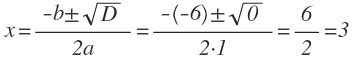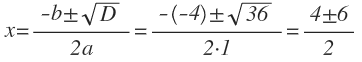|
Если дискриминант равен ноль, то уравнение имеет два одинаковых корня, котрые находятся так же как и при положительном дискриминанте. Но можно левую часть уравнения разложить на множители. Х^2 + 4х+ 4=0; (Х +2)(Х +2)=0 Х +2=0 и Х +2=0 , значит оба корня х=-2. При нулевом дискриминанте корень квадратного уравнения можно находить двумя способами. 1) По формуле x=-b/2a. 2) Разложением левой части уравнения на множители при помощи формулы сокращённого умножения. Множители приравниваются к нулю, решается линейное уравнение, находится корень. Пример 1. (Х^2 – икс во второй степени) Х^2 – 6х+ 9=0; Дискриминант равен ноль. Применить формулу x=-b/2a и можно получить: х=-(-6)/2*1=3. Корень уравнения равен 3. Пример 2. По формуле сокращённого умножения левая часть принимает вид (х-3)(х-з) (Я заменила (х-3) во второй степени разложением на два множителя). Приравнять левую часть к нулю (х-3)(х-з)=0; каждый множитель приравнять к нулю х-3=0 или х-3=0. В первом и втором случае получится одно и то же число 3. Ответ 3. система выбрала этот ответ лучшим Эл Лепсоид 4 года назад Не знаю, как сейчас учат в школе, но в наше время считалось, что при нахождении корней квадратного уравнения для начала рекомендовалось найти дискриминант этого уравнения и по его значению сразу определить, имеет ли уравнение корни, а если имеет, то сколько их – один или два. Сам дискриминант вычисляется по всем известной формуле (как, кстати, и корни уравнения): Если дискриминант получался отрицательным, то считается, что корней уравнение не имеет. Если положительный – можно найти два корня (см. картинку). А вот в случае, когда дискриминант равен нулю, оба корня (Х1 и Х2) становятся равны друг другу, т.к. X = Х1 = Х2 = (-b)/(2a). 88SkyWalker88 4 года назад Дискриминант может быть больше или меньше нуля или равняться нулю. Как видно из информации, представленной ниже, если дискриминант будет больше нуля, то уравнение будет иметь два корня. Если дискриминант равен нулю, то уравнение будет иметь один корень. Если дискриминант меньше нуля, то уравнение корней не имеет. Найти корень (если дискриминант равен нулю) можно по формуле, представленной в пункте 2. Galina7v7 7 лет назад Рассматривая квадратное уравнение: x^2 + px + q =0,решение : x1= -p /2 + V(D),а x2= -p /2 – V(D),где D дискриминант ,а V (D)-корень из дискриминанта.Значит ,если дискриминант D =0,то и корень из дискриминанта V(D)=0 ,тогда получим равные корни : ` х1=х2=-p/2.Для уравнения в общем виде: ax^2+bx+c=0,x1=x2=-b/2a.FantomeRU 5 лет назад Корни квадратного уравнения типа ax²+bx+c=0 (где a,b и c – коэффициенты) находятся в зависимости от результата дискриминанта. Если дискриминант получается равен нулю, то квадратное уравнение имеет только один корень и он вычисляется по следующей формуле: X=-b/2a. helpau 3 года назад Всё проще, чем даже с положительным дискриминантом. x=-(B(+/-)0)/(2A)=-B/(2A). В этом случае принято говорить, что существуют 2 одинаковых корня, а парабола пересекает ось X только в одной точке(кстати,x=-B/(2A)-центр параболы для любых значений C). Просто, по формуле корней. Квадратный корень нуля равен нулю. Вот и подставляете в формулу нуль вместо дискриминанта. Если дискриминант равен нулю, то у квадратного уравнения есть один корень, или говоря по другому, два корня равны между собой. Kuzmich291192 9 лет назад Пусть дано квадратное уравнение вида ax^2+bx+c=0, при чём a не равно 0. Если дискриминант данного уравнения равен нулю, то уравнение имеет один корень, который равен: x=-b/2a. moreljuba 6 лет назад Если дискриминант равняется нулю в уравнении, то его корень можно найти вот по этой формуле: В случае равенства дискриминанта нулю в конкретном уравнении вы сможете рассчитать всего один единственный корень. dmitr20 3 года назад В том случае, если дискриминант равен нулю, то должен получиться всего один корень. Корень дискриминанта при этом можно найти, используя следующую формулу: Формулу лучше запомнить, пригодится на экзаменах. Знаете ответ? |
Похоже, вы используете блокировщик рекламы. Наш сайт существует и развивается
только за счет дохода от рекламы.
Пожалуйста, добавьте нас в исключения блокировщика.
на главную
Дискриминант
квадратного уравнения
Поддержать сайт
Мы уже разобрали,
как решать квадратные уравнения.
Теперь давайте более подробно рассмотрим, что называют
дискриминантом квадратного уравнения.
Вернемся к нашей формуле для нахожденя корней квадратного уравнения.
Запомните!
Выражение «b2 − 4ac», которое находится под корнем,
принято называть дискриминантом и обозначать буквой «D».
По-другому, через дискриминант формулу нахождения корней квадратного уравнения можно записать так:
x1;2 = , где «D = b2 − 4ac»
По одной из версий термин «Дискриминант» произошел от латинского discriminantis, что означает «отличающий» или «различающий».
В зависимости от знака «D» (дискриминанта)
квадратное уравнение может иметь два, один или ни одного корня. Рассмотрим все три случая.
I случай
D > 0
(дискриминант больше нуля)
2x2 + 5x −7 = 0
D = b2 − 4ac
D = 52 − 4 · 2 · (−7)
D = 25 + 56
D = 81
D > 0
x1;2 =
x1;2 =
x1;2 =
| x1 = |
x2 = |
| x1 = |
x2 = |
| x1 = 1 |
x2 = −3 |
| x1 = 1 |
x2 = −3 |
Ответ: x1 = 1;
x2 = −3
Вывод: когда «D > 0» в квадратном уравнении два корня.
II случай
D = 0
(дискриминант равен нулю)
16x2 − 8x + 1 = 0
D = b2 − 4ac
D = (−8)2 − 4 · 16 · 1
D = 64 − 64
D = 0
x1;2 =
x1;2 =
x1;2 =
x =
x =
Ответ: x =
Вывод: когда «D = 0» в квадратном уравнении один корень.
III случай
D < 0
(дискриминант меньше нуля)
9x2 − 6x + 2 = 0
D = b2 − 4ac
D = (−6)2 − 4 · 9 · 2
D = 36 − 72
D = −36
D < 0
x1;2 =
x1;2 =
Ответ: нет действительных корней
Вывод: когда «D < 0» в квадратном уравнении нет корней.
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Надеюсь, изучив данную статью, вы научитесь находить корни полного квадратного уравнения.
С помощью дискриминанта решаются только полные квадратные уравнения, для решения неполных квадратных уравнений используют другие методы, которые вы найдете в статье “Решение неполных квадратных уравнений”.
Какие же квадратные уравнения называются полными? Это уравнения вида ах2 + b x + c = 0, где коэффициенты a, b и с не равны нулю. Итак, чтобы решить полное квадратное уравнение, надо вычислить дискриминант D.
D = b2 – 4ас .
В зависимости от того какое значение имеет дискриминант, мы и запишем ответ.
Если дискриминант отрицательное число (D < 0),то корней нет.
Если же дискриминант равен нулю, то х = (-b)/2a. Когда дискриминант положительное число (D > 0),
тогда х1 = (-b – √D)/2a , и х2 = (-b + √D)/2a .
Например. Решить уравнение х2 – 4х + 4= 0.
D = 42 – 4 · 4 = 0
x = (- (-4))/2 = 2
Ответ: 2.
Решить уравнение 2х2 + х + 3 = 0.
D = 12 – 4 · 2 · 3 = – 23
Ответ: корней нет.
Решить уравнение 2х2 + 5х – 7 = 0.
D = 52 – 4 · 2 · (–7) = 81
х1 = (-5 – √81)/(2·2)= (-5 – 9)/4= – 3,5
х2 = (-5 + √81)/(2·2) = (-5 + 9)/4=1
Ответ: – 3,5 ; 1.
Итак представим решение полных квадратных уравнений схемой на рисунке1.
По этим формулам можно решать любое полное квадратное уравнение.
ах2 + bx + c, иначе можно допустить ошибку. Например, в записи уравнения х + 3 + 2х2 = 0, ошибочно можно решить, что
а = 1, b = 3 и с = 2. Тогда
D = 32 – 4 · 1 · 2 = 1 и тогда уравнение имеет два корня. А это неверно. (Смотри решение примера 2 выше).
Поэтому, если уравнение записано не многочленом стандартного вида, вначале полное квадратное уравнение надо записать многочленом стандартного вида (на первом месте должен стоять одночлен с наибольшим показателем степени, то есть ах2, затем с меньшим – bx, а затем свободный член с.
При решении приведенного квадратного уравнения и квадратного уравнения с четным коэффициентом при втором слагаемом можно использовать и другие формулы. Давайте познакомимся и с этими формулами. Если в полном квадратном уравнении при втором слагаемом коэффициент будет четным (b = 2k), то можно решать уравнение по формулам приведенным на схеме рисунка 2.
Полное квадратное уравнение называется приведенным, если коэффициент при х2 равен единице и уравнение примет вид х2 + px + q = 0. Такое уравнение может быть дано для решения, либо получается делением всех коэффициентов уравнение на коэффициент а, стоящий при х2.
На рисунке 3 приведена схема решения приведенных квадратных
Пример. Решить уравнение
3х2 + 6х – 6 = 0.
Давайте решим это уравнение применяя формулы приведенные на схеме рисунка 1.
D = 62 – 4 · 3 · (– 6) = 36 + 72 = 108
√D = √108 = √(36 · 3) = 6√3
х1 = (-6 – 6√3 )/(2 · 3) = (6 ( -1- √(3)))/6 = –1 – √3
х2 = (-6 + 6√3 )/(2 · 3) = (6 ( -1+ √(3)))/6 = –1 + √3
Ответ: –1 – √3; –1 + √3
Можно заметить, что коэффициент при х в этом уравнении четное число, то есть b = 6 или b = 2k , откуда k = 3. Тогда попробуем решить уравнение по формулам , приведенным на схеме рисунка D1 = 32 – 3 · (– 6) = 9 + 18 = 27
√(D1) = √27 = √(9 · 3) = 3√3
х1 = (-3 – 3√3)/3 = (3 (-1 – √(3)))/3 = – 1 – √3
х2 = (-3 + 3√3)/3 = (3 (-1 + √(3)))/3 = – 1 + √3
Ответ: –1 – √3; –1 + √3. Заметив, что все коэффициенты в этом квадратном уравнении делятся на 3 и выполнив деление, получим приведенное квадратное уравнение x2 + 2х – 2 = 0 Решим это уравнение, используя формулы для приведенного квадратного 
D2 = 22 – 4 · (– 2) = 4 + 8 = 12
√(D2) = √12 = √(4 · 3) = 2√3
х1= (-2 – 2√3)/2 = (2 (-1 – √(3)))/2 = – 1 – √3
х2= (-2 + 2√3)/2 = (2 (-1+ √(3)))/2 = – 1 + √3
Ответ: –1 – √3; –1 + √3.
Как видим, при решении этого уравнения по различным формулам мы получили один и тот же ответ. Поэтому хорошо усвоив формулы приведенные на схеме рисунка 1 , вы всегда сможете решить любое полное квадратное уравнение.
© blog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
-
5 + 8 = 12;
-
13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
-
5 + 8 = 12;
-
12 = 12 — верное равенство.
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
Например
-
2x2 − x + 5 = 0
-
a = 2, b = −1, c = 5
Такое уравнение можно решить с помощью формулы дискриминанта.
Получай лайфхаки, статьи, видео и чек-листы по обучению на почту
Реши домашку по математике на 5.
Подробные решения помогут разобраться в самой сложной теме.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax2 + bx + c = 0:
-
Определим, чему равны коэффициенты a, b, c.
-
Вычислим значение дискриминанта по формуле D = b2 − 4ac.
-
Если дискриминант D < 0, то корней нет.
Если D = 0, то есть один корень, равный −b/2a.
Если D > 0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x2 – 4x + 2 = 0.
Как решаем:
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b2 – 4ac = (-4)2 – 4 * 3 * 2 = 16 – 24 = -8.
Ответ: D < 0, корней нет.
Пример 2. Решить уравнение: x2 – 6x + 9 = 0.
Как решаем:
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b2 – 4ac = (-6)2 – 4 * 1 * 9 = 36 – 36 = 0.
-
D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x2 – 4x – 5 = 0.
Как решаем:
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b2 – 4ac = (-4)2 – 4 * 1 * (-5) = 16 + 20 = 36.
-
D > 0, значит уравнение имеет два корня:
x1 = (4 + 6) : 2 = 5,
x2 = (4 – 6) : 2 = -1.
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно
на курсах по математике в Skysmart.
Как найти дискриминант квадратного уравнения
О чем эта статья:
Понятие квадратного уравнения
Уравнение — это равенство, содержащее переменную, значение которой нужно найти.
Например, х + 8 = 12 — это уравнение, содержащее переменную х.
Корень уравнения — это такое значение переменной, которое при подстановке в уравнение обращает его в верное числовое равенство.
Например, если х = 5, то при подстановке в уравнение мы получим:
13 = 12 — противоречие.
Значит, х = 5 не является корнем уравнения.
Если же х = 4, то при подстановке в уравнение мы получим:
12 = 12 — верное равенство.
Значит, х = 4 является корнем уравнения.
Решить уравнение — значит найти все его корни или доказать, что их не существует.
Квадратное уравнение — это уравнение вида ax2 + bx + c = 0, где a — первый или старший коэффициент, не равный нулю, b — второй коэффициент, c — свободный член.
Если все коэффициенты в уравнении отличны от нуля, то уравнение называется полным.
Такое уравнение можно решить с помощью формулы дискриминанта.
Понятие дискриминанта
Дискриминант квадратного уравнения — это выражение, равное b 2 − 4ac. Дискриминант в переводе с латинского означает «отличающий» или «различающий» и обозначается буквой D.
Дискриминант — отличный помощник, чтобы понять, сколько в уравнении корней.
Как решать квадратные уравнения через дискриминант
Алгоритм решения квадратного уравнения ax 2 + bx + c = 0:
Определим, чему равны коэффициенты a, b, c.
Вычислим значение дискриминанта по формуле D = b2 − 4ac.
Если дискриминант D 0, то у уравнения две корня, равные
Чтобы запомнить алгоритм решения полных квадратных уравнений и с легкостью его использовать, сохраните себе шпаргалку:
Примеры решения квадратных уравнений с помощью дискриминанта
Пример 1. Решить уравнение: 3x 2 – 4x + 2 = 0.
- Определим коэффициенты: a = 3, b = -4, c = 2.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 3 * 2 = 16 – 24 = -8.
Ответ: D 2 – 6x + 9 = 0.
- Определим коэффициенты: a = 1, b = -6, c = 9.
- Найдем дискриминант: D = b 2 – 4ac = (-6) 2 – 4 * 1 * 9 = 36 – 36 = 0.
D = 0, значит уравнение имеет один корень:
Ответ: корень уравнения 3.
Пример 3. Решить уравнение: x 2 – 4x – 5 = 0.
- Определим коэффициенты: a = 1, b = -4, c = -5.
- Найдем дискриминант: D = b 2 – 4ac = (-4) 2 – 4 * 1 * (-5) = 16 + 20 = 36.
D > 0, значит уравнение имеет два корня:
Ответ: два корня x1 = 5, x2 = -1.
Разобраться в решении квадратных уравнений на практике с классным преподавателем можно на курсах по математике в Skysmart.
Решить квадратное уравнение онлайн
На данной странице калькулятор онлайн помоежет решить квадратное уравнение. При решении выводится описание.
Квадратное уравнение — это уравнение вида ax 2 +bx+c=0 , где a не равно 0 .
Через дискриминант
a x 2 + b x + c = 0
Что бы решить квадратное уравнение, нужно найти все x . При подстановке должно выполняться равенство
ax 2 + bx + c = 0 .
Для начала находится дискриминант по формуле D = b 2 – 4ac :
- Если D > 0 , уравнение имеет два корня.
- Если D = 0 , уравнение имеет один корень.
- Если D > 0 , уравнение не имеет корней.
Корни квадратного уравнения находятся по формуле:
Решение задач по математике онлайн
//mailru,yandex,google,vkontakte,odnoklassniki,instagram,wargaming,facebook,twitter,liveid,steam,soundcloud,lastfm, // echo( ‘
Калькулятор онлайн.
Решение квадратного уравнения.
С помощью этой математической программы вы можете решить квадратное уравнение.
Программа не только даёт ответ задачи, но и отображает процесс решения двумя способами:
– с помощью дискриминанта
– с помощью теоремы Виета (если возможно).
Причём, ответ выводится точный, а не приближенный.
Например, для уравнения (81x^2-16x-1=0) ответ выводится в такой форме:
Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре. А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным решением.
Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень образования в области решаемых задач повышается.
Если вы не знакомы с правилами ввода квадратного многочлена, рекомендуем с ними ознакомиться.
В качестве переменной может выступать любая латинсая буква.
Например: ( x, y, z, a, b, c, o, p, q ) и т.д.
Числа можно вводить целые или дробные.
Причём, дробные числа можно вводить не только в виде десятичной, но и в виде обыкновенной дроби.
Правила ввода десятичных дробей.
В десятичных дробях дробная часть от целой может отделяться как точкой так и запятой.
Например, можно вводить десятичные дроби так: 2.5x – 3,5x^2
Правила ввода обыкновенных дробей.
В качестве числителя, знаменателя и целой части дроби может выступать только целое число.
Знаменатель не может быть отрицательным.
При вводе числовой дроби числитель отделяется от знаменателя знаком деления: /
Целая часть отделяется от дроби знаком амперсанд: &
Ввод: 3&1/3 – 5&6/5z +1/7z^2
Результат: ( 3frac<1> <3>- 5frac<6> <5>z + frac<1><7>z^2 )
При вводе выражения можно использовать скобки. В этом случае при решении квадратного уравнения введённое выражение сначала упрощается.
Например: 1/2(y-1)(y+1)-(5y-10&1/2)
Немного теории.
Квадратное уравнение и его корни. Неполные квадратные уравнения
Каждое из уравнений
( -x^2+6x+1<,>4=0, quad 8x^2-7x=0, quad x^2-frac<4><9>=0 )
имеет вид
( ax^2+bx+c=0, )
где x – переменная, a, b и c – числа.
В первом уравнении a = -1, b = 6 и c = 1,4, во втором a = 8, b = —7 и c = 0, в третьем a = 1, b = 0 и c = 4/9. Такие уравнения называют квадратными уравнениями.
Определение.
Квадратным уравнением называется уравнение вида ax 2 +bx+c=0, где x – переменная, a, b и c – некоторые числа, причём ( a neq 0 ).
Числа a, b и c — коэффициенты квадратного уравнения. Число a называют первым коэффициентом, число b — вторым коэффициентом и число c — свободным членом.
В каждом из уравнений вида ax 2 +bx+c=0, где ( a neq 0 ), наибольшая степень переменной x — квадрат. Отсюда и название: квадратное уравнение.
Заметим, что квадратное уравнение называют ещё уравнением второй степени, так как его левая часть есть многочлен второй степени.
Квадратное уравнение, в котором коэффициент при x 2 равен 1, называют приведённым квадратным уравнением. Например, приведёнными квадратными уравнениями являются уравнения
( x^2-11x+30=0, quad x^2-6x=0, quad x^2-8=0 )
Если в квадратном уравнении ax 2 +bx+c=0 хотя бы один из коэффициентов b или c равен нулю, то такое уравнение называют неполным квадратным уравнением. Так, уравнения -2x 2 +7=0, 3x 2 -10x=0, -4x 2 =0 – неполные квадратные уравнения. В первом из них b=0, во втором c=0, в третьем b=0 и c=0.
Неполные квадратные уравнения бывают трёх видов:
1) ax 2 +c=0, где ( c neq 0 );
2) ax 2 +bx=0, где ( b neq 0 );
3) ax 2 =0.
Рассмотрим решение уравнений каждого из этих видов.
Для решения неполного квадратного уравнения вида ax 2 +c=0 при ( c neq 0 ) переносят его свободный член в правую часть и делят обе части уравнения на a:
( x^2 = -frac Rightarrow x_ <1,2>= pm sqrt< -frac> )
Так как ( c neq 0 ), то ( -frac neq 0 )
Значит, неполное квадратное уравнение вида ax 2 +bx=0 при ( b neq 0 ) всегда имеет два корня.
Неполное квадратное уравнение вида ax 2 =0 равносильно уравнению x 2 =0 и поэтому имеет единственный корень 0.
Формула корней квадратного уравнения
Рассмотрим теперь, как решают квадратные уравнения, в которых оба коэффициента при неизвестных и свободный член отличны от нуля.
Решим квадратне уравнение в общем виде и в результате получим формулу корней. Затем эту формулу можно будет применять при решении любого квадратного уравнения.
Решим квадратное уравнение ax 2 +bx+c=0
Разделив обе его части на a, получим равносильное ему приведённое квадратное уравнение
( x^2+fracx +frac=0 )
Преобразуем это уравнение, выделив квадрат двучлена:
( x^2+2x cdot frac<2a>+left( frac<2a>right)^2- left( frac<2a>right)^2 + frac = 0 Rightarrow )
Подкоренное выражение называют дискриминантом квадратного уравнения ax 2 +bx+c=0 («дискриминант» по латыни — различитель). Его обозначают буквой D, т.е.
( D = b^2-4ac )
Теперь, используя обозначение дискриминанта, перепишем формулу для корней квадратного уравнения:
( x_ <1,2>= frac < -b pm sqrt> <2a>), где ( D= b^2-4ac )
Очевидно, что:
1) Если D>0, то квадратное уравнение имеет два корня.
2) Если D=0, то квадратное уравнение имеет один корень ( x=-frac <2a>).
3) Если D 0), один корень (при D = 0) или не иметь корней (при D
Теорема Виета
Приведённое квадратное уравнение ax 2 -7x+10=0 имеет корни 2 и 5. Сумма корней равна 7, а произведение равно 10. Мы видим, что сумма корней равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену. Таким свойством обладает любое приведённое квадратное уравнение, имеющее корни.
Сумма корней приведённого квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
Т.е. теорема Виета утверждает, что корни x1 и x2 приведённого квадратного уравнения x 2 +px+q=0 обладают свойством:
( left< begin x_1+x_2=-p \ x_1 cdot x_2=q end right. )
[spoiler title=”источники:”]
http://mozgan.ru/Math/QuadraticEquation
http://www.math-solution.ru/math-task/quadr-eq
[/spoiler]