Задачи на проценты: стандартный расчет с помощью пропорций
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X — 95%
Нужно составить пропорцию и найти x . Получаем:
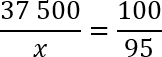
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:
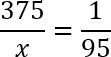
По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x — 80%
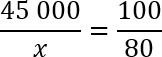
Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:
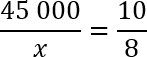
Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x · 10
Это простейшее линейное уравнение. Выразим из него переменную x :
x = 45 000 · 8 : 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x = 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Как решать пропорции – правила, методы и примеры вычислений
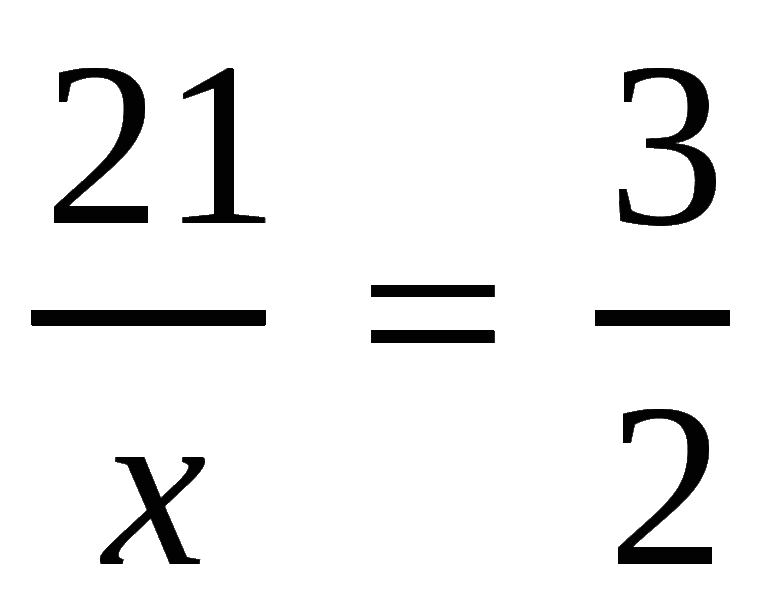
Общие сведения
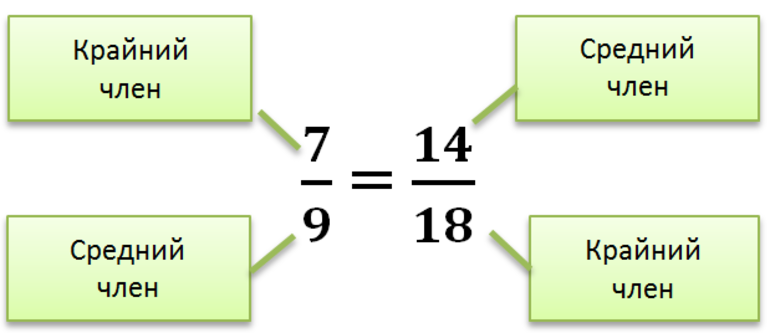
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.

Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.

Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.

В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
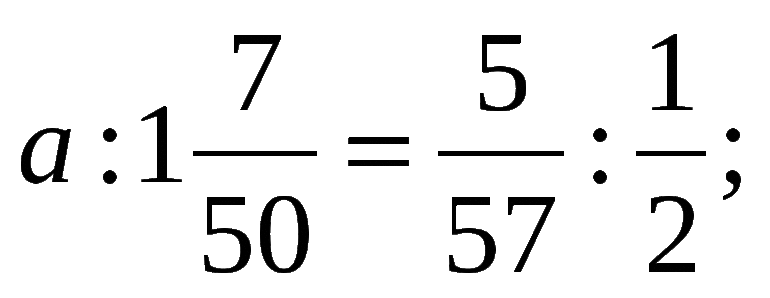
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
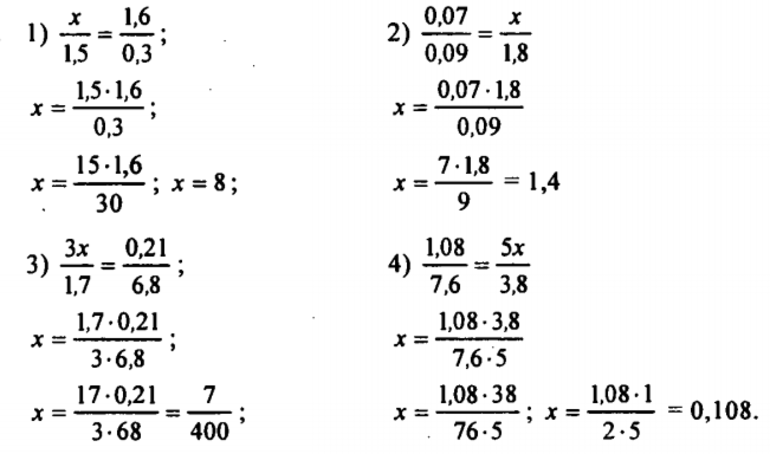
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
- Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
Решение уравнений с дробями

О чем эта статья:
5 класс, 6 класс, 7 класс
Понятие дроби
Прежде чем отвечать на вопрос, как найти десятичную дробь, разберемся в основных определениях, видах дробей и разницей между ними.
Дробь — это рациональное число, представленное в виде a/b, где a — числитель дроби, b — знаменатель. Есть два формата записи:
- обыкновенный вид — ½ или a/b,
- десятичный вид — 0,5.
Дробь — это одна из форм деления, записываемая с помощью дробной черты. Над чертой принято писать делимое (число, которое делим) — числитель. А под чертой всегда находится делитель (на сколько делим), его называют знаменателем. Черта между числителем и знаменателем означает деление.
Дроби бывают двух видов:
- Числовые — состоят из чисел. Например, 2/7 или (1,8 − 0,3)/5.
- Алгебраические — состоят из переменных. Например, (x + y)/(x − y). Значение дроби зависит от данных значений букв.
Дробь называют правильной, когда ее числитель меньше знаменателя. Например, 4/9 и 23/57.
Неправильная дробь — та, у которой числитель больше знаменателя или равен ему. Например, 13/5. Такое число называют смешанным — читается так: «две целых три пятых», а записывается — 2 3/5.
Основные свойства дробей
Дробь не имеет значения, если делитель равен нулю.
Дробь равняется нулю в том случае, если числитель равен нулю, а знаменатель отличен от нуля.
Дроби a/b и c/d называют равными, если a × d = b × c.
Если числитель и знаменатель дроби умножить или разделить на одно и то же натуральное число, то получится равная ей дробь.
Действия с дробями можно выполнять те же, что и с обычными числами: складывать, вычитать, умножать и делить. Также, дроби можно сравнивать между собой и возводить в степень.
Понятие уравнения
Уравнение — это математическое равенство, в котором неизвестна одна или несколько величин. Наша задача — найти неизвестные числа так, чтобы при их подстановке в пример получилось верное числовое равенство. Давайте на примере:
- Возьмем выражение 4 + 5 = 9. Это верное равенство, потому что 4+5 действительно 9. Если бы вместо 9 стояло любое другое число — мы бы сказали, что числовое равенство неверное.
- Уравнением можно назвать выражение 4 + x = 9, с неизвестной переменной x, значение которой нужно найти. Результат должен быть таким, чтобы знак равенства был оправдан, и левая часть равнялась правой.
Корень уравнения — то самое число, которое уравнивает выражения справа и слева, когда мы подставляем его на место неизвестной. В таком случае афоризм «зри в корень» — очень кстати при усердном решении уравнений.
Равносильные уравнения — это те, в которых совпадают множества решений. Другими словами, у них одни и те же корни.
Решить уравнение значит найти все его корни или убедиться, что корней нет.
Алгебраические уравнения могут быть разными, самые часто встречающиеся — линейные и квадратные. Расскажем и про них.
| Линейное уравнение выглядит так | ах + b = 0, где a и b — действительные числа.
Что поможет в решении:
|
|---|---|
| Квадратное уравнение выглядит так: | ax 2 + bx + c = 0, где коэффициенты a, b и c — произвольные числа, a ≠ 0. |
Понятие дробного уравнения
Дробное уравнение — это уравнение с дробями. Да, вот так просто. Но это еще не все. Чаще всего неизвестная стоит в знаменателе. Например, вот так:
Такие уравнения еще называют дробно-рациональными. В них всегда есть хотя бы одна дробь с переменной в знаменателе.
Если вы видите в знаменателях числа, то это уравнения либо линейные, либо квадратные. Решать все равно нужно, поэтому идем дальше. Примеры:
На алгебре в 8 классе можно встретить такое понятие, как область допустимых значений — это множество значений переменной, при которых это уравнение имеет смысл. Его используют, чтобы проверить корни и убедиться, что решение правильное.
Мы уже знаем все важные термины, их определения и наконец подошли к самому главному — сейчас узнаем как решить дробное уравнение.
Как решать уравнения с дробями
1. Метод пропорции
Чтобы решить уравнение методом пропорции, нужно привести дроби к общему знаменателю. А само правило звучит так: произведение крайних членов пропорции равно произведению средних. Проверим, как это работает.
Итак, у нас есть линейное уравнение с дробями:
В левой части стоит одна дробь — оставим без преобразований. В правой части видим сумму, которую нужно упростить так, чтобы осталась одна дробь.
После того, как в левой и правой части осталась одна дробь, можно применить метод пропорции и перемножить крест-накрест числители и знаменатели.
2. Метод избавления от дробей
Возьмем то же самое уравнение, но попробуем решить его по-другому.
В уравнении есть две дроби, от которых мы очень хотим избавиться. Вот, как это сделать:
- подобрать число, которое можно разделить на каждый из знаменателей без остатка;
- умножить на это число каждый член уравнения.
Ищем самое маленькое число, которое делится на 5 и 9 и без остатка — 45 как раз подходит. Умножаем каждый член уравнения на 45 и избавляемся от знаменателей. Вуаля!
Вот так просто мы получили тот же ответ, что и в прошлый раз.
Что еще важно учитывать при решении
- если значение переменной обращает знаменатель в 0, значит это неверное значение;
- делить и умножать уравнение на 0 нельзя.
Универсальный алгоритм решения
Определить область допустимых значений.
Найти общий знаменатель.
Умножить каждый член уравнения на общий знаменатель и сократить полученные дроби. Знаменатели при этом пропадут.
Раскрыть скобки, если нужно и привести подобные слагаемые.
Решить полученное уравнение.
Сравнить полученные корни с областью допустимых значений.
Записать ответ, который прошел проверку.
Курсы по математике от Skysmart помогут закрепить материал и разобраться в сложных темах.
Примеры решения дробных уравнений
Чтобы стать успешным в любом деле, нужно чаще практиковаться. Мы уже знаем, как решаются дробные уравнения — давайте перейдем к решению задачек.
Пример 1. Решить дробное уравнение: 1/x + 2 = 5.
- Вспомним правило х ≠ 0. Это значит, что область допустимых значений: х — любое число, кроме нуля.
- Отсчитываем справа налево в числителе дробной части три знака и ставим запятую.
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Решим обычное уравнение.
Пример 2. Найти корень уравнения
- Область допустимых значений: х ≠ −2.
- Умножим обе части уравнения на выражение, которое сократит оба знаменателя: 2(х+2)
- Избавимся от знаменателя. Умножим каждый член уравнения на х.
Переведем новый множитель в числитель..
Сократим левую часть на (х+2), а правую на 2.
Пример 3. Решить дробное уравнение:
-
Найти общий знаменатель:
Умножим обе части уравнения на общий знаменатель. Сократим. Получилось:
Выполним возможные преобразования. Получилось квадратное уравнение:
Решим полученное квадратное уравнение:
Получили два возможных корня:
Если x = −3, то знаменатель равен нулю:
Если x = 3 — знаменатель тоже равен нулю.
[spoiler title=”источники:”]
http://nauka.club/matematika/proportsii.html
http://skysmart.ru/articles/mathematic/reshenie-uravnenij-s-drobyami
[/spoiler]
Онлайн калькулятор пропорций
Формула пропорций
Пропо́рция — это равенство двух отношений, когда a:b=c:d
| средние | ||||||
| ╭ | члены | ╮ | ||||
| 1 | : | 10 | = | 7 | : | 70 |
| ╰ | крайние члены | ╯ | ||||
| 0,1 | = | 0,1 |
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d, то a⋅d=b⋅c
1 10 ✕ 7 70 1 ⋅ 70 = 10 ⋅ 7
Обращение пропорции: если a:b=c:d, то b:a=d:c
1 10 7 70 10 1 = 70 7
Перестановка средних членов: если a:b=c:d, то a:c=b:d
1 10 7 70 1 7 = 10 70
Перестановка крайних членов: если a:b=c:d, то d:b=c:a
1 10 7 70 70 10 = 7 1
Решение пропорции с одним неизвестным | Уравнение
1 : 10 = x : 70 1 10 = x 70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x = 1 ⋅ 70 10 = 7
Как посчитать пропорцию
Задача: нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию: 1 таблетка — 10 кг x таблеток — 70 кг Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение: 1 таблетка x таблеток ✕ 10 кг 70 кг x = 1 ⋅ 70 : 10 = 7 Ответ: 7 таблеток
Задача: за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию: 2 статьи — 5 часов x статей — 20 часов x = 2 ⋅ 20 : 5 = 8 Ответ: 8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и при расчёте процентов, и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
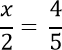
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
![]()
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.

Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
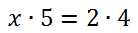
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
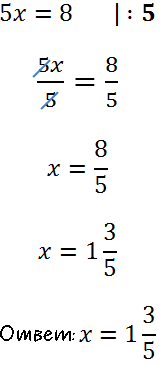
Рассмотрим другой пример уравнения с пропорцией.
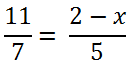
Такое уравнение также решается с помощью правила пропорции.
Важно!

Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
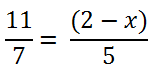
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
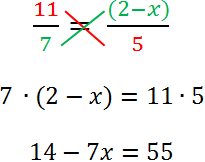
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
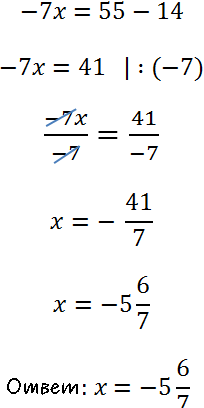
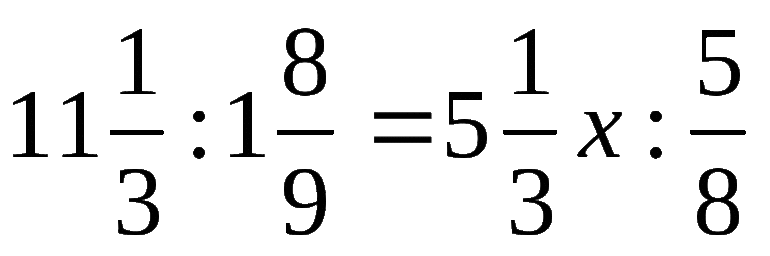
Иногда уравнения с пропорцией могут быть представлены следующим образом:
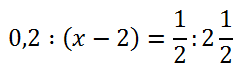
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
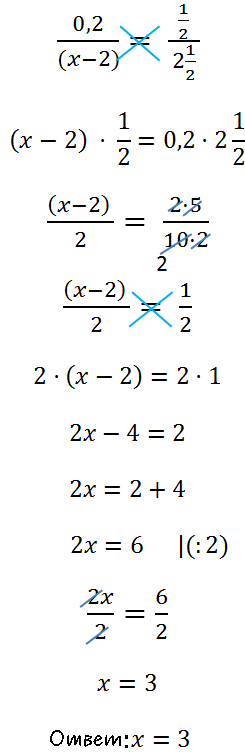
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Загрузить PDF
Загрузить PDF
Перекрестное умножение — это способ решения уравнения, обе части которого имеют вид дробей и неизвестная величина входит в состав числителя или знаменателя одной из них (или обеих). Перекрестное умножение позволит избавиться от дробей и привести уравнение к простому виду. Этот метод особенно полезен при решении пропорций.
-

1
Умножьте числитель левой дроби на знаменатель правой. Например, нам дано уравнение 2/x = 10/13. Умножьте 2 на 13. 2 * 13 = 26.[1]
-

2
Умножьте числитель правой дроби на знаменатель левой. Теперь умножьте x на 10. x * 10 = 10x. Можете поменять первый шаг и этот местами. Не важно, что вы умножите в первую очередь, а что во вторую; главное — перемножить по диагонали числитель одной дроби со знаменателем другой.[2]
-

3
Приравняйте ответы. Запишите, что 26 равно 10x. 26 = 10x. Последовательность записи ответов не имеет значения. Можете поменять их местами — равенство все равно сохранится. Только записывайте каждый ответ целиком в том виде, в каком его получили (10х — это 10х, а не 10, не х и не 10+х).[3]
- Итак, если вы решаете уравнение 2/x = 10/13, то у вас получится 2 * 13 = x * 10, или 26 = 10x.
-

4
Решите уравнение, чтобы найти неизвестную. Чтобы решить уравнение 26 = 10x, можно начать с поиска наибольшего общего делителя. Найдите число, на которое делятся нацело 26 и 10. Это будет 2; 26/2 = 13 и 10/2 = 5. Остается 13 = 5x. Теперь оставьте в правой части только x, разделив обе части на 5. Получится 13/5 = 5х/5, или х = 13/5. Если вы хотите получить ответ в виде десятичной дроби, можно просто разделить обе части уравнения на 10: 26/10 = 10х/10, или x = 2,6.[4]
Реклама
-

1
Умножьте числитель левой дроби на знаменатель правой. Например, нам дано такое уравнение: (x + 3)/2 = (x + 1)/4. Умножьте (x + 3) на 4, получится 4(x +3). Откройте скобки, получится 4x + 12.[5]
-

2
Умножьте числитель правой дроби на знаменатель левой.[6]
Сделайте все то же, что описано выше. Получится: (x +1) x 2 = 2(x +1). Откройте скобки, получим 2x + 2. -

3
Запишите полученные ответы в виде равенства и перенесите неизвестные в одну часть. У вас получилось уравнение 4x + 12 = 2x + 2. Перенесите все х в одну часть, а известные величины — в другую.
- Перенесем 2x к 4х. Если вычесть из обеих частей уравнения 2x, слева получится “4х – 2х + 12 = 2х + 12”, а справа останется только 2.
- Теперь перенесем 12 к 2. Если вычесть из обеих частей 12, то слева останется только 2х, а справа получится 2 – 12 = -10.
- Получилось уравнение 2x = -10.
-

4
Решите уравнение. Для этого осталось только найти неизвестную, разделив обе части на 2. 2х/2 = -10/2; получаем х = -5. Для проверки можно подставить это значение в изначальное уравнение. Получится -1 = -1.
Реклама
Советы
- Результат можно проверить, подставив его в изначальное уравнение. Если получится верное равенство, например 1 = 1, то вы решили уравнение правильно. Если равенстно неверно, например 0 = 1, вы допустили ошибку. Например, в примере из первой части этой статьи подставьте в уравнение 2,6: 2/(2,6) = 10/13. Умножьте левую часть на 5/5 и получится 10/13 = 10/13. Это равенство верно, значит, 2,6 — правильный ответ.
- Если в том же примере вы получили, скажем, 5, то при подсстановке этого значения получится 2/5 = 10/13. Если вы умножите левую часть на 5/5, у вас получится 10/25 = 10/13. Это равенство неверно, значит, при перекрестном умножении вы допустили ошибку.
Реклама
Об этой статье
Эту страницу просматривали 23 768 раз.
Была ли эта статья полезной?
Методика решения задач
на растворы с применением
правила креста
Многие важные вопросы изучения курса химии по
ряду причин исключены из школьной программы.
Среди них закон эквивалентов, разные способы
выражения концентрации растворов, правило
креста и многие другие. Однако на факультативных
занятиях, при подготовке ребят к олимпиадам без
них не обойтись. Да и в жизни ребятам они
пригодятся, особенно тем, кто свяжет будущую
профессию с химией (заводские лаборатории,
аптеки, научно-исследовательская работа, да и
просто химия в быту).
Особенно трудно в этом отношении молодым
учителям – у них нет той массы дополнительной
литературы, которую накопили старые учителя за
десятки лет работы в школе, а что издает
современная книгопечатная отрасль
промышленности – известно всем. Поэтому
предлагаемая методика решения задач на растворы
с применением правила креста, думается, хоть
сколько-то поможет молодым коллегам в этом деле.
«Конверт Пирсона»
Очень часто в лабораторной практике и при
решении олимпиадных задач приходится
встречаться со случаями приготовления растворов
с определенной массовой долей растворенного
вещества, смешением двух растворов разной
концентрации или разбавлением крепкого раствора
водой. В некоторых случаях можно провести
достаточно сложный арифметический расчет.
Однако это малопродуктивно. Чаще для этого лучше
применить правило смешения (диагональную модель
«конверта Пирсона», или, что то же самое, правило
креста).
Допустим, нужно приготовить раствор
определенной концентрации, имея в распоряжении
два раствора с более высокой и менее высокой
концентрацией, чем нужно нам. Тогда, если
обозначить массу первого раствора через m
1 ,
а второго – через m
2 , то при смешивании
общая масса смеси будет слагаться из суммы этих
масс. Пусть массовая доля растворенного вещества
в первом растворе – 1 , во втором – 2 , а в их смеси – 3 . Тогда общая масса
растворенного вещества в смеси будет слагаться
из масс растворенного вещества в исходных
растворах:
m
1 1 + m
2 2 = 3 (m
1 + m
2) .
Отсюда
m 1 ( 1 – 3) = m
2 ( 3 – 2),
m
1 /m
2 = ( 3 – 2)/( 1 – 3).
Видно, что отношение массы первого раствора к
массе второго раствора есть отношение разности
массовых долей растворенного вещества в смеси и
во втором растворе к разности соответствующих
величин в первом растворе и в смеси.
При решении задач на растворы с разными
концентрациями чаще всего применяют
диагональную схему правила смешении. При
расчетах записывают одну над другой массовые
доли растворенного вещества в исходных
растворах, справа между ними – его массовую долю
в растворе, который нужно приготовить, и вычитают
по диагонали из большего меньшее значение.
Разности их вычитаний показывают массовые доли
для первого и второго растворов, необходимые для
приготовления нужного раствора.
Для пояснения этого правила сначала решим
простейшую задачу.
ЗАДАЧА 1
Определите концентрацию раствора,
полученного при слиянии 150 г 30%-го и 250 г 10%-го
растворов какой-либо соли.
Дано:
m 1 = 150 г,
m
2 = 250 г,
1 = 30%,
2 = 10%.
Найти:
Решение
1-й способ (метод
пропорций).
Общая масса раствора:
m
3 = m
1 + m
2 = 150
+ 250 = 400 г.
Массу вещества в первом растворе находим
методом пропорций, исходя из определения:
процентная концентрация раствора показывает,
сколько граммов растворенного вещества
находится в 100 г раствора:
100 г 30%-го р-ра – 30 г в-ва,
150 г 30%-го р-ра – х
г в-ва,
х
= 150 30/100 = 45 г.
Для второго раствора составляем аналогичную
пропорцию:
100 г 10%-го р-ра – 10 г в-ва,
250 г 10%-го р-ра – y
г в-ва,
y
= 250 10/100 = 25 г.
Следовательно, 400 г нового раствора содержит 45 +
25 = 70 г растворенного вещества.
Теперь можно определить концентрацию нового
раствора:
400 г р-ра – 70 г в-ва,
100 г р-ра – z
г в-ва,
z
= 100 70/400 = 17,5 г, или 17,5%.
2-й способ
(алгебраический).
m
1 1 + m
2 2 = 3 (m
1 + m
2).
3
= (m
1 1
+ m
2 2)/(m
1
+ m
2).
В результате находим:
3 =
(150 30 + 250 10)/(150 + 250) = 17,5%.
3-й способ (правило
креста).
( 3
– 10)/(30 – 3) =
150/250.
(30 – 3) 150
= ( 3 – 10) 250,
4500 – 150 3
= 250 3 – 2500,
4500 – 2500 = 250 3 – 150 3 ,
7000 = 400 3 ,
3 = 7000/400 = 17,5%.
Ответ.
При слиянии взятых
растворов получится новый раствор с
концентрацией 3
= 17,5%.
Теперь решим задачи посложнее.
ЗАДАЧА 2
Определите, сколько нужно взять 10%-го раствора
соли и 30%-го раствора этой же соли для
приготовления 500 г 20%-го раствора.
Дано:
1 = 10%,
2 = 30%,
3 = 20%,
m
3 = 500 г.
Найти:
m
1 , m
2 .
Решение
Используем правило креста.
Для приготовления 500 г 20%-го раствора соли нужно
взять по 10 частей растворов исходных
концентраций.
Проверим правильность нашего решения, учитывая,
что 1 часть равна 500/(10 + 10) = 25 г.
250 г 10%-го р-ра – х
г соли,
х
= 250 10/100 = 25 г.
250 г 30%-го р-ра – y
г соли,
100 г 30%-го р-ра – 30 г соли,
y
= 250 30/100 = 75 г.
m
(р-ра) = 250 + 250 = 500 г.
m
(соли) = 25 + 75 = 100 г.
Отсюда находим 3:
500 г р-ра – 100 г соли,
100 г р-ра – 3 г соли,
3 =
100 100/500 = 20 г, или 20%.
Ответ
.
Для приготовления 500 г 20%-го
раствора нужно взять исходные растворы по 250 г
(m
1 = 250 г, m
2 = 250 г).
ЗАДАЧА 3
Определите, сколько нужно взять растворов
соли 60%-й и 10%-й концентраций для приготовления 300
г раствора 25%-й концентрации.
Дано:
1 = 60%,
2 = 10%,
3 = 25%,
3 = 300 г.
Найти:
m
1 , m
2 .
Решение
Масса одной части: 300/50 = 6 г.
m
1 = 6 15 = 90 г, m
2 = 6 35 =
210 г.
100 г 60%-го р-ра – 60 г соли,
90 г 60%-го р-ра – х
г соли,
х
= 54 г.
100 г 10%-го р-ра – 10 г соли,
210 г 30%-го р-ра – y
г соли,
y
= 21 г.
m
(соли) = 54 + 21 = 75 г.
Находим концентрацию нового раствора:
300 г р-ра – 75 г соли,
100 г р-ра – z
г соли,
z
= 100 75/300 = 25 г, или 25%.
Ответ
.
m
1 = 90 г, m
2
= 210 г.
Теперь перейдем к еще более сложным задачам.
ЗАДАЧА 4
Определите массу раствора
Nа 2 СО 3
10%-й концентрации и массу сухого
кристаллогидрата
Na 2 CO 3 10H 2 O,
которые нужно взять для приготовления 540 г
раствора 15%-й концентрации
.
Дано:
1 = 10%,
3 = 15%,
m
3 = 540 г.
Найти:
m
1 , m
2 .
Решение
1-й способ (через систему
уравнений с двумя неизвестными).
Определяем массу соли Na 2 CO 3 в 540 г
15%-го раствора:
100 г 15%-го р-ра – 15 г соли,
540 г 15%-го р-ра – z
г соли,
z
= 540 15/100 = 81 г.
Cоставляем систему уравнений:

Находим молярную массу:
Избавляемся от лишних неизвестных:
m
2 = 286y
/106;
100 г 10%-го р-ра – 10 г соли,
m
1 г 10%-го р-ра – х
г соли,
m
1 = 100х
/10 = 10х
.
Подставляем m
2 и m
1 в систему
уравнений:
![]()
С учетом того, что х
= 81 – y
, избавляемся
от второго неизвестного:
10(81 – y
) + 286y
/106 = 540.
y
= 270/7,3 = 37 г.
Тогда m
2 = 286y
/106 = 2,7 37 100 г – это масса необходимого
количества кристаллогидрата Na 2 СО 3 10H 2 O.
Далее находим: х
= 81 – y
= 81 – 37 = 44 г – это
масса соли из 10%-го раствора.
Находим массу 10%-го раствора:
100 г 10%-го р-ра – 10 г соли,
m
1 г 10%-го р-ра – 44 г соли,
m
1 = 100 44/10 = 440 г.
Видно, что так можно решить данную задачу –
способ надежный, но, к сожалению, достаточно
длинный, громоздкий и сложный. Им успешно могут
воспользоваться учащиеся с достаточно развитым
логическим мышлением. Для других он будет
сложноват.
2-й способ (правило
креста).
Допустим, что Na 2 СО 3 10H 2 O – это
«сухой раствор» (ведь он же содержит воду). Тогда
найдем его «концентрацию»:
286 г – 106 г соли,
100 г – х
г соли,
х
= 100 106/286 = 37 г, или 37%.
Применяем правило креста.
Находим массу одной части и массы веществ:
m
1 = 20 22 = 440 г, m
2 = 20 5 =
100 г.
Ответ.
Для приготовления 540 г
раствора Na 2 CO 3 15%-й концентрации
необходимо взять 440 г 10%-го раствора и 100 г
кристаллогидрата.
Таким образом, применение правила креста удобнее
и проще при решении подобных задач. Этот способ
более экономичен по времени и менее трудоемок.
Правило креста можно применять и в тех случаях,
когда нужно получить раствор меньшей
концентрации путем разбавления водой более
концентрированного раствора или получить более
концентрированный раствор путем добавления к
исходному раствору сухой смеси. Рассмотрим это
на примерах.
ЗАДАЧА 5
Сколько воды нужно добавить к 250 г раствора
соли для понижения его концентрации с 45% до 10%?
Дано:
1 = 45%,
3 = 10%,
m
1 = 250 г.
Найти:
Решение
Принимаем, что концентрация для добавляемой
воды – 2 = 0%.
Используем правило креста.
Определяем массу одной части через первый
раствор: 250/10 = 25 г.
Тогда масса необходимой воды равна:
m
2 = 25 35 = 875 г.
Проверим правильность решения.
Масса нового раствора:
m
3 = 250 + 875 = 1125 г.
250 г 45%-го р-ра – х
г соли,
100 г 45%-го р-ра – 45 г соли,
х
= 250 45/100 = 112,5 г.
Находим 3:
1125 г р-ра – 112,5 г соли,
100 г р-ра – y
г соли,
y
= 100 112,5/1125 = 10 г, или 10%.
Ответ
.
m
2 = 875 г.
ЗАДАЧА 6
Сколько сухой соли нужно добавить к 250 г
раствора 10%-й концентрации для ее увеличения до
45%?
Дано:
1 = 10%,
m
1 = 250 г,
3 = 45%.
Найти:
m
(с. с.).
Решение
Принимаем, что сухая соль – это раствор с 2 = 100%.
Используем правило креста.
Определяем массу одной части через первый
раствор: 250/55 = 4,5 г.
Определяем массу сухой соли:
m
(с. с.) = 4,5 35 = 158 г.
Проверяем правильность решения.
Масса нового раствора:
m
3 = 250 + 158 = 408 г.
Масса соли в исходном растворе:
100 г 10%-го р-ра – 10 г соли,
250 г 10%-го р-ра – х
г соли,
х
= 250 10/100 = 25 г.
Общая масса соли в новом растворе:
25 + 158 = 183 г.
Концентрация нового раствора:
408 г р-ра – 183 г соли,
100 г р-ра – y
г соли,
y
= 100 183/408 = 45 г, или 45%.
Ответ
.
m
(с. с.) = 158 г.
Думается, что опытный учитель всегда найдет
несколько способов решения любой задачи. Но как
учила меня моя первая учительница по химии
Клавдия Макаровна в школе № 17 г. Иркутска, так и я
стараюсь учить своих учеников: всегда глубоко
продумывать и понимать химическую сущность
задачи и находить наиболее рациональный способ
ее решения, а не просто подгонять под ответ в
конце учебника.
Сегодня мы продолжаем серию видеоуроков, посвященных задачам на проценты из ЕГЭ по математике. В частности, разберем две вполне реальных задачи из ЕГЭ и еще раз убедимся, насколько важно внимательно читать условие задачи и правильно его интерпретировать.
Итак, первая задача:
Задача. Только 95% и 37 500 выпускников города правильно решили задачу B1. Сколько человек правильно решили задачу B1?
На первый взгляд кажется, что это какая-то задача для кэпов. Наподобие:
Задача. На дереве сидело 7 птичек. 3 из них улетело. Сколько птичек улетело?
Тем не менее, давай все-таки сосчитаем. Решать будем методом пропорций. Итак, у нас есть 37 500 учеников — это 100%. А также есть некое число x
учеников, которое составляет 95% тех самых счастливчиков, которые правильно решили задачу B1. Записываем это:
37 500 — 100%
X
— 95%
Нужно составить пропорцию и найти x
. Получаем:
Перед нами классическая пропорция, но прежде чем воспользоваться основным свойством и перемножить ее крест-накрест, предлагаю разделить обе части уравнения на 100. Другими словами, зачеркнем в числителе каждой дроби по два нуля. Перепишем полученное уравнение:

По основному свойству пропорции, произведение крайних членов равно произведению средних членов. Другими словами:
x
= 375 · 95
Это довольно большие числа, поэтому придется умножать их столбиком. Напоминаю, что пользоваться калькулятором на ЕГЭ по математике категорически запрещено. Получим:
x
= 35 625
Итого ответ: 35 625. Именно столько человек из исходных 37 500 решили задачу B1 правильно. Как видите, эти числа довольно близки, что вполне логично, потому что 95% тоже очень близки к 100%. В общем, первая задача решена. Переходим к второй.
Задача на проценты №2
Задача. Только 80% из 45 000 выпускников города правильно решили задачу B9. Сколько человек решили задачу B9 неправильно?
Решаем по той же самой схеме. Изначально было 45 000 выпускников — это 100%. Затем из этого количества надо выбрать x
выпускников, которые должны составить 80% от исходного количества. Составляем пропорцию и решаем:
45 000 — 100%
x
— 80%

Давайте сократим по одному нулю в числителе и знаменателе 2-й дроби. Еще раз перепишем полученную конструкцию:

Основное свойство пропорции: произведение крайних членов равно произведению средних. Получаем:
45 000 · 8 = x
· 10
Это простейшее линейное уравнение. Выразим из него переменную x
:
x
= 45 000 · 8: 10
Сокращаем по одному нулю у 45 000 и у 10, в знаменателе остается единица, поэтому все, что нам нужно — это найти значение выражения:
x
= 4500 · 8
Можно, конечно, поступить так же, как в прошлый раз, и перемножить эти числа столбиком. Но давайте не будем сами себе усложнять жизнь, и вместо умножения столбиком разложим восьмерку на множители:
x
= 4500 · 2 · 2 · 2 = 9000 · 2 · 2 = 36 000
А теперь — самое главное, о чем я говорил в самом начале урока. Нужно внимательно читать условие задачи!
Что от нас требуется узнать? Сколько человек решили задачу B9 неправильно
. А мы только что нашли тех людей, которые решили правильно. Таких оказалось 80% от исходного числа, т.е. 36 000. Это значит, что для получения окончательного ответа надо вычесть из исходной численности учеников наши 80%. Получим:
45 000 − 36 000 = 9000
Полученное число 9000 — это и есть ответ к задаче. Итого в этом городе из 45 000 выпускников 9000 человек решили задачу B9 неправильно. Все, задача решена.
Я надеюсь, что этот ролик поможет тем, кто самостоятельно готовится к ЕГЭ по математике. А у меня на этом все. С вами был Павел Бердов. До новых встреч!:)
Это наиболее простая и довольно точная однородная разностная схема счета газодинамики. Ее шаблзн приведен на рис. 98; значения радиусов приписываются узлам сетки, значения скорости – границам пространственных интервалов на полуцелых слоях, а значения плотности, давления и внутренней энергии – серединам интервалов на целых слоях.
Построение схемы напоминает акустический «крест». Для простоты записи выберем равномерные по массе и времени шаги и t и аппроксимируем систему следующими разностными уравнениями:


Эти уравнения записаны в том порядке, который удобен для вычислений.
Обсудим разностное выражение для вязкого давления (65). Чтобы выполнить предельный переход от разностной схемы к уравнениям газодинамики, надо сначала устремить к нулю при фиксированном коэффициенте вязкости, а затем построить серию таких предельных решений для неограниченно уменьшающихся значений . Но это очень трудоемко. Поэтому на практике объединяют эти предельные переходы в один общий, полагая хотя законность такой процедуры не доказана (плотность введена в формулу для того, чтобы коэффициенты были безразмерны).
Таким образом, вязкое давление (65) принимает вид
где – скорость звука. Выражение (67) написано для плоского случая; но обычно им пользуются при любой симметрии задачи.
Аппроксимация. Из вида шаблона на рис. 98 и симметричного написания схемы (66) нетрудно заметить, что на течениях без сжатий, когда псевдовязкость (67) обращается в нуль, схема «крест» имеет локальную аппроксимацию
На течениях со сжатиями (в том числе – с ударными волнами) псевдовязкость отлична от нуля. Правда, квадратичный член в (67а) имеет величину но линейный член имеет величину и, тем самым, ухудшает порядок аппроксимации. Кроме того, вязкие члены записываются не вполне симметрично по времени. В итоге аппроксимация ухудшается до
Нахождение разностного решения. Схема (66) – явная; вычисления по ней проводятся следующим образом. Пусть все величины на исходном слое известны. Тогда из разностного уравнения импульса (66а) находим во всех интервалах; затем из второго уравнения (66б) определяем а из уравнения (66в) – .
Последним решается уравнение энергии (66г). Формально оно является неявным алгебраическим уравнением для определения в данном интервале. Но при каждом значении индекса уравнения (66г) решаются независимо, не образуя связанной системы уравнений, так что разностная схема, по существу, остается явной.
Замечание 1. Уравнение энергии в (66) можно сделать яным, используя в нем только значение с исходного слоя:
![]()
Это несколько упрощает расчет, не влияет на устойчивость, но заметно ухудшает точность, так как погрешность аппроксимации становится даже на гладких течениях. Такой вариант используется редко.
Устойчивость схемы можно исследовать методом разделения переменных, линеаризируя схему и замораживая коэффициенты. Громоздкие выкладки приводят к условию устойчивости типа Куранта.
Например, на гладких течениях с нулевой вязкостью схема устойчива при
Для идеального газа и условие (69) принимает вид где есть адиабатическая скорость звука. На течениях с ненулевой вязкостью ограничение на шаг несколько более сильное; при квадратичной вязкости условие устойчивости принимает вид

где – скачок скорости на ударной волне. Хотя это исследование не является строгим, тем не менее данное условие устойчивости хорошо подтверждается на практике.

Таким образом, «крест» – условно устойчивая схема. Отметим любопытное обстоятельство. Для расчета гладких течений вязкость не нужна. А если рассчитать без вязкости ударную волну (выбирая небольшое удовлетворяющее условию (70)), то получим «разболтку», изображенную на рис. 99. Этот расчет устойчив, поскольку амплитуда колебаний не возрастает со временем. Но сходимости к физически правильному решению при нет, так как на разрыве потеряна аппроксимация.
Сходимость газодинамической схемы «крест» не доказана. Однако эта схема успешно используется в расчетах примерно с 1950 г. и проверена на многих трудных задачах с известными точными решениями. При стремлении шагов к нулю наблюдалась сходимость к правильному решению, если шаги удовлетворяли условию устойчивости.
Замечание 2. Схема (66) неконсервативна; однако ее дисбаланс стремится к нулю при
Замечание 3. Газодинамические задачи с очень тонкими слоями особенно трудны для расчета. В самом деле, если , то для вычисления с удовлетворительной точностью по формуле (66в) надо знать радиусы с очень высокой точностью, сравнимой с ошибками округления на ЭВМ. В подобных задачах иногда приходится вести расчет с двойным числом знаков или специально видоизменять разностную схему.

Соблюдение Вашей конфиденциальности важно для нас. По этой причине, мы разработали Политику Конфиденциальности, которая описывает, как мы используем и храним Вашу информацию. Пожалуйста, ознакомьтесь с нашими правилами соблюдения конфиденциальности и сообщите нам, если у вас возникнут какие-либо вопросы.
Сбор и использование персональной информации
Под персональной информацией понимаются данные, которые могут быть использованы для идентификации определенного лица либо связи с ним.
От вас может быть запрошено предоставление вашей персональной информации в любой момент, когда вы связываетесь с нами.
Ниже приведены некоторые примеры типов персональной информации, которую мы можем собирать, и как мы можем использовать такую информацию.
Какую персональную информацию мы собираем:
- Когда вы оставляете заявку на сайте, мы можем собирать различную информацию, включая ваши имя, номер телефона, адрес электронной почты и т.д.
Как мы используем вашу персональную информацию:
- Собираемая нами персональная информация позволяет нам связываться с вами и сообщать об уникальных предложениях, акциях и других мероприятиях и ближайших событиях.
- Время от времени, мы можем использовать вашу персональную информацию для отправки важных уведомлений и сообщений.
- Мы также можем использовать персональную информацию для внутренних целей, таких как проведения аудита, анализа данных и различных исследований в целях улучшения услуг предоставляемых нами и предоставления Вам рекомендаций относительно наших услуг.
- Если вы принимаете участие в розыгрыше призов, конкурсе или сходном стимулирующем мероприятии, мы можем использовать предоставляемую вами информацию для управления такими программами.
Раскрытие информации третьим лицам
Мы не раскрываем полученную от Вас информацию третьим лицам.
Исключения:
- В случае если необходимо – в соответствии с законом, судебным порядком, в судебном разбирательстве, и/или на основании публичных запросов или запросов от государственных органов на территории РФ – раскрыть вашу персональную информацию. Мы также можем раскрывать информацию о вас если мы определим, что такое раскрытие необходимо или уместно в целях безопасности, поддержания правопорядка, или иных общественно важных случаях.
- В случае реорганизации, слияния или продажи мы можем передать собираемую нами персональную информацию соответствующему третьему лицу – правопреемнику.
Защита персональной информации
Мы предпринимаем меры предосторожности – включая административные, технические и физические – для защиты вашей персональной информации от утраты, кражи, и недобросовестного использования, а также от несанкционированного доступа, раскрытия, изменения и уничтожения.
Соблюдение вашей конфиденциальности на уровне компании
Для того чтобы убедиться, что ваша персональная информация находится в безопасности, мы доводим нормы соблюдения конфиденциальности и безопасности до наших сотрудников, и строго следим за исполнением мер соблюдения конфиденциальности.
Формула пропорций
Пропо́рция – это равенство двух отношений, когда a:b=c:d
отношение 1 :
10 равно отношению 7 :
70, что также можно записать в виде дроби:
1
10
=
7
70
читается как: «один относится к десяти так же, как семь относится к семидесяти»
Основные свойства пропорции
Произведение крайних членов равно произведению средних членов (крест-накрест): если a:b=c:d , то a⋅d=b⋅c
1
10
✕
7
70
1 ⋅
70 = 10 ⋅
7
Обращение пропорции: если a:b=c:d , то b:a=d:c
1
10
7
70
10
1
=
70
7
Перестановка средних членов: если a:b=c:d , то a:c=b:d
1
10
7
70
1
7
=
10
70
Перестановка крайних членов: если a:b=c:d , то d:b=c:a
1
10
7
70
70
10
=
7
1
Решение пропорции с одним неизвестным | Уравнение
1 :
10 = x
:
70
или
1
10
=
x
70
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение
x
=
1 ⋅
70
10
=
7
Как посчитать пропорцию
Задача:
нужно пить 1 таблетку активированного угля на 10 килограмм веса. Сколько таблеток нужно выпить, если человек весит 70 кг?
Составим пропорцию:
1 таблетка – 10 кг
x
таблеток – 70 кг
Чтобы найти икс, нужно перемножить два известных числа крест-накрест и поделить на противоположное значение:
1 таблетка
x
таблеток
✕
10 кг
70 кг
x
= 1 ⋅
70 :
10 = 7
Ответ:
7 таблеток
Задача:
за пять часов Вася пишет две статьи. Сколько статей он напишет за 20 часов?
Составим пропорцию:
2 статьи – 5 часов
x
статей – 20 часов
x
= 2 ⋅
20 :
5 = 8
Ответ:
8 статей
Будущим выпускникам школ могу сказать, что умение составлять пропорции мне пригодилось и , и для того, чтобы пропорционально уменьшать картинки, и в HTML-вёрстке интернет-страницы, и в бытовых ситуациях.
