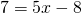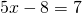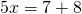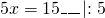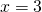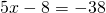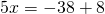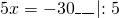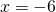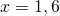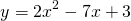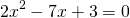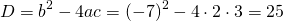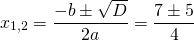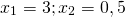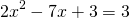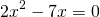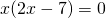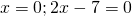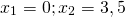Как найти икс пятое - Сайт, где вы сможете решить свои вопросы

На чтение 4 мин Просмотров 5.4к.

Как найти значение аргумента по значению функции? Это можно сделать с помощью формулы функции.

Если формула задана формулой вида y=f(x), чтобы найти значение аргумента по значению функции, надо в формулу вместо y подставить заданное значение функции и решить получившееся уравнение относительно икса.

1) Линейная функция задана формулой y=5x-8. Найти значение аргумента, при котором значение функции равно 7; -38;0.

Поменяем местами левую и правую часть, чтобы запись выглядела в привычном виде (знаки при этом менять не надо):

Это — линейное уравнение. Неизвестное — в одну сторону, известные — в другую (при переносе слагаемых из одной части в другую знаки меняются на противоположные):

Обе части уравнения делим на число, стоящее перед иксом:

2) При каком значении аргумента значение функции

Решаем квадратное уравнение.

При y=0 x=3 и x=0,5.

Это — неполное квадратное уравнение. Общий множитель x выносим за скобки

При y=3 x=0 и x=3,5.

Значение аргумента по заданному значению функции можно также найти с помощью графика. О том, как это сделать, мы будем говорить в следующий раз.

В прошлый раз мы находили значение функции по значению аргумента с помощью формулы.

Рассмотрим, как по данному графику функции найти y по x.

1) Пользуясь графиком линейной функции, изображенной на рисунке 1, найдите значение функции,если значение аргумента равно 1; 3; -3, -1; 0.

Аргумент — это x, функция — y.

Найти значение функции по значению аргумента — значит, по данному значению x найти, чему равен y.

Начнём с x=1. На оси абсцисс Ox находим x=1. Чтобы найти соответствующее значение y, надо из точки на Ox идти либо вверх, либо вниз, чтобы попасть на график.

От x=1 идём вверх. От полученной точки на графике надо двигаться либо влево, либо вправо, чтобы попасть на ось Oy. В данном случае идем влево и попадаем с ординатой y=2 (стрелочки помогают увидеть направление движения).

Следовательно, при x=1 y=2.

Аналогично, если x=3, идем вверх до пересечения с графиком, затем влево до пересечения с осью ординат Oy.

Получаем, что при x=3 y=4.

Если x=-3, чтобы попасть на график функции, нужно идти вниз, затем — вправо, до пересечения с осью Oy.

При x=-1 ни вверх, ни вниз двигаться не надо — эта точка уже на графике функции. Следовательно, y=0.

Записываем: при x=-1 y=0.

При x=0 идем до графика вверх и попадаем в точку с ординатой y=2.

2) На рисунке 2 изображен график функции y=f(x).

Пользуясь графиком, найдите значение функции, если значение аргумента равно 1; 3; 5; 7; -1; -5.

Чтобы по графику функции найти y по x, сначала надо от точки с данной абсциссой попасть на график, двигаясь вверх либо вниз, а затем от точки на графике идти к оси Oy, двигаясь влево или вправо.

При x=1 идем до графика функции вверх, затем влево — на ось Oy. Попадаем в точку с ординатой y=2.

Пишем: при x=1 y=2.

При x равном -1 и -5 идем сначала вверх, затем — вправо.

При иксах равных 3; 5 и 7 идём вниз и влево.

Обратите внимание: различным значениям икса может соответствовать одно значение y:

Дана следующая функция y=f(x) :
y = 2x – 10, если x > 0
y = 0, если x = 0
y = 2 * |x| – 1, если x

Требуется найти значение функции по переданному x .

Получить с клавиатуры значение x .
Если x больше 0, то вычислить выражение 2*x-10 , результат присвоить переменной y .

Иначе если x равен 0, то присвоить y значение 0.

Иначе присвоить y результат выражения 2*|x|-1 .

Вывести значение y на экран.

var x , y : integer ;
begin
readln ( x ) ;
if x > 0 then y : = 2 * x – 10
else
if x = 0 then y : = 0
else y : = 2 * abs ( x ) – 1 ;

writeln ( y ) ;
end .

main ( ) <
int x , y ;
scanf ( “%d” , & x ) ;
if ( x > 0 ) y = 2 * x – 10 ;
else
if ( x == 0 ) y = 0 ;
else
y = 2 * abs ( x ) – 1 ;

printf ( “%d
” , y ) ;
>

x = input ( )
x = int ( x )

if x > 0 :
y = 2 *x – 10
elif x == 0 :
y = 0
else :
y = 2 * abs ( x ) – 1

В КуМир функция взятия модуля от числа возвращает вещественное значение. Поэтому используется функция int(), чтобы привести к целому, иначе присвоение невозможно.

Источник

Калькулятор уравнений

Калькулятор уравнений предназначен для решения большинства типов уравнений и систем уравнений, таких как: линейные, квадратные, кубические, уравнения четвертой степени и более и т.д. Для решения уравнения введите уравнение и укажите неизвестную переменную, корни которой необходимо найти, например: x, y, a, b.

Для правильной работы с калькулятором необходимо ознакомиться с правилами ввода данных, указанных ниже. Калькулятор, принимает такие функции как: возведение в степень, извлечение корня n-ой степени, логарифм, любые тригонометрические функции, нод и нок чисел и т.д.

При решении квадратных уравнений рекомендуем воспользоваться калькулятором квадратных уравнений на сайте SmartCalculator.online. Калькулятор вычислит любой тип квадратного уравнения, включая неполные квадратные уравнения, найдет действительные и комплексные корни, а также построит график и найдет точки пересечения параболы с осью x.

Примеры ввода уравнений

x
2

–
4

x
–
2

x
2

–

4
·
x

+
7

(x^2-4)/(x-2)=x^2-4*x+7

2
·

x
3

–

3
·

x
2

1
2

2*x^3-(3/2)*x^2+1/2=0

Правила ввода чисел и функций

Содержание:

Десятичная дробь.
Обыкновенная дробь a/b.
Произведение чисел a*b.

Число пи (π).
Число Эйлера e.
Е – буква, означающая 10ⁿ.

Абсолютная величина. Модуль |x| числа Abs(x).

Квадратный корень sqrt(x).
Корень любой степени root(n, x).

Корень (в области вещественных чисел) real_root(n, x).
Возведение в степень n^(x) или pow(n, x).

Логарифм числа log(n, x).
Натуральный логарифм ln(n).
Наибольший общий делитель НОД gcd(n, m).
Наименьшее общее кратное НОК lcm(n, m).

Тригонометрические функции.
Синус угла sin(x).
Косинус угла cos(x).
Тангенс угла tan(x).
Котангенс угла cot(x).
Секанс угла sec(x).
Косеканс угла csc(x).

Обратные тригонометрические функции.
Арксинус угла asin(x).
Арккосинус угла acos(x).
Арктангенс угла atan(x).
Арккотангенс угла acot(x).
Арксеканс угла asec(x).
Арккосеканс угла acsc(x).

Выражения, содержащие множественное вложение функций и математических операций.

Десятичная дробь

Запись

:
Для записи десятичной дроби используйте точку

Пример

:
1.12

Обыкновенная дробь a/b

Запись

:
Для ввода обыкновенных дробей воспользуйтесь знаком «/»

Пример

:
1/2 или 3/4

Произведение чисел

Запись

:
Для записи произведения используйте знак «*»

Пример

:
5*4 или 2* – 5*(3^9)

Число пи (π)

Запись

:
Для записи числа π введите «π», либо «pi».

Пример

:
sin(π)

Число Эйлера e

е = 2.7182818284…

Запись

:
Для записи числа e введите 2.7182818284.

Е – буква, означающая 10ⁿ

Запись

:
Буква Е должна находится только в числе

Пример

:

16e+6
16e-4
3.96e+3

Абсолютная величина (модуль)

Запись

:
Abs(x)

Пример

:

|x| записывается как Abs(x)

|x-2|-|x+2| записывается как Abs(x-2)-Abs(x+2)

|x|/|y| записывается как Abs(x)/Abs(y)

Квадратный корень sqrt(x)

Запись

:
sqrt(x), где
x – любое число или выражение.

Пример

:

√3 записывается как sqrt(3)

√(3/5) записывается как sqrt(3/5)

√(3*3) записывается как sqrt(3*3)

Корень любой степени root(n, x)

Запись

:
root(n, x), где
n – подкореное выражение
x – степень корня
x, n – любые числа или выражения.
Для корня четной степени, подкореное выражение не может быть отрицательным.

Пример

:

Корень кубический из дроби 2/5
³√(2/5) записывается как root(2/5, 3)

Другие примеры
³√(2/5) записывается как root(1.5, 3)
^3/2√(3*5) записывается как root((3*5), 3/2)
^3/7√(1.5) записывается как root(1.5, 3/7)

Корень (в области вещественных чисел) real_root(n, x)

Если вам не нужно вычислять значение корня в области комплексных чисел, используйте функцию real_root(n, x) для нахождения вещественных корней.

Запись

:
real_root(n, x), где
n – подкореное выражение
x – степень корня
x, n – любые числа или выражения.

Пример

:
Выражение:

-2
3

Запись:
real_root(-2, 3)

Для возведения в степень используйте знак «^» либо функцию pow(n, x)

Пример

:

5³ записывается как 5^(3)
a^bc записывается как a^(b*c)
5^sin(x) записывается как 5^(sin(x))

Возведение в степень pow(n, x)

Запись

:
pow(n, x), где
n – основание
x – показатель степени
x, n – любые числа или выражения.

Пример

:

Пять в степени три

pow(5, 3)

Другие примеры

pow(12.5, 3)

pow((3-5), 3/2)

pow(1.5, sqrt(2))

Логарифм числа log(n, x)

Запись

:
log(n, x), где
n – число, логарифм которого требуется найти
x – основание логарифма.
x > 0, x ≠ 1, n > 0

Пример

:

Log5 34 (логарифм числа 34 по основанию 5), запишем как
log(34, 5)

Натуральный логарифм ln(n)
Основание равно числу Эйлера e
(е = 2.7182818284…)

Запись

:

ln(n), где
n > 0 <

Пример

:

Ln(7)

Наибольший общий делитель НОД gcd(n, m)

Запись

:

gcd(n, m), где
n, m – целые неотрицательные числа

Пример

:

НОД(12; 16) нужно записать как

gcd(12, 16)

Наименьшее общее кратное НОК lcm(n, m)

Запись

:

lcm(n, m), где
n, m – целые неотрицательные числа

Пример

:

НОК(4; 23) нужно записать как

lcm (4, 23)

Тригонометрические функции

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Синус угла sin(x)

Запись

:

sin(x)

Где

x – число, буква или выражение

Пример

:

Синус π/3

sin(π/3)

Синус 60° градусов

Sin(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Косинус угла cos(x)

Запись

:

Cos(x)

Где

x – число, буква или выражение

Пример

:

Косинус π/3

cos(π/3)

Косинус 60° градусов

cos(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Тангенс угла tan(x)

Запись

:

tan(x)

tan(x, measure)

Где

x – число, буква или выражение

Пример

:

Тангенс π/3

tan(π/3)

Тангенс 60° градусов

tan(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Котангенс угла cot(x)

Запись

:

Cot(x)

Где

x – число, буква или выражение

Пример

:

Котангенс π/3

cot(π/3)

Котангенс 60° градусов

cot(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Секанс угла sec(x)

Запись

:

sec(x)

Где

x – число, буква или выражение

Пример

:

Секанс π/3

sec(π/3)

Секанс 60° градусов

sec(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Косеканс угла csc(x)

Запись

:

csc(x)

Где

x – число, буква или выражение

Пример

:

Косеканс π/3

csc(π/3)

Косеканс 60° градусов

csc(60)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Обратные тригонометрические функции

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Арксинус asin(x)

Запись

:

asin(x)
Где
x – число, буква или выражение

Пример

:

Арксинус 1/3

asin(1/3)

Для вычисления тригонометрических функций в градусах в калькуляторе слева в верхнем углу выберете DEG, в радианах выберете RAD.

Арккосинус acos(x)

Запись

:

acos(x)
Где
x – число, буква или выражение

Пример

:

Арккосинус 1/3

acos(1/3)

Арктангенс atan(x)

Запись

:

atan(x)
Где
x – число, буква или выражение

Пример

:

Арктангенс 1/3

atan(1/3)

Арккотангенс acot(x)

Запись

:

acot(x)
Где
x – число, буква или выражение

Пример

:

Арккотангенс 1/3

acot(1/3)

Арксеканс asec(x)

Запись

:

asec(x)
Где
x – число, буква или выражение

Пример

:

Арксеканс 1/3

asec(1/3)

Арккосеканс acsc(x)

Запись

:

acsc(x)
Где
x – число, буква или выражение

Пример

:

Арккосеканс 1/3

Acsc(1/3)

Выражения, содержащие множественное вложение функций и математических операций

Любое выражение может содержать в себе множественное вложение функций, ограничение по длине выражения составляет 100 символов.
Введите выражение (максимальная длина 100 символов).

Примеры

:
root(2^(3.4), 2);
sin(x)+cos(x)
и т.д.

Вам могут также быть полезны следующие сервисы

Калькуляторы (Теория чисел)

Калькулятор выражений

Калькулятор упрощения выражений

Калькулятор со скобками

Калькулятор уравнений

Калькулятор суммы

Калькулятор пределов функций

Калькулятор разложения числа на простые множители

Калькулятор НОД и НОК

Калькулятор НОД и НОК по алгоритму Евклида

Калькулятор НОД и НОК для любого количества чисел

Калькулятор делителей числа

Представление многозначных чисел в виде суммы разрядных слагаемых

Калькулятор деления числа в данном отношении

Калькулятор процентов

Калькулятор перевода числа с Е в десятичное

Калькулятор экспоненциальной записи чисел

Калькулятор нахождения факториала числа

Калькулятор нахождения логарифма числа

Калькулятор квадратных уравнений

Калькулятор остатка от деления

Калькулятор корней с решением

Калькулятор нахождения периода десятичной дроби

Калькулятор больших чисел

Калькулятор округления числа

Калькулятор свойств корней и степеней

Калькулятор комплексных чисел

Калькулятор среднего арифметического

Калькулятор арифметической прогрессии

Калькулятор геометрической прогрессии

Калькулятор модуля числа

Калькулятор абсолютной погрешности приближения

Калькулятор абсолютной погрешности

Калькулятор относительной погрешности

Дроби

Калькулятор интервальных повторений

Учим дроби наглядно

Калькулятор сокращения дробей

Калькулятор преобразования неправильной дроби в смешанную

Калькулятор преобразования смешанной дроби в неправильную

Калькулятор сложения, вычитания, умножения и деления дробей

Калькулятор возведения дроби в степень

Калькулятор перевода десятичной дроби в обыкновенную

Калькулятор перевода обыкновенной дроби в десятичную

Калькулятор сравнения дробей

Калькулятор приведения дробей к общему знаменателю

Калькуляторы (тригонометрия)

Калькулятор синуса угла

Калькулятор косинуса угла

Калькулятор тангенса угла

Калькулятор котангенса угла

Калькулятор секанса угла

Калькулятор косеканса угла

Калькулятор арксинуса угла

Калькулятор арккосинуса угла

Калькулятор арктангенса угла

Калькулятор арккотангенса угла

Калькулятор арксеканса угла

Калькулятор арккосеканса угла

Калькулятор нахождения наименьшего угла

Калькулятор определения вида угла

Калькулятор смежных углов

Калькуляторы систем счисления

Калькулятор перевода чисел из арабских в римские и из римских в арабские

Калькулятор перевода чисел в различные системы счисления

Калькулятор сложения, вычитания, умножения и деления двоичных чисел

Системы счисления теория

N₂ | Двоичная система счисления

N₃ | Троичная система счисления

N₄ | Четырехичная система счисления

N₅ | Пятеричная система счисления

N₆ | Шестеричная система счисления

N₇ | Семеричная система счисления

N₈ | Восьмеричная система счисления

N₉ | Девятеричная система счисления

N₁₁ | Одиннадцатиричная система счисления

N₁₂ | Двенадцатеричная система счисления

N₁₃ | Тринадцатеричная система счисления

N₁₄ | Четырнадцатеричная система счисления

N₁₅ | Пятнадцатеричная система счисления

N₁₆ | Шестнадцатеричная система счисления

N₁₇ | Семнадцатеричная система счисления

N₁₈ | Восемнадцатеричная система счисления

N₁₉ | Девятнадцатеричная система счисления

N₂₀ | Двадцатеричная система счисления

N₂₁ | Двадцатиодноричная система счисления

N₂₂ | Двадцатидвухричная система счисления

N₂₃ | Двадцатитрехричная система счисления

N₂₄ | Двадцатичетырехричная система счисления

N₂₅ | Двадцатипятеричная система счисления

N₂₆ | Двадцатишестеричная система счисления

N₂₇ | Двадцатисемеричная система счисления

N₂₈ | Двадцативосьмеричная система счисления

N₂₉ | Двадцатидевятиричная система счисления

N₃₀ | Тридцатиричная система счисления

N₃₁ | Тридцатиодноричная система счисления

N₃₂ | Тридцатидвухричная система счисления

N₃₃ | Тридцатитрехричная система счисления

N₃₄ | Тридцатичетырехричная система счисления

N₃₅ | Тридцатипятиричная система счисления

N₃₆ | Тридцатишестиричная система счисления

Калькуляторы площади геометрических фигур

Площадь квадрата

Площадь прямоугольника

КАЛЬКУЛЯТОРЫ ЗАДАЧ ПО ГЕОМЕТРИИ

Калькуляторы (Комбинаторика)

Калькулятор нахождения числа перестановок из n элементов

Калькулятор нахождения числа сочетаний из n элементов

Калькулятор нахождения числа размещений из n элементов

Калькуляторы линейная алгебра и аналитическая геометрия

Калькулятор сложения и вычитания матриц

Калькулятор умножения матриц

Калькулятор транспонирование матрицы

Калькулятор нахождения определителя (детерминанта) матрицы

Калькулятор нахождения обратной матрицы

Длина отрезка. Онлайн калькулятор расстояния между точками

Онлайн калькулятор нахождения координат вектора по двум точкам

Калькулятор нахождения модуля (длины) вектора

Калькулятор сложения и вычитания векторов

Калькулятор скалярного произведения векторов через длину и косинус угла между векторами

Калькулятор скалярного произведения векторов через координаты

Калькулятор векторного произведения векторов через координаты

Калькулятор смешанного произведения векторов

Калькулятор умножения вектора на число

Калькулятор нахождения угла между векторами

Калькулятор проверки коллинеарности векторов

Калькулятор проверки компланарности векторов

Генератор Pdf с примерами

Тренажёры решения примеров

Тренажер по математике

Тренажёр таблицы умножения

Тренажер счета для дошкольников

Тренажер счета на внимательность для дошкольников

Тренажер решения примеров на сложение, вычитание, умножение, деление. Найди правильный ответ.

Тренажер решения примеров с разными действиями

Тренажёры решения столбиком

Тренажёр сложения столбиком

Тренажёр вычитания столбиком

Тренажёр умножения столбиком

Тренажёр деления столбиком с остатком

Калькуляторы решения столбиком

Калькулятор сложения, вычитания, умножения и деления столбиком

Калькулятор деления столбиком с остатком

Конвертеры величин

Конвертер единиц длины

Конвертер единиц скорости

Конвертер единиц ускорения

Цифры в текст

Калькуляторы (физика)

Механика

Калькулятор вычисления скорости, времени и расстояния

Калькулятор вычисления ускорения, скорости и перемещения

Калькулятор вычисления времени движения

Калькулятор времени

Второй закон Ньютона. Калькулятор вычисления силы, массы и ускорения.

Закон всемирного тяготения. Калькулятор вычисления силы притяжения, массы и расстояния.

Импульс тела. Калькулятор вычисления импульса, массы и скорости

Импульс силы. Калькулятор вычисления импульса, силы и времени действия силы.

Вес тела. Калькулятор вычисления веса тела, массы и ускорения свободного падения

Оптика

Калькулятор отражения и преломления света

Электричество и магнетизм

Калькулятор Закона Ома

Калькулятор Закона Кулона

Калькулятор напряженности E электрического поля

Калькулятор нахождения точечного электрического заряда Q

Калькулятор нахождения силы F действующей на заряд q

Калькулятор вычисления расстояния r от заряда q

Калькулятор вычисления потенциальной энергии W заряда q

Калькулятор вычисления потенциала φ электростатического поля

Калькулятор вычисления электроемкости C проводника и сферы

Конденсаторы

Калькулятор вычисления электроемкости C плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряженности E электрического поля плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления напряжения U (разности потенциалов) плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления расстояния d между пластинами в плоском конденсаторе

Калькулятор вычисления площади пластины (обкладки) S в плоском конденсаторе

Калькулятор вычисления энергии W заряженного конденсатора

Калькулятор вычисления энергии W заряженного конденсатора. Для плоского, цилиндрического и сферического конденсаторов

Калькулятор вычисления объемной плотности энергии w электрического поля для плоского, цилиндрического и сферического конденсаторов

Калькуляторы по астрономии

Вес тела на других планетах

Ускорение свободного падения на планетах Солнечной системы и их спутниках

Генераторы

Генератор примеров по математике

Генератор случайных чисел

Генератор паролей

Источник

Урок 17 Бесплатно Уравнение

Часто приходится описывать реальную ситуацию, процесс, явление с помощью математического языка.

Математический язык- универсальный язык, с помощью него можно однозначно и кратко описать многие закономерности, процессы, задачи и т.д.

Связать реальную жизнь и математическое описание любой ситуации нам позволяет математическая модель.

Описывая реальность с помощью математического языка, люди создают математические модели, превращающие слова в формулы, неравенства, равенства, уравнения и т.п.

Математическая модель дает возможность решать огромное количество практических (природных, технических, научных, экономических, социальных и других) задач.

Математические модели делят на:

Словесные.
Графические (схемы, графики, чертежи, рисунки и т.д.).
Аналитические (алгебраические: числовые равенства, неравенства, уравнения, формулы и т.д.).

На данном уроке подробно рассмотрим одну из аналитических математических моделей- уравнение.

Выясним, что такое уравнение и что называют корнем уравнения.

Рассмотрим простейшие виды уравнений.

Разберем способы и приемы решения уравнений с одним неизвестным.

Рассмотрим алгоритм и примеры решения задач с помощью уравнений.

Уравнения

Часто при решении задач приходится составлять равенства.

Два выражения (числовые или буквенные), соединенные знаком равно «=», образуют равенство.

В математике различают два вида равенств: тождества и уравнения.

Тождества- это числовые равенства, а также равенства, которые выполняются при всех допустимых значениях переменных, входящих в него.

Уравнение- это равенство, содержащее неизвестные числа, обозначенные буквами, значение которых можно определить.

Неизвестное число, входящее в уравнение, называют неизвестным членом уравнения (или просто «неизвестным»).

Чаще всего в математике неизвестные величины обозначают маленькими буквами латинского алфавита x, y, z.

У меня есть дополнительная информация к этой части урока!

Долгое время в математических выкладках не использовали буквенные обозначения и записывали выражения и уравнения словами.

В 1591 году французский ученый философ Франсуа Виет ввел буквенные обозначения. Он предложил использовать гласные буквы латинского алфавита для названия величин, а согласные для неизвестных.

Позже другой французский ученый, философ Рене Декарт предложил иную систему обозначений, связанную с латинскими буквами (которую используют по сегодняшний день).

Для неизвестных было предложено использовать последние буквы латинского алфавита (х, у, z), а для известных величин первые буквы латинского алфавита (а, b, c)

Пример 1:

4 + х = 18 является уравнением с неизвестной х.

12у — 5 = 19 является уравнением с неизвестной у.

(2 + z) — (3 — 1) = 2 является уравнением с неизвестной z.

Все три записи являются равенствами, в каждом из них есть неизвестное число, обозначенное буквой.

Пример 2:

4х — 18 не является уравнением, так как не является равенством.

24 — 5 = 19 не является уравнением, так как не содержит неизвестную.

у + 2 > 12 не является уравнением, так как не является равенством.

Решить уравнение- это значит найти неизвестное число, при котором из уравнения получается верное равенство.

Уравнение считается решенным, если все его решения найдены или доказано, что уравнение решения не имеет.

Значение неизвестного, обращающее уравнение в верное равенство, называют корнем уравнения.

Следовательно, если в уравнение вместо неизвестной подставить ее численное значение и получится верное числовое равенство, то это значение неизвестной будет решением этого уравнения.

Дано уравнение 12 — х + 3 = 10.

1) Пусть х равно 6, получаем

12 — 6 + 3 = 10

9 ≠ 10 (девять не равно десяти)

При подстановке вместо неизвестного число 6, получаем неверное числовое равенство 9 ≠ 10, т.е. число 6 не является корнем уравнения.

2) Пусть х равно 5, получаем

12 — 5 + 3 = 10

10 = 10

При подстановке вместо неизвестного число 5, получаем верное числовое равенство 10 = 10, т.е. число 5 является корнем уравнения.

Уравнение может иметь разное количество корней: существуют уравнения, имеющие один единственный корень, уравнения, имеющие два, три корня.

Встречаются уравнения, вообще не имеющие верного решения, и даже такие уравнения, решением которых являются бесконечное множество решений.

7 — х = 4 уравнение имеет один корень, х = 3, любое другое значение х будет давать неверное равенство.

х = х — 15 уравнение не имеет решения, так как любое значение неизвестного х будет данное равенство обращать в неверное, не существует таких чисел, которые были бы меньше самого себя.

0 ⋅ y = 0 уравнение имеет бесконечное множество верных решений, так как при умножении любого числа на 0, получается 0.

Уравнение, содержащее одну неизвестную, называют уравнением с одной неизвестной.

Уравнения с большим количеством неизвестным называют соответственно уравнением с двумя, тремя и т.д. неизвестными.

Такие уравнения и их решение будете рассматривать в старших классах.

Например, 26 — 2х = 23 — х— это уравнение с одной неизвестной х.

53 — х = 19у— это уравнение с двумя неизвестными х и у.

Любое уравнение имеет левую и правую часть.

Выражение, стоящее слева от знака равно, называют левой частью уравнения, а выражение, которое стоит справа, правой частью уравнения.

Каждый компонент, из которых состоит уравнение, называют членами этого уравнения.

Обычно все члены уравнения, содержащие неизвестное, следует группировать в левой части уравнения, а известные — в правой.

Чаще всего уравнение записывают в левой части страницы, справа делают письменные вычисления (вычислительные операции).

При решении уравнения каждое новое равенство записывается с новой строки (т.е. решение оформляется в виде столбика равенств).

Таким образом, знак равенства при решении уравнения используют только один раз в каждой строке.

Пройти тест и получить оценку можно после входа или регистрации

Памятка : «Решение уравнений», 5 класс

Обращаем Ваше внимание, что в соответствии с Федеральным законом N 273-ФЗ «Об образовании в Российской Федерации» в организациях, осуществляющих образовательную деятельность, организовывается обучение и воспитание обучающихся с ОВЗ как совместно с другими обучающимися, так и в отдельных классах или группах.

(Х – 87) – 27 = 36; Х-87 в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Х – 87 = 63; х в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

Проверка: (150 – 87) – 27 = 36;

87- ( 41 + У ) = 22; 41 + У в уравнении является вычитаемым . Чтобы найти неизвестное вычитаемое, нужно из уменьшаемого вычесть разность

41 + У = 65; У в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

Проверка: 87- ( 41 + 24 ) = 22;

(у – 35) + 12 = 32; у – 35 в уравнении является слагаемым. Чтобы найти неизвестное слагаемое , нужно из суммы вычесть известное слагаемое

у – 35 = 20; у в уравнении является уменьшаемым. Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое

(237 + х) – 583 = 149;

468 – ( 259 – х) = 382;

(237 + х) – 583 = 149;

237 + х = 149 + 583;

(237 + х) – 583 = 149;

237 + х – 583 = 149;

х – (583 – 237) = 149;

468 – ( 259 – х) = 382;

259 – х = 468 – 382;

468 – ( 259 – х) = 382; 468 – 259 + х = 382;

Решение уравнений, приведение подобных слагаемых

Пример 1: 8х-х=49 ; сначала запишем знаки умножения,

8*х-1*х=49 ; затем воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*7=49 ; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

Пример 2: 2х+5х+350=700 ; воспользуемся распределительным свойством (вынесем общую переменную за скобки)

Х*(2+5)+350=700 ; приведем подобные слагаемые (т.е. сложим числа в скобках)

7х является неизвестным слагаемым . Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

7х=350; х является неизвестным множителем . Чтобы найти неизвестный множитель , нужно произведение разделить на известный множитель

2*50 + 5*50 + 350 = 700;

100 + 250 + 350 = 700;

Пример: 270: х + 2 = 47;

( 270 : х — является слагаемым.

Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое

( х является делителем . Чтобы найти неизвестный делитель , нужно делимое разделить на частное)

Пример: а : 5 – 12 = 23;

Чтобы найти неизвестное уменьшаемое , нужно к разности прибавить вычитаемое )

( а является делимым. Чтобы найти неизвестное делимое , нужно частное умножить на делитель .

Курс повышения квалификации

Дистанционное обучение как современный формат преподавания

Сейчас обучается 929 человек из 80 регионов

Курс профессиональной переподготовки

Математика: теория и методика преподавания в образовательной организации

Сейчас обучается 686 человек из 75 регионов

Курс повышения квалификации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Сейчас обучается 313 человек из 69 регионов

Ищем педагогов в команду «Инфоурок»

Дистанционные курсы для педагогов

«Взбодрись! Нейрогимнастика для успешной учёбы и комфортной жизни»

Свидетельство и скидка на обучение каждому участнику

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

5 586 449 материалов в базе

Материал подходит для УМК

«Математика», Виленкин Н.Я., Жохов В.И. и др.

Самые массовые международные дистанционные

Школьные Инфоконкурсы 2022

33 конкурса для учеников 1–11 классов и дошкольников от проекта «Инфоурок»

«Психологические методы развития навыков эффективного общения и чтения на английском языке у младших школьников»

Свидетельство и скидка на обучение каждому участнику

Другие материалы

09.12.2019
256
2

08.12.2019
254
0

19.11.2019
200
2

18.11.2019
902
7

18.11.2019
311
0

17.11.2019
320
0

17.11.2019
294
10

17.11.2019
217
4

Вам будут интересны эти курсы:

Оставьте свой комментарий

Авторизуйтесь, чтобы задавать вопросы.

Добавить в избранное

15.12.2019 55857
DOCX 17.4 кбайт
6501 скачивание
Рейтинг: 5 из 5
Оцените материал:

Настоящий материал опубликован пользователем Кретинина Светлана Сергеевна. Инфоурок является информационным посредником и предоставляет пользователям возможность размещать на сайте методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайт

Если Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с сайта, Вы можете оставить жалобу на материал.

Автор материала

На сайте: 4 года и 5 месяцев
Подписчики: 0
Всего просмотров: 60537
Всего материалов: 9

Московский институт профессиональной
переподготовки и повышения
квалификации педагогов

Дистанционные курсы
для педагогов

663 курса от 690 рублей

Выбрать курс со скидкой

Выдаём документы
установленного образца!

Учителя о ЕГЭ: секреты успешной подготовки

Время чтения: 11 минут

В Забайкалье в 2022 году обеспечат интернетом 83 школы

Время чтения: 1 минута

Инфоурок стал резидентом Сколково

Время чтения: 2 минуты

В России действуют более 3,5 тысячи студенческих отрядов

Время чтения: 2 минуты

Ленобласть распределит в школы прибывающих из Донбасса детей

Время чтения: 1 минута

В ростовских школах рассматривают гибридный формат обучения с учетом эвакуированных

Время чтения: 1 минута

Минпросвещения подключит студотряды к обновлению школьной инфраструктуры

Время чтения: 1 минута

Подарочные сертификаты

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания, берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта и представлены на сайте исключительно для ознакомления. Авторские права на материалы принадлежат их законным авторам. Частичное или полное копирование материалов сайта без письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой зрения авторов.

Получите новую специальность с дополнительной скидкой 10%

Цена от 4900 740 руб. Промокод (до 23 февраля): Промокод скопирован в буфер обмена ПП2302 Выбрать курс Все курсы профессиональной переподготовки

Приемы решения уравнений в 5-6 классах
статья по алгебре (5 класс) на тему

Уравнения — не только одна из самых распространенных, но и одна из самых проблемных математических задач. Рассмотрим некоторые приемы решения простейших уравнений на уроках в 5-6 классах, которые в дальнейшем используем при решении более сложных уравнений. К концу обучения в 6 классе формируем обобщенный метод решения уравнений.

Скачать:

Вложение	Размер
priemy_zachetnaya_statya.docx	22.86 КБ

Предварительный просмотр:

Жарова Галия Шамратовна

Учитель математики МКОУ «Садовская СШ» Быковского района Волгоградской области тел. 8904-405-49-56

Приемы решения уравнений в 5-6 классах

Уравнение – самая простая и распространенная форма математической задачи. Решение уравнений — одна из проблем в математике. В 5-м классе изучение уравнений начинается с определения уравнения, его корней, что значит решить уравнение. Повторяются правила нахождения неизвестных компонентов сложения, вычитания. Решаются уравнения, которые содержат буквенные выражения только в одной части уравнения. Для их решения учащиеся должны выполнить последовательно несколько преобразований, каждое из которых освоено ими раньше: 395+х=864 или 59=81-k (№395 Математика 5 класс Н.Я. Виленкин и др.) Учащиеся 5 класса затрудняются решать уравнения такого типа, как (х + 121) — 38 =269. Алгоритм решения таких уравнений дан в №375 данного учебника.

Обычно такие уравнения решаются так:

чтобы найти уменьшаемое х +121,

надо к вычитаемому 38 прибавить разность 269:

х + 121 = 38 + 269;

Далее рассуждают так: чтобы найти неизвестное слагаемое Х, надо из суммы 307 вычесть известное слагаемое121:

Чаще всего ученики не видят в этом уравнении вычитаемого 38 и уменьшаемого (х+121). Если учащиеся имеют хорошие навыки решения простейших уравнений, можно решать подобные уравнения, приведя их к простейшим уравнениям. Рассмотрим этот прием на примерах решения уравнений из № 376 учебник Математика 5класс Н.Я.Виленкин и др.

Обозначим выражение, стоящее в скобках через a: х + 15 = а

Тогда получим такое уравнение:

Теперь возвращаемся к выражению, стоящему в скобках:

Подстановка 45-у = а;

Подстановка х+24= а;

Подстановка х – 15 = а;

Этот приём позволяет легко решать такие сложные уравнения.

Для тех учащихся, кто так и не усвоил правил нахождения неизвестных: слагаемого, вычитаемого, множителя и т.д., используется при решении простейших уравнений приём «по аналогии». Например, нужно решить уравнение: х – 284 = 127. В стороне от этого уравнения слабый ученик записывает простейший арифметический пример 7 — 3 = 4. Ученик смотрит, где в этом примере должен стоять х (на месте7). Как из этого простого примера найти 7? Надо к 3 прибавить 4. Значит, и в данном уравнении, чтобы найти х, надо 127 сложить с 284

Учащиеся 6-го класса осваивают новые методы решения уравнений. Вначале рассматривается возможность умножения или деления обеих частей на одно и то же отличное от нуля число. В обоих случаях делаются выводы о том, что при умножении (или делении) обеих частей уравнения на неравное нулю число получается новое уравнение с теми же корнями, что и заданное.

Далее осваивается способ переноса слагаемых из одной части уравнения в другую с переменой знака у слагаемого на противоположный. Так как обоснование этому способу также не дается (не изучались свойства равенства), то активно используется методические приемы с весами, с помощью которых учащиеся осознают смысл этого преобразования: все математические действия сопровождаются соответствующими действиями с весами. Покажем это на примере.

Решите уравнение х + 6 = 15

Вначале наполняем конкретным содержанием данную задачу: показываем картинку с весами или рассматриваем рисунок в учебнике. После выяснения соответствия картинки тексту задачи приступаем к решению уравнения.

Вынем из левой части уравнения число 6, это тоже самое, что снять с левой чаши весов гири в 5 кг и 1 кг. Чтобы равновесие не нарушилось, надо и с правой чаши весов снять гири массой в 6 кг, т.е. для сохранения равенства надо из правой части уравнения вычесть число 6.

После упрощения получаем

Просмотрев ход решения, можно сделать выводы: а) число 9 является корнем уравнения, б) при переносе членов из одной части уравнения в другую с переменой знаков получаем новое уравнение, но с тем же корнем.

После решения уравнения делаются выводы о возможности переноса членов, являющихся буквенными выражениями. Делается вывод, что любые слагаемые можно переносить из одной части уравнения в другую, изменяя при этом знаки.

В 6 классе учащиеся знакомятся с понятием модуля числа и учатся решать уравнения с модулем. Уравнения с модулем сводятся к простейшим уравнениям, в решении которых применяется определение модуля, учитывается, что под знаком модуля могут быть как положительные выражения, так и отрицательные, при этом модуль бывает только неотрицательным числом. Начнем с такого вида:

Решаем это уравнение как линейное: неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:

Теперь обе части уравнения делим на число, стоящее перед модулем икса:

источники:

http://infourok.ru/pamyatka-reshenie-uravneniy-klass-4004064.html

http://nsportal.ru/shkola/algebra/library/2016/02/10/priemy-resheniya-uravneniy-v-5-6-klassah

Источник

Калькулятор онлайн.
Решение показательных уравнений.

Этот математический калькулятор онлайн поможет вам решить показательное уравнение.
Программа для решения показательного уравнения не просто даёт ответ задачи, она приводит подробное
решение с пояснениями, т.е. отображает процесс получения результата.

Данная программа может быть полезна учащимся старших классов общеобразовательных школ при подготовке к контрольным работам и
экзаменам, при проверке знаний перед ЕГЭ, родителям для контроля решения многих задач по математике и алгебре.
А может быть вам слишком накладно нанимать репетитора или покупать новые учебники? Или вы просто хотите как можно быстрее
сделать домашнее задание по математике или алгебре? В этом случае вы также можете воспользоваться нашими программами с подробным
решением.

Таким образом вы можете проводить своё собственное обучение и/или обучение своих младших братьев или сестёр, при этом уровень
образования в области решаемых задач повышается.

Вы можете посмотреть теорию о показательной функции и
общие методы решения показательных уравнений.

Примеры подробного решения >>

Введите показательное уравнение

Наши игры, головоломки, эмуляторы:

Немного теории.

Показательная функция, её свойства и график

Напомним основные свойства степени. Пусть а > 0, b > 0, n, m – любые действительные числа. Тогда
1) aⁿ a^m = a^n+m

2) ( frac{a^n}{a^m} = a^{n-m} )

3) (aⁿ)^m = a^nm

4) (ab)ⁿ = aⁿ bⁿ

5) ( left( frac{a}{b} right)^n = frac{a^n}{b^n} )

6) aⁿ > 0

7) aⁿ > 1, если a > 1, n > 0

8) aⁿ < a^m, если a > 1, n < m

9) aⁿ > a^m, если 0< a < 1, n < m

В практике часто используются функции вида y = a^x, где a – заданное положительное число, x – переменная.
Такие функции называют показательными. Это название объясняется тем, что аргументом показательной функции является
показатель степени, а основанием степени — заданное число.

Определение. Показательной функцией называется функция вида y = a^x, где а — заданное число, a > 0, ( a neq 1)

Показательная функция обладает следующими свойствами

1) Область определения показательной функции — множество всех действительных чисел.
Это свойство следует из того, что степень a^x где a > 0, определена для всех действительных чисел x.

2) Множество значений показательной функции — множество всех положительных чисел.
Чтобы убедиться в этом, нужно показать, что уравнение a^x = b, где а > 0, ( a neq 1), не имеет корней,
если ( b leqslant 0), и имеет корень при любом b > 0.

3) Показательная функция у = a^x является возрастающей на множестве всех действительных чисел, если a > 1, и
убывающей, если 0 < a < 1.
Это следует из свойств степени (8) и (9)

Построим графики показательных функций у = a^x при a > 0 и при 0 < a < 1.

Использовав рассмотренные свойства отметим, что график функции у = a^x при a > 0 проходит через точку (0; 1) и
расположен выше оси Oх.
Если х < 0 и |х| увеличивается, то график быстро приближается к оси Oх (но не пересекает её).
Таким образом, ось Ох является горизонтальной асимптотой графика функции у = a^x при a > 0.
Если х > 0 и |х| увеличивается, то график быстро поднимается вверх.

График функции у = a^x при 0 < a < 1 также проходит через точку (0; 1) и расположен выше оси Ох.
Если х > 0 и увеличивается, то график быстро приближается к оси Ох (не пересекая её). Таким образом, ось Ох является
горизонтальной асимптотой графика.
Если х < 0 и |х| увеличивается, то график быстро поднимается вверх.

Показательные уравнения

Рассмотрим несколько примеров показательных уравнений, т.е. уравнений, в которых неизвестное содержится в показателе степени.
Решение показательных уравнений часто сводится к решению уравнения a^x = a^b где а > 0, ( a neq 1),
х — неизвестное. Это уравнение решается с помощью свойства степени: степени с одинаковым основанием а > 0, ( a neq 1) равны
тогда и только тогда, когда равны их показатели.

Решить уравнение 2^3x • 3^x = 576
Так как 2^3x = (2³)^x = 8^x, 576 = 24², то уравнение можно записать в виде
8^x • 3^x = 24², или в виде 24^x = 24², откуда х = 2.
Ответ х = 2

Решить уравнение 3^{х + 1} – 2 • 3^{x – 2} = 25
Вынося в левой части за скобки общий множитель 3^{х – 2}, получаем 3^{х – 2}(3³ – 2) = 25,
3^{х – 2} • 25 = 25,
откуда 3^{х – 2} = 1, x – 2 = 0, x = 2

Ответ х = 2

Решить уравнение 3^х = 7^х
Так как ( 7^x neq 0 ) , то уравнение можно записать в виде ( frac{3^x}{7^x} = 1 ), откуда ( left( frac{3}{7} right) ^x = 1 ), х = 0

Ответ х = 0

Решить уравнение 9^х – 4 • 3^х – 45 = 0
Заменой 3^х = t данное уравнение сводится к квадратному уравнению t² – 4t – 45 = 0. Решая это уравнение,
находим его корни: t₁ = 9, t₂ = -5, откуда 3^х = 9, 3^х = -5.
Уравнение 3^х = 9 имеет корень х = 2, а уравнение 3^х = -5 не имеет корней, так как показательная функция не
может принимать отрицательные значения.
Ответ х = 2

Решить уравнение 3 • 2^{х + 1} + 2 • 5^{x – 2} = 5^х + 2^{х – 2}
Запишем уравнение в виде
3 • 2^{х + 1} – 2^{x – 2} = 5^х – 2 • 5^{х – 2}, откуда
2^{х – 2} (3 • 2³ – 1) = 5^{х – 2}( 5 ² – 2 )
2^{х – 2} • 23 = 5^{х – 2}• 23
( left( frac{2}{5} right) ^{x-2} = 1 )
x – 2 = 0
Ответ х = 2

Решить уравнение 3^{|х – 1|} = 3^{|х + 3|}
Так как 3 > 0, ( 3 neq 1), то исходное уравнение равносильно уравнению |x-1| = |x+3|
Возводя это уравнение в квадрат, получаем его следствие (х – 1)² = (х + 3)², откуда
х² – 2х + 1 = х² + 6х + 9, 8x = -8, х = -1
Проверка показывает, что х = -1 — корень исходного уравнения.
Ответ х = -1

Источник

Запомните!

Уравнение — это равенство, содержащее букву, значение которой надо найти.

В уравнениях неизвестное обычно обозначается строчной латинской буквой. Чаще всего используют буквы
«x» [икс] и «y» [игрек].

Корень уравнения — это значение буквы, при котором из уравнения получается верное числовое равенство.
Решить уравнение — значит найти все его корни или убедиться, что корней нет.

Запомните!

Решив уравнение, всегда после ответа записываем проверку.

Информация для родителей

Уважаемые родители, обращаем ваше внимание на то, что в начальной школе и в 5 классе дети НЕ знают тему
«Отрицательные числа».

Поэтому они должны решать уравнения, используя только
свойства сложения, вычитания, умножения и деления. Методы решения уравнений для 5 класса приведены ниже.

Не пытайтесь объяснить решение уравнений через перенос чисел и букв
из одной части уравнения в другую с изменением знака.

Освежить знания по понятиям, связанным со сложением, вычитанием, умножением и делением вы можете в уроке
«Законы арифметики».

Решение уравнений на сложение и вычитание

Как найти неизвестное
слагаемое

x + 9 = 15

Как найти неизвестное
уменьшаемое

x − 14 = 2

Как найти неизвестное
вычитаемое

5 − x = 3

Чтобы найти неизвестное слагаемое, надо от суммы отнять известное слагаемое.

Чтобы найти неизвестное уменьшаемое, надо к разности прибавить вычитаемое.

Чтобы найти неизвестное вычитаемое, надо от уменьшаемого отнять разность.

x + 9 = 15
x = 15 − 9
x = 6

Проверка

6 + 9 = 15
15 = 15

x − 14 = 2
x = 14 + 2
x = 16

Проверка

16 − 2 = 14
14 = 14

5 − x = 3
x = 5 − 3
x = 2

Проверка

5 − 2 = 3
3 = 3

Решение уравнений на умножение и деление

Как найти неизвестный
множитель

y · 4 = 12

Как найти неизвестное
делимое

y : 7 = 2

Как найти неизвестный
делитель

8 : y = 4

Чтобы найти неизвестный множитель, надо произведение разделить на известный множитель.

Чтобы найти неизвестное делимое, надо частное умножить на делитель.

Чтобы найти неизвестный делитель, надо делимое разделить на частное.

y · 4 = 12
y = 12 : 4
y = 3

Проверка

3 · 4 = 12
12 = 12

y : 7 = 2
y = 2 · 7
y = 14

Проверка

14 : 7 = 2
2 = 2

8 : y = 4
y = 8 : 4
y = 2

Проверка

8 : 2 = 4
4 = 4

Ваши комментарии

Важно!

Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи

«ВКонтакте».

Оставить комментарий:

13 марта 2019 в 20:30

Mint Addict
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Mint Addict
Профиль
Благодарили: 0

Сообщений: 1

Составьте уравнение корни которого на 3 больше корней уравнения х² — 5х + 3 = 0

0
Спасибо thanks
Ответить

14 марта 2019 в 0:25
Ответ для Mint Addict

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

Эх, митрофанушка!
(x − 3)² − 5(x − 3) + 3 = 0.

0
Спасибо thanks
Ответить

25 марта 2017 в 19:12

Варя Соломахина
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Варя Соломахина
Профиль
Благодарили: 0

Сообщений: 2

Тема называется «Уравнения». Мне не понятно решение этих примеров, тесть уравнений. Помогите мне пожалуйста. Как их решать???
Например такой пример:
x+(x+5)=37
Решение

0
Спасибо thanks
Ответить

26 марта 2017 в 8:22
Ответ для Варя Соломахина

Руслан Лопатин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Руслан Лопатин
Профиль
Благодарили: 0

Сообщений: 1

х + х + 5=37
2х +5=37
2х=32
х=16

0
Спасибо thanks
Ответить

7 сентября 2016 в 21:53

Иван Баранов
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Иван Баранов
Профиль
Благодарили: 0

Сообщений: 3

решите уравнение ((х+2) · 81-3174): 21=34 используя теоремы о равносильности уравнений и правила тождественных преобразований

0
Спасибо thanks
Ответить

19 сентября 2016 в 15:11
Ответ для Иван Баранов

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

(x+2) · 81 ? 3174=714
(x+2) · 81 = 3000
x+2=
x=
x=
x=35

1
Спасибо thanks
Ответить

17 августа 2016 в 16:46

Александр Шаболтас
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Александр Шаболтас
Профиль
Благодарили: 0

Сообщений: 1

Здравствуйте, у меня возникают проблемы с решением подобных уравнений frown : (-3

) · (-2) =4 х ?

или

х=3. помогите пожалуйста

0
Спасибо thanks
Ответить

3 сентября 2016 в 19:46
Ответ для Александр Шаболтас

Юлия Анарметова
(^-^)
Профиль
Благодарили: 0

Сообщений: 11

(^-^)
Юлия Анарметова
Профиль
Благодарили: 0

Сообщений: 11

1 уравнение; умножим 1 часть чисел получим ( · =7) 7=4х-
7+ =4х
7 =4х
х= :4
х= =1.875
2 уравнение; х=3:
х= =10,5

0
Спасибо thanks
Ответить

15 августа 2016 в 22:24

Рустам Иманалиев
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Рустам Иманалиев
Профиль
Благодарили: 0

Сообщений: 1

Здравствуйте.Помогите пожалуйста решить такой пример.212*х=672.Учебник под общей редакцией Л. Катанина. Рабочая книга по математике для 4-го года обучения в начальной школе.Задание № 6. Счастливо!

0
Спасибо thanks
Ответить

19 сентября 2016 в 14:23
Ответ для Рустам Иманалиев

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

x=672: 212 = 3=3

0
Спасибо thanks
Ответить

3 августа 2016 в 23:32

Анастасия Ищенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анастасия Ищенко
Профиль
Благодарили: 0

Сообщений: 1

290093519 равно произвединию на 13

0
Спасибо thanks
Ответить

19 сентября 2016 в 14:20
Ответ для Анастасия Ищенко

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

290093519 = x · 13
x=290093519: 13
x=22314886
Уж не знаю, так ли понял задачу =)

0
Спасибо thanks
Ответить

28 марта 2016 в 21:37

Маша Берник
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Маша Берник
Профиль
Благодарили: 0

Сообщений: 1

4x-x=8.7

0
Спасибо thanks
Ответить

29 марта 2016 в 8:44
Ответ для Маша Берник

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

4x-x=8.7
3x=8,7
3x=87/10 |:3
x=87/30=29/10=2,9
проверка:
4*2,9-2,9=11,6-2,9=8,7
8,7=8,7

0
Спасибо thanks
Ответить

25 февраля 2016 в 19:40

Екатерина Богданова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Екатерина Богданова
Профиль
Благодарили: 0

Сообщений: 1

решить уравнения
1)??4х+2=-4
2)?4х+1=-4
решить неравенство
3)?х-1>2

0
Спасибо thanks
Ответить

26 февраля 2016 в 8:51
Ответ для Екатерина Богданова

Юрий Резник
(^-^)
Профиль
Благодарили: 0

Сообщений: 6

(^-^)
Юрий Резник
Профиль
Благодарили: 0

Сообщений: 6

Корень в 1) и 2) относится только к «4х», а в 3) к «х»? Или корень извлекается из всего выражения?

0
Спасибо thanks
Ответить

15 февраля 2016 в 16:41

Малика Ас?арова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Малика Ас?арова
Профиль
Благодарили: 0

Сообщений: 1

2(?-1)-3(?+2)<6(1+?)

0
Спасибо thanks
Ответить

20 февраля 2016 в 16:45
Ответ для Малика Ас?арова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

2x-2-3x-6<6+6x
-x-8<6+6x
7x>14
x>2

0
Спасибо thanks
Ответить

14 февраля 2016 в 14:28

Герман Волк
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Герман Волк
Профиль
Благодарили: 0

Сообщений: 2

(x:11) · 5 =110

0
Спасибо thanks
Ответить

20 февраля 2016 в 16:35
Ответ для Герман Волк

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

5x:55=110 | *55
275x=6050
x= 22

0
Спасибо thanks
Ответить

20 февраля 2016 в 20:24
Ответ для Герман Волк

Герман Волк
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Герман Волк
Профиль
Благодарили: 0

Сообщений: 2

Большое спасибо!

0
Спасибо thanks
Ответить

22 февраля 2016 в 2:06
Ответ для Герман Волк

Юрий Резник
(^-^)
Профиль
Благодарили: 0

Сообщений: 6

(^-^)
Юрий Резник
Профиль
Благодарили: 0

Сообщений: 6

А вот и нет!
Имеем:
· 5 = 110

Выражаем x:
x ·

= 110
x = 110 ·
x = 242

Проверим равенство исходного выражения:
(242: 11) · 5 = 110
(22) · 5 = 110
110 = 110

0
Спасибо thanks
Ответить

22 февраля 2016 в 8:49
Ответ для Герман Волк

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

И ведь не поспоришь, буду внимательнее!

0
Спасибо thanks
Ответить

18 января 2016 в 18:51

Эмиль Абасов
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Эмиль Абасов
Профиль
Благодарили: 0

Сообщений: 1

Пожалуйста, помогите с решением уравнений: Замените * одночленом так, чтобы получившееся равенство, было тождеством
(2,5a+3b)²=6,25a²+_*+9b²Упростите выражение:
а)(2x+6y)² — 24xy
б)b²+49-(b+7)²Представьте в виде многочлена выражение:
а)(x-6)²-x(x+8)
б)y(y-1)-(y-5)²Буду очень признателен за помощь в решении!!! Спасибо!

0
Спасибо thanks
Ответить

19 сентября 2016 в 11:23
Ответ для Эмиль Абасов

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

1) воспользуемся формулой квадрат суммы и раскроем скобки:
6,25a²+15ab+9b² — видим, что вместо * должно быть 15ab.
2) Раскрываем скобки при помощи тех же правил и приводим подобные:
а) 4x²+24xy+36y² ?24xy=4x² +36y²б)b²+49 ? b² ? 14b ? 49= ? 14b
3)Раскрываем скобки при помощи формулы квадрат разности и приводим подобные:
а)x² ? 12x + 36 ? x² ? 8x = 36 ? 20x
б)y² ? y ? y² +10y ?25=9y ?25

0
Спасибо thanks
Ответить

6 октября 2015 в 18:41

Юля Тулба
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Юля Тулба
Профиль
Благодарили: 0

Сообщений: 1

9x+28=2755

0
Спасибо thanks
Ответить

4 октября 2015 в 21:29

Анна Иложева
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Анна Иложева
Профиль
Благодарили: 0

Сообщений: 1

«сколько литров 23 градусной воды нужно смешать с 40 градусной водой чтобы получить 50 литров 37 градусной воды»

0
Спасибо thanks
Ответить

9 июня 2016 в 14:24
Ответ для Анна Иложева

Евгений Фёдоров
(^-^)
Профиль
Благодарили: 0

Сообщений: 60

(^-^)
Евгений Фёдоров
Профиль
Благодарили: 0

Сообщений: 60

23x + 40(50 ? x) = 50·37

0
Спасибо thanks
Ответить

21 сентября 2015 в 16:46

Камилла Назмутдинова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Камилла Назмутдинова
Профиль
Благодарили: 0

Сообщений: 1

собрали три карзины клубники в каждой по 10 кг и четыре карзины вишни по? кг сколько мджет быть кг в четырёх разных карзинах помагите пожалуйста cry у меня контрольная через четыри дня!

0
Спасибо thanks
Ответить

12 сентября 2016 в 11:23
Ответ для Камилла Назмутдинова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Предполагаю, что под знаком “?” кроется цифра «7».
Что сказано по условию? 3 корзины по 10 и 4 по 7. Какие варианты могут быть?
1) все корзины по 7 кг.
2) 1 корзина на 10 кг, 3 оставшиеся по 7 кг.
3) 2 корзины по 10кг, 2 корзины по 7 кг.
4) 3 корзины по 10кг, 1 корзина на 7кг.
Для получения количества кг в разных корзинах посчитаем:
1) 4 · 7 =28
2) 1 · 10 + 3 · 7 = 31
3) 2 · 10 + 2 · 7 = 34
4) 3 · 10 + 1 · 7 = 37

Убедительная просьба внимательно и полностью переписывать задачу. Невозможно ответить правильно на неправильную задачу.

0
Спасибо thanks
Ответить

6 сентября 2015 в 7:54

Андрей Шеин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Андрей Шеин
Профиль
Благодарили: 0

Сообщений: 1

Математика 4кл 1ч система школа <2100>автор Демидова, Козлова, Тонких. Стр 8 упр 5 как составить схему в виде отрезка и решение на эту задачу Если для разгадывания 3ребусов требуется 5минут, то сколько минут потребуется для разгадывания 9таких ребусов?(Будем считать, что каждый ребус разгадывается за одно и тоже время.) Составь и реши 3задачи, обратные даной.

0
Спасибо thanks
Ответить

2 сентября 2016 в 16:02
Ответ для Андрей Шеин

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Вычислим, сколько времени требуется на решение одного ребуса, для этого 5: 3=1 = . Для нахождения времени, затраченного на решение 9 таких ребусов, умножим количество ребусов на время для решения одного ребуса:
9 · = 15.
Примером задачи обратной данной может послужить например: Чтобы решить один ребус требуются 1 минута. Сколько потребуется, чтобы решить 5 ребусов?

0
Спасибо thanks
Ответить

5 сентября 2015 в 19:47

Диана Александрова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Диана Александрова
Профиль
Благодарили: 0

Сообщений: 1

Теплоход шёл 3,2ч по течению реки и 2,5ч против течения. Какой путь прошёл теплоход за всё это время, если его собственная скорость 28,8 км/ч, а скорость течения 2,2км/ч.
книга «Дидактические материалы по математике для 5 класса» А С.Чесноков, К.И.Нешков

0
Спасибо thanks
Ответить

2 сентября 2016 в 14:56
Ответ для Диана Александрова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Для определения пути, необходимо скорость умножить на время движения. Если теплоход идёт по течению, то к его скорости прибавляется скорость течения (течение несёт теплоход ускоряя его движение), а если против, то из его собственной скорости вычитается скорость реки. Для простоты и понимания обозначим
t₁-время движения по течению, t₂-время движения против течения, V₁-скорость теплохода, V₂-скорость реки, S₁-путь по течению, S₂-путь против течения, S — полный путь.
S = S₁+S₂=t₁_·(V₁ + V₂) + t₂ · (V₁ ? V₂)
S = 3,2 · (28,8 +2,2) + 2,5 · (28,8 ? 2,2) = 3,2 · 31 + 2,5 · 26,6 =99,2 + 66,5 = 165,7

Ответ: 165,7 км — общий путь катера.

Стоит отметить, что если речь идёт о пройденном расстоянии, то расчет производится по этой формуле. Если же мы говорим о расстоянии относительно начально точки, то следует вычислить разность между путём пройденым по течению и против. Т.к. путь против реки проходил назад, т.е. к первоначальной точки отплытия.

0
Спасибо thanks
Ответить

5 сентября 2015 в 12:52

Даниил Довгань
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Даниил Довгань
Профиль
Благодарили: 0

Сообщений: 1

5x?=25x

0
Спасибо thanks
Ответить

16 сентября 2015 в 19:51
Ответ для Даниил Довгань

Никита Семеренко
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Никита Семеренко
Профиль
Благодарили: 0

Сообщений: 2

X=5

0
Спасибо thanks
Ответить

16 августа 2015 в 11:36

Ольга Мартынова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Ольга Мартынова
Профиль
Благодарили: 0

Сообщений: 1

Помогите решить задачу. «Летние упражнения на каждый день. Я иду во 2 класс» автор — Ефимова И.В. Изд-во «Ранок». Задача на стр. 77. Реши задачу, воспользовавшись схемой. Игорь и Оля собирали грибы. Вместе они нашли на 4 гриба больше, чем нашел Игорь, и на 6 грибов больше, чем нашла Оля. Сколько грибов нашел каждый?

0
Спасибо thanks
Ответить

2 августа 2016 в 16:21
Ответ для Ольга Мартынова

Alex Feel
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Alex Feel
Профиль
Благодарили: 0

Сообщений: 1

И+О=И+4
О=4

И+О=6+О
И=6

О-Оля
И- Игорь

0
Спасибо thanks
Ответить

9 июля 2015 в 21:01

Дмитрий Рыжков
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Дмитрий Рыжков
Профиль
Благодарили: 0

Сообщений: 2

как обычно такой бред у вас что нето что школьник а взрослый непоймет-вот в теме(как найти уменьшаемое) смотрите у вас написано x ? 14 = 2 ; x = 14 + 2 ; x = 16 ; проверка:16 ? 2 = 14 ;14 = 14 и почему же в нахождении слагаемого и вычитаемого мы из слагаемого отнимаем второе слагаемое а тут почему-то отнимаем ответ сам, что это???

0
Спасибо thanks
Ответить

12 июля 2015 в 12:05
Ответ для Дмитрий Рыжков

Александр Середа-Четверг
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Александр Середа-Четверг
Профиль
Благодарили: 0

Сообщений: 1

Все правильно!

0
Спасибо thanks
Ответить

12 июля 2015 в 13:43
Ответ для Дмитрий Рыжков

Борис Гуров
(^-^)
Профиль
Благодарили: 1

Сообщений: 27

(^-^)
Борис Гуров
Профиль
Благодарили: 1

Сообщений: 27

Здравствуйте, Дмитрий.

Пожалуйста, разъясните еще раз, в чем Вы видите ошибку в уроке?

0
Спасибо thanks
Ответить

12 июля 2015 в 13:49
Ответ для Дмитрий Рыжков

Борис Гуров
(^-^)
Профиль
Благодарили: 1

Сообщений: 27

(^-^)
Борис Гуров
Профиль
Благодарили: 1

Сообщений: 27

Александр, спасибо, что принимаете участие в поиске ошибок и неточностей на нашем сайте.

На нашем сайте стоит задача: сделать максимально понятный и полезный ресурс для молодежи. Поэтому все диалоги по замечаниям к нашему интернет ресурсу внимательно изучаются.

Единственная просьба — это соблюдать нормы общения, а также уважать собеседника.

Сообщения на форуме читают также дети, поэтому вдвойне важно послужить примером уважительного и грамотного общения.

0
Спасибо thanks
Ответить

14 мая 2015 в 16:13

Дарья Белова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дарья Белова
Профиль
Благодарили: 0

Сообщений: 1

0
Спасибо thanks
Ответить

14 мая 2015 в 21:54
Ответ для Дарья Белова

Ярик Кравченко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Ярик Кравченко
Профиль
Благодарили: 0

Сообщений: 3

3.472

0
Спасибо thanks
Ответить

11 мая 2015 в 19:04

Алла Лучанинова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Алла Лучанинова
Профиль
Благодарили: 0

Сообщений: 2

Помогите решить уравнение

0
Спасибо thanks
Ответить

17 апреля 2016 в 16:02
Ответ для Алла Лучанинова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

(7-y) · 9=6 · 5
63-9y=30
-9y=-33
y=3=3
Проверка:

(7-3

) · 9 = 6 · 5
3 · 9 = 30
· 9 = 30
=30
30=30
Ответ: y=3

0
Спасибо thanks
Ответить

7 мая 2015 в 17:49

Мелани Ларикова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Мелани Ларикова
Профиль
Благодарили: 0

Сообщений: 2

помогите решить уравнение (пож) очень срочно! :
3,7y-2,5y+1,4y=3.38

0
Спасибо thanks
Ответить

11 мая 2015 в 16:43
Ответ для Мелани Ларикова

Алина Музычук
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Алина Музычук
Профиль
Благодарили: 0

Сообщений: 1

2.6 · 3y=3.38
3y=3.38 :2.6
3y=1.3
y=1.3 :3
y=

0
Спасибо thanks
Ответить

7 мая 2015 в 16:31

Мелани Ларикова
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Мелани Ларикова
Профиль
Благодарили: 0

Сообщений: 2

3,7y-2,5y+1,4y=3,38

0
Спасибо thanks
Ответить

9 мая 2015 в 8:31
Ответ для Мелани Ларикова

Аруна Аубакирова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Аруна Аубакирова
Профиль
Благодарили: 0

Сообщений: 1

3,7y-2,5y+1,4y=3,38
1,2y+1,4y=3,38
2,6y = 3,38
y = 3,38: 2,6
y = 1,3
Ответ:1,3

0
Спасибо thanks
Ответить

12 мая 2015 в 20:11
Ответ для Мелани Ларикова

Lena Derevianko
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Lena Derevianko
Профиль
Благодарили: 0

Сообщений: 1

kiss kiss

0
Спасибо thanks
Ответить

6 мая 2015 в 16:56

Егор Бебенин
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Егор Бебенин
Профиль
Благодарили: 0

Сообщений: 1

2x^2₊3x-3=x²-3x + ( ? 2 + x²)

0
Спасибо thanks
Ответить

16 апреля 2016 в 8:55
Ответ для Егор Бебенин

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Не ясно, для чего скобки в уравнении, но если нет ошибки, то решение такое:
2x²+3x-3=x²-3x-2+x²
2x²+3x-3-2x²+3x+2=0
6x=1
x=

0
Спасибо thanks
Ответить

5 мая 2015 в 19:45

Дарья Каспарьян
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Дарья Каспарьян
Профиль
Благодарили: 0

Сообщений: 1

ПОЖАЛУЙСТО РЕШИТИ УРАВНЕНИЕ
51,912:x+0,320=1,351
ЧЕМУ РАВЕН x РЕШИТЕ УМАЛЯЮ МНЕ НА ЗАВТРО ННУЖНО ПРИШЛА СО ШКОЛЫ УСТАЛА КТО РЕШИТ БЛАГОДАРНА ОЧЕНЬ ПЛИЗ РЕШИТЕ!!!!!! cry

0
Спасибо thanks
Ответить

15 апреля 2016 в 15:57
Ответ для Дарья Каспарьян

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

Понимаю, что поздно уже, но всё же:
51,912: Х + 0,32 = 1,351
51,912: Х=1,351-0,32
51,912: Х=1,031
Х?0
51,912=1,031Х
Х=51,912:1,031
Х=50.3511154219
Проверка:51.912/50.3511154219 + 0.32 = 1,351
1,351=1,351
Ответ: Х=50.3511154219

0
Спасибо thanks
Ответить

22 апреля 2015 в 15:00

Элана Золотова
(^-^)
Профиль
Благодарили: 0

Сообщений: 1

(^-^)
Элана Золотова
Профиль
Благодарили: 0

Сообщений: 1

x · 8 ? 4: 6 · 7 + 16=60 помогите решить уравнение

0
Спасибо thanks
Ответить

14 апреля 2016 в 13:51
Ответ для Элана Золотова

Евгений Колосов
(^-^)
Профиль
Благодарили: 12

Сообщений: 197

(^-^)
Евгений Колосов
Профиль
Благодарили: 12

Сообщений: 197

8 · x ? 4: 6 · 7 + 16=60
8 · x=60 ?16 +4 :6 · 7
8 · x=44+
8 · x=44 +
8 · x=44 8 · x=
x=
x=
x=
x=6
Проверка:
8 · ? +16= ? + 16= +16=44+16=60
60=60
Ответ: х=6

0
Спасибо thanks
Ответить

21 апреля 2015 в 15:00

Анюта Корниенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Анюта Корниенко
Профиль
Благодарили: 0

Сообщений: 3

х+256=958 и х+427=15698 помогите ( решение уровнений расписать надо )

0
Спасибо thanks
Ответить

21 апреля 2015 в 15:08
Ответ для Анюта Корниенко

Анюта Корниенко
(^-^)
Профиль
Благодарили: 0

Сообщений: 3

(^-^)
Анюта Корниенко
Профиль
Благодарили: 0

Сообщений: 3

срочно

0
Спасибо thanks
Ответить

21 апреля 2015 в 15:24
Ответ для Анюта Корниенко

Алина Гимадеева
(^-^)
Профиль
Благодарили: 0

Сообщений: 2

(^-^)
Алина Гимадеева
Профиль
Благодарили: 0

Сообщений: 2

х + 256 =958
х= 958 -256
х= 702
702 + 256=958

х+427 = 15698
х= 15698-427
х= 15271
15271+427=15698
вот smile

0
Спасибо thanks
Ответить

Источник

Калькулятор уравнений

Урок 17 Бесплатно Уравнение

Уравнения

Памятка : «Решение уравнений», 5 класс

Дистанционное обучение как современный формат преподавания

Математика: теория и методика преподавания в образовательной организации

Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО

Дистанционные курсы для педагогов

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

Материал подходит для УМК

Другие материалы

Вам будут интересны эти курсы:

Оставьте свой комментарий

Автор материала

Дистанционные курсы для педагогов

Подарочные сертификаты

Приемы решения уравнений в 5-6 классах статья по алгебре (5 класс) на тему

Скачать:

Предварительный просмотр:

Немного теории.

Информация для родителей

Решение уравнений на сложение и вычитание

Решение уравнений на умножение и деление

Ваши комментарии

Вам также может понравиться

Нет цены иска как исправить

Как составить историю бизнеса

Фоллаут 4 как найти ядерные блоки

Добавить комментарий Отменить ответ

Дистанционные курсы
для педагогов

Приемы решения уравнений в 5-6 классах
статья по алгебре (5 класс) на тему