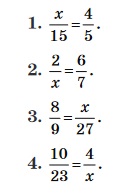Некоторые линейные уравнения имеют вид, который сильно напоминает обыкновенную пропорцию.
Например, рассмотрим такое уравнение.
Для решения уравнения с пропорцией используют правило пропорции или,
как его называют по-другому, правило креста.
Подробно понятие пропорции мы рассматривали в уроке
«Пропорции».
В этом уроке мы вспомним только основные моменты необходимые для решения уравнений с пропорцией.
Правило пропорции или правило креста
Запомните!
Произведение крайних членов пропорции равно произведению средних.
По-другому сформулировать правило выше можно так: если нарисовать крест поверх пропорции,
то произведения членов пропорции, которые лежат на концах креста, равны .
Вернемся к нашему уравнению. Решим его, использую правило пропорции.
Нарисуем поверх пропорции крест.
Теперь по правилу пропорции (правило креста) запишем пропорцию
в виде равенства произведений крайних и средних членов пропорции.
Вспомним правило деления и
решим уравнение до конца.
В ответе не забудем выделить целую часть у дроби.
Рассмотрим другой пример уравнения с пропорцией.
Такое уравнение также решается с помощью правила пропорции.
Важно!
Если в члене пропорции присутствуют знаки «+» или «−»,
обязательно заключайте этот член пропорции в скобки перед использованием правила пропорции.
Если вы не заключите в скобки такой член пропорции, то с большей вероятностью сделаете ошибку, когда
будете использовать правило пропорции.
После заключения в скобки члена пропорции «(2 − x)» используем правило пропорции
для дальнейшего решения.
Теперь раскроем скобки с помощью
правила раскрытия
скобок.
Из урока «Решение линейных уравнений» используем
правило переноса и
правило деления для уравнений.
Не забудем при делении на отрицательное число, использовать
правило знаков.
Иногда уравнения с пропорцией могут быть представлены следующим образом:
Чтобы было проще использовать правило пропорции (правило креста) нужно записать исходное уравнение,
в общем для пропорции виде.
Для этого нужно вспомнить, что знак деления «:» можно заменить на дробную черту.
Другие примеры решения уравнений с пропорцией
-
=
18 · x = 6 · 3x
18x = 18x
18x − 18x = 0
0 = 0
Ответ: x — любое число
-
=
3x · 6,8 = 0,21 · 1,7
20,4 x=
·
20
x =
=204x · 1000 = 21 · 17 · 10 |:(204 · 1000)
x =
x =
x =
x =
x =
Ответ: x =
Ваши комментарии
Важно!
Чтобы оставить комментарий, вам нужно войти на наш сайт при помощи
«ВКонтакте».

Оставить комментарий:
Математика
6 класс
Урок № 5
Пропорции
Перечень рассматриваемых вопросов:
- Понятие пропорции.
- Основное свойство пропорции.
- Как правильно составить пропорцию.
- Как найти неизвестный член пропорции.
Тезаурус
Равенство двух отношений называют пропорцией.
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Основная литература
- Никольский С. М. Математика. 6 класс. Учебник для общеобразовательных учреждений // С. М. Никольский, М. К. Потапов, Н. Н. Решетников и др. — М.: Просвещение, 2017. — 258 с.
Дополнительная литература
- Чулков П. В. Математика: тематические тесты. 5-6 кл. // П. В. Чулков, Е. Ф. Шершнёв, О. Ф. Зарапина — М.: Просвещение, 2009. — 142 с.
- Шарыгин И. Ф. Задачи на смекалку: 5-6 кл. // И. Ф. Шарыгин, А. В. Шевкин — М.: Просвещение, 2014. — 95 с.
Теоретический материал для самостоятельного изучения
Основное свойство пропорции: произведение крайних членов пропорции равно произведению её средних членов.
Если один член пропорции неизвестен и необходимо его определить, то говорят, что нужно решить пропорцию.
Рассмотрим 3 способа нахождения неизвестного члена пропорции.
1 способ.
2 способ.
Способ 3.
Задача.
Решение:
Ответ:
1) можно;
2) можно;
3) нельзя;
4) нельзя.
Разбор решения заданий тренировочного модуля
№1. Тип задания: сортировка элементов по категориям.
№2. Тип задания: Подстановка элементов в пропуски в тексте.
Найдите неизвестный член пропорции.
Для нахождения неизвестного члена пропорции воспользуемся основным свойством пропорции, из которого следует: чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Ответ: 3.
Рассмотрим решение пропорций на конкретных примерах.
Решить уравнения с пропорцией:
1) 25 : x = 10 : 18
Здесь x — неизвестный средний член пропорции. Чтобы найти неизвестный средний член пропорции, произведение крайних членов разделим на известный средний член:
25 и 10 сокращаем на 5. Затем 18 и 2 сокращаем на 2.
Ответ: 45.
Здесь y — неизвестный крайний член пропорции. Чтобы найти неизвестный крайний член пропорции, произведение средних членов делим на известный крайний член:
Ответ: 13,5.
При решении пропорций с десятичными дробями удобно для упрощения вычислений использовать основное свойство дроби.
Чтобы найти неизвестный средний член пропорции, произведение крайних членов делим на известный средний член пропорции:
В числителе после запятой в общей сложности два знака, в знаменателе — один. Поэтому, умножив и числитель, и знаменатель на 100, мы получим дробь, равную данной. В числителе умножение на 100 распределим так: каждый из множителей умножим на 10. В знаменателе 0,6 умножим на 10 и результат умножим на 10:
Сокращаем 24 и 6 на 6, 10 и 45 — на 5:
Еще раз сокращаем 4 и 2 на 2:
Ответ: 18.
Решение пропорций с обыкновенными дробями и смешанными числами удобнее записывать в строчку.
Чтобы найти неизвестный крайний член пропорции, произведение средних членов разделим на известный крайний член:
Смешанные числа переводим в неправильные дроби:
Ответ: 28.
При решении более сложных пропорций удобно использовать непосредственно основное свойство пропорции.
Произведение крайних членов пропорции равно произведению средних членов:
Здесь удобно упростить уравнение, разделив обе части на 5:
Ответ: 10,5.
Произведение крайних членов пропорции равно произведению ее средних членов:
Для упрощения вычислений удобно умножить каждую часть уравнения на 10:
Это — линейное уравнение. Неизвестные — в одну сторону, известные — в другую, изменив при этом их знаки:
Обе части уравнения делим на число, стоящее перед иксом:
Ответ: 1,12.
Составление и решение пропорций в математике
Пропорции — что это в математике
Валя съела 3 яблока из пяти. Какую часть яблок съела Валя?
Вначале узнаем, какую часть яблок составляет 1 яблоко. Всего у Вали было 5 яблок, значит, одно из них — это 1 5 часть всех яблок. Тогда 3 съеденных яблока составляют 3 5 всех яблок.
Тот же ответ получим, если 3 разделим на пять.
Получается, что 3 яблока соотносятся с пятью яблоками как 3 к 5.
Другой вариант записи ответа отмечают в виде десятичной дроби и процентов: 3 5 = 0 , 6 или 60%.
Отношением двух чисел называют частное этих чисел.
Отношение показывает, во сколько раз одно число больше другого. Или какую часть первое число составляет от второго.
Термин «отношение» применяют в случаях, когда нужно выразить одну величину в долях другой. Например, одну площадь в долях другой площади. Это операцию выполняют с помощью деления.
Делимое в выражении отношения называют предыдущим членом. Делитель называют последующим членом.
В задаче 1 предыдущий член — это 3, последующий — 5.
Если есть два равных отношения, то они образуют пропорцию.
Пропорцией называют равенство двух отношений.
Даны два отношения: 3,8:2 и 5,7:3.
Можно ли составить из этих выражений пропорцию?
Найдем значения каждого из отношений:
3 , 8 : 2 = 1 , 9 ; 5 , 7 : 3 = 1 , 9 .
Значения выражений оказались равными, значит, эти отношения равны.
Тогда можно записать равенство: 3,8:2=5,7:3.
Такое равенство называется пропорцией.
Ответ: да, можно составить из этих отношений чисел пропорцию.
С помощью буквенных символов пропорцию можно записать так: a : b = c : d или a b = c d .
Полученное равенство читают: «Отношение a к b равно отношению c к d» или «a относится к b, как c относится к d».
Числа a и d в пропорции называют крайними членами пропорции.
Числа b и c — средними членами пропорции.
Назовите крайние и средние члены пропорции 42:6=49:7.
Крайние члены пропорции — 42 и 7.
Средние члены пропорции — 6 и 49.
Определите средние члены пропорции 25 5 = 35 7 .
Средние члены пропорции — 5 и 35.
Понятие «пропорция» пришло из латинского языка. Слово в переводе означает соразмерность, определенное соотношение частей между собой.
Основное свойство пропорции, правило
Основное свойство пропорции
В верной пропорции произведение крайних членов равно произведению средних членов:
Определите, верна ли пропорция 6:2=9:3.
В верной пропорции произведение крайних членов равно произведению средних членов.
Произведение крайних членов равно произведению 6 и 3. Получим 6 * 3 = 18 .
Произведение средних членов равно произведению 2 и 9. Получим 2 * 9 = 18 .
Значит, 6:2=9:3. Пропорция верна.
Обратное утверждение тоже верно:
Если произведение средних членов равно произведению крайних членов, то пропорция верна.
Пропорция 60:12=10:2 верна, потому что 60 * 2 = 12 * 10 = 120 .
Если поменять в это пропорции местами средние члены, получим 60:10=12:2. Эта пропорция тоже верна. При перестановке произведение крайних и средних членов не изменилось.
Если в пропорции поменять крайние члены — 2:10=12:60, то произведение тоже не изменится.
Пропорция будет верной, если поменять местами средние члены или крайние члены.
Если какой-то из членов пропорции неизвестен, то его можно найти.
По основному свойству пропорции можно найти ее неизвестный член, если все остальные компоненты известны.
Найдите неизвестный член пропорции: 4,8:b=8:2,5.
Используем основное свойство пропорции: произведение крайних членов = произведению средних членов.
Получим 4 , 8 * 2 , 5 = b * 8 .
b = 4 , 8 * 2 , 5 : 8 ;
Составление и решение пропорций
Запишите пропорцию: 6 так относится к 18, как 9 относится к 27.
Слово «относится» заменяем на знак деления.
Получаем два отношения: 6:18 и 9:27.
Если эти два отношения равны, то получаем верную пропорцию.
6 : 18 = 9 : 27 ; 1 3 = 1 3 , получили верную пропорцию.
Запишите пропорцию и проверьте ее: отношение 2 к 1 4 равно отношению 3 к 1 15 .
Записываем отношения: 2 1 4 и 3 1 15 .
Составляем пропорцию: 2 1 4 = 3 1 15 .
Проверяем, верна ли пропорция.
Для этого воспользуемся основным свойством пропорции: произведение крайних членов = произведению средних членов.
2 * 1 15 ≠ 1 4 * 3 ; 2 15 ≠ 3 4 . Условие равенства произведений не выполнилось, значит, пропорция не верна.
Определите, верна ли пропорция: 1 , 4 0 , 7 = 3 , 4 1 , 7 .
Чтобы проверить, верна ли пропорция, воспользуемся основным свойством пропорции.
Запишем произведения крайних и средних членов пропорции:
1 , 4 * 1 , 7 = 2 , 38 ; 0 , 7 * 3 , 4 = 2 , 38 .
Значит, произведение крайних членов равно произведению средних членов.
1 , 4 * 1 , 7 = 0 , 7 * 3 , 4 ; 2 , 38 = 2 , 38 .
Вывод: пропорция верна.
Примеры уравнений с решением для 6 класса
Решите уравнение: 8 , 8 4 2 5 = n 0 , 12 .
Чтобы найти неизвестный член пропорции, используем основное свойство пропорции. Находим произведение крайних и средних членов. Выражаем неизвестный компонент.
8 , 8 4 2 5 = n 0 , 12 ; 8 , 8 * 0 , 12 = 4 2 5 * n . Из равенства выражаем n : n = 8 , 8 * 0 , 12 4 2 5 Представим смешанное число 4 2 5 в виде десятичной дроби. Для этого приведем дробную часть смешанного числа к дроби со знаменателем 10 : домножим числитель и знаменатель 2 . 4 2 5 = 4 2 * 2 н а 5 * 2 = 4 4 10 . Такое смешанное число записываем в виде десятичной дроби, отделяя целую часть запятой: 4 4 10 = 4 , 4 . Тогда n = 8 , 8 * 0 , 12 4 , 4 . Сокращаем получившуюся дробь: 0 , 12 и 4 , 4 делятся на 4 . n = 8 , 8 * 0 , 03 1 , 1 ; 8 , 8 и 1 , 1 делятся на 1 , 1 . n = 8 * 0 , 03 1 ; n = 0 , 24 .
Найдите неизвестный член пропорции: 1 1 2 : 2 1 4 = 6 : m .
Используем основное свойство пропорций. Записываем равенства произведений крайних и средних членов.
1 1 2 * m = 2 1 4 * 6 . И выражаем m : m = 2 1 4 * 6 : 1 1 2 . Переводим смешанные числа в неправильные дроби: m = 2 * 4 + 1 4 * 6 : 1 * 2 + 1 2 ; m = 9 4 * 6 : 3 2 . Натуральное число переводим в обыкновенную дробь со знаменателем 1 и умножаем на первую дробь: m = 9 4 * 6 1 : 3 2 ; m = 9 * 6 4 * 1 : 3 2 . Чтобы разделить обыкновенные дроби, нужно домножить дробь на взаимно обратную данной: m = 9 * 6 4 * 1 * 2 3 ; m = 9 * 6 * 2 4 * 1 * 3 . Сокращаем получившееся выражение. 4 и 2 делятся нацело на 2 . 9 и 3 делятся нацело на 3 . m = 3 * 6 * 1 2 * 1 * 1 . Для чисел 6 и 2 общий делитель 2 : m = 3 * 3 * 1 1 * 1 * 1 ; m = 9 .
Решите уравнение: 0,25:x=3,75:3.
По основному свойству пропорции получим: 0 , 25 * 3 = x * 3 , 75 .
x = 0 , 25 * 3 : 3 , 75 ; x = 0 , 75 : 3 , 75 . Делить на десятичную дробь нельзя. Преобразуем ее в натуральное число.
После запятой в дроби 3 , 75 два знака, значит, нужно домножить ее на единицу с таким оличеством нулей. Это сто.
Но чтобы выражение осталось неизменным, нужно домножить на сто и делимое.
x = 0 , 75 * 100 : 3 , 75 * 100 ; x = 75 : 375 ; x = 0 , 2 .
Найдите неизвестное: k : 3 1 2 = 0 , 4 : 2 4 5
Чтобы найти неизвестный компонент пропорции, нужно воспользоваться основным свойством дроби.
По основному свойству дроби произведение крайних членов равно произведению средних членов.
Получим: k * 2 4 5 = 3 1 2 * 0 , 4 .
Выразим k : k = 3 1 2 * 0 , 4 : 2 4 5 .
Переведем 0,4 в обыкновенную дробь: 0 , 4 = 4 10 . Эта дробь сократима: числитель и знаменатель делятся на 2 нацело: 4 10 = 4 : 2 10 : 2 = 2 5 .
Записываем полученное выражение:
k = 3 1 2 * 2 5 : 2 4 5 .
1 действие — умножение.
Переводим смешанное число в неправильную дробь и умножаем на вторую: числитель на числитель, знаменатель на знаменатель.
3 1 2 * 2 5 = 3 * 2 + 1 2 * 2 5 = 7 2 * 2 5 = 7 * 2 2 * 5 .
Сокращаем дробь: есть одинаковые числа в числителе и знаменателе.
2 действие — деление.
Теперь делим полученное число на 2 4 5 .
Смешанное число переводим в неправильную дробь.
Умножаем 7 5 на взаимно обратную дробь.
7 5 : 2 4 5 = 7 5 : 2 * 5 + 4 5 = 7 5 : 14 5 = 7 5 * 5 14 = 7 * 5 5 * 14 = 7 * 5 5 * 14 = 7 14 = 1 2 = 0 , 5 .
Урок 22 Бесплатно Пропорции
Чтобы узнать название темы урока, обратите внимание на картинку.
Попробуйте отгадать ребус.
На этом уроке вы узнаете, что называют пропорцией, выведете основное свойство пропорции и с помощью него научитесь решать задачи и уравнения.
Слово «пропорция» (proportio) в переводе с латинского – соразмерность, отношение частей (соотношение).
Пропорция
В IV веке до н.э. древнегреческий математик Евдокс Книдский дал определение пропорции, состоящей из величин любой природы, а не только из натуральных величин.
Пропорции применяли с древности при решении различных задач.
Древние греки использовали пропорцию и ее свойство для строительства сооружений, при создании произведений искусства (скульптуры, статуи), в ремесленническом деле и др.
Соблюдение пропорций, определенных соотношений, активно используется и в настоящее время в архитектуре, искусстве, музыке, при решении физических задач.
В географии и моделировании пропорциональные зависимости применяют при создании уменьшенной копии реального объекта.
В швейных технологиях – для изменения размеров выкройки изделия до нужного размера.
В химии для проведения успешной реакции рассчитывают пропорциональное отношение химических веществ.
В медицине и фармацевтике используют пропорции при изготовлении лекарственных препаратов.
В кулинарии, например, с помощью пропорции можно рассчитать рецепт одного и того же блюда для разного количества гостей.
Разберем, что же такое пропорция в математическом понимании.
Возьмем два отношения: (mathbf<frac<36><9>>) и (mathbf<frac<12><3>>) и эти отношения равны, так как (mathbf<36div9=4>) и (mathbf<12div3=4>), значит (mathbf<frac<36><9>= frac<12><3>>)
Равенство двух отношений называют пропорцией.
С помощью букв запишем пропорцию из двух отношений так: (mathbf) или (mathbf<frac= frac>).
Эту математическую запись читают так: «Отношение a к b равно отношению c к d» или «a так относится к b, как c относится к d».
Все члены пропорции не равны нулю: (mathbf).
Числа a и d называют крайними членами пропорции.
Числа b и c называют средними членами пропорции.
У меня есть дополнительная информация к этой части урока!
В мире существует «золотая пропорция», которую называют «золотым сечением». Это пропорциональное деление отрезка на различные по размеру части, но в таком соотношении к друг другу, что меньший отрезок так относится к большему, как больший ко всей величине.
Приблизительное значение «золотого сечения» равно 1,618… Число это продолжается бесконечно после запятой, и оно не периодично.
В процентном выражении целая часть относится к большей, как большая к меньшей, примерно так: 62% и 38% соответственно.
Обозначают число «золотого сечения» математической буквой (mathbf<varphi>) (фи).
Мир живой и неживой природы, мир творений человека полон красоты, симметрии и гармонии. Этот мир описывается законом «золотого сечения».
Рассмотрим только несколько примеров, где присутствует и используется правило «золотого сечения».
Считается, что длина фаланг пальцев и длина кисти руки, средний палец и мизинец, или высота лица и расстояние от кончика подбородка до центральной точки соединения губ у пропорционального человека находятся в определенных отношениях, соответствуя правилу «золотого сечения».
Форма тела ящериц, стрекоз, бабочек соответствует закону «золотого сечения»: отношение грудной и брюшной части тела приближенно равны значению «золотого сечения».
Спиралевидная форма ракушек тоже описывается числом (mathbf<varphi>) (фи).
«Золотая пропорция» была обнаружена в египетских пирамидах, произведениях искусства, архитектуре и применяется до сих пор в разных областях жизни человека
Пройти тест и получить оценку можно после входа или регистрации
Как решать пропорции – правила, методы и примеры вычислений
Общие сведения
Изучение какого-либо термина в математике начинается с определения. Пропорцией вида x / y = v / z (x: y = v: z) называется равенство отношений двух чисел. Она представлена в виде правильной дроби, и состоит из следующих элементов, которые называются крайними (x и z) и средними (y и v) членами.
Следует отметить, что в некоторых сферах пропорциональная зависимость может быть представлена в немного другом виде. В этом случае знак равенства не указывается. Для удобства используется символ деления «:». Записывается в таком виде: a: b: c. Объяснение такой записи очень простое: для приготовления какого-либо вещества нужно использовать «а» частей одного компонента, b — другого и с — третьего.
Знак равенства не имеет смысла указывать, поскольку этот тип пропорциональной зависимости является абстрактным. Неизвестно, какой результат получится на выходе. Если взять за единицу измерения массу в кг, то и конечный результат получится в кг. В этом случае решать пропорцию не нужно — достаточно просто подставить данные, и получить результат.
Бывают случаи, когда следует посчитать пропорцию в процентах. Пример — осуществление некоторых финансовых операций.
Сферы применения
Пропорция получила широкое применение в физике, алгебре, геометрии, высшей и прикладной математике, химии, кулинарии, фармацевтике, медицине, строительстве и т. д. Однако ее нужно применять только в том случае, когда элементы соотношения не подчиняются какому-либо закону (методика исследования величин такого типа будет рассмотрена ниже), и не являются неравенствами.
В алгебре существует класс уравнений, представленных в виде пропорции. Они бывают простыми и сложными. Для решения последних существует определенный алгоритм. Кроме того, в геометрии встречается такие термин, как «гомотетия» или коэффициент подобия. Он показывает, во сколько раз увеличена или уменьшена фигура относительно оригинала.
Масштаб в географии является также пропорцией, поскольку он показывает количество см или мм, которые содержатся в какой-либо единице, зависящей от карты (например, в 1 см = 10 км). Специалисты применяютправило пропорции в высшей и прикладной математике. Расчет количества реактивов, вступающих в реакцию, для получения другого вещества применяется также пропорциональная зависимость.
Каждая хозяйка также применяет это соотношение для приготовления различных блюд и консерваций. В этом случае пропорция имеет немного другой вид: 1:2. Все компоненты берутся частями с одинаковыми размерностями или единицами измерения. Например, на 1 кг клубники необходимо 2 кг сахара. Расшифровывается такое соотношение следующим образом: 1 часть одного и 2 части другого компонентов.
В фармацевтике она также применяется, поскольку необходимо очень точно рассчитать массовую долю для каждого компонента лекарственного препарата. В медицине используется пропорциональная зависимость для назначения лекарства больному, дозировка которого зависит от массы тела человека.
Для приготовления различных строительных смесей она также используется, однако у нее такой же вид, как и для кулинарии. Например, для приготовления бетона М300 необходимы такие компоненты: цемент (Ц), щебень (Щ), песок (П) и вода (В). Далее следует воспользоваться таким соотношением, в котором единицей измерения является ведро: 1: 5: 3: 0,5. Запись расшифровывается следующим образом: для приготовления бетонной смеси необходимо 1 ведро цемента, 5 щебня, 3 песка и 0,5 воды.
Основные свойства
Для решения различных задач нужно знать основные свойства пропорции. Они действуют только для соотношения x / y = v / z. К ним можно отнести следующие формулы:
- Обращение или обратное пропорциональное соотношение: [x / y = v / z] = [y / x = z / v].
- Перемножение «крест-накрест»: x * z = y * v.
- Перестановка: x / v = y / z и v / x = z / y.
- Увеличение или уменьшение: x + у / y = v + z / z и x — у / y = v — z / z.
- Составление через арифметические операции сложения и вычитания: (x + v) / (y + z) = x / y = v / z и (x — v) / (y — z) = x / y = v / z.
Первое свойство позволяет перевернуть правильные дроби соотношений двух величин. Это следует делать одновременно для левой и правой частей. Умножение по типу «крест-накрест» считается главным соотношением. С помощью его решаются уравнения и упрощаются выражения, в которых нужно избавиться от дробных частей. Найти неизвестный член пропорции можно также с помощью второго свойства, формулировка которого следующая: произведение крайних эквивалентно произведению средних элементов (членов).
Очень часто члены соотношения необходимо переставить для оптимизации вычислений. Для этого применяется свойство перестановки. При этом следует внимательно подставлять значения в формулу, поскольку неправильные действия могут существенно исказить результат решения. Этого можно не заметить. Для осуществления проверки следует подставить значение неизвестной в исходную пропорцию. Если равенство соблюдается, то получен верный результат. В противном случае необходимо найти ошибку или повторить вычисления.
Увеличение или уменьшение пропорции следует производить по четвертому свойству. Основной принцип: равенство сохраняется в том случае, когда уменьшение или увеличение числителя происходит на значение, которое находится в знаменателе. Нельзя отнимать от пропорции (от числителя и знаменателя равные числовые значения), поскольку соотношение не будет выполняться. Это является распространенной ошибкой, которая влечет за собой огромные погрешности при расчетах или неверное решение экзаменационных заданий.
Составить пропорцию можно с помощью вычитания и сложения. Этот прием применяется редко, но в некоторых заданиях может использоваться. Суть его заключается в следующем: отношение суммы крайнего и среднего элемента к суммарному значению других крайнего и среднего членов, которое равно отношению крайнего к среднему значению. Однако не ко всем выражениям можно применять свойства пропорции. Следует рассмотреть методику их определения.
Методика исследования
Пропорция применима только к линейным законам изменения величин. Примером этого является поведение простой тригонометрической функции z = sin (p). Величина «z» — зависимая переменная, которая называется значением функции. Переменная «p» — независимая величина или аргумент. В данном контексте она принимает значения углов в градусах. Для демонстрации того, что пропорция «не работает» необходимо подставить некоторые данные.
Кроме того, нужна таблица значений тригонометрических функций некоторых углов. Необходимо предположить, что p = 30, тогда z = sin (30) = 0,5. По свойству пропорции можно найти значение функции при р = 60, не используя таблицу. Для этого нужно составить пропорцию с неизвестным: 30 / 0,5 = 60 / х. Чтобы найти х («икс»), нужно воспользоваться свойством умножения «крест-накрест»: 60 * 0,5 = 30 * х. Уравнение решается очень просто: х = 60 * 0,5 / 30 = 30 / 30 = 1. Ответ получен очень быстро, и нет необходимости смотреть табличное значение.
В этом случае не так все просто. Если воспользоваться вышеописанной таблицей, то z = sin (60) = [3^(½)] / 2. Полученное значение не равно 1. Причина несоответствия — нелинейность функции. Математики для облегчения вычислений предлагают методику определения нелинейных выражений. Она состоит из следующих положений:
- Записать функцию.
- Рассмотреть составные части.
- Если простой тип, перейти к 5 пункту.
- Сложная — разложить на простые элементы, а затем перейти к 5 пункту.
- Определить тип зависимости ее значения от аргумента: линейная или нелинейная. Если получен второй тип, то свойства пропорции применить невозможно.
- Определить тип линейности, построив график.
По таким правилам были исследовано огромное количество функций. К нелинейным относятся следующие: прямые и обратные тригонометрические, гиперболические, показательные, логарифмические и сложные математические, состоящие из нелинейных зависимостей.
К прямым тригонометрическим относятся sin (p), cos (p), tg (p) и ctg (p), а к обратным — arcsin (p), arccos (p), arctg (p) и arcctg (p). Следует отметить, что гиперболическими являются sh, ch, th, cth, sech и csch. Показательная — z = a^y, а логарифмической — функция, имеющая операцию логарифмирования. Простые линейные могут объединяться с нелинейными. В таких случаях правило пропорции также не соблюдается.
Универсальный алгоритм
Алгоритм позволяет решать уравнения, и найти неизвестный член пропорции. Для его реализации следует знать теорию о пропорциях, и методику обнаружения нелинейных функций. Он состоит из нескольких шагов, которые помогут правильно вычислить необходимую величину:
- Записать соотношение пропорции.
- Проанализировать выражение в пункте под первым номером на наличие нелинейных функций и составляющих.
- Применить свойство умножения «крест-накрест».
- Перенести неизвестные в левую сторону, а известные — в правую. Необходимо обратить внимание на знаки: умножение — деление, сложение — вычитание и положительная величина становится отрицательной.
- Решить уравнение.
Существуют различные приложения, позволяющие решить пропорцию. Онлайн-калькулятор позволяет вычислить неизвестный компонент очень быстро. Кроме того, результат вычислений отображается после проведения расчетов. Для реализации последнего пункта необходимо рассмотреть некоторые типы равенств с неизвестными.
Уравнения с пропорцией
Существуют уравнения в виде обыкновенной дроби, в которых необходимо найти неизвестную величину. Для этого нужно рассмотреть основные их виды:
Различаются они степенным показателем. У первого типа степень переменной соответствует 1, второго — двойке, третьего — тройке и четвертого — четверке. При решении таких типов нужно выписать знаменатели отдельно, и решить их. Такие корни не являются решением исходной пропорции, поскольку знаменатели должны быть отличны от нулевого значения.
Решение линейного типа сводится к применению правила «крест-накрест». После чего нужно руководствоваться четвертым пунктом универсального алгоритма. Квадратное уравнение (ap 2 + bp + c = 0) решается при помощи разложения на множители (существует высокая вероятность сокращения степени с последующим упрощением выражения) или с использованием дискриминанта (D = b 2 — 4ac). Корни зависят от его значения:
- Два корня, когда D > 0: р1 = (-b — [D]^(½)) / 2a и р2 = (-b + [D]^(½)) / 2a.
- При D равном 0 (один): р = (-b) / 2a.
- Если D 2 — t — 5t + 5 =t 2 -5t -2t + 10. Перенести все слагаемые в левую сторону с противоположными знаками: t 2 — t — 5t + 5 + 5t — t 2 — 10 + 2t = 0. Приведя подобные слагаемые, выражение будет иметь такой вид: t = 5. Решением пропорции является значение t = 5.
Таким образом, для решения пропорций необходимо знать основные свойства, определение типа выражения по методике и алгоритм расчета.
[spoiler title=”источники:”]
http://ladle.ru/education/matematika/6class/proporcii
http://nauka.club/matematika/proportsii.html
[/spoiler]
Летняя онлайн-школа, задание 25 июня для 6 класса. Повторяем как решать уравнения на пропорции.
Сначала повторим определение пропорции, основное свойство пропорции и правило нахождения неизвестного члена пропорции.
Пропорция — это равенство двух отношений.
В верной пропорции произведение крайних членов равно произведению средних членов.
Чтобы найти неизвестный средний член пропорции, надо произведение крайних членов разделить на известный средний член пропорции.
Реши уравнения на нахождения неизвестного члена пропорции. Ответы отправь в форме.
Форма для заполнения ответов на задания
Уравнения на пропорции в ОГЭ
В огэ уравнения на нахождение неизвестного члена пропорции встречаются в первой части. Это 9 задание и оценивается в 1 балл.
Пример 1
Решение:
Находим неизвестный член пропорции, используя основное свойство пропорции.
Условие: х отличен от 4.
Получилось линейное уравнение 5(х — 12) = 3(х — 4).
Раскрываем скобки и приводим подобные слагаемые.
5х — 60 = 3х — 12,
5х — 3х = — 12 + 60,
2х = 48,
х = 48 : 2,
х = 24.
Ответ: 24.
Пример 2
Решение: Представим 2 в виде обыкновенной дроби и применим основное свойство пропорции.
Условие: х не равен 5.
7 / ( х — 5) = 2/1,
2(х — 5) = 7,
Раскрываем скобки, используя распределительное свойство умножения относительно вычитания.
2х — 10 = 7.
Переносим в правую часть уравнения числа, изменив знак.
2х = 7 + 10,
2х = 17,
х = 17 : 2,
х = 8,5.
Ответ: 8,5.
Вернуться к выбору заданий 6 класса.
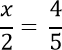

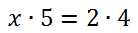
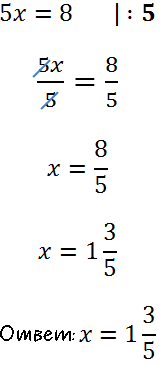
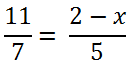

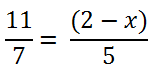
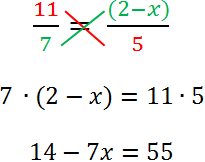
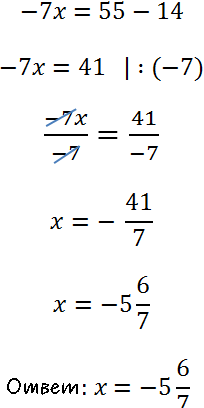
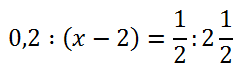
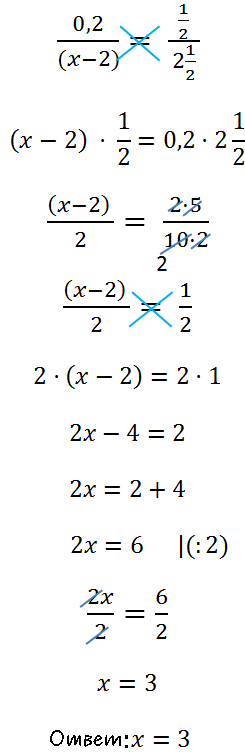










![Rendered by QuickLaTeX.com [x = frac{{mathop {25}limits^5 cdot mathop {18}limits^9 }}{{mathop {10}limits_{mathop 2limits_1 } }}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-b64124f5ea643ccafd168677f25ce6d7_l3.png)
![Rendered by QuickLaTeX.com [y = frac{{mathop {21}limits^3 cdot 9}}{{mathop {14}limits_2 }}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-ebf824933369d4dcb478e11568683894_l3.png)
![Rendered by QuickLaTeX.com [z = frac{{mathop {45}limits^9 cdot mathop {24}limits^4 }}{{mathop 6limits_1 cdot mathop {10}limits_2 }}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-e11bb58bd11e3b24df630575ca2457e0_l3.png)
![Rendered by QuickLaTeX.com [z = frac{{9 cdot mathop 4limits^2 }}{{mathop 2limits_1 }}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-de131f323ce68efa8ec0eb67a303012f_l3.png)
![Rendered by QuickLaTeX.com [k = frac{{mathop {49}limits^7 cdot mathop {23}limits^1 cdot 4}}{{mathop {23}limits_1 cdot mathop 7limits_1 }}]](https://www.for6cl.uznateshe.ru/wp-content/ql-cache/quicklatex.com-d88c55fec4572e70aab7860b8d80c055_l3.png)