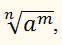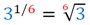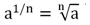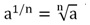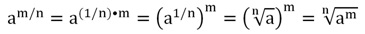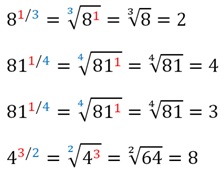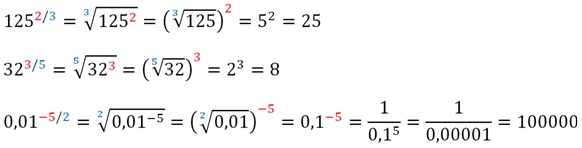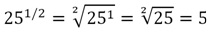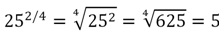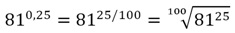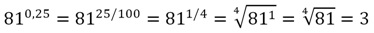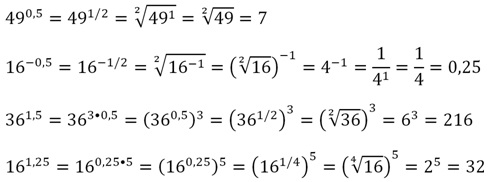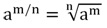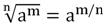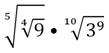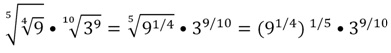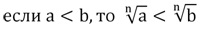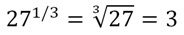Как найти икс в степени в дроби

Часто преобразование и упрощение математических выражений требует перехода от корней к степеням  и наоборот. Данная статья рассказывает о том, как осуществлять перевод корня в степень и обратно. Рассматривается теория, практические примеры и наиболее распространенные ошибки.

Переход от степеней с дробными показателями к корням

Допустим, мы имеем число с показателем степени в виде обыкновенной дроби – amn. Как записать такое выражение в виде корня?

Ответ вытекает из самого определения степени! 

В соответствии с определением, степень amn можно представить в виде корня amn.

Например: 325=325, 123-34=123-34.

Однако, как уже было сказано, не следует забывать про условия: a > 0 ;   m ∈ ℤ ;   n ∈ ℕ .

Так, выражение -813 нельзя представить в виде -813, так как запись -813 попросту не имеет смысла – степень отрицательных чисел на определена.При этом, сам корень -813 имеет смысл.

Переход от  степеней с выражениями в основании и дробными показателями осуществляется аналогично на всей области допустимых значений (далее – ОДЗ) исходных выражений в основании степени. 

Например, выражение x2+2x+1-412 можно представить в виде квадратного корня x2+2x+1-4.Выражение в степени x2+x·y·z-z3-73 переходит в выражение x2+x·y·z-z3-73 для всех x, y, z из ОДЗ данного выражения.

Как представить корень в виде степени?

Обратная замена корней степенями, когда вместо выражения с корнем записывается выражения со степенью, также возможна. Просто перевернем равенство из предыдущего пункта и получим:

amn=amn

Опять же, переход очевиден для положительных чисел a. Например, 764=764, или27-53=27-53.

Для отрицательных a корни имеют смысл. Например -426, -23. Однако, представить эти корни в виде степеней  -426 и -213 нельзя.  

Можно ли вообще преобразовать такие выражения со степенями? Да, если произвести некоторые предварительные преобразования. Рассмотрим, какие.

Используя свойства степеней, можно выполнить преобразования  выражения -426.

-426=-12·426=426.

Так как 4>0, можно записать: 

426=426.

В случае с корнем нечетной степени из отрицательного числа, можно записать:

-a2m+1=-a2m+1.

Тогда выражение -23 примет вид:

-23=-23=-213.

Разберемся теперь, как корни, под которыми содержатся выражения, заменяются на степени, содержащие эти выражения в основании. 

Обозначим буквой A некоторое выражение. Однако не будем спешить с представлением Amn в виде Amn. Поясним, что здесь имеется в виду. Например, выражение х-323, основываясь на равенстве из первого пункта, хочется представить в виде x-323. Такая замена возможна только при x-3≥0, а для остальных икс из ОДЗ она не подходит, так как для отрицательных a формула amn=amn не имеет смысла.

Таким образом, в рассмотренном примере преобразование вида Amn=Amn является преобразованием, сужающим ОДЗ, а из-за неаккуратного применения формулы Amn=Amn нередко возникают ошибки. 

Чтобы правильно перейти от корня Amn к степени Amn, необходимо соблюдать несколько пунктов:

• В случае, если число m – целое и нечетное, а n – натуральное и четное, то формула  Amn=Amn справедлива на всей ОДЗ переменных.
• Если m – целое и нечетное, а n – натуральное и нечетное,то выражение Amn можно заменить:
   – на Amn для всех значений переменных, при которых A≥0;
   – на –Amn для  для всех значений переменных, при которых A<0;
• Если  m – целое и четное, а n – любое натуральное число, то Amn можно заменить на Amn.

Сведем все эти правила в таблицу и приведем несколько примеров их использования.

Вернемся к выражению х-323. Здесь m=2 – целое и четное число, а n=3 – натуральное число. Значит, выражение х-323 правильно будет записать в виде:

х-323=x-323.

Приведем еще один пример с корнями и степенями.

x+5-35=x+5-35, x>-5–x-5-35, x<-5

Обоснуем результаты, приведенные в таблице. Если число m – целое и нечетное, а n – натуральное и четное, для всех переменных из ОДЗ в выражении Amn значение A положительно или неотрицательно (при m>0). Именно поэтому  Amn=Amn.

Во втором варианте, когда  m – целое, положительное и нечетное, а n – натуральное и нечетное, значения Amn разделяются. Для переменных из ОДЗ, при которых A неотрицательно, Amn=Amn=Amn. Для переменных, при которых A отрицательно, получаем Amn=-Amn=-1m·Amn=-Amn=-Amn=-Amn.

Аналогично рассмотрим и следующий случай, когда m – целое и четное, а n – любое натуральное число. Если значение Aположительно или неотрицательно, то для таких значений переменных из ОДЗ Amn=Amn=Amn. Для отрицательных A получаем Amn=-Amn=-1m·Amn=Amn=Amn.

Таким образом, в третьем случае для всех переменных из ОДЗ можно записать Amn=Amn.

Степенью положительного числа  а  с рациональным

показателем

где  m – целое число, а  n – натуральнее  (n > 1), называют корень  n-й  степени из числа  a^m.

ПРИМЕР:

Если  а >
0  и  х – произвольное дробное число, представленное в виде

где  m –
целое, а  n –
натуральное, то:

Если  а = 0  и  х – дробное положительное число, то: 

a^x = 0. 

Формулу

в элементарной
математике обычно рассматривают только при 
а ≥ 0, так
как при отрицательных значениях  а  выражение

а следовательно, и

может не иметь значения
(в множестве действительных чисел). Дробные показатели могут быть не только
положительные, но и отрицательные, т. е. любыми рациональными числами.

ПРИМЕР:

Такие выражения, как:

не имеют смысла.

ПРИМЕР:

Дробное число  0,75  можно представить в виде дроби так:

Значение степени с
дробным показателем не зависит от выбора способа записи
числа  х  в виде дроби;
представляя дробное
число  х  в виде отношения
целого числа к натуральному
разными способами, всегда будем получать один и тот же результат.

ПРИМЕР:

Пусть  а
> 0. Тогда

и значит,

a ≥
0,  n ∈ N,  n ≥ 2.


ПРИМЕР:

ПРИМЕР:

ПРИМЕР:

Если основания
степеней положительны, то свойства степени с целым показателем остаются
справедливыми и для степеней с любым дробным показателем.


Действия над степенями с любыми рациональными показателями
выполняют по тем же правилам, что и действия над степенями с натуральными показателями.


Для любых рациональных
 u  и  v  и действительного  a > 0  верны равенства:

Дробная степень числа

• Дробный показатель степени
• Действия над степенями с дробными показателями

Дробный показатель

Число с дробным показателем степени равно корню с показателем, равным знаменателю, и подкоренным числом в степени, равной числителю.

Чтобы разобраться, почему число в дробной степени равно корню, надо вспомнить правило извлечения корня из степени:

Чтобы извлечь корень из степени, надо показатель степени разделить на показатель корня:

Следовательно, если показатель степени не делится на показатель корня, то получается дробная степень:

Поэтому извлечение корня всегда может быть заменено возведением в степень.

Действия над степенями с дробными показателями

Действия над степенями с дробными показателями совершаются по тем же правилам, которые установлены для степеней с целым показателем.

При доказательстве этого положения, будем сначала предполагать, что члены дробей:    и  ,  служащих показателями степеней, положительны.

В частном случае  n  или  q  могут равняться единице.

При умножении дробных степеней с одинаковыми основаниями их показатели складываются:

При делении дробных степеней с одинаковыми основаниями из показателя делимого вычитается показатель делителя:

Чтобы возвести степень в другую степень, в случае дробных показателей, достаточно перемножить показатели степеней:

Чтобы извлечь корень из дробной степени, достаточно показатель степени разделить на показатель корня:

Правила действий применимы не только к положительным дробным показателям, но и к отрицательным.

План урока:

Степень с рациональным показателем

Свойства дробных степеней и операции с ними

Сравнение степеней

Степень с рациональным показателем

Напомним, что в 7 классе мы впервые познакомились с понятием степени, причем тогда рассматривались случаи, когда показателем степени является натуральное число. В 8 классе понятие степени было расширено, теперь в него включались случаи, когда показатель являлся целым числом. Настоятельно рекомендуем перечитать соответствующие уроки. Сегодня же мы можем сделать ещё один шаг вперед и рассмотреть степени с рациональными показателями.

При расширении понятия степени важно обеспечить то, чтобы уже известные правила работы с целыми степенями работали и для дробных показателей. Одно из свойств степеней выглядит так:

(a^m)ⁿ = a^mn

Подставим в эту формулу следующие значения переменных:

а = 3

m = 1/6

n = 6

Мы специально выбрали эти числа такими, чтобы произведение mn равнялось единице:

mn = (1/6)•6 = 1

Подставляем эти значения:

(3^1/6)⁶ = 3^1/6•6 = 3¹ = 3

Получили, что

(3^1/6)⁶ = 3

Однако по определению корня n-ой степени число, дающее при возведении в шестую степень тройку, является корнем шестой степени из трех. То есть можно записать:

С помощью подобных преобразований нам удалось указать, чему равно число, возведенное в дробную степень. Аналогично можно показать, что для любого а > 0 справедлива формула:

Действительно, если возвести левую часть в n-ую степень, то получим:

(а^1/n)ⁿ = a^1/n•n = a

Значит, по определению корня n-ой степени

Ограничение а > 0 необходимо для того, чтобы не рассматривать случаи, когда подкоренное выражение является отрицательным.

Продолжим наши рассуждения. Чему будет равна степень а^m/n? Ясно, что дробь m/n можно представить в виде:

m/n = (1/n)•m

C учетом этого выполним преобразование:

В результате несложных преобразований нам удалось получить формулу, позволяющую возводить число в степень, у которой рациональный показатель!

Приведем несколько примеров вычисления дробных степеней:

Часто при вычислениях удобнее сначала извлечь корень из числа, а потом полученный результат возвести в степень:

Напомним, что одну и ту же дробь можно представить разными способами, например:

1/2 = 2/4 = 3/6 = 4/8 = 5/10 = 0,5

Возникает вопрос – изменится ли значение дробной степени, если мы приведем дробь к новому знаменателю? Очевидно, что нет, но всё же убедимся в этом на примере. Сначала возведем в степень 1/2 число 25:

Теперь заменим дробь 1/2 на идентичную ей дробь 2/4:

Результат не изменился. В общем случае есть смысл максимально сократить дробь перед вычислением, чтобы избежать операций с большими числами. Особенно это касается десятичных дробей. Например, пусть необходимо вычислить значение выражения 81^0,25. По определению десятичной дроби можно записать, что 0,25 = 25/100. Тогда вычислить 81^0,25 можно так:

Согласитесь, возводить число 81 в 25-ую степень не очень легко! Поэтому поступим иначе. Сократим дробь 25/100:

0,25 = 25/100 = 25/(25•4) = 1/4

Теперь вычисления будет более простыми:

Вообще легко запомнить, что 0,25 = 1/4, а 0,5 = 1/2. Замена десятичных дробей обыкновенными дробями сильно упрощает вычисления. Приведем примеры:

Свойства дробных степеней и операции с ними

Когда мы изучали степени с целыми показателями, мы выяснили, что правила работы с ними ничем не отличаются от правил работы со степенями с натуральным показателем. Оказывается, эти же правила работают и для степеней с рациональным показателем. Сформулируем основные свойства дробных степеней.

Например, справедливы следующие действия:

5^0,5•5^2,5 = 5^{0,5 + 2,5} = 5³ = 125

19^5/3•19^1/3 = 19^{5/3 + 1/3} = 19² = 361

29,36^–0,37•29,36^1,37 = 29,36^{–0,37 + 1,37} = 29,36¹ = 29,36

Вот несколько примеров подобных вычислений:

17^4,5:17^3,5 = 17^4,5–3,5 = 17¹ = 1

4^9,36:4^6,36 = 4^9,36–6,36 = 4³ = 64

20¹²:20¹⁴ = 20^12–14 = 20^–2

Проиллюстрируем это правило примерами:

(6^0,25)⁸ = 6^0,25•8 = 6² = 36

(9^3/2)² = 9^(3/2)•2 = 9³ = 729

(25⁴)^0,125 = 25^4•0,125 = 25^0,5 = 5

Покажем, как можно применять данное правило:

4^1/6•16^1/6 = (4•64)^1/6 = 64^1/6 = 2

0,5^1,5•50^1,5 = (0,5•50)^1,5 = 25^1,5 = 25^1+0,5 = 25¹•25^0,5 = 25•5 = 125

4,9^0,5•10^0,5 = (4,9•10)^0,5 = 49^0,5 =7

Это правило можно применять следующим образом:

360^0,5:10^0,5 = (360:10)^0,5 = 36^0,5 = 6

500³:50³ = (500:50)³ = 10³ = 1000

6,25^1/4:0,01^1/4 = (6,25:0,01)^1/4 = 625^1/4 = 5

Заметим, что степени очень удобны тем, что с их помощью легко упростить работу с корнями, ведь если

то верное и обратное:

То есть любое выражение с корнями в виде степени с рациональным показателем.

Пример. Вычислите значение выражения

Решение. Корней много, поэтому для удобства заменим их степенями

Получили тоже самое выражение, но в более компактном виде. Посчитаем его значение:

(9^1/4)^1/5•3^9/10 = (9^0,25)^0,2•3^0,9 = 9^0,25•0,2•3^0,9 = 9^0,05•3^0,9 = (3²)^0,05•3^0,9 =

=3^2•0,05•3^0,9 = 3^0,1•3^0,9 = 3^0,1•0,9 = 3¹ = 3

Ответ: 3.

Пример. Упростите выражение

(81ⁿ⁺¹– 65•81ⁿ)^0,25

Решение. Степень 81ⁿ⁺¹можно представить как произведение:

81ⁿ⁺¹ = 81ⁿ•81¹ = 81•81ⁿ

С учетом этого можно записать:

(81ⁿ⁺¹– 65•81ⁿ)^0,25 = (81•81ⁿ– 65•81ⁿ)^0,25 = (81ⁿ(81 – 65))^0,25 =

= (81ⁿ•16)^0,25 = 81^0,25n •16^0,25 = 81^0,25n •16^1/4 = 2•81^0,25n

Ответ: 2•81^0,25n.

Сравнение степеней

Напомним, что из двух корней n-ой степени больше тот, у которого больше подкоренное выражение:

Отсюда следует вывод, что если a<b, то

а^1/n<b^1/n

теперь возведем каждую часть этого неравенства в степень m. Тогда получим неравенство:

а^m/n<b^m/n

Получили, что из двух степеней с одинаковыми показателями меньше та, у которой меньше основание (правила сравнения будем нумеровать, чтобы на них удобнее было ссылаться):

В частности, справедливы следующие неравенства:

23^3,75< 24^3,75

63^4/3< 64^4/3

0,008^0,002< 0,008^0,002

Здесь мы рассматривали случаи, когда показатель степени является положительным числом. А что делать, если он отрицательный? Тогда степень следует «перевернуть», воспользовавшись уже известной вам формулой:

a^–n = 1/aⁿ = (1/а)ⁿ

Пример. Сравните выражения с рациональным показателем степени:

20^–3,14 и 50^–3,14

Решение. Избавимся от знака минус в показателе:

20^–3,14 = (1/20)^3,14 = 0,05^3,14

50^–3,14 = (1/50)^3,14 = 0,02^3,14

Получили две степени с одинаковым и, что принципиально важно, положительным показателем. Из них больше та, у которой больше основание. То есть из неравенства 0,02 < 0,05 следует, что

0,02^3,14< 0,05^3,14

Это означает, что

50^–3,14< 20^–3,14

Ответ: 50^–3,14< 20^–3,14.

Особенным является случай, когда показатель степени равен нулю. Напомним, что любое число в нулевой степени (кроме самого нуля) равно единице, а выражение 0⁰ не имеет смысл. Это значит, что числа в нулевой степени равны друг другу, даже если у них разные основания:

25⁰ = 26⁰ = 1

9,36⁰ = 9,37⁰ = 1

18,3546⁰ = 12,3647⁰ = 1

Несколько сложнее сравнивать числа, у которых одинаковые основания, но различные показатели. Здесь возможны три случая – основание либо равно единице, либо больше неё, либо меньше неё.

На основании этого правила можно записать, что:

5^3,14< 5^3,15

45^–0,563< 45^0,001

1,235^–5,623< 1,235^–4,958

Единица в любой степени равна самой себе. Поэтому, если у двух чисел в основании записана именно она, то они должны быть равны друг другу:

1^–7,56 = 1^–0,15 = 1^0,236 = 1 ^521,36 = 1

Осталось рассмотреть случай, когда основание меньше единицы (но всё равно положительное). В таком случае ситуация становится противоположной – чем больше степень, тем меньше число. Проиллюстрируем это на примере. Пусть надо сравнить числа 0,5^7,6 и 0,5^8,9. Заменим дробь 0,5 так, чтобы вместо нее получилась степень с основанием, большим единицы:

0,5 = 1/2 = 1/(2¹) = 2^–1

Итак, 0,5 = 2^–1. Тогда можно записать, что:

0,5^7,6 = (2^–1)^7,6 = 2^–7,6

0,5^8,9 = (2^–1)^8,9 = 2^–8,9

Такие числа мы уже умеем сравнивать. Так как

– 8,9 <– 7,6

то и

2^–8,9< 2^–7,6

Следовательно, 0,5^7,6> 0,5^8,9.

Например, справедливы неравенства:

0,99⁷> 0,99^7,24

0,57^15,36> 0,57^16,47

0,49^0,04> 0,49^0,05

Рассмотрим чуть более сложное задание на сравнение степеней, где надо использовать одновременно несколько правил.

Пример. Докажите, что

0,9^0,9 + 0,8^0,8 + 0,7^0,7< 28^1/3

Решение. Напрямую вычислить значение выражений в правой и левой части затруднительно. Однако мы можем усиливать неравенство, чтобы получить более простые выражения.

Усилить неравенство – это значит увеличить его меньшую или уменьшить большую часть. Например, неравенство 10 < 20 усилится, если вместо 10 написать большее число (11 < 20), или вместо 20 написать меньшее число (10 < 19). Очевидно, что если усиленное неравенство верное, то и изначальное (ослабленное) также справедливо.

Очевидно, что можно легко посчитать значение выражения 27^1/3:

Также ясно, что 27^1/3< 28^1/3 (правило 1). Усилим исходное неравенство:

0,9^0,9 + 0,8^0,8 + 0,7^0,7< 27^1/3 (1)

Действительно, если (1) справедливо, то мы можем записать двойное неравенство

0,9^0,9 + 0,8^0,8 + 0,7^0,7< 27^1/3< 28^1/3

Опустив здесь среднюю часть, получим исходное неравенство. Так как 27^1/3 = 3, мы можем переписать (1) так:

0,9^0,9 + 0,8^0,8 + 0,7^0,7<3 (2)

Далее будем работать с левой частью. Очевидно, что 0,8^0,8< 0,9^0,8 (снова используем правило 1). С другой стороны, 0,9^0,8< 0,9^0,7 (правило 3). Значит, можно записать двойное неравенство:

0,8^0,8< 0,9^0,8<0,9^0,7

или просто 0,8^0,8<0,9^0,7. Абсолютно аналогично можно записать, что

0,7^0,8< 0,9^0,7<0,9^0,7

Или 0,7^0,8<0,9^0,7. Наконец, в силу правила (3), 0,9^0,9<0,9^0,7. Итак, имеем три неравенства:

0,9^0,9<0,9^0,7

0,8^0,8<0,9^0,7

0,7^0,8<0,9^0,7

Их левые части стоят в (2). Следовательно, можно усилить (2):

0,9^0,7 + 0,9^0,7 + 0,9^0,7<3

3•0,9^0,7< 3

Поделим обе части на 3:

0,9^0,7< 1

Заменим единицу равным ему выражением 1^0,7:

0,9^0,7<1^0,7 (4)

Из правила 1 следует, что (4) справедливо. Но мы получили его, усиливая исходное неравенство. Из справедливости более сильного неравенства следует и справедливость более слабого. Следовательно, из справедливости (4) вытекает верность исходного неравенства, которое и надо было доказать.