Как найти импульс первого шарика до взаимодействия

Словами этот закон сохранения можно сформулировать так:

В замкнутой системе сумма импульсов тел не меняется со временем.

Формула:

[ large boxed{ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} + ldots + vec{p_{n}} = const}]

Помним, что при сложении векторов учитываем их направления.

Примечания:

1. Импульс иногда называют количеством движения. Рекомендую освежить в памяти, какие виды импульсов есть в физике и что такое импульс.
2. Формулировку закона сохранения импульса можно упростить:

В замкнутой системе вектор ( vec{p_{text{общ}}})  не меняется.

Математики данный факт запишут таким способом:

[ large boxed{ vec{p_{text{общ}}} = const}]

Дополнительно читайте о том, какие системы можно считать замкнутыми, и какие виды систем в физике есть.

Пояснения к формуле закона сохранения импульса

Пусть, несколько тел двигаются в замкнутой системе.

В начальный момент времени сложим векторы ( vec{p} ) импульсов всех тел, входящих в систему.

В результате получим новый вектор, обозначим его ( vec{p_{text{общ}}} ). Этот вектор – импульс всей системы, как единого целого.

Время идет. Тела продолжают двигаться и соударяться. При ударах их импульсы будут меняться (и по направлению, и по модулю).

После каждого удара будем с помощью геометрии складывать новые импульсы тел.

При этом выяснится следующее: складывая новые импульсы тел, мы будем получать все тот же вектор ( vec{p_{text{общ}}} ), который был получен нами в начале.

Импульс сохраняется, на примере бильярдных шаров

Предположим, мы склонились над гладким бильярдным столом и смотрим на него сверху. Рассмотрим три бильярдных шара на столе (рис. 1). Массы шаров одинаковые.

( m_{1} = m_{2} = m_{3})

Шары под номерами 2 и 3 покоятся. Значит, их начальные скорости и импульсы равны нулю.

Шар №2: ( vec{v_{2text{до}}} = 0),  импульс ( vec{p_{2text{до}}} = 0)

Для третьего шара ( vec{v_{3text{до}}} = 0) и ( vec{p_{3text{до}}} = 0)

Еще один шар движется со скоростью ( vec{v_{1text{до}}} ) по направлению к шарам 2 и 3.

Его вектор импульса обозначен ( vec{p_{1text{до}}} ) на рисунке.

Сложим импульсы всех шаров, чтобы найти общий вектор импульса системы

[ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} ]

[ vec{p_{1}} + 0 + 0 = vec{p_{1}} ]

То есть, импульс первого шара равен импульсу всех шаров системы (рис. 2) до удара

[ vec{p_{1}} = vec{p_{text{общ.до}}} ]

Во время удара шар 1 подействовал на шары 2 и 3 силой и передал им импульс.

После удара шар под номером 1 остановился, а шары 2 и 3 пришли в движение.

Примечание: в бильярде иногда бывает такое, шар передает свой импульс полностью шару, о который он ударяется.

Направления, в которых двигаются шары 2 и 3, указаны векторами их импульсов ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ) на рисунке 3.

Рассмотрим векторы импульсов шаров 2 и 3 подробнее. Совместим их начала и дорисуем параллелограмм (рис. 4), чтобы сложить импульсы ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ).

В результате сложения получим вектор, обозначенный на рисунке 5 красной стрелкой и символом ( vec{p_{text{общ.после}}} )

Сравним векторы ( vec{p_{text{общ.до}}} ) и ( vec{p_{text{общ.после}}} ). Как видно из рисунка 6, у векторов совпадают длины и направления. Если у векторов совпадают обе характеристики, то векторы равны. О равенстве векторов подробно написано тут.

Запишем математически равенство векторов:

[ vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}} ].

Общий импульс системы до удара = общему импульсу системы после удара.

Это выражение и есть закон сохранения импульса.

Далее, советую почитать о способе решения задач, связанных с только что изученной темой. Переходите по ссылке, чтобы правильно составить формулу закона сохранения для двух случаев —  абсолютно упругий и абсолютно неупругий удар (откроется в новой вкладке).

Комментарии преподавателя

Импульс тела. Закон сохранения импульса.

Законы Ньютона позволяют решать различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано, например, с нахождением ускорения движущегося тела, если известны все действующие на это тело силы. А затем по ускорению определяют и другие величины (мгновенную скорость, перемещение и др.).

Но часто бывает очень сложно определить действующие на тело силы. Поэтому для решения многих задач используют ещё одну важнейшую физическую величину — импульс тела.

• Импульсом тела р называется векторная физическая величина, равная произведению массы тела на его скорость

p = mv.

Импульс — векторная величина. Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

За единицу импульса в СИ принимают импульс тела массой 1 кг, движущегося со скоростью 1 м/с. Значит, единицей импульса тела в СИ является 1 кг • м/с.

При расчётах пользуются уравнением для проекций векторов: рх = mvx.

В зависимости от направления вектора скорости по отношению к выбранной оси X проекция вектора импульса может быть как положительной, так и отрицательной.

Слово «импульс» (impulsus) в переводе с латинского означает «толчок». В некоторых книгах вместо термина «импульс» используется термин «количество движения».

Эта величина была введена в науку примерно в тот же период времени, когда Ньютоном были открыты законы, названные впоследствии его именем (т. е. в конце XVII в.).

При взаимодействии тел их импульсы могут изменяться. В этом можно убедиться на простом опыте.

Два шарика одинаковой массы подвешивают на нитяных петлях к укреплённой на кольце штатива деревянной линейке, как показано на рисунке а.

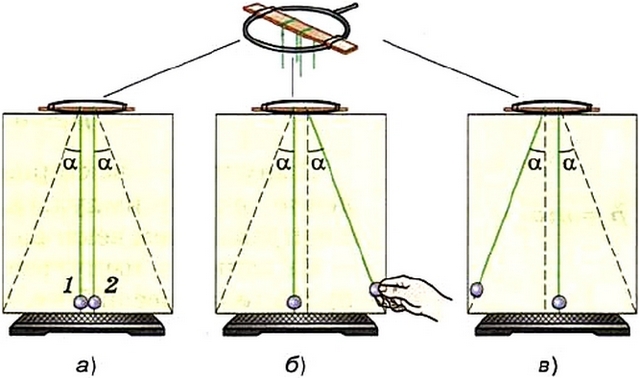
Рис.  Демонстрация закона сохранения импульса

Шарик 2 отклоняют от вертикали на угол а (рис. б) и отпускают. Вернувшись в прежнее положение, он ударяет по шарику 1 и останавливается. При этом шарик 1 приходит в движение и отклоняется на тот же угол а (рис. в).

В данном случае очевидно, что в результате взаимодействия шаров импульс каждого из них изменился: на сколько уменьшился импульс шара 2, на столько же увеличился импульс шара 1.

Если два или несколько тел взаимодействуют только между собой (т. е. не подвергаются воздействию внешних сил), то эти тела образуют замкнутую систему.

Импульс каждого из тел, входящих в замкнутую систему, может меняться в результате их взаимодействия друг с другом. Но

• векторная сумма импульсов тел, составляющих замкнутую систему, не меняется с течением времени при любых движениях и взаимодействиях этих тел

В этом заключается закон сохранения импульса.

Закон сохранения импульса выполняется и в том случае, если на тела системы действуют внешние силы, векторная сумма которых равна нулю. Покажем это, воспользовавшись для вывода закона сохранения импульса вторым и третьим законами Ньютона. Для простоты рассмотрим систему, состоящую только из двух тел — шаров массами m1 и m2, которые движутся прямолинейно навстречу друг другу со скоростями v1 и v2 (рис.).

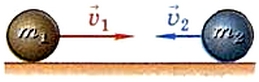
Рис. Система из двух тел — шаров, движущихся прямолинейно навстречу друг другу

Силы тяжести, действующие на каждый из шаров, уравновешиваются силами упругости поверхности, по которой они катятся. Значит, действие этих сил можно не учитывать. Силы сопротивления движению в данном случае малы, поэтому их влияние мы тоже не будем учитывать. Таким образом, можно считать, что шары взаимодействуют только друг с другом.

Из рисунка видно, что через некоторое время шары столкнутся. Во время столкновения, длящегося в течение очень короткого промежутка времени t, возникнут силы взаимодействия F1 и F2, приложенные соответственно к первому и второму шару. В результате действия сил скорости шаров изменятся. Обозначим скорости шаров после соударения буквами v1 и v2.

В соответствии с третьим законом Ньютона силы взаимодействия шаров равны по модулю и направлены в противоположные стороны:

По второму закону Ньютона каждую из этих сил можно заменить произведением массы и ускорения, полученного каждым из шаров при взаимодействии:

m1а1 = -m2а2.

Ускорения, как вы знаете, определяются из равенств:

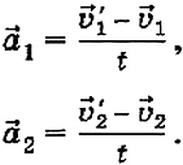
Заменив в уравнении для сил ускорения соответствующими выражениями, получим:

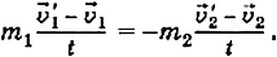
В результате сокращения обеих частей равенства на t получим:

m1(v’1 – v1) = -m2(v’2 – v2).

Сгруппируем члены этого уравнения следующим образом:

m1v1′ + m2v2′ = m1v1 = m2v2. (1)

Учитывая, что mv = p, запишем уравнение (1) в таком виде:

P’1 + Р’2 = P1 + Р2.(2)

Левые части уравнений (1) и (2) представляют собой суммарный импульс шаров после их взаимодействия, а правые — суммарный импульс до взаимодействия.

Значит, несмотря на то, что импульс каждого из шаров при взаимодействии изменился, векторная сумма их импульсов после взаимодействия осталась такой же, как и до взаимодействия.

Уравнения (1) и (2) являются математической записью закона сохранения импульса.

Поскольку в данном курсе рассматриваются только взаимодействия тел, движущихся вдоль одной прямой, то для записи закона сохранения импульса в скалярной форме достаточно одного уравнения, в которое входят проекции векторных величин на ось X:

m1v’1x + m2v’2х= m1v1x + m2v2x.

Использованные источники: 

• http://znaika.ru/catalog/10-klass/physics/
• https://www.youtube.com/watch?v=RiPcl0-v40s
• https://www.youtube.com/watch?v=GdoZwHDYmp8

другом (первый за вторым) со скоростями v1= 9 м/с и v2= 4 м/с соответственно. После столкновения шаров происходит упругий удар, в результате которого скорость первого шара уменьшается на Δv= 5 м/с, и шарики раскатываются в разные стороны. Определи скорость второго шарика после столкновения. (Ответ округли до десятых.) Шаг 1. Найди импульс первого шарика до взаимодействия: p1= кг·м/с. Шаг 2. Найди импульс второго шарика до взаимодействия: p2= кг·м/с. Шаг 3. Найди суммарный импульс двух шариков до взаимодействия, учитывая, что шарики движутся друг за другом (первый за вторым): p= кг·м/с. Шаг 4. Найди скорость первого шарика после взаимодействия: V1= м/с. Шаг 5. Найди импульс первого шарика после взаимодействия: P1= кг·м/с. Шаг 6. Обозначив скорость второго шарика после взаимодействия как V, запиши импульс P второго шарика после взаимодействия: = ⋅. Шаг 7. Обрати внимание, что в результате упругого столкновения шарики будут двигаться в разные стороны. Запиши суммарный импульс шариков после взаимодействия: p′=∣∣ − ⋅ ∣∣.

Шаг 8. Поскольку два шарика являются замкнутой системой, то для них выполняется закон сохранения импульса: импульс системы до взаимодействия равен импульсу системы после взаимодействия. Составь уравнение согласно закону сохранения импульса: =∣∣ − ⋅ ∣∣ — и реши его относительно V с точностью до десятых: V = м/с.