Как найти импульс поступательно движущегося тела

Импульсом
материальной точки называют вектор p,
равный произведению массы m
точки на ее скорость v
в данной системе отсчета.

.

(12.1)

Импульс
материальной точки является одной из
важнейших ее динамических характеристик,
зависящих как от скорости движения
точки, так и от ее инертности (массы).

Второй
закон Ньютона для материальной точки
т
(7.1) можно записать в виде:

.
(12.2)

Выражение
(12.2) является более общей записью этого
закона, который можно трактовать
следующим образом: «Скорость
изменения импульса p
материальной точки равна сумме сил,
действующих на эту точку».
В такой форме второй закон Ньютона можно
применять для тел и в случае их переменной
массы.

Импульсом
P
системы материальных точек называют
геометрическую
сумму импульсов всех материальных точек
системы.

.
(12.3)

Импульс
P
тела массой m,
состоящего из материальных точек, в
случае его поступательного движения
со скоростью v
равен:

.

В
этом случае импульс тела является мерой
его движения. Однако эта характеристика
не может служить универсальной мерой
для всех форм движения. Поясним это
следующими примерами.

1. Например,
   если однородное тело правильной формы
   (шар или куб) равномерно вращается
   вокруг неподвижной оси, проходящей
   через центр симметрии, то легко проверить,
   что векторная сумма (12.3) импульсов всех
   материальных точек равна нулю при любой
   угловой скорости тела. Следовательно,
   импульс тела не может служить мерой
   его вращательного
   движения
   .

2. Два
   тела массой 1кг и 2кг, соответственно,
   свободно падая с высот 20м и 5м, имеют
   у поверхности Земли одинаковые импульсы.
   Однако, как показывают опыты, при ударе
   о Землю первое тело способно сжать две
   одинаковые пружины на столько же,
   насколько второе тело может сжать
   только одну из этих пружин. Таким
   образом, импульс тела не может полностью
   количественно охарактеризовать
   динамические свойства тел даже при
   поступательном движении.

Единой
мерой различных форм движения служит
физическая величина, называемая энергией.

§13. Энергия

Установлено,
что все формы движения превращаются
друг в друга в строго определенных
количественных соотношениях. Именно
это обстоятельство и позволило ввести
понятие об энергии, т.е. позволило
измерять различные формы движения и
взаимодействия единой мерой.

Энергия
механической системы количественно
характеризует ее с точки зрения возможных
в ней превращений движения. Эти превращения
обусловлены взаимодействием тел системы,
как между собой, так и с внешними телами.

Важность
понятия энергии определяется еще и тем,
что энергия подчиняется закону сохранения.
Это означает, что если взаимодействием
данной системы с окружающим миром можно
пренебречь, то в этой системе при любых
процессах энергия может только
превращаться из одной формы в другую,
сохраняя свое значение. Понятие энергии
связывает воедино все явления природы.
Поэтому вводят понятия механической
энергии (механика), внутренняя энергия
(термодинамика), электромагнитная
энергия (электричество и магнетизм),
ядерная энергия (ядерная физика) и др.

Механическую
энергию разделяют на два вида: кинетическую
и потенциальную энергии.

Кинетическая
энергия

Кинетическая
энергия Е_к
материальной точки является мерой ее
механического движения.

Пусть
на материальную точку массой m,
движущуюся со скоростью v
действует сила F.
На малом участке dr
эта сила совершает работу A,
равную
Fdr,
а скорость материальной точки изменяется
от v
до значения v+dv.

Из
второго закона Ньютона для материальной
точки m
следует:

.

Отсюда,
.

Работа,
совершаемая силой F
при
возрастании скорости материальной
точки от v₁
до v₂,
равна:

.

Здесь
учтено, что
.
(см.2.6)

Величина
называется кинетической энергией
материальной точкит.

Таким
образом, можно сказать, что работа,
совершаемая над материальной точкой
произвольной силой, равна изменению
кинетической энергии этой точки:

.
(13.1)

Если
работа силы положительна, то кинетическая
энергия частицы возрастает, если
отрицательна, то убывает.

Это
позволяет интерпретировать кинетическую
энергию частицы как запас работы, которую
совершили над ней внешние силы. Этот
запас может расходоваться (кинетическая
энергия убывает), и тогда внешние силы
совершают отрицательную работу. Говорят,
что кинетическая энергия израсходована
на работу против
внешних сил.

Кинетическая
энергия – величина аддитивная. Это
означает, что кинетическая энергия Е_к
системы N
материальных точек равна сумме
кинетических энергий всех точек, входящих
в эту систему.

,
(13.2)

где

–
масса и скорость i-ой
материальной точки.

Полученные
результаты можно обобщить на случай
произвольной системы материальных
точек.

Если
записать соотношение (13.1) для каждой
материальной точки и затем все уравнения
сложить, то мы получим:

А_{всех
сил}
=
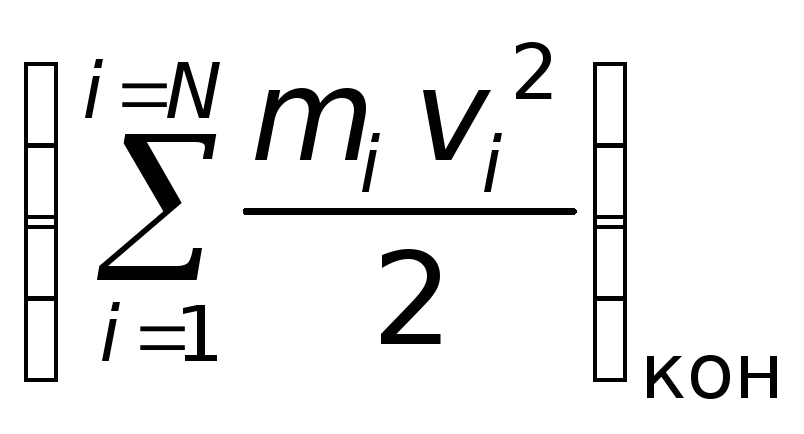–= (Е_к)_кон
– (Е_к)_нач.
(13.3)

Таким
образом, работа
всех сил, действующих на систему
материальных точек, равна приращению
кинетической энергии этой системы.

Полученное
выражение выражает теорему
об изменении кинетической энергии:
приращение
кинетической энергии системы материальных
точек равно сумме работ всех приложенных
к системе внешних и внутренних сил.

Важность
полученного результата заключается в
том, что приращение кинетической энергии
системы определяется работой не только
внешних
сил (сил со стороны тел, не включенных
в рассматриваемую систему), но и работой
внутренних
сил, т.е. силами взаимодействия между
материальными точками системы.

Как
мы увидим в дальнейшем, внутренние силы
не могут изменить импульс всей системы
материальных точек.

Потенциальная
энергия частицы во внешнем силовом
поле.

Введем
понятие силового поля.

Если
в каждой точке данного пространства
известны величина направление силы,
действующей на рассматриваемую частицу,
то говорят, что в этом пространстве
задано поле сил
или силовое поле.

Мы
ограничимся рассмотрением полей сил,
не зависящих от времени,
т.е. стационарных
полей.

Например,
в каждой точке пространства данной
аудитории на частицу массой m
действует сила гравитации со стороны
Земли, равная mg
и направленная к центру Земли. Можно
сказать, что в данной аудитории действует
гравитационное поле сил.

Другой
пример: при движении материальной точки
по поверхности стола на нее со стороны
поверхности действует сила трения,
равная μN
и направленная противоположно скорости
ее движения. Говорят, что на поверхности
стола действует поле сил трения.

Вводя
понятие работы, мы говорим, что действие
силы на каком-либо участке характеризуется
работой, т.е. сила совершает работу на
данном участке. Например, при движении
тела из точки 1 в точку 2 по поверхности
стола силы трения будут совершать
работу. Очевидно, что работа сил трения
будет зависеть от того, по какому пути
будет двигаться тело из точки 1 в точку
2. Чем длиннее путь, пройденный телом,
тем больше работа сил трения, хотя при
этом отправная и конечные точки пути
одни и те же.

Однако,
можно выделить класс сил, которые
обладают замечательным свойством –
работа,
совершаемая силой при перемещении
частицы из точки 1 в точку 2, не
зависит от формы пути,
по которому частица перемещается из
т.1 в т.2 ( рис. 13.1).

Это
означает, что
,

где
–
работа при перемещении частицы из 1 в 2
по траектории 1-а-2;

–
работа при перемещении частицы из 1 в 2
по траектории 1-b-2.

Т

Рис.13.1.
Работа
консервативных сил

не
зависит от формы траектории, по

которой
частица перемещается из т.1 в т.2.

акие силы называютсяконсервативными.
Если такое свойство сохраняется и для
силовых полей, меняющихся со временем
(не стационарных полей), то такие силы
называются потенциальными.
Консервативные силы – это частный
случай потенциальных сил.

Изменение
направления движения частицы на
противоположное вызывает изменение
знака работы консервативной силы, так
как
меняет свой знак. Поэтому, при перемещении
частицы по любому замкнутому контуруL,
например, 1-а-2-b-1,
работа консервативной силы тождественно
равна 0. Это обстоятельство позволяет
записать условие консервативности сил
в следующей математической форме:

.
(13.4)

Кружок
на знаке интеграла означает суммирование
по замкнутому контуру. Тождество (13.4)
является необходимым
условием консервативности сил F_кон.
Условие (13.4) не может быть достаточным
условием консервативности сил данного
поля. Для этого нужно доказать, что это
условие выполняется для любого
замкнутого контура. Как это сделать, мы
узнаем позже, когда познакомимся с
понятием ротора векторной функции.

К
неконсервативным
силам относятся диссипативные
(силы трения) и
гироскопические
силы, с которыми мы познакомимся попозже.

Введем
понятие потенциальной энергии. Допустим,
что на частицу в пространстве действуют
консервативные силы. В этом случае
говорят, что задано потенциальное поле
сил. Из определения консервативных сил
ясно, что работа, совершаемая силами
потенциального поля над частицей,
зависит только от взаимного расположения
начальной 1 и конечной 2 точек пути. Это
означает, что работу в этом случае можно
выразить в виде:

,
(13.5)

где

–
некоторые значения функции состояния
частицы, зависящие только от ее координат.
Эту функцию и называютпотенциальной
энергией.

Из
соотношения (13.5) следует, что работа
сил потенциального поля равна убыли
потенциальной энергии частицы:

.
(13.6)

Выражение
(13.5) позволяет найти зависимость
потенциальной энергии частиц от координат
только с точностью до постоянного
слагаемого С,
не влияющего величину разности
.
Поэтому в каждой конкретной задаче для
получения однозначной зависимостиU_пот
от
координат выбирают точку, для которой
потенциальную энергию частицы (или
системы) условно считают равной нулю.

Используя
выражение (13.5), можно дать определение
потенциальной энергии. Потенциальная
энергия системы в произвольном состоянии
равна работе, которую должны совершить
потенциальные силы при переводе системы
из этого состояния в состояние, где U_п2
равна нулю.

В
качестве примера рассмотрим однородное
силовое поле и поле центральных сил.

а)
Однородное поле.

Если
во всех точках рассматриваемого
пространства силы поля равны и по
величине и по направлению, то такое поле
называется однородным.

Работа,
совершаемая постоянной силой F,
равна (11.4):

.

Очевидно,
что эта работа не зависит от формы
траектории, а зависит только от начального
и конечного положения точек движения
r₁
и
r₂.
Следовательно, однородное силовое поле
потенциально.

Например,
гравитационное поле вблизи поверхности
Земли в пределах небольшой области
(r<<R_Земли)
можно считать однородным: F=mg=
const.
Тогда работа сил тяжести будет равна:
А
= mg(r₂
–
r₁)
= mgr
= mgrcos(g,r)
= mg(h₂
– h₁)
= –U_пот.

Итак,
работа сил тяжести будет равна: А
= –(U_кон
– U_нач).

Следовательно,
потенциальная энергия в однородном
поле сил тяжести равна:

U(h)
= mgh
+ C.
(13.8)

Константу
С
удобнее всего выбрать равной нулю. Это
означает, что на высоте h
равной нулю потенциальная энергия U(0)
будет считаться тоже равной нулю. Начало
отсчета высоты h
выбирается произвольно из соображений
удобства решения задачи. Таким образом,
потенциальная энергия материальной
точки, поднятой на высоту h,
возрастает на величину mgh.

б)
Поле центральных
сил

Аналогичным
образом вычисляется потенциальная
энергия для различных потенциальных
полей: сначала доказывается, что данное
поле сил потенциально и затем вычисляется
работа этих сил при переходе системы
из начального положения в конечное,
причем по наиболее удобной траектории.
Подобным образом получают выражение
для потенциальной энергии данного поля.

Рассмотрим
поле центральных сил. Если все
силы данного поля направлены к одной
точке (или от нее), а их величина зависит
только от расстояния до этой точки,
называемой силовым
центром,
то такое поле называется центральным
полем сил. Это определение можно записать
в математической форме:

F
=
f(r)
e_r,
(13.9)

где
e_r
– единичный вектор, задающий направление
радиус-вектора точки поля относительно
силового центра, т.е.
r
= re_r.
Элементарная работа такой силы будет
равна А
= f(r)e_rdr.
С учетом соотношения (2.6) произведение
e_rdr
равно:

.
Следовательно, dА
= f(r)×dr.
Работа этой силы на произвольном пути
от точки 1 до точки 2 равна:

.
(13.10)

Полученное
выражение зависит только от вида функции
f(r)
и от значений r₁
и r₂,
и никак не зависит от формы траектории
движения и поэтому является потенциальным.

Рассмотрим
гравитационное взаимодействие двух
материальных точек М
и
т. По
закону всемирного тяготения сила
взаимодействия по модулю равна:
.
Если рассматривать силу, действующую
на точку т,
то можно сказать, что гравитационное
силовое поле, создаваемое материальной
точкой М,
действует на точку т
с силой F.

Другими
словами, материальная точка М
создает поле центральных сил с силовым
центром в точке М.

Поместим
начало отсчета в точку М.

Тогда
в векторном виде сила гравитации,
действующая на точку т,
примет следующий вид:

.

(13.11)

При
перемещении точки т
из r₁
в точку r₂
силы гравитации совершат работу:

.
(13.12)

Сравнивая
полученное выражение с (13.6), получим,
что потенциальная энергия частицы т
в гравитационном поле точки М
равна:

.
(13.13)

При
большом удалении точек друг от друга
(),
сила их гравитационного взаимодействия
стремится к нулю, и, следовательно,
должна стремиться к нулю и потенциальная
энергия. Поэтому в данном случае константуС
можно положить равной нулю.

Выражение
(13.13) является точным для расчета
потенциальной энергии частицы т
в гравитационном поле точки М.
Выражение (13.8) является приближенным
расчетным соотношением для вычисления
потенциальной энергии частицы в
гравитационном поле. Покажем это.

Можно
доказать, что тело сферической формы
массой М
создает вне себя точно такое же
гравитационное поле, как материальная
точка такой же массы, помещенная в центр
шара. Следовательно, при поднятии тела
массой т
с поверхности, например, Земли на высоту
h
ее потенциальная энергия меняется на
величину

.
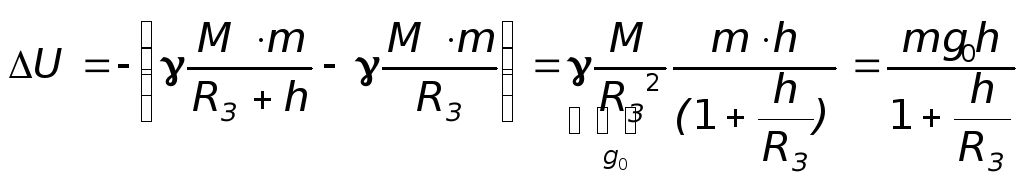(13.14)

Если
h<<R_Земли,
то это выражение переходит в (13.8).

Таким
образом, если все перемещения происходят
вблизи поверхности Земли, то можно
пользоваться выражением (13.8), если нет
– то надо использовать более точное
выражение (13.14).

Если
в силовом потенциальном поле находится
система невзаимодействующих
между собою материальных точек, то
потенциальная энергия такой системы в
этом силовом поле будет равна сумме
потенциальных энергий каждой точки в
отдельности: U_сист
= U_i

Если
частицы системы взаимодействуют между
собой, то для того чтобы найти потенциальную
энергию всей системы, нужно к потенциальной
энергии частиц во внешнем силовом поле
добавить потенциальную энергию их
взаимодействия.

Соседние файлы в папке Лекции по физике

• #
• #
• #
• #

Оглавление:

• Основные теоретические сведения
  • Импульс тела
  • Закон сохранения импульса
  • Сохранение проекции импульса
  • Многомерный случай ЗСИ. Векторный метод

Основные теоретические сведения

Импульс тела

К оглавлению…

Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:

Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.

Общий импульс системы тел равен векторной сумме импульсов всех тел системы:

Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):

где: p_н – импульс тела в начальный момент времени, p_к – в конечный. Главное не путать два последних понятия.

Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.

Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.

Закон сохранения импульса

К оглавлению…

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:

Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.

Сохранение проекции импульса

К оглавлению…

Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.

Многомерный случай ЗСИ. Векторный метод

К оглавлению…

В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:

В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m1v1 = (m1 + m2)v
Неупругое столкновение движущихся тел	± m1v1 ± m2v2 = ±(m1 + m2)v
В начальный момент система тел неподвижна	0 = m1v’1 – m2v’2
До взаимодействия тела двигались с одинаковой скоростью	(m1 + m2)v = ± m1v’1 ± m2v’2

Сохранение  проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁ + m₂)v

Отсюда скорость равна:

Алиса Никитина | Просмотров: 20k

Импульс в физике

Любое тело, обладающее скоростью, обладает импульсом.

Тело всегда движется туда, куда направлен вектор его скорости.

Импульс тела – это вектор. Он сонаправлен с вектором скорости тела.

Покоящееся тело импульса не имеет — если тело не движется, его импульс равен нулю.

Физики различают два вектора – импульс тела и импульс силы.

Импульса тела, формула

Возьмем вектор ( vec{v} ) скорости тела (рис. 1), умножим его на ( m ) массу тела (масса — скаляр), получим новый вектор, обозначим его ( p ). Длина этого вектора отличается от длины скорости, а направление – совпадает.

Подробнее о умножении вектора на число написано тут.

Рис. 1. Вектор скорости тела умножаем на скаляр — массу тела, получаем вектор импульса тела

[ large boxed{ vec{v} cdot m = vec{p} }]

( vec{v} left( frac{ text{м}}{с} right) ) – скорость тела, вектор

( m left( text{кг} right) ) – масса тела, скаляр (просто число)

( vec{p} left( text{кг} cdot frac{ text{м}}{c} right) ) – импульс тела, вектор, он сонаправлен со скоростью тела

Если тело не движется, оно импульсом не обладает ( vec{p} = 0 ).

Импульс силы, формула

На тело может действовать сила, например, когда тело соударяется с каким-то другим телом. Тела взаимодействуют с помощью сил. Что такое сила, написано тут.

Действие происходит не мгновенно, а в течение какого-то промежутка времени.

Возьмем вектор ( vec{F} ) силы, действующей на тело (рис. 2), умножим его на ( Delta t ) кусочек времени, в течение которого сила действовала (время — скаляр), получим новый вектор. Для этого вектора не придумали специального обозначения.

Рис. 2. Вектор силы, действующей на тело, умножаем на скаляр – промежуток времени, в течение которого сила действовала, получаем вектор импульса силы

[ large boxed{overrightarrow {F cdot Delta t }}]

( vec{F} left( H right) ) – сила, действующая на тело, вектор

( Delta t left( c right) ) – время воздействия силы (просто число). Можно пояснить так:

Пусть сила действовала несколько секунд. Тогда ( Delta t = t — t_{0} ) – разница между двумя положениями секундной стрелки на часах.

• ( t left( c right) ) – конечное положение стрелки,
• ( t_{0} left( c right) ) – начальное положение стрелки.

Длины векторов силы и импульса силы отличаются, а направления – совпадают.

Если сила не действует ( vec{F} = 0 ), то вектор импульса силы отсутствует ( vec{F} cdot Delta t = 0 ).

Импульс тела и импульс силы связаны. В этой статье подробно описана связь между этими векторами.

Оценка статьи:

Загрузка…