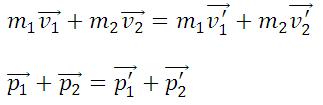Как найти импульс шара до удара

Заключение – дополнение к тексту

Мы применили закон сохранения импульса (одного из основных законов природы) к абсолютно неупругому и абсолютно упругому удару шаров.

При абсолютно неупругом ударе шары (тела) не сохраняют свою форму, то есть испытывают пластическую деформацию. К такому удару

можно отнести удар свинцовых шаров. При неупругом ударе не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. При неупругом ударе механическая энергия полностью или частично переходит во внутреннюю энергию тел (тела нагреваются). В случае нецентрального (косого) удара тел их общий импульс и общая скорость после абсолютно неупругого удара находятся путём векторного сложения импульсов отдельных тел.

При абсолютно упругом ударе (сюда можно грубо приближённо отнести удар стальных шаров) выполняется и закон сохранения импульса, и закон сохранения механической энергии. При упругом ударе механическая энергия шаров частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию шаров. Шары приобретают скорости

направления и модули которых определяются законами сохранения полного импульса и полной энергии системы. Последний 3) частный случай говорит о том, что если лёгкий шарик испытает абсолютно упругий удар о неподвижную стенку, то он отскочит от неё без потери скорости. Пусть теперь шарик падает на неподвижную стенку под углом.

Тогда нормальная составляющая скорости шарика изменит своё направление на обратное, а по модулю останется прежней. Тангенциальная же составляющая скорости не изменится, поэтому угол падения будет равен углу отражения.

На рисунке вектора скорости падения и скорости отражения шарика перенесены в точку падения. Вектор изменения скорости направлен вверх перпендикулярно поверхности стенки. Такие же направления имеют импульсы шарика до удара и после удара о стенку, а вектор приращения импульса шарика

направлен по нормали от стенки.

В молекулярной физике происходит то же самое, когда молекулы газа ударяются о стенку сосуда. Проявляется это давлением газа на стенку сосуда.

Подумаем, что можно найти, если в условии задачи сказано, что шарик летит под прямым углом к движущейся навстречу стенке и между ними происходит упругий удар:

Сразу можно сказать, что скорость шарика относительно движущейся стенки равна

(см. занятие 12 на относительность движения). От стенки шарик отскочит со скоростью

относительно стенки, а относительно земли его скорость после удара

Далее можно найти импульс шара относительно земли до и после удара. Сможем найти изменение его импульса, его кинетическую энергию до и после удара.

Изменение кинетической энергии даст работу, совершённую силой упругости за время удара. Работу же можно выразить через произведение силы удара на перемещение стенки за время удара и найти силу удара.

Таким образом, через данные в условии задачи сможем охарактеризовать упругий удар между шаром и движущейся стенкой.

Абсолютно неупругий удар и абсолютно упругий удар – это предельные случаи кратковременного взаимодействия шаров (тел). При взаимодействии реальных тел имеют место и упругие, и неупругие деформации. Формула, связывающая скорости шаров до удара и после удара имеет вид:

коэффициент восстановления относительной скорости при ударе. В случае абсолютно неупругого удара он равен нулю; в случае абсолютно упругого удара он равен единице.

При ударе реальных тел этот коэффициент принимает промежуточные значения между нулём и единицей. Для стали этот коэффициент равен 0,56.

К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.

Предыдущая запись: Занятие 23. Импульс системы тел. Центр масс системы

Следующая запись:Задачи 1 – 4 к занятиям 22 – 24

Первая запись на канале: Занятие 1. Физика. Механика. Кинематика

Лабораторная работа № 2

Тема: Изучение закона сохранения импульса

Цель: экспериментально проверить справедливость закона сохранения импульса тел при прямом упругом соударении

Оборудование: 1. Два металлических шарика разной массы.

                        2. Рама для подвеса шариков.

                        3. Измерительная линейка.

Теория

   Величина, равная произведению массы материальной точки на ее скорость, называется импульсом.

p=mυ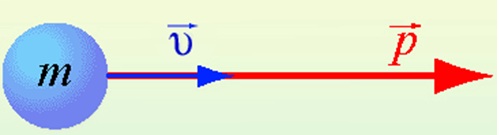  

p — импульс тела

m — масса тела

υ — скорость тела   

   Импульс тела направлен в ту же сторону, что и скорость тела.

   Единицей измерения импульса в СИ является 1 кг·м/с.

   Изменение импульса тела происходит при взаимодействии тел, например, при ударах.

   Для системы материальных точек полный импульс равен сумме импульсов. При этом следует иметь в виду, что импульс – это векторная величина, и поэтому в общем случае импульсы складываются как векторы, т.е. по правилу параллелограмма.

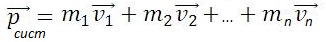
   Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой. Замкнутая система – это система тел, которые взаимодействуют только друг с другом.

   Закон сохранения импульса: в замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

m₁, m₂ — массы взаимодействующих тел, кг

υ₁, υ₂ — скорости тел до столкновения, м/с

υ’₁, υ’₂ — скорости тел после столкновения, м/с

   Закон сохранения импульса можно сформулировать и так: если на тела системы действуют только силы взаимодействия между ними («внутренние силы»), то полный импульс системы тел не изменяется со временем, т.е. сохраняется. Этот закон применим к системе, состоящей из любого числа тел. Отметим еще раз, что импульс – величина векторная, поэтому сохранение полного импульса означает сохранение не только его величины, но и направления.

   Закон сохранения импульса выполняется при распаде тела на части и при абсолютно неупругом ударе, когда соударяющиеся тела соединяются в одно. Если распад или удар происходят в течение малого промежутка времени, то закон сохранения импульса приближенно выполняется для этих процессов даже при наличии внешних сил, действующих на тела системы со стороны тел, не входящих в нее, т.к. за малое время внешние силы не успевают значительно изменить импульс системы.

   Под ударом в механике понимается кратковременное взаимодейс­твие двух или более тел,  возникающее в результате их соприкосно­вения (соударение шаров, удар молота о наковальню и др.). Самым простым является прямой (центральный) удар, то есть такой удар, при котором скорости соударяющихся тел до удара направлены по линии, соединя­ющей центры тел. При соударении взаимодействие  длится такой короткий промежуток времени (иногда измеряемый тысячными долями секунды) и возни­кают столь большие внутренние силы взаимодействия, что внешними силами можно пренебречь и систему соударяющихся тел можно считать замкнутой и применять к ней закон сохранения импульса.

   В зависимости от упругих свойств тел соударения могут проте­кать весьма различно. Принято выделять два крайних случая: абсо­лютно упругий и абсолютно неупругий удары.

   Абсолютно упругим называется удар, при котором после взаимодействия тела полностью восстанавливают свою форму. Таких ударов в природе не существует, так как всегда часть энергии затрачивается на необратимую деформацию тел. Однако для некоторых  тел, например стальных закаленных шаров, потерями механической энергии при столкновении можно пренебречь и считать удар абсолютно упру­гим. В случае центрального абсолютно упругого удара двух тел с массами m₁, m₂  и скоростями υ₁, υ₂  до удара и υ′₁, υ′₂ после удара можно записать закон сохранения импульса тел:

   Абсолютно неупругим называется удар, при котором после соп­рикосновения тел они не восстанавливают полностью свою форму, со­единяются вместе и движутся как единое целое с одной скоростью. При этом ударе часть их механической энергии переходит в работу деформации тел (внутреннюю энергию). Столкновение двух шаров из пластилина, когда после столкновения шары слипаются и движутся вместе, является примером абсолютно неупругого удара. В случае центрального абсолютно неупругого удара двух тел с массами m₁, m₂  движущихся со скоростями υ₁, υ₂  до удара и υ′ после удара можно записать законы сохранения импульса тел:

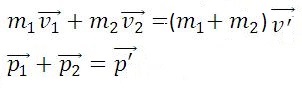
   Закон сохранения импульса служит основой для объяснения обширного круга явлений природы, применяется в различных науках:

1. Закон строго выполняется в явлениях отдачи при выстреле, явлении реактивного движения, взрывных явлениях и явлениях столкновения тел.
2. Закон сохранения импульса применяют: при расчетах скоростей тел при взрывах и соударениях; при расчетах реактивных аппаратов; в военной промышленности при проектировании оружия; в технике – при забивании свай, ковке металлов и т.д

Описание работы

Установка состоит из двух стальных шаров, на длинных подвесах и измерительной линейки под шарами. Центры масс соприкасающихся шарв лежат на одном уровне от точки подвеса. Отведя один из шаров (например, большей массы) в сторону и отпустив его, можно произвести прямой (центральный) удар шаров.

Если до столкновения один из шаров покоился υ₂=0, то выражение закона сохранения импульса упростится. При прямом ударе оба шара после столкновения движутся по одной прямой, поэтому от векторной формы записи закона сохранения импульса можно перейти к алгебраической и учитывая, что после столкновения оба шара движутся в одном направлении, получим:

m₁∙υ₁= m₁∙υ′₁ + m₂∙υ′₂ 

   

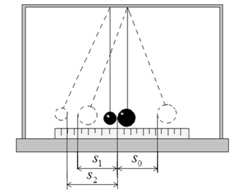
   рис. 2

   Для определения скорости первого шара υ₁ до удара  и скоростей шаров υ′₁ и υ′₂ после удара воспользуемся законом сохранения механической энергии. Потенциальная энергия шара в положении максимального отклонения равняется его кинетической энергии при ударе 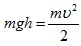, отсюда .

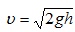   Высоту подъёма шара можно определить по его максимальному отклонению s от положения равновесия (рис.3,а).

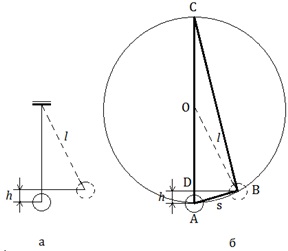
рис. 3

Треугольник АВС прямоугольный (опирается на диаметр). Катет АВ является средней пропорциональной величиной между гипотенузой АС=2l и своей проекцией на гипотенузу АD  (рис.3,б):  АВ²=АС·AD то есть 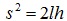, откуда 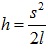. Следовательно, величины скоростей можно выразить так: 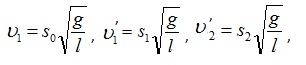где S₀,  S₁ – максимальные отклонения первого шара до и после удара; S₂ – максимальное отклонение второго шара после удара.

Запишем уравнение закона сохранения через выражения скоростей:

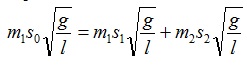  или  m₁∙S₀= m₁∙S₁ + m₂∙S₂.

Таким образом, проверка закона сохранения импульса в данной работе сводится к проверке справедливости последнего уравнения.

 При малых углах отклонения шара от положения равновесия S₀,  S₁ и S₂ можно заменить соответствующими величинами, отсчитанными по горизонтальной шкале.

Выполнение работы.

1. Перенесите рисунок 2 в отчет по работе.

2. Подготовьте в тетради таблицу для записи результатов измерений и вычислений:

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1
2
3

3. Определите массы шаров m₁ и m₂. Запишите их результат в таблицу.

4. Отрегулируйте подвеску шаров так, чтобы их центры и точка касания находились на одной горизонтальной линии.

5. Отклоните шар большей массы на 3 см от положения расновесия (S₀) и затем отпустите его. Заметьте максимальное отклонение шара большей массы после удара (S₁). Повторите опыт 5 раз и найдите среднее значение отклонения S_1ср. Запишите его в таблицу (S₁).

6. Повторите опыт, но теперь заметьте после удара максимальное отклонение шара с меньшей массой (S₂). Повторите опыт 5 раз, и найдите среднее значение отклонения S_2ср. Запишите его в таблицу (S₂).

7. Повторите опыт, отклоняя шар большей массы на 4 см и 5 см. Результаты измерений запишите в таблицу.

8. Используя значения S₀, S₁ и S₂, вычислите импульс шара до удара m₁∙S₀ и сумму импульсов шаров после удара  m₁∙S₁ + m₂∙S₂ и внесите в таблицу их результаты.

9. Сравните импульс шара до удара с суммой импульсов шаров после удара. Запишите вывод по полученным результатам работы.

10. Ответьте на контрольные вопросы.

Контрольные вопросы

1. Что называется импульсом материальной точки? По какой формуле он находится? В каких единицах он измеряется?

2. Импульс – величина векторная или скалярная?

3. Запишите формулу и формулировку закона сохранения импульса.

4. При каких условиях выполняется закон сохранения импульса?

5. Какое соударение называется абсолютно упругим?

6. Для каких видов соударений выполняется закон сохранения импульса?

Вариант выполнения измерений.

1. Определяем массы шариков m₁ и m₂  при помощи динамометра (или весов) и записываем в таблицу:

m₁=62 г

m₂=27,5 г

2. Отклоняем большой шар от положения расновесия на 3 см и отпускаем его. 

S₀=3 см=30 мм

Замечаем его максимальное отклонение после удара. Повторяем опыт 5 раз, находим среднее значение отклонения и записываем в таблицу S_1ср.

S₁=13мм   S₁=15мм   S₁=18мм    S₁=14мм   S₁=16мм

S_1ср=(13мм+15мм+18мм+14мм+16мм)/5=15,2 мм

3. Повторяем этот же опыт, но теперь замечаем после удара отклонение шара меньшей массы. Повторяем опыт 5 раз, находим среднее значение и записываем в таблицу S_2ср.

S₂=31мм   S₂=34мм   S₂=36мм    S₂=35мм   S₂=32мм

S_2ср=(31мм+34мм+36мм+35мм+32мм)/5=34мм

4. Повторяем опыт, отклоняя шар большей массы на 4 см и 5 см. 

S₀=4 см=40 мм

S₁=18 мм   S₁=19 мм   S₁=23 мм    S₁=22 мм   S₁=18 мм

S_1ср=(18 мм+19 мм+23 мм+22 мм+18 мм)/5=20 мм

S₂=43 мм   S₂=44 мм   S₂=46 мм    S₂=47 мм   S₂=45 мм

S_2ср=(43 мм + 44 мм + 46 мм + 47 мм + 45 мм)/5=45 мм

S₀=5 см=50 мм

Результаты измерений записываем в таблицу.

№	m1, г	m2, г	S0, мм	S1, мм	S2, мм	m1∙S0, г∙мм с	m1∙S1, г∙мм с	m2∙S2, г∙мм с	m1∙S1 + m2∙S2, г∙мм с
1	62,0	27,5	30	15	34
2	62,0	27,5	40	20	45
3	62,0	27,5	50	25	56

Словами этот закон сохранения можно сформулировать так:

В замкнутой системе сумма импульсов тел не меняется со временем.

Формула:

[ large boxed{ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} + ldots + vec{p_{n}} = const}]

Помним, что при сложении векторов учитываем их направления.

Примечания:

1. Импульс иногда называют количеством движения. Рекомендую освежить в памяти, какие виды импульсов есть в физике и что такое импульс.
2. Формулировку закона сохранения импульса можно упростить:

В замкнутой системе вектор ( vec{p_{text{общ}}})  не меняется.

Математики данный факт запишут таким способом:

[ large boxed{ vec{p_{text{общ}}} = const}]

Дополнительно читайте о том, какие системы можно считать замкнутыми, и какие виды систем в физике есть.

Пояснения к формуле закона сохранения импульса

Пусть, несколько тел двигаются в замкнутой системе.

В начальный момент времени сложим векторы ( vec{p} ) импульсов всех тел, входящих в систему.

В результате получим новый вектор, обозначим его ( vec{p_{text{общ}}} ). Этот вектор – импульс всей системы, как единого целого.

Время идет. Тела продолжают двигаться и соударяться. При ударах их импульсы будут меняться (и по направлению, и по модулю).

После каждого удара будем с помощью геометрии складывать новые импульсы тел.

При этом выяснится следующее: складывая новые импульсы тел, мы будем получать все тот же вектор ( vec{p_{text{общ}}} ), который был получен нами в начале.

Импульс сохраняется, на примере бильярдных шаров

Предположим, мы склонились над гладким бильярдным столом и смотрим на него сверху. Рассмотрим три бильярдных шара на столе (рис. 1). Массы шаров одинаковые.

( m_{1} = m_{2} = m_{3})

Шары под номерами 2 и 3 покоятся. Значит, их начальные скорости и импульсы равны нулю.

Шар №2: ( vec{v_{2text{до}}} = 0),  импульс ( vec{p_{2text{до}}} = 0)

Для третьего шара ( vec{v_{3text{до}}} = 0) и ( vec{p_{3text{до}}} = 0)

Еще один шар движется со скоростью ( vec{v_{1text{до}}} ) по направлению к шарам 2 и 3.

Его вектор импульса обозначен ( vec{p_{1text{до}}} ) на рисунке.

Сложим импульсы всех шаров, чтобы найти общий вектор импульса системы

[ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} ]

[ vec{p_{1}} + 0 + 0 = vec{p_{1}} ]

То есть, импульс первого шара равен импульсу всех шаров системы (рис. 2) до удара

[ vec{p_{1}} = vec{p_{text{общ.до}}} ]

Во время удара шар 1 подействовал на шары 2 и 3 силой и передал им импульс.

После удара шар под номером 1 остановился, а шары 2 и 3 пришли в движение.

Примечание: в бильярде иногда бывает такое, шар передает свой импульс полностью шару, о который он ударяется.

Направления, в которых двигаются шары 2 и 3, указаны векторами их импульсов ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ) на рисунке 3.

Рассмотрим векторы импульсов шаров 2 и 3 подробнее. Совместим их начала и дорисуем параллелограмм (рис. 4), чтобы сложить импульсы ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ).

В результате сложения получим вектор, обозначенный на рисунке 5 красной стрелкой и символом ( vec{p_{text{общ.после}}} )

Сравним векторы ( vec{p_{text{общ.до}}} ) и ( vec{p_{text{общ.после}}} ). Как видно из рисунка 6, у векторов совпадают длины и направления. Если у векторов совпадают обе характеристики, то векторы равны. О равенстве векторов подробно написано тут.

Запишем математически равенство векторов:

[ vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}} ].

Общий импульс системы до удара = общему импульсу системы после удара.

Это выражение и есть закон сохранения импульса.

Далее, советую почитать о способе решения задач, связанных с только что изученной темой. Переходите по ссылке, чтобы правильно составить формулу закона сохранения для двух случаев —  абсолютно упругий и абсолютно неупругий удар (откроется в новой вкладке).

Amaxar 777

Высший разум

(105281)


1 год назад

Непонятно, на каком этапе в такой задаче вообще может возникнуть сложность (особенно при доступе к учебнику и к интернету)
-) Вам даны: масса, скорость в момент перед ударом. Значит вы можете найти импульс перед ударом.
-) Вы знаете, на какую высоту шарик подлетел после удара. Значит, вы можете найти скорость в момент после удара (можете через ЗСЭ, можете через формулы кинематики для равноускоренного движения). Далее найдете импульс после удара.
-) Если вы найдете импульсы до и после удара, вы сможете найти, на сколько изменился импульс в процесе удара, это и будет приращением импульса и ответом на первый вопрос задачи.
-) Воспльзуйтесь соотношением:
N Δt = Δp
и найдите N. Получите ответ на второй вопрос задачи.

Задача №47

Определить импульс р, полученный стенкой
при ударе о нее шарика массой m
= 300 г, если шарик двигался со скоростью
v = 8 м/с под углом α = 60º к
плоскости стенки. Удар о стенку считать
упругим.

Дано:

m = 0,3 кг

v₀ = 8 м/с

α = 60º

Найти: p = ?

Решение:

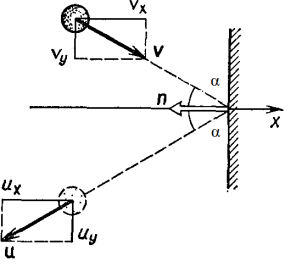
Рисунок 1

Стенка неподвижна, поэтому система
отсчета, связанная с ней, будет
инерциальной. Удар о стенку упругий;
следовательно, можно воспользоваться
законом сохранения механической энергии.
Из него, учитывая, что масса стенки много
больше массы шара, следует равенство
модулей скоростей шара |v| до и |u| после
удара.

Покажем, что угол отражения шарика от
стенки равен углу падения шара. Спроецируем
векторы

и

на координатные оси Ох и Оу (рис.1).
Так как стенка гладкая, то
.
Учитывая, кроме того, что |v| = |u|, получим u_x
= –v_x а отсюда следует равенство
углов падения и отражения.

Для определения импульса, полученного
стенкой, воспользуемся законом сохранения
импульса. Для нашего случая этот закон
можно записать в виде

,

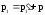где 
и

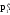
– импульсы шара до и после удара ().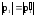
Отсюда импульс, полученный стенкой,

.

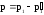Из рис. 2 видно, что вектор р сонаправлен
с осью Ох и его модуль 

p = |р| = 2p₁sinα.

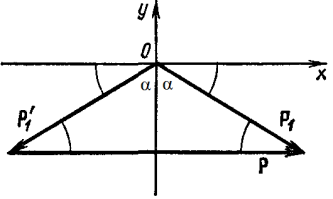
Рисунок 2

Подставив сюда выражение импульса p₁
= mv, получим

.

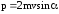Подставляя исходные данные и проверяя
размерность, получаем:

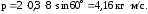
Ответ:
4,16 кг∙м/с.

Соседние файлы в предмете Физика

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #