В этой главе…
- Измеряем количество движения
- Вычисляем импульс
- Выясняем связь между силой и изменением импульса
- Разбираемся с законом сохранения импульса
- Знакомимся с разными типами столкновений
Эта глава посвящена понятиям, которые следует учитывать при изучении движения объектов, а именно с импульсом и моментом импульса. Оба эти понятия играют большую роль в двух разделах механики: кинематике, посвященной изучению движения объектов, и динамике, посвященной изучению взаимодействия объектов. Владея этими понятиями, можно легко описывать поведение объектов при столкновениях: с какой скоростью продолжат движение сталкивающиеся объекты (не хотелось бы, чтобы на их месте были ваш автомобиль или велосипед), в каком направлении продолжит движение теннисный мячик после столкновения с ракеткой, насколько глубоко дротик для игры в дартс вонзится в мишень и т.п. Чтобы получить ответы на эти и многие другие вопросы, нужно очень хорошо представлять себе, что такое импульс и момент импульса. Описанию именно этих понятий и посвящается данная глава.
Содержание
- Изучаем количество движения
- Получаем импульс
- Связываем работу силы и изменение импульса
- Пример: вычисляем импульс бильярдного шара
- Пример: определяем импульс капель дождя
- Изучаем закон сохранения импульса
- Измеряем скорость с помощью закона сохранения импульса
- Измеряем начальную скорость пули с помощью закона сохранения импульса
- Упругие и неупругие столкновения
- Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
- Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
- Упругие столкновение на прямой
- Упругое столкновение с более тяжелым объектом
- Упругое столкновение с более легким объектом
- Упругие столкновения в одной плоскости
Изучаем количество движения
В физике импульсом называется количество движения, которое приобретает тело под действием заданной силы за определенное время. Играя в бильярд, нетрудно убедиться в разнообразных проявлениях импульса. Чем сильнее и быстрее удар кия по шару, тем интенсивнее движется шар. Чем больше столкновений испытает шар, тем менее интенсивным становится его движение.
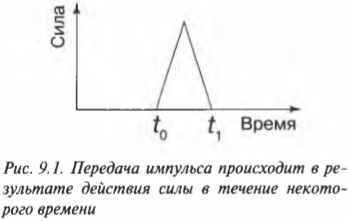
В повседневных ситуациях мы привыкли говорить, что тому или иному объекту или событию придают импульс. Рассмотрим процесс передачи импульса более подробно на примере бильярдного кия и шара. Процесс передачи импульса начинается в момент ( t_0 ) первого соприкосновения кия с шаром и заканчивается в момент ( t_1 ) утраты контакта между кием и шаром. В общем зависимость силы воздействия кия на шар от времени имеет сложный характер. Однако доя простоты можно положить, что она линейно возрастает от нулевого значения в момент ( t_0 ) первого соприкосновения, достигает максимального значения в момент наибольшего контакта, а потом снижается до нуля в момент ( t_1 ) утраты контакта между кием и шаром. Эта идеализированная зависимость силы взаимодействия кия и шара от времени графически показана на рис. 9.1.
Время взаимодействия кия и шара очень мало (несколько долей секунды), и зафиксировать характер изменения силы можно только с помощью очень точного оборудования. Обычно физики используют не точные мгновенные значения, а усредненные величины. Например, в данном примере приобретенный шаром импульс ( mathbf{p} ) равен произведению средней силы взаимодействия ( mathbf{overline{F}} ) и времени взаимодействия ( Delta{t}=t_1-t_0 ):
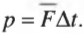
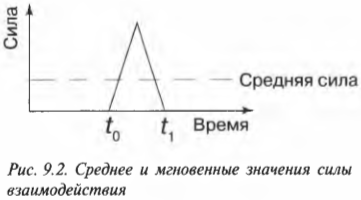
Обратите внимание, что эта формула связывает векторы силы и импульса. Действительно, импульс — это вектор, обладающий некоторой величиной и направлением, совпадающим с направлением силы, например результирующей векторной суммы всех действующих на объект сил.
Из этой формулы ясно, что изменение импульса измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Получаем импульс
Изменение импульса (т.е. определенного количества движения) объекта означает изменение характера его движения. Причем это изменение зависит от массы и скорости объекта, поскольку импульс равен произведению скорости и массы объекта. Импульс является очень важной физической концепцией, которая используется не только в начальном курсе физики, но и в некоторых очень сложных разделах физики, например в физике элементарных частиц, где компоненты атомов носятся с огромными скоростями. Именно на основании анализа импульсов до и после столкновения элементарных частиц ученые могут делать выводы о поведении субатомного мира.
Общая идея импульса понятна даже тем, кому незнакомо это понятие. Не так уж легко остановить тележку, которая катится по склону горы. Дело в том, что тележка массивна и обладает большой скоростью. Еще труднее остановить огромный нефтяной танкер. Порой для полной остановки крупного танкера требуется около 30 км тормозного пути! И все это из-за огромного импульса, которым он обладает.
Чем больше масса движущегося объекта (представьте себе огромный танкер) и чем больше скорость объекта (представьте себе быстро плывущий танкер), тем больше импульс объекта.
Итак, импульс объекта равен:
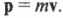
Как видите, импульс — это вектор с определенной величиной и направлением (о векторах подробнее рассказывается в главе 4). Импульс, как и количество движения, измеряется в системе СИ в ньютонах в секунду (Н·с), а в системе СГС — в динах-секундах (дин·с).
Связываем работу силы и изменение импульса
Придать объекту импульс так же просто, как ударить клюшкой для гольфа по мячу. Достаточно применить элементарные алгебраические преобразования ко второму закону Ньютона и мы получим связь между работой силы и изменением импульса. С чего начать? Начнем со связи силы и скорости. Как известно, ускорение определяется следующей формулой:
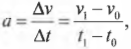
где ( Delta{v} ) — это изменение скорости за промежуток времени ( Delta{t} ), ( v_0 ) — это начальная скорость в момент времени ( t_0 ), a ( v_1 ) — это конечная скорость в момент времени ( t_1 ). Теперь, если умножить обе части этой формулы на массу объекта ( m ), то слева получим:
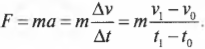
Теперь, чтобы получить связь силы с импульсом объекта, умножим эту формулу на промежуток времени ( Delta{t} ) и получим:
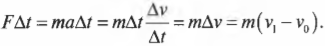
Посмотрите повнимательнее на правую часть формулы ( m(v_1-v_0) ). Поскольку импульс объекта с массой ( m ) равен ( p=mv ), то эта часть формулы выражает разницу конечного ( p_1=mv_1 ) и начального ( p_0=mv_0 ) импульса, т.е.:
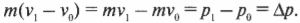
Следовательно, в итоге получим:
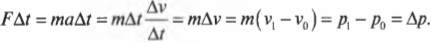
Итак, справа имеем силу, умноженную на промежуток времени ее действия, т.е. ( FDelta{t} ), а слева — изменение импульса ( Delta{p} ). Убирая промежуточные выкладки, получим искомую формулу связи силы и изменения импульса объекта:
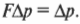
Произведение силы на время ее действия называется импульсом силы за то же время. (Его не следует путать с понятием импульс объекта ( p=mv ). Применение обоих этих понятий часто приводит к путанице, и потому понятие импульс силы используется довольно редко. — Примеч. ред.)
Пример: вычисляем импульс бильярдного шара
С помощью приведенных выше уравнений можно связать действующую на объект силу и приобретенный им импульс. Попробуем применить полученные знания при игре в бильярд. Допустим, что время контакта кия с бильярдным шаром приблизительно равно 5 мс (1 миллисекунда, или сокращенно 1 мс, равна 10-3 с). Насколько нужно изменить импульс неподвижного бильярдного шара, чтобы загнать его в лузу с отскоком от боковой стенки?
Пусть шар имеет массу 200 г (т.е. 0,2 кг). Допустим, что путем тщательных замеров и вычислений стало известно, что для попадания в лузу с отскоком от боковой стенки шару нужно приобрести скорость 20 м/с. Какую силу нужно приложить к кию для выполнения этой задачи?
Итак, в начальный момент времени шар покоится, т.е. начальная скорость ( v_0 ) = 0, а его конечная скорость ( v_1 ) должна быть равна 20 м/с. Вычислим необходимое изменение импульса по уже известной нам формуле:
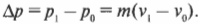
Подставив значения получим:
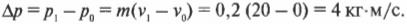
Итак, необходимо изменить импульс шара на 4 кг·м/с. Вычислим, какую силу нужно для этого приложить за промежуток времени 5 мс по известной формуле:
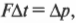
откуда
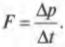
Подставив значения, получим:
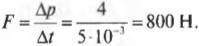
Итак, чтобы загнать бильярдный шар в лузу с отскоком от боковой стенки нужно прилагать к кию силу 800 Н в течение 5 мс.
Пример: определяем импульс капель дождя
После триумфальной демонстрации своих физических познаний в бильярдной попробуем использовать их в более привычной ситуации. Предположим, что на обратном пути домой внезапно начался дождь. Не беда, ведь под рукой есть зонт. Допустим, что на раскрытый зонт ежесекундно со средней скоростью около 10 м/с падает приблизительно 100 г капель воды. Вопрос: с какой силой нужно удерживать зонт массой 1 кг, чтобы удержать его под таким дождем?
Чтобы удержать зонт даже в отсутствие дождя, потребуется сила, равная весу зонта, то есть:
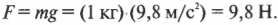
А как же подсчитать воздействие капель дождя? Предположим, что капли после падения на зонт почти мгновенно стекают по его почти горизонтальной поверхности. Даже в этом случае нам нужно учесть не только их массу, но и уменьшение скорости из-за встречи с зонтом. Действительно, летящие капли имеют начальную скорость 10 м/с, а после падения на зонт останавливаются, т.е. приобретают нулевую конечную скорость. Итак, имеем изменение импульса капель дождя, вызванное взаимодействием с зонтом. Попробуем оценить это изменение с помощью известной формулы:
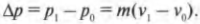
Подставляя значения, получим:
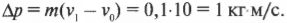
Такое изменение импульса капель происходит ежесекундно. Свяжем теперь его с известной нам формулой:
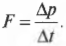
Подставив значения, получим:
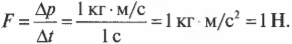
Итак, помимо силы 9,8 Н для удержания сухого зонта потребуется еще дополнительная сила 1 Н для компенсации торможения капель, т.е. всего потребуется сила 10,8 Н.
Наибольшую трудность при вычислениях изменения импульса под действием силы вызывает оценка времени действия этой силы. Поэтому при решении задач, связанных с изменением импульса, при столкновениях объектов обычно стремятся использовать другие параметры процесса, например скорость до и после столкновения, избегая оценок трудновычислимых параметров.
Изучаем закон сохранения импульса
Согласно этому закону, в изолированной системе без внешних сил общий импульс всех объектов системы до столкновений между ними равен общему импульсу всех объектов системы после столкновений между ними.
Если для анализа импульсов взаимодействующих объектов использовать приведенные выше формулировки с указанием силы и времени ее действия, то на это придется затратить чрезвычайно много усилий. Закон сохранения импульса позволяет избежать этих сложностей. Дело в том, что, применяя этот закон, можно полностью исключить из рассмотрения силы и время их действия.
Допустим, что два беспечных пилота космических кораблей А и Б не смогли избежать лобового столкновения своих машин. Во время столкновения корабль Б воздействовал на корабль А со средней силой ( F_{АБ} ). Согласно известной формуле о связи между силой и изменением импульса, получим для корабля А:
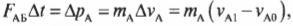
где ( m_{А} ) — это масса корабля A, ( v_{А1} ) — скорость корабля А после столкновения и ( v_{А0} ) — скорость корабля А до столкновения.
Аналогично, во время столкновения корабль А воздействовал на корабль Б со средней силой ( F_{БА} ). Опять по известной формуле о связи между силой и изменением импульса, получим для корабля Б:
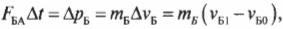
где ( m_{Б} ) — это масса корабля Б, ( v_{Б1} ) — скорость корабля Б после столкновения и ( v_{Б0} ) — скорость корабля Б до столкновения.
Сложим оба последних равенства и получим следующее уравнение:
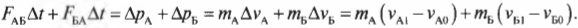
Опустим промежуточные выкладки и оставим только крайние левую и правую части этого равенства. Причем в правой части соберем отдельно члены начального и конечного состояний и получим:
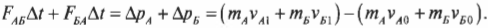
Сумма ( m_Av_{A1}+m_Бv_{Б1} ) означает суммарный конечный импульс ( p_{1}=p_{A1}+p_{Б1} ) двух кораблей после столкновения, а сумма ( m_Av_{A0}+m_Бv_{Б0} ) — суммарный начальный импульс ( p_{0}=p_{A0}+p_{Б0} ) двух кораблей до столкновения. Следовательно, последнее уравнение можно переписать в следующем виде:
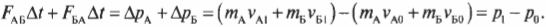
Если теперь ввести обозначение ( sum!{F} ) для суммы этих двух сил ( F_{АБ}+F_{БА} ), то получим:
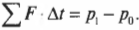
При работе с изолированной, или замкнутой, системой объектов внешних сил нет. Именно такая ситуация рассматривается в данном примере.
Если два космических корабля столкнутся при отсутствии внешних сил, то согласно третьему закону Ньютона, ( F_{АБ}=-F_{БА} ). Иначе говоря, в замкнутой системе имеем:
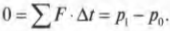
А это означает, что:

Это равенство означает, что в изолированной системе без внешних сил начальный импульс двух сталкивающихся объектов до их столкновения равняется конечному импульсу после столкновения, что соответствует закону сохранения импульса.
Извлекаем тепло из суммарного импульса.
Всегда ли сохраняется суммарный импульс объектов при их лобовом столкновении и сцеплении? В реальном мире далеко не всегда. Дело в том, что часто при столкновениях объектов они необратимо деформируются и часть их кинетической энергии расходуется на необратимую деформацию и рассеивается в виде тепловой энергии. Однако для точного расчета такого преобразования кинетической энергии в тепловую требуется учесть много других сложных физических процессов. Эти процессы обычно не рассматриваются в начальном курсе физики, а тем более в этом курсе.
Измеряем скорость с помощью закона сохранения импульса
Попробуем применить закон сохранения импульса для расчета некоторых параметров движения. Предположим, что при игре в хоккей игрок А с массой 100 кг решил применить силовой прием против другого неподвижного игрока Б тоже с массой 100 кг (который оказался его братом-близнецом). Для этого игрок А разогнался до скорости 11 м/с, грубо толкнул игрока Б и, схватив его руками, устроил потасовку. С какой скоростью будут двигаться оба сцепившихся руками игрока после столкновения?
Будем считать, что в данном примере мы имеем дело с замкнутой системой (см. предыдущий раздел), поскольку мы пренебрегаем всеми внешними силами, включая силу трения. Хотя в вертикальном направлении на хоккеистов со стороны ледяного катка действует нормальная сила (подробнее о ней см. в главе 6), но она равна по величине весу игроков и противоположна по направлению и в сумме дает нуль.
Итак, рассмотрим горизонтальные проекции импульсов игроков. Согласно закону сохранения импульса, имеем:
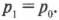
Подставим в эту формулу массу и начальную скорость игроков (на самом деле нужно подставить массу ( m_А ) и начальную скорость ( v_{А0} ) только игрока А, поскольку игрок Б имел нулевую начальную скорость):
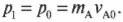
Конечный импульс ( p_1 ) должен быть равен произведению общей массы ( m_А+m_Б ) игроков на их конечную скорость ( v_{АБ1} ), т.е. получаем:
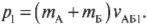
Из двух последних уравнений получаем:
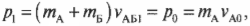
откуда легко можно выразить конечную скорость ( v_{АБ1} ):
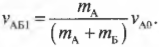
Подставляя значения, получим:
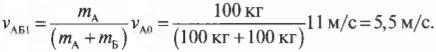
Конечная скорость двух игроков равна половине начальной скорости одного игрока. Этого следовало ожидать, ведь масса движущихся объектов увеличилась вдвое, а поскольку импульс сохраняется, то скорость должна уменьшиться во столько же раз.
Измеряем начальную скорость пули с помощью закона сохранения импульса
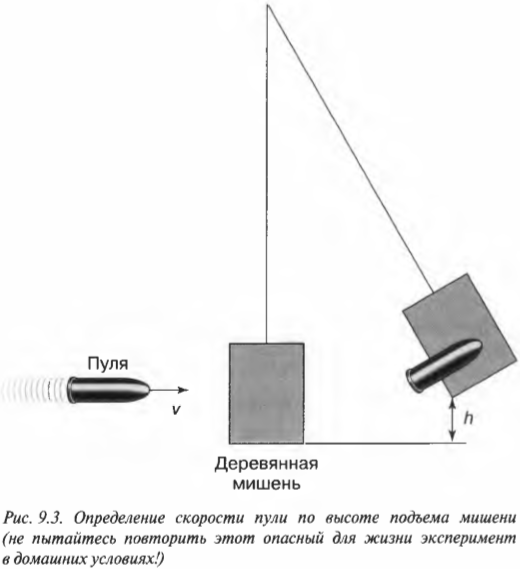
Закон сохранения импульса очень удобно использовать для определения скорости объекта, если ее нельзя или очень трудно измерить с помощью секундомера. Предположим, что изготовитель пуль хочет знать, какой будет начальная скорость новой пули. Как ему поступить? Для решения этой задачи ему предложили использовать приспособление, показанное на рис. 9.3.
Как оно может помочь? Оказывается, что если выстрелить пулей с массой ( m ) в массивную деревянную мишень с массой ( M ) и пуля застрянет в мишени, то, как и в примере с хоккеистами, конечная скорость мишени с пулей ( v_1 ) будет зависеть от начальной скорости пули ( v_0 ). Как именно? Для конкретного ответа на этот вопрос попробуем использовать закон сохранения импульса.
Итак, начальный суммарный импульс пули и мишени равен:
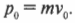
Поскольку пуля застряла в мишени, то конечный суммарный импульс пули и мишени равен:
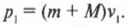
Если пренебречь потерями энергии на преодоление трения при попадании пули в мишень, то согласно закону сохранения импульса, эти два импульса должны быть равны:
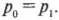
Тогда:
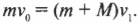
и искомая начальная скорость равна:
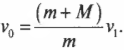
Итак, остается только определить конечную скорость ( v_1 ) мишени с застрявшей в ней пулей. Для этого нужно вспомнить закон сохранения энергии, который описывается в главе 8. Ведь после попадания пули мишень отклонится и поднимется на некоторую максимальную высоту ( h ), на которой ее скорость станет равной нулю. В этой точке ее кинетическая энергия ( frac{(m+M)v^2_1}{2} ) преобразуется в потенциальную ( (m+M)gh ). Итак, согласно закону сохранения энергии получим:
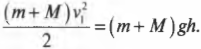
Откуда легко вывести формулу для конечной скорости мишени с застрявшей в ней пулей ( v_1 ):
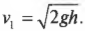
Подставим эту формулу в прежнее выражение для искомой начальной скорости пули:
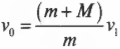
и получим:
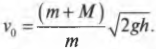
Пусть пуля имеет массу 50 г, деревянная мишень — 10 кг, а после попадания пули в нее мишень отклонилась и поднялась на максимальную высоту 0,5 м. Подставляя значения в приведенную выше формулу, получим:
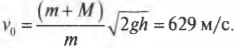
Таким образом, мы определили начальную скорость пули. Изготовитель пуль будет просто в восторге от такого простого и удобного способа.
Упругие и неупругие столкновения
Изучение физики на примере столкновений разных тел — это очень интересное и увлекательное занятие. Во многом это объясняется тем, что многие вычисления значительно упрощаются благодаря закону сохранения импульса (более подробно он рассматривается в предыдущих разделах этой главы). Однако, как мы уже убедились в предыдущих примерах, в некоторых столкновениях одного этого закона недостаточно и нужно применять закон сохранения энергии. Это особенно полезно для анализа столкновений объектов со скоростями, векторы которых направлены не вдоль одной прямой (как в предыдущих примерах), а лежат в одной плоскости.
В реальной жизни такие ситуации происходят сплошь и рядом. Например, при изучении причин дорожно-транспортного происшествия часто требуется проанализировать начальные и конечные скорости столкнувшихся автомобилей. При сортировке вагонов нужно учитывать начальные и конечные скорости сталкивающихся вагонов и составов.
Что происходит в таких столкновениях, если столкнувшиеся объекты не “слипаются” друг с другом? Рассмотрим более общий пример: пусть два бильярдных шара сталкиваются дуг с другом с разными скоростями, направленными друг к другу под произвольным углом. Как определить их величину и направление их скоростей после столкновения? Для этого потребуется не только закон сохранения импульса, но и закон сохранения энергии.
Когда сталкивающиеся объекты отскакивают друг от друга: упругие столкновения
В реальном мире при столкновении тел всегда наблюдаются потери энергии на деформацию и рассеивание тепла. В некоторых случаях эти потери столь малы, что ими можно пренебречь, как, например, при столкновении двух бильярдных шаров. В физике такие столкновения с сохранением кинетической энергии сталкивающихся объектов называют упругими столкновениями. Итак, в упругом столкновении сохраняется общая кинетическая энергия замкнутой системы объектов, т.е. суммарная кинетическая энергия после столкновения равна суммарной кинетической энергии до столкновения.
Когда сталкивающиеся объекты не отскакивают друг от друга: неупругие столкновения
Если во время столкновения объектов какая-то часть энергии тратится на работу каких-то неконсервативных сил (например, на преодоление силы трения, деформацию и т.п.), то кинетическая энергия системы не сохраняется. Она частично преобразуется в другие формы энергии. Такие столкновения в физике называют неупругими столкновениями. Итак, в неупругом столкновении общая кинетическая энергия замкнутой системы объектов не сохраняется, т.е. суммарная кинетическая энергия после столкновения не равна суммарной кинетической энергии до столкновения. Примеры неупругих столкновений можно наблюдать в дорожно-транспортных происшествиях, когда столкнувшиеся машины деформируют друг друга или даже сцепляются и движутся как единое целое.
Совсем не обязательно, чтобы после неупругого столкновения объекты сцеплялись друг с другом. Достаточно, чтобы часть кинетической энергии “утрачивалась”, т.е. переходила в другую форму, например в тепловую энергию. Неупругое столкновение внешне может быть очень похоже на упругое столкновение, например при касательном столкновении двух машин с образованием легких повреждений. На образование этих повреждений необратимо тратится часть кинетической энергии, но машины могут независимо продолжить движение.
Упругие столкновение на прямой
Итак, мы уже выяснили, что при упругом столкновении кинетическая энергия сталкивающихся объектов сохраняется. Проще всего изучать особенности упругого столкновения, когда векторы скоростей находятся на одной прямой. Рассмотрим идеализированный пример столкновения двух машин с совершенно упругими (т.е. недеформирую- щимися) бамперами, которые движутся по прямой.
Упругое столкновение с более тяжелым объектом
Предположим, что вы решили прокатиться на автомобиле А с массой 300 кг и на скорости около 10 м/с столкнулись с внезапно остановившимся перед вами другим автомобилем Б с массой 400 кг. Какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 300 кг имел начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 400 кг — начальную скорость ( v_{Б0} ) = 0. Если считать систему двух автомобилей замкнутой, то их общий импульс должен сохраняться, то есть:
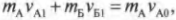
где ( v_{А1} ) — это конечная скорость автомобиля А после столкновения, a ( v_{Б1} ) — это конечная скорость автомобиля Б после столкновения.
У нас есть одно уравнение с двумя неизвестными ( v_{А1} ) и ( v_{Б1} ). Чтобы их найти, нужно иметь еще одно уравнение, связывающее эти неизвестные. Как насчет кинетической энергии? Действительно, поскольку столкновение было упругим, то кинетическая энергия объектов должна сохраняться, т.е. должно выполняться равенство:
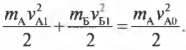
Теперь у нас есть два уравнения и две неизвестных величины. С помощью простых алгебраических операций можно легко получить выражения для неизвестных скоростей ( v_{А1} ) и ( v_{Б1} ):
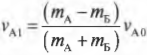
и
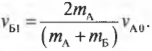
Подставляя значения в обе эти формулы, получим:
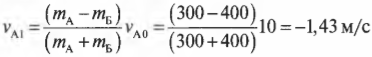
и
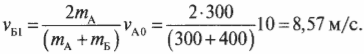
Анализируя полученные значения, можно легко восстановить ход событий. Итак, автомобиль А на скорости 10 м/с столкнулся с неподвижным автомобилем Б. После столкновения автомобиль А отскочил назад (об этом свидетельствует отрицательный знак конечной скорости ( v_{А1} )) со скоростью 1,43 м/с, а автомобиль Б начал движение вперед со скоростью 8,57 м/с. Автомобиль А легче автомобиля Б, а что если бы было наоборот?
Упругое столкновение с более легким объектом
Предположим, что в предыдущем примере движущийся автомобиль А тяжелее неподвижного автомобиля Б. Пусть автомобиль А с массой 400 кг на скорости около 10 м/с сталкивается с внезапно остановившимся перед вами другим автомобилем Б с массой 300 кг. Вопрос остается прежним: какими будут скорости обоих автомобилей после их упругого столкновения?
Итак, до столкновения автомобиль А с массой ( m_А ) = 400 кг имеет начальную скорость ( v_{А0} ) = 10 м/с, а автомобиль Б с массой ( m_Б ) = 300 кг — начальную скорость ( v_{Б0} ) = 0. Используем уже известные нам формулы скоростей ( v_{А1} ) и ( v_{Б1} ):
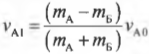
и
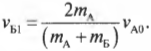
Подставим в них новые значения и получим:
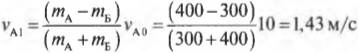
и
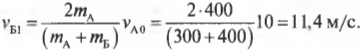
Как видите, более тяжелый движущийся автомобиль А после столкновения с более легким автомобилем Б смог продолжить движение в том же направлении, но с меньшей скоростью. Причем часть своего импульса он передал более легкому автомобилю Б.
Упругие столкновения в одной плоскости
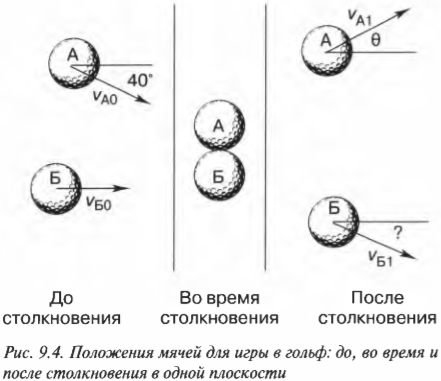
Столкновения объектов не всегда происходят по прямой линии. Например, бильярдные шары сталкиваются так, что векторы их скоростей могут быть направлены не вдоль одной прямой, а находится в одной плоскости под произвольным углом друг к другу. В этом случае нужно учитывать не только величину, но и направление скорости. Пусть во время игры в гольф два игрока одновременно (простим им это нарушение правил) ударяют по разным мячам А и Б, мячи упруго сталкиваются и продолжают движение, как показано на рис. 9.4. Какими будут скорости мячей после столкновения?
Попробуем решить эту задачу, учитывая, что мячи имеют одинаковую массу ( m ) = 46 г. Мяч А имеет начальную скорость ( v_{А0} ) = 1,0 м/с, а мяч Б — начальную скорость ( v_{Б0} ) = 2,0 м/с. Кроме того, пусть нам известны направления векторов начальных скоростей обоих мячей (см. рис. 9.4).
Для решения задачи нам потребуются закон сохранения импульса и закон сохранения энергии. Поскольку столкновение считается упругим, то кинетическая энергия системы сохраняется, т.е. согласно закону сохранения энергии, имеем:
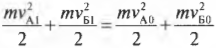
или в более простой форме:
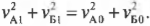
Если подставить вместо скоростей их компоненты по осям X и Y, то получим:
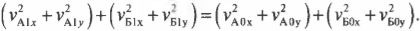
Так как трение здесь не учитывается, то в процессе столкновения внутренние силы упругого взаимодействия мячей направлены только по вертикальной оси Y. Эти силы не изменяют компоненты импульсов мячей по горизонтальной оси X:
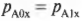
и
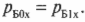
Отсюда следует, что компоненты скоростей мячей по горизонтальной оси X после столкновения тоже не изменяются:
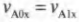
и
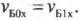
(То есть компоненты скоростей мячей по горизонтальной оси X в результате столкновения не изменились.)
Соотношение, полученное ранее из закона сохранения энергии:
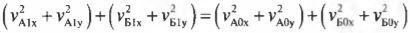
с учетом постоянства компонент скоростей по оси X теперь будет иметь следующий вид:
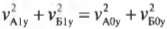
или (поскольку ( v_{Б0у} ) = 0);
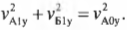
Согласно закону сохранения импульса, для компонент импульса по вертикальной оси Y имеем( mv_{А1у}+mv_{Б1у}=mv_{А0у}+mv_{Б0у} ) или в более простой форме (поскольку ( v_{Б0у} ) = 0):
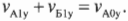
Из двух последних равенств нетрудно получить выражения для компонент скоростей по вертикальной оси Y:
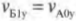
и
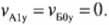
Как видите, при таком упругом столкновении у мячей остались прежними их компоненты скоростей по горизонтальной оси X, и они “обменялись” компонентами скоростей по вертикальной оси Y. Это значит, что мяч А продолжит движение с нулевой компонентой ( v_{А1у} ), т.е. по горизонтали, а мяч Б продолжит движение под углом ( alpha ), который легко вычислить по формуле:
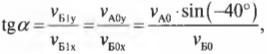
где знак “минус” перед значением угла означает, что на рис. 9.4 угол откладывается в направлении против часовой стрелки.
А скорости мячей после столкновения будут равны
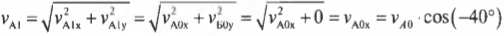
и:
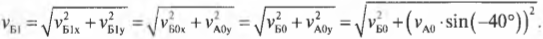
Подставив значения, получим:
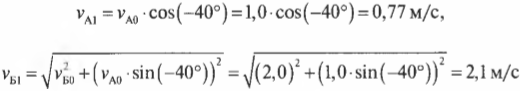
и
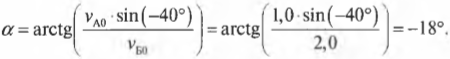
Глава 9. Двигаем объекты: количество движения и импульс
3 (60%) 5 votes
Макеты страниц
В качестве примера практического применения новой формы второго закона Ньютона рассмотрим задачу об абсолютно упругом ударе шара массой  о неподвижную стенку (рис. 4.11).
о неподвижную стенку (рис. 4.11).
Допустим, что шар до удара имеет скорость  и движется перпендикулярно стенке. Нужно найти скорость
и движется перпендикулярно стенке. Нужно найти скорость  с которой он будет двигаться после удара, и импульс, который получит стенка во время удара.
с которой он будет двигаться после удара, и импульс, который получит стенка во время удара.
Рассмотрим отдельно последовательные стадии удара.
С момента соприкосновения в шаре и стенке начнут развиваться деформации. Вместе с ними будут возникать постепенно возрастающие упругие силы  действующие на стенку и на шар и тормозящие движение шара. Нарастание деформаций и сил прекратится в тот момент, когда скорость шара обратится в нуль:
действующие на стенку и на шар и тормозящие движение шара. Нарастание деформаций и сил прекратится в тот момент, когда скорость шара обратится в нуль: 
Таким образом, для этой стадии удара мы знаем начальное и конечное значение количества движения шара и по ним можем определить импульс, полученный за это время шаром от стенки. Сила в это время меняет свое значение от нуля до некоторой максимальной
величины, поэтому выразить импульс прямо через силу довольно сложно. Введем так называемую среднюю силу: средней силой будем называть постоянную силу  сообщающую телу такой же импульс, какой сообщает ему переменная сила за то же время.
сообщающую телу такой же импульс, какой сообщает ему переменная сила за то же время.
Для импульса средней силы, которая действовала на шар при его деформации, теперь можно записать уравнение второго закона Ньютона:  Так
Так  то окончательно получим:
то окончательно получим:

Изменение количества движения шара за первую половину удара и импульс, полученный шаром, оказываются равными начальному количеству движения, взятому с обратным знаком.
Во время второй половины удара после полной остановки шара упругие силы заставят его двигаться в обратном направлении. Деформации, а вместе с ними упругие силы, начнут уменьшаться. При этом все значения деформаций и сил повторятся в обратном порядке за такое же время. Следовательно, во время второй стадии удара шар получит от стенки дополнительно такой же импульс  как и на первой стадии. Теперь подставим в уравнение второго закона Ньютона
как и на первой стадии. Теперь подставим в уравнение второго закона Ньютона  найденные значения импульса и скоростей, соответствующие второй половине удара. Так как
найденные значения импульса и скоростей, соответствующие второй половине удара. Так как  то получим
то получим

Приравнивая левые части выражений, записанных для первой и второй половин удара, находим:

После упругого удара о стенку по нормали шар будет иметь скорость  равную по модулю начальной скорости
равную по модулю начальной скорости  и противоположно ей направленную. Полный импульс, полученный шаром за все время удара, и полное изменение количества движения будут равны
и противоположно ей направленную. Полный импульс, полученный шаром за все время удара, и полное изменение количества движения будут равны 

Рис. 4.11.
По третьему закону Ньютона стенка получит от шара такой же импульс  но направленный в противоположную сторону.
но направленный в противоположную сторону.
Допустим, что стенка испытывает за одну секунду  таких ударов. Во время каждого удара стенка получит импульс
таких ударов. Во время каждого удара стенка получит импульс  Всего за секунду стенка получит импульс
Всего за секунду стенка получит импульс  Зная этот импульс, можно вычислить среднюю силу
Зная этот импульс, можно вычислить среднюю силу  которая действует на стенку и создается ударами шаров. Полный импульс, полученный стенкой, будет
которая действует на стенку и создается ударами шаров. Полный импульс, полученный стенкой, будет

где  время, в течение которого произошли
время, в течение которого произошли  ударов. Подставляя
ударов. Подставляя  найдем, что за одну секунду на стенку будет действовать средняя сила
найдем, что за одну секунду на стенку будет действовать средняя сила 
Рассмотренный пример особенно важен потому, что именно таким образом подсчитываются силы давления газа на стенки сосуда. Как вы узнаете в курсе молекулярной физики, давление газа на стенки сосуда возникает за счет импульсов, которые сообщают стенке при ударах быстро движущиеся молекулы газа. При этом предполагают, что каждый удар молекулы является абсолютно упругим. Проведенные нами расчеты полностью применимы к этому случаю. Вся трудность расчета давления газа состоит в правильном подсчете числа ударов  молекул о стенки сосуда за единицу времени. Заметим также, что совпадение модуля силы с модулем импульса, сообщаемого этой силой за единицу времени, часто используется в решении многих практических задач.
молекул о стенки сосуда за единицу времени. Заметим также, что совпадение модуля силы с модулем импульса, сообщаемого этой силой за единицу времени, часто используется в решении многих практических задач.
Отметим, наконец, что в наших рассуждениях скрывается одно недосказанное предположение о том, что время, затраченное на создание деформаций во время удара, равно времени снятия деформаций. Немного позже мы докажем его справедливость.
Заключение – дополнение к тексту
Мы применили закон сохранения импульса (одного из основных законов природы) к абсолютно неупругому и абсолютно упругому удару шаров.
При абсолютно неупругом ударе шары (тела) не сохраняют свою форму, то есть испытывают пластическую деформацию. К такому удару
можно отнести удар свинцовых шаров. При неупругом ударе не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. При неупругом ударе механическая энергия полностью или частично переходит во внутреннюю энергию тел (тела нагреваются). В случае нецентрального (косого) удара тел их общий импульс и общая скорость после абсолютно неупругого удара находятся путём векторного сложения импульсов отдельных тел.
При абсолютно упругом ударе (сюда можно грубо приближённо отнести удар стальных шаров) выполняется и закон сохранения импульса, и закон сохранения механической энергии. При упругом ударе механическая энергия шаров частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию шаров. Шары приобретают скорости
направления и модули которых определяются законами сохранения полного импульса и полной энергии системы. Последний 3) частный случай говорит о том, что если лёгкий шарик испытает абсолютно упругий удар о неподвижную стенку, то он отскочит от неё без потери скорости. Пусть теперь шарик падает на неподвижную стенку под углом.
Тогда нормальная составляющая скорости шарика изменит своё направление на обратное, а по модулю останется прежней. Тангенциальная же составляющая скорости не изменится, поэтому угол падения будет равен углу отражения.
На рисунке вектора скорости падения и скорости отражения шарика перенесены в точку падения. Вектор изменения скорости направлен вверх перпендикулярно поверхности стенки. Такие же направления имеют импульсы шарика до удара и после удара о стенку, а вектор приращения импульса шарика
направлен по нормали от стенки.
В молекулярной физике происходит то же самое, когда молекулы газа ударяются о стенку сосуда. Проявляется это давлением газа на стенку сосуда.
Подумаем, что можно найти, если в условии задачи сказано, что шарик летит под прямым углом к движущейся навстречу стенке и между ними происходит упругий удар:
Сразу можно сказать, что скорость шарика относительно движущейся стенки равна
(см. занятие 12 на относительность движения). От стенки шарик отскочит со скоростью
относительно стенки, а относительно земли его скорость после удара
Далее можно найти импульс шара относительно земли до и после удара. Сможем найти изменение его импульса, его кинетическую энергию до и после удара.
Изменение кинетической энергии даст работу, совершённую силой упругости за время удара. Работу же можно выразить через произведение силы удара на перемещение стенки за время удара и найти силу удара.
Таким образом, через данные в условии задачи сможем охарактеризовать упругий удар между шаром и движущейся стенкой.
Абсолютно неупругий удар и абсолютно упругий удар – это предельные случаи кратковременного взаимодействия шаров (тел). При взаимодействии реальных тел имеют место и упругие, и неупругие деформации. Формула, связывающая скорости шаров до удара и после удара имеет вид:
коэффициент восстановления относительной скорости при ударе. В случае абсолютно неупругого удара он равен нулю; в случае абсолютно упругого удара он равен единице.
При ударе реальных тел этот коэффициент принимает промежуточные значения между нулём и единицей. Для стали этот коэффициент равен 0,56.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Занятие 23. Импульс системы тел. Центр масс системы
Следующая запись:Задачи 1 – 4 к занятиям 22 – 24
Первая запись на канале: Занятие 1. Физика. Механика. Кинематика
Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:

Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:

Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
![]()
Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:


Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:

Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:

Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
 На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
 Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
 Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20k
Словами этот закон сохранения можно сформулировать так:
В замкнутой системе сумма импульсов тел не меняется со временем.
Формула:
[ large boxed{ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} + ldots + vec{p_{n}} = const}]
Помним, что при сложении векторов учитываем их направления.
Примечания:
- Импульс иногда называют количеством движения. Рекомендую освежить в памяти, какие виды импульсов есть в физике и что такое импульс.
- Формулировку закона сохранения импульса можно упростить:
В замкнутой системе вектор ( vec{p_{text{общ}}}) не меняется.
Математики данный факт запишут таким способом:
[ large boxed{ vec{p_{text{общ}}} = const}]
Дополнительно читайте о том, какие системы можно считать замкнутыми, и какие виды систем в физике есть.
Пояснения к формуле закона сохранения импульса
Пусть, несколько тел двигаются в замкнутой системе.
В начальный момент времени сложим векторы ( vec{p} ) импульсов всех тел, входящих в систему.
В результате получим новый вектор, обозначим его ( vec{p_{text{общ}}} ). Этот вектор – импульс всей системы, как единого целого.
Время идет. Тела продолжают двигаться и соударяться. При ударах их импульсы будут меняться (и по направлению, и по модулю).
После каждого удара будем с помощью геометрии складывать новые импульсы тел.
При этом выяснится следующее: складывая новые импульсы тел, мы будем получать все тот же вектор ( vec{p_{text{общ}}} ), который был получен нами в начале.
Импульс сохраняется, на примере бильярдных шаров
Предположим, мы склонились над гладким бильярдным столом и смотрим на него сверху. Рассмотрим три бильярдных шара на столе (рис. 1). Массы шаров одинаковые.
( m_{1} = m_{2} = m_{3})

Рис. 1. Шар 1 движется по направлению к покоящимся шарам 2 и 3
Шары под номерами 2 и 3 покоятся. Значит, их начальные скорости и импульсы равны нулю.
Шар №2: ( vec{v_{2text{до}}} = 0), импульс ( vec{p_{2text{до}}} = 0)
Для третьего шара ( vec{v_{3text{до}}} = 0) и ( vec{p_{3text{до}}} = 0)
Еще один шар движется со скоростью ( vec{v_{1text{до}}} ) по направлению к шарам 2 и 3.
Его вектор импульса обозначен ( vec{p_{1text{до}}} ) на рисунке.
Сложим импульсы всех шаров, чтобы найти общий вектор импульса системы
[ vec{p_{1}} + vec{p_{2}} + vec{p_{3}} ]
[ vec{p_{1}} + 0 + 0 = vec{p_{1}} ]
То есть, импульс первого шара равен импульсу всех шаров системы (рис. 2) до удара
[ vec{p_{1}} = vec{p_{text{общ.до}}} ]

Рис. 2. До удара вектор импульса системы шаров равен вектору импульса первого шара
Во время удара шар 1 подействовал на шары 2 и 3 силой и передал им импульс.
После удара шар под номером 1 остановился, а шары 2 и 3 пришли в движение.
Примечание: в бильярде иногда бывает такое, шар передает свой импульс полностью шару, о который он ударяется.
Направления, в которых двигаются шары 2 и 3, указаны векторами их импульсов ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ) на рисунке 3.

Рис. 3. После удара шар 1 остановился, шары 2 и 3 пришли в движение, стрелками указано направление движения шаров
Рассмотрим векторы импульсов шаров 2 и 3 подробнее. Совместим их начала и дорисуем параллелограмм (рис. 4), чтобы сложить импульсы ( vec{p_{2text{после}}} ) и ( vec{p_{3text{после}}} ).

Рис. 4. Совместим начала векторов импульса шаров 2 и 3 после удара для их сложения
В результате сложения получим вектор, обозначенный на рисунке 5 красной стрелкой и символом ( vec{p_{text{общ.после}}} )

Рис. 5. Общий вектор импульса системы получим, складывая векторы импульса шаров 2 и 3 после удара
Сравним векторы ( vec{p_{text{общ.до}}} ) и ( vec{p_{text{общ.после}}} ). Как видно из рисунка 6, у векторов совпадают длины и направления. Если у векторов совпадают обе характеристики, то векторы равны. О равенстве векторов подробно написано тут.

Рис. 6. Сравнивая вектор импульса системы до удара с вектором импульса системы послу удара обнаружим их равенство
Запишем математически равенство векторов:
[ vec{p_{text{общ.до}}} = vec{p_{text{общ.после}}} ].
Общий импульс системы до удара = общему импульсу системы после удара.
Это выражение и есть закон сохранения импульса.
Далее, советую почитать о способе решения задач, связанных с только что изученной темой. Переходите по ссылке, чтобы правильно составить формулу закона сохранения для двух случаев — абсолютно упругий и абсолютно неупругий удар (откроется в новой вкладке).






