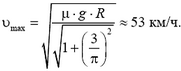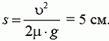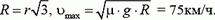Мякишев Г.Я., Кондрашева Л., Крюков С. Работа сил трения //Квант. — 1991. — № 5. — С. 37-39.
По специальной договоренности с редколлегией и редакцией журнала “Квант”
Сила трения, как и любая другая сила, совершает работу и соответственно изменяет кинетическую энергию тела при условии, если точка приложения силы перемещается в выбранной системе отсчета. Однако сила трения существенно отличается от других, так называемых консервативных, сил (тяготения и упругости), так как ее работа зависит от формы траектории. Вот почему работу сил трения ни при каких обстоятельствах нельзя представить в виде изменения потенциальной энергии системы. Кроме того, дополнительные сложности при вычислении работы создает специфика силы трения покоя. Здесь существует ряд стереотипов физического мышления, которые хотя и лишены смысла, но очень устойчивы.
Мы рассмотрим несколько вопросов, связанных с не вполне правильным пониманием роли силы трения в изменении энергии системы тел.
О силе трения скольжения
Нередко говорят, что сила трения скольжения всегда совершает отрицательную работу и это приводит к увеличению внутренней (тепловой) энергии системы.
Такое утверждение нуждается в важном уточнении — оно справедливо только в том случае, если речь идет не о работе одной отдельно взятой силы трения скольжения, а о суммарной работе всех таких сил, действующих в системе. Дело в том, что работа любой силы зависит от выбора системы отсчета и может быть отрицательной в одной системе, но положительной в другой. Суммарная же работа всех сил трения, действующих в системе, не зависит от выбора системы отсчета и всегда отрицательна. Вот конкретный пример.
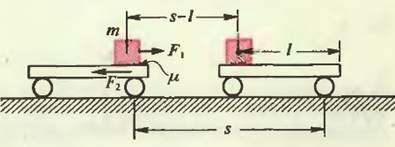
Рис. 1
Положим кирпич на движущуюся тележку так, чтобы он начал по ней скользить (рис. 1). В системе отсчета, связанной с землей, сила трения F1, действующая на кирпич до, прекращения скольжения, совершает положительную работу A1. Одновременно сила трения F2, действующая на тележку (и равная по модулю первой силе), совершает отрицательную работу A2, по модулю большую, чем работа A1, так как путь тележки s больше пути кирпича s – l (l — путь кирпича относительно тележки). Таким образом, получаем
(~A_1 = mu mg(s – l), A_2 = -mu mgs) ,
и полная работа сил трения
(~A_{tr} = A_1 + A_2 = -mu mgl < 0) .
Поэтому кинетическая энергия системы убывает (переходит в тепло):
(~Delta E_k = -mu mgl) .
Этот вывод имеет общее значение. Действительно, работа двух сил (не только сил трения), осуществляющих взаимодействие между телами, не зависит от выбора системы отсчета (докажите это самостоятельно). Всегда можно перейти к системе отсчета, относительно которой одно из тел покоится. В ней работа силы трения, действующей на движущееся тело, всегда отрицательна, так как сила трения направлена против относительной скорости. Но она отрицательна и в любой другой системе отсчета. Следовательно, всегда, при любом количестве тел в системе, Atr < 0. Эта работа и уменьшает механическую энергию системы.
О силе трения покоя
При действии между соприкасающимися телами силы трения покоя ни механическая, ни внутренняя (тепловая) энергия этих тел не изменяется. Значит ли это, что работа силы трения покоя равна нулю? Как и в первом случае, такое утверждение правильно только по отношению к полной работе сил трения покоя над всеми взаимодействующими телами. Одна же отдельно взятая сила трения покоя может совершать работу, причем как отрицательную, так и положительную.
Рассмотрим, например, книгу, лежащую на столе в набирающем скорость поезде. Именно сила трения покоя сообщает книге такую же скорость, как у поезда, т. е. увеличивает ее кинетическую энергию, совершая определенную работу при этом. Другое дело, что такая же по модулю, но противоположная по направлению сила действует со стороны книги на стол, а значит, и на поезд в целом. Эта сила совершает точно такую же работу, но только отрицательную. В результате получается, что полная работа двух сил трения покоя равна нулю, и механическая энергия системы тел не меняется.
О движении автомобиля без проскальзывания колес
Самое устойчивое заблуждение связано именно с этим вопросом.
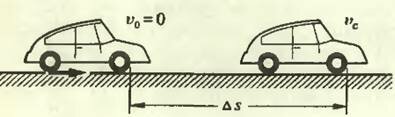
Рис. 2
Пусть автомобиль вначале покоится, а затем начинает разгоняться (рис. 2). Единственной внешней силой, сообщающей автомобилю ускорение, является сила трения покоя Ftr действующая на ведущие колеса (мы пренебрегаем силой сопротивления воздуха и силой трения качения). Согласно теореме о движении центра масс, импульс силы трения равен изменению импульса автомобиля:
(~F_{tr} Delta t = Delta(M upsilon_c) = M upsilon_c) ,
если скорость центра масс в начале движения равнялась нулю, а в конце υc. Приобретая импульс, т. е. увеличивая свою скорость, автомобиль одновременно получает и определенную порцию кинетической энергии. А поскольку импульс сообщается силой трения, естественно считать, что и увеличение кинетической энергии определяется работой этой же силы. Вот это-то утверждение оказывается совершенно неверным. Сила трения ускоряет автомобиль, но работы при этом не совершает. Как же так?
Рис. 3
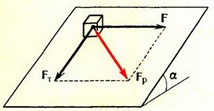
Вообще говоря, ничего парадоксального в этой ситуации нет. В качестве примера достаточно рассмотреть совсем простую модель — гладкий кубик с прикрепленной сбоку пружинкой (рис. 3). Кубик, придвигают к стене, сжимая пружинку, а затем отпускают. «Отталкиваясь» от стены, наша система (кубик с пружинкой) приобретает определенные импульс и кинетическую энергию. Единственной внешней силой, действующей по горизонтали на систему, является, очевидно, сила реакции стены Fp. Именно она и сообщает системе ускорение. Однако никакой работы при этом, конечно, не совершается — ведь точка приложения этой силы неподвижна (в системе координат, связанной с землей), хотя сила действует некоторое конечное время Δt.
Аналогичная ситуация возникает и при разгоне автомобиля без проскальзывания. Точка приложения силы трения, действующей на ведущее колесо автомобиля, т. е. точка соприкосновения колеса с дорогой, в любой момент покоится относительно дороги (в системе отсчета, связанной с дорогой). При движении автомобиля она исчезает в одной точке и сразу же появляется в соседней.
Не противоречит ли сказанное закону сохранения механической энергии? Конечно же, нет. В нашем случае с автомобилем изменение кинетической энергии системы происходит за счет ее внутренней энергии, выделяющейся при сгорании топлива.
Для простоты рассмотрим чисто механическую систему: игрушечный автомобиль с пружинным заводом. Двигатель такого автомобиля использует не внутреннюю энергию топлива, а потенциальную энергию сжатой пружины. Вначале пружина заведена, и ее потенциальная энергия Ep1 отлична от нуля. Если двигатель игрушки — просто растянутая пружина, то (~E_{p1} = frac{k (Delta l)^2}{2}). Кинетическая энергия равна нулю, и полная начальная энергия автомобиля E1 = Ep1. В конечном состоянии, когда деформация пружины исчезнет, потенциальная энергия равна нулю, а кинетическая энергия (~E_{k2} = frac{M upsilon_c^2}{2}). Полная энергия E2 = Ek2. Согласно закону сохранения энергии (трением мы пренебрегаем),
(~frac{M upsilon_c^2}{2} = frac{k (Delta l)^2}{2}) .
В случае реального автомобиля
(~frac{M upsilon_c^2}{2} = Delta U) ,
где ΔU — энергия, полученная при сгорании топлива.
Если колеса автомобиля проскальзывают, то Atr<0, так как точка соприкосновения колес с дорогой движется против направления силы трения. Следовательно,
(~frac{M upsilon_c^2}{2} = frac{k (Delta l)^2}{2} + A_{tr}) .
Видно, что кинетическая энергия автомобиля в конечном состоянии оказывается меньше, чем в отсутствие проскальзывания.
Задача по физике. Объясните решение.
Ученик
(105),
закрыт
10 лет назад
профессор Де Жа Ву
Мудрец
(18606)
10 лет назад
Импульс силы равен произведению силы на время действия этой силы:
F* (t1 – t0).
Время действия силы задана условием и равно 20 сек.
Сила же находится из 2-го закона Ньютона:
F = ma = 1000кг*(20/20) [м/сек**2] = 1000 н.
Искомый импульс сила = 1000 н. * 20 сек = 2*10**4 [н*сек] = 20 [кн*сек]
NB Критику, не знающему физики (см. ниже ответ) : разгоняющей силой (силой тяги авто) и является сила трения: на абсолютно гладкой (скользкой) и ровной поверхности автомобиль не будет способен передвигаться.
LaFleurNike
Гуру
(3748)
10 лет назад
Из ур-ния профессора Де Жа Ву F=ma получается, что по горизонтали действовала только сила трения, которая разгоняла авто?
По-моему в этой задаче нужно знать еще силу тяги авто, тогда можно будет найти ответ
Сила
трения
– сила, возникающая при движении одного
тела по поверхности другого, направлена
простив скорости.
Точка
приложения
находится на границе раздела
соприкасающихся тел.
Причина
возникновения:
все тела имеют шероховатости, при
движении тела зацепляются друг за друга
неровностями, скорость уменьшается.
Тело останавливается. При этом разрываются
межмолекулярные связи, и возникает
сила трения.
Виды
сил трения:
1.
Трение покоя – самая большая сила
трения.
2.
Сила трения скольжения.
3.
Трение качения – самая малая.
Любая
сила трения зависит:
1.
От площади соприкасающихся поверхностей.
2.
От качества обработки поверхности.
3.
От вида материала, из которого сделаны
тела.
Fтр=μmg
Fтр=μN
μ
– коэффициент трения
g
– ускорение свободного падения = 9,8м/с
Есть
сухое
и влажное
трение, влажное меньше сухого.
8. Импульс тела и импульс силы. Второй закон Ньютона.
Импульс
– толчок, количество движения.
Импульс
тела
– физическая векторная величина, равная
произведению массы тела на скорость.
=m*
[кг*м/с]
Импульс
силы
(
*Δt)
– произведение силы, действующей на
тело, на время ее действия.(
*Δt)=[H*c]
[H*c=(кг*м)/с²*с=кг*м/с]
– эти единицы измерения эквивалентны.
Второй
закон Ньютона через импульс:
a=F/m;
F=ma
a=(V-Vo)/Δt
F=m*(V-Vo)/Δt
F*Δt=
m*(V-Vo)
F*Δt=
m*V–m*Vo
– второй закон Ньютона через импульс
F*Δt=P-Po
P-Po=Δp
F*Δt=Δp
Импульс
силы равен изменению импульса тела.
Следствия
из второго закона Ньютона:
F=Δp/Δt
Сила, действующая на тело равна изменению
импульса тела в единицу времени.
Импульс
– универсальная величина, т.е. он остается
неизменным в любых системах отсчета,
при любых скоростях.
9. Закон сохранения импульса. Реактивное движение.
Закон
сохранения импульса
– универсальный закон природы, который
выполняется в замкнутых
системах
– это системы, где взаимодействуют
между собой только тела, входящие в эту
систему, а другие тела вне этой системы
с ними не взаимодействуют.
В
замкнутых системах тела могут
взаимодействовать двумя способами:
1.
Упругое взаимодействие
– после взаимодействия тела движутся
отдельно.
2.
Неупругое взаимодействие
– после взаимодействия тела движутся
как единое целое.
После
неупругого взаимодействия система тел
будет двигаться в ту сторону, куда
движется тело с большей массой.
Закон
сохранения импульса:
в замкнутой системе геометрическая
(векторная) сумма импульсов тел до
взаимодействия равна геометрической
сумме импульсов тел после взаимодействия.
m1*
1+m2*
2=m1*
1′+
m2*
2′=const
Реактивное
движение
– движение, возникающее при отделении
частей замкнутой системы друг от друга,
при этом выполняется закон сохранения
импульса.
Примеры:
отдача при выстреле, движение кальмаров,
медуз, бабочек, ракет, пароходов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
17.05.2015430.93 Кб221.pdf
- #
- #
Баканина Л.П. Силы трения // Квант. — 1973. — № 9. — С. 68-71.
По специальной договоренности с редколлегией и редакцией журнала «Квант»
Сила трения часто вызывает у поступающих в вуз серьезные затруднения, особенно сила трения покоя. Чему равна ее величина? Как она направлена? Попытаемся ответить на эти вопросы, разобрав несколько конкретных примеров. Задачи, рассмотренные в статье, в разные годы предлагались на вступительных экзаменах в Московский физико-технический институт, и многие абитуриенты не смогли с ними справиться.
Прежде всего вспомним некоторые особенности сил сухого трения, возникающего между двумя твердыми телами. При непосредственном взаимодействии (соприкосновении) этих тел возникают силы, действующие на каждое из них. Согласно третьему закону Ньютона эти силы равны по величине и противоположны по направлению. Составляющие этих сил, направленные перпендикулярно соприкасающимся поверхностям, называют силами нормального давления. Составляющие, направленные вдоль поверхности, называют силами трения.
Пусть тело лежит на горизонтальном столе. Будем действовать на него горизонтальной силой, величина которой постепенно увеличивается. До тех пор, пока эта сила меньше определенной величины Fmax, тело будет сохранять состояние покоя потому, что на тело со стороны стола действует сила трения покоя, по величине равная приложенной силе. Направление силы трения противоположно возможному перемещению. Если бы не было трения, тело сразу начало бы скользить. Можно сказать, что тело «пытается» начать скользить, но трение удерживает его на месте. Если же величина воздействия больше Fmax, возникает скольжение. Сила трения скольжения, как известно, не зависит от величины сил, действующих на тело вдоль поверхности:
Fск = μ∙N.
Величина силы нормального давления N не зависит ни от величины касательных взаимодействий, ни от свойств трущихся поверхностей.
Опыт показывает, что обычно Fск несколько меньше Fmax. Однако отличие это невелико, и при решении почти всех задач считают, что Fск = Fmax. Это приближение стало настолько привычным, что его обычно даже и не оговаривают. Точно так же пренебрегают зависимостью силы трения от скорости. На рисунке 1 пунктиром изображена (несколько преувеличено) зависимость силы трения от скорости, наблюдаемая на опыте, а сплошной линией — обычное упрощенное представление этой зависимости.

Рис. 1.
Перейдем теперь к разбору конкретных задач, при решении которых особенности сил трения играют существенную роль.
Задача 1. Поезд, подходя к станции со скоростью υ = 72 км/ч, начинает равномерно тормозить. Каково наименьшее время торможения поезда до полной остановки, безопасное для спящих пассажиров? Коэффициент трения пассажира о полку μ = 0,2.
При торможении поезда скорость движения полки, на которой лежит пассажир, уменьшается, и если бы пассажир сохранил прежнюю скорость, он начал бы скользить по полке вперед, по ходу движения поезда. Однако, как только он начинает или, вернее, как только он «пытается» начать скользить, возникает сила трения. Она сообщает пассажиру тормозящее ускорение. Если это ускорение равно ускорению поезда, скорость пассажира все время равна скорости полки, на которой он лежит, и пассажир не скользит по полке. Максимальное возможное ускорение может сообщить максимальная сила трения покоя, которая, как мы уже говорили, приближенно равна Fcк = μ·N. Согласно второму закону Ньютона
m·amax= μ·N,
где m — масса спящего пассажира, а N — сила его нормального давления на полку. Для горизонтальной полки N = m·g и amax = μ·g. Значит, ускорение поезда, при котором пассажиры не падают с полок, a ≤ μ·g.
Время торможения до полной остановки
Задача 2. Автомобиль, трогаясь с места, равномерно набирает скорость, двигаясь по горизонтальному участку дороги, представляющему собой дугу окружности в 30° радиуса R = 100 м. С какой максимальной скоростью автомобиль может выехать на прямой участок пути? Коэффициент трения колес о землю μ = 0,3.
Единственная внешняя горизонтальная сила, действующая на автомобиль, — это сила трения. Разгон, как мы предполагаем, происходит без проскальзывания, следовательно, мы имеем дело с силой трения покоя. Только эта сила и может сообщить автомобилю необходимое ускорение.
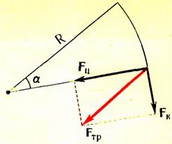
Рис. 2.
Так как движение автомобиля по окружности — это движение с ускорением, сила трения должна быть направлена под углом к скорости (рис.2). При этом составляющая Fk, направленная вдоль скорости, сообщает автомобилю необходимое для разгона ускорение, а составляющая Fn, направленная по радиусу окружности, изменяет направление скорости так, чтобы автомобиль двигался по окружности. Центростремительное ускорение 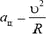
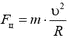
Как известно, пройденный путь, ускорение и скорость в конце пути связаны соотношением 2aц∙s = υ2. Отсюда 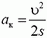
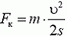
Геометрическая сумма сил Fк и Fц не должна превышать максимальной силы трения покоя Fтр = μ∙m∙g. Так как эти силы перпендикулярны друг другу, то в конце разгона
Отсюда
Задача 3. Небольшой кубик массы m покоится на шероховатой плоскости, наклоненной к горизонту под углом α. Коэффициент трения μ = 2·tg α. Определить, с какой минимальной горизонтальной силой F, лежащей в плоскости склона (рис. 3), нужно толкать, кубик, чтобы он начал двигаться.
Рис. 3.
При μ > tg α под действием только силы тяжести кубик не будет скользить по наклонной плоскости, так как направленная вдоль наклонной плоскости проекция силы тяжести Fт = m∙g∙sin α меньше максимальной силы трения покоя Fтр = μ∙m∙g∙cos α. Если приложить горизонтальную силу F, то результирующая сила, действующая вдоль наклонной плоскости, будет равна (см. рис. 3).
Если Fp ≥ Fтр, кубик начнет скользить, так как сила трения покоя уже не может его уравновесить. Минимальное значение необходимой для этого силы F можно найти из условия
F2 + (m∙g∙sin α)2 = (μ∙m∙g∙cos α)2.
Отсюда
Задача 4. Хоккейная шайба падает на лед под углом α к вертикали со скоростью υ0. С какой скоростью шайба начнет скользить по льду, если после удара о лед она не подпрыгивает? Коэффициент трения шайбы о лед равен μ.
Изменение количества движения, согласно второму закону Ньютона, равно импульсу действующей силы. По условию задачи вертикальная составляющая вектора количества движения за время удара обращается в нуль. Значит, импульс силы нормального давления на поверхность N·Δt равен
N·Δt = m·υ0·cos α,
где Δt — время удара, а N — средняя сила давления шайбы на лед во время удара.
Так как по условию задачи шайба после удара скользит, сила трения во время удара — это сила трения скольжения Fск = μ·N. Время соударения Δt очень мало, а m·Δυверт — конечная величина, поэтому сила нормального давления при ударе гораздо больше веса шайбы. Среднее значение силы трения во время удара
Импульс силы трения за время удара
Fтр·Δt = μ·N·Δt = μ·m·υ0·cos α.
Изменение горизонтальной составляющей количества движения шайбы за время удара равно
m·υ – m·υ0·sin α = –μ·m·υ0·cos α,
откуда υ = υ0·sin α – μ·υ0·cos α.
Если коэффициент трения μ очень мал, изменение горизонтальной составляющей количества движения шайбы тоже мало, и приближенно можно считать, что для горизонтальной проекции выполняется закон сохранения количества движения.
Следует отметить, что приведенное решение справедливо только тогда, когда μ ≤ tg α. Попробуйте разобраться самостоятельно, что будет происходить в случае, если μ > tg α.
Упражнения
1. Тело опускают без начальной скорости на ленту транспортера, движущуюся со скоростью υ = 3,6 км/ч. Коэффициент трения между телом и лентой μ = 1. Какой путь пройдет тело по ленте?
2. Изучая дорожное происшествие, автоинспектор установил, что след торможения автомобиля, ехавшего по асфальтовой дороге, равен 60 м. С какой скоростью ехал автомобиль, если коэффициент трения колес об асфальт при торможении равен 0,5?
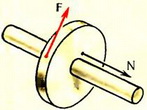
3. Маховик радиуса R = 0,2 м насажен на закрепленную горизонтальную ось радиуса r = 0,02 м. Сила трения между маховиком и осью Fск = 103 Н. Для того чтобы легче было снять маховик с оси, к его ободу прикладывается сила F = 80 Н, создающая вращающий момент относительно оси (рис. 4). С какой минимальной силой N нужно тянуть маховик вдоль оси, чтобы снять его?
Рис. 4.
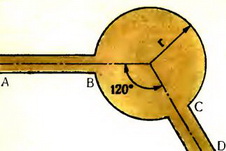
4. Две дороги, АВ и CD, направленные под углом 120° друг к другу, выходят на круглую асфальтированную площадь радиуса r = 68 м (рис. 5). С какой максимальной постоянной скоростью может ехать по площади автомобиль, чтобы попасть с одной дороги на другую, если коэффициент трения между асфальтом и шинами автомобиля μ = 0,4?
Рис. 5.
Ответы
1.
2. υ = 87 км/ч.
3. N = 600 Н.
4.
You should upgrade or use an alternative browser.
-
Forums
-
Homework Help
-
Introductory Physics Homework Help
What is the impulse of friction?
-
Thread starter
Jason03 -
Start date
May 16, 2008
- May 16, 2008
-
- #1
I know the impulse is the area under the curve…
[tex]mv_{1} + F_{avg}Delta{t} = mv_{} [/tex]
Answers and Replies
- May 16, 2008
- #2
What is the impulse of friction?
How does that change your equation?
- May 16, 2008
-
- #3
This equation allowed me to come up with the correct answer
[tex] mv_{1} + P-T(Delta{t}) = mv_{2}[/tex]
- May 16, 2008
- #4
heres the graph for the problem…http://img91.imageshack.us/img91/6935/graphmp3.jpg [Broken]
im trying to find the average Force at T = 8 seconds…but its not working
- May 16, 2008
- #5
- May 16, 2008
- #6
[tex] mv_{1} + P-T(Delta{t}) = mv_{2}[/tex]
but I tried solving for time at 8 seconds… finding the area under the curve which is just a rectange and triangle…but the answer comes up incorrect
as far as area it should just be [tex](L * W) + (.5*b*h)[/tex]
- May 16, 2008
- #7
I used this equation to solve for time at 5 seconds…and it worked…[tex] mv_{1} + P-T(Delta{t}) = mv_{2}[/tex]
That equation is not quite right. That second term (P) is a force, not an impulse. (It should be the area under that curve.)
but I tried solving for time at 8 seconds… finding the area under the curve which is just a rectange and triangle…but the answer comes up incorrectas far as area it should just be [tex](L * W) + (.5*b*h)[/tex]
Looks fine to me. Show me the details. What did you get for the impulse due to the force P? The impulse due to the friction force T?
- Jul 9, 2010
- #8
Don’t forget that Impulse is NET force * time. So if you have the graph of the force of the engine vs. time, you need to subtract out kinetic friction, which is considered constant over the time.
If the MR2 that kept up well with the viper was a Spyder, that is I think 137 hp and not 115 hp.
Suggested for: What is the impulse of friction?
- Dec 13, 2022
- Mar 12, 2023
- Apr 12, 2023
- Aug 29, 2022
- Apr 6, 2022
- Nov 26, 2022
- Dec 26, 2022
- Jan 24, 2023
- May 7, 2022
- Apr 11, 2023
-
Forums
-
Homework Help
-
Introductory Physics Homework Help