Как найти импульс спустя время - Сайт, где вы сможете решить свои вопросы

Импульс

Второй закон Ньютона в импульсной форме
Пример вычисления силы
Импульс системы тел
Закон сохранения импульса
Закон сохранения проекции импульса

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: импульс тела, импульс системы тел, закон сохранения импульса.

Импульс тела — это векторная величина, равная произведению массы тела на его скорость:

Специальных единиц измерения импульса нет. Размерность импульса — это просто произведение размерности массы на размерность скорости:

$[p]=[m]cdot [upsilon ]= frac{displaystyle kgcdot m}{displaystyle c}$ .

Почему понятие импульса является интересным? Оказывается, с его помощью можно придать второму закону Ньютона несколько иную, также чрезвычайно полезную форму.

к оглавлению ▴

Второй закон Ньютона в импульсной форме

Пусть vec{F} — равнодействующая сил, приложенных к телу массы . Начинаем с обычной записи второго закона Ньютона:

С учётом того, что ускорение тела vec{a} равно производной вектора скорости, второй закон Ньютона переписывается следующим образом:

$mfrac{displaystyle dvec{upsilon } }displaystyle {dt}=vec{F}$ .

Вносим константу под знак производной:

$frac{displaystyle d(mvec{upsilon } )}{displaystyle dt}= vec{F}$ .

Как видим, в левой части получилась производная импульса:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{F}$ . ( 1)

Соотношение ( 1) и есть новая форма записи второго закона Ньютона.

Второй закон Ньютона в импульсной форме. Производная импульса тела есть равнодействующая приложенных к телу сил.

Можно сказать и так: результирующая сила, действующая на тело, равна скорости изменения импульса тела.

Производную в формуле ( 1) можно заменить на отношение конечных приращений:

$frac{displaystyle Delta vec{displaystyle p} }{Delta displaystyle t}= vec{displaystyle F}$ . ( 2)

В этом случае vec{F} есть средняя сила, действующая на тело в течение интервала времени Delta t . Чем меньше величина Delta t , тем ближе отношение к производной , и тем ближе средняя сила vec{F} к своему мгновенному значению в данный момент времени.

В задачах, как правило, интервал времени Delta t достаточно мал. Например, это может быть время соударения мяча со стенкой, и тогда vec{F} — средняя сила, действующая на мяч со стороны стенки во время удара.

Вектор в левой части соотношения ( 2) называется изменением импульса за время Delta t . Изменение импульса — это разность конечного и начального векторов импульса. А именно, если $vec{p} _{0}$ — импульс тела в некоторый начальный момент времени, vec{p} — импульс тела спустя промежуток времени Delta t , то изменение импульса есть разность:

$Delta vec{p} = vec{p} -vec{p} _{0}$ .

Подчеркнём ещё раз, что изменение импульса — это разность векторов (рис. 1):

Рис. 1. Изменение импульса

Пусть, например, мяч летит перпендикулярно стенке (импульс перед ударом равен $vec{p} _{0}$ ) и отскакивает назад без потери скорости (импульс после удара равен $vec{p}= -vec{p} _{0}$ ). Несмотря на то, что импульс по модулю не изменился ( $p= p _{0}$ ), изменение импульса имеется:

$Delta vec{p} = vec{p} -vec{p} _{0}= -vec{p} _{0}-vec{p} _{0}= -2vec{p} _{0}$ .

Геометрически эта ситуация показана на рис. 2:

Рис. 2. Изменение импульса при отскоке назад

Модуль изменения импульса, как видим, равен удвоенному модулю начального импульса мяча: $Delta p= 2p_{0}$ .

Перепишем формулу ( 2) следующим образом:

, ( 3)

или, расписывая изменение импульса, как и выше:

$vec{p} -vec{p} _{0}=vec{F} Delta t$ .

Величина называется импульсом силы. Специальной единицы измерения для импульса силы нет; размерность импульса силы равна просто произведению размерностей силы и времени:

(Обратите внимание, что Hcdot c оказывается ещё одной возможной единицей измерения импульса тела.)

Словесная формулировка равенства ( 3) такова: изменение импульса тела равно импульсу действующей на тело силы за данный промежуток времени. Это, разумеется, снова есть второй закон Ньютона в импульсной форме.

к оглавлению ▴

Пример вычисления силы

В качестве примера применения второго закона Ньютона в импульсной форме давайте рассмотрим следующую задачу.

Задача. Шарик массы m= 100 г, летящий горизонтально со скоростью м/с, ударяется о гладкую вертикальную стену и отскакивает от неё без потери скорости. Угол падения шарика (то есть угол между направлением движения шарика и перпендикуляром к стене) равен $alpha = 60^{circ}$ . Удар длится с. Найти среднюю силу,
действующую на шарик во время удара.

Решение. Покажем прежде всего, что угол отражения равен углу падения, то есть шарик отскочит от стены под тем же углом alpha (рис. 3).

Рис. 3. К задаче (вид сверху)

Тут всё дело в том, что стена — гладкая. Это значит, что трения между шариком и стеной нет. Следовательно, со стороны стены на шарик действует единственная сила vec{N} — сила упругости, направленная перпендикулярно стене (рис. 4).

Рис. 4. К задаче

Согласно ( 3) имеем: . Отсюда следует, что вектор изменения импульса сонаправлен с вектором vec{N} , то есть направлен перпендикулярно стене в сторону отскока шарика (рис. 5).

Рис. 5. К задаче

Векторы $vec{p} _{0}$ и
vec{p} равны по модулю
(так как скорость шарика не изменилась). Поэтому треугольник, составленный из векторов $vec{p} _{0}$ , vec{p} и , является равнобедренным. Значит, угол между векторами vec{p} и равен alpha , то есть угол отражения действительно равен углу падения.

Теперь заметим вдобавок, что в нашем равнобедренном треугольнике есть угол $60^{circ}$ (это угол падения); стало быть, данный треугольник — равносторонний. Отсюда:

$Delta p= p_{0}= mupsilon = 0,1cdot 6= 0,6~Hcdot c$ .

И тогда искомая средняя сила, действующая на шарик:

$N= frac{displaystyle Delta p}{displaystyle Delta t}= frac{displaystyle 0,6}{displaystyle 0,01}= 60~H$ .

к оглавлению ▴

Импульс системы тел

Начнём с простой ситуации системы двух тел. А именно, пусть имеются тело 1 и тело 2 с импульсами $vec{p} _{1}$ и $vec{p} _{2}$ соответственно. Импульс vec{p} системы данных тел — это векторная сумма импульсов каждого тела:

$vec{p} = vec{p} _{1}+vec{p} _{2}$ .

Оказывается, для импульса системы тел имеется формула, аналогичная второму закону Ньютона в виде ( 1). Давайте выведем эту формулу.

Все остальные объекты, с которыми взаимодействуют рассматриваемые нами тела 1 и 2, мы будем называть внешними телами. Силы, с которыми внешние тела действуют на тела 1 и 2, называем внешними силами. Пусть $vec{F} _{1}$ — результирующая внешняя сила, действующая на тело 1. Аналогично $vec{F} _{2}$ — результирующая внешняя сила, действующая на тело 2 (рис. 6).

Рис. 6. Система двух тел

Кроме того, тела 1 и 2 могут взаимодействовать друг с другом. Пусть тело 2 действует на тело 1 с силой vec{T} . Тогда тело 1 действует на тело 2 с силой . По третьему закону Ньютона силы vec{T} и равны по модулю и противоположны по направлению: . Силы vec{T} и — это внутренние силы, действующие в системе.

Запишем для каждого тела 1 и 2 второй закон Ньютона в форме ( 1):

$frac{displaystyle dvec{displaystyle p} _ {displaystyle 1}}{displaystyle dt}=vec{F} _{1}+vec{T}$ , ( 4)

$frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}=vec{F} _{2}+{vec{T}}$ . ( 5)

Сложим равенства ( 4) и ( 5):

$frac{displaystyle dvec{displaystyle p} _{displaystyle 1}}{displaystyle dt}+frac{displaystyle dvec{displaystyle p} _{displaystyle 2}}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}+vec{T} +{vec{T}}$ .

В левой части полученного равенства стоит сумма производных, равная производной суммы векторов $vec{p} _{1}$ и $vec{p} _{2}$ . В правой части имеем в силу третьего закона Ньютона:

$frac{displaystyle d(vec{displaystyle p} _{displaystyle 1}+vec{displaystyle p} _{displaystyle 2})}{displaystyle dt}= vec{F} _{1}+vec{F} _{2}$ .

Но $vec{p} _{1}+vec{p} _{2}= vec{p}$ — это импульс системы тел 1 и 2. Обозначим также $vec{F} _{1}+vec{F} _{2}= vec{F} _{external}$ — это результирующая внешних сил, действующих на систему. Получаем:

$frac{dvec{displaystyle p} }{displaystyle dt}= vec{F} _{external}$ . ( 6)

Таким образом, скорость изменения импульса системы тел есть равнодействующая внешних сил, приложенных к системе. Равенство ( 6), играющее роль второго закона Ньютона для системы тел, мы и хотели получить.

Формула ( 6) была выведена для случая двух тел. Теперь обобщим наши рассуждения на случай произвольного количества тел в системе.

Импульсом системы тел тел называется векторная сумма импульсов всех тел, входящих в систему. Если система состоит из тел, то импульс этой системы равен:

$vec{p} = vec{p} _{1}+vec{p} _{2}+...+vec{p} _{N}$ .

Дальше всё делается совершенно так же, как и выше (только технически это выглядит несколько сложнее). Если для каждого тела записать равенства, аналогичные ( 4) и ( 5), а затем все эти равенства сложить, то в левой части мы снова получим производную импульса системы, а в правой части останется лишь сумма внешних сил (внутренние силы, попарно складываясь, дадут нуль ввиду третьего закона Ньютона). Поэтому равенство ( 6) останется справедливым и в общем случае.

к оглавлению ▴

Закон сохранения импульса

Система тел называется замкнутой, если действия внешних тел на тела данной системы или пренебрежимо малы, или компенсируют друг друга. Таким образом, в случае замкнутой системы тел существенно лишь взаимодействие этих тел друг с другом, но не с какими-либо другими телами.

Равнодействующая внешних сил, приложенных к замкнутой системе, равна нулю: $vec{F} _{external}= vec{0}$ . В этом случае из ( 6) получаем:

$frac{displaystyle dvec{displaystyle p} }{displaystyle dt}= vec{0}$ .

Но если производная вектора обращается в нуль (скорость изменения вектора равна нулю), то сам вектор не меняется со временем:

Закон сохранения импульса. Импульс замкнутой системы тел остаётся постоянным с течением времени при любых взаимодействиях тел внутри данной системы.

Простейшие задачи на закон сохранения импульса решаются по стандартной схеме, которую мы сейчас покажем.

Задача. Тело массы $m_{1}= 800$ г движется со скоростью $upsilon _{1}= 3$ м/с по гладкой горизонтальной поверхности. Навстречу ему движется тело массы $m_{2}= 200$ г со скоростью $upsilon _{2}= 13$ м/с. Происходит абсолютно неупругий удар (тела слипаются). Найти скорость тел после удара.

Решение. Ситуация изображена на рис. 7. Ось направим в сторону движения первого тела.

Рис. 7. К задаче

Поскольку поверхность гладкая, трения нет. Поскольку поверхность горизонтальная, а движение происходит вдоль неё, сила тяжести и реакция опоры уравновешивают друг друга:

$m_{1}vec{g} +vec{N} _{1}= vec{0}$ ,
$m_{2}vec{g} +vec{N} _{2}= vec{0}$ .

Таким образом, векторная сумма сил, приложенных к системе данных тел, равна нулю. Это значит, что система тел замкнута. Стало быть, для неё выполняется закон сохранения импульса:

$vec{p} _{before~hitting}= vec{p} _{after~hitting}$ . ( 7)

Импульс системы до удара — это сумма импульсов тел:

$vec{p} _{before~hitting}= m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}}$ .

После неупругого удара получилось одно тело массы $m_{1}+m_{2}$ , которое движется с искомой скоростью :

$vec{p} _{after~hitting}= (m_{1}+m_{2})vec{upsilon }$ .

Из закона сохранения импульса ( 7) имеем:

$m_{1}vec{upsilon _{1}} +m_{2}vec{upsilon _{2}} = (m_{1}+m_{2})vec{upsilon }$ .

Отсюда находим скорость тела, образовавшегося после удара:

$vec{upsilon} = frac{displaystyle m_{displaystyle 1}vec{displaystyle upsilon _{displaystyle 1}} +displaystyle m_{displaystyle 2}vec{displaystyle upsilon _{displaystyle 2}} }{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

Переходим к проекциям на ось :

$upsilon _{x}= frac{displaystyle m_{displaystyle 1}displaystyle upsilon _{displaystyle 1x}+displaystyle m_{displaystyle 2}upsilon _{displaystyle 2x}}{displaystyle m_{displaystyle 1}+displaystyle m_{displaystyle 2}}$ .

По условию имеем: $upsilon _{1x}= 3$ м/с, $upsilon _{2x}= -13$ м/с, так что

$upsilon _{x}= frac{displaystyle 0,8cdot 3-0,2cdot 13}{displaystyle 0,8+0,2}= -0,2frac{m}{c}$ .

Знак минус указывает на то, что слипшиеся тела двигаются в сторону, противоположную оси . Искомая скорость: м/с.

к оглавлению ▴

Закон сохранения проекции импульса

Часто в задачах встречается следующая ситуация. Система тел не является замкнутой (векторная сумма внешних сил, действующих на систему, не равна нулю), но существует такая ось , сумма проекций внешних сил на ось равна нулю в любой момент времени. Тогда можно сказать, что вдоль данной оси наша система тел ведёт себя как замкнутая, и проекция импульса системы на ось сохраняется.

Покажем это более строго. Спроектируем равенство ( 6) на ось :

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= F_{external,x}$ .

Если проекция равнодействующей внешних сил обращается в нуль, $F_{external,x}= 0$ , то

$frac{displaystyle dp_{displaystyle x}}{displaystyle dt}= 0$ .

Следовательно, проекция $p_{x}$ есть константа:

$p_{x}= const$ .

Закон сохранения проекции импульса. Если проекция на ось суммы внешних сил, действующих на систему, равна нулю, то проекция $p_{x}$ импульса системы не меняется с течением времени.

Давайте посмотрим на примере конкретной задачи, как работает закон сохранения проекции импульса.

Задача. Мальчик массы , стоящий на коньках на гладком льду, бросает камень массы со скоростью upsilon под углом alpha к горизонту. Найти скорость , с которой мальчик откатывается назад после броска.

Решение. Ситуация схематически показана на рис. 8. Мальчик изображён прямогольником.

Рис. 8. К задаче

Импульс системы «мальчик + камень» не сохраняется. Это видно хотя бы из того, что после броска появляется вертикальная составляющая импульса системы (а именно, вертикальная составляющая импульса камня), которой до броска не было.

Стало быть, система, которую образуют мальчик и камень, не замкнута. Почему? Дело в том, что векторная сумма внешних сил не равна нулю во время броска. Величина больше, чем сумма Mg+mg , и за счёт этого превышения как раз и появляется вертикальная компонента импульса системы.

Однако внешние силы действуют только по вертикали (трения нет). Стало быть, сохраняется проекция импульса на горизонтальную ось . До броска эта проекция была равна нулю. Направляя ось в сторону броска (так что мальчик поехал в направлении отрицательной полуоси), получим:

$-Mu+mupsilon _{0}cos alpha = 0$ ,

откуда

$u=frac{mupsilon _{0}cos alpha }{M}$ .

Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Импульс» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
07.05.2023

Источник

Законы, сформулированных Ньютоном, позволяют решить различные практически важные задачи, касающиеся взаимодействия и движения тел. Большое число таких задач связано, например, с нахождением ускорения движущегося тела, если известны все действующие на это тело силы. А далее по ускорению можно определить и другие величины, такие как перемещение, мгновенную скорость и др.

Прежде чем сформулировать закон сохранения импульса, давайте введем понятие импульса и проследим, каким образом связано это понятие с законами Ньютона, с которыми мы познакомились ранее.

Основным законом динамики, как мы уже говорили, является второй закон Ньютона, связывающий ускорение тела с его массой m и силой , действующей на это тело:

Зная связь ускорения тела со скоростью его движения и предполагая, что масса тела не изменяется с течением времени, выражение можно переписать несколько в ином виде:

Полученное выражение показывает, что результат действия силы можно понимать и несколько иначе, чем мы делали это раньше: действие силы на тело приводит к изменению некоторой величины, характеризующей это тело, которая равна произведению массы тела на скорость его движения. Эту величину называют импульсом тела :

Направление вектора импульса тела всегда совпадает с направлением вектора скорости движения.

Слово “импульс” в переводе с латинского означает “толчок”. В некоторых книгах вместо термина “импульс” используется термин “количество движения”.

Эта величина была введена в науку примерно в тот же период времени, когда Ньютоном были открыты законы, названные впоследствии его именем. Ещё в первой половине XVII века понятие импульса введено Рене Декартом. Так как физическое понятие массы в то время отсутствовало, он определил импульс как произведение «величины тела на скорость его движения». Позже такое определение было уточнено Исааком Ньютоном. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

Поскольку , то за единицу импульса в СИ принимают импульс тела массой 1 кг, движущегося со скорость 1 м/с. Соответственно единицей импульса тела в СИ является 1 кг * м/c.

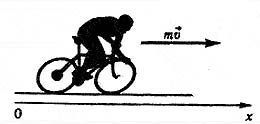
При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, то такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой.

Этот фундаментальный закон природы называется законом сохранения импульса. Он является следствием из второго и третьего законов Ньютона.

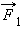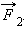Рассмотрим какие-либо два взаимодействующих тела, входящих в состав замкнутой системы. Силы взаимодействия между этими телами обозначим через и По третьему закону Ньютона 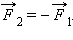Если эти тела взаимодействуют в течение времени t, то импульсы сил взаимодействия одинаковы по модулю и направлены в противоположные стороны: 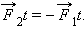Применим к этим телам второй закон Ньютона:

где 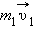и – и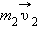мпульсы тел в начальный момент времени, 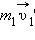и – и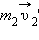мпульсы тел в конце взаимодействия. Из этих соотношений следует:

Это равенство означает, что в результате взаимодействия двух тел их суммарный импульс не изменился. Рассматривая теперь всевозможные парные взаимодействия тел, входящих в замкнутую систему, можно сделать вывод, что внутренние силы замкнутой системы не могут изменить ее суммарный импульс, т. е. векторную сумму импульсов всех тел, входящих в эту систему.

Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны. Примером может служить реактивное движение.

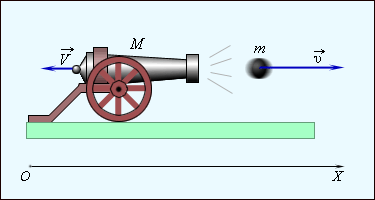
При стрельбе из орудия возникает отдача – снаряд движется вперед, а пушка– откатывается назад. Снаряд и пушка – два взаимодействующих тела. Скорость, которую приобретает пушка при отдаче, зависит только от скорости снаряда и отношения масс. Если скорости пушки и снаряда обозначить через 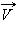и 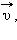а их массы через M и m, то на основании закона сохранения импульса можно записать в проекциях на ось OX:

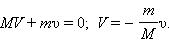
Если тело покоится, импульс равен нулю. Ненулевым импульсом обладает любое, движущееся тело. Например, когда мяч покоится, его импульс равен нулю. После удара он приобретает импульс. Импульс тела изменяется, так как изменяется скорость.

Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Пример. Масса мяча равна 400 г, скорость, которую приобрел мяч после удара – 30 м/с. Сила, с которой нога действовала на мяч – 1500 Н, а время удара 8 мс. Найти импульс силы и изменение импульса тела для мяча.

Изменение импульса тела:

Как определить изменение импульса тела? Необходимо найти численное значение импульса в один момент времени, затем импульс через промежуток времени. От второй найденной величины отнять первую. Внимание! Вычитать надо вектора, а не числа. То есть из второго вектора импульса отнять первый вектор. Смотрите вычитание векторов.

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Источник

Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:

a→=∆v→∆t=v2→-v1→∆t.

Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:

F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.

Изменение импульса

Определение 1

Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.

Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).

Определение 2

Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.

Импульс относят к векторным величинам. Существует еще одна формулировка определения.

Определение 3

Изменение импульса тела равняется импульсу силы.

При обозначении импульса p→ второй закон Ньютона записывается как:

F→∆t=∆p→.

Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:

FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.

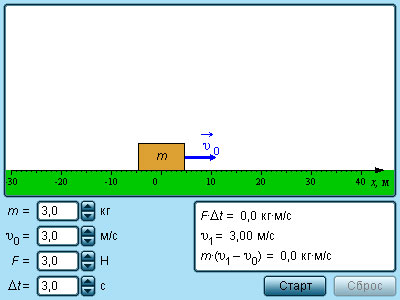
Рисунок 1.16.1. Модель импульса тела.

Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.

Определение 4

Одномерное движение – это движение тела по одной из координатный осей.

Пример 1

На примере рассмотрим свободное падение тела с начальной скоростью v0под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:

Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.

Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fсриз временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.

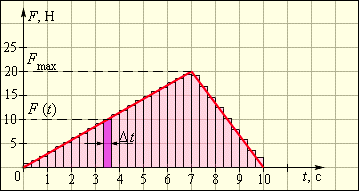
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)

Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δtiна промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti_,тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.

Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].

Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.

Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.

То есть, из примера видно Fср=12Fmax=10 Н.

Определение средней силы

Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.

Тогда формула импульса приобретает вид:

p=mv=12,5 кг·м/с.

Чтобы определить среднюю силу Fсрво время удара, необходимо Fср=p∆t=1,56·103 Н.

Получили очень большое значение, которое равняется телу массой 160 кг.

Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.

Пример 2

Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.

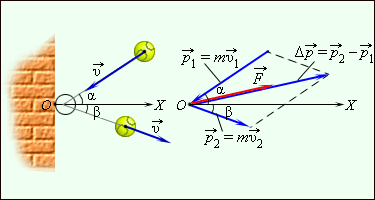
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.

Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.

Источник

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p₀ – p = m(v₀ – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p₀ = 2p = 2mv₀
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v₀. Модули конечного и начального импульсов равны: p = p₀. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

положителен, если его направление совпадает с направлением оси ОХ;
отрицателен, если он направлен противоположно направлению оси ОХ.

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m₁v₁ = (m₁ + m₂)v
Неупругое столкновение движущихся тел	± m₁v₁ ± m₂v₂ = ±(m₁ + m₂)v
В начальный момент система тел неподвижна	0 = m₁v’₁ – m₂v’₂
До взаимодействия тела двигались с одинаковой скоростью	(m₁ + m₂)v = ± m₁v’₁ ± m₂v’₂

Сохранение проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁+ m₂)v

Отсюда скорость равна:

Задание EF17556

Импульс частицы до столкновения равен −p₁, а после столкновения равен −p₂, причём p₁= p, p₂= 2p, −p₁⊥−p₂. Изменение импульса частицы при столкновении Δ−p равняется по модулю:

а) p

б) p√3

в) 3p

г) p√5

Алгоритм решения

1.Записать исходные данные.

2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.

3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.

4.Подставить известные значения и вычислить.

Решение

Запишем исходные данные:

• Модуль импульса частицы до столкновения равен: p₁= p.

• Модуль импульса частицы после столкновения равен: p₂= 2p.

• Угол между вектором начального и вектором конечного импульса: α = 90^о.

Построим чертеж:

Так как угол α = 90^о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:

Δp=√p21+p22

Подставим известные данные:

Δp=√p2+(2p)2=√5p2=p√5

Ответ: г

pазбирался: Алиса Никитина | обсудить разбор

Задание EF17695

На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?

а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно

б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено

в) в интервалах 0–1 и 1–2 двигалось равномерно

г) в интервалах 0–1 и 1–2 двигалось равноускорено

Алгоритм решения

1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.

2.Сделать вывод о том, как зависит характер движения от импульса.

3.На основании вывода и анализа графика установить характер движения тела на интервалах.

Решение

Импульс тела есть произведение массы тела на его скорость:

p = mv

Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.

На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.

Верный ответ: б.

Ответ: б

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22730

Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.

Алгоритм решения

1.Записать исходные данные.

2.Записать закон сохранения импульса применительно к задаче.

3.Записать формулу кинетической энергии тела.

4.Выполнить общее решение.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса камня: m₁ = 3 кг.

• Масса тележки с песком: m₂ = 15 кг.

• Кинетическая энергия тележки с камнем: E_k = 2,25 Дж.

Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:

m1v1+m2v2=(m1+m2)v

Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:

m1v1cosα=(m1+m2)v

Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:

Ek=(m1+m2)v22

Отсюда скорость равна:

v=√2Ekm1+m2

Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:

v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2

Подставим известные данные и произведем вычисления:

v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)

Ответ: 6

pазбирался: Алиса Никитина | обсудить разбор

Задание EF22520

Снаряд, имеющий в точке О траектории импульсp₀, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:

а) −−→AB

б) −−→BC

в) −−→CO

г) −−→OD

Алгоритм решения

1.Сформулировать закон сохранения импульса и записать его в векторной форме.

2.Применить закон сохранения импульса к задаче.

3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.

Решение

Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:

−p1+−p2=−p′
1+−p′2

Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:

−p0=−p1+−p2

Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:

−p2=−p0−−p1

Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.

Ответ: а

pазбирался: Алиса Никитина | обсудить разбор

Задание EF18122

Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?

Ответ:

а) 27 г

б) 64 г

в) 81 г

г) 100 г

Алгоритм решения

1.Записать исходные данные и перевести единицы измерения величин в СИ.

2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.

3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.

4.Выполнить решение задачи в общем виде.

5.Подставить известные данные и вычислить искомую величину.

Решение

Запишем исходные данные:

• Масса пластилиновой пули: m = 9 г.

• Скорость пластилиновой пули: v = 20 м/с.

• Максимальный угол отклонения нити: α = 60°.

Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.

После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:

mv=(m+M)V

После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.

Закон сохранения энергии для точки В:

(m+M)V22=(m+M)gh

V22=gh

Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:

V=√2glcosα

Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в

pазбирался: Алиса Никитина | обсудить разбор

Алиса Никитина | Просмотров: 19.9k

Источник

I. Механика

Тестирование онлайн

Импульс тела

Пуля 22-го калибра имеет массу всего 2 г. Если кому-нибудь бросить такую пулю, то он легко сможет поймать ее даже без перчаток. Если же попытаться поймать такую пулю, вылетевшую из дула со скоростью 300 м/с, то даже перчатки тут не помогут.

Если на тебя катится игрушечная тележка, ты сможешь остановить ее носком ноги. Если на тебя катится грузовик, следует уносить ноги с его пути.

Импульс это векторная величина, которая определяется по формуле

Импульс служит мерой того, насколько велика должна быть сила, действующая в течение определенного времени, чтобы остановить или разогнать его с места до данной скорости.

Направление вектора импульса всегда совпадает с направлением вектора скорости.

Импульс силы

Это векторная величина, которая определяется по формуле

Изменение импульса тела равно импульсу равнодействующей всех сил, действующих на тело. Это иная формулировка второго закона Ньютона

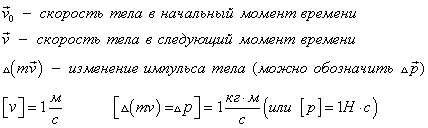
Рассмотрим задачу, которая демонстрирует связь импульса силы и изменения импульса тела.

Изменение импульса тела

Пример. Оценить среднюю силу со стороны пола, действующую на мяч во время удара.

1) Во время удара на мяч действуют две силы: сила реакции опоры, сила тяжести.

Сила реакции изменяется в течение времени удара, поэтому возможно найти среднюю силу реакции пола.

2) Изменение импульса тела изображено на рисунке

3) Из второго закона Ньютона

Главное запомнить

1) Формулы импульса тела, импульса силы;
2) Направление вектора импульса;
3) Находить изменение импульса тела

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Источник

Импульс

Второй закон Ньютона в импульсной форме

Пример вычисления силы

Импульс системы тел

Закон сохранения импульса

Закон сохранения проекции импульса

Изменение импульса тела:

Главное запомнить

Изменение импульса

Определение средней силы

Относительный импульс

Изменение импульса тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар

Абсолютно упругий удар

Пуля пробила стенку

Радиус-вектор тела повернул на 180 градусов

Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали

Второй закон Ньютона в импульсном виде

Реактивное движение

Суммарный импульс системы тел

Закон сохранения импульса

Закон сохранения импульса в проекции на горизонтальную ось

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Сохранение проекции импульса

I. Механика

Тестирование онлайн

Импульс тела

Импульс силы

Изменение импульса тела

Главное запомнить

Вывод второго закона Ньютона в общем виде

График F(t). Переменная сила

Вам также может понравиться

Как найти сумму авансовых платежей

Коржи для медовика получились жесткими как исправить

Как найти русскую невесту

Добавить комментарий Отменить ответ