Задача №47
Определить импульс р, полученный стенкой
при ударе о нее шарика массой m
= 300 г, если шарик двигался со скоростью
v = 8 м/с под углом α = 60º к
плоскости стенки. Удар о стенку считать
упругим.
Дано:
m = 0,3 кг
v0 = 8 м/с
α = 60º
Найти: p = ?
Решение:
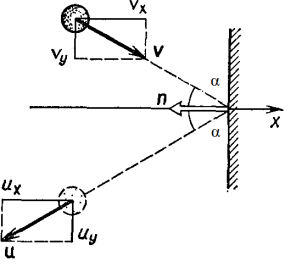
Рисунок 1
Стенка неподвижна, поэтому система
отсчета, связанная с ней, будет
инерциальной. Удар о стенку упругий;
следовательно, можно воспользоваться
законом сохранения механической энергии.
Из него, учитывая, что масса стенки много
больше массы шара, следует равенство
модулей скоростей шара |v| до и |u| после
удара.
Покажем, что угол отражения шарика от
стенки равен углу падения шара. Спроецируем
векторы

и
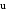
на координатные оси Ох и Оу (рис.1).
Так как стенка гладкая, то
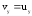 .
.
Учитывая, кроме того, что |v| = |u|, получим ux
= –vx а отсюда следует равенство
углов падения и отражения.
Для определения импульса, полученного
стенкой, воспользуемся законом сохранения
импульса. Для нашего случая этот закон
можно записать в виде
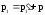 ,
,
где 
и
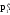
– импульсы шара до и после удара (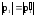 ).
).
Отсюда импульс, полученный стенкой,
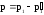 .
.
Из рис. 2 видно, что вектор р сонаправлен
с осью Ох и его модуль
p = |р| = 2p1sinα.
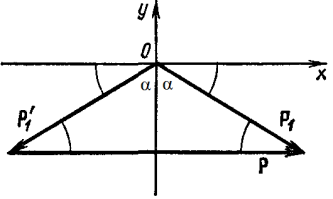
Рисунок 2
Подставив сюда выражение импульса p1
= mv, получим
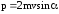 .
.
Подставляя исходные данные и проверяя
размерность, получаем:
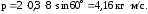
Ответ:
4,16 кг∙м/с.
Соседние файлы в предмете Физика
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
В качестве примера практического применения новой формы второго закона Ньютона рассмотрим задачу об абсолютно упругом ударе шара массой  о неподвижную стенку (рис. 4.11).
о неподвижную стенку (рис. 4.11).
Допустим, что шар до удара имеет скорость  и движется перпендикулярно стенке. Нужно найти скорость
и движется перпендикулярно стенке. Нужно найти скорость  с которой он будет двигаться после удара, и импульс, который получит стенка во время удара.
с которой он будет двигаться после удара, и импульс, который получит стенка во время удара.
Рассмотрим отдельно последовательные стадии удара.
С момента соприкосновения в шаре и стенке начнут развиваться деформации. Вместе с ними будут возникать постепенно возрастающие упругие силы  действующие на стенку и на шар и тормозящие движение шара. Нарастание деформаций и сил прекратится в тот момент, когда скорость шара обратится в нуль:
действующие на стенку и на шар и тормозящие движение шара. Нарастание деформаций и сил прекратится в тот момент, когда скорость шара обратится в нуль: 
Таким образом, для этой стадии удара мы знаем начальное и конечное значение количества движения шара и по ним можем определить импульс, полученный за это время шаром от стенки. Сила в это время меняет свое значение от нуля до некоторой максимальной
величины, поэтому выразить импульс прямо через силу довольно сложно. Введем так называемую среднюю силу: средней силой будем называть постоянную силу  сообщающую телу такой же импульс, какой сообщает ему переменная сила за то же время.
сообщающую телу такой же импульс, какой сообщает ему переменная сила за то же время.
Для импульса средней силы, которая действовала на шар при его деформации, теперь можно записать уравнение второго закона Ньютона:  Так
Так  то окончательно получим:
то окончательно получим:

Изменение количества движения шара за первую половину удара и импульс, полученный шаром, оказываются равными начальному количеству движения, взятому с обратным знаком.
Во время второй половины удара после полной остановки шара упругие силы заставят его двигаться в обратном направлении. Деформации, а вместе с ними упругие силы, начнут уменьшаться. При этом все значения деформаций и сил повторятся в обратном порядке за такое же время. Следовательно, во время второй стадии удара шар получит от стенки дополнительно такой же импульс  как и на первой стадии. Теперь подставим в уравнение второго закона Ньютона
как и на первой стадии. Теперь подставим в уравнение второго закона Ньютона  найденные значения импульса и скоростей, соответствующие второй половине удара. Так как
найденные значения импульса и скоростей, соответствующие второй половине удара. Так как  то получим
то получим

Приравнивая левые части выражений, записанных для первой и второй половин удара, находим:

После упругого удара о стенку по нормали шар будет иметь скорость  равную по модулю начальной скорости
равную по модулю начальной скорости  и противоположно ей направленную. Полный импульс, полученный шаром за все время удара, и полное изменение количества движения будут равны
и противоположно ей направленную. Полный импульс, полученный шаром за все время удара, и полное изменение количества движения будут равны 

Рис. 4.11.
По третьему закону Ньютона стенка получит от шара такой же импульс  но направленный в противоположную сторону.
но направленный в противоположную сторону.
Допустим, что стенка испытывает за одну секунду  таких ударов. Во время каждого удара стенка получит импульс
таких ударов. Во время каждого удара стенка получит импульс  Всего за секунду стенка получит импульс
Всего за секунду стенка получит импульс  Зная этот импульс, можно вычислить среднюю силу
Зная этот импульс, можно вычислить среднюю силу  которая действует на стенку и создается ударами шаров. Полный импульс, полученный стенкой, будет
которая действует на стенку и создается ударами шаров. Полный импульс, полученный стенкой, будет

где  время, в течение которого произошли
время, в течение которого произошли  ударов. Подставляя
ударов. Подставляя  найдем, что за одну секунду на стенку будет действовать средняя сила
найдем, что за одну секунду на стенку будет действовать средняя сила 
Рассмотренный пример особенно важен потому, что именно таким образом подсчитываются силы давления газа на стенки сосуда. Как вы узнаете в курсе молекулярной физики, давление газа на стенки сосуда возникает за счет импульсов, которые сообщают стенке при ударах быстро движущиеся молекулы газа. При этом предполагают, что каждый удар молекулы является абсолютно упругим. Проведенные нами расчеты полностью применимы к этому случаю. Вся трудность расчета давления газа состоит в правильном подсчете числа ударов  молекул о стенки сосуда за единицу времени. Заметим также, что совпадение модуля силы с модулем импульса, сообщаемого этой силой за единицу времени, часто используется в решении многих практических задач.
молекул о стенки сосуда за единицу времени. Заметим также, что совпадение модуля силы с модулем импульса, сообщаемого этой силой за единицу времени, часто используется в решении многих практических задач.
Отметим, наконец, что в наших рассуждениях скрывается одно недосказанное предположение о том, что время, затраченное на создание деформаций во время удара, равно времени снятия деформаций. Немного позже мы докажем его справедливость.
Заключение – дополнение к тексту
Мы применили закон сохранения импульса (одного из основных законов природы) к абсолютно неупругому и абсолютно упругому удару шаров.
При абсолютно неупругом ударе шары (тела) не сохраняют свою форму, то есть испытывают пластическую деформацию. К такому удару
можно отнести удар свинцовых шаров. При неупругом ударе не выполняется закон сохранения механической энергии, но выполняется закон сохранения полной энергии. При неупругом ударе механическая энергия полностью или частично переходит во внутреннюю энергию тел (тела нагреваются). В случае нецентрального (косого) удара тел их общий импульс и общая скорость после абсолютно неупругого удара находятся путём векторного сложения импульсов отдельных тел.
При абсолютно упругом ударе (сюда можно грубо приближённо отнести удар стальных шаров) выполняется и закон сохранения импульса, и закон сохранения механической энергии. При упругом ударе механическая энергия шаров частично или полностью переходит в потенциальную энергию упругой деформации. Затем тела принимают первоначальную форму, отталкивая друг друга. Потенциальная энергия упругой деформации снова переходит в кинетическую энергию шаров. Шары приобретают скорости
направления и модули которых определяются законами сохранения полного импульса и полной энергии системы. Последний 3) частный случай говорит о том, что если лёгкий шарик испытает абсолютно упругий удар о неподвижную стенку, то он отскочит от неё без потери скорости. Пусть теперь шарик падает на неподвижную стенку под углом.
Тогда нормальная составляющая скорости шарика изменит своё направление на обратное, а по модулю останется прежней. Тангенциальная же составляющая скорости не изменится, поэтому угол падения будет равен углу отражения.
На рисунке вектора скорости падения и скорости отражения шарика перенесены в точку падения. Вектор изменения скорости направлен вверх перпендикулярно поверхности стенки. Такие же направления имеют импульсы шарика до удара и после удара о стенку, а вектор приращения импульса шарика
направлен по нормали от стенки.
В молекулярной физике происходит то же самое, когда молекулы газа ударяются о стенку сосуда. Проявляется это давлением газа на стенку сосуда.
Подумаем, что можно найти, если в условии задачи сказано, что шарик летит под прямым углом к движущейся навстречу стенке и между ними происходит упругий удар:
Сразу можно сказать, что скорость шарика относительно движущейся стенки равна
(см. занятие 12 на относительность движения). От стенки шарик отскочит со скоростью
относительно стенки, а относительно земли его скорость после удара
Далее можно найти импульс шара относительно земли до и после удара. Сможем найти изменение его импульса, его кинетическую энергию до и после удара.
Изменение кинетической энергии даст работу, совершённую силой упругости за время удара. Работу же можно выразить через произведение силы удара на перемещение стенки за время удара и найти силу удара.
Таким образом, через данные в условии задачи сможем охарактеризовать упругий удар между шаром и движущейся стенкой.
Абсолютно неупругий удар и абсолютно упругий удар – это предельные случаи кратковременного взаимодействия шаров (тел). При взаимодействии реальных тел имеют место и упругие, и неупругие деформации. Формула, связывающая скорости шаров до удара и после удара имеет вид:
коэффициент восстановления относительной скорости при ударе. В случае абсолютно неупругого удара он равен нулю; в случае абсолютно упругого удара он равен единице.
При ударе реальных тел этот коэффициент принимает промежуточные значения между нулём и единицей. Для стали этот коэффициент равен 0,56.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Пишите комментарии. Спасибо.
Предыдущая запись: Занятие 23. Импульс системы тел. Центр масс системы
Следующая запись:Задачи 1 – 4 к занятиям 22 – 24
Первая запись на канале: Занятие 1. Физика. Механика. Кинематика
Пётр написал всё верно, за исключением того, что перпендикулярная к стенке составляющая часть импульса – не mx*cos(60), а mx*sin(60), т. к. Вы указали, что угол падения шарика отсчитывается от плоскости стенки.
Потому ответ не mx, а 2 * mx * sin(60) = sqrt(3) * mx ~ 46.8 кг*м/с.
Роман ПоповМастер (1030)
12 лет назад
а почему импульс , точнее его нормальная составляющая, умножается на 2?
Maxepsut
Гуру
(2510)
По закону сохранения импульса (ЗСИ). У шарика до удара был один импульс в этой плоскости, а после удара стал другой. Изменение импульса шарика: 2 * mx * sin(a). Откуда оно взялось? От удара. Куда делось (по ЗСИ)? Передалось стенке (других объектов нет).
Передалось же полностью, т.к. удар, по условию, можно считать упругим. Хотя в реальности не вся эта энергия уходит на движение, а часть – на нагрев: как стенки, так и шарика.
Тема: Определить импульс силы, полученный стенкой (Прочитано 9392 раз)
0 Пользователей и 1 Гость просматривают эту тему.
himik
Шарик массой m = 100 г, летевший со скоростью Vx = 5 см/с под углом 600 к плоскости стенки, упруго ударился о неё и отскочил с той же по модулю скоростью. Определите импульс силы, полученный стенкой.
Источник неизвестен. Спасибо.

Записан
djek
« Последнее редактирование: 16 Сентября 2012, 20:57 от djek »

Записан
djek
Второй закон Ньютона для тела массой m, на которое действует сила F в течении времени Δt, записывается следующим образом:
[ vec F cdot Δt = m cdot vec υ – m cdot vec υ_0 = Delta vec p, ]
где υ и υ0 – начальная и конечная скорости тела, m·υ, m·υ0 – импульсы тела в начальный момент времени и через время Δt; Δp – изменение импульса тела за время Δt; F·Δt – импульс силы, действующей на тело.
Так как импульс есть величина векторная, то изменение импульса шарика найдем как векторную разность конечного и начального импульсов шарика
[ Delta vec{p}=vec{p}-{{vec{p}}_{0}}=mcdot vec{upsilon }-mcdot {{vec{upsilon }}_{0}} ]
Модуль скорости постоянен: υ = υ0. Из ΔОСВ
[ begin{align}
& frac{Delta p}{2}={{p}_{0}}cdot sin alpha \
& Delta p=2cdot {{p}_{0}}cdot sin alpha =2cdot mcdot upsilon cdot sin alpha \
end{align}
]
Импульс силы, который получила, стена равен по модулю, но противоположен по знаку импульсу силы шарика
« Последнее редактирование: 17 Сентября 2012, 11:06 от djek »

Записан

