Как найти импульс стержня

Момент
импульса. Момент сил. Уравнение
моментов.

При
анализе вращательного движения, как
твердого тела, так и материальной
точки важной характеристикой движения
является момент импульса.

Моментом
импульса называется
векторное произведение радиус-вектора
на вектор импульса:
.
Соответственно модуль момента импульса
равен:,
а направлен он перпендикулярно
радиус-вектору и вектору скорости,
согласно правилу нахождения векторного
произведения.

Влияние
сил, действующих на тело, на величину
момента импульса можно учесть,
используя II
закон Ньютона. Для этого возьмем
производную момента импульса по
времени:

.

Здесь
учтено, что
,
а скорость и импульс совпадают по
направлению и их векторное произведение
равно 0. Во втором слагаемом учтено,
что согласно второму закону Ньютона
.

Величина,
представляющая собой векторное
произведение радиуса-вектора на силу
называется момент
сил.:

.

Полученный
результат ):

,

называется
уравнение
моментов.
Согласно ему скорость изменения
момента импульса равна моменту
равнодействующей сил. Это соотношение
подобно второму закон Ньютона,
утверждающему, что скорость изменения
импульса равна равнодействующей
приложенных сил.

Как
видно из определения, момент сил,
так же как момент импульса зависит
от выбора точки, из которой проводится
радиус вектор. Поэтому в уравнении
моментов эти величины должны
рассчитываться относительно одной
и той же точки.

Пара
сил

Возможна
ситуация, когда суммарный момент сил
не будет зависеть от точки отсчета.
Таким будет момент двух сил, если
они удовлетворяют условию:
.
Действительно, тогда:

Рис. 14
Пара сил

И
модуль момента импульса окажется
равным:
,
гдеl-плечо
(
расстояние
между линиями действия сил)

Закон
сохранения момента импульса

Если
рассматривать движение не одной
материальной точки, а системы
материальных точек, то окажется, что
в уравнении моментов нужно учитывать
только моменты внешних сил. Моменты
сил взаимодействия частей системы
на результат не влияют. И для системы
материальных точек (и для твердого
тела) уравнение моментов примет вид:

.

Здесь
под
надо понимать суммарный момент
импульса системы:,
где– момент импульса отдельной материальной
точки, а в правой части стоит сумма
моментов внешних сил:.

Из
данного уравнения следует, что

при
равенстве нулю суммарного момента
внешних сил суммарный момент импульса
тела (или системы тел) остается
постоянным.

Это
утверждение и является законом
сохранения момента импульса (ЗСМИ).
Так же, как и закон сохранения импульса
(ЗСИ), ЗСМИ должен выполняться в
замкнутой системе. Но кроме этого
возможна ситуация, когда тело находится
в поле внешней силы (система
незамкнута), а момент этой силы равен
нулю. Такие силы называются центрально
симметричными
или просто центральными.
Математически такая сила может быть
представлена в виде:
.
Нетрудно видеть, что векторное
произведение такой силы на радиус
вектор равен нулю.

Таким
образом ЗСМИ выполняется в
замкнутой системе и в поле центральных
сил.

Примеры
центральных
сил: сила
гравитационного притяжения планет
Солнцем, сила кулоновского взаимодействия
ядра и электронов в атоме.

Особенности
описания движения твердого тила

При
движении твердого тела необходимо
учитывать как перемещение тела в
пространстве в целом, так и поворот
его вокруг оси, проходящей через центр
масс. Для анализа движения твердого
тела его мысленно разбивают на
множество материальных точек. Скорость
каждой из них может быть представлена
как сумма двух скоростей:
,
где– скорость отдельной (i–той)
точки,
– скорость центра масс твердого тела,
а–
скорость этой точки относительно
центра масс. Проанализировав движение
отдельной точки, пользуясь выводами
динамики материальной точки, можно
затем результат просуммировать (или
проинтегрировать) для тела в целом.
При этом удобнее применять именно
операцию интегрирования, для чего
отдельные части (точки) тела принимаются
бесконечно малыми.

Движение
центра масс

Согласно
второму закону Ньютона для отдельно
взятой элементарной массы, которую
считаем материальной точкой, с учетом
внешних сил
и
сил взаимодействиямежду отдельными массами этого тела
можно записать:

Просуммировав
получим равенство:

Учитывая,
что согласно третьему закону Ньютона

,и так далее, получим, что сумма сил
взаимодействия окажется равной нулю
и в данном равенстве останутся только
внешние силы:

Учтем,
что положение центра масс определяется
по формуле.:
,
тогда:. Дважды продифференцировав это
равенство получим:

.

А
это значит, что основное уравнение
динамики (II
закон Ньютона), для центра масс
записывается так же, как и для
материальной точки, но с учетом только
внешних сил (для материальной точки
все силы внешние):

.

Здесь

– равнодействующая внешних сил, а–
масса всего твердого тела.

Ускорение
центра масс твердого тела, умноженное
на полную массу тела, равняется
равнодействующей внешних сил,
действующих на тело.

Вращение
вокруг неподвижной оси.

Рассмотрим
тело произвольной формы,

вращающееся
вокруг оси Oz.

Разобьем
его на элементарные
массы
.

Для
каждой из них можно записать

уравнение
моментов с учетом моментов

внешних
сил


и сил взаимодействия
:

Запишем
проекцию этого равенства на ось z:

Рис
15. Вращение вокруг

Момент
импульса
связан со скоростьюнеподвижной оси

тела
и его импульсом:
.
А при

вращательном
движении его можно записать через
угловую скорость, используя взаимосвязь
и:
.
В результате получим:

,
где(α – угол между радиусом вектором и
осьюz)

Величина
называетсямоментом
инерции (в
данном случае i-той
элементарной массы):

Далее
просуммируем приведенное выше
равенство по всему твердому телу:

.

Учитывая,
что сумма моментов сил взаимодействия
(внутренних) равна нулю, а угловое
ускорение для всех точек одинаково,
получим:

.

И
окончательно, уравнение
динамики вращения твердого тела имеет
вид:

,

где
М_z
проекция
суммарного момента внешних сил на
ось вращения, а

–
момент
инерции твердого тела.

Момент
инерции.

Приведенная
выше формула для расчета инерции:
– удобна для расчета момента инерции
системы из нескольких тел, если эти
тела можно считать материальными
точками (случай, так называемых,
дискретных масс). Но если мы хотим
вычислить момент инерции твердого
тела (непрерывное распределение масс)
необходимо использовать операцию
интегрирования:

.

Здесь
dm
– элементарная
бесконечно малая масса, аналог m_i
в
предшествующем анализе.

Например,
если стержень вращается вокруг одного
из своих концов, момент инерции находим
следующим образом: выделяем элементарную
массу (бесконечно тонкий слой стержня
толщиной dx)
dm:

.

Радиус
вращения в данном случае обозначен
x
(смотри
рисунок). Подставив dm
и x
вместо
R
в интеграл, получим:

.

Здесь
l
-длина стержня, m-масса
стержня.

Итак,
момент инерции стержня относительно
оси проходящей через один из его
концов равен:

.

Для
того чтобы определить момент инерции
стержня относительно оси, проходящей
через его середину, надо изменить
пределы интегрирования:

Момент
инерции тела зависит от положения
оси, относительно которой оно вращается.

Теорема
Штейнера.

Теорема
Штейнера позволяет сосчитать момент
инерции J
тела, имеющего
массу m,
относительно
произвольной оси, если известен его
момент инерции относительно центра
масс J_c.

Рассмотрим
2 оси: осьCC’
, проходящую через центр масс и
произвольную OO’.

Положение
элементарной массы задается вектором

Момент
инерции этой элементарной массы
относительно оси OO’
будет равен:

Рис.
17. К теореме Штайнера.

.

Просуммировав
это равенство по всему

объему:

,

и
приняв во внимание, что для центра
масс координата
,
в итоге получим:

.

Это
соотношение называется теорема
Штейнера, здесь
a
– расстояние от центра масс до оси
OO’,
относительно которой считается момент
инерции.

Моменты
инерции различных тел:

Момент
инерции стержня относительно оси,
проходящей через центр масс и
перпендикулярной стержню:

Момент
инерции цилиндра или диска, относительно
его оси:

Момент
инерции шара относительно его центра
масс:

Кинетическая
энергия и работа при вращении твердого
тела.

Кинетическая
энергия вращающегося тела находится
суммированием кинетических энергий
элементарных масс (материальных
точек), на которые мы мысленно разбиваем
твердое тело. Кинетическая энергия
одной элементарной массы m_i:

.

При
суммировании
учтем, что, а

.

В
результате оказывается, что кинетическая
энергия вращающегося тела
может быть подсчитана по формуле:

Эта
формула по структуре повторяет
формулу расчета кинетической энергии
при поступательном движении
.

Аналогично
формуле для расчета работы при
поступательном движении
записывается работа при вращательном
движении:

,

Здесь

момент силы, поворачивающий тело на
угол.

Кинетическая
энергия при плоском движении.

Плоское
движение – такое движение, при котором
любая точка твердого тела остается в
какой-то одной своей плоскости. Самый
простой пример: катящийся цилиндр
или диск. В этом случае кинетическая
энергия складывается из кинетической
энергии поступательного движения и
кинетической энергии вращения вокруг
оси цилиндра (или диска):

.

J_c
– момент инерции цилиндра (или диска)
относительно его оси.

Гироскопический
эффект. Прецессия.

Г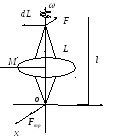ироскоп
– массивное тело, имеющее ось симметрии,
которое вращается вокруг этой оси с
очень большой угловой скоростью. Какую
скорость мы можем считать «очень
большой»? Это требование важно для
случая, когда гироскоп участвует в
дополнительном вращательном движении
с угловой скоростью .Тогда, при
выполнении условия
,
можно считать, что направление момента
импульса совпадает с осью вращения
гироскопа:

.

Рис. 18 Гироскопический
эффект Если
на гироскоп подействовать силой

(на
чертеже она направлена от нас), то
возникающий момент сил направлен
перпендикулярно этой силе (см. рис).
Согласно уравнению моментов:

вектор
изменения момента импульса совпадает
по направлению с вектором момента
силы. А это значит, что ось гироскопа
будет стремиться повернуться в
направлении перпендикулярном приложенной
силе. То есть в приведенном примере
мы действуем на гироскоп от нас, а
он наклоняется в сторону – влево. Это
одно из проявлений гироскопического
эффекта.

Если
сила, стремящаяся повернуть ось
гироскопа, действует постоянно, то
может возникнуть прецессия
гироскопа. Рассмотрим
в качестве примера волчок (гироскоп),
ось которого наклонена. Тогда сила
тяжести mg
и реакция
опоры N
создают
пару сил, стремящуюся опрокинуть
волчок. Но момент этих сил направлен
перпендикулярно оси волчка и так же
направлен вектор изменения импульса.
В этой ситуации ось волчка будет
вращаться вокруг вертикали, проведенной
из точки опоры волчка (см. рисунок).

Для
того, чтобы определить частоту
прецессии рассмотрим эту ситуа-

цию
более подробно. Момент сил пары сил
можно считать относительно

любой
точки. Относительно точки опоры
волчка момент сил будет равен ,модуль его
соответственно ,где α – угол между
радиус-вектором (направленным вдоль
оси волчка) и силой тяжести.

:

Рис 19.
Прецессия гироскопа

С
другой стороны, если за время dt
ось волчка
повернется на dφ,
то модуль изменения вектора момента
импульса будет равен (см. рисунок)
.Подставив
эти результаты в уравнение моментов,
приняв во внимание при этом, что
,
получим:.
Отсюда следует, что частота прецессии
равна:

.

Чем
меньше частота вращения волчка-гироскопа,
тем больше частота прецессии.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение.

Будем рассматривать движение системы «стержень – пуля»
относительно системы отсчета, начало которой расположено в центре стержня О,
а ось  совпадает с осью вращения и направлена «на
нас» (рис. 14). В момент удара на  систему действуют силы тяжести

и
реакции опоры – оси. Линии действия сил реакции оси и тяжести, действующих на стержень,
и силы тяжести, действующей на пулю, проходят через центр стержня О. Таким
образом, все внешние силы являются центральными, их моменты относительно центра
О равны нулю, следовательно, при столкновении выполняется закон
сохранения момента импульса:

,                                                          
(1)

где
 и – моменты
импульса системы относительно центра  непосредственно до удара
(рис. 14, а) и сразу после него (рис. 14, б) соответственно[1].

До
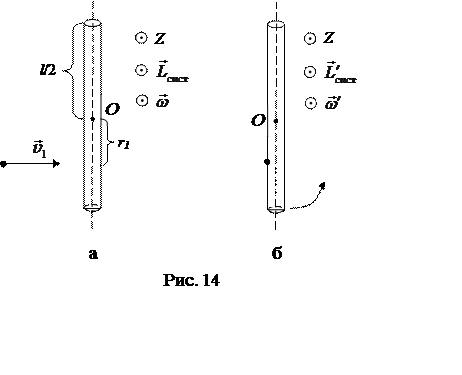
взаимодействия стержень был неподвижен, поэтому момент импульса системы равен
моменту импульса пули:

,             (2)

где
 – момент инерции пули относительно оси
вращения;

 – угловая скорость пули непосредственно
перед ударом.

Примем
пулю за материальную точку, тогда ее момент инерции относительно оси вращения

.                                       
    (3)

Модуль
угловой скорости пули выражается через модуль линейной скорости  и расстояние  от
точки попадания пули до оси

,                                                     
  (4)

где

Направление
 (рис. 14, а – «на нас») определяется по
правилу буравчика в соответствии с направлением вращения.

После
взаимодействия пули и стержня система начинает вращение как одно целое с
угловой скоростью  поэтому

,                          
 (5)

где
 – угловая скорость системы непосредственно
после удара.

Момент
инерции стержня относительно оси вращения, которая в рассматриваемом случае
совпадает с осью симметрии стержня, определяется по формуле:

.                                                   
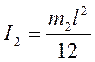
 (6)

Подставив
формулы (2) и (5) в уравнение (1), получим соотношение:

.                                          
    (7)

Отсюда

.                                             
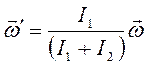
   (8)

Заметим, что моменты импульса пули до и после удара можно
вычислить, основываясь на определении момента импульса материальной точки:
 и .

При
анализе выражения (8) можно сделать два вывода:

1)
угловая скорость системы во втором состоянии сонаправлена с угловой скоростью пули
в первом состоянии: ;

2)
так как моменты инерции величины положительные, модуль угловой скорости  определяется по формуле:

.                                             
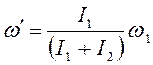
 (9)

Подставим
выражения (3), (4) и (6) в равенство (9):

.  (10)

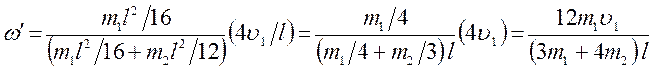
Подставим
данные задачи в уравнение (10) и получим:

 рад/с.

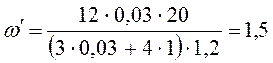
Ответ: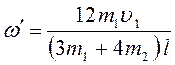,  рад/с.

Библиографический список

1. С
а в е л ь е в  И. В. Курс общей физики: В 5 кн. Кн. 1. Механика / И. В. С
а в е л ь е в. М., 1998. 336 с.

2. Я в о р с к и й  Б. М. Курс физики / Б. М.  Я в о
р с к и й, А. А.  Д е т л а ф, Л. Б.  М и л к о в с к а я. М., 2001. 718
с.

3. Т
р о ф и м о в а Т. И. Курс физики / Т. И.  Т р о ф и м о в а. М., 2004. 542
с.

4. Физический
энциклопедический словарь / Под ред. А. М. Прохорова. 
М., 1984. 940 с.

5.
Д ж а н к о л и  Д. Физика / Д.  Д ж а н к о л и.  М., 1989. Т. 1. 667 с.

6.
Н и к и т и н  Н. Н. Курс теоретической механики / Н. Н.  Н и к и т и н. М., 1990.
607 с.

_________________________________________________

Учебное
издание

ДРОЗДОВА Илга
Анатольевна,  ТОДЕР Георгий Борисович

ЗАКОНЫ  СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ  РЕШЕНИЯ  ЗАДАЧ)

Редактор Т. С. Паршикова

***

Подписано в печать     . 02.2010.
Формат 60 ´ 84 ¹/₁₆.

Плоская печать. Бумага офсетная. Усл.
печ. л. 2,4. Уч.-изд. л. 2,6.

Тираж 800 экз.  Заказ         .

**

Редакционно-издательский
отдел ОмГУПСа

Типография ОмГУПСа

*

644046, г. Омск, пр. Маркса, 35

И. А.
ДРОЗДОВА,  Г. Б. ТОДЕР

ЗАКОНЫ 
СОХРАНЕНИЯ  В  МЕХАНИКЕ

(ПРИМЕРЫ 
РЕШЕНИЯ  ЗАДАЧ)

ОМСК  200

9

Определение

Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:

p = mv

Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).

Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).

Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.

Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:

10 г = 0,01 кг

Импульс равен:

p = mv = 0,01∙300 = 3 (кг∙м/с)

Относительный импульс

Определение

Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:

p_1отн2 = m₁v_1отн2 = m₁(v₁ – v₂)

p_1отн2 — импульс первого тела относительно второго, m₁ — масса первого тела, v_1отн2 — скорость первого тела относительно второго, v₁ и v₂ — скорости первого и второго тела соответственно в одной и той же системе отсчета.

Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.

Сначала переведем единицы измерения в СИ:

15 т = 15000 кг

p_1отн2 = m₁(v₁ – v₂) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙10³ (кг∙м/с)

Изменение импульса тела

ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:

∆p = p – p₀ = p + (– p₀)

∆p — изменение импульса тела, p — конечный импульс тела, p₀ — начальный импульс тела

Частные случаи определения изменения импульса тела

Абсолютно неупругий удар
	Конечная скорость после удара: v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0.
Абсолютно упругий удар
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p.
Пуля пробила стенку
	Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v)
Радиус-вектор тела повернул на 180 градусов
	Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали
	Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:

Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.

В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.

Вычисляем:

Второй закон Ньютона в импульсном виде

Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела

Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?

Из формулы импульса силы выразим модуль силы:

Реактивное движение

Определение

Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.

Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.

Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.

Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:

V = a∆t

Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:

Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел

Определение

Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:

Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.

Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса

Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.

Закон сохранения импульса в проекции на горизонтальную ось

Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:

Важно!

При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.

Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)

Неупругое столкновение с неподвижным телом	m1v1 = (m1 + m2)v
Неупругое столкновение движущихся тел	± m1v1 ± m2v2 = ±(m1 + m2)v
В начальный момент система тел неподвижна	0 = m1v’1 – m2v’2
До взаимодействия тела двигались с одинаковой скоростью	(m1 + m2)v = ± m1v’1 ± m2v’2

Сохранение  проекции импульса

В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.

Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.

Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:

m₂v₂ = (m₁ + m₂)v

Отсюда скорость равна:

Алиса Никитина | Просмотров: 19.9k