Импульс тела — векторная физическая величина, обозначаемая как p и равная произведению массы тела на его скорость:
p = mv
Единица измерения импульса — килограмм на метр в секунду (кг∙м/с).
Направление импульса всегда совпадает с направлением скорости (p↑↓v), так как масса — всегда положительная величина (m > 0).
Пример №1. Определить импульс пули массой 10 г, вылетевшей со скоростью 300 м/с. Сопротивлением воздуха пренебречь.
Импульс пули есть произведение массы на ускорение. Прежде чем выполнить вычисления, нужно перевести единицы измерения в СИ:
10 г = 0,01 кг
Импульс равен:
p = mv = 0,01∙300 = 3 (кг∙м/с)
Относительный импульс
Определение
Относительный импульс — векторная физическая величина, равная произведению массы тела на относительную скорость:
p1отн2 = m1v1отн2 = m1(v1 – v2)
p1отн2 — импульс первого тела относительно второго, m1 — масса первого тела, v1отн2 — скорость первого тела относительно второго, v1 и v2 — скорости первого и второго тела соответственно в одной и той же системе отсчета.
Пример №2. Два автомобиля одинаковой массы (15 т) едут друг за другом по одной прямой. Первый — со скоростью 20 м/с, второй — со скоростью 15 м/с относительно Земли. Вычислите импульс первого автомобиля в системе отсчета, связанной со вторым автомобилем.
Сначала переведем единицы измерения в СИ:
15 т = 15000 кг
p1отн2 = m1(v1 – v2) = 15000(20 – 15) = 75000 (кг∙м/с) = 75∙103 (кг∙м/с)
Изменение импульса тела
ОпределениеИзменение импульса тела — векторная разность между конечным и начальным импульсом тела:
∆p = p – p0 = p + (– p0)
∆p — изменение импульса тела, p — конечный импульс тела, p0 — начальный импульс тела
Частные случаи определения изменения импульса тела
Абсолютно неупругий удар |
|
|
|
Конечная скорость после удара:
v = 0. Конечный импульс тела: p = 0. Модуль изменения импульса тела равен модулю его начального импульса: ∆p = p0. |
Абсолютно упругий удар |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p. |
Пуля пробила стенку |
|
|
|
Модуль изменения импульса тела равен разности модулей начального и конечного импульсов: ∆p = p0 – p = m(v0 – v) |
Радиус-вектор тела повернул на 180 градусов |
|
|
|
Модуль изменения импульса тела равен удвоенному модулю начального (конечного) импульса: ∆p = 2p0 = 2p = 2mv0 |
Абсолютно упругое отражение от горизонтальной поверхности под углом α к нормали |
|
|
|
Модули конечной и начальной скоростей равны: v = v0. Модули конечного и начального импульсов равны: p = p0. Угол падения равен углу отражения: α = α’ Модуль изменения импульса в этом случае определяется формулой:
|
Пример №3. Шайба абсолютно упруго ударилась о неподвижную стену. При этом направление движения шайбы изменилось на 90 градусов. Импульс шайбы перед ударом равен 1 кг∙м/с. Чему равен модуль изменения импульса шайбы в результате удара? Ответ округлите до десятых.
В данном случае 90 градусов и есть 2α (угол между векторами начального и конечного импульсов), в то время как α — это угол между вектором импульса и нормалью. Учтем, что при абсолютно упругом отражении модули конечного и начального импульсов равны.
Вычисляем:

Второй закон Ньютона в импульсном виде
Второй закон Ньютона говорит о том, что ускорение тела прямо пропорционально силе, действующей на него. Записывается он так:

Но ускорение определяется отношением разности конечной и начальной скоростей ко времени, в течение которого менялась скорость:

Подставим это выражение во второй закон Ньютона и получим:

Или:

F∆t — импульс силы, ∆p — изменение импульса тела
Пример №4. Тело движется по прямой в одном направлении. Под действием постоянной силы за 3 с импульс тела изменился на 6 кг∙м/с. Каков модуль силы?
Из формулы импульса силы выразим модуль силы:

Реактивное движение
Определение
Реактивное движение — это движение, которое происходит за счет отделения от тела с некоторой скоростью какой-либо его части. В отличие от других видов движения реактивное движение позволяет телу двигаться и тормозить в безвоздушном пространстве, достигать первой космической скорости.
Ракета представляет собой систему двух тел: оболочки массой M и топлива массой m. v — скорость выброса раскаленных газов. ∆m/∆t — расход реактивного топлива, V — скорость ракеты.
Второй закон Ньютона в импульсном виде:

Реактивная сила:

Второй закон Ньютона для ракеты:

Пример №5. Космический корабль массой 3000 кг начал разгон в межпланетном пространстве, включив реактивный двигатель. Из сопла двигателя каждую секунду выбрасывается 3 кг горючего газа со скоростью 600 м/с. Какой будет скорость корабля через 20 секунд после разгона? Изменением массы корабля во время разгона пренебречь. Принять, что поле тяготения, в котором движется корабль, пренебрежимо мало.
Корабль начинает движение из состояния покоя. Поэтому скорость будет равна:
V = a∆t
Выразим ускорение из второго закона Ньютона для ракеты:

Изменение импульса определяется произведением суммарной массы выброшенного горючего на скорость его выброса. Так как мы знаем, сколько выбрасывалось горючего каждую секунду, формула примет вид:
![]()
Отсюда ускорение равно:

Выразим формулу для скорости и сделаем вычисления:

Суммарный импульс системы тел
Определение
Суммарный импульс системы тел называется полным импульсом системы. Он равен векторной сумме импульсов всех тел, которые входят в эту систему:


Пример №6. Найти импульс системы, состоящей из двух тел. Векторы импульсов этих тел указаны на рисунке.
Между векторами прямой угол (его косинус равен нулю). Модуль первого вектора равен 4 кг∙м/с (т.к. занимает 2 клетки), а второго — 6 кг∙м/с (т.к. занимает 3 клетки). Отсюда:

Закон сохранения импульса
Закон сохранения импульсаПолный импульс замкнутой системы сохраняется:

Левая часть выражения показывает векторную сумму импульсов системы, состоящей из двух тел, до их взаимодействия. Правая часть выражения показывает векторную сумму этой системы после взаимодействия тел, которые в нее входят.
Закон сохранения импульса в проекции на горизонтальную ось
Если до и после столкновения скорости тел направлены вдоль горизонтальной оси, то закон сохранения импульса следует записывать в проекциях на ось ОХ. Нельзя забывать, что знак проекции вектора:
- положителен, если его направление совпадает с направлением оси ОХ;
- отрицателен, если он направлен противоположно направлению оси ОХ.
Важно!
При неупругом столкновении двух тел, движущихся навстречу друг другу, скорость совместного движения будет направлена в ту сторону, куда до столкновения двигалось тело с большим импульсом.
Частные случаи закона сохранения импульса (в проекциях на горизонтальную ось)
| Неупругое столкновение с неподвижным телом | m1v1 = (m1 + m2)v |
| Неупругое столкновение движущихся тел | ± m1v1 ± m2v2 = ±(m1 + m2)v |
| В начальный момент система тел неподвижна | 0 = m1v’1 – m2v’2 |
| До взаимодействия тела двигались с одинаковой скоростью | (m1 + m2)v = ± m1v’1 ± m2v’2 |
Сохранение проекции импульса
В незамкнутых системах закон сохранения импульса выполняется частично. Например, если из пушки под некоторым углом α к горизонту вылетает снаряд, то влияние силы реакции опоры не позволит орудию «уйти под землю». В момент отдачи оно будет откатываться от поверхности земли.
Пример №7. На полу лежит шар массой 2 кг. С ним сталкивается шарик массой 1 кг со скоростью 2 м/с. Определить скорость первого шара при условии, что столкновение было неупругим.
Если столкновение было неупругим, скорости первого и второго тел после столкновения будут одинаковыми, так как они продолжат двигаться совместно. Используем для вычислений следующую формулу:
m2v2 = (m1 + m2)v
Отсюда скорость равна:

Задание EF17556
Импульс частицы до столкновения равен −p1, а после столкновения равен −p2, причём p1 = p, p2 = 2p, −p1⊥−p2. Изменение импульса частицы при столкновении Δ−p равняется по модулю:
а) p
б) p√3
в) 3p
г) p√5
Алгоритм решения
1.Записать исходные данные.
2.Построить чертеж, обозначить векторы начального и конечного импульсов, а также вектор изменения импульса. Для отображения вектора изменения импульса использовать правило сложения векторов методом параллелограмма.
3.Записать геометрическую формулу для вычисления длины вектора изменения импульса.
4.Подставить известные значения и вычислить.
Решение
Запишем исходные данные:
• Модуль импульса частицы до столкновения равен: p1 = p.
• Модуль импульса частицы после столкновения равен: p2 = 2p.
• Угол между вектором начального и вектором конечного импульса: α = 90о.
Построим чертеж:

Так как угол α = 90о, вектор изменения импульса представляет собой гипотенузу треугольника, катами которого являются вектора начального и конечного импульсов. Поэтому изменение импульса можно вычислить по теореме Пифагора:
Δp=√p21+p22
Подставим известные данные:
Δp=√p2+(2p)2=√5p2=p√5
Ответ: г
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17695
 На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
На рисунке приведён график зависимости проекции импульса на ось Ox тела, движущегося по прямой, от времени. Как двигалось тело в интервалах времени 0–1 и 1–2?
а) в интервале 0–1 не двигалось, а в интервале 1–2 двигалось равномерно
б) в интервале 0–1 двигалось равномерно, а в интервале 1–2 двигалось равноускорено
в) в интервалах 0–1 и 1–2 двигалось равномерно
г) в интервалах 0–1 и 1–2 двигалось равноускорено
Алгоритм решения
1.Записать формулу, связывающую импульс тема с его кинематическими характеристиками движения.
2.Сделать вывод о том, как зависит характер движения от импульса.
3.На основании вывода и анализа графика установить характер движения тела на интервалах.
Решение
Импульс тела есть произведение массы тела на его скорость:
p = mv
Следовательно, импульс и скорость тела — прямо пропорциональные величины. Если импульс с течением времени не меняется, то скорость тоже. Значит, движение равномерное. Если импульс растет линейно, то и скорость увеличивается линейно. В таком случае движение будет равноускоренным.
На участке 0–1 импульс тела не менялся. Следовательно, на этом участке тело двигалось равномерно. На участке 1–2 импульс тела увеличивался по линейной функции, следовательно, на этом участке тело двигалось равноускорено.
Верный ответ: б.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22730
 Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Камень массой 3 кг падает под углом α = 60° к горизонту в тележку с песком общей массой 15 кг, покоящуюся на горизонтальных рельсах, и застревает в песке (см. рисунок). После падения кинетическая энергия тележки с камнем равна 2,25 Дж. Определите скорость камня перед падением в тележку.
Алгоритм решения
1.Записать исходные данные.
2.Записать закон сохранения импульса применительно к задаче.
3.Записать формулу кинетической энергии тела.
4.Выполнить общее решение.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса камня: m1 = 3 кг.
• Масса тележки с песком: m2 = 15 кг.
• Кинетическая энергия тележки с камнем: Ek = 2,25 Дж.
Так как это абсолютно неупругий удар, закон сохранения импульса принимает вид:
m1v1+m2v2=(m1+m2)v
Учтем, что скорость тележки изначально была равна нулю, а к ее движению после столкновения привела только горизонтальная составляющая начальной скорости камня:
m1v1cosα=(m1+m2)v
Выразить конечную скорость системы тел после столкновения мы можем через ее кинетическую энергию:
Ek=(m1+m2)v22
Отсюда скорость равна:
v=√2Ekm1+m2
Выразим скорость камня до столкновения через закон сохранения импульса и подставим в формулу найденную скорость:
v1=(m1+m2)vm1cosα=(m1+m2)m1cosα·√2Ekm1+m2
Подставим известные данные и произведем вычисления:
v1=(3+15)3cos60o·√2·2,253+15=12·√0,25=12·0,5=6 (мс)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF22520
 Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
Снаряд, имеющий в точке О траектории импульсp0, разорвался на два осколка. Один из осколков имеет импульс −p1
. Импульс второго осколка изображается вектором:
а) −−→AB
б) −−→BC
в) −−→CO
г) −−→OD
Алгоритм решения
1.Сформулировать закон сохранения импульса и записать его в векторной форме.
2.Применить закон сохранения импульса к задаче.
3.Выразить из закона импульс второго осколка и найти на рисунке соответствующий ему вектор.
Решение
Согласно закону сохранения импульса, импульс замкнутой системы тел сохраняется. Записать его можно так:
−p1+−p2=−p′
1+−p′2
Можем условно считать осколки замкнутой системой, так как они не взаимодействуют с другими телами. Применяя к ним закон сохранения импульса, получим:
−p0=−p1+−p2
Отсюда импульс второго осколка равен векторной разности импульса снаряда и импульса первого осколка:
−p2=−p0−−p1
Известно, что разностью двух векторов является вектор, начало которого соответствует вычитаемому вектору, а конец — вектору уменьшаемому. В нашем случае вычитаемый вектор — вектор импульса первого осколка. Следовательно, начало вектора импульса второго осколка лежит в точке А. Уменьшаемый вектор — вектор импульса снаряда. Следовательно, конец вектора лежит в точке В. Следовательно, искомый вектор — −−→AB.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18122
Летящая горизонтально со скоростью 20 м/с пластилиновая пуля массой 9 г попадает в груз неподвижно висящий на нити длиной 40 см, в результате чего груз с прилипшей к нему пулей начинает совершать колебания. Максимальный угол отклонения нити от вертикали при этом равен α = 60°. Какова масса груза?
Ответ:
а) 27 г
б) 64 г
в) 81 г
г) 100 г
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения величин в СИ.
2.Сделать чертеж, отобразив начальное, промежуточное и конечное положение тел.
3.Записать закон сохранения импульса для момента столкновения и закон сохранения механической энергии для момента максимального отклонения нити от положения равновесия.
4.Выполнить решение задачи в общем виде.
5.Подставить известные данные и вычислить искомую величину.
Решение
Запишем исходные данные:
• Масса пластилиновой пули: m = 9 г.
• Скорость пластилиновой пули: v = 20 м/с.
• Максимальный угол отклонения нити: α = 60°.
Переведем единицы измерения величин в СИ:

Сделаем чертеж:

Нулевой уровень — точка А.
После неупругого столкновения пули с грузом они начинают двигаться вместе. Поэтому закон сохранения импульса для точки А выглядит так:
mv=(m+M)V
После столкновения система тел начинается двигаться по окружности. Точка В соответствует верхней точке траектории. В этот момент скорость системы на мгновение принимает нулевое значение, а потенциальная энергия — максимальное.
Закон сохранения энергии для точки В:
(m+M)V22=(m+M)gh
V22=gh
Высоту h можно определить как произведение длины нити на косинус угла максимального отклонения. Поэтому:
V=√2glcosα
Подставим это выражение в закон сохранения импульса для точки А и получим:

Выразим массу груза:

Ответ: в
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 20k
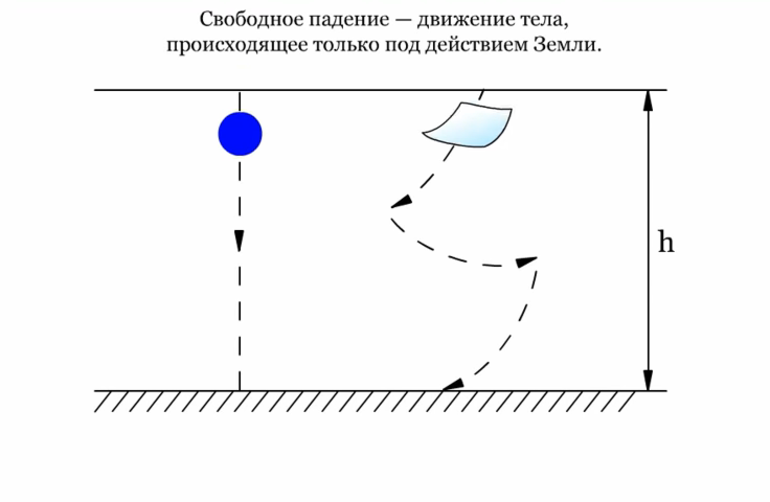
Все вы в своей жизни наблюдали за тем, что тела, не имеющие опоры или подвеса, падают вниз. В чем причина такого падения? Конечно же в том, что на все тела у поверхности Земли действует сила тяжести.
Свободным падением тела называется движение тела только под действием силы тяжести.
Проведем мысленный эксперимент. Представьте, что одновременно начинают падение мяч, камень, лист дерева и перо птицы. В какой очередности упадут эти тела?
Первым упадут камень и мяч, затем перо и лист.
Почему? На перо и лист оказывает заметное влияние сила сопротивления воздуха, направленная против силы тяжести.
Падение тела не может считаться свободным, если сила сопротивления воздуха сравнима с силой тяжести.
Еще в конце XVI века знаменитый итальянский ученый Г. Галилей предположил, что все тела падают с одинаковым ускорением и опытным путем доказал, что это предположение верно.

Согласно биографии Галилео Галилея, написанной его учеником Винченцо Вивиани, в 1589 году Галилей провёл эксперимент, сбросив два шара различной массы (ядро и мушкетную пулю) со знаменитой падающей башни в Пизе, чтобы продемонстрировать, что время падения не зависит от массы шара. С помощью этого эксперимента Галилей якобы обнаружил, что тела упали практически одновременно, тем самым доказав, что в отсутствии сопротивления воздуха все тела падают на Землю равноускоренно и что в данной точке Земли ускорение всех тел при падении одно и то же.

Исаак Ньютон доказал справедливость выводов Галилео простым опытом.

В стеклянную трубку он поместил дробинку, пробку и перышко. Если резко перевернуть расположенную вертикально трубку, то быстрее всего упадет дробинка, за ней кусочек пробки и потом плавно опустится перышко. Если же из трубки откачать воздух и опять резко перевернуть её,то все три тела опустятся на дно одновременно.
Какие выводы можно сделать из опыта Ньютона?
1. Тела падают с одинаковым ускорением.
2. Существует сила сопротивления воздуха
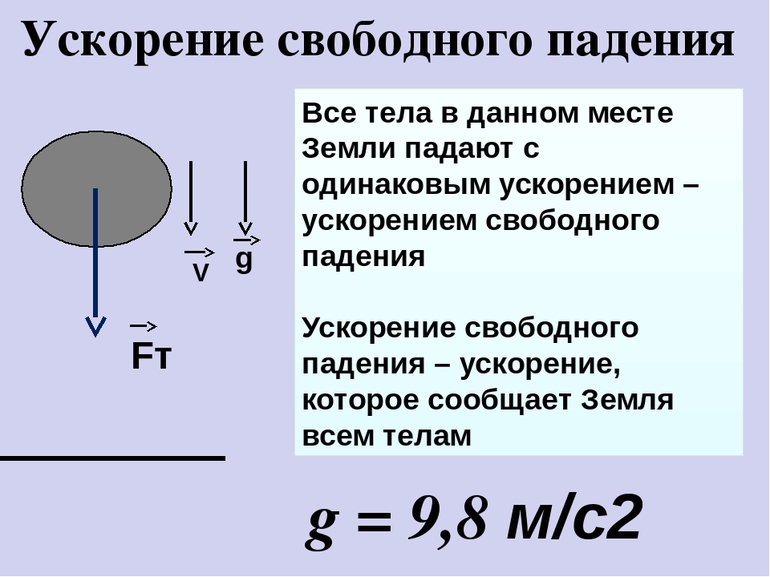
Ускорение, с которым тела падают на Землю, называется ускорением свободного падения.
Ускорение свободного падения – ускорение, сообщаемое телу, поднятому над Землей, силой тяжести.
Вектор ускорения свободного падения обозначается символом g.
g=9,8 м/с2≈10м/с2
Из закона всемирного тяготения: 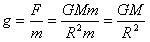
Ускорение свободного падения:
1) Всегда направлено по вертикали вниз
2) Не зависит от массы падающего тела
3) Зависит от географической широты. Так как Земля не шар, а эллипсоид вращения, т.е. радиус Земли на полюсе меньше, чем радиус Земли на экваторе.
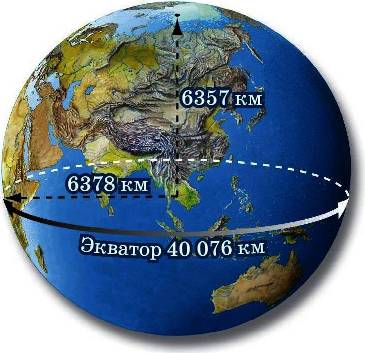
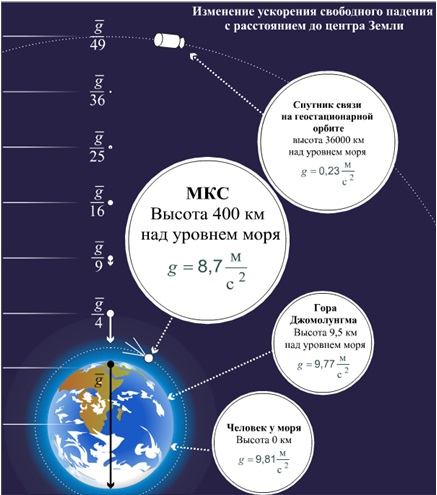
Поэтому сила тяжести и вызвемое ей ускорение больше на полюсе, чем на экваторе. g изменяется примерно от 9,83 м/с2 на полюсах до 9,78 м/с2 на экваторе. На широте Москвы g = 9,81523 м/с2. Обычно, если в расчетах не требуется высокая точность, то числовое значение g у поверхности Земли принимают равным 9,8 м/с2 или даже 10 м/с2.
4) Зависит от высоты над уровнем моря
Рассмотрим несколько примеров движения тел под действием силы тяжести. При решении подобных задач очень важно правильно выполнить чертеж, на котором указать направление осей и всех векторных величин.
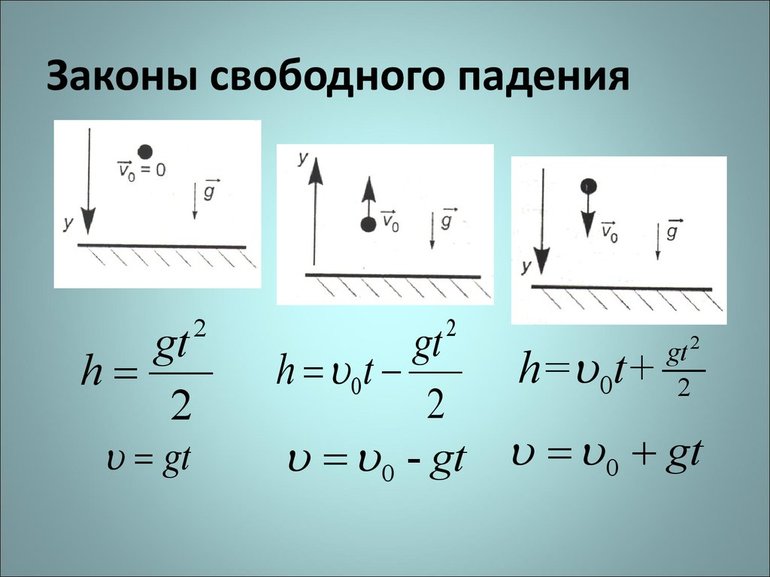
Простым примером свободного падения является падение тела с некоторой высоты h без начальной скорости.
Анализируем рисунок.
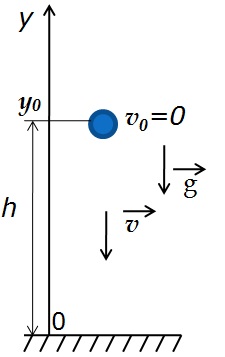
Свободное падение является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело падало s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальная скорость движения равна нулю v0=0
Проекция конечной скорости на ось y отрицательна vу =-v
Начальная координата тела y0=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и vу=-v, получаем -v=0-gt
Упростив выражение, получим формулу для нахождения скорости свободно падающено тела в любой момент времени:
v=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и sу=-h, получаем -h=0-gt2/2
Упростив выражение, получим формулу для нахождения перемещения тела при свободном падении в любой момент времени:
h=gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0=0 и y0=h, получаем y=h-gt2/2
То есть, формула для нахождения координаты тела при свободном падении в любой момент времени:
y=h-gt2/2
2. Тело брошено вертикально вверх.
Как будет двигаться тело, брошенное вертикально вверх?
Если бросить тело вертикально вверх, то некоторое время оно будет двигаться вверх. Действующая на него сила тяжести направлена вниз и сообщает ему ускорение g, тоже направленное вниз. Поэтому скорость тела будет уменьшаться со временем и в некоторый момент она станет равной нулю, после чего тело начнет падать вниз с увеличивающейся скоростью.
Анализируем рисунок.
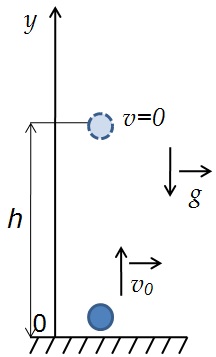
Движение тела, брошенного вертикально вверх тоже является прямолинейным движением с постоянным ускорением a=g, значит, к нему применимы все формулы для равноускоренного движения.
Так как тело движется вертикально, то будем рассматривать его движение вдоль оси y, которую направим вертикально вверх.
Тогда проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Проекция начальной скорости движения на ось y положительна v0y=v0
Конечная скорость в верхней точке равна нулю v =0
Начальная координата тела равна нулю y0=0, а конечная координата равна высоте, на которую тело поднимется y=h
Теперь работаем с формулами.
Проекция скорости на ось y при равноускоренном движении находится по формуле
vу=v0у+ayt
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и vу=v, получаем, что скорость тела, брошенного вертикально в любой момент времени:
v=v0-gt
Если учесть, что в верхней точке v =0, получим 0=v0-gt
Упростив выражение, получим формулу для нахождения начальной скорости тела, брошенного вертикально:
v0=gt
Проекция перемещения на ось y при равноускоренном движении находится по формуле
sу=v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 и sу=h, получим формулу для нахождения перемещения тела, брошенного вертикально, в любой момент времени:
h=v0t-gt2/2
Уравнение координаты при равноускоренном движении находится по формуле
y=y0+v0уt+ayt2/2
учитывая, что тело движется с ускорением свободного падения и gy=-g, а также то, что v0y=v0 , y0=0 и y=h, получаем формулу для нахождения координаты тела, брошенного вертикально, в любой момент времени:
y=v0t-gt2/2
3. Тело брошено горизонтально.
Как будет двигаться тело, брошенное горизонтально?
Если тело бросить горизонтально, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
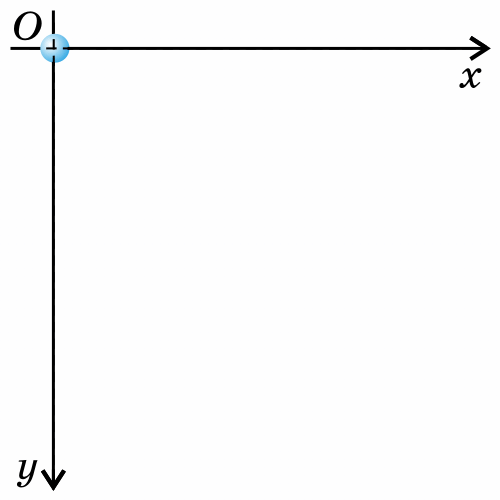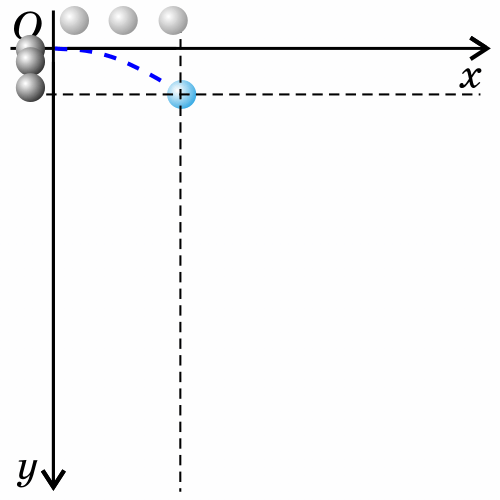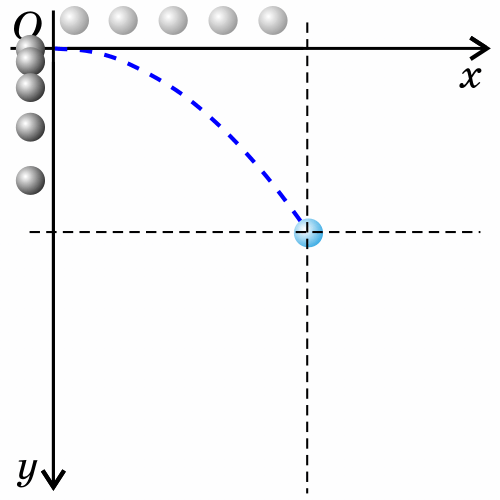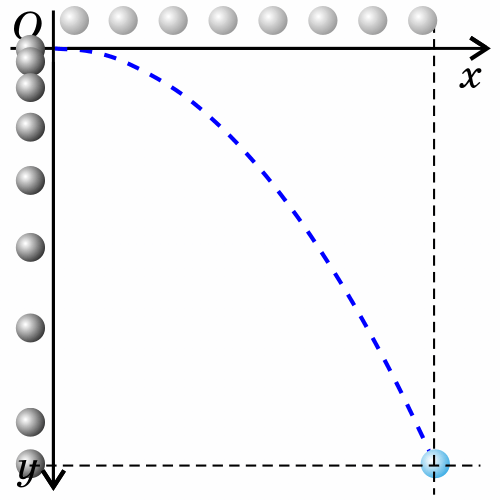
Такое движение тела рассматривают как два движения: по горизонтали – вдоль оси х, и по вертикали – вдоль оси y.
Анализируем рисунок.
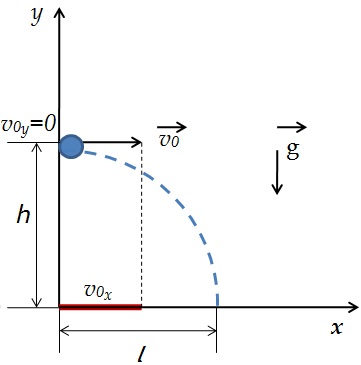
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, с которой тело бросили s=h, а проекция перемещения на ось y отрицательна: sy=-h
Начальные координаты тела х0=0 y0=h
Проекция начальной скорости на ось х равна v0х=v0
Проекция начальной скорости на ось y равна v0y=0
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси х нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0=const
Уравнение перемещения (дальность полета): l=v0х·t= v0·t
Уравнение координаты: x= x0 + v0·t
По вертикали, т.е. вдоль оси y тело свободно падает с высоты h. Поэтому при рассмотрении движения вдоль оси y применимы формулы для свободного падения.
Уравнение скорости: v=g·t
Уравнение перемещения: h=g·t2/2
Уравнение координаты: y= y0-g·t2/2
4. Тело брошено под углом к горизонту.
Как будет двигаться тело, брошенное под углом к горизонту?
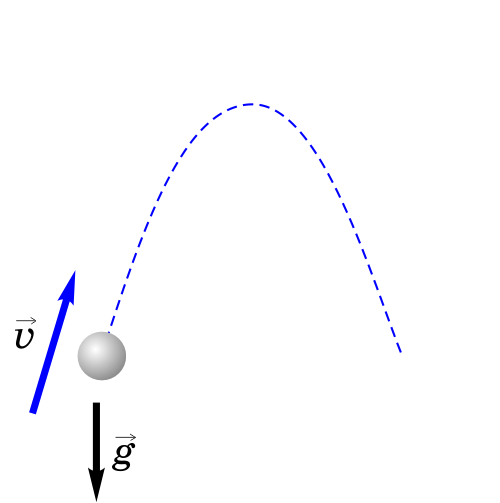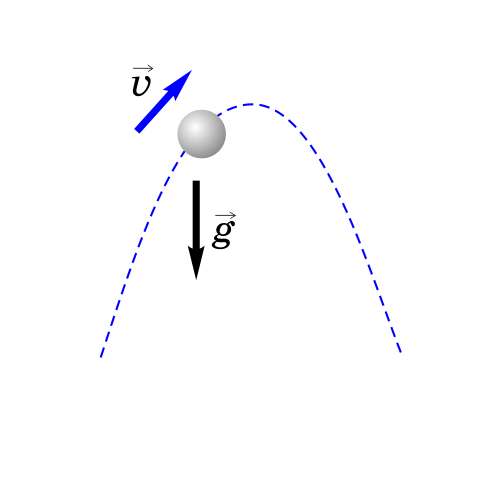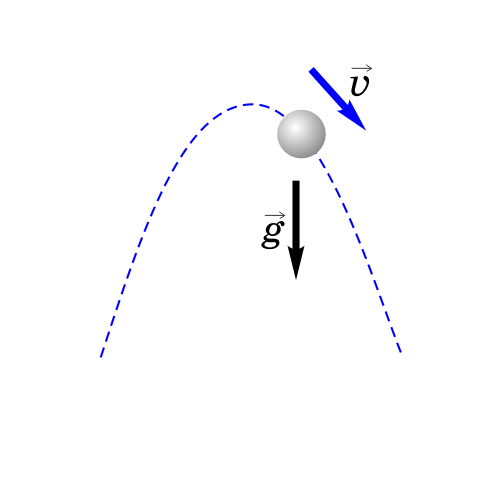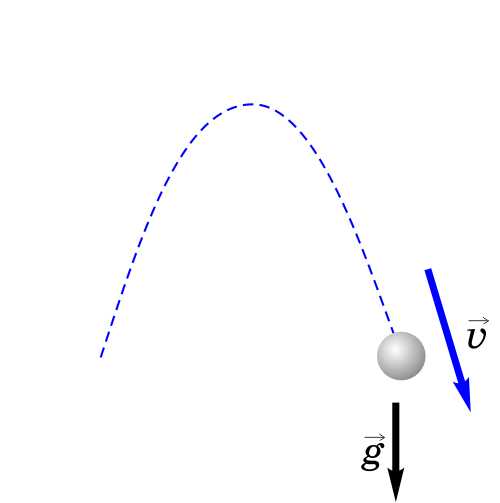
Если тело бросить под углом к горизонту, оно будет двигаться криволинейно — по параболе, хотя на тело все время действует сила тяжести, направленная вертикально вниз.
Такое движение тела рассматривают как два движения: по горизонтали – вдоль оси х, и по вертикали – вдоль оси y.
Анализируем рисунок.
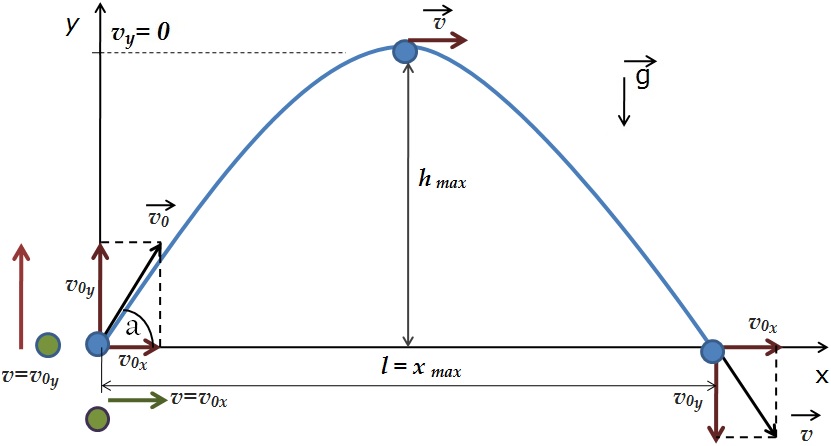
Ось y направим вертикально вверх. Проекция ускорения на ось y отрицательна gy=-g
Перемещение тела равно по модулю высоте, на которую тело поднимется s=h, а проекция перемещения на ось y полжительна: sy=h
Начальные координаты тела равны нулю х0=0 y0=0
Проекция начальной скорости на ось х равна v0х=v0·cosa
Проекция начальной скорости на ось y равна v0y=v0·sina
h – максимальная высота, на которую тело поднимется. На этой высоте проекция скорости на ось y равна 0.
Перемещение тела вдоль оси х это дальность полета sх=l=х-х0
Теперь работаем с формулами.
По горизонтали, т.е. вдоль оси х тело движется равномерно (т.к. нет ускорения) с постоянной скоростью, равной проекции начальной скорости на ось х. Поэтому при рассмотрении движения вдоль оси ОХ нужно пользоваться формулами, полученными для равномерного движения.
Уравнение скорости: v0x=v0·cosa=const
Уравнение перемещения (дальность полета): l=vxt= v0·cosa·t
Уравнение координаты: x= x0 + v0·cosa·t
По вертикали, т.е. вдоль оси y тело движется сначало равнозамедленно, подобно телу, брошенному вертикально вверх со скоростью, равной проекции начальной скорости на ось y, а затем равноускоренно (свободно падая).
Проекция ускорения на ось y gy= -g , проекция начальной скорости на ось y v0у=v0·sina, начальная координата y0=0
Таким образом, применимы формулы, которые мы использовали ранее для равноускоренного движения по вертикали.
Уравнение скорости: vy=v0·sina-g·t
Уравнение перемещения (максимальная высота полета): h=v0·sina·t-g·t2/2
Уравнение координаты: y= v0·sina·t-g·t2/2
Время полета в 2 раза больше времени подъема тела на максимальную высоту
t= 2·tmax = 2·v0·sina/g
Скорость тела находится по теореме Пифагора: ![]()
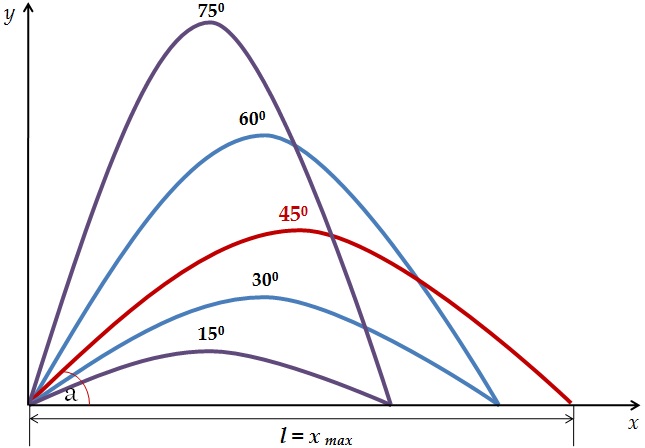 .
.
l = x max= v02·sin2a /g
Дальность полета максимальна, когда максимален sin2a.
Максимальное значение синуса равно единице при угле 2a=900, откуда a = 450
Для углов, дополняющих друг друга до 900 дальность полета одинакова.
Расширения для Joomla
Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:
a→=∆v→∆t=v2→-v1→∆t.
Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:
F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.
Изменение импульса
Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.
Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).
Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.
Импульс относят к векторным величинам. Существует еще одна формулировка определения.
Изменение импульса тела равняется импульсу силы.
При обозначении импульса p→ второй закон Ньютона записывается как:
F→∆t=∆p→.
Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:
FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.
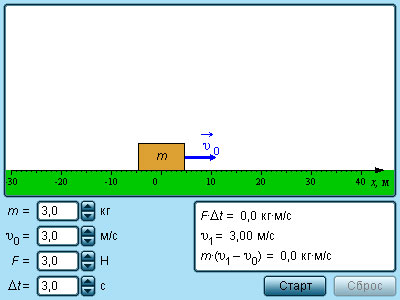
Рисунок 1.16.1. Модель импульса тела.
Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.
Одномерное движение – это движение тела по одной из координатный осей.
На примере рассмотрим свободное падение тела с начальной скоростью v0 под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:
Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.
Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fср из временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.
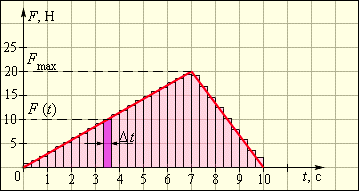
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)
Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δti на промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti, тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.
Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].
Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.
Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.
То есть, из примера видно Fср=12Fmax=10 Н.
Определение средней силы
Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.
Тогда формула импульса приобретает вид:
p=mv=12,5 кг·м/с.
Чтобы определить среднюю силу Fср во время удара, необходимо Fср=p∆t=1,56·103 Н.
Получили очень большое значение, которое равняется телу массой 160 кг.
Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.
Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.
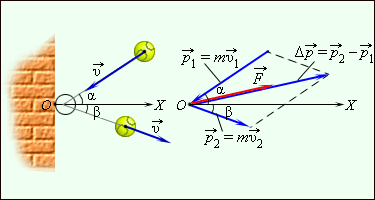
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.
Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.
Здравствуйте!
Если это билет по физике, то обычными детскими рассуждениями как выше Вы не сможете обойтись. Для полного ответа на эти вопросы нужно вывести зависимости и построить графики.
1. Рассмотрим падение тела с некоторой высоты H0:
Уравнение движения будет описываться формулой соответ. равноускоренному движению с начальной сокрость равной нулю.
Здесь же следут сказать, что обычно сопротивлением воздуха пренебрегают, так как иначе задача будет нелинейной и решить ее аналитически не поучится (действительно: сопротивление воздуха зависит нелинейно от квадрата скорости объекта, его размеров и формы) .
S(t)=g*t*t/2, где g=9,81 Н/м – ускорение свободного падения у поверхности земли. В этом случае уравнение положения объекта над замлей будет таким:
H(t)=H0-S(t)=H0-g*t*t/2.
Уравнение скорости падающего тела можно найти взяв первую производную от уравения движения по времени:
V(t)=g*t.
2. Теперь можно перейти к анализу импульса и потенциальной энергии:
Импульс тела: P=m*V, где m – масса тела.
В нашем случае подставляем уравнение скорости: P(t)=m*g*t.
График линейный с углом наклона: phi=arctg(m*g)=arctg(9,81*m)

Потенциальная энергия тела: W=m*g*h
В нашем случае подставляем уравнение падения:
W(t)=m*g*(H0-g*t*t/2)=H0*m*g-m*g*g*t*t/2.
График квадратичный, т. е. парабола.
Найдем параметры параболы (выкладки опускаю, думаю что математику вы знаете) .
Первый корень уравнения: t_падения=КОРЕНЬ (2*H0/g).
Координаты вершины параболы: W0=m*g*H0

Общие сведения
Основоположником создания учения о движении стал Аристотель. Он утверждал, что скорость падения тела зависит от его веса. Значит, тяжёлый предмет сможет долететь до Земли быстрее, чем лёгкий. Если же на объект не будут воздействовать какие-либо силы, его движение невозможно.

Но Галилео Галилей, известный итальянский изобретатель и физик, изучая падение различных предметов и их инерцию, смог опровергнуть догадки Аристотеля. Результаты его исследований были революционными в науке. При этом даже была выпущена книга «Беседы и математические доказательства, касающиеся двух новых отраслей науки, относящихся к механике и местному движению», в которой были изложены основные размышления Галилея.
За дату рождения кинематики как науки можно принять 20 января 1700 года. В это время проходило заседание Академии наук, на котором Пьер Вариньона не только дал определения понятиям скорость, ускорение, но и описал их в дифференциальном виде. Уже после Ампер использовал для изучения процессов вариационное исчисление. Наглядные опыты провёл Лейбниц, а потом. профессор МГУ Н. А. Любимов смог продемонстрировать появление невесомости при свободном падении.
Под невесомостью понимают состояние тела, при котором силы взаимодействия с опорой, существующие из-за гравитационного притяжения, не оказывают никакого влияния. Такое положение имеет место, когда воздействующие на тело внешние силы можно охарактеризовать массовостью, например, тяготения.
В этом случае силы поля сообщают всем частицам предмета в любом из его положений равные по модулю и направлению ускорения, либо при движении возникают одинаковые по модулю скорости всех частиц тела. Например, поступательное движение. Состояние невесомости особо ярко проявляется в начальный момент при падении тела в атмосфере. Это связано с тем, что сопротивление воздуха ещё невелико.
Таким образом, для существования свободного падения нужно выполнение как минимум двух условий:
- малость или отсутствие сопротивления среды;
- действие лишь одной силы тяжести.
Что интересно, движение вверх тоже считается свободным падением, несмотря на обратное интуитивное восприятие, поэтому траектория движения может иметь форму как участка параболы, так и отрезка прямой. Например, камень, брошенный с небольшой высоты или поверхности под любым углом.
Опыт Галилея
Падение относится к реальному движению. Любое взаимодействие с Землёй приводит к изменению скорости из-за чего возникает ускорение. В 1553 году итальянец Джованни Бенедетти заявил, что 2 тела с разной массой, но одинаковой формы, брошенные в одной среде за одинаковое время пролетят равные расстояния. Это утверждение нуждалось в доказательстве, так как противоречило общепринятому на тот момент времени пониманию процессов. В частности, высказываниям Аристотеля.

Одним из экспериментаторов стал Галилей. Для проведения опыта учёному понадобилось:
- стофунтовое ядро;
- однофунтовый шар.
Существует мнение, что вместо шара учёный использовал мушкетную пулю. Эксперимент заключался в следующем. Подняв 2 предмета на Пизанскую башню, Галилей сбросил их одновременно. Наблюдающие люди воочию смогли убедиться, что 2 тела упали на землю одновременно. Когда же один из учеников Аристотеля упрекнул итальянца, что на такой малой высоте невозможно оценить достоверно разницу, экспериментатор ответил: «Проделайте опыт самостоятельно, вы найдёте, что более тяжёлый предмет опередит тот, что легче на 2 пальца, поэтому, когда первый упадёт на землю, то второй будет от него на расстоянии толщины двух пальцев».

В своих работах Галилей рассуждал, что если связать верёвкой 2 тела разной тяжести, то с большим весом, по мнению Аристотеля, предмет будет лететь быстрее. Причём лёгкий объект начнёт замедлять падение тяжёлого. Но так как система в целом тяжелее, чем отдельно взятые тела, падать она должна быстрее самого тяжёлого тела. Другими словами, возникает противоречие, значит, предположение о влиянии веса на скорость падения неверно.
Сегодня эксперимент, подтверждающий доводы Галилея, может провести самостоятельно, пожалуй, каждый интересующийся. Такой опыт часто демонстрируют в средних классах общеобразовательной школы. Для этого нужно взять 2 трубки, длиной более метра и поместить в них 2 шарика разной массы. Затем создать внутри вакуум и одновременно их перевернуть. Если все условия соблюдены верно, то 2 тела опустятся на дно ёмкостей одновременно.
Если же опыт повторить не в вакууме, на шары будет действовать сила сопротивления, поэтому время падения уже не будет совпадать. Причём зависеть оно будет от формы предмета и его плотности.
Закон ускорения
Формула для свободного падения была выведена из выражения, определяющего силу тяжести: F = m * g. В соответствии с законом, падение предметов выполняется с одним и тем же ускорением вне зависимости от массы тела. По сути, это частный случай равноускоренного движения, обусловленное силой тяжести.
Для количественного анализа нужно ввести систему координат, взяв начало у поверхности Земли. Тогда можно рассмотреть падение тела массой m с высоты y0. Причём вращением планеты и сопротивлением воздушной среды нужно пренебречь.
Дифференциальное уравнение будет иметь вид: my = – mg, где: g — ускорение свободного падения. Само же дифференцирование выполняется по времени. При заданных начальных условиях y = y0 и беря во внимание проекцию скорости на вертикальную ось после интегрирования, зависимость переменных от t примет вид:
- v = v0 + gt;
- y = y0 + v0t — (gt2 / 2).
Из полученных формул становится понятно, почему свободное падение не зависит от массы тела. При этом если начальная скорость будет равна нулю, то есть при падении предмету не сообщается импульс, текущее движение пропорционально времени, а пройденный путь определяется его квадратом.
Как показали эксперименты, если сопротивления воздуха нет, ускорение для любых летящих предметов по отношению к Земле составит 9,8 м / с2. Формулы, которые используются при расчёте величин, совпадают с выражениями, справедливыми для любого равноускоренного движения. Например, если тело падает без начальной скорости, его скорость можно найти по формуле: V2 = g * t, а высоту падения определить так: h = (gt2 / 2).
Следует отметить, что при удалении предмета от Земли значение свободного движения уменьшается. Причём из-за формы планеты на экваторе оно будет составлять 9,78 м / с2, а с противоположной стороны — 9,832 м / с2. Чтобы определить значение в любом месте, используют нитяной маятник. Его период колебаний определяется по формуле: T = 2p√(l / g), где l — длина нити.
Значения силы тяжести также зависит от строения земной коры и содержащихся в недрах полезных ископаемых. С учётом этого рассчитываются гравитационные аномалии: Δg = g — gср. Например, если g > gcp, то с большой вероятностью в земле содержатся залежи железной руды, в ином случае — нефти или газа.
Решение задач
Свободно двигаться, то есть не испытывать действие сторонних сил, могут любые тела в вакууме. Но в реальности на них оказывается воздействие как атмосферными явлениями, так и сопротивлением среды. При решении задач учитывается только сила тяжести, а вот остальными явлениями пренебрегают, считая их ничтожно малыми.
Вот некоторые из типовых задач, используемые при обучении в среднеобразовательных школах:

- Деревянная бочка падает с 30 метров. Какова будет её скорость перед столкновением с Землёй? Так как рассматривается свободное падение, для решения нужно использовать формулу: v2 = 2 * g * h. Отсюда, v = √(2 * g * h) = (2 * 9,81 м / с2 * 30 м) = 24,26 м/с.
-
Тело вылетает вертикально вверх со скоростью 45 м/с. Какой высоты оно достигнет перед изменением направления полёта и сколько для этого понадобится времени. Для начала следует записать формулу скорости: v = v0 — gt. Отсюда можно рассчитать время полёта: t = v0 / g = 45 / 9,8 = 4,6 c. Теперь можно определить максимальную высоту: h = vot — (gt 2 / 2) = 45 м / с * 4,6 с — 9,8 м / с2 * (4,6 c)2 / 2 = 207 м — 103,7 м = 103,3 м.
-
Камень летит со скоростью 30 м/с. Найти время, за которое он достигнет 25 метров. Система уравнений, описывающая движение, будет выглядеть так: h = v0t — (gt2 / 2); 25 = 30t — 5t2. Полученные уравнения в системе называются квадратными, поэтому нужно выразить одно из другого и определить корни: t2 — 6t + 5 = 0. В результате должно получиться время, равное одной секунде.
Рассмотренные задания довольно простые. Но есть и повышенной сложности, требующие не только знания формул, но и умения выполнять анализ. Вот одно из таких.
Мяч бросили с горки под углом к горизонту. Через время, равное t = 0,5 c он достигнет наибольшей высоты, а t2 = 2,5 он упадёт. Определить высоту горки, ускорение падения принять равное g = 10 м / с2. Скорость движущегося предмета можно представить в координатной плоскости x и y. В горизонтальном направлении сил, оказывающих воздействие, нет. Движение равномерное. Наибольшая высота будет достигнута при h = H + v0y * t1 — (gt21 / 2).
Вертикальную составляющую можно вычислить, руководствуясь геометрическими принципами: v0y = v0 * sin (a). Учитывая, что h = (gt2 / 2), для высоты горки можно записать: H = (g * (t21 + t22) / 2) — t1 * v0 sin (a). Так как gt1 = v0 sin (a), то рабочая формула примет вид: H = (g * (t21 + t22) / 2) — gt21. После подстановки данных в ответе должна получиться высота равная 30 метров. Задача решена.






