Как найти импульс тела формула физика

Импульс

Размерность	LMT⁻¹
Единицы измерения
СИ	кг·м/с
СГС	г·см/с
Примечания
векторная величина

И́мпульс (коли́чество движе́ния) — векторная физическая величина, являющаяся мерой механического движения тела.

В классической механике импульс тела равен произведению массы этого тела на его скорость направление импульса совпадает с направлением вектора скорости:

В релятивистской физике импульс вычисляется как:

${displaystyle {vec {p}}={frac {m{vec {v}}}{sqrt {1-v^{2}/c^{2}}}},}$

где — скорость света; в пределе для малых формула переходит в классическую.

Важнейший физический закон, в котором фигурирует импульс тела, — второй закон Ньютона:

${displaystyle {frac {{mbox{d}}{vec {p}}}{{mbox{d}}t}}={vec {F}},}$

здесь — время, vec{F} — сила, приложенная к телу.

В записи через импульс (в отличие от — ускорение) закон применим не только в классической, но и в релятивистской механике.

В самом общем виде, определение звучит: импульс — это аддитивный интеграл движения механической системы, связанный согласно теореме Нётер с фундаментальной симметрией — однородностью пространства.

Понятие «импульс» имеет обобщения в теоретической механике, для случая наличия электромагнитного поля (как для частицы в поле, так и для самого поля), а также в квантовой механике.

История появления термина[править | править код]

Средневековые натурфилософы, в соответствии с учением Аристотеля, полагали, что для поддержания движения непременно требуется некоторая сила, без силы движение прекращается. Часть учёных выдвинула возражение против этого утверждения: почему брошенный камень продолжает двигаться, хотя связь с силой руки утрачена?

Для ответа на подобные вопросы Жан Буридан (XIV век) изменил ранее известное в философии понятие «импетус». По Буридану, летящий камень обладает «импетусом», который сохранялся бы в отсутствие сопротивления воздуха. При этом «импетус» прямо пропорционален скорости. В другом месте он пишет о том, что тела с бо́льшим весом способны вместить больше импетуса.

В первой половине XVII века Рене Декартом было введено понятие «количества движения». Он высказал предположение о том, что сохраняется не только количество движения одного тела, изолированного от внешних воздействий, но и любой системы тел, взаимодействующих лишь друг с другом. Физическое понятие массы в то время ещё не было формализовано — и он определил количество движения как произведение «величины тела на скорость его движения». Под скоростью Декарт подразумевал абсолютную величину (модуль) скорости, не учитывая её направление. Поэтому теория Декарта согласовывалась с опытом лишь в некоторых случаях (например, Валлис, Рен и Гюйгенс в 1678 году использовали её для исследования абсолютно упругого столкновения в системе центра масс).

Валлис в 1668 году первым предложил считать количество движения не скалярной, а направленной величиной, учитывая направления с помощью знаков «плюс» и минус”^[1]. В 1670 году он окончательно сформулировал закон сохранения количества движения. Экспериментальным доказательством закона послужило то, что новый закон позволял рассчитывать неупругие удары, а также удары в любых системах отсчёта.

Закон сохранения количества движения был теоретически доказан Исааком Ньютоном через третий и второй закон Ньютона. Согласно Ньютону, «количество движения есть мера такового, устанавливаемая пропорционально скорости и массе».

Формальное абстрактное определение[править | править код]

Импульсом называется сохраняющаяся физическая величина, связанная с однородностью пространства (то есть инвариант относительно трансляций).

Из свойства однородности пространства следует независимость лагранжиана замкнутой системы от её положения в пространстве: для хорошо изолированной системы её поведение не зависит от того, в какое место пространства она помещена. По теореме Нётер из этой однородности следует сохранение некоторой физической величины, которую и называют импульсом.

В разных разделах физики применительно к реальным задачам даются более конкретные определения импульса, с которыми можно работать и производить расчёты.

Определения импульса тела в механике[править | править код]

Классическая механика[править | править код]

В классической механике полным импульсом системы материальных точек называется векторная величина, равная сумме произведений масс материальных точек на их скорости:

${vec p}=sum _{{i}}m_{i}{vec {v}}_{i},$

соответственно, величина ${vec p}_{i}=m_{i}{vec {v}}_{i}$ называется импульсом одной материальной точки. Это векторная величина, направленная в ту же сторону, что и скорость частицы. Единицей измерения импульса в Международной системе единиц (СИ) является килограмм-метр в секунду (кг·м/с).

Импульс тела конечных размеров находится путём его мысленного разбиения на малые части, которые можно считать материальными точками, с последующим интегрированием по ним:

{displaystyle {vec {p}}=int rho (x,y,z){vec {v}}(x,y,z)dxdydz.}

Стоящее под интегралом произведение называют плотностью импульса.

Релятивистская механика[править | править код]

В релятивистской механике импульсом системы материальных точек называется величина:

${displaystyle {vec {p}}=sum _{i}{frac {m_{i}{vec {v}}_{i}}{sqrt {1-v_{i}^{2}/c^{2}}}},}$

где m_i — масса -й материальной точки, vec v_i — её скорость.

Также вводится четырёхмерный импульс, который для одной материальной точки массой определяется как:

${displaystyle p_{mu }=(E/c,{vec {p}})=left({frac {mc}{sqrt {1-v^{2}/c^{2}}}},{frac {m{vec {v}}}{sqrt {1-v^{2}/c^{2}}}}right).}$

На практике часто применяются соотношения между массой, импульсом и энергией частицы:

${displaystyle E^{2}-mathbf {p} ^{2}c^{2}=m^{2}c^{4},qquad qquad mathbf {p} ={frac {E}{c^{2}}},mathbf {v} .}$

Свойства импульса[править | править код]

Сохранение импульса следует из второго и третьего законов Ньютона: записав второй закон для каждой из составляющих систему материальных точек, представив силу, действующую на каждую точку, как внешнюю ${displaystyle {vec {F}}_{i,ext}}$ плюс силу взаимодействия со всеми остальными точками, затем просуммировав, получим:

${displaystyle {frac {d{vec {p}}}{dt}}=sum _{i}{frac {d{vec {p}}_{i}}{dt}}=sum _{i}{vec {F}}_{i}=sum _{i}left({vec {F}}_{i,ext}+sum _{j,jneq j}{vec {F}}_{i,j}right)=sum _{i}{vec {F}}_{i,ext}+sum _{i}sum _{j,jneq i}F_{i,j}.}$

Первое слагаемое равно нулю из-за компенсации внешних сил, а второе — вследствие третьего закона Ньютона (слагаемые ${displaystyle {vec {F}}_{a,b}}$ и ${displaystyle {vec {F}}_{b,a}}$ в двойной сумме попарно уничтожают друг друга).

Импульс не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[2]. Свойства сохранения кинетической энергии, сохранения импульса и второго закона Ньютона достаточно для получения математического выражения импульса^[3]^[4].

При наличии электромагнитного взаимодействия между материальными точками третий закон Ньютона может не выполняться — и тогда сохранения суммы импульсов точек не будет. В таких случаях, особенно в релятивистской механике, удобнее включать в понятие «система» не только совокупность точек, но и поле взаимодействия между ними. Соответственно, будут учтены не только импульсы составляющих систему частиц, но и импульс поля взаимодействия. При этом вводится величина — тензор энергии-импульса, которая в полной мере удовлетворяет законам сохранения.

Что касается 4-импульса, то для системы не взаимодействующих материальных точек их совокупный 4-импульс равен сумме по всем частицам. При наличии взаимодействия такое суммирование теряет смысл.

Обобщённый импульс[править | править код]

В теоретической механике в целом[править | править код]

В теоретической механике обобщённым импульсом называется частная производная лагранжиана системы по обобщённой скорости:

${displaystyle p_{i}={{partial {mathcal {L}}} over {partial {dot {q}}_{i}}}.}$

Обобщенный импульс, как и не обобщённый, обозначается буквой обычно из контекста ясно, о чём идёт речь.

Размерность обобщённого импульса зависит от размерности обобщённой координаты. Если размерность $q_{i}$ — длина, то $p_{i}$ будет иметь размерность обычного импульса, если же координатой $q_{i}$ выступает угол (величина безразмерная), то $p_{i}$ обретёт размерность момента импульса. Если лагранжиан системы не зависит от некоторой обобщённой координаты, то из уравнений Лагранжа ${displaystyle dp_{i}/dt=0.}$

Если обобщённая координата — это обычная координата (и тогда её производная по времени — просто скорость), а внешних полей нет, обобщённый импульс тождественен обычному. Так, для свободной частицы функция Лагранжа имеет вид:

${mathcal L}=-mc^{2}{sqrt {1-v^{2}/c^{2}}}$

, отсюда: ${displaystyle {vec {p}}=m{vec {v}}/{sqrt {1-v^{2}/c^{2}}}}$

Для частицы в электромагнитном поле[править | править код]

В электромагнитном поле лагранжиан частицы будет отличаться от приведённого выше наличием дополнительных членов, а именно ${displaystyle {mathcal {L}}=-mc^{2}{sqrt {1-v^{2}/c^{2}}}-qvarphi +q{vec {v}}cdot {vec {A}}.}$ Соответственно, обобщённый импульс частицы равен:

${mathbf {p}}={frac {m{mathbf {v}}}{{sqrt {1-v^{2}/c^{2}}}}}+q{mathbf A},$

где — векторный потенциал электромагнитного поля, — заряд частицы; в выражении для фигурировал также скалярный потенциал varphi .

Импульс электромагнитного поля[править | править код]

Электромагнитное поле, как и любой другой материальный объект, обладает импульсом, который легко можно найти, проинтегрировав вектор Пойнтинга по объёму:

${mathbf p}={frac {1}{c^{2}}}int {mathbf S}dV={frac {1}{c^{2}}}int [{mathbf E}times {mathbf H}]dV$

(в системе СИ).

Существованием импульса у электромагнитного поля объясняется, например, такое явление как давление электромагнитного излучения.

Импульс в квантовой механике[править | править код]

Определение через оператор[править | править код]

В квантовой механике оператором импульса частицы называют оператор — генератор группы трансляций. Это эрмитов оператор, собственные значения которого отождествляются с импульсом системы частиц. В координатном представлении для системы нерелятивистских частиц он имеет вид:

${hat {{mathbf {P}}}}=sum _{j}{hat {{mathbf {p}}}}_{j}=sum _{j}-ihbar nabla _{j}$

где $nabla _{j}$ — оператор набла, соответствующий дифференцированию по координатам -ой частицы.

Гамильтониан системы выражается через оператор импульса:

${hat {H}}=sum _{i}{frac {1}{2m_{i}}}{hat {{mathbf {p}}}}_{i}^{2}+U({mathbf {r_{1}}},dots )$ .

Для замкнутой системы ( U=0 ) оператор импульса коммутирует с гамильтонианом, и импульс сохраняется.

Определение через волны де Бройля[править | править код]

Формула де Бройля связывает импульс и длину волны де Бройля рассматриваемого объекта.

Модуль импульса обратно пропорционален длине волны

$p={frac hlambda }$

где — постоянная Планка.

Для частиц не очень высокой энергии, движущихся со скоростью vll c (скорости света), модуль импульса равен p=mv (где — масса частицы), и:

${displaystyle lambda ={frac {h}{p}}={frac {h}{mv}}}$

Следовательно, длина волны де Бройля тем меньше, чем больше модуль импульса.

В векторном виде это записывается как:

${displaystyle {vec {p}}={frac {h}{2pi }}{vec {k}}=hbar {vec {k}}}$

где {vec k} — волновой вектор.

Как и в классической механике, в квантовой имеет место сохранение импульса в изолированных системах^[5]^[6]. В тех явлениях, когда проявляются корпускулярные свойства частиц, их импульс записывается «классически» как p=mv , а если проявляются волновые свойства, действует^[7] связь ${displaystyle p=hlambda ^{-1}}$ . При этом, как и в классической механике, сохранение импульса выступает следствием симметрии относительно сдвигов по координатам^[8].

Импульс в гидродинамике[править | править код]

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа При этом вместо импульса фигурирует вектор плотности импульса, совпадающий по смыслу с вектором плотности потока массы

Поскольку в турбулентном потоке характеристики состояния вещества (в том числе плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока в соответствии с методом О. Рейнольдса получаются путём осреднения уравнений Навье-Стокса^[9].

Если в согласии с методом Рейнольдса представить , где черта сверху — знак осреднения, а штрих — отклонения от среднего, то вектор осреднённой плотности импульса приобретёт вид:

{displaystyle {overline {vec {s}}}={overline {rho {vec {v}}}}={overline {rho }}~{overline {vec {v}}}+{vec {S}},}

где — вектор плотности флуктуационного потока массы (или «плотность турбулентного импульса»^[9]).

Импульсное представление в квантовой теории поля[править | править код]

В квантовой теории поля часто употребляется импульсное представление на основе использования преобразования Фурье. Его преимуществами являются: удобство описания физических систем при помощи энергий и импульсов, а не при помощи пространственно-временных координат; более компактная и наглядная структура динамических переменных^[10].

См. также[править | править код]

Импульс силы
Момент импульса
Электрический импульс

Примечания[править | править код]

↑ Григорьян А. Т. Механика от античности до наших дней. — М.: Наука, 1974.
↑ ¹ ² ³ Айзерман, 1980, с. 49.
↑ Айзерман, 1980, с. 54.
↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» Архивная копия от 1 января 2015 на Wayback Machine // УФН, 59, с. 325—362, (1956)
↑ Перкинс Д.^[en] Введение в физику высоких энергий. — М., Мир, 1975. — c. 94
↑ Широков Ю. М., Юдин Н. П. Ядерная физика. — М.: Наука, 1972. — С. 276. — 670 с.
↑ Фейнман Р. Ф. ]. Фейнмановские лекции по физике. Вып. 1 Современная наука о природе. Законы механики.. — М.: Едиториал УРСС, 2004. — С. 194. — 440 с. — ISBN 5-354-00699-6.
↑ Ферми Э. Квантовая механика. — М.: Мир, 1968. — С. 183. — 367 с.
↑ ¹ ² Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
↑ Боголюбов Н. Н., Ширков Д. В. Квантовые поля. — М., Наука, 1980. — с. 25

Литература[править | править код]

Арнольд В. И. Математические методы классической механики. — 5-е изд., стереотипное. — М.: Едиториал УРСС, 2003. — 416 с. — 1500 экз. — ISBN 5-354-00341-5.
Ландау Л. Д., Лифшиц Е. М. Механика. — Издание 4-е, исправленное. — М.: Наука, 1988. — 215 с. — («Теоретическая физика», том I). — ISBN 5-02-013850-9.
Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7.
Сивухин Д. В. Общий курс физики. — Издание 4-е. — М.: Физматлит, 2002. — Т. I. Механика. — 792 с. — ISBN 5-9221-0225-7.
Айзерман М. А. Классическая механика. — М.: Наука, 1980. — 368 с.

Источник

Основные теоретические сведения

Импульс тела

К оглавлению…

Импульсом (количеством движения) тела называют физическую векторную величину, являющуюся количественной характеристикой поступательного движения тел. Импульс обозначается р. Импульс тела равен произведению массы тела на его скорость, т.е. он рассчитывается по формуле:

Направление вектора импульса совпадает с направлением вектора скорости тела (направлен по касательной к траектории). Единица измерения импульса – кг∙м/с.

Общий импульс системы тел равен векторной сумме импульсов всех тел системы:

Изменение импульса одного тела находится по формуле (обратите внимание, что разность конечного и начального импульсов векторная):

где: p_н – импульс тела в начальный момент времени, p_к – в конечный. Главное не путать два последних понятия.

Абсолютно упругий удар – абстрактная модель соударения, при которой не учитываются потери энергии на трение, деформацию, и т.п. Никакие другие взаимодействия, кроме непосредственного контакта, не учитываются. При абсолютно упругом ударе о закрепленную поверхность скорость объекта после удара по модулю равна скорости объекта до удара, то есть величина импульса не меняется. Может поменяться только его направление. При этом угол падения равен углу отражения.

Абсолютно неупругий удар – удар, в результате которого тела соединяются и продолжают дальнейшее своё движение как единое тело. Например, пластилиновый шарик при падении на любую поверхность полностью прекращает свое движение, при столкновении двух вагонов срабатывает автосцепка и они так же продолжают двигаться дальше вместе.

Закон сохранения импульса

К оглавлению…

При взаимодействии тел импульс одного тела может частично или полностью передаваться другому телу. Если на систему тел не действуют внешние силы со стороны других тел, такая система называется замкнутой.

В замкнутой системе векторная сумма импульсов всех тел, входящих в систему, остается постоянной при любых взаимодействиях тел этой системы между собой. Этот фундаментальный закон природы называется законом сохранения импульса (ЗСИ). Следствием его являются законы Ньютона. Второй закон Ньютона в импульсной форме может быть записан следующим образом:

Как следует из данной формулы, в случае если на систему тел не действует внешних сил, либо действие внешних сил скомпенсировано (равнодействующая сила равна нолю), то изменение импульса равно нолю, что означает, что общий импульс системы сохраняется:

Аналогично можно рассуждать для равенства нулю проекции силы на выбранную ось. Если внешние силы не действуют только вдоль одной из осей, то сохраняется проекция импульса на данную ось, например:

Аналогичные записи можно составить и для остальных координатных осей. Так или иначе, нужно понимать, что при этом сами импульсы могут меняться, но именно их сумма остается постоянной. Закон сохранения импульса во многих случаях позволяет находить скорости взаимодействующих тел даже тогда, когда значения действующих сил неизвестны.

Сохранение проекции импульса

К оглавлению…

Возможны ситуации, когда закон сохранения импульса выполняется только частично, то есть только при проектировании на одну ось. Если на тело действует сила, то его импульс не сохраняется. Но всегда можно выбрать ось так, чтобы проекция силы на эту ось равнялась нулю. Тогда проекция импульса на эту ось будет сохраняться. Как правило, эта ось выбирается вдоль поверхности по которой движется тело.

Многомерный случай ЗСИ. Векторный метод

К оглавлению…

В случаях если тела движутся не вдоль одной прямой, то в общем случае, для того чтобы применить закон сохранения импульса, нужно расписать его по всем координатным осям, участвующим в задаче. Но решение подобной задачи можно сильно упростить, если использовать векторный метод. Он применяется если одно из тел покоится до или после удара. Тогда закон сохранения импульса записывается одним из следующих способов:

В этих формулах буквой υ обозначены скорости тел до соударения, а буквой u обозначены скорости тел после соударения. Из правил сложения векторов следует, что три вектора в этих формулах должны образовывать треугольник. Для треугольников применяется теорема косинусов. Если правильно записать соответствующую теорему косинусов, то зачастую получается уравнение из которого можно найти нужную величину. Однако, иногда к правильно записанной теореме косинусов еще нужно будет добавить правильно записанный закон сохранения энергии (смотрите следующий раздел). В этом случае получится система уравнений из которых наверняка можно будет найти нужную величину.

Источник

Если на тело массой m за определенный промежуток времени Δt действует сила F→, тогда следует изменение скорости тела ∆v→=v2→-v1→. Получаем, что за время Δt тело продолжает движение с ускорением:

a→=∆v→∆t=v2→-v1→∆t.

Основываясь на основном законе динамики, то есть втором законе Ньютона, имеем:

F→=ma→=mv2→-v1→∆t или F→∆t=mv2→-mv1→=m∆v→=∆mv→.

Изменение импульса

Определение 1

Импульс тела, или количество движения – это физическая величина, равная произведению массы тела на скорость его движения.

Импульс тела считается векторной величиной, которая измеряется в килограмм-метр в секунду (кг м/с).

Определение 2

Импульс силы – это физическая величина, равняющаяся произведению силы на время ее действия.

Импульс относят к векторным величинам. Существует еще одна формулировка определения.

Определение 3

Изменение импульса тела равняется импульсу силы.

При обозначении импульса p→ второй закон Ньютона записывается как:

F→∆t=∆p→.

Данный вид позволяет формулировать второй закон Ньютона. Сила F→ является равнодействующей всех сил, действующих на тело. Равенство записывается как проекции на координатные оси вида:

FxΔt=Δpx; FyΔt=Δpy; FzΔt=Δpz.

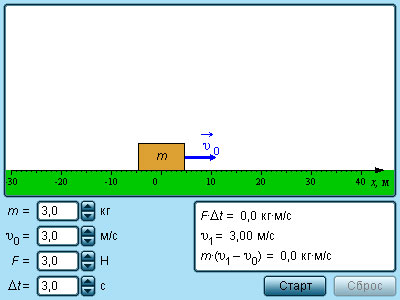
Рисунок 1.16.1. Модель импульса тела.

Изменение проекции импульса тела на любую из трех взаимно перпендикулярных осей равно проекции импульса силы на эту же ось.

Определение 4

Одномерное движение – это движение тела по одной из координатный осей.

Пример 1

На примере рассмотрим свободное падение тела с начальной скоростью v0под действием силы тяжести за промежуток времени t. При направлении оси OY вертикально вниз импульс силы тяжести Fт=mg, действующий за время t, равняется mgt. Такой импульс равняется изменению импульса тела:

Fтt=mgt=Δp=m(v–v0), откуда v=v0 + gt.

Запись совпадает с кинематической формулой определения скорости равноускоренного движения. По модулю сила не изменяется из всего интервала t. Когда она изменяема по величине, тогда формула импульса требует подстановки среднего значения силы Fсриз временного промежутка t. Рисунок 1.16.2 показывает, каким образом определяется импульс силы, которая зависит от времени.

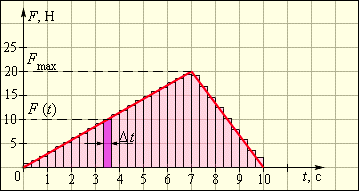
Рисунок 1.16.2. Вычисление импульса силы по графику зависимости F(t)

Необходимо выбрать на временной оси интервал Δt, видно, что сила F(t) практически неизменна. Импульс силы F(t)Δt за промежуток времени Δt будет равняться площади заштрихованной фигуры. При разделении временной оси на интервалы на Δtiна промежутке от от 0 до t, сложить импульсы всех действующих сил из этих промежутков Δti_,тогда суммарный импульс силы будет равняться площади образования при помощи ступенчатой и временной осей.

Применив предел (Δti→0), можно найти площадь, которая будет ограничиваться графиком F(t) и осью t. Использование определения импульса силы по графику применимо с любыми законами, где имеются изменяющиеся силы и время. Данное решение ведет к интегрированию функции F(t) из интервала [0; t].

Рисунок 1.16.2 показывает импульс силы, находящийся на интервале от t1=0 с до t2=10.

Из формулы получим, что Fср(t2-t1)=12Fmax(t2-t1)=100 Н·с=100 кг·м/с.

То есть, из примера видно Fср=12Fmax=10 Н.

Определение средней силы

Имеются случаи, когда определение средней силы Fср возможно при известных времени и данных о сообщенном импульсе. При сильной ударе по мячу с массой 0,415 кг можно сообщить скорость, равную v=30 м/с. Приблизительным временем удара является значение 8·10–3 с.

Тогда формула импульса приобретает вид:

p=mv=12,5 кг·м/с.

Чтобы определить среднюю силу Fсрво время удара, необходимо Fср=p∆t=1,56·103 Н.

Получили очень большое значение, которое равняется телу массой 160 кг.

Когда движение происходит по криволинейной траектории, то начальное значение p1→ и конечное
p2→ могут быть различны по модулю и по направлению. Для определения импульса ∆p→ применяют диаграмму импульсов, где имеются векторы p1→ и p2→, а ∆p→=p2→-p1→ построен по правилу параллелограмма.

Пример 2

Для примера приводится рисунок 1.16.2, где нарисована схема импульсов мяча, отскакивающего от стены. При подаче мяч с массой m со скоростью v1→ налетает на поверхность под углом α к нормали и отскакивает со скоростью v2→ с углом β. При ударе в стену мяч подвергался действию силы F→, направленной также, как и вектор ∆p→.

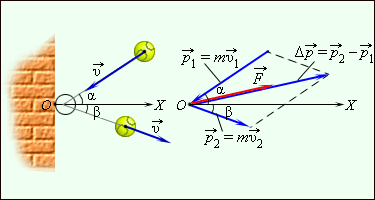
Рисунок 1.16.3. Отскакивание мяча от шероховатой стенки и диаграмма импульсов.

Если происходит нормальное падение мяча с массой m на упругую поверхность со скоростью v1→=v→, тогда при отскоке она изменится на v2→=-v→. Значит, за определенный промежуток времени импульс изменится и будет равен ∆p→=-2mv→. Используя проекции на ОХ, результат запишется как Δpx=–2mvx. Из рисунка 1.16.3 видно, что ось ОХ направлена от стенки, тогда следует vx<0 и Δpx>0. Из формулы получим, что модуль Δp связан с модулем скорости, который принимает вид Δp=2mv.

Источник

Импульс тела — это физическая векторная величина, равная произведению массы тела на его скорость

Каждое тело, которое имеет массу и скорость, так же имеет и импульс.

Пусть на тело массой в течение некоторого малого промежутка времени Δt действовала сила F. Под действием этой силы скорость тела изменилась на . Следовательно, тело на промежутке Δt двигалось с ускорением

$Large vec a=frac{Delta vecupsilon }{Delta t}=frac{vec upsilon _2-vecupsilon_1}{Delta t}$

На основе Второго закон Ньютона

$Large vec F=m vec a=mfrac{(vec upsilon _2-vecupsilon _1)}{Delta t}$

А если немного преобразовать, то у нас получится:

Физическая величина, равная произведению массы тела на скорость его движения, называется импульсом тела . А физическая величина, равная произведению силы на время ее действия, называется импульсом силы .

Импульс тела – векторная величина. Единицей измерения импульса в СИ является килограмм-метр в секунду (кг·м/с)

В Формуле мы использовали :

— Импульс тела

— Масса тела

— Скорость тела

Источник

История появления термина[править | править код]

Формальное абстрактное определение[править | править код]

Определения импульса тела в механике[править | править код]

Классическая механика[править | править код]

Релятивистская механика[править | править код]

Свойства импульса[править | править код]

Обобщённый импульс[править | править код]

В теоретической механике в целом[править | править код]

Для частицы в электромагнитном поле[править | править код]

Импульс электромагнитного поля[править | править код]

Импульс в квантовой механике[править | править код]

Определение через оператор[править | править код]

Определение через волны де Бройля[править | править код]

Импульс в гидродинамике[править | править код]

Импульсное представление в квантовой теории поля[править | править код]

См. также[править | править код]

Примечания[править | править код]

Литература[править | править код]

Оглавление: