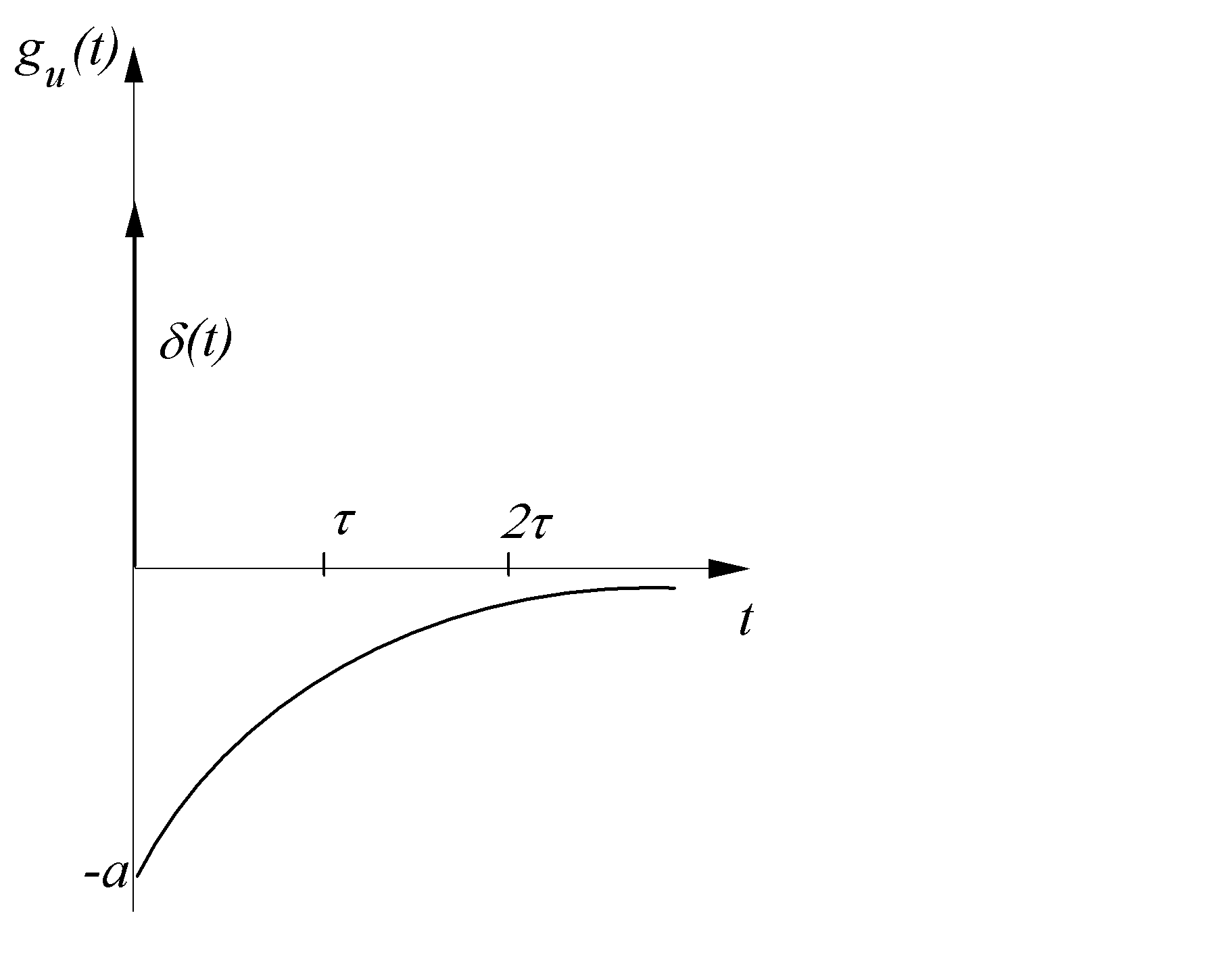Как найти импульсную характеристику цепи

Импульсная
(весовая) характеристика или импульсная
функция
цепи –
это ее обобщенная характеристика,
являющаяся временной функцией, численно
равная реакции цепи на единичное
импульсное воздействие на ее входе при
нулевых начальных условиях (рис. 13.14);
другими словами, это отклик цепи,
свободной от начального запаса энергии
на дельта-функцию Дирана
на ее входе.

Функцию
можно определить, рассчитав переходную

или передаточную
функцию цепи.

Расчет функции
с использованием переходной функции
цепи. Пусть при входном воздействии
реакцией линейной электрической цепи
является .
Тогда в силу линейности цепи при входном
воздействии, равном производной ,
реакция цепи будет равна производной
.

Как отмечалось,
при ,
реакция цепи ,
а если ,
то реакция цепи будет ,
т.е. импульсная функция

.

Согласно свойству
выборки
произведение
.
Таким образом, импульсная функция цепи

.
(13.8)

Если ,
то импульсная функция имеет вид

.
(13.9)

Следовательно,
размерность импульсной характеристики
равна размерности переходной
характеристики, поделенной на время.

Расчет функции
с использованием передаточной функции
цепи. Согласно выражению (13.6), при
воздействии на вход функции ,
откликом функции будет переходная
функция
вида:

.

С другой стороны,
известно, что изображение производной
функции по времени ,
при ,
равно произведению .

Откуда ,

или ,
(13.10)

т.е. импульсная
характеристика
цепи равна обратному преобразованию
Лапласа ее передаточной
функции.

Пример.
Найдем импульсную функцию цепи, схемы
замещения которой представлены на рис.
13.12, а;
13.13.

Решение

Переходная и
передаточная функции этой цепи били
получены ранее:

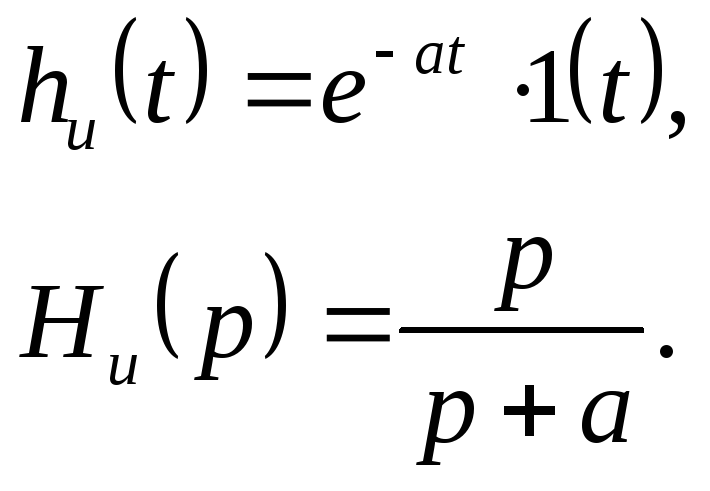
Тогда, согласно
выражению (13.8)

,

где .

График импульсной
характеристики
цепи представлен на рис. 13.15.

Выводы

Импульсная
характеристика
введена по тем же двум причинам, что и
переходная характеристика .

1. Единичное
импульсное воздействие
– скачкообразное и потому довольно
тяжелое для любой системы или цепи
внешнее воздействие. Следовательно,
важно знать реакцию системы или цепи
именно при таком воздействии, т.е.
импульсную характеристику .

2. При помощи
некоторого видоизменения интеграла
Дюамеля можно, зная
вычислить реакцию системы или цепи на
любое внешнее возмущение (см. далее пп.
13.4, 13.5).

4. Интеграл наложения (дюамеля).

Пусть произвольный
пассивный двухполюсник (рис. 13.16, а)
подключается к источнику непрерывно
изменяющегося с момента
напряжения(рис. 13.16,б).

Требуется найти
ток
(или напряжение) в любой ветви двухполюсника
после замыкания ключа.

Задачу решим в два
этапа. Сначала искомую величину найдем
при включении двухполюсника на единичный
скачок напряжения, который задается
единичной ступенчатой функцией
.

Известно, что
реакцией цепи на единичный скачок
является переходная
характеристика (функция)
.

Например, для
–
цепи переходная функция по току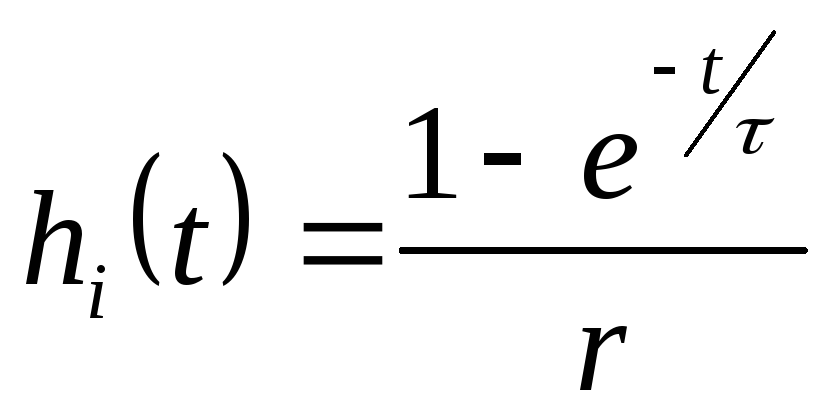(см. п.2.1), для–
цепи переходная функция по напряжению.

На втором этапе
непрерывно изменяющееся напряжение
заменим ступенчатой функцией с
элементарными прямоугольными скачками(см. рис. 13.16б).
Тогда процесс изменения напряжения
можно представить как включение при
постоянного напряжения,
а затем как включение элементарных
постоянных напряжений,
смещенных относительно друг друга на
интервалы времении имеющих знак плюс для возрастающей и
минус для падающей ветви заданной кривой
напряжения.

Составляющая
искомого тока в момент
от постоянного напряженияравна:

.

Составляющая
искомого тока от элементарного скачка
напряжения
,
включаемого в момент времениравна:

.

Здесь аргументом
переходной функции является время
,
поскольку элементарный скачок напряженияначинает действовать на времяпозднее замыкания ключа или, иначе
говоря, поскольку промежуток времени
между моментомначала действия этого скачка и моментом
времениравен.

Элементарный
скачок напряжения

,

где
– масштабный коэффициент.

Поэтому искомая
составляющая тока

.

Элементарные
скачки напряжения включаются на интервале
времени от
до момента,
для которого определяется искомый ток.
Поэтому, суммируя составляющие тока от
всех скачков, переходя к пределу при,
и учитывая составляющую тока от начального
скачка напряжения,
получаем:

.

Последняя формула
для определения тока при непрерывном
изменении приложенного напряжения

(13.11)

называется
интегралом
наложения (суперпозиции)
или интегралом
Дюамеля
(первой формой записи этого интеграла).

Аналогично решается
задача при подключении цепи и источнику
тока. Согласно этому интегралу реакция
цепи, в общем виде,
в некоторый моментпосле
начала воздействияопределяется всей той частью воздействия,
которая имела место до момента времени.

Заменой переменных
и интегрированием по частям можно
получить другие формы записи интеграла
Дюамеля, эквивалентные выражению
(13.11):

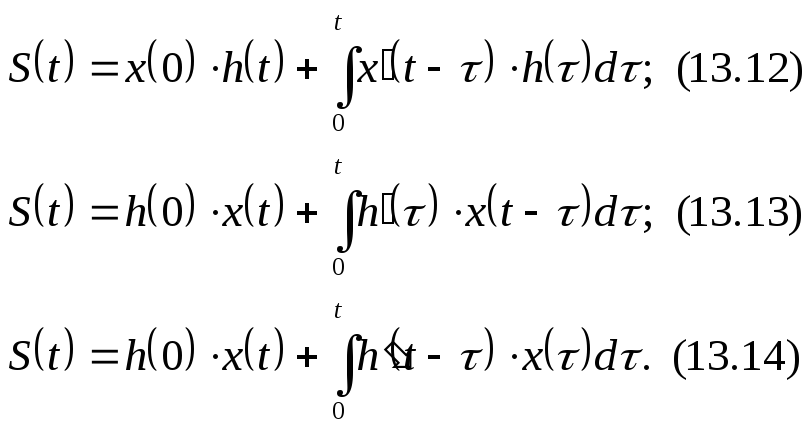
Выбор формы записи
интеграла Дюамеля определяется удобством
расчета. Например, в случае, если
выражается экспоненциальной функцией,
удобной оказывается формула (13.13) или
(13.14), что обуславливается простотой
дифференцирования экспоненциальной
функции.

При
илиудобно применять форму записи, в которой
слагаемое перед интегралом обращается
в нуль.

Произвольное
воздействие
может быть представлено также в виде
суммы последовательно включаемых
импульсов, как это изображено на рис.
13.17.

При бесконечно
малой длительности импульсов
получим формулы интеграла Дюамеля,
аналогичные (13.13) и (13.14).

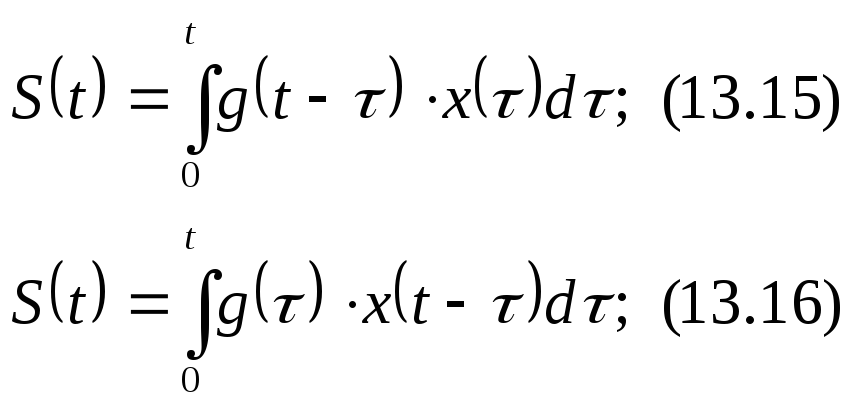
Эти же формулы
можно получить из соотношений (13.13) и
(13.14), заменив а них производную функцию
импульсной функцией.

Вывод.

Таким образом, на
основе формул интеграла Дюамеля (13.11) –
(13.16) и временных характеристик цепи
имогут быть определены временные функции
откликов цепина произвольные воздействия.

Соседние файлы в папке ДРТЦ дляЗАО

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

В основе временного метода лежит понятие переходной и импульсной характеристик цепи. Переходной характеристикой цепи называют реакцию цепи на воздействие в форме единичной функции (7.19). Обозначается переходная характеристика цепи g(t). Импульсной характеристикой цепи называют реакцию цепи на воздействие единичной импульсной функции (d-функции) (7.21). Обозначается импульсная характеристика h(t). Причем, g(t) и h(t) определяются при нулевых начальных условиях в цепи. В зависимости от типа реакции и типа воздействия (ток или напряжение) переходные и импульсные характеристики могут быть безразмерными величинами, либо имеют размерность А/В или В/А.

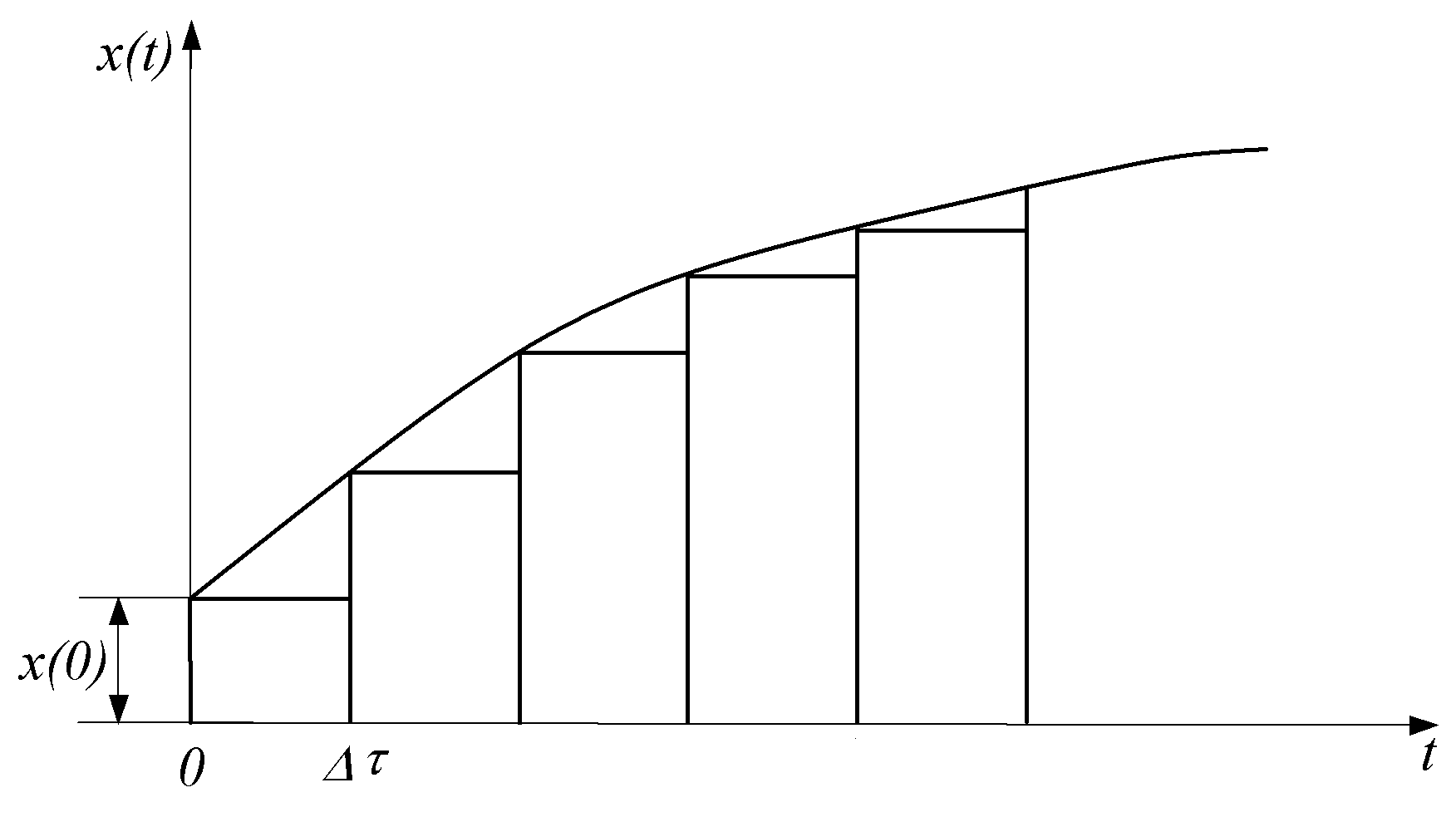
Использование понятий переходной и импульсной характеристик цепи позволяет свести расчет реакции цепи от действия непериодического сигнала произвольной формы к определению реакции цепи на простейшее воздействие типа единичной 1(t) или импульсной функции d(t), с помощью которых аппроксимируется исходный сигнал. При этом результирующая реакция линейной цепи находится (с использованием принципа наложения) как сумма реакций цепи на элементарные воздействия 1(t) или d(t).

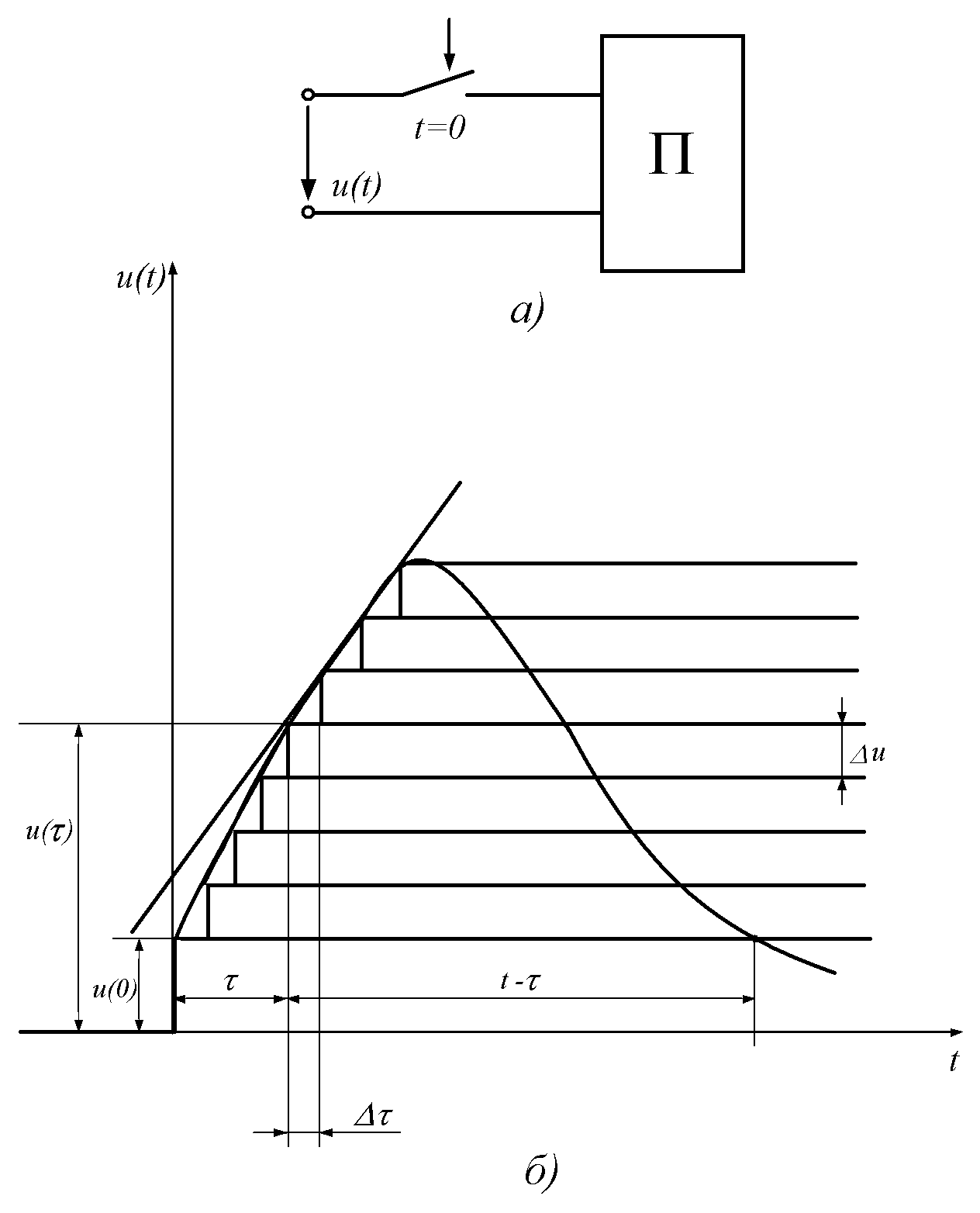
Между переходной g(t) и импульсной h(t) характеристиками линейной пассивной цепи существует определенная связь. Ее можно установить, если представить единичную импульсную функцию через предельный переход разности двух единичных функций величины 1/t, сдвинутых друг относительно друга на время t (см. рис. 7.4):

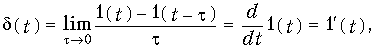
т. е. единичная импульсная функция равна производной единичной функции. Так как рассматриваемая цепь предполагается линейной, то соотношение (8.1) сохраняется и для импульсных и переходных реакций цепи

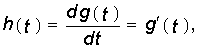
т. е. импульсная характеристика является производной от переходной характеристики цепи.

Уравнение (8.2) справедливо для случая, когда g(0) = 0 (нулевые начальны е условия для цепи). Если же g(0) ¹ 0, то представив g(t) в виде g(t) = 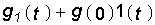, где 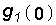= 0, получим уравнение связи для этого случая:

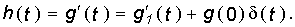
Для нахождения переходных и импульсных характеристик цепи можно использовать как классический, так и операторный методы. Сущность классического метода состоит в определении временной реакции цепи (в форме напряжения или тока в отдельных ветвях цепи) на воздействие единичной 1(t) или импульсной d(t) функции. Обычно классическим методом удобно определять переходную характеристику g(t), а импульсную характеристику h(t) находить с помощью уравнений связи (8.2), (8.3) или операторным методом.

Пример. Найдем классическим методом переходную характеристику по напряжению для цепи, изображенной на рис. 8.1. Численно g_u(t) для данной цепи совпадает с напряжением на емкости при подключении ее в момент t= 0 к источнику напряжения U₁ = l В:

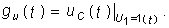
Закон изменения напряжения u_C(t) определяется уравнением (6.27), где необходимо положить U= l В:

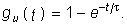
При нахождении характеристик g(t) и h(t) операторным методом пользуются изображениями функций 1(t), d(t) и методикой расчета переходных процессов, изложенных в гл. 7.

Пример. Определим операторным методом переходную характеристику g_u(t) RС-цепи (см. рис. 8.1). Для данной цепи в соответствии с законом Ома в операторной форме (7.35) можем записать:

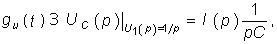
где

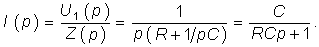
Окончательно получаем

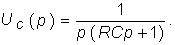
Отсюда по теореме разложения (7.31) находим

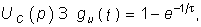
т. е. то же значение, что и полученное классическим методом.

Следует отметить, что величина I(р) в уравнении (8.4) численно равна изображению переходной проводимости. Аналогичное изображение импульсной характеристики численно равно операторной проводимости цепи

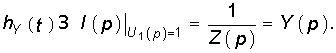
Например, для RС-цепи (см. рис. 8.1) имеем:

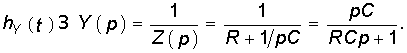
Применив к Y(p) теорему разложения (7.30), получим:

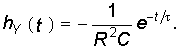
Следует отметить, что формула (8.5) определяет свободную составляющую реакции цепи при единичном импульсном воздействии. В общем случае в реакции цепи, кроме экспоненциальных составляющих свободного режима при t > 0 присутствует импульсное слагаемое, отображающее воздействие при t = 0 единичного импульса. Действительно, если учесть, что для RС-контура (см. рис. 8.1) переходная характеристика по току при U= 1(t) согласно (6.28) будет

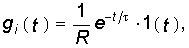
то после дифференцирования (8.6) согласно (8.2) получаем импульсную характеристику RС-цепи h_i(t) в виде

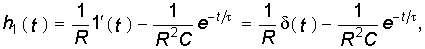
т. е. реакция h_i(t) содержит два слагаемых — импульсное и экспоненциальное.

Физический смысл первого слагаемого в (8.7) означает, что при t = 0 в результате воздействия на цепь импульсного напряжения d(t) зарядный ток мгновенно достигает бесконечно большого значения, при этом за время от 0_– до 0₊ элементу емкости передается конечный заряд и она скачком заряжается до напряжения I/RC. Второе слагаемое определяет свободный процесс в цепи при t> 0 и обусловлено разрядом конденсатора через короткозамкнутый вход (так как при t> 0 d(t) = 0, что равносильно КЗ входа) с постоянной времени t = RC. Из этого следует, что при d(t)-импульсном воздействии на RС-цепь нарушается непрерывность заряда на емкости (второй закон коммутации). Аналогично нарушается и условие непрерывности тока в индуктивности (первый закон коммутации), если к цепи, содержащей элемент индуктивности воздействовать напряжением в виде d(t).

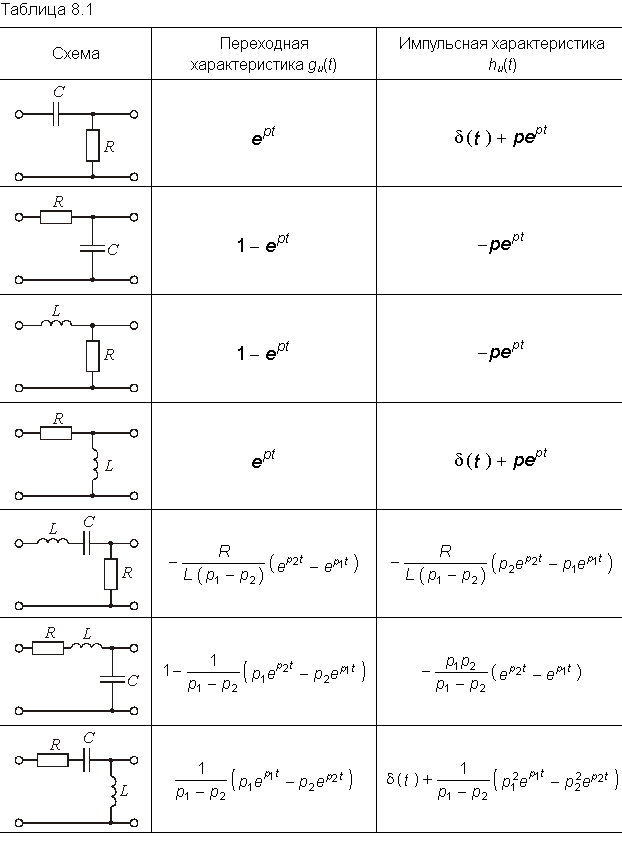
В табл. 8.1 сведены значения переходной и импульсных характеристик по току и напряжению для некоторых цепей первого и второго порядка.

В линейной теории цепей автоматического управления и в других дисциплинах часто пользуются понятиями переходной характеристики и импульсной переходной характеристики какой-либо системы или цепи.
Аналогично вводят понятие переходной характеристики любой цепи или системы, например для четырехполюсника переходной характеристикой называется реакция (напряжение или ток) на выходе при единичном ступенчатом воздействии на входе.
Понятие переходной характеристики h(t) как реакции (отклика) системы (или как выходной величины, за которую может быть принята любая из функций системы) на единичное ступенчатое воздействие, приложенное к ее входу (причем, за вход системы может быть принята любая ветвь или два вывода), применимо не только к электрическим цепям, но и к любым физическим системам — механическим, пневматическим, гидравлическим, электромеханическим и т. д. Так, переходные характеристики rL-, rС- и rLC-цепей, если, например, в качестве выходной величины выбраны токи, даются формулами (14.14), (14.26), (14.60), (14.63) при U = 1, а если выбраны напряжения на емкостных элементах, то формулами (14.25), (14.59), (14.62) также при U = 1.

Переходная характеристика введена в основном по двум причинам.
1. Единичное ступенчатое воздействие 1(t) — скачкообразное, и поэтому довольно тяжелое для любой системы внешнее воздействие. Следовательно, важно знать реакцию системы именно при таком воздействии. Иные, например, всевозможные плавные воздействия будут для системы легче.
2. Если определена характеристика h(t), то при помощи интеграла Дюамеля (см. раздел и раздел) можно определить реакцию системы при любой форме внешних воздействий.

Существует еще один вид внешнего воздействия, называемый единичным импульсом, дельта-функцией d(t) или функцией Дирака, которое определяется как производная
по времени единичной функции



и представляет собой предельный случай импульса очень большого значения и очень малой продолжительности (рис. 14.39), когда его длительность стремится к нулю, но площадь сохраняется равной единице.
Действительно, оставляя сейчас в стороне вопрос о законности операций дифференцирования разрывной функции 1(t), но отметив, что в теории обобщенных функций эти операции достаточно строго обоснованы, найдем площадь единичного импульса:

Рис. 14.39

Импульсной переходной функцией или характеристикой (весовой функцией) системы (например, четырехполюсника) k(t) называется реакция на выходе, если на входе действует внешнее возмущение в виде единичного импульса δ(t). Поскольку внешние возмущения 1(t) и δ(t) связаны равенством (14.83), то при h(0+)=0 получаем, что подобным же равенством связаны и их реакции на выходе системы, т. е.

В справедливости (14.84) можно убедиться непосредственно, вычислив h(t), k(t) и dh(t)/dt для любой цепи.
Если же , то соотношение (14.84) обобщается:

Например, если при включении rС-цепи на единичный импульс напряжения в качестве выходной величины рассматривается ток, то



Так как при t — 0 в составе приложенного напряжения имеется дельта-функция и в этот момент по второму закону коммутации , то дельта-функция должна быть и в составе тока, что и объясняет наличие второго слагаемого в правой части (14.85).

Импульсная переходная характеристика k(t) введена по тем же двум причинам, что и h(t).
1. Единичный импульс — скачкообразное и поэтому довольно тяжелое возмущение для системы или цепи; оно тяжелее, чем плавное возмущение. Следовательно, важно знать реакцию системы или цепи на это возмущение.
2. При помощи некоторого видоизменения интеграла Дюамеля можно, зная k(t), вычислить реакцию системы или цепи на любое внешнее возмущение (см. раздел).
Реализацию внешнего воздействия в виде единичного импульса напряжения δ(t) обычно представляют как экспоненциальное воздействие с очень большой начальной ординатой и очень малой постоянной времени t, так что



где — площадь, ограничиваемая экспоненциальным импульсом, т. е.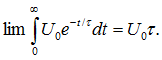

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 26 декабря 2018 года; проверки требуют 12 правок.

Импульсная переходная функция (весовая функция, импульсная характеристика) — выходной сигнал динамической системы как реакция на входной сигнал в виде дельта-функции Дирака. В цифровых системах входной сигнал представляет собой простой импульс минимальной ширины (равной периоду дискретизации для дискретных систем) и максимальной амплитуды. В применении к фильтрации сигнала называется также ядром фильтра. Находит широкое применение в теории управления, обработке сигналов и изображений, теории связи и других областях инженерного дела.

Определение[править | править код]

Импульсной характеристикой системы называется её реакция на единичный импульс при нулевых начальных условиях.

Свойства[править | править код]

Выходной сигнал линейной системы может быть получен как свертка его входного сигнала и импульсной характеристики системы :

,

либо, в случае цифровой системы

.

Для того чтобы система была физически реализуема в реальном времени, её импульсная переходная функция должна удовлетворять условию: при В противном случае система нереализуема, поскольку отклик на выходе системы не может появиться раньше, чем поступающее на вход системы воздействие, вызывающее отклик (см. статью физически реализуемая система).

Применение[править | править код]

Анализ систем[править | править код]

Восстановление частотной характеристики[править | править код]

Важным свойством импульсной характеристики является тот факт, что на её основе может быть получена комплексная частотная характеристика, определяемая как отношение комплексного спектра сигнала на выходе системы к комплексному спектру входного сигнала.

Комплексная частотная характеристика (КЧХ) является аналитическим выражением комплексной функции. КЧХ строится на комплексной плоскости и представляет собой кривую траектории конца вектора в рабочем диапазоне изменения частот, называемую годографом КЧХ. Для построения КЧХ обычно требуется 5-8 точек в рабочем диапазоне частот: от минимально реализуемой частоты до частоты среза (частоты окончания эксперимента). КЧХ, так же, как и временная характеристика будет давать полную информацию о свойствах линейных динамических систем.^[1]

Частотная характеристика фильтра определяется как преобразование Фурье (дискретное преобразование Фурье в случае цифрового сигнала) от импульсной характеристики.

Цифровая фильтрация[править | править код]

Импульсная переходная функция системы рассматривается только для дискретных сигналов, если же сигналы непрерывные, то фиксируются их значения только для дискретных моментов времени, кратных периоду прерывания сигнала в системе.

Фильтр с характеристикой типа «приподнятый косинус» (ФПК) — особый электронный фильтр, часто встречающийся в телекоммуникационных системах благодаря возможности минимизировать межсимвольные искажения.

Импульсный отклик такого фильтра описывается следующей формулой:

, в выражении через sinc функцию.

См. также[править | править код]

• Переходный процесс
• Переходная функция
• Передаточная функция

Примечания[править | править код]