-
Индексы по простому модулю.
Опр.
Пусть m
– модуль, а, в – взаимно простые с
модулем числа. Число S
принадлежащее a,
такое что as≡b(mod
m)
называется индексом по основанию а.
ind
ab.

Пр.
Пусть
m=13, a = 2.
23≡8(mod
13) 24≡16(mod
13), 24≡3(mod
13) ind23=4
26≡12(mod
6), ind12=6.
Теорема:
Пусть m
– модуль, g
– первообразный корень по модулю m,
тогда для любого b,
такого что НОД(b,m)=1,
существует такое S,
что gs
≡b(mod
m)
и все такие индексы S
явл. Неотрицательными числами некоторого
класса по модулю m.
Д-во:
пользуясь теоремой, что g
– первообразный корень g,
g2,…,gr(m)…
все степени различные и образуют
приведенную систему вычетов по модулю
m.
Т.к.
НОД(b,m)=1,
то b
попадет в какой-то класс, значит существует
S
принадлежащий N,
такой что gs≡b(mod
m).
Возьмем какой-нибудь S1,
такой что gS1
≡ b(mod
m),
gS
≡ b(mod
m),
Тогда
эти модули сравнимы по модулю порядка
P(g)=

(m).
S
≡ S1(mod
(m)).
Докажем,
что если взять два вычета из одного
класса они являются индексами
S
≡ k(mod
(m)),
gS
≡ gk
(mod
m),
но g≡b(mod
m),
тогда и gk≡b(mod
m),
значит k
– тоже индекс. k=indgb.
Доказанно.
Теорема:
Пусть НОД(b,m)=1
и НОД(с,m)=1
g
первообразный корень по модулю m,
b≡c(mod
m)
<=> indgb≡indgс(mod
(m)).
Д-во:
необходимость. Пусть b≡c(mod
m).
Теперь

значит ind
g
b
≡ ind
g
b(mod
(m)).
Т.к.
степень сравнения по модулю m,
то показатель сравнения по модулю
(m).
Достаточность:
Пусть indgb≡indgс(mod
(m)),
тогда имеем

,
т.е. b≡c(mod
m).
-
Теорема о свойствах индексов и следствие из нее.
Опр.
Пусть m
– модуль, а, в – взаимно простые с
модулем числа. Число S
принадлежащее a,
такое что as≡b(mod
m)
называется
индексом по основанию а. ind
ab.

Свойства
индексирования: 1) Пусть НОД(b,m)=1
и НОД(a,m)=1,
g
– первообразный корень по модулю m,
тогда indg
ab
≡ indg
a
+
+
indg
b
(mod
(m)).
Д-во:
gind
g
ab
≡
ab(mod
m),
в то же время
ab≡gind
g a
*
gind
g b
= gind
g a+
ind g b(mod
m). теперь
indg
ab
≡ indg
a
+ indg
b
(mod
(m)). Д-но.
-
Пусть
НОД(a,m)=1,
g
– первообразный корень по модулю m,
тогда
Indsak=k
indga(mod
m). Д-во:
K=0,
indg
a0
≡
0
indg
a(mod
m)
Indga0
= Indg1=0
левая
часть верно. k=1,
indg
a1
≡1
indg
a(mod
m) –
верно.
k>1,
indg
ak
≡
indg
a
тогда
по замечанию
indg
ak
=
.
Д-НО.
Опр.
Пусть

Пусть
НОД(b,m)=1
и НОД(a,m)=1,
g
– первообразный корень по модулю m,
тогда

.
Д-во:

по
предыдущему свойству


,


Но
по опр.

=
,
т.е.
.
Д-но.
-
Формула перехода от системы индексов с основанием к системе индексов с основанием (пример 1).
g,
g1
– первообразные корни по модулю m.
НОД(a,m)=1
a=gα(mod
m)
a=g1α1(mod
m) α =indga
=
indgg1α1(mod
ᵠ(m))
indga
=
α1
indgg1(mod
ᵠ(m))
indga
=
indg1a
indgg1(mod
ᵠ(m))
Пример:
ind
1043
=
13 ind 643
=
?
Решение:
ind1043
=
ind643
* ind106(mod
58)
13=
ind643*57(mod
58) ind 106=57
ind643
= 45 (mod 58)
-
Таблица
индексов по

.
Опр.
Пусть
m
– модуль, a,b
–взаимно простые с модулем числа. Число
sϵN
такое, что as=b(mod
m)
, называется индексом b
по модулю а.
indab
aindab=b(mod
m)
m=11
ᵠ(m)=10
25=–1(mod
11) или 25=10(mod
11)
2 –
первообразный корень по модулю 11
Р(2)=10,
т.е. 2 – первообразный корень.
Пояснение:
2=2(mod
11)
23=8(mod
11)
26=9(mod
11)
27=7(mod
11)
28=3(mod
11)
29=6(mod
11)
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
ind |
0 |
1 |
8 |
2 |
4 |
9 |
7 |
3 |
6 |
5 |
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Макеты страниц
Индексы по простому модулю.
Пусть g есть первообразный корень по модулю  . Тогда числа
. Тогда числа

образуют приведенную систему вычетов по модулю  . Поэтому любое число а, взаимно простое с
. Поэтому любое число а, взаимно простое с  , сравнимо с одним и только с одним из чисел ряда (1).
, сравнимо с одним и только с одним из чисел ряда (1).
Если  то k называется индексом числа а по модулю
то k называется индексом числа а по модулю  при основании g и обозначается символом
при основании g и обозначается символом  а или
а или  . Если k — другое число, для которого
. Если k — другое число, для которого  , то
, то  и, согласно предложению
и, согласно предложению  Таким образом, множество индексов данного числа а образуют класс вычетов по модулю
Таким образом, множество индексов данного числа а образуют класс вычетов по модулю  Из определения индекса вытекает, что из
Из определения индекса вытекает, что из  следует
следует 
Пример. Пусть  Число 2 есть первообразный корень по модулю 13. Индексы чисел
Число 2 есть первообразный корень по модулю 13. Индексы чисел  при основании
при основании  таковы:
таковы:

С помощью этой таблицы по данному числу а находится его индекс по модулю 13. Следующая таблица позволяет по данному индексу находить соответствующее число:

С помощью индексов умножение по модулю  можно свести к сложению по модулю
можно свести к сложению по модулю  аналогично тому, как, используя логарифмы, можно свести обычное умножение чисел к сложению.
аналогично тому, как, используя логарифмы, можно свести обычное умножение чисел к сложению.
ТЕОРЕМА 5.12. Если числа а, b взаимно простые с  — любое натуральное число, то
— любое натуральное число, то

Доказательство. По определению индексов чисел а и b имеем:

отсюда находим произведение

Следовательно,  есть один из индексов произведения
есть один из индексов произведения  т. е.
т. е.

Из сравнения  следует, что
следует, что

поэтому  есть один из индексов степени
есть один из индексов степени  , т. е.
, т. е.

Примеры. 1. Пусть  тогда
тогда 
2. Решить сравнение 
Данное сравнение равносильно такому:

Отсюда следует, что 
ТЕОРЕМА 5.12. Пусть  — мультипликативная группа классов вычетов, взаимно простых с
— мультипликативная группа классов вычетов, взаимно простых с  и С есть аддитивная группа классов вычетов по модулю
и С есть аддитивная группа классов вычетов по модулю  Отображение
Отображение  , ставящее в соответствие каждому элементу а группы
, ставящее в соответствие каждому элементу а группы  элемент
элемент  а группы С, есть изоформизм группы
а группы С, есть изоформизм группы  на группу С.
на группу С.
Доказательство. Согласно определению индекса, соответствие  является биективным. Кроме того, сохраняется операция умножения в группе
является биективным. Кроме того, сохраняется операция умножения в группе  так как из сравнения
так как из сравнения

следует, что

Следовательно,  есть изоморфизм группы на группу С.
есть изоморфизм группы на группу С.
В обычной арифметике основой теории логарифмов является изоморфизм мультипликативной группы положительных действительных чисел и аддитивной группы всех действительных чисел. Доказанная теорема, являющаяся основной в теории индексов, объясняет причину сходства теории логарифмов (в обычной арифметике) и теории индексов (по простому модулю).
Показателем, или мультипликативным порядком, целого числа 


Показатель определен только для чисел 






Чтобы показать зависимость показателя 





Свойства[править | править код]
, поэтому можно считать, что показатель задан на классе вычетов
по модулю
.
. В частности,
и
, где
— функция Кармайкла, а
— функция Эйлера.
; если
, то
- Если
— простое число и
, то
— все решения сравнения
.
- Если
— простое число, то
— образующая группы
.
- Если
— количество классов вычетов с показателем
, то
. А для простых модулей даже
.
- Если
— простое число, то группа вычетов
циклична и потому, если
, где
— образующая,
, а
— взаимно просто с
, то
. В общем случае для произвольного модуля
можно вывести аналогичную формулу, пользуясь теоремой о структуре мультипликативной группы вычетов
.
Пример[править | править код]
Так как 



Вычисление[править | править код]
Если известно разложение модуля 








Приложения[править | править код]
Характеры Дирихле[править | править код]
Характер Дирихле 





См. также[править | править код]
- Дискретное логарифмирование
- Функция Кармайкла
Примечания[править | править код]
- ↑ Бухштаб, 1966, с. 140.
- ↑ Виноградов, 1972, с. 92.
Литература[править | править код]
- Бухштаб А. А. Теория чисел. — М.: Просвещение, 1966.
- Виноградов И. М. Основы теории чисел. — М.: Наука, 1972.

Python задачи
Найти номер минимального по модулю элемента массива. Например, в массиве [20, -3, -5, 2, 5] минимальным по модулю элементом является число 2. По индексу число 2 – третье, тк отсчёт с нуля.Разбор задачи на Python
Что такое модуль числа
Если очень грубо объяснять, то минусы отбрасываются. Например, |-4| = 4, модуль числа минус четыре, равен четырём.
Почти у всех языков программирования есть встроенная функция, которая возвращает модуль числа. Так как нужно найти номер (индекс) элемента с минимальным по модулю, а не сам элемент (его значение), то при поиске необходимо сохранять индекс найденного элемента.
Алгоритм поиска индекса минимального по модулю элемента массива
1) Вводим какую-то переменную и присваиваем ей индекс первого элемента массива 0, предполагая, что первый элемент массива и является минимальным по модулю.
2) Начинаем в цикле перебор массива со второго элемента и до конца. При этом в цикле в заголовке условного оператора (if) сравниваем модуль текущего элемента с модулем элемента, чей индекс хранится в переменной первой переменной.
3) Если абсолютное значение текущего элемента массива меньше, чем элемента с индексом, которое записано в нашу переменную, то в теле условного оператора присваиваем новый индекс текущего элемента.
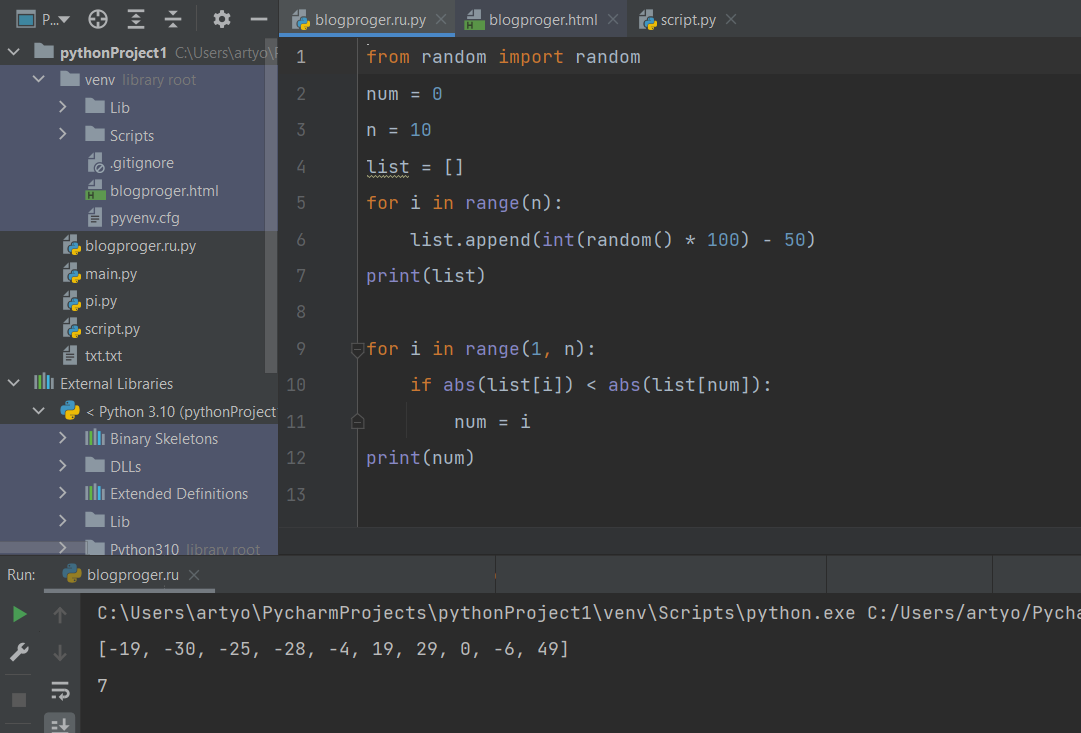
Поиск минимального модуля числа в массиве
from random import random
num = 0
n = 10
list = []
for i in range(n):
list.append(int(random() * 100) – 50)
print(list)
for i in range(1, n):
if abs(list[i]) < abs(list[num]):
num = i
print(num)
Python задачи
Все задачи на python
Репост статьи
2 ноября 2022 г.
Комментарии могут оставлять только зарегестрированные пользователи!
Комментарии
Ваш комментарий будет первым !


3.2 Индексы
Пусть  – группа,
– группа,  – её элемент,
– её элемент, 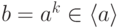 . Число
. Число  называется дискретным логарифмом элемента
называется дискретным логарифмом элемента  по основанию
по основанию  (пишут
(пишут 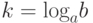 ). В случае, когда
). В случае, когда  – примитивный корень по модулю
– примитивный корень по модулю  , дискретный логарифм
, дискретный логарифм  ещё называют индексом числа
ещё называют индексом числа  по модулю
по модулю  при основании
при основании  . Пишут:
. Пишут:  . Когда примитивный корень
. Когда примитивный корень  фиксирован, можно также писать:
фиксирован, можно также писать:  .
.
Дискретное логарифмирование в произвольной группе является трудноразрешимой задачей. Приведём один из примеров, когда оно всё-таки легко осуществимо.
Пример 3.7 Вычислить дискретный логарифм числа  по основанию
по основанию 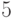 по модулю
по модулю  .
.
Решение. Порядок мультипликативной группы поля вычетов по модулю 102673 равен  . Число, являющееся произведением большого количества небольших чисел, называется гладким. Для дискретного логарифмирования в таком поле существует алгоритм Полига-Хэллмана, который мы сейчас применим.
. Число, являющееся произведением большого количества небольших чисел, называется гладким. Для дискретного логарифмирования в таком поле существует алгоритм Полига-Хэллмана, который мы сейчас применим.
Если  – решение нашей задачи, и
– решение нашей задачи, и  ,
,  ,
,  ,
, 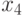 – остатки от деления
– остатки от деления  на
на 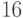 ,
, 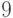 ,
, 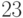 и
и 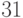 соответственно, то
соответственно, то
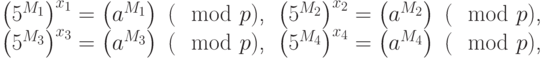
где
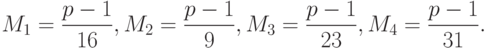
Наоборот, если мы найдём  ,
,  ,
,  и
и 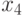 , а решение
, а решение  задачи всегда существует (так как
задачи всегда существует (так как 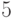 – примитивный корень), то
– примитивный корень), то  будет совпадать с единственным решением
будет совпадать с единственным решением  системы:
системы:
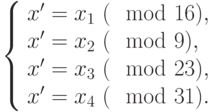
Итак, для решения задачи, по китайской теореме об остатках нужно найти:

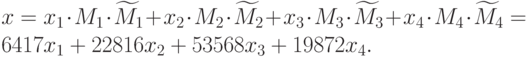
Следовательно, нам нужно найти  ,
,  ,
,  ,
, 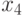 .
.
Имеем:

Поскольку порядок группы  равен 23, а группы
равен 23, а группы 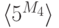 – всего 31, то при различных
– всего 31, то при различных  ,
, 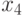 величины
величины  и
и  пробегают, соответственно, по 23 и 31 различным значениям.
пробегают, соответственно, по 23 и 31 различным значениям.
Тогда  и
и 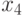 можно найти полным перебором, проверив
можно найти полным перебором, проверив 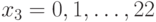 ,
,  . В нашем случае
. В нашем случае 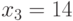 ,
,  . Числа
. Числа 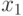 и
и 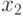 также можно искать полным перебором, но для них можно ещё уменьшить количество попыток. Будем искать
также можно искать полным перебором, но для них можно ещё уменьшить количество попыток. Будем искать

где 
Имеем:
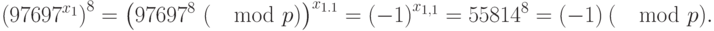
То есть  . Отсюда
. Отсюда 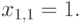
Далее,

Проверим оба варианта  :
:


Отсюда 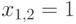 .
.
Далее,

Опять, из двух вариантов выбираем верный: 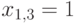 .
.
Наконец,
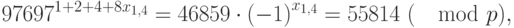
откуда 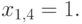 Проверяем:
Проверяем:

Аналогично находим  .
.
По китайской теореме об остатках находим  .
.
Для небольших  бывает удобно вычислять все степени примитивного корня и строить на основе этих вычислений две таблицы, называемые таблицами индексов. Таблицы индексов используются для быстрого решения некоторых задач по модулю простого числа
бывает удобно вычислять все степени примитивного корня и строить на основе этих вычислений две таблицы, называемые таблицами индексов. Таблицы индексов используются для быстрого решения некоторых задач по модулю простого числа  .
.
Приведем эти таблицы для примитивного корня 2 по модулю 37:
|
|
Например, чтобы определить индекс по числу 13, нужно в первой таблице перейти к столбцу “1” и строке “3”. Итак,  . Наоборот, для нахождения числа по его индексу 11 нужно во второй таблице перейти в столбец “1” строку “1”. Имеем:
. Наоборот, для нахождения числа по его индексу 11 нужно во второй таблице перейти в столбец “1” строку “1”. Имеем:  .
.
Пример 3.8 Решим с помощью таблицы индексов сравнение:

Будем далее использовать примитивный корень  и построенные для него выше таблицы. Правую часть сравнения заменяем положительным вычетом:
и построенные для него выше таблицы. Правую часть сравнения заменяем положительным вычетом:

“Индексируем” левую и правую части сравнения:

Находим в первой таблице для простого числа 37 значение 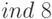 и
и 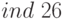 и подставляем в сравнение. Получим:
и подставляем в сравнение. Получим:
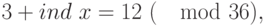
Откуда
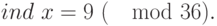
По второй таблице находим число, соответствующее индексу 9. Получим: 
Пример 3.9 С помощью индексов решить сравнение:

Индексируем сравнение:
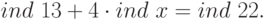
По первой таблице индексов находим:  ,
,  . Отсюда:
. Отсюда:  , или
, или 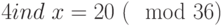 . Последнему сравнению удовлетворяют
. Последнему сравнению удовлетворяют 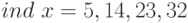 . Для каждого из них по второй таблице индексов найдем
. Для каждого из них по второй таблице индексов найдем  .
.



