
«Высшая ловкость состоит в том, чтобы всему знать истинную цену», — французский писатель XVII века Франсуа де Ларошфуко знал ценность цены — простите за тавтологию.
Всем нам не раз приходилось и оценивать, и сравнивать цены различных товаров или продуктов, как говорится, «на глазок».
Но такой подход не всегда дает объективный результат. Кроме того, как быть в ситуации, когда нужно сравнить цены большого количества совершенно разных вещей да еще за разные периоды времени?
Поэтому давайте разбираться с индексами цен, коих немало предусмотрено наукой эконометрикой специально для конкретных целей оценивания и анализа хозяйственной деятельности.
Понятие об индексах. Индексный метод
Индекс — это обобщающий относительный показатель, характеризующий изменение уровня общественного явления во времени, по сравнению с программой развития, планом, прогнозом или его соотношение в пространстве. Наиболее распространена сравнительная характеристика во времени. В этом случае индексы выступают как относительные величины динамики.

Индекс цен общий: формула
Индексный метод является также важнейшим аналитическим средством выявления связей между явлениями. При этом применяются уже не отдельные индексы, а их системы. В статистической практике индексы применяются при анализе развития всех отраслей экономики, на всех этапах экономической работы. В условиях рыночной экономики особенно возросла роль индексов цен, доходов населения, фондового рынка и территориальных индексов.
Элиминирование, то есть расчет влияния отдельных факторов на обобщающий показатель, может осуществляться также индексным методом. Этот метод применяется для расчленения экономических показателей.
Индексы являются разновидностью относительных величин. Индексы применяются в анализе хозяйственной деятельности с целью характеристики экономических явлений, состоящих из элементов, которые не следует суммировать.
Технически любой индекс представляет собой показатель, определяемый как соотношение двух каких-либо величин. Последние являются, по существу, определенными состояниями известного признака. С помощью индексов осуществляются сравнения фактических показателей с базисными, то есть, как правило, с плановыми и с показателями предшествующих периодов.
Индивидуальный индекс цен
В индексе выделяют 3 элемента:
- индексируемый показатель — это показатель, соотношение уровней которого характеризует индекс;
- сравниваемый уровень — это тот уровень, который сравнивают с другим;
- базисный уровень — это тот уровень, с которым производится сравнение.
Для расчета индекса необходимо найти отношение сравниваемого уровня к базисному и выразить его в виде коэффициента, если база сравнения приравнивается к единице, или в процентах, если база сравнения принимается за 100%. Обычно расчеты индексов производятся в форме коэффициентов с точностью до третьего знака после запятой, т. е. до 0,001, в форме процентов — до десятых долей процента, т.е. до 0,1%.
Для удобства построения индексов используется специальная символика:
- i — символ индексируемого показателя — индекс, характеризующий изменение уровня элемента явления;
- I — с подстрочным индексируемым показателем — для группы элементов или всей совокупности в целом;
- q — количество проданных товаров или произведенной продукции в натуральном выражении;
- p — цена за единицу товара;
- 0 — базисный период;
- 1 — отчетный период.

Таблица 1. Пример расчета индивидуальных индексов
Индивидуальные индексы характеризуют изменение отдельного элемента явления. Индивидуальный индекс цен определяется как отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде, то есть по формуле:
![]()
Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях:
![]()
Рассчитаем индивидуальные индексы цен:

Индекс цен общий: формула расчета
Все рассмотренные нами индексы характеризуют относительное изменение уровней отдельных элементов явления и называются индивидуальными индексами. Однако большинство изучаемых статистикой общественных явлений и процессов состоят из многих элементов, которые могут быть как однородными, так и неоднородными.
Однородные явления можно непосредственно суммировать и исчислять индексы, характеризующие изменение не одного элемента, а группы элементов или всей совокупности в целом. Такие индексы называются общими индексами.
Если же отдельные элементы явления неоднородны, то непосредственное суммирование их невозможно или бессмысленно и тогда необходимо привести их к сопоставимому виду. Все товары имеют стоимость, а стоимости товаров можно суммировать.
Переход от натуральных показателей к стоимостным позволяет преодолеть несуммарность натурально-вещественных элементов совокупности. Но изменение стоимости товаров обусловлено совместным изменением двух факторов — количества товаров и цен на них, а нам необходимо определить изменение каждого из этих факторов в отдельности.
Для изучения изменения одного фактора необходимо абстрагироваться от изменения второго, взаимосвязанного с ним фактора и построить общий индекс в агрегатной форме.
Агрегатные индексы качественных показателей строятся при весах — объемных показателях отчетного периода. Так, агрегатный индекс цен по формуле немецкого экономиста Э.Пааше:
![]()
В числителе индекса — товарооборот отчетного периода, в знаменателе — товарооборот отчетного периода в ценах базисного периода, а разность между ними характеризует: с позиции продавца — абсолютное изменение товарооборота за счет изменения цен, с позиции покупателя — экономию (перерасход) населения от изменения цен на товары:
![]()
Рассчитаем агрегатный индекс цен по данным нашего примера:
![]()
В качестве весов в индексах качественных показателей могут быть использованы не только абсолютные объемные показатели, но и показатели их структуры, то есть доли.
В статистической практике используется также индекс цен, построенный с базисными весами по формуле Э.Ласпейреса:
![]()
Общий индекс цен показывает, во сколько раз изменилась стоимость продукции в результате изменения цен, или сколько процентов составил рост (снижение) стоимости продукции из-за изменения цен. Значение индекса, уменьшенное на 100%, показывает, на сколько процентов изменилась стоимость продукции в результате изменения цен.
Разность числителя и знаменателя показывает, на сколько денежных единиц изменилась стоимость продукции в результате роста (уменьшения) цен.
Источник: "grandars.ru"
Кто и как впервые рассчитал индекс потребительских цен
Как считать инфляцию? Сегодня анализ экономики немыслим без расчета индексов цен. С их помощью мы сегодня определяем, насколько подорожала жизнь в нашей стране, под какой процент нужно положить деньги в банк, чтобы не потерять. Формула расчета индекса цен выкристаллизовывалась постепенно на основе трудов разных экономистов.
И все же основным автором принято считать выходца из семьи гугенотов Этьена Ласпейреса, преподававшего в основных немецких университетах XIX века, в том числе в Риге и Тарту.
Эрнст Луи Этьен Ласпейрес родился 28 ноября 1834 года в саксонском городе Галле в семье профессора юриспруденции. Французское звучание имени будущего экономиста объясняется тем, что это была семья кальвинистов (или гугенотов), предки которых в конце XVII века иммигрировали из Французского королевства в более веротерпимую на тот момент Священную Римскую империю. Сначала они поселились в Берлине, а позднее оказались в Саксонии.
По достижении 19 лет Этьен Ласпейрес отправился изучать юриспруденцию и общественные финансы. К тому времени университет Галле объединился с университетом города Виттенберг. Молодой человек также учился в университетах Тюбингена, Геттингена и Берлина. В 1859 году Ласпейрес получил степень доктора философии в области политических наук и общественных финансов в университете города Гейдельберга.
Всю дальнейшую жизнь Ласпейрес посвятил карьере ученого. Он занимал различные посты в высших учебных заведениях Гейдельберга, Базеля, политехническом институте Риги, университете Дерпта (Тарту). Два последних города к тому времени уже входили в состав Российской империи, но говорили там, а тем более преподавали научные дисциплины на немецком.
Затем он преподавал в Карлсруэ, а в возрасте 40 лет осел в университете Гессена, где возглавлял кафедру политологии вплоть до выхода на пенсию в 1900 году. В процессе своей деятельности Ласпейрес основал семинар по политической научной статистике, активно участвовал в работе Международного статистического института и регулярно принимал участие в его конференциях.
В 1893 году он съездил в Чикаго, где за его командировочные расходы пришлось доплатить дополнительно три тысячи марок. Ласпейрес умер 4 августа 1913 года, не дожив года до начала Первой мировой войны. Похоронен профессор в Гессене, на старинном кладбище Альте Фридхоф, на котором погребены и другие деятели науки, в том числе Вильгельм Конрад Рентген, открывший икс-излучение.
Как считать цены
Как уже сказано выше, Ласпейрес не был первым в его поколении экономистов, посчитавшим индекс цен. Первым, скорее, следует считать Шарля Дюто, описавшего модель ценовых индексов в 1738 году. Почти параллельно с ним индекс цен построил в 1764 году итальянский экономист Карли, — по среднеарифметической формуле, без применения какой-либо системы взвешивания.
Индексы, построенные Дюто и Карли по принципу невзвешенной средней, применялись в теории и на практике того времени, однако порядок осреднения цен вызывал сомнения. В 1850-х годах в Калифорнии и Австралии началась «золотая лихорадка» — открыли новые месторождения золота. В экономике того времени это вызвало обесценение денег и рост цен. Исследованием этой проблемы занялся современник Ласпейреса английский экономист Стэнли Джевонс.
Он предложил считать общий индекс цен по формуле средней геометрической из отношений цен на отдельные товары. Средняя арифметическая и геометрическая довольно долго конкурировали в построении индексов. Недостатком данной модели было то, что все товары считались равнозначимыми.
Тут и оказалась эффективной формула Ласпейреса, который предложил использовать для расчета индекса среднюю арифметическую взвешенную.
При этом в качестве веса он использовал удельный вес выручки от продажи данного первого товара в базисном периоде в общей величине базовой выручки. Такой порядок взвешивания привел к формуле агрегатного индекса цен с базисными весами.
В разработке формулы индекса цен большой вклад принадлежит другому немецкому экономисту — Герману Пааше, который предложил усреднять относительные изменения цен на отдельные товары по формуле средней гармонической взвешенной.
И хотя аналогичный индекс был построен английским экономистом Томасом Маном на две с половиной сотни лет раньше, в экономической литературе его принято называть индексом Пааше. Формулы Ласпейреса и Пааше учитывают изменения цен при предположении, что количество товаров неизменно.
Отличие формул двух экономистов в том, что Ласпейрес берет количество товара в базисном периоде, а Пааше — в текущем. Недостаток формулы Пааше в том, что она не учитывает упавший спрос на товары, поэтому при исчислении индекса цен по Пааше необходимо делать поправки для формировании правильной системы весов.
Но этот недостаток не брался в расчет советской экономической наукой, которая не обращала внимания на такой показатель как колебания спроса. Поэтому в советской статистике при расчете индекса цен ориентировались на формулу Пааше. Только с 1991 года, когда страна перешла к рыночной экономике, начали считать по формуле Ласпейреса, принятой в международной практике.
Преимущества этой формулы в том, что сам расчет индекса и его последующие перерасчеты проводить с ее помощью значительно легче. Проще установить веса, поскольку достаточно иметь данные о стоимости продаж указанных товаров в базисный период. Именно поэтому в большинстве стран индексы инфляции строятся по формуле средней арифметической взвешенной.
Правда и ложь индекса цен
Впрочем, говорить о том, что формула расчета инфляции, предложенная Этьеном Ласпейресом более века назад, является универсальной, тоже нельзя. Об изъянах этой математической функции не говорит сегодня только ленивый. Ведь как ни крути она построена не на сплошном исследовании цен, а на выборочном.
Можно взять стоимость картофеля в магазине на окраине Краснодара, а можно — в супермаркете в центре Москвы. Результаты окажутся разными. Есть и другая составляющая формулы Ласпейреса, игра с которой позволяет статистическим органам манипулировать с показателями инфляции. Речь идет о тех самых весах.
Ведь продуктов в потребительской корзине много, каждый из них человек потребляет в разных количествах. Соответственно, и влияние их на общий уровень цен в корзине различно.
Но в том-то и дело, что определить точно, сколько россияне ежедневно потребляют мяса, а сколько помидоров, невозможно. Один — вегетарианец, второй предпочитает яичнице огурцы, поэтому и инфляция у каждого из нас своя, не совпадающая с теми цифрами, которые выдают статистические исследования.
Зато последние, путем пересмотра доли каждого продукта в потребительской корзине, имеют возможность как занижать свой показатель, так и завышать, — как больше нравится считающему. Что интересно, в России «весовые коэффициенты» каждого продукта в общей «корзине» Росстат начал публиковать всего несколько лет назад. До этого людям, знавшим правила эконометрии, ознакомиться с ними было практически невозможно.
А сами «веса», как признаются государственные статистики, меняются каждый год «в зависимости от изменения потребительских предпочтений россиян». Поди проверь… Наконец, при расчете инфляции важен не только учет стоимости каждого товара, но и определение доли населения, которое покупает их именно по таким ценам. Особенно в России, где разрыв между самыми бедными и самыми богатыми — один из самых больших в мире.
И формула Ласпейреса не позволяет это сделать. Хотя, возможно, со временем появится другая, более совершенная. Возможно, ее создаст кто-то из отечественных математиков. Но пока приходится пользоваться тем, что придумали немцы.
Источник: "lenta.ru"
Индексы цен
В макроэкономическом анализе важным показателем (кроме перечисленных в предыдущем параграфе) считается общий уровень цен. В реальной жизни цены меняются непрерывно, одни товары дешевеют, другие дорожают. Для того чтобы определить, на какую величину возросли или снизились цены, используют индексы цеп. Индекс цен — относительный показатель, характеризующий соотношение цен во времени.
При исчислении индексов цен обычно цены базового года принимают за 100 %, а цены других лет оценивают по отношению к этим 100 %. В общем виде индекс цен можно определить по формуле:
Индекс цен текущего года = (Цены текущего года / Цены базового года) х 100%.
Существует несколько видов индексов. Широкое применение получили индексы оптовых цен, индексы розничных (потребительских) цен, индексы цен — дефляторы ВНП, индексы импортных и экспортных цен и др.
Индекс оптовых цен (индекс цен производителей) включает три группы товаров, а именно:
- конечные товары, готовые для использования;
- промежуточные товары;
- сырье, подготовленное для дальнейшей переработки.
Этот индекс показывает изменение среднего уровня продажных цен промышленных и строительных предприятий и компаний, сельскохозяйственных предприятий. Индекс потребительских (розничных) цен рассчитывается для группы товаров и услуг, входящих в потребительскую корзину среднего городского жителя:
ИПЦ = (Потребительская корзина в текущих ценах / Потребительская корзина в ценах базового года) х 100.
Важное место среди индексов цен занимает дефлятор ВНП, в котором «корзина» включает все конечные товары и услуги.
Этот индекс отражает изменение в ценах не только на товары широкого потребления, но и на все товары. Он позволяет сравнивать реальный и номинальный ВНП. Величина дефлятора определяется по формуле:
Дефлятор ВНП = (Реальный ВНП / Номинальный ВНП) х 100%.
Индексы цен используются также для исчисления уровня инфляции. Уровень инфляции определяется как процентное изменение цен:
Уровень инфляции = (цены текущего периода — цены прошлого периода) х 100 %.
Источник: "studme.org"
Статистические индексы
Само слово «индекс» (index) означает «показатель». Обычно этот термин используется для некоторой обобщающей характеристики изменений. Например, индекс Доу Джонса, индекс деловой активности, индекс объема промышленного производства и т.д. Гораздо реже термин «индекс» используется как обобщенный показатель состояния, например, известный индекс интеллектуального развития IQ.
В практике статистики индексы, наряду со средними величинами, являются наиболее распространенными статистическими показателями. Но индексы имеют три принципиальных отличия:
- Во-первых, индексы позволяют измерить изменение сложных явлений (неоднородных статистических совокупностей).
Например, нужно определить, как изменились за год расходы жителей г. Луганска на городской транспорт. Для ответа на этот вопрос необходимо знать численность пассажиров, перевезенных за год каждым видом транспорта.
Нужно рассчитать среднемесячную численность пассажиров или взять точные данные из отчетов по месяцам, умножить численность на тариф перевозки (и число месяцев его действия – в случае использования среднемесячной численности) и полученные величины просуммировать.
То же нужно сделать по данным за прошлый год. Затем сопоставить сумму расходов за последний год с суммой за прошлый год. То есть это не просто средние двух чисел, как при расчете, например, темпов динамики или приростов, а получение и сравнение некоторых агрегатированных величин.
- Во-вторых, индексы позволяют проанализировать изменения – выявить роль отдельных факторов. Например, можно определить, как изменилась сумма выручки городского транспорта за счет изменения численности пассажиров, изменения тарифов, наконец, за счет соотношения в объеме перевозок разными видами транспорта.
- В-третьих, индексы являются показателями сравнений не только с прошлым периодом (сравнение во времени), но и с другой территорией (сравнение в пространстве), а также с нормативами. Например, интересно знать, не только как изменилось среднедушевое потребление мяса в Украине в данном году по сравнению с прошлым годом (или с каким-либо другим периодом), но и сравнить показатели среднедушевого потребления мяса в Украине и в развитых странах Запада, Востока.
А также провести сравнение с нормативной величиной, отвечающей нормам рационального питания. Очевидно, что каждое направление сравнения вносит что-то новое.
Индексы для измерения динамики экономических изменений
Индекс – это показатель сравнений двух состояний одного и того же социально-экономического явления и представляет собой относительную величину, получаемую в результате сопоставления уровней сложных явлений во времени, в пространстве или с планом.
Индекс – это показатель, который сочетает в себе качества средних и относительных величин одновременно. Обычно индексы применяют для характеристики сложных совокупностей единиц наблюдения, то есть состоящих из разнородных элементов, непосредственное суммирование которых невозможно в силу их несоизмеримости.
Для определения общего объема реализации продуктов суммировать данные разнородные товары в натуральных единицах их учета, просто, нельзя, так как результат будет бессмысленным. Для получения обобщающих показателей в сложных статистических совокупностях необходимо применять индексный метод.
Например, в магазине ассортимент товаров состоит из разновидностей, первичный учет которых ведется в натуральных единицах измерения: молоко – в литрах, мясо – в килограммах, консервы – в банках, торты – в штуках, макароны – в пачках и т.д.
Индексный метод представляет собой совокупность приемов, которая исторически возникла для измерения динамики социально-экономических явлений. Это сравнительно молодой метод в статистике. В простейшей форме его стали применять более 100 лет тому назад, но по-настоящему этот метод начал развиваться значительно позднее, когда появились большие теоретические работы и практические исследования в этой области.
Основой индексного метода при определении изменений в производстве и обращении товаров является переход от натурально-вещественной формы выражения товарных масс к стоимостным (денежным) измерителям.
Именно посредством денежного выражения стоимости отдельных товаров устраняется их несравнимость как потребительских стоимостей и достигается единство. В зависимости от степени охвата и характера подвергнутых обобщению единиц изучаемой совокупности все индексы, употребляемые в статистике, делятся на два класса:
- Индивидуальные (элементарные) индексы – это относительные числа, характеризующие изменения во времени показателей, относящихся к однородному объекту (к одной статистической совокупности), или изменения во времени показатели одновременно существующих однородных объектов (изменения уровней однотипных явлений).
Индивидуальные индексы вычисляются просто. Если, например, требуется показать динамику цены или производительности труда, урожайности пшеницы или любой другой культуры с помощью индивидуальных индексов, то берут величину текущего периода и делят ее на величину сравниваемого периода.
- Общие (сложные) индексы выражают сводные (обобщающие) результаты совместного изменения всех единиц сложной статистической совокупности или изменение сложных общественных явлений во времени.
Общие индексы подразделяются на:
- индексы объемных показателей;
- индексы качественных показателей.
К объемным показателям относятся:
- физический объем продукции (обозначается буквой q). Выражается в натуральных единицах объема: кг, литры, метры, мешки, банки, ящики;
- объем продукции или услуг (товарооборот), выраженный в стоимостной форме (обозначается буквами qp). Выражается в денежной форме: грн., доллар.
К качественным показателям относятся:
- цена продукции или услуг (обозначается буквой p). Выражается в денежной форме: грн., доллар;
- себестоимость продукции или услуг (обозначается буквой z). Выражается в денежной форме: грн., доллар;
- затраты на производство продукции (обозначается буквами qz). Выражается в денежной форме: грн., доллар.
При вычислении индексов различают:
- сравниваемый уровень (отчетный период);
- уровень, с которым производится сравнение, называемый базисным.
Если показатель относится к сравниваемому (отчетному) уровню, то индексируемой величине присваивается символ «1» (например, p1 – цена товара за отчетный период), а если показатель относится к базисному периоду, то индексируемой величине присваивается символ «0» (например, q0 — объем продукции за базисный период).
Выбор базы сравнения определяется целью исследований. В индексах, характеризующих изменение индексируемой величины во времени, за базисную величину принимают размер показателя в каком-либо периоде, предшествующем отношению. При этом возможны два способа расчета индексов – цепной и базисный:
- Цепные индексы получают сопоставлением текущих уровней с предшествующим, т.е. база сравнения непрерывно меняется.
- Базисные индексы получают сопоставлением текущих уровней с уровнем периода, принятого за базу сравнения, т.е. база сравнения остается неизменной.
При использовании индексов как показателей выполнения плана, за базу сравнения принимаются плановые показатели. В статистике индивидуальные индексы принято обозначать буквой «i», а общие индексы – буквой «I». Рассмотрим порядок вычисления индивидуальных индексов.
Как уже отмечалось, индивидуальные индексы определяются как отношение уровня исследуемого показателя за отчетный период к уровню того же показателя за базисный период. При этом основным элементом индексного отношения является индексируемая величина, под которой понимается значение показателя за отчетный период.
Ее всегда записывают в числителе индексного отношения. Индивидуальные индексы цены продукции или услуг определяются по формуле:
![]()
где в числителе — цена продукции в текущем (отчетном) периоде; в знаменателе — цена продукции в базисном периоде.
Индивидуальные индексы для статистических исследований вычисляются крайне редко, так однородных совокупностей практически не бывает.
Основной формой общих индексов являются агрегатные индексы («aggrega» (лат.) – присоединять). В числителе и знаменателе общих индексов в агрегатной форме содержатся соединенные наборы (агрегаты) элементов изучаемых сложных статистических совокупностей.
Для достижения сопоставимости разнородных единиц в сложных статистических совокупностях в индексные соотношения вводят специальные сомножители – так называемые, соизмерители.
Они необходимы для перехода от натуральных измерений разнородных единиц к однородным показателям. При этом в числителе и знаменателе общего индекса изменяются лишь значения индексируемой величины, а их соизмерители остаются постоянными величинами и фиксируются на одном уровне (текущего или базисного периода).
Это необходимо для того, чтобы на величине индекса называлось лишь влияние фактора, который определяет изменения индексируемой величины. Общий индекс цены:
![]()
Цена является качественным показателем, поэтому соизмерителем берем количественный показатель физического объема q1 и отношение цены в отчетном периоде p1 к базисному p0).
Рассмотрим индексный метод изучения динамики сложных статистических совокупностей на примерах. Пусть имеются сведения о ценах и реализации товаров за два периода. Эти данные приведены в таблице 2:

Таблица 2. Сведения о ценах и реализации товаров
Как видно из таблицы, совокупность товаров разнородная (единицы измерения). Определим агрегатный индекс цен:

т.е. цены возросли в целом на 13,9%. В данном примере цена – индексируемый показатель, а объем — вес, взятый за отчётный период.
Можно в качестве весов взять объем и за базисный период. Тогда агрегатный индекс цен будет иметь вид:

т.е. цены возросли на 14,4 % (114,4-100 = 14,4%).
Используя два варианта расчета, получаем разное значение индекса цен. Какой из них ближе к реальному и принимать за действительный — зависит от цели исследований.
Правила построения общих индексов:
- в исходные данные вводят необходимые буквенные обозначения;
- записывают формулу общего индекса;
- числитель и знаменатель формулы общего индекса расписывают в табличном виде;
- производят промежуточные расчеты;
- результаты вычислений подставляют в формулу общего индекса;
- вычисляют общий индекс и делают выводы.
При анализе хозяйственной деятельности предприятий и организаций использование общих индексов в ряде случаев затруднено из-за отсутствия отдельных отчетных данных, особенно при вычислении планируемых показателей. Поэтому на практике часто используют формулы расчета общих индексов как величин, средних из соответствующих индивидуальных индексов.
В этом смысле общий индекс изучаемого явления рассматривается как результат изменения уровня данного явления у отдельных единиц совокупности. В процессе осреднения индивидуальных индексов веса подбираются такими, чтобы был возможен алгебраический переход от общего индекса в форме средней величины к общему индексу в агрегатной форме.
И наоборот, агрегатная форма общего индекса позволяет выбрать взвешивающий показатель при расчете общего индекса в виде средней величины. При изучении коммерческой деятельности предприятий приходится осуществлять индексные сопоставления более чем за два периода.
Поэтому индексные величины могут вычисляться как с постоянной, так и с переменной базами сравнения. При этом, если задача анализа состоит в получении характеристик изменения изучаемого явления во всех последующих периодах по сравнению с начальным, то вычисляются базисные индексы. Но если требуется охарактеризовать последовательное изменение изучаемого явления из периода в период, то вычисляются цепные индексы.
В зависимости от задачи исследований и характера исходной информации, базисные и цепные индексы исчисляются как индивидуальные (однотоварные), так и общие. Способы расчета индивидуальных базисных и цепных индексов аналогичны расчету относительных величин динамики. Общие индексы, в зависимости от их вида (экономического содержания), вычисляются с переменными и постоянными весами – соизмерителями.
Источник: "ekonomstat.ru"
Система индексов цен
Индекс цен исторически является одним из первых экономических индексов. Практически задачи индекса цен в основном сводятся к оценке изменений цен во времени (индексы динамики) или в пространстве (территориальные индексы). Построение системы индексов цен базируется на общеметодологических принципах, согласно которым в ней выделяются индивидуальные, сводные индексы и индексы средних цен (тарифов).
Индивидуальный индекс динамики определяется как отношение цены конкретного i-го товара текущего периода к цене предыдущего периода или к цене одного из периодов динамического ряда, принятого за базу сравнения (0):
![]()
Для индивидуальных индексов цен не представляет труда переход от цепных к базисным индексам (свойство круговой сходимости индексов). Обозначим последовательные периоды ряда динамики цен от 0 до n. Исходя из свойства круговой сходимости индексов величину базисного индекса цен можно определить как произведение цепных.
Индивидуальные индексы цен позволяют решать многие практические задачи, но основной задачей является изучение динамики цен разнородной совокупности товаров и услуг. Эта задача решается с помощью сводных индексов, характеризующих среднее изменение цен изучаемой совокупности товаров и услуг.
Сводный (общий) индекс цен относится к числу классических показателей, разработкой которого исследователи занимаются с XVII в. Наиболее широкое применение в статистической практике получили агрегатные формулы сводных индексов цен, разработанные в середине XVIII в. немецкими учеными Э. Ласпейресом и Г. Пааше.
Индекс Ласпейреса:
![]()
Индекс Пааше:
![]()
Числитель и знаменатель в приведенных индексах состоят из агрегатов, включающих индексируемую величину р и вес q. Различие между индексами Ласпейреса и Пааше заключается в выборе периодов весов. В индексе Ласпейреса берутся веса базисного или предшествующего периода, а в индексе Пааше — текущего периода.
При использовании в индексе Ласпейреса весов одного и того же базисного периода в течение длительного времени получают систему сводных индексов цен с постоянными весами, что позволяет учитывать свойство круговой сходимости индексов:

Таблица 4. Динамика цен по двум товарам-представителям одной из групп продукции дробильно-размольного оборудования
В статистической практике при расчете сводных индексов цен широко применяются различные модификации агрегатных формул, в частности в виде формул среднеарифметических и среднегармонических с использованием индивидуальных индексов (ip).
Индекс Пааше (средняя гармоническая формула):

Индекс Ласпейреса (средняя арифметическая формула):

Выражение сводного индекса через индивидуальные (ip) позволяет наглядно представить как динамику цен по отдельным товарам, так и их роль в формировании сводного индекса. Необходимо отметить, что в индексе Пааше используются переменные веса, поэтому свойством транзитивности, или круговой сходимости, этот индекс не обладает. В индексе Ласпейреса могут применяться как переменные, так и постоянные веса.
В статистической практике при исчислении цепных и базисных индексов цен широко используется средняя арифметическая формула Ласпейреса с постоянными весами. При этом применяется рекурсивный принцип построения модифицированной формулы Ласпейреса. Пример расчета приведен выше в таблице 4.
При широком использовании в экономической практике индивидуальных и сводных индексов цен определенный интерес представляет исчисление индекса динамики средних цен.
Средние цены, а следовательно, и индекс средних цен определяются по достаточно однородным группам товаров и при условии, что все товары, входящие в группу, измеряются одинаковыми количественными единицами (тоннами, литрами и т.д.).
Средние цены определяются путем деления стоимости (Σpiqi) на общее количество изучаемых единиц в группе (Σqi). Индексы средних цен (тарифов) правомерно исчислять не только по достаточно однородным группам товаров (услуг), но и по одному виду товаров, произведенному или реализованному по совокупности территориальных единиц (районов, области и т.д.) или в разрезе временных периодов (месяцев, кварталов и т.д.).
Средние цены и индексы средних цен, исчисленные по отдельным товарным группам, можно агрегировать в более укрупненные группы и в целом по изучаемой совокупности, используя те же формулы сводных индексов цен, что и при агрегировании цен конкретных товаров, но в этом случае сводный индекс будет характеризовать среднее изменение средних цен, что важно иметь в виду при интерпретации и использовании таких индексов.
Источник: "bibliotekar.ru"
Индивидуальный и общий индексы цен
Индексы являются важнейшим видом обобщающих статистических показателей. Они используются для характеристики динамики явлений, сравнений по различным территориям, при контроле и разработке плановых заданий. Наравне со средними величинами они представляют собой один из самых распространенных видов статистических показателей.
Слово «индекс» (index) в переводе с латыни означает указатель, показатель. В статистике этот термин имеет специфическое значение.
Индекс – это относительная величина, характеризующая изменение сложных общественных явлений во времени, пространстве или по сравнению с планом. Индекс является результатом сравнения двух одноименных величин, поэтому необходимо различать величину сравнения (числителя индексного отношения) и базу сравнения (знаменатель).
Выбор базы сравнения определяется целью исследования; при изучении динамики в качестве базы используются данные какого-либо предыдущего периода; при контроле за выполнением плана – плановые данные; при территориальных сравнениях – данные другой территории. Величину сравнения обычно называют показателем отчетного периода, базу сравнения называют показателем базисного периода.
Если базисный уровень при исчислении индекса принимается за единицу, то индексы вычисляются в виде коэффициентов, а если базисный уровень принимается за 100, то индекс вычисляют в виде процентов. На основании вычисления можно определить, во сколько раз отчетная величина больше или меньше базисной или на сколько процентов она больше или меньше базисной.
Статистика изучает в основном сложные экономические явления, которые состоят из элементов непосредственно несоизмеримых.
Так, если электромеханический завод производит несколько видов продукции, то данные о выпуске продукции в натуральном выражении суммировать нельзя. Для того, чтобы показать общее изменение выпуска по нескольким видам продукции и вычисляются индексы. С их помощью можно дать обобщенную характеристику изменения себестоимости, цен, выпуска по нескольким видам продукции.
При всем их разнообразии экономические индексы подразделяются на индивидуальные и общие индексы. Индивидуальным называется индекс, характеризующий изменение объема производства, объема продажи, уровня производительности труда и т.д. в отношении какого-нибудь одного продукта. Индивидуальный индекс цен характеризует изменение цены по каждому виду продукции:
![]()
где в числителе — цена отчетного периода, в знаменателе — цена базисного периода.
Общим (агрегатным) называется индекс, характеризующий общее (среднее) изменение объема производства, объема продаж, уровней цен и т.д. в отношении совокупности рядов товаров. Например, индексы, показывающие изменение общего объема производства различных видов продукции или изменение уровня цен различных видов товаров в целом. При расчете общих индексов возникает проблемы соизмерения показателей по отдельным товарам.
Соизмеримость отдельных показателей достигается путем взвешивания, суть которого состоит в том, что при вычислении абстрагируются от влияния изменения одной из сторон изучаемого явления, принимая ее за неизменную величину.
Так, при расчете индекса объема проданной продукции неизменными величинами будут цены, а при расчете индекса цен – количество проданной продукции. Та сторона изучаемого явления, от влияния изменения которой абстрагируются, принимая ее за неизменную, называется весами индекса.
Перед общим (агрегатным) индексом качественного показателя ставится задача измерить не только относительное изменение уровня но и абсолютную величину того экономического эффекта, который получен в текущем периоде в результате этого изменения. В данном случае сумму экономии покупателей за счет снижения цен, или сумму их дополнительных расходов, если цены повысились.
Для получения общего индекса цен нужно построить его так, чтобы отразилось влияние только фактора изменения цен, и было бы исключено влияние изменения количества проданных товаров. Это возможно в том случае, если для обоих сравниваемых периодов количество проданных товаров будет взято одинаковое.
Количество проданных товаров следует брать в текущем периоде, так как только на приобретении этого количества потребитель может экономить в результате снижения цен или перерасходовать в результате их повышения.
Общий индекс цен Пааше:
![]()
где p – индексируемая величина; q – веса.
В числителе индекса дана суммарная стоимость проданных в текущем периоде товаров по ценам текущего периода, а в знаменателе – стоимость того же количества товаров, но рассчитанная по ценам базисного периода.
Экономия (перерасход) от изменения цен:
![]()
В статистике используются и другие формы представления общих индексов цен – Ласпейреса и Фишера.
Общий индекс цен Ласпейреса:
![]()
Общий индекс цен Фишера:

Источник: "life-prog.ru"
Общий индекс цен. Индекс Пааше
В условиях современной экономики и эконометрики важное место среди индексов качественных показателей отводится индексу цен, который представляет собой показатели динамики уровня цен. При помощи индекса потребительских цен (ИПЦ) проводится оценка динамики цен на товары производственного и непроизводственного потребления.
ИПЦ отражает динамику цен конечного потребления, измеряет общее изменение стоимости фиксированного набора потребительских товаров и услуг («потребительская корзина»), а также является одним из основных показателей, характеризующих уровень инфляции. ИПЦ используется при корректировке минимального размера труда, расчета ставок налогов и т.д.
В 1874 г. немецкий экономист Г. Пааше предложил агрегатный индекс цен с отчетными весами. Формула агрегатного индекса цен Пааше определяется так:
![]()
где в числителе — фактическая стоимость продукции отчетного периода;
в знаменателе — условная стоимость товаров, которые реализованы в отчетном периоде, по базисным ценам.
Индекс цен Пааше показывает, во сколько раз возрос или уменьшился в среднем уровень цен на массу товара, реализованную в отчетном периоде, или сколько процентов составляет его рост (снижение) в отчетном периоде по сравнению с базисным периодом, т. е. он показывает, на сколько товары в отчетном периоде стали дороже (дешевле), чем в базисном.
В 1864 г. немецкий экономист Э. Ласпейрес предложил индекс, отражающий изменение цен, который строится по продукции базисного периода. Формула агрегатного индекса цен Ласпейреса рассчитывается как отношение:
![]()
Индекс цен Ласпейреса показывает, на сколько изменились цены в отчетном периоде по сравнению с базисным, но по продукции, которая была реализована в базисном периоде, и экономию (перерасход), который можно было бы получить от изменения цен. Индекс цен Ласпейреса также показывает, во сколько раз товары базисного периода подорожали (подешевели) в результате изменения цен на них в отчетном периоде.
Американский экономист И. Фишер предложил «идеальный» индекс цен, который назвали его именем, представляющий собой среднюю геометрическую произведения двух агрегатных индексов цен Ласпейреса и Пааше:

Идеальность данной формулы заключается в том, что индекс является обратимым во времени, т. е. при перестановке базисного и отчетного периодов полученный обратный индекс представляет собой величину, обратную величине первоначального индекса.
Недостаток формулы состоит в том, что она лишена конкретного экономического содержания (разность между числителем и знаменателем не показывает никакой реальной экономии или потерь вследствие изменения цен).
Средний гармонический индекс цен
Средний гармонический индекс цен применяется тогда, когда неизвестны значения p1, q1 но дано их произведение и индивидуальные индексы цен ip = p1/p0 а сводный индекс должен быть исчислен с отчетными весами.
Индивидуальные индексы определены таким образом, чтобы средний гармонический индекс совпал с агрегатным. Выражая из формулы индивидуальных индексов цен неизвестное значение р0 = p1/ip, подставляем его в знаменатель агрегатной формулы и получим средний гармонический индекс цен, который равен формуле Пааше:

Весами индивидуальных индексов iр в индексе является стоимость отдельных видов продукции отчетного периода в ценах того же периода p1q1.
Средний арифметический индекс цен
Средний арифметический индекс цен получают в том случае, если из индивидуального индекса цен ip = p1/p0 выразить цену отчетного периода p1 = i0p0, а затем подставить ее в числитель агрегатного индекса цен. Данный индекс аналогичен агрегатному индексу Ласпейреса и имеет формулу:

В этом индексе весами осредненных индивидуальных индексов служит объем товарооборота в базисном периоде.
Источник: "univer-nn.ru"
Общий индекс цен. Индекс Ласпейреса
В большинстве экономически развитых стран общие индексы цен на потребительские товары, рассчитанные по отношению к одному из периодов, выбранному в качестве базисного, ежегодно публикуются и используются для характеристики процесса инфляции.

Таблица 3. Агрегатные, арифметические и гармонические формы индексов цен
Применяется индекс Ласпейреса, отличающийся от индекса Пааше тем, что в формуле в качестве весовых коэффициентов берутся q0, т. е. объемы реализации в базисном периоде. Индекс Ласпейреса обладает рядом весьма серьезных преимуществ перед индексом Пааше.
В частности, имея данные о значениях индекса Ласпейреса в двух произвольно выбранных годах, легко исчислить, как изменились цены в период между этими годами индекс Пааше сделать этого не позволяет из-за различия в весовых коэффициентах. Эта особенность имеет особое значение в ретроспективном анализе, когда приходится принимать во внимание балансовые оценки долгосрочных активов, приобретения.
С помощью индексов Ласпейреса легко построить аналитический баланс, в котором ценовые различия элиминированы. Общий индекс цен по формуле Этьена Ласпейреса:
![]()
В отечественной статистике до 1992 г. общий индекс цен рассчитывался по формуле Пааше, используя гармоническую его форму. Связано это было с простотой получения данных о текущем товарообороте (P,Qj) в связи со сплошной ежемесячной статистической отчетностью и незначительным изменением цен.
Однако после 1992 г., когда был осуществлен переход к рыночным отношениям и принята новая методика расчета индекса потребительских цен, он стал рассчитываться так же, как и в большинстве стран, по формуле Ласпейреса.
Контроль за изменением цен на отдельные виды товаров, а также на потребительские товары в целом осуществляется с помощью индексов цен. Существует два основных вида индекса цен частный, или индивидуальный, (ip) и общий, или агрегатный, (Iр). Именно последний используется для характеристики инфляции.
В статистике разработано несколько алгоритмов расчета агрегатного индекса цен, различающихся системой весовых коэффициентов в формуле расчета. Наибольшую известность получили индексы Карли, Маршалла, Пааше, Ласпейреса, Фишера. В нашей стране традиционно используется индекс Пааше, предусматривающий взвешивание цен по весам отчетного периода, в качестве которых выступают объемы реализованных товаров в натуральных измерителях.
Источник: "economy-ru.info"
Содержание:
- 1 Понятие об индексах. Индексный метод
- 1.1 Индивидуальный индекс цен
- 1.2 Индекс цен общий: формула расчета
- 2 Кто и как впервые рассчитал индекс потребительских цен
- 2.1 Как считать цены
- 2.2 Правда и ложь индекса цен
- 3 Индексы цен
- 4 Статистические индексы
- 4.1 Индексы для измерения динамики экономических изменений
- 5 Система индексов цен
- 6 Индивидуальный и общий индексы цен
- 7 Общий индекс цен. Индекс Пааше
- 7.1 Средний гармонический индекс цен
- 7.2 Средний арифметический индекс цен
- 8 Общий индекс цен. Индекс Ласпейреса
Предположим, что за два периода производятся и потребляются 3 блага. В таблице представлены количество и цена (за единицу) каждого из товаров.
Рассчитайте:
индекс Ласпейреса,
индекс Пааше
индекс Фишера (2013 – базисный период).
| Годы | 2013 | 2014 | ||
|---|---|---|---|---|
| цена | количество | цена | количество | |
| книги | 10 | 10 | 15 | 8 |
| джинсы | 27 | 6 | 24 | 7 |
| телевизоры | 655 | 3 | 425 | 5 |
Решение:
Агрегатный индекс цен, в котором вес принят на уровне отчётного периода (q1) называется формулой Пааше:

где
p1 – цена текущего периода,
p0 – цена базисного периода,
q1 – количество товара в отчётном периоде (вес индекса).
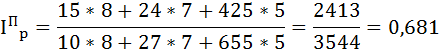
или 68,1%.
Значит, цены на все товары вместе снизились в отчётном периоде по сравнению с базисным на 31,9%.
Агрегатный индекс цен, в котором вес принят на уровне базисного периода (q0) называется формулой Ласпейреса:

где
p1 – цена текущего периода,
p0 – цена базисного периода,
q0 – количество товара в базисном периоде (вес индекса).
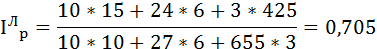
или 70,5%.
Следовательно, стоимость жизни снизилась на 29,5%.
Индекс Фишера представляет собой среднее геометрическое индекса Ласпейреса и индекса Пааше:
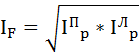
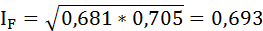
Следовательно, общий уровень цен упал на 30,7%.
Индексы Пааше, Ласпейреса и Фишера
Пример решения задачи
Задача
Имеются
данные о продаже различных товаров:
| Товар |
Ед. измерения |
Базисный период |
Отчетный период |
||
|
цена (руб.) |
объем продаж |
цена (руб.) |
объем продаж |
||
| А | кг | 7.6 | 108 | 9.3 | 82 |
| Б | л. | 12.5 | 54 | 11.9 | 68 |
| В | шт. | 13.9 | 91 | 13.2 | 106 |
Вычислить
общие индексы цен по методикам:
-
Ласпейреса;
Пааше;
Эджворта-Маршалла;
Лоу;
«идеальной» Фишера;
Рассчитать сводные индексы товарооборота и физического объема, пользуясь
формулами Ласпейреса и Пааше.
Проверить взаимосвязь индексов.
Определить сумму экономии (перерасхода), получаемую населением от изменения
цен.
Решение
На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:
ВКонтакте
WhatsApp
Telegram
Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.
Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.
Индексы цен по формуле Пааше, Ласпейреса,
Маршалла-Эджворта, Лоу
1) Индекс цен по
формуле Ласпейреса:
2) По формуле Пааше:
3) По формуле Маршалла-Эджворта:
4) По формуле Лоу:
Индекс цен Фишера
5) Индекс Фишера:
Индекс физического объема Пааше и Ласпейреса
6) Индекс
физического объема по формуле Ласпейреса:
Индекс
физического объема по формуле Пааше:
Индекс товарооборота, взаимосвязь между
индексами и сумма перерасхода населения от изменения цен
Индекс
товарооборота:
7) Между
рассчитанными индексами существует следующая взаимосвязь:
8) Сумма
перерасхода населения от изменения цен:
В связи с
увеличением цен население переплатило по сравнению с базисным периодом 24,4
руб.

Информация по индексу потребительских цен подготовлена по данным: Федеральной службы государственной статистики.
Что такое индекс потребительских цен
Индекс потребительских цен (ИПЦ, индекс инфляции, англ. Consumer Price Index, CPI) — это один из видов индексов цен, созданный для измерения среднего уровня цен на товары и услуги (потребительской корзины) за определённый период в экономике, является одним из главных показателей, на основании, которого, определяют уровень инфляции, отображает динамику цен на товары и услуги, которые приобретает население для непроизводственного потребления.
Для чего необходим индекс
Указанный индекс ежемесячно составляет Федеральная служба государственной статистики, и характеризуют уровень инфляции. В качестве базового периода выступает предыдущий месяц или декабрь предыдущего года.
Используется для расчета инфляции за расчетный период.
Формула расчета
Стоимость потребительской корзины из хлеба, молока и соли составила 165 руб, а в том же месяце предыдущего года данная корзина стоила 160 руб.
- Годовой ИПЦ будет равен: 165 / 160 * 100 = 103,1.
- Если индекс выше 100%, то это говорит о инфляции.
Индекс роста потребительских цен по годам в таблице
(отдельно на товары и услуги на сайте не публикуем)
| Период | В % к декабрю предпредыдущего года (нарастающим итогом с начала года) |
В % к предыдущему месяцу текущего года |
В % к соответствующему месяцу предпредыдущего года |
Индекс потребительских цен в 2023 году |
|||
| Май 2023 г. | |||
| Апрель 2023 г. | |||
| Март 2023 г. | |||
| Февраль 2023 г. | |||
| Январь 2023 г. | 100,84 | — | 111,77 |
Индекс потребительских цен в 2022 году |
|||
| Декабрь 2022 г. | 111,94 | 100,78 | |
| Ноябрь 2022 г. | 111,07 | 100,37 | 111,98 |
| Октябрь 2022 г. | 110,66 | 100,18 | 112,63 |
| Сентябрь 2022 г. | 110,46 | 100,05 | 113,68 |
| Август 2022 г. | 110,40 | 99,48 | 114,30 |
| Июль 2022 г. | 110,98 | 99,61 | 115,10 |
| Июнь 2022 г. | 111,41 | 99,65 | 115,90 |
| Май 2022 г. | 111,80 | 100,12 | 117,10 |
| Апрель 2022 г. | 111,67 | 101,56 | 117,83 |
| Март 2022 г. | 109,95 | 107,61 | 116,69 |
| Февраль 2022 г. | 102,17 | 101,17 | 109,15 |
| Январь 2022 г. | 100,99 | — | 108,73 |
Индекс потребительских цен в 2021 году |
|||
| Декабрь 2021 г. | 108,39 | 100,82 | — |
| Ноябрь 2021 г. | 107,51 | 100,96 | 108,40 |
| Октябрь 2021 г. | 106,49 | 101,11 | 108,13 |
| Сентябрь 2021 г. | 105,32 | 100,60 | 107,40 |
| Август 2021 г. | 104,69 | 100,17 | 106,68 |
| Июль 2021 г. | 104,51 | 100,31 | 106,46 |
| Июнь 2021 г. | 104,19 | 100,69 | 106,50 |
| Май 2021 г. | 103,48 | 100,74 | 106,02 |
| Апрель 2021 г. | 102,72 | 100,58 | 105,53 |
| Март 2021 г. | 102,13 | 100,66 | 105,79 |
| Февраль 2021 г. | 101,46 | 100,78 | 105,67 |
| Январь 2021 г. | 100,67 | — | 105,19 |
Индекс потребительских цен в 2020 году |
|||
| Декабрь 2020 г. | 104,91 | 100,83 | — |
| Ноябрь 2020 г. | 104,05 | 100,71 | 104,42 |
| Октябрь 2020 г. | 103,32 | 100,43 | 103,99 |
| Сентябрь 2020 г. | 102,88 | 99,93 | 103,67 |
| Август 2020 г. | 103,0 | 100,0 | 103,6 |
| Июль 2020 г. | 103,0 | 100,4 | 103,4 |
| Июнь 2020 г. | 102,6 | 100,2 | 103,2 |
| Май 2020 г. | 102,4 | 100,3 | 103,0 |
| Апрель 2020 г. | 102,1 | 100,8 | 103,1 |
| Март 2020 г. | 101,3 | 100,6 | 102,5 |
| Февраль 2020 г. | 100,7 | 100,3 | 102,3 |
| Январь 2020 г. | 100,4 | — | 102,4 |
Индекс потребительских цен в 2019 году |
|||
| Декабрь 2019 г. | 103,0 | 100,4 | — |
| Ноябрь 2019 г. | 102,7 | 100,3 | 103,5 |
| Октябрь 2019 г. | 102,4 | 100,1 | 103,8 |
| Сентябрь 2019 г. | 102,3 | 99,8 | 104,0 |
| Август 2019 г. | 102,4 | 99,8 | 104,3 |
| Июль 2019 г. | 102,7 | 100,2 | 104,6 |
| Июнь 2019 г. | 102,5 | 100,0 | 104,7 |
| Май 2019 г. | 102,4 | 100,3 | 105,1 |
| Апрель 2019 г. | 102,1 | 100,3 | 105,2 |
| Март 2019 г. | 101,8 | 100,3 | 105,3 |
| февраль 2019 г. | 101,5 | 101,4 | 105,2 |
| январь 2019 г. | 101,0 | — | 105,0 |
Индекс потребительских цен в 2018 году |
|||
| декабрь 2018 г. | 104,3 | 100,8 | — |
| ноябрь 2018 г. | 103,4 | 100,5 | 103,8 |
| октябрь 2018 г. | 102,9 | 100,4 | 103,5 |
| сентябрь 2018 г. | 102,5 | 100,2 | 103,4 |
| август 2018 г. | 102,4 | 100,0 | 103,1 |
| июль 2018 г. | 102,4 | 100,3 | 102,5 |
| июнь 2018 г. | 102,1 | 100,5 | 102,3 |
| май 2018 г. | 101,6 | 100,4 | 102,4 |
| апрель 2018 г. | 101,2 | 100,4 | 102,4 |
| март 2018 г. | 100,8 | 100,3 | 102,4 |
| февраль 2018 г. | 100,5 | 100,2 | 102,2 |
| январь 2018 г. | 100,3 | — | 102,2 |
Индекс потребительских цен в 2017 году |
|||
| декабрь 2017 г. | 102,5 | 100,4 | — |
| ноябрь 2017 г. | 102,1 | 100,2 | 102,5 |
| октябрь 2017 г. | 101,9 | 100,2 | 102,7 |
| сентябрь 2017 г. | 101,7 | 99,9 | 103,0 |
| август 2017 г. | 101,8 | 99,5 | 103,3 |
| июль 2017 г. | 102,4 | 100,1 | 103,9 |
| июнь 2017 г. | 102,3 | 100,6 | 104,4 |
| май 2017 г. | 101,7 | 100,4 | 104,1 |
| апрель 2017 г. | 101,3 | 100,3 | 104,1 |
| март 2017 г. | 101,0 | 100,1 | 104,3 |
| февраль 2017 г. | 100,8 | 100,2 | 104,6 |
| январь 2017 г. | 100,6 | — | 105,0 |
Индекс потребительских цен в 2016 году |
|||
| январь 2016 г. | 101,0 | — | 109,8 |
| февраль 2016 г. | 101,6 | 100,6 | 108,1 |
| март 2016 г. | 102,1 | 100,5 | 107,3 |
| апрель 2016 г. | 102,5 | 100,4 | 107,3 |
| май 2016 г. | 102,9 | 100,4 | 107,3 |
| июнь 2016 г. | 103,3 | 100,4 | 107,5 |
| июль 2016 г. | 103,9 | 100,5 | 107,2 |
| август 2016 г. | 103,9 | 100,0 | 106,9 |
| сентябрь 2016 г. | 104,1 | 100,2 | 106,4 |
| октябрь 2016 г. | 104,5 | 100,4 | 106,1 |
| ноябрь 2016 г. | 105,0 | 100,4 | 105,8 |
| декабрь 2016 г. | н/д | — | |
Индексы потребительских цен в 2015 году |
|||
| январь 2015 г. | 103,9 | — | 112,3 |
| февраль 2015 г. | 106,2 | 102,2 | 112,8 |
| март 2015 г. | 107,4 | 101,2 | 112,6 |
| апрель 2015 г. | 107,9 | 100,5 | 111,8 |
| май 2015 г. | 108,3 | 100,4 | 111,6 |
| июнь 2015 г. | 108,5 | 100,2 | 111,7 |
| июль 2015 г. | 109,4 | 100,8 | 113,4 |
| август 2015 г. | 109,8 | 100,4 | 114,1 |
| сентябрь 2015 г. | 110,5 | 100,6 | 113,8 |
| октябрь 2015 г. | 111,2 | 100,7 | 113,1 |
| ноябрь 2015 г. | 112,1 | 100,8 | 111,9 |
| декабрь 2015 г. | 112,9 | 100,8 | — |
Индексы потребительских цен в 2014 году |
|||
| январь 2014 г. | 100,6 | — | 106,1 |
| февраль 2014 г. | 101,3 | 100,7 | 106,2 |
| март 2014 г. | 102,3 | 101,0 | 106,9 |
| апрель 2014 г. | 103,2 | 100,9 | 107,3 |
| май 2014 г. | 104,2 | 100,9 | 107,6 |
| июнь 2014 г. | 104,8 | 100,6 | 107,8 |
| июль 2014 г. | 105,3 | 100,5 | 107,5 |
| август 2014 г. | 105,6 | 100,2 | 107,6 |
| сентябрь 2014 г. | 106,3 | 100,7 | 108,0 |
| октябрь 2014 г. | 107,1 | 100,8 | 108,3 |
| ноябрь 2014 г. | 108,5 | 101,3 | 109,1 |
| декабрь 2014 г. | 111,4 | 102,6 | — |
Индексы потребительских цен в 2013 году |
|||
| январь 2013 г. | 101,0 | — | 107,1 |
| февраль 2013 г. | 101,5 | 100,6 | 107,3 |
| март 2013 г. | 101,9 | 100,3 | 107,0 |
| апрель 2013 г. | 102,4 | 100,5 | 107,2 |
| май 2013 г. | 103,1 | 100,7 | 107,4 |
| июнь 2013 г. | 103,5 | 100,4 | 106,9 |
| июль 2013 г. | 104,4 | 100,8 | 106,5 |
| август 2013 г. | 104,5 | 100,1 | 106,5 |
| сентябрь 2013 г. | 104,7 | 100,2 | 106,1 |
| октябрь 2013 г. | 105,3 | 100,6 | 106,3 |
| ноябрь 2013 г. | 105,9 | 100,6 | 106,5 |
| декабрь 2013 г. | 106,5 | 100,5 | — |
Индексы потребительских цен в 2012 году |
|||
| январь 2012 г. | 100,5 | — | 104,2 |
| февраль 2012 г. | 100,9 | 100,4 | 103,7 |
| март 2012 г. | 101,5 | 100,6 | 103,7 |
| апрель 2012 г. | 101,8 | 100,3 | 103,6 |
| май 2012 г. | 102,3 | 100,5 | 103,6 |
| июнь 2012 г. | 103,2 | 100,9 | 104,3 |
| июль 2012 г. | 104,5 | 101,2 | 105,6 |
| август 2012 г. | 104,6 | 100,1 | 105,9 |
| сентябрь 2012 г. | 105,2 | 100,6 | 106,6 |
| октябрь 2012 г. | 105,6 | 100,5 | 106,5 |
| ноябрь 2012 г. | 106,0 | 100,3 | 106,5 |
| декабрь 2012 г. | 106,6 | 100,5 | — |
Индексы потребительских цен в 2011 году |
|||
| январь 2011 г. | 102,4 | 109,6 | |
| февраль 2011 г. | 103,2 | 100,8 | 109,5 |
| март 2011 г. | 103,8 | 100,6 | 109,5 |
| апрель 2011 г. | 104,3 | 100,4 | 109,6 |
| май 2011 г. | 104,8 | 100,5 | 109.6 |
| июнь 2011 г. | 105,0 | 100,2 | 109,4 |
| июль 2011 г. | 105,0 | 100,0 | 109,0 |
| август 2011 г. | 104,7 | 99,8 | 108,2 |
| сентябрь 2011 г. | 104,7 | 100,0 | 107,2 |
| октябрь 2011 г. | 105,2 | 100,5 | 107,2 |
| ноябрь 2011 г. | 105,6 | 100,4 | 106,8 |
| декабрь 2011 г. | 106,1 | 100,4 | — |
Индексы потребительских цен в 2010 году |
|||
| январь 2010 г. | 101.6 | 108,0 | |
| февраль 2010 г. | 102,5 | 100,9 | 107,2 |
| март 2010 г. | 103,2 | 100,6 | 106,5 |
| апрель 2010 г. | 103,5 | 100,3 | 106,0 |
| май 2010 г. | 104,0 | 100,5 | 106,0 |
| июнь 2010 г. | 104,4 | 100,4 | 105,8 |
| июль 2010 г. | 104,8 | 100,4 | 105,5 |
| август 2010 г. | 105,4 | 100,6 | 106,1 |
| сентябрь 2010 г. | 106,2 | 100,8 | 107,0 |
| октябрь 2010 г. | 106,8 | 100,5 | 107,5 |
| ноябрь 2010 г. | 107,6 | 100,8 | 108,1 |
| декабрь 2010 г. | 108,8 | 101,1 | |
Индексы потребительских цен в 2009 году |
|||
| январь 2009 г. | 102.4 | 113.4 | |
| февраль 2009 г. | 104.1 | 101.7 | |
| март 2009 г. | 105.4 | 101.3 | |
| апрель 2009 г. | 106.2 | 100.7 | |
| май 2009 г. | 106.8 | 100.6 | |
| июнь 2009 г. | 107.4 | 100.6 | |
| июль 2009 г. | 108.1 | 100.6 | |
| август 2009 г. | 108.1 | 100.0 | |
| сентябрь 2009 г. | 108.1 | 100.0 | |
| октябрь 2009 г. | 108.1 | 100.0 | |
| ноябрь 2009 г. | 108.4 | 100.3 | |
| декабрь 2009 г. | 108.8 | 100.4 | |
Индексы потребительских цен в 2008 году |
|||
| январь 2008 г. | 102.3 | 112.6 | |
| февраль 2008 г. | 103.5 | 101.2 | |
| март 2008 г. | 104.8 | 101.2 | |
| апрель 2008 г. | 106.3 | 101.4 | |
| май 2008 г. | 107.7 | 101.4 | |
| июнь 2008 г. | 108.7 | 101.0 | |
| июль 2008 г. | 109.3 | 100.5 | |
| август 2008 г. | 109.7 | 100.4 | |
| сентябрь 2008 г. | 110.6 | 100.8 | |
| октябрь 2008 г. | 111.6 | 100.9 | |
| ноябрь 2008 г. | 112.5 | 100.8 | |
| декабрь 2008 г. | 113.3 | 100.7 | |
Индексы потребительских цен в 2007 году |
|||
| январь 2007 г. | 101.7 | 108.2 | |
| февраль 2007 г. | 102.8 | 101.1 | |
| март 2007 г. | 103.4 | 100.6 | |
| апрель 2007 г. | 104.0 | 100.6 | |
| май 2007 г. | 104.7 | 100.6 | |
| июнь 2007 г. | 105.7 | 101.0 | |
| июль 2007 г. | 106,6 | 100,9 | |
| август 2007 г. | 106,7 | 100,1 | |
| сентябрь 2007 г. | 107,5 | 100,8 | |
| октябрь 2007 г. | 109,3 | 101,6 | |
| ноябрь 2007 г. | 110,6 | 101,2 | |
| декабрь 2007 г. | 111,9 | 101,1 | |
Индексы потребительских цен в 2006 году |
|||
| январь 2006 г. | 102.4 | 110.7 | |
| февраль 2006 г. | 104.1 | 101.7 | |
| март 2006 г. | 105.0 | 100.8 | |
| апрель 2006 г. | 105.4 | 100.4 | |
| май 2006 г. | 105.9 | 100.5 | |
| июнь 2006 г. | 100.3 | ||
| июль 2006 г. | 106,9 | 100.7 | |
| август 2006 г. | 107,1 | 100.2 | |
| сентябрь 2006 г. | 107,2 | 100.1 | |
| октябрь 2006 г. | 107,5 | 100.3 | |
| ноябрь 2006 г. | 108,2 | 100.6 | |
| декабрь 2006 г. | 109,0 | 100.8 | |
Индексы потребительских цен в 2005 году |
|||
| январь 2005 г. | 102.6 | 112.7 | |
| февраль 2005 г. | 103.9 | 101.2 | 113.0 |
| март 2005 г. | 105.3 | 101.3 | |
| апрель 2005 г. | 106.5 | 101.1 | |
| май 2005 г. | 107.3 | 100.8 | |
| июнь 2005 г. | 108.0 | 100.6 | |
| июль 2005 г. | 108.5 | 100.5 | |
| август 2005 г. | 108.3 | 99.9 | |
| сентябрь 2005 г. | 108.6 | 100.3 | |
| октябрь 2005 г. | 109.2 | 100.6 | |
| ноябрь 2005 г. | 110.0 | 100.7 | |
| декабрь 2005 г. | 110.9 | 100.8 | |
Индексы потребительских цен в 2004 году |
|||
| январь 2004 г. | 101.8 | 111.3 | |
| февраль 2004 г. | 102.8 | 101.0 | 110.6 |
| март 2004 г. | 103.5 | 100.8 | 110.3 |
| апрель 2004 г. | 104.6 | 101.0 | 110.2 |
| май 2004 г. | 105.3 | 100.7 | 110.2 |
| июнь 2004 г. | 106.1 | 100.8 | |
| июль 2004 г. | 107.1 | 100.9 | |
| август 2004 г. | 107.6 | 100.4 | |
| сентябрь 2004 г. | 108.0 | 100.4 | 111.4 |
| октябрь 2004 г. | 109.3 | 101.1 | |
| ноябрь 2004 г. | 110.5 | 101.1 | |
| декабрь 2004 г. | 111.7 | 101.1 | |
Индексы потребительских цен в 2003 году |
|||
| январь 2003 г. | 102.4 | 114.3 | |
| февраль 2003 г. | 104.1 | 101.6 | 114.8 |
| март 2003 г. | 105.2 | 101.1 | 114.8 |
| апрель 2003 г. | 106.2 | 101.0 | 114.6 |
| май 2003 г. | 107.1 | 100.8 | 113.6 |
| июнь 2003 г. | 107.9 | 100.8 | 113.9 |
| июль 2003 г. | 108.7 | 100.7 | |
| август 2003 г. | 108.3 | 99.6 | 113.3 |
| сентябрь 2003 г. | 108.6 | 100.3 | 113.3 |
| октябрь 2003 г. | 109.7 | 101.0 | 113.2 |
| ноябрь 2003 г. | 110.8 | 101.0 | 112.5 |
| декабрь 2003 г. | 101.1 | 112.0 | |
Индексы потребительских цен в 2002 году |
|||
| январь 2002 г. | 103.1 | 119.0 | |
| февраль 2002 г. | 104.3 | 101.2 | 117.7 |
| март 2002 г. | 105.4 | 101.1 | 116,8 |
| апрель 2002 г. | 106.6 | 101.2 | |
| май 2002 г. | 108.4 | 101.7 | |
| июнь 2002 г. | 109.0 | 100.5 | |
| июль 2002 г. | 109.8 | 100.7 | |
| август 2002 г. | 109.9 | 100.1 | 115,1 |
| сентябрь 2002 г. | 110.3 | 100.4 | 114,9 |
| октябрь 2002 г. | 111.5 | 101.1 | 114.8 |
| ноябрь 2002 г. | 113.3 | 101.6 | |
| декабрь 2002 г. | 115.1 | 101.5 | |
Индексы потребительских цен в 2001 году |
|||
| январь 2001 г. | 102.8 | ||
| февраль 2001 г. | 105.1 | 102.3 | 122.2 |
| март 2001 г. | 107.1 | 101.9 | 123.7 |
| апрель 2001 г. | 109.0 | 101.8 | 124.8 |
| май 2001 г. | 110.9 | 101.8 | 124.8 |
| июнь 2001 г. | 112.7 | 101.6 | |
| июль 2001 г. | 113.2 | 100.5 | 122.1 |
| август 2001 г. | 113.2 | 100.0 | 120.9 |
| сентябрь 2001 г. | 113.9 | 100.6 | 120.0 |
| октябрь 2001 г. | 115.2 | 101.1 | |
| ноябрь 2001 г. | 116.7 | 101.4 | |
| декабрь 2001 г. | 118,6 | 101.6 | |
Индексы потребительских цен в 2000 году |
|||
| январь 2000 г. | 102.3 | ||
| февраль 2000 г. | 101 | ||
| март 2000 г. | 104.1 | 100.6 | |
| апрель 2000 г. | 105.0 | 100.9 | |
| май 2000 г. | 106.8 | 101.8 | |
| июнь 2000 г. | 109.5 | 102.6 | |
| июль 2000 г. | 111.5 | 101.8 | |
| август 2000 г. | 112.6 | 101.0 | |
| сентябрь 2000 г. | 114.1 | 101.3 | |
| октябрь 2000 г. | 116.5 | 102.1 | 119.4 |
| ноябрь 2000 г. | 101.5 | ||
| декабрь 2000 г. | 120.2 | 101.6 | |
Индексы потребительских цен в 1999 году |
|||
| январь 1999 г. | 108.4 | ||
| февраль 1999 г. | 112.9 | 104.1 | 203.3 |
| март 1999 г. | 116.0 | 102.8 | 207.6 |
| апрель 1999 г. | 119.5 | 103.0 | |
| май 1999 г. | 122.2 | 102.2 | |
| июнь 1999 г. | 101.9 | ||
| июль 1999 г. | 128.0 | 102.8 | |
| август 1999 г. | 129.5 | 101.2 | |
| сентябрь 1999 г. | 101.5 | ||
| октябрь 1999 г. | 101.4 | ||
| ноябрь 1999 г. | 134.8 | 101.2 | |
| декабрь 1999 г. | 101.3 | ||
Индексы потребительских цен в 1998 году |
|||
| январь 1998 г. | 101.5 | 101.5 | 110.1 |
| февраль 1998 г. | 102.4 | 100.9 | 109.4 |
| март 1998 г. | 103.1 | 100.6 | 108.5 |
| апрель 1998 г. | 103.5 | 100.4 | 107.9 |
| май 1998 г. | 104.0 | 100.5 | 107.5 |
| июнь 1998 г. | 104.1 | 100.1 | 106.4 |
| июль 1998 г. | 104.2 | 100.2 | 105.6 |
| август 1998 г. | 119.0 | 103.7 | 121.0 |
| сентябрь 1998 г. | 149.6 | 138.4 | 152,2 |
| октябрь 1998 г. | 156.4 | 104.5 | 158,8 |
| ноябрь 1998 г. | 165.3 | 105.7 | 166,8 |
| декабрь 1998 г. | 184.4 | 111.6 | 184.4 |
Индексы потребительских цен в 1997 году |
|||
| январь 1997 г. | 102.3 | 102.3 | |
| февраль 1997 г. | 103.8 | 101.5 | |
| март 1997 г. | 105.4 | 101.4 | |
| апрель 1997 г. | 106.4 | 101.0 | |
| май 1997 г. | 107.4 | 100.9 | 114.6 |
| июнь 1997 г. | 108.6 | 101.1 | |
| июль 1997 г. | 109.6 | 100.9 | |
| август 1997 г. | 109.5 | 99.9 | |
| сентябрь 1997 г. | 108.7 | 99.7 | |
| октябрь 1997 г. | 109.3 | 100.2 | |
| ноябрь 1997 г. | 110.0 | 100.6 | 111.5 |
| декабрь 1997 г. | 111.0 | 101.0 | 111.0 |
Индексы потребительских цен в 1996 году |
|||
| январь 1996 г. | 104.1 | 104.1 | 204 |
| февраль 1996 г. | 107.0 | 102.8 | 189 |
| март 1996 г. | 110.0 | 102.8 | 179 |
| апрель 1996 г. | 112.4 | 102.2 | 168 |
| май 1996 г. | 114.2 | 101.6 | 158 |
| июнь 1996 г. | 115.5 | 101.2 | 150 |
| июль 1996 г. | 116.4 | 100.7 | |
| август 1996 г. | 116.1 | 99.8 | |
| сентябрь 1996 г. | 116.5 | 100.3 | |
| октябрь 1996 г. | 117.9 | 101.2 | |
| ноябрь 1996 г. | 120.1 | 101.9 | |
| декабрь 1996 г. | 121.8 | 101.4 | 121.8 |
Индексы потребительских цен в 1995 году |
|||
| январь 1995 г. | 118 | 117,8 | 315 |
| февраль 1995 г. | 131 | 111 | 316 |
| март 1995 г. | 142 | 108,9 | 320 |
| апрель 1995 г. | 154 | 108.5 | 320 |
| май 1995 г. | 167 | 107.9 | 323 |
| июнь 1995 г. | 178 | 106.7 | 325 |
| июль 1995 г. | 187 | 105.4 | 325 |
| август 1995 г. | 196 | 104.6 | 325 |
| сентябрь 1995 г. | 205 | 104.5 | 314 |
| октябрь 1995 г. | 214 | 104.7 | 286 |
| ноябрь 1995 г. | 224 | 104.5 | 261 |
| декабрь 1995 г. | 231 | 103.2 | 231 |
Индексы потребительских цен в 1994 году |
|||
| январь 1994 г. | 118 | 118 | 881 |
| февраль 1994 г. | 131 | 111 | 782 |
| март 1994 г. | 140 | 107 | 699 |
| апрель 1994 г. | 152 | 108 | 639 |
| май 1994 г. | 163 | 107 | 579 |
| июнь 1994 г. | 172 | 106 | 512 |
| июль 1994 г. | 182 | 105 | 440 |
| август 1994 г. | 190 | 105 | 366 |
| сентябрь 1994 г. | 205 | 108 | 321 |
| октябрь 1994 г. | 236 | 115 | 309 |
| ноябрь 1994 г. | 270 | 115 | 304 |
| декабрь 1994 г. | 315 | 116 | 315 |
Индексы потребительских цен в 1993 году |
|||
| январь 1993 г. | 126 | 126 | 950 |
| февраль 1993 г. | 157 | 125 | 858 |
| март 1993 г. | 188 | 120 | 794 |
| апрель 1993 г. | 224 | 119 | 774 |
| май 1993 г. | 264 | 118 | 817 |
| июнь 1993 г. | 317 | 120 | 823 |
| июль 1993 г. | 388 | 122 | 910 |
| август 1993 г. | 488 | 126 | в 10.6 раз |
| сентябрь 1993 г. | 601 | 123 | в 11.7 раз |
| октябрь 1993 г. | 718 | 120 | в 11.3 раз |
| ноябрь 1993 г. | 836 | 116 | в 10.5 раз |
| декабрь 1993 г. | 940 | 113 | 940 |
Индексы потребительских цен в 1992 году |
|||
| январь 1992 г. | 345 | 345 | 846 |
| февраль 1992 г. | 477 | 138 | в 11.1 раз |
| март 1992 г. | 619 | 130 | в 13.6 раз |
| апрель 1992 г. | 753 | 122 | в 10.1 раз |
| май 1992 г. | 843 | 112 | в 11.0 раз |
| июнь 1992 г. | в 10.0 раз | 119 | в 13.0 раз |
| июль 1992 г. | в 11.1 раз | 111 | в 14.3 раз |
| август 1992 г. | в 12.1 раз | 109 | в 15.4 раз |
| сентябрь 1992 г. | в 13.4 раз | 112 | в 17.0 раз |
| октябрь 1992 г. | в 16.5 раз | 123 | в 20.2 раз |
| ноябрь 1992 г. | в 20.8 раз | 126 | в 23.4 раз |
| декабрь 1992 г. | в 26.1 раз | 125 | в 26.1 раз |
Увидели опечатку? Выделите фрагмент и нажмите Ctrl+Enter
Подпишитесь на соцсети
Публикуем обзор статьи, как только она выходит. Отдельно информируем о важных изменениях закона.
 Поделиться с друзьями
Поделиться с друзьями
-
Методы расчета индексов цен.
Основная
характеристика динамики цен производится
при помощи расчетов индексов цен.
Индекс
цен – это относительный показатель,
выраженный в коэффициентах или процентах,
характеризующий изменение цен во времени
(индекс динамики) или в пространстве
(территориальный индекс).
Индексы
цен делятся на индивидуальные (частные)
и общие.
Индивидуальный
индекс цен
характеризует соотношение уровней цен
одного вида товаров.
Общий
индекс цен
– относительная величина, характеризующая
изменение цен совокупности ряда
разнородных товаров.
В
зависимости от поставленных задач и
наличия исходных данных для расчета
индексов цен могут применяться различные
формы индексов: агрегатная, средняя
арифметическая и средняя гармоническая,
реже – геометрическая форма.
Все
эти формы индексов рассматриваются в
курсе общей теории статистики.
В
настоящее время Госкомстат России
рассчитывает индексы цен для двух
секторов: производственного и
потребительского.
В
потребительском
секторе рассчитывается индекс
потребительских цен на основные товары
и услуги (ИПЦ).
В
производственном
секторе рассчитывается несколько
индексов:
-
Индекс
цен предприятий-производителей на
промышленную продукцию; -
Индекс
цен приобретения материально-технических
ресурсов для основного производства; -
Индекс
цен реализации на сельскохозяйственную
продукцию; -
Индекс
цен в капитальном строительстве; -
Индекс
цен на грузовые перевозки.
Индекс
потребительских цен
характеризует изменение во времени
общего уровня цен на товары и услуги,
приобретаемые населением для
непроизводственного потребления. Он
исчисляется как отношение стоимости
фактического фиксированного набора
товаров и услуг в текущем периоде к его
стоимости в базисном периоде.
Фиксированный
набор товаров и услуг – это репрезентативная
выборка групп товаров и услуг, наиболее
часто потребляемых населением. Такой
набор одинаков для всех регионов России.
В него включаются три группы:
продовольственные товары, непродовольственные
товары и платные услуги населению.
Расчет
ИПЦ производится ежемесячно и
ежеквартально на базе статистических
данных, полученных в ходе наблюдения
за ценами. Кроме того, для расчета ИПЦ
используют данные о структуре фактических
потребительских расходов населения за
предыдущий период.
Расчет
ИПЦ
производится в несколько этапов:
-
Определяются
индивидуальные индексы цен на отдельные
виды товаров и по отдельному городу
как частное от деления средних
сопоставимых цен:
![]() (1)
(1)
Средние
сопоставимые цены по отдельному региону
определяются как средняя арифметическая,
взвешенная по доле населения отдельных
районов региона в общей численности
населения региона:
![]() (2),
(2),
где
рк,i
– тариф k-того
района в i-том
месяце;
dk
– доля численности населения k-того
района.
-
Определяют
агрегатные индексы цен на отдельные
товары, товарные группы и услуги в целом
по региону, экономическому району, РФ
с использованием территориальных
весов.
 (3),
(3),
где
p0,kdk
– произведение доли численности
населения на уровень тарифов в периоде,
принятом за базисный.
-
Исходя
из агрегатных индексов цен по товарам
и услугам в целом по региону, экономическому
району, РФ и доли расходов на приобретение
отдельных товаров в потребительских
расходах населения определяют сводные
индексы цен в целом по всем товарам и
услугам и отдельно по группам:
продовольственным товарам,
непродовольственным товарам и платным
услугам населению. Расчет производится
по формуле Ласпейреса:
 (4)
(4)
В
условиях резкого изменения структуры
производства базисного и текущего
периода для расчетов сводного индекса
цен используется модифицированная
формула индекса Ласпейреса которая
имеет следующий вид:

(5),
где
t
– текущий период;
t-1
– предыдущий период;
pt-1q0
=p0q0![]() .
.
Достоинством
данной формулы является то, что в качестве
весов используется товарооборот
базисного периода, который последовательно
умножается на последнее значение индекса
цен.
Расчет
сводного ИПЦ на федеральном и региональных
уровнях производится еженедельно. Для
определения индекса за более
продолжительный период (месяц, квартал
и т.д.) используется цепной метод, т.е.
перемножаются ИПЦ недельные (месячные
и т.д.).
Для
характеристики уровня инфляции в
потребительском секторе, для индексации
доходов населения используется общий
ИПЦ, но органами статистики рассчитывается
система индексов потребительских цен.
В нее включаются:
-
Сводный
индекс потребительских цен полного
набора потребительских товаров и услуг,
приобретаемых на одну семью и по этому
же набору без товаров необязательного
пользования (ювелирных изделий, легковых
автомобилей, алкогольных напитков и
табачных изделий); -
ИПЦ
для отдельных социально-экономических
групп населения с различным уровнем
доходов (10 децильных групп семей); -
Индексы
стоимости прожиточного минимума; -
Индексы
на отдельные товары и услуги.
Анализ
динамики цен в производственном секторе
экономики проводится путем расчета
индекса цен
производителей промышленной
продукции. Данный индекс определяется
двумя методами: цепным и базисным.
Базисный
индекс
показывает, во сколько раз изменились
цены в отчетном периоде по сравнению с
базисным. Он рассчитывается путем
деления цены текущего месяца на цену
товара в период, принятый за базисный.
Используется
базисный метод только в том случае,
когда анализируются цены на товары,
производимые в течение нескольких лет.
Месячный
индекс текущего периода определяется
путем деления базисного индекса текущего
периода на базисный индекс предшествующего
периода.
Пример:
базисный индекс цен производителей на
стиральные машины в марте составил
100,3%, а в апреле – 100,8%. Определить, на
сколько процентов изменились цены за
апрель.
Iапр
=
![]()
Следовательно,
за апрель цены возросли на 0,4%.
При
использовании цепного
метода
месячный индекс определяется путем
отнесения цены товара в текущем месяце
к цене товара в предыдущем месяце. При
необходимости определения цепного
индекса за длительный период производится
перемножение месячных индексов.Цепной
метод расчета используется при частой
смене производимой продукции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
