Индексы совокупных доходов рабочих и служащих в текущих ценах, реальных доходов рабочих и служащих, покупательной способности денег, номинальной заработной платы, индекс номинальной располагаемой заработной платы, реальной заработной платы
Среднемесячная зарплата за вычетом налогов рабочих и служащих в базисном году составила 2300 руб, в отчетном 2500 руб., цены на потребительские товары и услуги повысились в отчетном периоде по сравнению с базисным на 25 %. Выплаты трансфертов (в ценах соответствующих лет) на одного рабочего и служащего составили в базисном году 310 руб., в отчетном – 480 руб. Доля налогов в общей зарплате составила в базисном периоде 12 %, в отчетном – 18 %.
Определите:
- индекс совокупных доходов рабочих и служащих в текущих ценах;
- индекс реальных доходов рабочих и служащих;
- индекс покупательной способности денег;
- индекс номинальной заработной платы;
- индекс номинальной располагаемой заработной платы;
- индекс реальной заработной платы.
Решение.
- Индекс совокупных доходов рабочих и служащих в текущих ценах определяется как:
где СДН1, СДН0 – номинальные совокупные доходы населения в базисном и отчетном периодах.
- Индекс реальных доходов рабочих и служащих:
где РДН0, РДН1 – реальные совокупные доходы населения в базисном и отчетном периодах.
Реальные доходы – это номинальные доходы с поправкой на индекс потребительских цен:
Так как индекс покупательной способности денег равен обратной величине индекса потребительских цен (Ip):
Тогда:
Несмотря на то, что номинальные доходы рабочих и служащих возросли на 9,2 %, реальные – снизились (87,4 – 100= — 12,6) на 12,6%.
- Индекс покупательной способности рубля равен:
Таким образом, покупательная способность рубля сократилась на 20%.
- Индекс номинальной заработной платы:
где Ном.ЗП0, Ном.ЗП1 – номинальная зарплата отчетного и базисного периодов.
5. Номинальная располагаемая заработная плата. (Ном.РЗП) равна номинальной (НомЗП) за вычетом налогов и обязательных платежей (НП).
Следовательно,
где dНПо, dНП1 – доля налогов в номинальной заработной плате в базисном и отчетном периодах.
6. Реальная заработная плата равна номинально располагаемой заработной плате умноженной на индекс покупательной способности рубля.
Индекс реальной заработной платы составит:
Таким образом, проведя несложные вычисления, мы приходим к выводу, о том, что номинальная заработная плата за анализируемый период возросла на 8,7 % (2500 – 2300 = 200 руб.), причем, в связи с ростом на 6% налогов, номинальная располагаемая заработная плата увеличилась на 1,3 %. Учитывая тот факт, что цены на потребительские товары и услуги также повысились (+25%), реальная заработная плата в отчетном периоде снизилась на 13 % по сравнению с базисным. С учетом выплаты трансфертов сокращение реальных доходов населения составило 12,6%.
Потребитель рассматривает свой денежный
доход как средство для приобретения
тех или иных благ. Изменения дохода,
происходящие одновременно с изменениями
цен, благоприятны или неблагоприятны
для него в зависимости от того, как
изменяются при этом его возможности
как покупателя.
По этой причине различают
номинальный
(денежный) и реальный
доход. Слово “реальный” восходит к
латинскому res, означающему вещь, предмет,
дело. Реальный доход, если вернуться к
первоначальному значению слова, должен
означать вещественное, предметное
содержание дохода потребителя. Строго
говоря, его можно полно охарактеризовать
лишь перечислив все те блага, которые
он мог бы приобрести в соответствии со
своими предпочтениями, с указанием
количества каждого покупаемого блага.
Выразить его каким-либо одним числом
невозможно.
Но ряд изобретенных
статистиками показателей устроен
наподобие стрекозиного глаза: как
стрекоза видит только движущиеся
предметы, так и эти показатели, не
оценивая уровень
какого-либо явления, тем не менее могут
охарактеризовать его изменение.
Поэтому мы, отказавшись от попыток
численно выразить реальный доход,
рассмотрим возможности численной оценки
его изменения.
В сравнительно простых
случаях, когда уровень явления выражается
одним числом, в качестве характеристики
изменения удобно использовать индекс
соответствующей величины — отношение
“нового” уровня (его называют текущим)
к “старому”, с которым производится
сравнение (его называют базисным):
|
I |
В этой лекции мы всюду будем использовать
одну и ту же букву для обозначения
сравниваемых величин, применяя нуль
для базисных значений и единицу для
текущих.
По этой схеме мы легко можем
построить индекс номинального дохода
Y:
|
IНД |
Если же мы не можем выразить каждый из
уровней одним числом, но мы хотим получить
ответ на вопрос как, в каком направлении,
во сколько раз увеличилось, улучшилось,
усилилось или уменьшилось, ухудшилось,
ослабилось то или иное явление, то
построение соответствующего индекса
становится значительно более сложной
задачей.
Итак, мы хотим построить индекс реального
дохода. Рассмотрим вначале самые простые
случаи.
1. Пусть цены всех благ
остались без изменения. В этом случае
естественно считать, что реальный доход
изменился в такой же пропорции, что и
номинальный: IРД
= IНД.
Если, например, номинальный доход
изменился с 1000 до 2000 руб. в месяц, то при
условии постоянства цен можно считать,
что индекс реального дохода равен 2.
Это, разумеется, не означает, что
потребитель захочет купить каждого
товара в два раза больше: предметов
первой необходимости он купит столько
же или ненамного больше, значительно
больше купит тех товаров, которые относят
к предметам роскоши, а так называемых
низших благ приобретет меньше (см. лекцию
15, раздел 1). Во всяком случае, он перейдет
на более высокий уровень потребления,
и в качестве меры повышения его
благосостояния вполне уместно принять
рост его номинального дохода, поскольку
все прочие факторы остаются неизменными.
2. Допустим, что цена может
изменяться, но человек потребляет
один-единственный товар. При денежном
доходе Y
и цене Р
он может купить его в количестве q
= Y/P. Здесь потребление
выражается одним числом, которое в этом
случае и есть реальный доход.
Поэтому индекс реального
дохода:
|
IРД |
Но отношение Y1/Y0—
это индекс номинального дохода, а Р1/Р0
— это индекс цены, который мы обозначим
IР.
Мы пришли к выражению:
|
IРД |
которое легко интерпретировать:
рост денежного дохода увеличивает
возможности покупателя в IНД
раз, а рост цен в IP
раз во столько же раз эти возможности
снижает.
3. Пусть теперь человек приобретает
много разных благ. Если все цены и
денежный доход изменились в одной и той
же пропорции, то бюджетная линия не
изменила своего положения и выбор
потребителя остался прежним. Индекс
реального дохода при этом равен единице.
Если же все цены изменились
в одной и той же пропорции в а раз, а
номинальный доход — в b
раз, то такое изменение равносильно
изменению дохода в b/а
раз (при первоначальных ценах), т. е. IРД
= b/а.
Величина b—
это, очевидно, индекс номинального
дохода; величина а
есть индекс каждой цены в отдельности,
а так как эта величина одна и та же для
всех товаров, естественно считать, что
в такой ситуации индекс цен равен а.
Таким образом, мы и в этом случае приходим
к соотношению (1) для индекса реального
дохода.
И в общем случае, когда цены и денежный
доход изменяются в различных пропорциях,
равенство (1) представляется весьма
привлекательным из-за наглядности и
естественности его смысловой интерпретации.
Но мы пока не можем им воспользоваться,
поскольку мы нерешенную задачу определения
изменения реального дохода сводим к
также еще не решенной задаче определения
совместного изменения всех цен, когда
они изменяются по-разному.
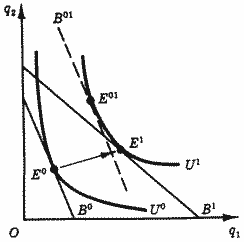
Приглядимся внимательнее
к поведению потребителя при изменении
цен и дохода (рис. 1). Его выбор в базисном
периоде определяется бюджетной линией
В0,
и он выбирает точку Е0
на кривой безразличия U0.
В текущем периоде он перемещается в
точку Е1,
лежащую на новой бюджетной линии B1.
При этом потребитель достигает уровня
удовлетворения своих потребностей,
соответствующего кривой безразличия
U1.
Рис. 1.
Изменение выбора при изменении денежного
дохода и цен
Изменение реального дохода
целесообразно связать с изменением
благополучия потребителя. Можно ли
достигнуть нового уровня при неизменных
ценах за счет изменения денежного
дохода? Так как наклон бюджетной линии
определяется соотношением цен, переместим
бюджетную линию В0
параллельно самой себе до касания с
кривой безразличия U1.
На графике новое положение касательной
обозначено В01,
а точка касания — Е01.
Она характеризует набор благ, эквивалентный
по полезности набору Е1,
но достигаемый при постоянных ценах
только за счет изменения номинального
дохода. Поскольку бюджетные линии В01
и В1
обеспечивают потребителю один и тот же
уровень благополучия, мы должны приписать
им одинаковое значение реального дохода.
А тогда мы можем измерить
изменение реального дохода как изменение
денежного дохода, требуемое для перехода
в точку Е01.
Если q1,
q2,
…, qn—
объемы потребления благ, а P1,
P2,
…, Pn
— цены (мы переходим от
двумерной иллюстрации к общему случаю),
для индекса реального дохода мы получаем
выражение:
|
|
Знаменатель этого выражения
равен базисному уровню номинального
дохода, а числитель – денежному доходу,
соответствующему точке Е01
при базисных ценах. Итак, в принципе мы
можем оценить изменение реального
дохода у отдельного потребителя; при
этом мы существенно используем его
систему предпочтений. Действительно,
повышение одной-единственной цены при
прочих равных условиях может заметно
снизить ваш реальный доход, если
подорожавший товар вами любим и
потребляется в больших количествах.
Если же вы к нему равнодушны и потребляете
немного, то и подорожание этого товара
не изменит заметным образом вашего
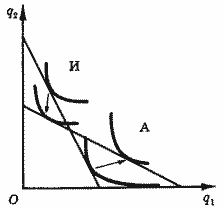
реального дохода. Рис. 2 иллюстрирует
изменение цен на два товара в противоположных
направлениях, благоприятное для одного
потребителя и неблагоприятное для
другого.
Рис. 2.
На рисунке совмещены карты безразличия
Антона и Игоря. У них разные вкусы. Одно
и то же изменение стипендии и цен
оказалось благоприятным для Антона и
неблагоприятным для Игоря.
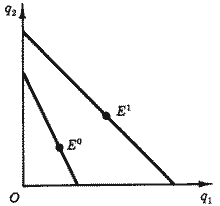
Рис. 3.
Наблюдаемые характеристики потребителя
Но можем ли мы воспользоваться равенством
(2) практически? Ведь потребитель не
формулирует своих предпочтений в явном
виде, он лишь реализует их в своем
поведении.
Сторонний наблюдатель
(например, статистик) может зафиксировать
точки Е0
и Е1,
соответствующие покупкам в базисном и
текущем периодах, но он не может “увидеть”
точку Е01.
Все, что можно оценить объективно по
наблюдениям в базисном и текущем
периодах, изображено на рис. 3: это
бюджетные линии, определяемые номинальным
доходом и ценами, и объемы покупок. На
рисунке точка Е0
лежит выше новой бюджетной линии, что
свидетельствует об увеличении реального
дохода. Оперируя только наблюдаемыми
данными, мы вынуждены несколько
поступиться теоретической чистотой
формулы (2) и заменить точку Е01
точкой Е1:
|
|
Здесь числитель характеризует
затраты на покупку набора Е1
в базисных ценах; он несколько больше,
чем числитель в формуле (2), так что
выражение (3) дает завышенное по сравнению
с (2) значение индекса реального дохода.
Постарайтесь самостоятельно убедиться
в справедливости последнего утверждения.
Обратимся теперь к определению индекса
цен. Здесь мы можем использовать тот же
подход, который позволил нам определить
индекс реального дохода.
Если бы все цены изменились
в одной и той же пропорции, то индекс
цен совпадал бы с индексом каждой цены
в отдельности. Обратимся снова к рис.
1. Переход от базисной бюджетной линии
В0
к линии В01
(и соответственно к точке E01)
мог бы произойти и без изменения денежного
дохода, только за счет пропорционального
изменения цен. Если бы каждая из цен
изменилась в а
раз, затраты на покупку товаров,
соответствующих точке Е01,
составили бы:
|
|
Но точка Е01
выбрана нами потому, что она эквивалентна
по полезности точке E1
— точке выбора потребителя при фактическом
изменении цен и изменившемся денежном
доходе.
Поэтому пропорциональное изменение
цен, эквивалентное по полезности
фактическому их изменению, должно
удовлетворять соотношению:
|
|
и значение коэффициента а, отвечающее
этому условию, мы можем принять за индекс
цен для данного потребителя:
|
|
И так же, как при определении
индекса реального дохода, для практических
расчетов нам пришлось бы в этом выражении
заменить ненаблюдаемую точку Е01
наблюдаемой точкой Е1:
|
|
Сравните выражения (4) и (5) и попытайтесь
выяснить, какое из них дает большее
значение для индекса цен.
Легко убедиться, что при использовании
выражений (2) для индекса реального
дохода и (4) для индекса цен равенство
(1) остается справедливым:
|
|
Точно так же равенства (3) и (5) согласованы
с формулой (1).
До сих пор мы рассматривали индекс
реального дохода отдельного потребителя,
а также индекс цен с точки зрения
отдельного потребителя. Каждая домохозяйка
в принципе могла бы, ведя учет своих
покупок и используя данные о ценах на
различные товары, рассчитать для себя
оба индекса. Каждый из них будет отражать
и общие для всех семей условия — рыночные
цены на все товары, — и особые условия
каждой семьи — доход, потребительские
привычки, вкусы, пристрастия.
Но статистические органы интересуются
не отдельными потребителями, а их
совокупностями – населением в целом или
определенными его группами.
Формулы (3) и (5) могут быть легко перенесены
и на совокупности потребителей.
Достаточно лишь заменить
в них индивидуальные объемы потребления
q1,
q2,
…, qn
рыночными объемами Q1,
Q2,
…, Qn:
|
|
|
|
Что же стоит за этой формальной
подстановкой?
В статистике используется много различных
способов усреднения величин. Приведенные
здесь общие индексы являются определенного
рода средними из индексов для отдельных
потребителей. В этом смысле можно
говорить, что они выражают общие для
всех индивидов тенденции изменения
реальных доходов и цен.
Получение количественных оценок сложных
экономических характеристик, не
выражаемых одним числом, – таких, как
реальный доход или цены на все
потребительские товары, – непростая
задача, и ее решение наталкивается на
различные теоретические и практические
трудности. Пути их преодоления
рассматриваются в следующих разделах
лекции.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Главным показателем инфляции выступает темп (или уровень) инфляции, который рассчитывается как процентное отношение разницы уровней цен текущего и предыдущего года к уровню цен предыдущего года:
−Pп.г.)Pп.г.
·100 %
,
где Pт.г. — общий уровень цен текущего года,
— общий уровень цен предыдущего года.
Таким образом, темпы инфляции характеризуют процентное изменение общего уровня цен (на сколько процентов от уровня цен предыдущего года изменились цены в текущем году).
Рост уровня цен приводит к снижению покупательной способности денег.
Под покупательной способностью (ценностью) денег понимают количество товаров и услуг, которое можно купить на одну денежную единицу.
Если цены на товары повышаются, то на одну и ту же сумму денег можно купить меньше товаров, чем раньше, поэтому ценность денег падает.
Виды инфляции в зависимости от темпов роста
|
Вид инфляции |
Темп роста инфляции, % в год |
Характеристика |
|
Нормальная |
(3)–(5) |
Инфляция поддаётся контролю, может способствовать росту инвестиций и наращиванию объёмов выпуска продукции |
|
Умеренная (ползучая) |
(5)–(10) |
Масштабы не приводят к серьёзным нарушениям в экономике, но способствуют сокращению объёмов производства |
|
Галопирующая |
(20)–(20)(0) |
Является серьёзной экономической проблемой, затрудняет возможность прогнозирования экономической ситуации, приводит к росту социальной нестабильности |
|
Гиперинфляция |
(200) и выше |
Является губительной для экономики, разрушает экономические связи, обесценивает сбережения населения |
Виды инфляции в зависимости от формы проявления:
- открытая (явная) инфляция проявляется в наблюдаемом росте общего уровня цен;
- cкрытая (подавленная) инфляция имеет место в случае, когда цены устанавливает государство, причём на уровне ниже, чем рыночные. Главная форма проявления скрытой инфляции — дефицит товаров.
Расчёт суммы, имеющей такую же покупательную способность
Инфляция снижает покупательную способность денег, то есть приводит к обесцениванию денег.
Для того чтобы рассчитать, какая сумма понадобится через (t) лет при годовой инфляции (i) %, чтобы приобрести то же количество товаров и услуг, необходимо воспользоваться формулой сложного процента:
где (S) — сумма с покупательной способностью, равной первоначальной сумме;
(P) — первоначальная сумма;
(i) — величина инфляции в процентах;
(t) — число лет.
Реальный и номинальный доход компании
Номинальный доход — доход компании, полученный в текущем году.
Реальный доход — доход, отражающий реальную покупательную способность денег, «очищенный» от инфляции.
Вычисление реального дохода проводят по формуле сложного дисконта:
где (P) — реальный доход компании;
(S) — номинальный доход компании;
(i) — инфляция в процентах;
(t) — число лет.
Понижающий коэффициент, на который делят номинальный доход компании, называется индексом инфляции.
Формула вычисления реального дохода через индекс инфляции принимает следующий вид:
где (P) — реальный доход компании;
(S) — номинальный доход компании;
В том случае, если периоды и уровень инфляции равны, индекс инфляции рассчитывается по следующей формуле:
где (I) — индекс инфляции (за несколько периодов);
(i) — уровень инфляции в процентах;
(t) — число периодов.
В том случае, если периоды инфляции равны, а уровни инфляции различаются, индекс инфляции рассчитывается по следующей формуле:
·(1+i2100)
·…
·(1+in100)
,
где (I) — индекс инфляции (за несколько периодов);
— уровень инфляции в процентах в n-ом периоде.
Рост реального дохода компании
Инфляция снижает покупательную способность денег, поэтому вводят понятия роста номинального и реального дохода.
Рост номинального дохода (темп прироста) за год рассчитывается как отношение дохода текущего года к доходу прошлого года.
−Дп.г.)Дп.г.
·100
,
где
Дт.г.
— доход, полученный в текущем году;
— доход, полученный в прошлом году.
Рост реального дохода за год — это темп прироста номинального дохода, уменьшенный на величину инфляции.
где
РД
— темпы прироста за год реального дохода компании;
— темпы прироста за год номинального дохода компании;
— темпы инфляции за год.
Только рост реального дохода может свидетельствовать о положительной динамике развития компании.

|
������ 19. ������� ����� � ��� ��������� ������ ��������� ������ ����������� ������������� ���� �������� ����� ��� �������� ��� ������������ ��� ��� ���� ����. ��������� ������, ������������ ������������ � ����������� ���, ������������ ��� �������������� ��� ���� � ����������� �� ����, ��� ���������� ��� ���� ��� ����������� ��� ����������. �� ���� ������� ��������� ����������� (��������) � �������� �����. ����� “��������” �������� � ���������� res, ����������� ����, �������, ����. �������� �����, ���� ��������� � ��������������� �������� �����, ������ �������� ������������, ���������� ���������� ������ �����������. ������ ������, ��� ����� ����� ���������������� ���� ���������� ��� �� �����, ������� �� ��� �� ���������� � ������������ �� ������ ��������������, � ��������� ���������� ������� ����������� �����. �������� ��� �����-���� ����� ������ ����������. �� ��� ������������ ������������ ����������� ������� ��������� ������������ �����: ��� �������� ����� ������ ���������� ��������, ��� � ��� ����������, �� �������� ������� ������-���� �������, ��� �� ����� ����� ���������������� ��� ���������. ������� ��, ����������� �� ������� �������� �������� �������� �����, ���������� ����������� ��������� ������ ��� ���������. � ������������ ������� �������, ����� ������� ������� ���������� ����� ������, � �������� �������������� ��������� ������ ������������ ������ ��������������� �������� — ��������� “������” ������ (��� �������� �������) � “�������”, � ������� ������������ ��������� (��� �������� ��������): � ���� ������ �� ����� ����� ������������ ���� � �� �� ����� ��� ����������� ������������ �������, �������� ���� ��� �������� �������� � ������� ��� �������. �� ���� ����� �� ����� ����� ��������� ������ ������������ ������ Y: ���� �� �� �� ����� �������� ������ �� ������� ����� ������, �� �� ����� �������� ����� �� ������ ���, � ����� �����������, �� ������� ��� �����������, ����������, ��������� ��� �����������, ����������, ���������� �� ��� ���� �������, �� ���������� ���������������� ������� ���������� ����������� ����� ������� �������. ����, �� ����� ��������� ������ ��������� ������. ���������� ������� ����� ������� ������. 1. ����� ���� ���� ���� �������� ��� ���������. � ���� ������ ����������� �������, ��� �������� ����� ��������� � ����� �� ���������, ��� � �����������: I�� = I��. ����, ��������, ����������� ����� ��������� � 1000 �� 2000 ���. � �����, �� ��� ������� ����������� ��� ����� �������, ��� ������ ��������� ������ ����� 2. ���, ����������, �� ��������, ��� ����������� ������� ������ ������� ������ � ��� ���� ������: ��������� ������ ������������� �� ����� ������� �� ��� ��������� ������, ����������� ������ ����� ��� �������, ������� ������� � ��������� �������, � ��� ���������� ������ ���� ���������� ������ (��. ������ 15, ������ 1). �� ������ ������, �� �������� �� ����� ������� ������� �����������, � � �������� ���� ��������� ��� �������������� ������ ������� ������� ���� ��� ������������ ������, ��������� ��� ������ ������� �������� �����������. 2. ��������, ��� ���� ����� ����������, �� ������� ���������� ����-������������ �����. ��� �������� ������ Y � ���� � �� ����� ������ ��� � ���������� q = Y/P. ����� ����������� ���������� ����� ������, ������� � ���� ������ � ���� �������� �����. ������� ������ ��������� ������
�� ��������� Y1/Y0— ��� ������ ������������ ������, � �1/�0 — ��� ������ ����, ������� �� ��������� I�. �� ������ � ��������� ������� ����� ����������������: ���� ��������� ������ ����������� ����������� ���������� � I�� ���, � ���� ��� � IP ��� �� ������� �� ��� ��� ����������� �������. 3. ����� ������ ������� ����������� ����� ������ ����. ���� ��� ���� � �������� ����� ���������� � ����� � ��� �� ���������, �� ��������� ����� �� �������� ������ ��������� � ����� ����������� ������� �������. ������ ��������� ������ ��� ���� ����� �������. ���� �� ��� ���� ���������� � ����� � ��� �� ��������� � � ���, � ����������� ����� — � b ���, �� ����� ��������� ����������� ��������� ������ � b/� ��� (��� �������������� �����), �. �. I�� = b/�. �������� b— ���, ��������, ������ ������������ ������; �������� � ���� ������ ������ ���� � �����������, � ��� ��� ��� �������� ���� � �� �� ��� ���� �������, ����������� �������, ��� � ����� �������� ������ ��� ����� �. ����� �������, �� � � ���� ������ �������� � ����������� (1) ��� ������� ��������� ������. � � ����� ������, ����� ���� � �������� ����� ���������� � ��������� ����������, ��������� (1) �������������� ������ ��������������� ��-�� ����������� � �������������� ��� ��������� �������������. �� �� ���� �� ����� �� ���������������, ��������� �� ���������� ������ ����������� ��������� ��������� ������ ������ � ����� ��� �� �������� ������ ����������� ����������� ��������� ���� ���, ����� ��� ���������� ��-�������. ����������� ������������ � ��������� ����������� ��� ��������� ��� � ������ (���. 1). ��� ����� � �������� ������� ������������ ��������� ������ �0, � �� �������� ����� �0 �� ������ ����������� U0. � ������� ������� �� ������������ � ����� �1, ������� �� ����� ��������� ����� B1. ��� ���� ����������� ��������� ������ �������������� ����� ������������, ���������������� ������ ����������� U1. ���. 1. ��������� ������ ��� ��������� ��������� ������ � ��� ��������� ��������� ������ ������������� ������� � ���������� ������������ �����������. ����� �� ���������� ������ ������ ��� ���������� ����� �� ���� ��������� ��������� ������? ��� ��� ������ ��������� ����� ������������ ������������ ���, ���������� ��������� ����� �0 ����������� ����� ���� �� ������� � ������ ����������� U1. �� ������� ����� ��������� ����������� ���������� �01, � ����� ������� — �01. ��� ������������� ����� ����, ������������� �� ���������� ������ �1, �� ����������� ��� ���������� ����� ������ �� ���� ��������� ������������ ������. ��������� ��������� ����� �01 � �1 ������������ ����������� ���� � ��� �� ������� ������������, �� ������ ��������� �� ���������� �������� ��������� ������. � ����� �� ����� �������� ��������� ��������� ������ ��� ��������� ��������� ������, ��������� ��� �������� � ����� �01. ���� q1, q2, …, qn— ������ ����������� ����, � P1, P2, …, Pn — ���� (�� ��������� �� ��������� ����������� � ������ ������), ��� ������� ��������� ������ �� �������� ���������
����������� ����� ��������� ����� ��������� ������ ������������ ������, � ��������� – ��������� ������, ���������������� ����� �01 ��� �������� �����. ����, � �������� �� ����� ������� ��������� ��������� ������ � ���������� �����������; ��� ���� �� ����������� ���������� ��� ������� ������������. �������������, ��������� �����-������������ ���� ��� ������ ������ �������� ����� ������� ������� ��� �������� �����, ���� ������������ ����� ���� ����� � ������������ � ������� �����������. ���� �� �� � ���� ���������� � ����������� �������, �� � ����������� ����� ������ �� ������� �������� ������� ������ ��������� ������. ���. 2 ������������ ��������� ��� �� ��� ������ � ��������������� ������������, ������������� ��� ������ ����������� � ��������������� ��� �������. ���. 2. �� ������� ��������� ����� ����������� ������ � �����. � ��� ������ �����. ���� � �� �� ��������� ��������� � ��� ��������� ������������� ��� ������ � ��������������� ��� �����. ���. 3. ����������� �������������� ����������� �� ����� �� �� ��������������� ���������� (2) �����������? ���� ����������� �� ����������� ����� ������������ � ����� ����, �� ���� ��������� �� � ����� ���������. ��������� ����������� (��������, ���������) ����� ������������� ����� �0 � �1, ��������������� �������� � �������� � ������� ��������, �� �� �� ����� “�������” ����� �01. ���, ��� ����� ������� ���������� �� ����������� � �������� � ������� ��������, ���������� �� ���. 3: ��� ��������� �����, ������������ ����������� ������� � ������, � ������ �������. �� ������� ����� �0 ����� ���� ����� ��������� �����, ��� ��������������� �� ���������� ��������� ������. �������� ������ ������������ �������, �� ��������� ��������� ����������� ������������� �������� ������� (2) � �������� ����� �01 ������ �1:
����� ��������� ������������� ������� �� ������� ������ �1 � �������� �����; �� ��������� ������, ��� ��������� � ������� (2), ��� ��� ��������� (3) ���� ���������� �� ��������� � (2) �������� ������� ��������� ������. ������������ �������������� ��������� � �������������� ���������� �����������. ��������� ������ � ����������� ������� ���. ����� �� ����� ������������ ��� �� ������, ������� �������� ��� ���������� ������ ��������� ������. ���� �� ��� ���� ���������� � ����� � ��� �� ���������, �� ������ ��� �������� �� � �������� ������ ���� � �����������. ��������� ����� � ���. 1. ������� �� �������� ��������� ����� �0 � ����� �01 (� �������������� � ����� E01) ��� �� ��������� � ��� ��������� ��������� ������, ������ �� ���� ����������������� ��������� ���. ���� �� ������ �� ��� ���������� � � ���, ������� �� ������� �������, ��������������� ����� �01, ��������� ��
�� ����� �01 ������� ���� ������, ��� ��� ������������ �� ���������� ����� E1 — ����� ������ ����������� ��� ����������� ��������� ��� � ������������ �������� ������. ������� ���������������� ��������� ���, ������������� �� ���������� ������������ �� ���������, ������ ������������� �����������
� �������� ������������ �, ���������� ����� �������, �� ����� ������� �� ������ ��� ��� ������� �����������:
� ��� ��, ��� ��� ����������� ������� ��������� ������, ��� ������������ �������� ��� �������� �� � ���� ��������� �������� ������������� ����� �01 ����������� ������ �1:
�������� ��������� (4) � (5) � ����������� ��������, ����� �� ��� ���� ������� �������� ��� ������� ���. ����� ���������, ��� ��� ������������� ��������� (2) ��� ������� ��������� ������ � (4) ��� ������� ��� ��������� (1) �������� ������������:
����� ��� �� ��������� (3) � (5) ����������� � �������� (1). �� ��� ��� �� ������������� ������ ��������� ������ ���������� �����������, � ����� ������ ��� � ����� ������ ���������� �����������. ������ ����������� � �������� ����� ��, ���� ���� ����� ������� � ��������� ������ � ����� �� ��������� ������, ���������� ��� ���� ��� �������. ������ �� ��� ����� �������� � ����� ��� ���� ����� ������� — �������� ���� �� ��� ������, — � ������ ������� ������ ����� — �����, ��������������� ��������, �����, �����������. �� �������������� ������ ������������ �� ���������� �������������, � �� �������������� – ���������� � ����� ��� ������������� ��� ��������. ������� (3) � (5) ����� ���� ����� ���������� � �� ������������ ������������. ���������� ���� �������� � ��� �������������� ������ ����������� q1, q2, …, qn ��������� �������� Q1, Q2, …, Qn:
��� �� ����� �� ���� ���������� ������������? � ���������� ������������ ����� ��������� �������� ���������� �������. ����������� ����� ����� ������� �������� ������������� ���� �������� �� �������� ��� ��������� ������������. � ���� ������ ����� ��������, ��� ��� �������� ����� ��� ���� ��������� ��������� ��������� �������� ������� � ���. ��������� �������������� ������ ������� ������������� �������������, �� ���������� ����� ������, – �����, ��� �������� ����� ��� ���� �� ��� ��������������� ������, – ��������� ������, � �� ������� ������������� �� ��������� ������������� � ������������ ���������. ���� �� ����������� ��������������� � ��������� �������� ������. |








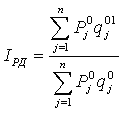 ,
,
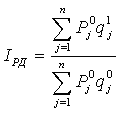 ,
,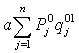
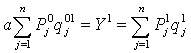 ,
,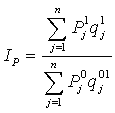 ,
,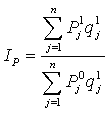 ,
,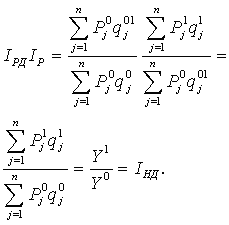 ,
,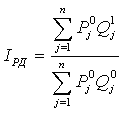 ;
;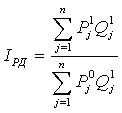 . (8)
. (8)
 ,
,


 ,
,

 ,
,
 ,
,
 ,
,
 ,
,
 ;
;
 .
.
