Индивидуальный индекс цен
Индивидуальный
индекс цен определяется
как отношение цены отдельного товара
в отчетном периоде к цене его в базисном
периоде, то есть по формуле: ![]() .
.
Разность между числителем и знаменателем
его покажет абсолютное изменение цены
за единицу товара в рублях ![]() .
.
Рассчитаем
индивидуальные индексы цен (9):
По
телевизорам: ![]() или
или
110% и ![]() тыс.руб,
тыс.руб,
т.е. цена телевизора увеличилась на 0,3
тыс.руб., или на 10% (110-100).
По
видеомагнитофомам: ![]() или 90% и
или 90% и ![]() тыс.руб
тыс.руб
т.е. цена видеомагнитофона снизилась
на 0,2 тыс.руб или на 10%.
Индивидуальный индекс товарооборота
Индивидуальный
индекс товарооборота характеризует
изменение товарооборота по одному
товару и строится как отношение
товарооборота отчетного периода ![]() к
к
товарообороту базисного периода ![]() ,
,
то есть по формуле:
![]()
Разница
между числителем и знаменателем его
покажет абсолютное изменение товарооборота
в рублях за счет двух фактров: изменения
количества проданного товара и изменения
цены этого товара, то есть ![]()
Рассчитаем
индивидуальные индексы товарооборота
(10):
По
телевизорам: ![]() или 99% и
или 99% и ![]() млн.руб,
млн.руб,
то есть товарооборот по телевизорам
стал меньше на 12 млн.руб, или на 1%
(99-100%).
По
видеомагнитофонам: ![]() или 112.5% и
или 112.5% и ![]() млн.руб,
млн.руб,
то есть товарооборот по видеомагнитофонам
увеличился на 50 млн.руб. или на 12,5%
(12,5-100%).
Рассмотренные
нами индивидуальные
индексы взаимосвязаны между собой так
же, как сами индексируемые показатели:
индекс товарооборота равен произведению
индекса физического объема товарооборота
на идекс цен, то есть ![]()
Проверим
взаимосвязь исчисленных индивидуальных
индексов:
-
По
телевизорам: 0,99 = 0,9*1,1 -
По
видеомагнитофонам: 1,125 = 1,25*0,9
Кроме
того, полученные данные позволяют
рассчитать абсолютные
показатели изменения товарооборота по
отдельным товарам за счет отдельных
факторов.
Так,
по телевизорам общее изменение
товарооборота составило: ![]() млн.руб,
млн.руб,
то есть товарооборот по телевизорам в
отчетном периоде по сравнению с базисным
стал меньше на 12 млн.руб. Эта величина
может быть разложена на две:
1.
за счет изменения количества проданных
товаров: ![]() млн.руб,
млн.руб,
то есть за счет уменьшения количества
проданных телевизоров на 40 тыс.штук
товарооборот стал меньше на 120 млн.руб.
2.
за счет изменения цен: ![]() млн.руб,
млн.руб,
то есть за счет роста цены одного
телевизора на 0,3 тыс.руб товарооборот
возрос на 108 млн.руб.
Проверим
взаимосвязь исчисленных показателей: ![]() млн.руб.
млн.руб.
По
видеомагнитофонам имеем изменение
товарооборота на 50 млн.руб.
1.
за счет изменения количества проданных
товаров: ![]()
2.
за счет изменения цен: ![]()
Товарооборот
по видеомагнитофонам увеличился на 50
млн.руб. За счет увеличения количества
проданных видеомагнитофонов на 50
тыс.штук товарооборот возрос на 100
млн.руб, а за счет снижения цен на
видеомагнитофоны на 0,2 тыс.руб за штуку
стал меньше на 50 млн.руб.
Общие индексы
большинство
изучаемых статистикой общественных
явлений и процессов состоят из многих
элементов, которые могут быть как
однородными, так и неоднородными. Однородные
явления можно непосредственно суммировать
и исчислять индексы, характеризующие
изменение не одного элемента, а группы
элементов или всей совокупности в целом.
Такие индексы называются общими
индексами. Так,
можно суммировать количество
проданных однородных
товаров по
группе фирм и исчислить общий
индекс физического объема товарооборотапо
формуле:
![]() ,
,
где знак ![]() означает
означает
суммирование данных о количестве одного
товара по нескольким фирмам. Можно
суммировать товарооборот по нескольким
товарам и исчислять общий индекс
товарооборота по формуле ![]() ,
,
где знак ![]() означает
означает
суммирование товарооборота по группе
товаров.
Если
же отдельные элементы явления неоднородны,
то непосредственное суммирование их
невозможно или бессмысленно и тогда
необходимо привести их к сопоставимому
виду. Все товары имеют стоимость, а
стоимости товаров можно суммировать.
Переход от натуральных показателей к
стоимостным позволяет преодолеть
несуммарность натурально-вещественных
элементов совокупности. Но изменение
стоимости товаров обусловлено совместным
изменением двух факторов — количества
товаров и цен на них, а нам необходимо
определить изменение каждого из этих
факторов в отдельности. Для изучения
изменения одного фактора необходимо
абстрагироваться от изменения второго,
взаимосвязанного с ним фактора и
построить общий индекс в агрегатной
форме.
Так, агрегатный
индекс физического объема товарооборота должен
показать изменение количества
проданныхразнородных
товаров,
поэтому в числителе его берется отчетное
количество товаров (q1),
а в знаменателе — базисное (q0),
т.е. индексируемый показатель изменяется,
а взвешивание производится в одних и
тех же ценах базисного период (p0):
![]() .
.
В
числителе этого индекса — условная
величина товарооборота отчетного
периода в ценах базисного периода, в
знаменателе — реальная величина
товарооборота базисного периода.
Разность между числителем и знаменателем
индекса покажет абсолютное изменение
товарооборота за счет изменения
физического объема товарооборота:
![]()
Рассчитаем агрегатный
индекс физического объема товарооборота по
данным нашего примера:
![]() или 98,75% и
или 98,75% и ![]() млн.руб.,
млн.руб.,
то есть количество проданных магазином
товаров в среднем стало меньше на 1,25%
(98,75 — 100%), что привело к уменьшению
товарооборота на 20 млн.руб.
Агрегатные
индексы качественных показателей
строятся при весах — объемных показателях
отчетного периода. Так, агрегатный
индекс цен по формуле немецкого экономиста
Э.Пааше:
![]()
В
числителе индекса — товарооборот
отчетного периода, в знаменателе —
товарооборот отчетного периода в ценах
базисного периода, а разность между
ними характеризует: с позиции продавца
— абсолютное изменение товарооборота
за счет изменения цен, с позиции покупателя
— экономию (перерасход) населения от
изменения цен на товары: ![]() .
.
Рассчитаем
агрегатный индекс цен по данным нашего
примера:
![]() или 103.7% и
или 103.7% и ![]() млн.руб,
млн.руб,
то есть в среднем цены на товары возрасли
на 3,7%, что привело к росту товарооборота
на 58 млн.руб.
В
качестве весов в индексах качественных
показателей могут быть использованы
не только абсолютные объемные показатели,
но и показатели их структуры, то есть
доли.
В
статистической практике используется
также индекс цен, построенный с базисными
весами по формуле Э.Ласпейреса:
![]()
Агрегатный
индекс товарооборота исчисляется по
формуле:
![]() или 102.4%.
или 102.4%.
Разность между числителем и знаменателем
этого индекса характеризует абсолютное
изменение товарооборота за счет двух
фактров: изменения количества проданных
товаров и цен на них: ![]() млн.руб,
млн.руб,
то есть товарообот в отчетном периоде
по сравнению с базисным увеличился на
38 млн.руб. или на 2,4%.
Агрегатные
индексы объемных и качественных
показателей, построенные с различными
весами, взаимосвязаны между собой так
же, как индивидуальные индексы:
произведение агрегатного индекса
физического объема товарообора на
агрегатный индекс цен, дает агрегатный
индекс товарооборота:
![]()
Мы
получили систему взаимосвязанных
агрегатных индексов, каждый из которых
позволяет определить изменение
индексируемого показателя в относительном
выражении (%). Кроме того, по этим индексам
можно определить изменение обобщающего
показателя — товарооборота за счет
отдельных факторов в абсолютном выражении
как разность между числителем и
знаменателем соответствующего индекса.
Абсолютные показатели изменения
товарооборота за счет отдельных факторов
взаимосвязаны следующим образом.
![]()
Проверим
взаимосвязь показателей, исчисленных
по данным нашего примера:
1.
аграгатных индексов: 1,024 = 0,975*1,037
2.
абсолютных изменений: +38 млн.руб = — 20 +
58 млн.руб.
Аналогичным
образом строятся системы агрегатных
индексов других экономических
показателей.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
22.02.201663.49 Кб91.doc
- #
22.02.2016240.09 Кб221.docx
- #
- #
- #
- #
- #
- #
- #
- #
- #
По данным Федеральной службы государственной статистики о средних ценах на уголь и объемах его производства в РФ за три года:
| Год | Цена за 1 т, руб. | Произведено, тыс. т. |
|---|---|---|
| 2011 | 1005 | 336 293 |
| 2012 | 955 | 356 781 |
| 2013 | 962 | 351 232 |
при условии 100 %-й реализации угля в каждом году, определите цепные и базисные индивидуальные индексы цен, физического объема реализации и товарооборота. Проверьте взаимосвязь цепных и базисных индексов.
Решение:
1. а) Цепные индивидуальные индексы цен на уголь вычисляются с меняющейся от индекса к индексу базой сравнения:
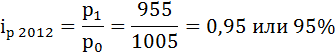
где
р1 – цена угля в 2012 году (текущем),
р0 – цена угля в 2011 году (базисном).
В 2012 году в Российской Федерации наблюдается снижение цен на уголь по сравнению с 2011 годом на 5%.
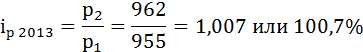
где
р2 – цена угля в 2013 году (текущем),
р1 – цена угля в 2012 году (базисном).
В 2013 году в РФ цены на уголь по сравнению с 2012 годом возросли на 0,7%.
б) Базисные индивидуальные индексы цен на уголь вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода:
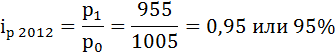
где
р1 – цена угля в 2012 году (текущем),
р0 – цена угля в 2011 году (базисном).
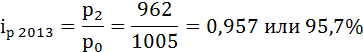
где
р2 – цена угля в 2013 году (текущем),
р0 – цена угля в 2011 году (базисном).
Проверим взаимосвязь цепных индексов.
Если последовательно перемножить цепные индексы, можно получить конечный базисный индекс:
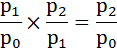
И действительно:
0,95 × 1,007 = 0,957
Проверим взаимосвязь базисных индексов:
Зная последовательные значения базисных индексов, легко рассчитать на их основе конечный цепной индекс:
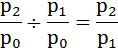
0,957 / 0,95 = 1,007
2. а) Цепные индивидуальные индексы физического объема реализации угля вычисляются, аналогично. То есть с меняющейся от индекса к индексу базой сравнения:
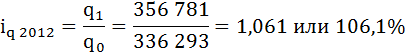
где
q1 – физический объем реализации угля в 2012 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
В 2012 году в РФ наблюдается рост физического объема реализации угля по сравнению с 2011 годом на 6,1%.
В 2013 году в РФ физический объем реализации угля по сравнению с 2012 годом снизился на 1,6%:
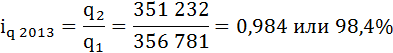
где
q2 – физический объем реализации угля в 2013 году (текущем),
q1 – физический объем реализации угля в 2012 году (базисном).
б) Базисные индивидуальные индексы физического объёма на уголь вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода.
Базисный индекс 2012 года совпадает с величиной цепного индекса 2012 года:
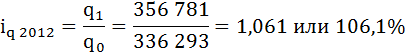
где
q1 – физический объем реализации угля в 2012 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
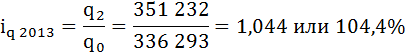
где
q2 – физический объем реализации угля в 2013 году (текущем),
q0 – физический объем реализации угля в 2011 году (базисном).
Физический объем реализации угля в 2013 году вырос на 4,4% по сравнению с 2011 годом.
Проверим взаимосвязь цепных индексов.
Если последовательно перемножить цепные индексы, можно получить конечный базисный индекс:
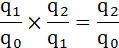
1,061 × 0,984 = 1,044
Проверим взаимосвязь базисных индексов:
Зная последовательные значения базисных индексов, легко рассчитать на их основе конечный цепной индекс:
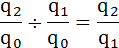
1,044 / 1,061 = 0,984
3. а) Рассчитаем цепные индивидуальные индексы товарооборота:
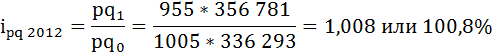
где
рq1 – товарооборот угля в 2012 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
В 2012 году в РФ наблюдается рост товарооборота угля по сравнению с 2011 годом на 0,8%.
В 2013 году в РФ товарооборот угля по сравнению с 2012 годом упал на 0,8%:
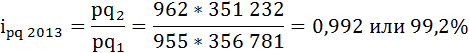
где
рq2 – товарооборот угля в 2013 году (текущем),
рq1 – товарооборот угля в 2012 году (базисном).
б) Базисные индивидуальные индексы товарооборота угля вычисляются с постоянной базой сравнения, то есть в знаменателе всех индексов находится индексируемая величина базисного периода.
Базисный индекс товарооборота 2012 года совпадает с величиной цепного индекса товарооборота 2012 года:
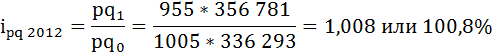
где
рq1 – товарооборот угля в 2012 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
Базисный индекс товарооборота в 2013 году будет равен:
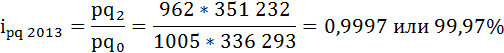
где
рq2 – товарооборот угля в 2013 году (текущем),
рq0 – товарооборот угля в 2011 году (базисном).
Товарооборот угля в 2013 году по сравнению с 2011 годом снизился на 0,03%.
Проверим взаимосвязь цепных индексов товарооборота.
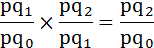
Взаимосвязь наблюдается:
1,008 × 0,992 = 0,9997
Проверим взаимосвязь базисных индексов товарооборота:
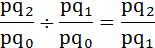
0,9997/ 1,008 = 0,992.
Индивидуальный индекс физического объема товарооборота
Так, для изучения изменения количества проданных товаров (физического объема продаж) следует построить индивидуальный индекс физического объема товарооборота как отношение количества товара одного вида, проданного в отчетном периоде, к количеству того же товара, проданного в базисном периоде (iq = q1 / q0 ). Поскольку базисный уровень индексируемого показателя приравнивается к 1 или 100%, то разность между полученным индексом и 1 или 100% характерзиует относительную величину изменения количества проданного товара. По этому индексу можно определить и абсолютное изменение количества проданного товара в натуральном выражении как разность между числителем и знаменателем индекса .
Произведем расчет индивидуальных индексов физического объема товарооборота.
По телевизорам: или 90% и рассчитываем
тыс.шт, то есть в отчетном периоде по сравнению с базисным было продано телевизоров на 40 тыс.штук, или на 10% меньше, чем в базисном году.
По видеомагнитофонам: , и рассчитываем
тыс.шт, то есть количество проданных видеомагнитофонов возрасло на 50 тыс. штук или на 25%.
Индивидуальный индекс цен
Индивидуальный индекс цен определяется как отношение цены отдельного товара в отчетном периоде к цене его в базисном периоде, то есть по формуле: . Разность между числителем и знаменателем его покажет абсолютное изменение цены за единицу товара в рублях
.
Рассчитаем индивидуальные индексы цен (9):
По телевизорам: или 110% и
тыс.руб, т.е. цена телевизора увеличилась на 0,3 тыс.руб., или на 10% (110-100).
По видеомагнитофомам: или 90% и
тыс.руб т.е. цена видеомагнитофона снизилась на 0,2 тыс.руб или на 10%.
Индивидуальный индекс товарооборота
Индивидуальный индекс товарооборота характеризует изменение товарооборота по одному товару и строится как отношение товарооборота отчетного периода к товарообороту базисного периода
, то есть по формуле:
Разница между числителем и знаменателем его покажет абсолютное изменение товарооборота в рублях за счет двух фактров: изменения количества проданного товара и изменения цены этого товара, то есть
Рассчитаем индивидуальные индексы товарооборота (10):
По телевизорам: или 99% и
млн.руб, то есть товарооборот по телевизорам стал меньше на 12 млн.руб, или на 1% (99-100%).
По видеомагнитофонам: или 112.5% и
млн.руб, то есть товарооборот по видеомагнитофонам увеличился на 50 млн.руб. или на 12,5% (12,5-100%).
Рассмотренные нами индивидуальные индексы взаимосвязаны между собой так же, как сами индексируемые показатели: индекс товарооборота равен произведению индекса физического объема товарооборота на идекс цен, то есть
Проверим взаимосвязь исчисленных индивидуальных индексов:
- По телевизорам: 0,99 = 0,9*1,1
- По видеомагнитофонам: 1,125 = 1,25*0,9
Кроме того, полученные данные позволяют рассчитать абсолютные показатели изменения товарооборота по отдельным товарам за счет отдельных факторов.
Так, по телевизорам общее изменение товарооборота составило: млн.руб, то есть товарооборот по телевизорам в отчетном периоде по сравнению с базисным стал меньше на 12 млн.руб. Эта величина может быть разложена на две:
1. за счет изменения количества проданных товаров: млн.руб, то есть за счет уменьшения количества проданных телевизоров на 40 тыс.штук товарооборот стал меньше на 120 млн.руб.
2. за счет изменения цен: млн.руб, то есть за счет роста цены одного телевизора на 0,3 тыс.руб товарооборот возрос на 108 млн.руб.
Проверим взаимосвязь исчисленных показателей: млн.руб.
По видеомагнитофонам имеем изменение товарооборота на 50 млн.руб.
1. за счет изменения количества проданных товаров:
2. за счет изменения цен:
Товарооборот по видеомагнитофонам увеличился на 50 млн.руб. За счет увеличения количества проданных видеомагнитофонов на 50 тыс.штук товарооборот возрос на 100 млн.руб, а за счет снижения цен на видеомагнитофоны на 0,2 тыс.руб за штуку стал меньше на 50 млн.руб.
Пример 7.1. На основе данных о реализации товаров определите:
1) Индивидуальные индексы цен и физического объема продаж.
2) Общий индекс цен.
3) Общий индекс товарооборота в сопоставимых ценах.
4) Общий индекс товарооборота в действующих ценах.
5) Продемонстрируйте взаимосвязь исчисленных общих индексов.
6) Разложите на факторы изменение товарооборота за счет изменения цен и физического объема продаж.

Решение.
1) Индивидуальные индексы цен:
IpA=P1/P0=48/40=1,20 (рост на 20%);
IpA=150/120=1,25 (рост на 25%).
Индивидуальные индексы физического объема:
IqA= Q1/Q0=550/500=1,10 (рост на 10%)
IqA=70/80=0,875 (снижение на 12,5%)
2) Общий индекс цен

3) Общий индекс товарооборота в сопоставимых ценах

4) Общий индекс товарооборота в действующих ценах

5) Взаимосвязь исчисленных общих индексов.
![]()
6) Абсолютный прирост товарооборота за счет фактора изменения цен
![]()
Абсолютный прирост товарооборота за счет фактора изменения физического объема товарооборота
![]()
Абсолютный прирост товарооборота за счет совокупного действия факторов

Выводы. Товарооборот в действующих ценах увеличился на 24,66% за счет повышения цен 21,38% и за счет роста физического объема продаж на 2,7%.
Товарооборот в действующих ценах увеличился на 7300 руб., в том числе на 6500 руб. за счет повышения цен и на 800 руб. за счет роста физического объема продаж.
Пример 7.2. На основе данных о реализации товаров определите:
1) Общий индекс цен.
2) Общий индекс товарооборота в сопоставимых ценах.
3) Общий индекс товарооборота в действующих ценах.
4) Разложите на факторы изменение товарооборота за счет изменения цен и физического объема продаж.

Решение.
1) Так как в исходных данных отсутствует информация о количестве проданных товаров, но имеются данные о динамике цен, поэтому необходимо использовать общий индекс цен в среднегармонической форме.

2) Общий индекс товарооборота в сопоставимых ценах
 .
.
3) Общий индекс товарооборота в действующих ценах

Взаимосвязь исчисленных общих индексов
![]()
4) Абсолютный прирост товарооборота за счет фактора изменения цен
![]()
Абсолютный прирост товарооборота за счет фактора изменения физического объема товарооборота
![]()
Абсолютный прирост товарооборота за счет совокупного действия факторов

Пример 7.3. На основе данных о реализации товаров определите:
1) Общий индекс цен.
2) Общий индекс товарооборота в сопоставимых ценах.
3) Общий индекс товарооборота в действующих ценах.
4) Разложите на факторы изменение товарооборота за счет изменения цен и физического объема продаж.

Решение.
1) Так как в исходных данных отсутствует информация о количестве проданных товаров, но имеются данные о динамике физического объема продаж, поэтому необходимо использовать общий индекс физического объема товарооборота (в сопоставимых ценах) в среднеарифметической форме. Отсюда общий индекс цен (7.13)
 .
.
2) Общий индекс товарооборота в сопоставимых ценах в среднеарифметической форме.
 .
.
Результаты для пунктов 3 и 4 данного примера полностью совпадают с соответствующими пунктами примера 7.2.
Пример 7.4. Имеются данные о производстве однородной продукции на двух предприятиях. Определите изменение средней себестоимости:
1) общее;
2) за счет изменения себестоимости единицы продукции;
3) за счет изменения структуры выпуска продукции;
4) показать взаимосвязь исчисленных индексов.

Решение.
На изменение средней себестоимости влияют два фактора: а) себестоимость единицы продукции на каждом предприятии и б) структура выпуска продукции.
1) Для анализа изменения средней себестоимости Z необходимо рассчитать средние себестоимости за 2009 и 2010 гг.
 Руб.,
Руб.,
 Руб.
Руб.
Тогда индекс средней себестоимости (индекс переменного состава).

Таким образом, средняя себестоимость снизилась на 1,21% за счет совместного действия двух факторов. В абсолютном выражении себестоимость снизилась на 54 коп. (![]() ).
).
2) Изменение средней себестоимости за счет изменения себестоимости единицы продукции позволяет учесть индекс себестоимости постоянного состава

Таким образом, средняя себестоимость увеличилась на 3,29% за счет изменения себестоимости единицы продукции на каждом предприятии. В абсолютном выражении себестоимость возросла на 1,40 руб. (![]() ).
).
3) Изменение структуры выпуска продукции (т. е. изменение доли предприятий в общем выпуске продукции) учитывает индекс структурных сдвигов.

Таким образом, средняя себестоимость уменьшилась на 4,35% за счет изменения структуры выпуска продукции. В абсолютном выражении себестоимость уменьшилась на 1,94 руб. (![]() ).
).
4) Взаимосвязь системы индексов:
![]() =1,0329×0,9565= 0,9879.
=1,0329×0,9565= 0,9879.
Взаимосвязь абсолютных изменений:
![]() =1,40+(–1,94)=–0,54.
=1,40+(–1,94)=–0,54.
E Обратите внимание – по условиям примера себестоимость продукции возросла на ВСЕХ предприятиях, но средняя себестоимость снизилась на 54 коп.!
Пример 7.5. На основе данных о реализации товаров рассчитайте индексы Дюто, Карли, Джевонса, Ласпейреса, Пааше, Эджворта-Маршалла, Уолша, Фишера, а также геометрические индексы Ласпейреса, Пааше и Торнквиста.

Решение.
1) Индекс цен Дюто  .
.
2) Индекс цен Карли 
3) Индекс цен Джевонса 
4) Индекс цен Ласпейреса 
5) Индекс цен Пааше 
6) Индекс цен Эджворта-Маршалла 
7) Индекс цен Уолша 
8) Индекс цен Фишера ![]() .
.
9) Геометрический индекс цен Ласпейреса

10) Геометрический индекс цен Пааше

11) Индекс цен Торнквиста

Таблица 7.1. Расчет общих индексов цен
|
Товар |
P0 |
Q0 |
P1 |
Q1 |
|
P0×Q0 |
P0×Q1 |
P1×Q0 |
P1×Q1 |
|
А |
60 |
80 |
75 |
66 |
1,25 |
4800 |
3960 |
6000 |
4950 |
|
Б |
25 |
120 |
27 |
180 |
1,08 |
3000 |
4500 |
3240 |
4860 |
|
В |
5 |
220 |
6 |
300 |
1,20 |
1100 |
1500 |
1320 |
1800 |
|
Итого |
90 |
108 |
8900 |
9960 |
10560 |
11610 |
Продолжение таблицы 7.1
|
Товар |
|
P0×Q |
P1×Q |
|
P0×QГеом |
P1×QГеом |
|
А |
73 |
4380 |
5475 |
72,66 |
4359,82 |
5449,77 |
|
Б |
150 |
3750 |
4050 |
146,97 |
3674,24 |
3968,17 |
|
В |
260 |
1300 |
1560 |
256,90 |
1284,52 |
1541,43 |
|
Итого |
9430 |
11085 |
9318,57 |
10959,37 |
Окончание таблицы 7.1
|
Товар |
|
|
|
|
А |
4800/8900=0,53933 |
4950/11610=0,42636 |
0,48284 |
|
Б |
3000/8900=0,33707 |
4860/11610=0,41860 |
0,37784 |
|
В |
1100/8900=0,12360 |
1800/11610=0,15504 |
0,13932 |
|
Итого |
1,00000 |
1,00000 |
1,00000 |
| < Предыдущая | Следующая > |
|---|



