В этой статье мы рассмотрим, что такое правило Ленца и какого его практическое применение. Это правило позволяет быстро определить направление индукционного тока. На самом деле, правило Ленца тесно связано с принципом сохранения энергии — об этом также читайте в этой статье.

Формулировка
Правило Ленца обычно формулируется следующим образом:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
Википедия
Давайте расшифруем это предложение.
Давайте расшифруем это предложение. Давайте начнем с причины. Причиной протекания индукционного тока является изменяющийся поток магнитной индукции B через поверхность, охватываемую контуром, в котором должен протекать электрический ток.
Противодействие причине здесь заключается в том, что когда поток увеличивается, магнитное поле Bind, создаваемое индукционным током, направлено так, чтобы уменьшить поток. И наоборот, когда поток уменьшается, индуцированное магнитное поле направлено так, чтобы усилить поток. В общем, если поле B перпендикулярно плоской поверхности, охватывающей замкнутый проводник, то
Когда ФB уменьшается, то Вind параллельно В.
Когда ФB увеличивается, то Bind антипараллельно B.
В более общем случае необходимо задать условие для углов между этими векторами.
Как только мы установили, как направлен вектор магнитной индукции Bind (внутри контура), мы должны связать индукционный ток с этим вектором и определить его направление.
Пример правила Ленца в действии
Теперь мы покажем правило Ленца в действии; вот конкретный пример.
В магнитном поле, создаваемом прямолинейным проводником с током, имеется круговой контур (кольцо), лежащий в одной плоскости с проводником (рис. 2а.). Ток в прямолинейном проводнике течет вверх. В каком направлении будет течь электрический ток в кольце, если мы прижмем его к проводнику?

Ток в прямолинейном проводнике создает вокруг себя магнитное поле. Для определения направления вектора магнитной индукции в кольце мы используем хорошо известный метод правой руки. Мы располагаем большой палец так, как направлен электрический ток, а пальцы покажут нам магнитное поле, «оборачивающееся» вокруг этого электрического тока. Справа от проводника, где находится кольцо, линии поля идут «внутрь», как показано на рис. 2б.

Сближение кольца вызывает увеличение потока магнитного поля, проникающего через кольцо (увеличивается значение магнитной индукции B). Согласно правилу Ленца, ток в кольце должен протекать таким образом, чтобы вектор магнитного поля Bind, создаваемого этим током, был направлен противоположно вектору, вызывающему явление индукции B. То есть, вектор Bind направлен «в нашу сторону». (рис. 2в).

Снова применим правило правой руки. На этот раз мы укажем большим пальцем вектор индукции Bind, а остальные пальцы покажут нам направление индукционного тока. Он будет протекать против часовой стрелки.
Правило Ленца и закон сохранения энергии
То, что «скрывается» под правилом Ленца — это фундаментальный принцип сохранения энергии в физике. Вы узнаете об этом, прочитав данный подраздел.
Посмотрите на следующую экспериментальную установку (см. рисунок 3).
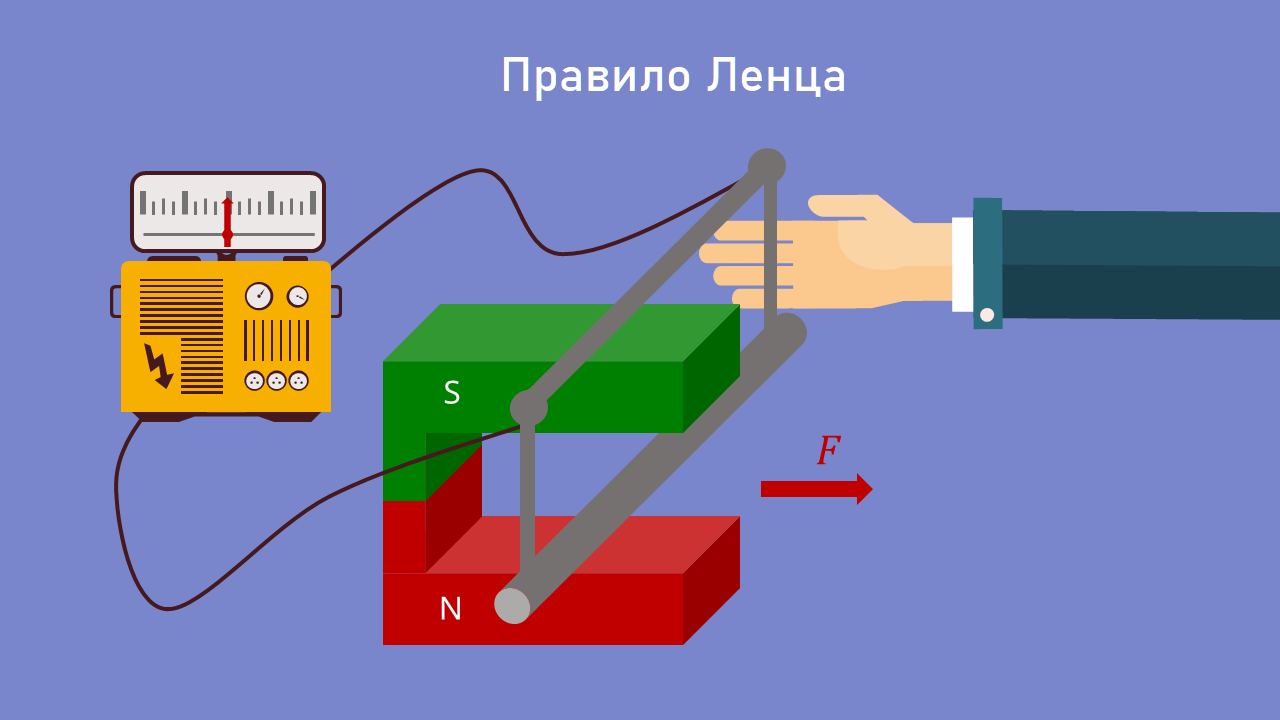
Для эксперимента подвесьте качели проводника в магнитном поле подковообразного магнита. Подковообразный магнит располагается так, чтобы северный полюс находился внизу, а южный — вверху. Вы подключаете проводник к амперметру вне магнитного поля, поэтому во всей цепи нет источника.
В эксперименте мы теперь перемещаем качели проводника в направлении, перпендикулярном силовым линиям магнитного поля, в нашем случае «из подковообразного магнита». Для перемещения качающегося проводника нужна сила F. Когда частицы движутся в магнитном поле, действует сила Лоренца, происходит разделение зарядов, а значит, и возникает индукционный ток. Это можно наблюдать по отклонению стрелки амперметра.
Для определения направления индукционного тока применяется правило левой руки. Большой палец указывает направление, в котором электроны перемещаются под действием силы F, т.е. «из подковы». Ваш указательный палец указывает направление магнитного поля, от северного к южному полюсу. Наконец, средний палец указывает направление, в котором электроны притягиваются силой Лоренца. На конце проводника, в сторону которого указывает ваш средний палец, образуется избыток электронов и это приводит к изменению направления тока.
Однако, в силу правила Ленца, точно в тот же момент должна действовать противодействующая сила F‘, направленная в противоположную сторону от причины F. Эта противодействующая сила создается индукционным током, который, так сказать, пытается восстановить исходное состояние.
Вы можете еще раз проверить направление силы F‘ с помощью правила левой руки. На этот раз большой палец указывает направление движения электронов. Итак, в проводнике, который перемещается под действием силы F внутри магнита , большой палец направлен в плоскость рисунка, а указательный палец снова направлен от северного полюса к южному. Затем средний палец указывает направление силы F’. Это направление согласуется с правилом Ленца и действует в направлении, противоположном направлению движения проводника. Чтобы проиллюстрировать это, мы провели эти рассуждения одно за другим. В реальном эксперименте, однако, все это происходит параллельно.
Можно также сравнить правило Ленца с поведением детей (аналог индукционного тока). Когда их родители (аналог причины) говорят им что-то, они сначала хотят сделать прямо противоположное. Если вы будете помнить об этой мнемонике, вы гарантированно не забудете правило Ленца.
Сохранение энергии для индукции также может быть соблюдено только с помощью правила Ленца.
Чтобы проверить это, вы можете провести следующий мысленный эксперимент. Если бы сила из F‘ была направлена в противоположную сторону, то есть равна силе F, раскачивание качелей ускорялось бы все больше и больше. И это без добавления дополнительной энергии извне. Таким образом, можно было бы создать вечный двигатель, что противоречит закону сохранения энергии.
Применение
Правило Ленца необходимо для многих применений в технике. Например, в вихретоковом тормозе. Этот тормоз не изнашивается, поскольку отсутствует трение. Тормозная сила генерируется магнитными полями. Например, такие тормоза есть у поездов и грузовиков. Электродвигатели также работают по этому принципу.
Правило Ленца защитит вас, даже если в вашу машину ударит молния. Клетка Фарадея также основана на этом принципе.
Все металлодетекторы, которые вы знаете по аэропортам или магазинам, работают одинаково. Они генерируют магнитное поле с помощью катушки. Если в магнитном поле находится металлический предмет, в нем индуцируются вихревые токи. Согласно правилу Ленца, эти токи направлены таким образом, что противодействуют причине возникновения тока. Поэтому магнитное поле детектора становится слабее. Это также уменьшает ток в металлодетекторе, эта разница измеряется, что приводит, например, к сигналу тревоги.
Металлодетекторы также используются в некоторых светофорах, только здесь катушка расположена в асфальте под машинами. Таким образом, светофор, так сказать, замечает, что автомобиль ждет, и по возможности переключает его на зеленый. Как видите, правило Ленца важно для многих областей электротехники, а также в повседневной жизни.
Список использованной литературы
- Мякишев Г. Я. Физика: Учеб. для 11 кл. общеобразоват. учреждений. – М.: Просвещение, 2010.
- Касьянов В. А. Физика. 11 кл.: Учеб. для общеобразоват. учреждений. – М.: Дрофа, 2005.
- Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.
Если присоединить катушку, в которой возникает индукционный ток, к гальванометру, можно обнаружить, что направление этого тока зависит от того, приближается ли магнит к катушке, или удаляется от нее. Причем возникающий индукционный ток взаимодействует с магнитом — притягивает или отталкивает его.
Катушка с протекающей по ней током подобна магниту с двумя полюсами — северным и южным. Направление индукционного тока определяет, какой конец катушки играет роль северного полюса, из которого выходят линии магнитной индукции. В каких случаях катушка будет притягивать магнит, а в каких отталкивать, можно предсказать, опираясь на закон сохранения энергии.
Взаимодействие индукционного тока с магнитом
Если магнит приближать к катушке, то в ней появится индукционный ток такого направления, что магнит обязательно отталкивается. Для сближения магнита и катушки при этом нужно совершить положительную работу. Катушка становится подобной магниту, обращенному одноименным полюсом к приближающемуся к ней магниту. Одноименные же полюсы отталкиваются. При удалении магнита, наоборот, в катушке возникает ток такого направления, чтобы появилась притягивающая магнит сила.
Представьте, что все было бы иначе. Тогда при введении магнита в катушку он сам бы устремлялся в нее. Это противоречит закону сохранения энергии, так как при этом увеличилась бы кинетическая энергия при одновременном возникновении индукционного тока, который также затрачивает часть энергии. Кинетическая энергия и энергия тока в этом случае возникали бы из ничего, без затрат энергии, что невозможно.
Справедливость вывода можно подтвердить с помощью следующего опыта. Пусть на свободно вращающемся стержне закреплены два алюминиевых кольца: с разрезом и без разреза. Если поднести магнит к кольцу без разреза, оно будет отталкиваться. Если поднести его к кольцу с разрезом, ничего не произойдет. Это связано с тем, что в нем не возникает индукционный ток. Этому препятствует разрез. Но если отдалять магнит от кольца без разреза, то оно начнет притягиваться.
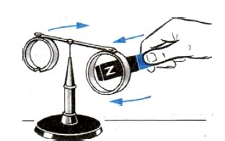
Опыты показывают, что притягивание или отталкивание кольца с индукционным током зависит от того, удаляется магнит, или притягивается. А различаются они характером изменения линий магнитной индукции, пронизывающих поверхность, ограниченную кольцом. В первом случае (рис. а) магнитный поток увеличивается, во втором (рис. б) — уменьшается. То же самое можно наблюдать в опытах с магнитом и проводящей катушкой.
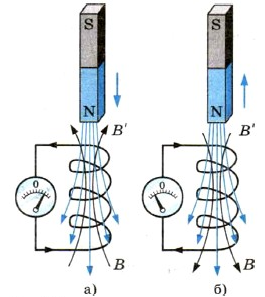
Причем в первом случае линии индукции B’ магнитного поля, созданного возникшем в катушке индукционным током, выходят из верхнего конца катушки, та как катушка отталкивает магнит. Во втором же случае напротив, они входят в этот конец.
Правило Ленца
Описанные выше опыты позволяют делать вывод, что при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с такой индукцией, которая увеличивает магнитный поток через витки катушки.
Правило направления индукционного тока носит название правила Ленца.
Правило Ленца
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.
Применять правило Ленца для нахождения направления индукционного тока Ii в контуре надо так:
- Установить направление линий магнитной индукции →B внешнего магнитного поля.
- Выяснить, увеличивается ли поток магнитной индукции этого поля через поверхность, ограниченную контуром (ΔΦ>0), или уменьшается (ΔΦ<0).
- Установить направление линий магнитной индукции →B‘ магнитного поля индукционного тока Ii. Эти линии должны быть согласно правилу Ленца направлены противоположно линиям →B при ΔΦ>0 и иметь одинаковое с ними направление при ΔΦ<0.
- Зная направление линий магнитной индукции →B‘, найти направление индукционного тока Ii, пользуясь правилом правой руки.
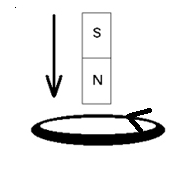
Пример №1. Найти направление индукционного тока, возникающего в кольце во время приближения к нему магнита (см. рисунок).
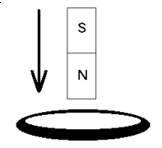
Линии магнитной индукции магнита обращены в сторону кольца, так как он направлен к нему северным полюсом. Так как магнит приближается к кольцу, магнитный поток увеличивается. Следовательно, кольцо отталкивается. Тогда оно обращено к магниту одноименным — северным — полюсом. Применим правило правой руки. Так как линии магнитной индукции выходят из северного полюса, направим к нему большой палец. Теперь четыре пальца руки покажут направление индукционного тока. В нашем случае он будет направлен против направления хода часовой стрелки.
Задание EF17577
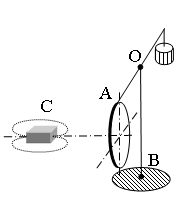 Медное кольцо на горизонтальном коромысле поворачивается вокруг вертикальной оси ОВ под действием движущегося магнита С. Установите соответствие между направлением движения магнита, вращением коромысла с кольцом и направлением индукционного тока в кольце.
Медное кольцо на горизонтальном коромысле поворачивается вокруг вертикальной оси ОВ под действием движущегося магнита С. Установите соответствие между направлением движения магнита, вращением коромысла с кольцом и направлением индукционного тока в кольце.
 К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
К каждой позиции первого столбца подберите соответствующую позицию второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
| МАГНИТ | ПОВОРОТ КОРОМЫСЛА И ТОК В КОЛЬЦЕ | ||
| А) | движется по направлению к кольцу, северный полюс обращён к кольцу | 1) | коромысло с кольцом поворачивается, отталкиваясь от магнита, ток идёт по часовой стрелке |
| Б) | движется к кольцу, к кольцу обращён южный полюс |
2) | коромысло с кольцом поворачивается, отталкиваясь от магнита, ток идёт против часовой стрелки |
| 3) | коромысло с кольцом поворачивается, притягиваясь к магниту, ток идёт по часовой стрелке | ||
| 4) | коромысло с кольцом поворачивается, притягиваясь к магниту, ток идёт против часовой стрелки |
Алгоритм решения
- Записать правило Ленца.
- В соответствии с правилом Ленца установить, что произойдет, если к кольцу поднести магнит северным полюсом.
- В соответствии с правилом Ленца установить, что произойдет, если к кольцу поднести магнит южным полюсом.
Решение
Запишем правило Ленца:
Возникающий в замкнутом контуре индукционный ток своим магнитным полем противодействует тому изменению магнитного потока, которым он вызван.
Следовательно, если поднести к кольцу магнит северным полюсом, линии магнитной индукции поля, образованного магнитом, будут направлены в сторону кольца (т.к. они выходят из северного полюса). Тогда в кольце образуется такой ток, при котором с той стороны, с которой подносят магнит, тоже сформируется северный полюс. Используем правило правой руки и расположим большой палец правой руки так, чтобы он указывал в сторону северного полюса кольца с индукционным током. Тогда четыре пальца покажут направление этого тока. Следовательно, индукционный ток направлен по часовой стрелке.
Если поднести к кольцу магнит южным полюсом, линии магнитной индукции поля, образованного магнитом, будут направлены в сторону от кольца (т.к. они выходят из северного полюса). Тогда в кольце образуется такой ток, при котором с той стороны, с которой подносят магнит, тоже сформируется южный полюс. Используем правило правой руки и получим, что в этом случае индукционный ток будет направлен против часовой стрелки.
Так как магнит подносят к кольцу, а не отодвигают от него, то кольцо всегда будет отталкиваться, поскольку в нем возникают силы противодействия. Следовательно, позиции А соответствует строка 1, а позиции Б — строка 2.
Ответ: 12
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18621
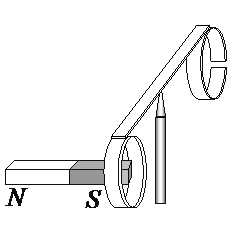 На рисунке запечатлён тот момент демонстрации по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится вблизи сплошного металлического кольца. Если магнит выдвигать из алюминиевого кольца, то кольцо перемещается вслед за магнитом. Это движение кольца – результат действия
На рисунке запечатлён тот момент демонстрации по проверке правила Ленца, когда все предметы неподвижны. Южный полюс магнита находится вблизи сплошного металлического кольца. Если магнит выдвигать из алюминиевого кольца, то кольцо перемещается вслед за магнитом. Это движение кольца – результат действия
Ответ:
а) силы гравитационного взаимодействия между кольцом и магнитом
б) силы Ампера, действующей со стороны магнитного поля магнита на кольцо, по которому идёт индукционный ток
в) кулоновских (электростатических) сил, которые возникают при движении магнита относительно кольца
г) воздушных потоков, вызванных движением руки и магнита
Алгоритм решения
- Проанализировать предложенные варианты ответа.
- Установить природу взаимодействия магнита и кольца.
- Выбрать верный ответ.
Решение
Гравитационные силы между магнитом и кольцом ничтожно малы при данных массах и расстояниях, поэтому они не могли вызвать притяжения кольца к магниту.
Кулоновские силы характеризуют силу электростатического взаимодействия зарядов. Поскольку магнит не имеет заряда, между ним и кольцом такие силы не возникают.
Металлическое кольцо достаточно тяжелое для того, чтобы заставить его стремительно двигаться вслед за магнитом.
Но вариант с силой Ампера подходит, так как сила Ампера — это сила, с которой действует магнитное поле на проводник с током. В момент, когда магнит двигают в стороны от кольца, магнитный поток, пронизывающий его, меняется. Это вызывает образование в кольце индукционного тока, который также порождает магнитное поле, противодействующее магнитному полю постоянного магнита.
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор
Задание EF19032
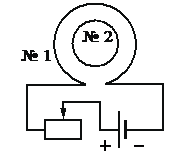 Катушка №1 включена в электрическую цепь, состоящую из источника напряжения и реостата. Катушка № 2 помещена внутрь катушки № 1 и замкнута (см. рисунок).
Катушка №1 включена в электрическую цепь, состоящую из источника напряжения и реостата. Катушка № 2 помещена внутрь катушки № 1 и замкнута (см. рисунок).
Из приведённого ниже списка выберите два правильных утверждения, характеризующих процессы в цепи и катушках при перемещении ползунка реостата вправо.
Ответ:
А) Сила тока в катушке № 1 увеличивается.
Б) Вектор индукции магнитного поля, созданного катушкой № 1, всюду увеличивается.
В) Магнитный поток, пронизывающий катушку № 2, увеличивается.
Г) Вектор индукции магнитного поля, созданного катушкой № 2, в центре этой катушки направлен от наблюдателя.
Д) В катушке № 2 индукционный ток направлен по часовой стрелке.
Алгоритм решения
- Проверить истинность каждого утверждения.
- Выбрать только истинные утверждения.
Решение
Согласно утверждению А, при перемещении ползунка реостата вправо сила тока в катушке №1 увеличивается. Перемещая ползунок реостата вправо, мы увеличиваем сопротивление. Следовательно, сила тока уменьшается. Утверждение А — неверно.
Согласно утверждению Б, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №1, всюду увеличивается. Так как сила тока уменьшается, вектор индукции магнитного поля ослабевает. Утверждение Б — неверно.
Согласно утверждению В, при перемещении ползунка реостата вправо магнитный поток, пронизывающий катушку №2, увеличивается. Так как магнитное поле ослабевает, будет уменьшаться и магнитный поток, пронизывающий катушку № 2. Утверждение В — неверно.
Согласно утверждению Г, при перемещении ползунка реостата вправо вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки направлен от наблюдателя. В катушке №1 ток течёт по часовой стрелке, и по правилу буравчика эта катушка будет создавать магнитное поле, направленное от наблюдателя. В силу того, что сила тока в цепи уменьшается, будет уменьшаться и магнитный поток, пронизывающий вторую катушку. При этом согласно правилу Ленца во второй катушке будет создаваться индукционный ток, который направлен так, чтобы своим магнитным полем противодействовать изменению магнитного потока, которым он вызван. В этом случае вектор индукции магнитного поля, созданного катушкой №2, в центре этой катушки сонаправлен с внешним полем и направлен от наблюдателя. Утверждение Г — верно.
Согласно утверждению Д, при перемещении ползунка реостата вправо в катушке №2 индукционный ток направлен по часовой стрелке. По правилу правой руки, индукционный ток в катушке 2 направлен по часовой стрелке. Утверждение Д — верно.
Ответ: ГД
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 7.9k
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 5 мая 2022 года; проверки требуют 8 правок.
Правило Ленца определяет направление индукционного тока и гласит:
Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.
— Сивухин Д. В. § 65. Правило Ленца // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 268. — 688 с.
Правило сформулировано в 1833 году Э. Х. Ленцем. Позднее оно было обобщено на все физические явления в работах Ле Шателье (1884 год) и Брауна (1887 год), это обобщение известно как принцип Ле Шателье — Брауна.
Эффектной демонстрацией правила Ленца является опыт Элиу Томсона.
Физическая суть правила[править | править код]
Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока 
где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.
Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменением величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур.
Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.
Ссылки[править | править код]
- Демонстрация правила Ленца на примере прибора Петраевского (видео)
Примечания[править | править код]
- ↑ Сивухин Д. В. § 64. Электромагнитная индукция // Общий курс физики. — М.: Наука, 1977. — Т. III. Электричество. — С. 265. — 688 с.
Направление индукционного тока в контуре зависит от того, увеличивается или уменьшается магнитный поток через этот контур.
Убедимся в этом на опыте с помощью прибора, изображённого на рисунке (1).

Рис. (1). Опыт № (1)
Узкая алюминиевая пластинка с двумя алюминиевыми кольцами на концах (одно — сплошное, другое — с разрезом) находится на стойке и может свободно вращаться вокруг вертикальной оси.
Попытаемся внести полосовой магнит северным полюсом в сплошное кольцо (рис. (1)). Оно уходит от магнита, как будто отталкивается от него, поворачивая при этом всю пластинку. Повторим эксперимент, будем подносить магнит к кольцу южным полюсом. Результат будет точно таким же. Кольцо оттолкнется. Если подносить магнит к кольцу с прорезью, то ничего не произойдет. Замена полюса магнита изменений тоже не вносит.
Данное явление можно объяснить следующим образом:
при приближении магнита к кольцу без прорези возрастает магнитный поток сквозь площадь кольца. Так как кольцо замкнуто, то в нем возникает индукционный ток.
В кольце с разрезом ток циркулировать не может.
Ток в сплошном кольце создаёт магнитное поле, поэтому кольцо приобретает свойства магнита. Кольцо отталкивается от магнита. Значит, кольцо и магнит обращены друг к другу одноименными полюсами, а векторы магнитной индукции их полей направлены в противоположные стороны.
Магнитное поле индукционного тока противодействует увеличению внешнего магнитного потока через кольцо.
Внося полосовой магнит, мы увеличиваем интенсивность магнитного поля, действующего со стороны магнита на кольцо. В кольце возникает магнитное поле, которое ослабляет поле полосового магнита, то есть направлено противоположно внешнему. Значит, ток в кольце будет направлен по часовой стрелке.
Направление индукционного тока в кольце определяется правилом правой руки.
Поменяем направление полосового магнита. Из кольца будем удалять магнит. Кольцо будет двигаться за магнитом. Получается, что кольцо притягивается к магниту.
Объяснение: притяжение возможно только в том случае, если кольцо и магнит обращены друг к другу разноименными полюсами. В этом случае направление векторов магнитной индукции магнитных полей кольца и магнита совпадают.
Магнитное поле, создаваемое индукционным током, поддерживает уменьшающийся магнитный поток через площадь кольца.
Убирая полосовой магнит из кольца, мы уменьшаем интенсивность магнитного поля, действующего со стороны магнита на кольцо. Магнитное поле кольца будет поддерживать поле полосового магнита, значит, сонаправлено внешнему магнитному полю. Поэтому, ток в кольце будет направлен против часовой стрелки.
Общее правило впервые сформулировал российский ученый Эмилий Христианович Ленц в (1834) году:
правило Ленца
Индукционный ток в замкнутом проводящем контуре принимает такое направление, что он ослабляет первопричину своего возникновения.
Источники:
Рис. 1. Опыт № 1. © ЯКласс.
Электромагнитная индукция
-
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
-
Магнитный поток
-
ЭДС индукции
-
Закон электромагнитной индукции Фарадея
-
Правило Ленца
-
Взаимодействие магнита с контуром
-
Закон Фарадея + Правило Ленца = Снятие модуля
-
Вихревое электрическое поле
-
ЭДС индукции в движущемся проводнике
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: явление электромагнитной индукции, магнитный поток, закон электромагнитной индукции Фарадея, правило Ленца.
Опыт Эрстеда показал, что электрический ток создаёт в окружающем пространстве магнитное поле. Майкл Фарадей пришёл к мысли, что может существовать и обратный эффект: магнитное поле, в свою очередь, порождает электрический ток.
Иными словами, пусть в магнитном поле находится замкнутый проводник; не будет ли в этом проводнике возникать электрический ток под действием магнитного поля?
Через десять лет поисков и экспериментов Фарадею наконец удалось этот эффект обнаружить. В 1831 году он поставил следующие опыты.
1. На одну и ту же деревянную основу были намотаны две катушки; витки второй катушки были проложены между витками первой и изолированы. Выводы первой катушки подключались к источнику тока, выводы второй катушки — к гальванометру (гальванометр — чувствительный прибор для измерения малых токов). Таким образом, получались два контура: «источник тока — первая катушка» и «вторая катушка — гальванометр».
Электрического контакта между контурами не было, только лишь магнитное поле первой катушки пронизывало вторую катушку.
При замыкании цепи первой катушки гальванометр регистрировал короткий и слабый импульс тока во второй катушке.
Когда по первой катушке протекал постоянный ток, никакого тока во второй катушке не возникало.
При размыкании цепи первой катушки снова возникал короткий и слабый импульс тока во второй катушке, но на сей раз в обратном направлении по сравнению с током при замыкании цепи.
Вывод.
Меняющееся во времени магнитное поле первой катушки порождает (или, как говорят, индуцирует) электрический ток во второй катушке. Этот ток называется индукционным током.
Если магнитное поле первой катушки увеличивается (в момент нарастания тока при замыкании цепи), то индукционный ток во второй катушке течёт в одном направлении.
Если магнитное поле первой катушки уменьшается (в момент убывания тока при размыкании цепи), то индукционный ток во второй катушке течёт в другом направлении.
Если магнитное поле первой катушки не меняется (постоянный ток через неё), то индукционного тока во второй катушке нет.
Обнаруженное явление Фарадей назвал электромагнитной индукцией (т. е. «наведение электричества магнетизмом»).
2. Для подтверждения догадки о том, что индукционный ток порождается переменным магнитным полем, Фарадей перемещал катушки друг относительно друга. Цепь первой катушки всё время оставалась замкнутой, по ней протекал постоянный ток, но за счёт перемещения (сближения или удаления) вторая катушка оказывалась в переменном магнитном поле первой катушки.
Гальванометр снова фиксировал ток во второй катушке. Индукционный ток имел одно направление при сближении катушек, и другое — при их удалении. При этом сила индукционного тока была тем больше, чем быстрее перемещались катушки.
3. Первая катушка была заменена постоянным магнитом. При внесении магнита внутрь второй катушки возникал индукционный ток. При выдвигании магнита снова появлялся ток, но в другом направлении. И опять-таки сила индукционного тока была тем больше, чем быстрее двигался магнит.
Эти и последующие опыты показали, что индукционный ток в проводящем контуре возникает во всех тех случаях, когда меняется «количество линий» магнитного поля, пронизывающих контур. Сила индукционного тока оказывается тем больше, чем быстрее меняется это количество линий. Направление тока будет одним при увеличении количества линий сквозь контур, и другим — при их уменьшении.
Замечательно, что для величины силы тока в данном контуре важна лишь скорость изменения количества линий. Что конкретно при этом происходит, роли не играет — меняется ли само поле, пронизывающее неподвижный контур, или же контур перемещается из области с одной густотой линий в область с другой густотой.
Такова суть закона электромагнитной индукции. Но, чтобы написать формулу и производить расчёты, нужно чётко формализовать расплывчатое понятие «количество линий поля сквозь контур».
к оглавлению ▴
Магнитный поток
Понятие магнитного потока как раз и является характеристикой количества линий магнитного поля, пронизывающих контур.
Для простоты мы ограничиваемся случаем однородного магнитного поля. Рассмотрим контур площади , находящийся в магнитном поле с индукцией
.
Пусть сначала магнитное поле перпендикулярно плоскости контура (рис. 1).

Рис. 1.
В этом случае магнитный поток определяется очень просто — как произведение индукции магнитного поля на площадь контура:
(1)
Теперь рассмотрим общий случай, когда вектор образует угол
с нормалью к плоскости контура (рис. 2).

Рис. 2.
Мы видим, что теперь сквозь контур «протекает» лишь перпендикулярная составляющая вектора магнитной индукции
(а та составляющая, которая параллельна контуру, не «течёт» сквозь него). Поэтому, согласно формуле (1), имеем
. Но
, поэтому
(2)
Это и есть общее определение магнитного потока в случае однородного магнитного поля. Обратите внимание, что если вектор параллелен плоскости контура (то есть
), то магнитный поток становится равным нулю.
А как определить магнитный поток, если поле не является однородным? Укажем лишь идею. Поверхность контура разбивается на очень большое число очень маленьких площадок, в пределах которых поле можно считать однородным. Для каждой площадки вычисляем свой маленький магнитный поток по формуле (2), а затем все эти магнитные потоки суммируем.
Единицей измерения магнитного потока является вебер (Вб). Как видим,
Вб = Тл · м = В · с. (3)
Почему же магнитный поток характеризует «количество линий» магнитного поля, пронизывающих контур? Очень просто. «Количество линий» определяется их густотой (а значит, величиной — ведь чем больше индукция, тем гуще линии) и «эффективной» площадью, пронизываемой полем (а это есть не что иное, как
). Но множители
и
как раз и образуют магнитный поток!
Теперь мы можем дать более чёткое определение явления электромагнитной индукции, открытого Фарадеем.
Электромагнитная индукция — это явление возникновения электрического тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего контур.
к оглавлению ▴
ЭДС индукции
Каков механизм возникновения индукционного тока? Это мы обсудим позже. Пока ясно одно: при изменении магнитного потока, проходящего через контур, на свободные заряды в контуре действуют некоторые силы — сторонние силы, вызывающие движение зарядов.
Как мы знаем, работа сторонних сил по перемещению единичного положительного заряда вокруг контура называется электродвижущей силой (ЭДС): . В нашем случае, когда меняется магнитный поток сквозь контур, соответствующая ЭДС называется ЭДС индукции и обозначается
.
Итак, ЭДС индукции — это работа сторонних сил, возникающих при изменении магнитного потока через контур, по перемещению единичного положительного заряда вокруг контура.
Природу сторонних сил, возникающих в данном случае в контуре, мы скоро выясним.
к оглавлению ▴
Закон электромагнитной индукции Фарадея
Сила индукционного тока в опытах Фарадея оказывалась тем больше, чем быстрее менялся магнитный поток через контур.
Если за малое время изменение магнитного потока равно
, то скорость изменения магнитного потока — это дробь
(или, что тоже самое, производная
магнитного потока по времени).
Опыты показали, что сила индукционного тока прямо пропорциональна модулю скорости изменения магнитного потока:
Модуль поставлен для того, чтобы не связываться пока с отрицательными величинами (ведь при убывании магнитного потока будет ). Впоследствии мы это модуль снимем.
Из закона Ома для полной цепи мы в то же время имеем: . Поэтому ЭДС индукции прямо пропорциональна скорости изменения магнитного потока:
(4)
ЭДС измеряется в вольтах. Но и скорость изменения магнитного потока также измеряется в вольтах! Действительно, из (3) мы видим, что Вб/с = В. Стало быть, единицы измерения обеих частей пропорциональности (4) совпадают, поэтому коэффициент пропорциональности — величина безразмерная. В системе СИ она полагается равной единице, и мы получаем:
(5)
Это и есть закон электромагнитной индукции или закон Фарадея. Дадим его словесную формулировку.
Закон электромагнитной индукции Фарадея. При изменении магнитного потока, пронизывающего контур, в этом контуре возникает ЭДС индукции, равная модулю скорости изменения магнитного потока.
к оглавлению ▴
Правило Ленца
Магнитный поток, изменение которого приводит к появлению индукционного тока в контуре, мы будем называть внешним магнитным потоком. А само магнитное поле, которое создаёт этот магнитный поток, мы будем называть внешним магнитным полем.
Зачем нам эти термины? Дело в том, что индукционный ток, возникающий в контуре, создаёт своё собственное магнитное поле, которое по принципу суперпозиции складывается с внешним магнитным полем.
Соответственно, наряду с внешним магнитным потоком через контур будет проходить собственный магнитный поток, создаваемый магнитным полем индукционного тока.
Оказывается, эти два магнитных потока — собственный и внешний — связаны между собой строго определённым образом.
Правило Ленца . Индукционный ток всегда имеет такое направление, что собственный магнитный поток препятствует изменению внешнего магнитного потока .
Правило Ленца позволяет находить направление индукционного тока в любой ситуации.
Рассмотрим некоторые примеры применения правила Ленца.
Предположим, что контур пронизывается магнитным полем, которое возрастает со временем (рис. (3)). Например, мы приближаем снизу к контуру магнит, северный полюс которого направлен в данном случае вверх, к контуру.
Магнитный поток через контур увеличивается. Индукционный ток будет иметь такое направление, чтобы создаваемый им магнитный поток препятствовал увеличению внешнего магнитного потока. Для этого магнитное поле, создаваемое индукционным током, должно быть направлено против внешнего магнитного поля.
Индукционный ток течёт против часовой стрелки, если смотреть со стороны создаваемого им магнитного поля. В данном случае ток будет направлен по часовой стрелке, если смотреть сверху, со стороны внешнего магнитного поля, как и показано на (рис. (3)).

Рис. 3. Магнитный поток возрастает
Теперь предположим, что магнитное поле, пронизывающее контур, уменьшается со временем (рис. 4). Например, мы удаляем магнит вниз от контура, а северный полюс магнита направлен на контур.

Рис. 4. Магнитный поток убывает
Магнитный поток через контур уменьшается. Индукционный ток будет иметь такое направление, чтобы его собственный магнитный поток поддерживал внешний магнитный поток, препятствуя его убыванию. Для этого магнитное поле индукционного тока должно быть направлено в ту же сторону , что и внешнее магнитное поле.
В этом случае индукционный ток потечёт против часовой стрелки, если смотреть сверху, со стороны обоих магнитных полей.
к оглавлению ▴
Взаимодействие магнита с контуром
Итак, приближение или удаление магнита приводит к появлению в контуре индукционного тока, направление которого определяется правилом Ленца. Но ведь магнитное поле действует на ток! Появится сила Ампера, действующая на контур со стороны поля магнита. Куда будет направлена эта сила?
Если вы хотите хорошо разобраться в правиле Ленца и в определении направления силы Ампера, попробуйте ответить на данный вопрос самостоятельно. Это не очень простое упражнение и отличная задача для С1 на ЕГЭ. Рассмотрите четыре возможных случая.
1. Магнит приближаем к контуру, северный полюс направлен на контур.
2. Магнит удаляем от контура, северный полюс направлен на контур.
3. Магнит приближаем к контуру, южный полюс направлен на контур.
4. Магнит удаляем от контура, южный полюс направлен на контур.
Не забывайте, что поле магнита не однородно: линии поля расходятся от северного полюса и сходятся к южному. Это очень существенно для определения результирующей силы Ампера. Результат получается следующий.
Если приближать магнит, то контур отталкивается от магнита. Если удалять магнит, то контур притягивается к магниту. Таким образом, если контур подвешен на нити, то он всегда будет отклоняться в сторону движения магнита, словно следуя за ним. Расположение полюсов магнита при этом роли не играет .
Уж во всяком случае вы должны запомнить этот факт — вдруг такой вопрос попадётся в части А1
Результат этот можно объяснить и из совершенно общих соображений — при помощи закона сохранения энергии.
Допустим, мы приближаем магнит к контуру. В контуре появляется индукционный ток. Но для создания тока надо совершить работу! Кто её совершает? В конечном счёте — мы, перемещая магнит. Мы совершаем положительную механическую работу, которая преобразуется в положительную работу возникающих в контуре сторонних сил, создающих индукционный ток.
Итак, наша работа по перемещению магнита должна быть положительна . Это значит, что мы, приближая магнит, должны преодолевать силу взаимодействия магнита с контуром, которая, стало быть, является силой отталкивания .
Теперь удаляем магнит. Повторите, пожалуйста, эти рассуждения и убедитесь, что между магнитом и контуром должна возникнуть сила притяжения.
к оглавлению ▴
Закон Фарадея + Правило Ленца = Снятие модуля
Выше мы обещали снять модуль в законе Фарадея (5). Правило Ленца позволяет это сделать. Но сначала нам нужно будет договориться о знаке ЭДС индукции — ведь без модуля, стоящего в правой части (5), величина ЭДС может получаться как положительной, так и отрицательной.
Прежде всего, фиксируется одно из двух возможных направлений обхода контура. Это направление объявляется положительным . Противоположное направление обхода контура называется, соответственно, отрицательным . Какое именно направление обхода мы берём в качестве положительного, роли не играет — важно лишь сделать этот выбор.
Магнитный поток через контур считается положительным , если магнитное поле, пронизывающее контур, направлено туда, глядя откуда обход контура в положительном направлении совершается против часовой стрелки. Если же с конца вектора магнитной индукции положительное направление обхода видится по часовой стрелке, то магнитный поток считается отрицательным
.
ЭДС индукции считается положительной , если индукционный ток течёт в положительном направлении. В этом случае направление сторонних сил, возникающих в контуре при изменении магнитного потока через него, совпадает с положительным направлением обхода контура.
Наоборот, ЭДС индукции считается отрицательной , если индукционный ток течёт в отрицательном направлении. Сторонние силы в данном случае также будут действовать вдоль отрицательного направления обхода контура.
Итак, пусть контур находится в магнитном поле . Фиксируем направление положительного обхода контура. Предположим, что магнитное поле направлено туда, глядя откуда положительный обход совершается против часовой стрелки. Тогда магнитный поток положителен:
.
Предположим, далее, что магнитный поток увеличивается . Согласно правилу Ленца индукционный ток потечёт в отрицательном направлении (рис. 5).

Рис. 5. Магнитный поток возрастает
Стало быть, в данном случае имеем . Знак ЭДС индукции оказался противоположен знаку скорости изменения магнитного потока. Проверим это в другой ситуации.
А именно, предположим теперь, что магнитный поток убывает . По правилу Ленца индукционный ток потечёт в положительном направлении. Стало быть,
(рис. 6).

Рис. 6. Магнитный поток возрастает
Таков в действительности общий факт: при нашей договорённости о знаках правило Ленца всегда приводит к тому, что знак ЭДС индукции противоположен знаку скорости изменения магнитного потока :
(6)
Тем самым ликвидирован знак модуля в законе электромагнитной индукции Фарадея.
к оглавлению ▴
Вихревое электрическое поле
Рассмотрим неподвижный контур, находящийся в переменном магнитном поле. Каков же механизм возникновения индукционного тока в контуре? А именно, какие силы вызывают движение свободных зарядов, какова природа этих сторонних сил?
Пытаясь ответить на эти вопросы, великий английский физик Максвелл открыл фундаментальное свойство природы: меняющееся во времени магнитное поле порождает поле электрическое . Именно это электрическое поле и действует на свободные заряды, вызывая индукционный ток.
Линии возникающего электрического поля оказываются замкнутыми, в связи с чем оно было названо вихревым электрическим полем . Линии вихревого электрического поля идут вокруг линий магнитного поля и направлены следующим образом.
Пусть магнитное поле увеличивается. Если в нём находится проводящий контур, то индукционный ток потечёт в соответствии с правилом Ленца — по часовой стрелке, если смотреть с конца вектора . Значит, туда же направлена и сила, действующая со стороны вихревого электрического поля на положительные свободные заряды контура; значит, именно туда направлен вектор напряжённости вихревого электрического поля.
Итак, линии напряжённости вихревого электрического поля направлены в данном случае по часовой стрелке (смотрим с конца вектора , (рис. 7).

Рис. 7. Вихревое электрическое поле при увеличении магнитного поля
Наоборот, если магнитное поле убывает, то линии напряжённости вихревого электрического поля направлены против часовой стрелки (рис. 8).

Рис. 8. Вихревое электрическое поле при уменьшении магнитного поля
Теперь мы можем глубже понять явление электромагнитной индукции. Суть его состоит именно в том, что переменное магнитное поле порождает вихревое электрическое поле. Данный эффект не зависит от того, присутствует ли в магнитном поле замкнутый проводящий контур или нет; с помощью контура мы лишь обнаруживаем это явление, наблюдая индукционный ток.
Вихревое электрическое поле по некоторым свойствам отличается от уже известных нам электрических полей: электростатического поля и стационарного поля зарядов, образующих постоянный ток.
1. Линии вихревого поля замкнуты, тогда как линии электростатического и стационарного полей начинаются на положительных зарядах и оканчиваются на отрицательных.
2. Вихревое поле непотенциально: его работа перемещению заряда по замкнутому контуру не равна нулю. Иначе вихревое поле не могло бы создавать электрический ток! В то же время, как мы знаем, электростатическое и стационарное поля являются потенциальными.
Итак, ЭДС индукции в неподвижном контуре — это работа вихревого электрического поля по перемещению единичного положительного заряда вокруг контура .
Пусть, например, контур является кольцом радиуса и пронизывается однородным переменным магнитным полем. Тогда напряжённость
вихревого электрического поля одинакова во всех точках кольца. Работа
силы
, с которой вихревое поле действует на заряд
, равна:
Следовательно, для ЭДС индукции получаем:
к оглавлению ▴
ЭДС индукции в движущемся проводнике
Если проводник перемещается в постоянном магнитном поле, то в нём также появляется ЭДС индукции. Однако причиной теперь служит не вихревое электрическое поле (оно не возникает — ведь магнитное поле постоянно), а действие силы Лоренца на свободные заряды проводника.
Рассмотрим ситуацию, которая часто встречается в задачах. В горизонтальной плоскости расположены параллельные рельсы, расстояние между которыми равно . Рельсы находятся в вертикальном однородном магнитном поле
. По рельсам движется тонкий проводящий стержень
со скоростью
; он всё время остаётся перпендикулярным рельсам (рис. 9).

Рис. 9. Движение проводника в магнитном поле
Возьмём внутри стержня положительный свободный заряд . Вследствие движения этого заряда вместе со стержнем со скоростью
на заряд будет действовать сила Лоренца:
Направлена эта сила вдоль оси стержня, как показано на рисунке (убедитесь в этом сами — не забывайте правило часовой стрелки или левой руки!).
Сила Лоренца играет в данном случае роль сторонней силы: она приводит в движение свободные заряды стержня. При перемещении заряда
от точки
к точке
наша сторонняя сила совершит работу:
(Длину стержня мы также считаем равной .) Стало быть, ЭДС индукции в стержне окажется равной:
(7)
Таким образом, стержень аналогичен источнику тока с положительной клеммой
и отрицательной клеммой
. Внутри стержня за счёт действия сторонней силы Лоренца происходит разделение зарядов: положительные заряды двигаются к точке
, отрицательные — к точке
.
Допустим сначала,что рельсы непроводят ток.Тогда движение зарядов в стержне постепенно прекратится. Ведь по мере накопления положительных зарядов на торце и отрицательных зарядов на торце
будет возрастать кулоновская сила, с которой положительный свободный заряд
отталкивается от
и притягивается к
— и в какой-то момент эта кулоновская сила уравновесит силу Лоренца. Между концами стержня установится разность потенциалов, равная ЭДС индукции (7).
Теперь предположим, что рельсы и перемычка являются проводящими. Тогда в цепи возникнет индукционный ток; он пойдёт в направлении
(от «плюса источника»
к «минусу» N). Предположим, что сопротивление стержня равно
(это аналог внутреннего сопротивления источника тока), а сопротивление участка
равно
(сопротивление внешней цепи). Тогда сила индукционного тока найдётся по закону Ома для полной цепи:
Замечательно, что выражение (7) для ЭДС индукции можно получить также с помощью закона Фарадея. Сделаем это.
За время наш стержень
проходит путь
и занимает положение
(рис. 9). Площадь контура возрастает на величину площади прямоугольника
:
Магнитный поток через контур увеличивается. Приращение магнитного потока равно:
Скорость изменения магнитного потока положительна и равна ЭДС индукции:
Мы получили тот же самый результат, что и в (7). Направление индукционного тока, заметим, подчиняется правилу Ленца. Действительно, раз ток течёт в направлении , то его магнитное поле направлено противоположно внешнему полю
и, стало быть, препятствует возрастанию магнитного потока через контур.
На этом примере мы видим, что в ситуациях, когда проводник движется в магнитном поле, можно действовать двояко: либо с привлечением силы Лоренца как сторонней силы, либо с помощью закона Фарадея. Результаты будут получаться одинаковые.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Электромагнитная индукция» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
07.05.2023

