Как найти индукцию формулы физика

Электромагнитная индукция

Явление электромагнитной индукции

Электромагнитная индукция – явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.

Явление электромагнитной индукции было открыто М. Фарадеем.

Опыты Фарадея

• На одну непроводящую основу были намотаны две катушки: витки первой катушки были расположены между витками второй. Витки одной катушки были замкнуты на гальванометр, а второй – подключены к источнику тока. При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
• Первая катушка была подключена к источнику тока, вторая, подключенная к гальванометру, перемещалась относительно нее. При приближении или удалении катушки фиксировался ток.
• Катушка замкнута на гальванометр, а магнит движется – вдвигается (выдвигается) – относительно катушки.

Опыты показали, что индукционный ток возникает только при изменении линий магнитной индукции. Направление тока будет различно при увеличении числа линий и при их уменьшении.

Сила индукционного тока зависит от скорости изменения магнитного потока. Может изменяться само поле, или контур может перемещаться в неоднородном магнитном поле.

Объяснения возникновения индукционного тока

Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна ЭДС. Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.

Электроны в неподвижном проводнике могут приводиться в движение только электрическим полем. Это электрическое поле порождается изменяющимся во времени магнитным полем. Его называют вихревым электрическим полем. Представление о вихревом электрическом поле было введено в физику великим английским физиком Дж. Максвеллом в 1861 году.

Свойства вихревого электрического поля:

• источник – переменное магнитное поле;
• обнаруживается по действию на заряд;
• не является потенциальным;
• линии поля замкнутые.

Работа этого поля при перемещении единичного положительного заряда по замкнутому контуру равна ЭДС индукции в неподвижном проводнике.

Магнитный поток

Магнитным потоком через площадь ​( S )​ контура называют скалярную физическую величину, равную произведению модуля вектора магнитной индукции ​( B )​, площади поверхности ​( S )​, пронизываемой данным потоком, и косинуса угла ​( alpha )​ между направлением вектора магнитной индукции и вектора нормали (перпендикуляра к плоскости данной поверхности):

Обозначение – ​( Phi )​, единица измерения в СИ – вебер (Вб).

Магнитный поток в 1 вебер создается однородным магнитным полем с индукцией 1 Тл через поверхность площадью 1 м², расположенную перпендикулярно вектору магнитной индукции:

Магнитный поток можно наглядно представить как величину, пропорциональную числу магнитных линий, проходящих через данную площадь.

В зависимости от угла ​( alpha )​ магнитный поток может быть положительным (( alpha ) < 90°) или отрицательным (( alpha ) > 90°). Если ( alpha ) = 90°, то магнитный поток равен 0.

Изменить магнитный поток можно меняя площадь контура, модуль индукции поля или расположение контура в магнитном поле (поворачивая его).

В случае неоднородного магнитного поля и неплоского контура магнитный поток находят как сумму магнитных потоков, пронизывающих площадь каждого из участков, на которые можно разбить данную поверхность.

Закон электромагнитной индукции Фарадея

Закон электромагнитной индукции (закон Фарадея):

ЭДС индукции в замкнутом контуре равна и противоположна по знаку скорости изменения магнитного потока через поверхность, ограниченную контуром:

Знак «–» в формуле позволяет учесть направление индукционного тока. Индукционный ток в замкнутом контуре имеет всегда такое направление, чтобы магнитный поток поля, созданного этим током сквозь поверхность, ограниченную контуром, уменьшал бы те изменения поля, которые вызвали появление индукционного тока.

Если контур состоит из ​( N )​ витков, то ЭДС индукции:

Сила индукционного тока в замкнутом проводящем контуре с сопротивлением ​( R )​:

При движении проводника длиной ​( l )​ со скоростью ​( v )​ в постоянном однородном магнитном поле с индукцией ​( vec{B} )​ ЭДС электромагнитной индукции равна:

где ​( alpha )​ – угол между векторами ​( vec{B} )​ и ( vec{v} ).

Возникновение ЭДС индукции в движущемся в магнитном поле проводнике объясняется действием силы Лоренца на свободные заряды в движущихся проводниках. Сила Лоренца играет в этом случае роль сторонней силы.

Движущийся в магнитном поле проводник, по которому протекает индукционный ток, испытывает магнитное торможение. Полная работа силы Лоренца равна нулю.

Количество теплоты в контуре выделяется либо за счет работы внешней силы, которая поддерживает скорость проводника неизменной, либо за счет уменьшения кинетической энергии проводника.

Важно!
Изменение магнитного потока, пронизывающего замкнутый контур, может происходить по двум причинам:

• магнитный поток изменяется вследствие перемещения контура или его частей в постоянном во времени магнитном поле. Это случай, когда проводники, а вместе с ними и свободные носители заряда, движутся в магнитном поле;
• вторая причина изменения магнитного потока, пронизывающего контур, – изменение во времени магнитного поля при неподвижном контуре. В этом случае возникновение ЭДС индукции уже нельзя объяснить действием силы Лоренца. Явление электромагнитной индукции в неподвижных проводниках, возникающее при изменении окружающего магнитного поля, также описывается формулой Фарадея.

Таким образом, явления индукции в движущихся и неподвижных проводниках протекают одинаково, но физическая причина возникновения индукционного тока оказывается в этих двух случаях различной:

• в случае движущихся проводников ЭДС индукции обусловлена силой Лоренца;
• в случае неподвижных проводников ЭДС индукции является следствием действия на свободные заряды вихревого электрического поля, возникающего при изменении магнитного поля.

Правило Ленца

Направление индукционного тока определяется по правилу Ленца: индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток.

Алгоритм решения задач с использованием правила Ленца:

• определить направление линий магнитной индукции внешнего магнитного поля;
• выяснить, как изменяется магнитный поток;
• определить направление линий магнитной индукции магнитного поля индукционного тока: если магнитный поток уменьшается, то они сонаправлены с линиями внешнего магнитного поля; если магнитный поток увеличивается, – противоположно направлению линий магнитной индукции внешнего поля;
• по правилу буравчика, зная направление линий индукции магнитного поля индукционного тока, определить направление индукционного тока.

Правило Ленца имеет глубокий физический смысл – оно выражает закон сохранения энергии.

Самоиндукция

Самоиндукция – это явление возникновения ЭДС индукции в проводнике в результате изменения тока в нем.

При изменении силы тока в катушке происходит изменение магнитного потока, создаваемого этим током. Изменение магнитного потока, пронизывающего катушку, должно вызывать появление ЭДС индукции в катушке.

В соответствии с правилом Ленца ЭДС самоиндукции препятствует нарастанию силы тока при включении и убыванию силы тока при выключении цепи.

Это приводит к тому, что при замыкании цепи, в которой есть источник тока с постоянной ЭДС, сила тока устанавливается через некоторое время.

При отключении источника ток также не прекращается мгновенно. Возникающая при этом ЭДС самоиндукции может превышать ЭДС источника.

Явление самоиндукции можно наблюдать, собрав электрическую цепь из катушки с большой индуктивностью, резистора, двух одинаковых ламп накаливания и источника тока. Резистор должен иметь такое же электрическое сопротивление, как и провод катушки.

Опыт показывает, что при замыкании цепи электрическая лампа, включенная последовательно с катушкой, загорается несколько позже, чем лампа, включенная последовательно с резистором. Нарастанию тока в цепи катушки при замыкании препятствует ЭДС самоиндукции, возникающая при возрастании магнитного потока в катушке.

При отключении источника тока вспыхивают обе лампы. В этом случае ток в цепи поддерживается ЭДС самоиндукции, возникающей при убывании магнитного потока в катушке.

ЭДС самоиндукции ​( varepsilon_{is} )​, возникающая в катушке с индуктивностью ​( L )​, по закону электромагнитной индукции равна:

ЭДС самоиндукции прямо пропорциональна индуктивности катушки и скорости изменения силы тока в катушке.

Индуктивность

Электрический ток, проходящий по проводнику, создает вокруг него магнитное поле. Магнитный поток ​( Phi )​ через контур из этого проводника пропорционален модулю индукции ​( vec{B} )​ магнитного поля внутри контура, а индукция магнитного поля, в свою очередь, пропорциональна силе тока в проводнике.

Следовательно, магнитный поток через контур прямо пропорционален силе тока в контуре:

Индуктивность – коэффициент пропорциональности ​( L )​ между силой тока ​( I )​ в контуре и магнитным потоком ​( Phi )​, создаваемым этим током:

Индуктивность зависит от размеров и формы проводника, от магнитных свойств среды, в которой находится проводник.

Единица индуктивности в СИ – генри (Гн). Индуктивность контура равна 1 генри, если при силе постоянного тока 1 ампер магнитный поток через контур равен 1 вебер:

Можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 ампер за 1 с в нем возникает ЭДС самоиндукции 1 вольт.

Энергия магнитного поля

При отключении катушки индуктивности от источника тока лампа накаливания, включенная параллельно катушке, дает кратковременную вспышку. Ток в цепи возникает под действием ЭДС самоиндукции.

Источником энергии, выделяющейся при этом в электрической цепи, является магнитное поле катушки.

Для создания тока в контуре с индуктивностью необходимо совершить работу на преодоление ЭДС самоиндукции. Энергия магнитного поля тока вычисляется по формуле:

Основные формулы раздела «Электромагнитная индукция»

Алгоритм решения задач по теме «Электромагнитная индукция»:

1. Внимательно прочитать условие задачи. Установить причины изменения магнитного потока, пронизывающего контур.

2. Записать формулу:

• закона электромагнитной индукции;
• ЭДС индукции в движущемся проводнике, если в задаче рассматривается поступательно движущийся проводник; если в задаче рассматривается электрическая цепь, содержащая источник тока, и возникающая на одном из участков ЭДС индукции, вызванная движением проводника в магнитном поле, то сначала нужно определить величину и направление ЭДС индукции. После этого задача решается по аналогии с задачами на расчет цепи постоянного тока с несколькими источниками.

3. Записать выражение для изменения магнитного потока и подставить в формулу закона электромагнитной индукции.

4. Записать математически все дополнительные условия (чаще всего это формулы закона Ома для полной цепи, силы Ампера или силы Лоренца, формулы кинематики и динамики).

5. Решить полученную систему уравнений относительно искомой величины.

6. Решение проверить.

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 20 мая 2021 года; проверки требуют 16 правок.

Магнитная индукция
Размерность	MT−2I−1
Единицы измерения
СИ	Тл
СГС	Гс
Примечания
Векторная величина

Классическая электродинамика
Электричество · Магнетизм
Электростатика Закон Кулона Теорема Гаусса Электрический дипольный момент Электрический заряд Электрическая индукция Электрическое поле Электростатический потенциал
Магнитостатика Закон Био — Савара — Лапласа Закон Ампера Магнитный момент Магнитное поле Магнитный поток Магнитная индукция
Электродинамика Векторный потенциал Диполь Потенциалы Лиенара — Вихерта Сила Лоренца Ток смещения Униполярная индукция Уравнения Максвелла Электрический ток Электродвижущая сила Электромагнитная индукция Электромагнитное излучение Электромагнитное поле
Электрическая цепь Закон Ома Законы Кирхгофа Индуктивность Радиоволновод Резонатор Электрическая ёмкость Электрическая проводимость Электрическое сопротивление Электрический импеданс
Ковариантная формулировка Тензор электромагнитного поля Тензор энергии-импульса 4-потенциал 4-ток
См. также: Портал:Физика

Магни́тная инду́кция — векторная физическая величина, являющаяся силовой характеристикой магнитного поля, а именно характеристикой его действия на движущиеся заряженные частицы и на обладающие магнитным моментом тела.

Стандартное обозначение: ; единица измерения в СИ — тесла (Тл), в СГС — гаусс (Гс) (связь: 1 Тл = 10⁴ Гс).

Величина магнитной индукции фигурирует в ряде важнейших формул электродинамики, включая уравнения Максвелла.

Для измерения магнитной индукции используются магнитометры-тесламетры. Также она может быть найдена расчётным путём — в статической ситуации для этого достаточно знать пространственное распределение токов.

Вектор в общем случае зависит от координат рассматриваемой точки и времени . Он не инвариантен относительно преобразований Лоренца и изменяется при смене системы отсчёта.

Физический смысл[править | править код]

Магнитная индукция — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

(по величине ).

Косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (вектор перпендикулярен им обоим и направлен по правилу левой руки).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в предполагаемое однородным (на расстояниях порядка размера рамки) магнитное поле, к произведению силы тока в рамке на её площадь. Момент сил зависит от ориентации рамки и достигает максимального значения при каких-то определённых углах. Звёздочка у символа указывает на то, что заряд или ток являются «пробными», то есть используемыми именно для регистрации поля, в отличие от тех же величин без звёздочки.

Магнитная индукция выступает основной, фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля .

Способы расчёта[править | править код]

Общий случай[править | править код]

В общем случае расчёт магнитной индукции проводится совместно с расчётом электрической составляющей электромагнитного поля посредством решения системы уравнений Максвелла:

,

где — магнитная постоянная, — магнитная проницаемость, — диэлектрическая проницаемость, а — скорость света в вакууме. Через обозначена плотность заряда (Кл/м³) и через плотность тока (А/м²).

Магнитостатика[править | править код]

В магнитостатическом пределе^[3] расчёт магнитного поля может быть выполнен с использованием формулы Био—Савара—Лапласа. Вид этой формулы несколько различен для ситуаций, когда поле создаётся текущим по проводу током и когда оно создаётся объёмным распределением тока:

.

В магнитостатике эта формула играет ту же роль, что закон Кулона в электростатике. Формула позволяет вычислить магнитную индукцию в вакууме. Для случая магнитной среды необходимо использовать уравнения Максвелла (без слагаемых с производными по времени).

Если заранее очевидна геометрия поля, помогает теорема Ампера о циркуляции магнитного поля^[4] (эта запись является интегральной формой уравнения Максвелла для в вакууме):

.

Здесь — произвольная поверхность, натянутая на выбранный замкнутый контур .

Простые примеры

Вектор магнитной индукции прямого провода с током на расстоянии от него составляет

,

где — единичный вектор вдоль окружности, по оси симметрии которой проложен провод. Предполагается, что среда однородна.

Вектор магнитной индукции прямого внутри соленоида с током и числом витков на единицу длины равен

,

где — единичный вектор вдоль оси соленоида. Здесь также предполагается однородность магнетика, которым заполнен соленоид.

Связь с напряжённостью[править | править код]

Магнитная индукция и напряжённость магнитного поля связаны через соотношение

,

где — магнитная проницаемость среды (вообще говоря, это тензорная величина, но в большинстве реальных случаев её можно считать скаляром, то есть просто константой конкретного материала).

Основные уравнения[править | править код]

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в большое число уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, — это электростатика.

Некоторые из уравнений:

из которого следуют выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле,

• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

  

(это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля

  .

Оно входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля, и в лагранжиан электромагнитного поля, и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Типичные значения[править | править код]

характерные значения магнитной индукции

объект	, Тл	объект	, Тл
магнитоэкранируемая комната	10-14	солнечное пятно	0,15
межзвёздное пространство	10-10	небольшой магнит (Nd-Fe-B)	0,2
магнитное поле Земли	5*10-5	большой электромагнит	1,5
1 см от провода с током 100 А	2*10-3	сильный лабораторный магнит	10
небольшой магнит (феррит)	0,01	поверхность нейтронной звезды	108

Примечания[править | править код]

См. также[править | править код]

• Векторный потенциал
• Уравнения Максвелла
• Электромагнитное поле
• Тензор электромагнитного поля
• Напряжённость магнитного поля

Магнитная индукция

Магнитная индукция — это силовая характеристика магнитного поля в выбранной точке пространства. Она определяет силу, с которой магнитное поле воздействует на заряженную частицу, что движется внутри него. Магнитная индукция считается фундаментальной характеристикой магнитного поля (как напряжённость для электрического поля).

Магнитная индукция описывает магнитную силу (вектор) на тестовом объекте (например, на куске железа) в каждой точке пространства. Простыми словами: если естественный магнит поднести к магнитным веществам (таким, как железо, никель, кобальт и т. д.), это вызовет в них магнитные свойства, которые называются “магнитной индукцией”. Магнитная индукция используется для создания искусственных магнитов.

Магнитная индукция также называется плотностью магнитного потока.

Магнитная индукция измеряется:

• в системе СИ единицей тесла (Тл),
• в системе СГС единицей гаусс (Гс).

Соотношение между Тл и Гс: 1 Тл = 10 000 Гс.

Магнитная индукция — это векторная величина и обозначается буквой B со стрелочкой:

Индукция (от лат. inducere — вводить, наведение) — производство токов в цепи под действием магнита или другого тока.

Формулы вычисления магнитной индукции

Формула магнитной индукции:

Где:

• B — индукция магнитного поля (в Тл)
• Mmax — максимальный крутящий момент магнитных сил, приложенных к рамке (в Нм)
• l — длина проводника (в м)
• S — площадь рамки (в м²)

Другие формулы, где встречается B

Эти формулы также можно использовать для её расчёта.

Сила Ампера:

Где:

• Fa — сила Ампера (в Н — ньютон)
• I — сила тока (в А — ампер)
• B — индукция магнитного поля (в Тл)
• L — длина проводника (в м)
• α — угол между вектором В и одним из направлений (силы тока, скорости или др.; измеряется в рад. или град.)

Сила Лоренца:

Где:

• Fл — сила Лоренца (в Н — ньютон)
• q — заряд частицы (в Кл — кулон)
• v — скорость (в м/с)
• B — индукция (в Тл)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Магнитный поток:

Где:

• Ф — магнитный поток (в Вб – вебер)
• B — индукция (в Тл)
• S — площадь рамки (в м²)
• α — угол между вектором В и одним из направлений (силы тока, скорости, или др.; измеряется в рад. или град.))

Электромагнитная индукция и магнитная индукция: какая между ними разница?

Электромагнитная индукция — это производство электродвижущей силы, создаваемой в результате относительного движения между магнитным полем и проводником.

Магнитная индукция может производить постоянный магнит, но может и не производить.

Электромагнитная индукция создаёт ток, но таким образом, что этот созданный ток противодействует изменению магнитного поля.

В электромагнитной индукции используются магниты и электрические цепи, а в магнитной индукции используются только магниты и магнитные материалы.

Узнайте также про:

• Магнитное поле,
• Магнитное поле Земли,
• Уравнения Максвелла
• Напряженность электрического поля.

Часто бывает, что задачу не удается решить из-за того, что под рукой нет нужной формулы. Выводить формулу с  самого начала – дело не самое быстрое, а у нас на счету каждая минута.

Ниже мы собрали вместе основные формулы по теме «Электричество и Магнетизм». Теперь, решая задачи, вы сможете пользоваться этим материалом как справочником, чтобы не терять время на поиски нужной информации.

Ежедневная рассылка с полезной информацией для студентов всех направлений – на нашем телеграм-канале.

Магнетизм: определение

Магнетизм – это взаимодействие движущихся электрических зарядов, происходящее посредством магнитного поля.

Поле – особая форма материи. В рамках стандартной модели существует электрическое, магнитное, электромагнитные поля, поле ядерных сил, гравитационное поле и поле Хиггса. Возможно, есть и другие гипотетические поля, о которых мы пока что можем только догадываться или не догадываться вовсе. Сегодня нас интересует магнитное поле.

Магнитная индукция

Так же, как заряженные тела создают вокруг себя электрическое поле, движущиеся заряженные тела порождают магнитное поле. Магнитное поле не только создается движущимися зарядами (электрическим током), но еще и действует на них. По сути магнитное поле можно обнаружить только по действию на движущиеся заряды. А действует оно на них с силой, называемой силой Ампера, о которой речь пойдет позже.

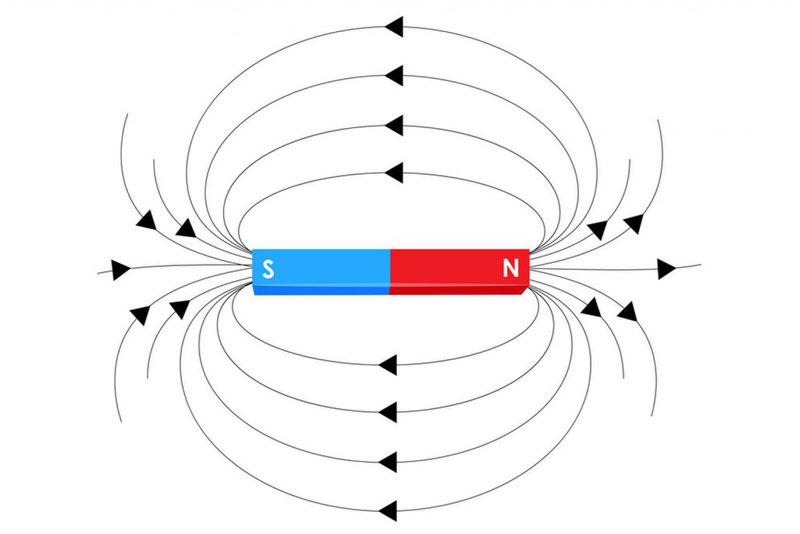
Прежде чем мы начнем приводить конкретные формулы, нужно рассказать про магнитную индукцию.

Магнитная индукция – это силовая векторная характеристика магнитного поля.

Она обозначается буквой B и измеряется в Тесла (Тл). По аналогии с напряженностью для электрического поля Е магнитная индукция показывает, с какой силой магнитное поле действует на заряд.

Кстати, вы найдете много интересных фактов на эту тему в нашей статье про теорию магнитного поля и интересные факты о магнитном поле Земли.

Как определять направление вектора магнитной индукции? Здесь нас интересует практическая сторона вопроса. Самый частый случай в задачах – это магнитное поле, создаваемое проводником с током, который может быть либо прямым, либо в форме окружности или витка.

Для определения направления вектора магнитной индукции существует правило правой руки. Приготовьтесь задействовать абстрактное и пространственное мышление!

Если взять проводник в правую руку так, что большой палец будет указывать на направление тока, то загнутые вокруг проводника пальцы покажут направление силовых линий магнитного поля вокруг проводника. Вектор магнитной индукции в каждой точке будет направлен по касательной к силовым линиям.

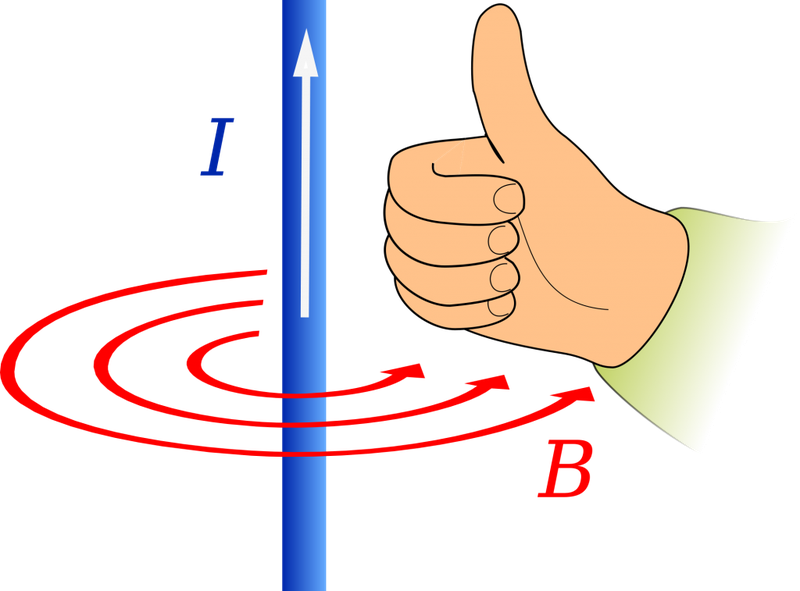
Сила Ампера

Представим, что есть магнитное поле с индукцией B. Если мы поместим в него проводник длиной l, по которому течет ток силой I, то поле будет действовать на проводник с силой:

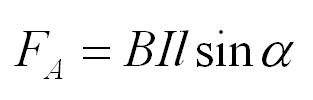
Это и есть сила Ампера. Угол альфа – угол между направлением вектора магнитной индукции и направлением тока в проводнике.

Направление силы Ампера определяется по правилу левой руки: если расположить левую руку так, чтобы в ладонь входили линии магнитной индукции, а вытянутые пальцы указывали бы направление тока, отставленный большой палец укажет направление силы Ампера.

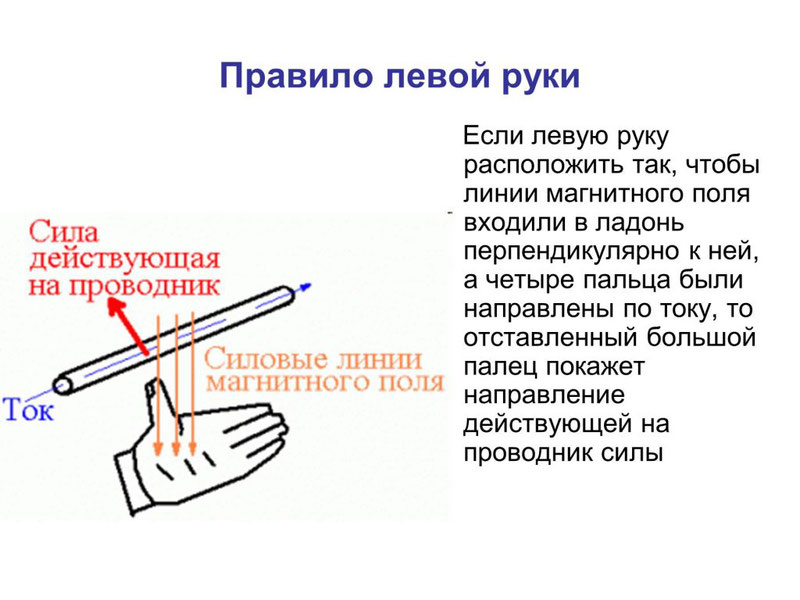
Сила Лоренца

Мы выяснили, что поле действует на проводник с током. Но если это так, то изначально оно действует отдельно на каждый движущийся заряд. Сила, с которой магнитное поле действует на движущийся в нем электрический заряд, называется силой Лоренца. Здесь важно отметить слово «движущийся», так на неподвижные заряды магнитное поле не действует.

Итак, частица с зарядом q движется в магнитном поле с индукцией В со скоростью v, а альфа – это угол между вектором скорости частицы и вектором магнитной индукции. Тогда сила, которая действует на частицу:

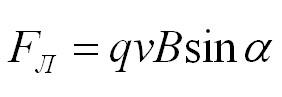
Как определить направление силы Лоренца? По правилу левой руки. Если вектор индукции входит в ладонь, а пальцы указывают на направление скорости, то отогнутый большой палец покажет направление силы Лоренца. Отметим, что так направление определяется для положительно заряженных частиц. Для отрицательных зарядов полученное направление нужно поменять на противоположное.

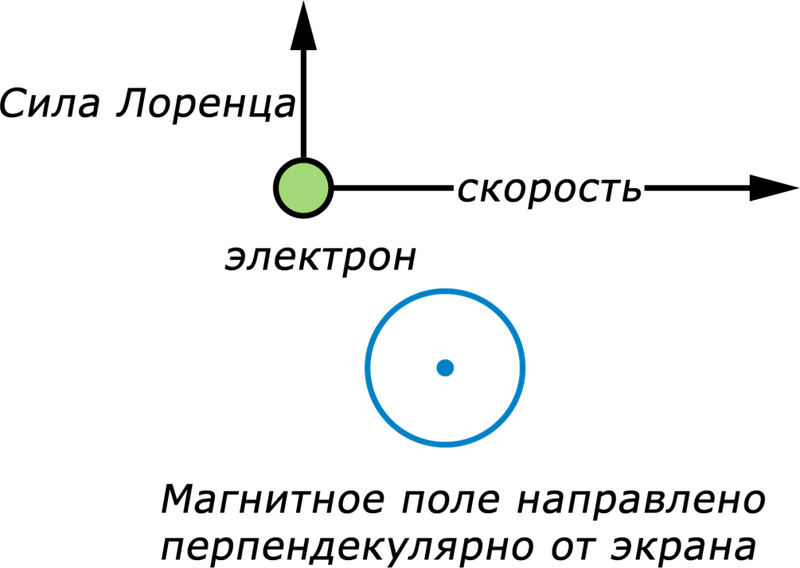
Если частица массы m влетает в поле перпендикулярно линиям индукции, то она будет двигаться по окружности, а сила Лоренца будет играть роль центростремительной силы. Радиус окружности и период обращения частицы в однородном магнитном поле можно найти по формулам:

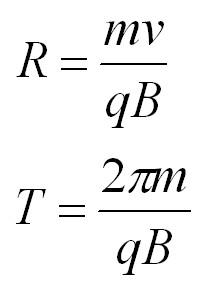
Взаимодействие токов

Рассмотрим два случая. Первый – ток течет по прямому проводу. Второй – по круговому витку. Как мы знаем, ток создает магнитное поле.

В первом случае магнитная индукция провода с током I на расстоянии R от него считается по формуле:

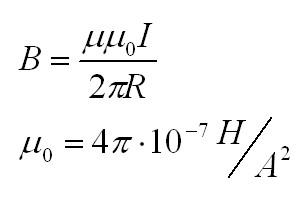
Мю – магнитная проницаемость вещества, мю с индексом ноль – магнитная постоянная.

Во втором случае магнитная индукция в центре кругового витка с током равна:

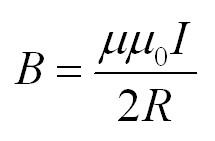
Также при решении задач может пригодиться формула для магнитного поля внутри соленоида. Соленоид – это катушка, то есть множество круговых витков с током.

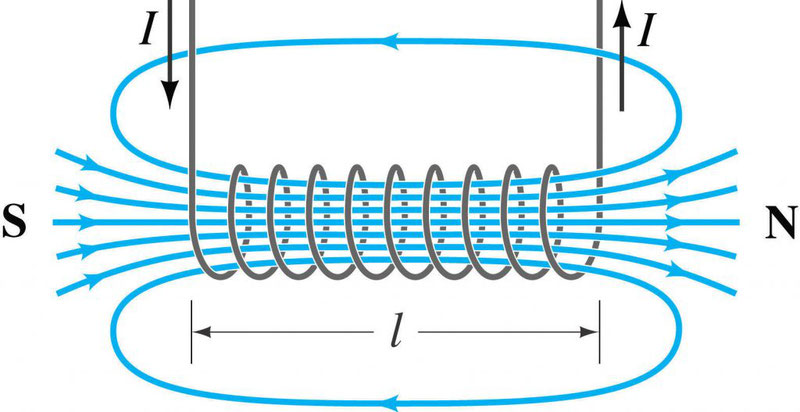
Пусть их количество – N, а длина самого соленоилда – l. Тогда поле внутри соленоида вычисляется по формуле:

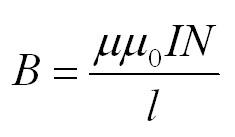
Кстати! Для наших читателей сейчас действует скидка 10% на любой вид работы

Магнитный поток и ЭДС

Если магнитная индукция – векторная характеристика магнитного поля, то магнитный поток – скалярная величина, которая также является одной из самых важных характеристик поля. Представим, что у нас есть какая-то рамка или контур, имеющий определенную площадь. Магнитный поток показывает, какое количество силовых линий проходит через единицу площади, то есть характеризует интенсивность поля. Измеряется в Веберах (Вб) и обозначается Ф.

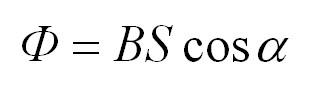
S – площадь контура, альфа – угол между нормалью (перпендикуляром) к плоскости контура и вектором В.

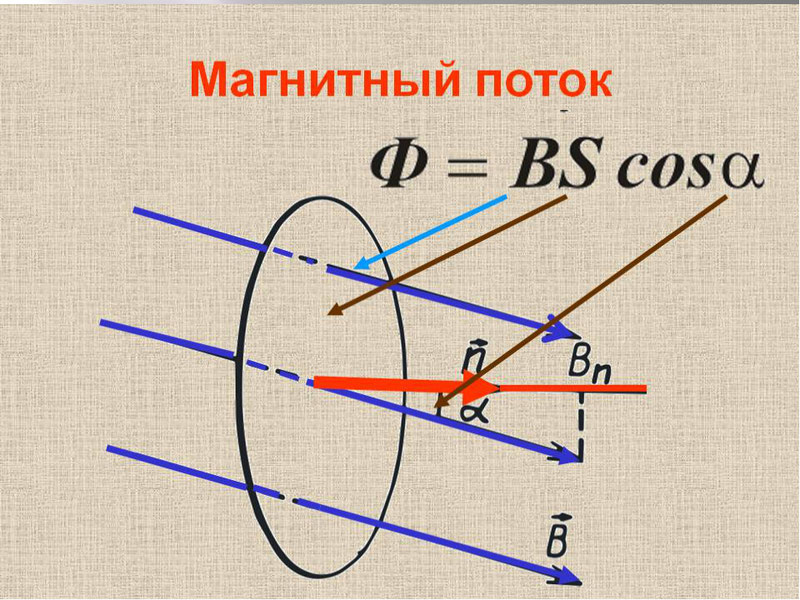
При изменении магнитного потока через контур в контуре индуцируется ЭДС, равная скорости изменения магнитного потока через контур. Кстати, подробнее о том, что такое электродвижущая сила, вы можете почитать в еще одной нашей статье.

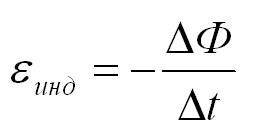
По сути формула выше – это формула для закона электромагнитной индукции Фарадея. Напоминаем, что скорость изменения какой-либо величины есть не что иное, как ее производная по времени.

Для магнитного потока и ЭДС индукции также справедливо обратное. Изменение тока в контуре приводит к изменению магнитного поля и, соответственно, к изменению магнитного потока. При этом возникает ЭДС самоиндукции, которая препятствует изменению тока в контуре. Магнитный поток, который пронизывает контур с током, называется собственным магнитным потоком, пропорционален силе тока в контуре и вычисляется по формуле:

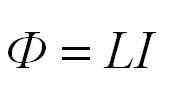
L – коэффициент пропорциональности, называемый индуктивностью, который измеряется в Генри (Гн). На индуктивность влияют форма контура и свойства среды. Для катушки с длиной l и с числом витков N индуктивность рассчитывается по формуле:

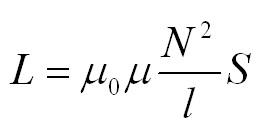
Формула для ЭДС самоиндукции:

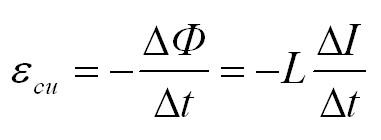
Энергия магнитного поля

Электроэнергия, ядерная энергия, кинетическая энергия. Магнитная энергия – одна из форм энергии. В физических задачах чаще всего нужно рассчитывать энергию магнитного поля катушки. Магнитная энергия катушки с током I и индуктивностью L равна:

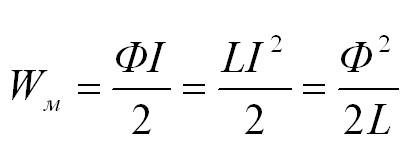
Объемная плотность энергии поля:

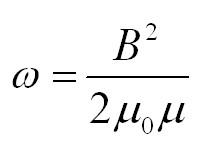
Конечно, это не все основные формулы раздела физики «электричество и магнетизм», однако они часто могут помочь при решении стандартных задач и расчетах. Если же вам попалась задача со звездочкой, и вы никак не можете подобрать к ней ключ, упростите себе жизнь и обратитесь за решением в сервис студенческой помощи.

Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].

Вектор индукции магнитного поля: главные понятия

Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.

Вектор магнитной индукции однородного поля и неоднородного

Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.

Вектор индукции магнитного поля: важные формулы

Важно!

Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.

Модуль вектора индукции магнитного поля: производные формулы

Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:

[B=frac{F_{max }}{I cdot L}]

В вакууме модуль индукции будет равен:

[mathrm{B}=mu 0 cdot mathrm{H}]

Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)

[vec{F}=B cdot q cdot v cdot sin alpha]

[B=frac{F}{sin alpha cdot q v}]

В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика.  Под символом q подразумевается заряд в магнитном поле.

Как определяется направление вектора индукции магнитного поля?

За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}]  используют направление, в котором устанавливается под воздействием поля  утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.

Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].

Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.

Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:

• Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.

• Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.

Задания по теме

Разберем примеры, в которых будет задействована данная формула и свойства.

Пример 1

Условие задачи:

Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.

Решение задачи следующее:

Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.

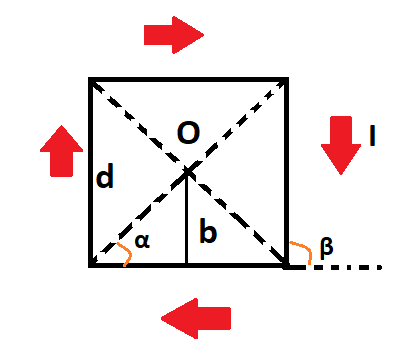
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B₁+B₂+B₃+B₄ 

Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B₁

В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.

Чтобы формула подошла к данной задачи, ее применяют в следующем виде:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]

углы α и β, которые отмечены на рисунке:

[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]

Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]

Поскольку у нас квадратная форма, то следует заметить следующее:

[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]

Возьмем выведенные формулы и получим конечное выражение, то есть:

[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Пример 2

Условие задачи:

Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.

Решение задачи:

В точке А получается из двух частей проводника, то есть:

[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]

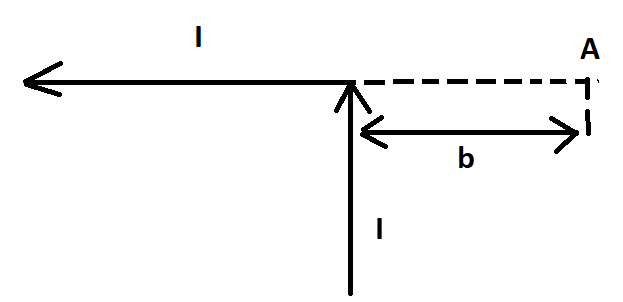
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.

Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:

[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]

В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].

Индукция бесконечного проводника в точке А была бы равна:

[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]

Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:

[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]

Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]