Как найти индукцию магнитного поля в квадрате

где
v
– скорость направленного движения
свободных носителей заряда. Умножив В
на количество свободных носителей
заряда в элементе проводника dl,
получим индукцию магнитного поля,
созданную этим элементом проводника с
током,

поскольку
env
= j*,

;

поскольку
dl^.j
= dl^.j
(dl
и j совпадают
по направлению),

.

Таким
образом, индукция магнитного поля,
созданного элементом dl
проводника с током I
на расстоянии r
от элемента проводника, определяется
выражением

.

Это выражение и
представляет собой закон Био–Савара–Лапласа.

Из
закона видно, что вектор магнитной
индукции dB
всегда перпендикулярен плоскости, в
ко-торой лежат векторы dl
и r.
Его направление определяется по правилу
правого винта.

Модуль
вектора dB
определяется из выражения

,

где

– угол между векторами dl
и r.

______________________

*
Здесь j
– вектор плотности тока.

Необходимо
учесть, что полученное выражение
позволяет рассчитать индукцию магнитного
поля, созданную одним бесконечно малым
элементом проводника dl
с током I.

Для
того чтобы найти магнитную индукцию,
созданную всем
проводником,
необходимо использовать принцип
суперпозиции, т. е. просуммировать
векторы dB,
созданные каждым элементом проводника
в интересующей нас точке.

3.4.1. Индукция магнитного поля отрезка прямолинейного проводника с током

Для всех бесконечно
малых элементов dl
отрезка векторы dl
и r
лежат в плоскости листа.
Поэтому векторы dB,
созданные в выбранной нами точке
различными элементами проводника
направлены одинаково – перпендикулярно
плоскости листа. Следовательно, сложение
векторов dB
можно заменить сложением их модулей
dB.

И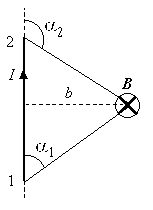з
рисунка видно, чтоr
= b/sin

(b
– расстояние от проводника до инте-ресующей
нас точки), и

.

Тогда
индукция, созданная элементом проводника
dl,
равна

.

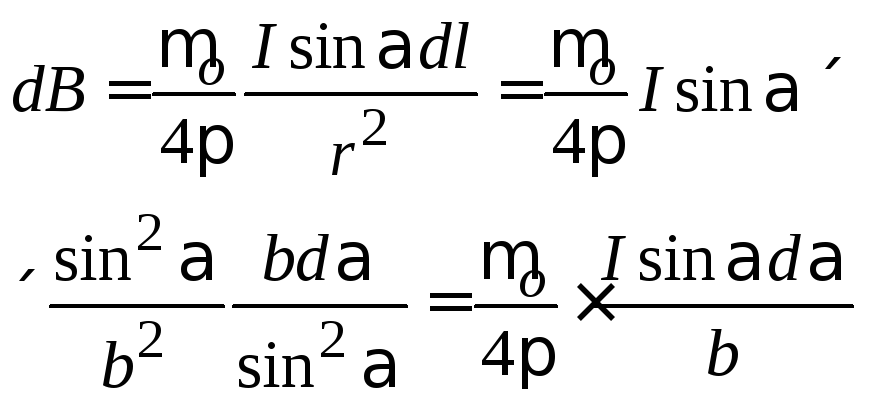Индукция
магнитного поля, созданного всем
проводником, может быть найдена как
интеграл от dB
в пределах от  ₁
до + ₂:

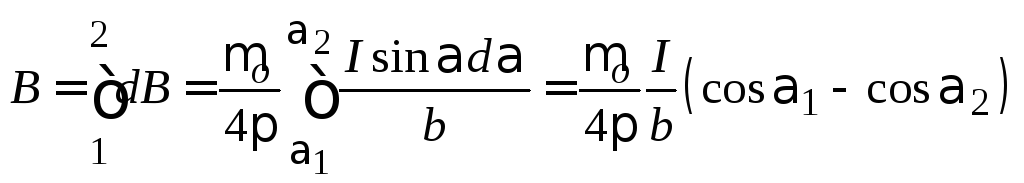
Иногда
удобнее воспользоваться другим
выражением:

(обратите
внимание на рисунок, показывающий углы
₁
и ₂).

О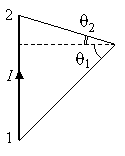братите
также внимание на то, что если точка
расположена так, как показано на следующем
рисунке, то₂
меняет знак и формула для расчёта
магнитного поля прямолинейного отрезка
записывается следующим образом:

.

3.4.2. Индукция магнитного поля бесконечно длинного прямолинейного проводника с током

Если
длина прямого проводника бесконечно
велика, то ₁
= 0, а ₂
= .

В
этом случае индукция магнитного поля,
созданного проводником, будет равна

.

Т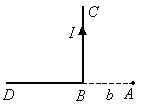аким
образом, индукция магнитного поля,
созданного бесконечно длинным проводником
прямо пропорциональна току в проводнике
и обратно пропорциональна расстоянию
от проводника до интересующей нас точки.

Дополнительно
рассмотрим магнитное поле, созданное
бесконечным проводником, который изогнут
под прямым углом.

Ограничимся
получением расчётной формулы для точки
А,
расположенной на продолжении одной из
половин проводника.

Участок
DB
в точке А
не создаёт магнитного поля, так как для
него ₁
и ₂
равны 0.

Для
участка ВС
₁
= 90⁰,
₂
= -180⁰.
Поэтому индукция, созданная этим
участком, равна

.

Таким
образом, индукция магнитного поля в
точке А
равна половине индукции, созданной
прямым бесконечно длинным проводником
с таким же током.

3.4.3. Индукция магнитного поля в центре квадрата

Рассмотрим
квадрат со стороной а, в котором течёт
токI.

Все
стороны квадрата создают в его центре
одинаковое магнитное поле. Поэтому если
индукция, созданная одной стороной,
равна В,
то магнитная индукция, созданная всеми
сторонами, равна 4В.

В
рассматриваемом случае ₁
= 45⁰,
а ₂
= 135⁰
(см. рисунок).

Индукция магнитного
поля, созданного одной стороной, равна:

.

Соответственно
индукция магнитного поля, созданного
всеми сторонами, равна

.

В показанном на
рисунке случае индукция магнитного
поля направлена перпендикулярно
плоскости квадрата на нас.

3.4.4. Расчёт магнитного поля замкнутого кругового тока (витка с током).

Пусть
радиус витка равен R,
а ток в нём – I.

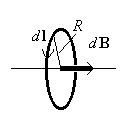
Вначале рассмотрим расчёт
поля в центре витка.

Каждый
элемент тока будет создавать индукцию,
направленную вдоль оси витка. Поэтому,
как и в предыдущем случае, сложение dB
алгебраическое и

,

(в
каждой точке 
= 90⁰)

.

Поле
на оси витка на расстоянии bот центра
витка рассчитывается несколько сложнее.Вэтом случае векторыdBне параллельны друг другу.

При суммировании
составляющие векторов dB,
перпендикулярные оси, уничтожаются, а
параллельные оси – складываются.

Из рисунка видно,
что

;

.

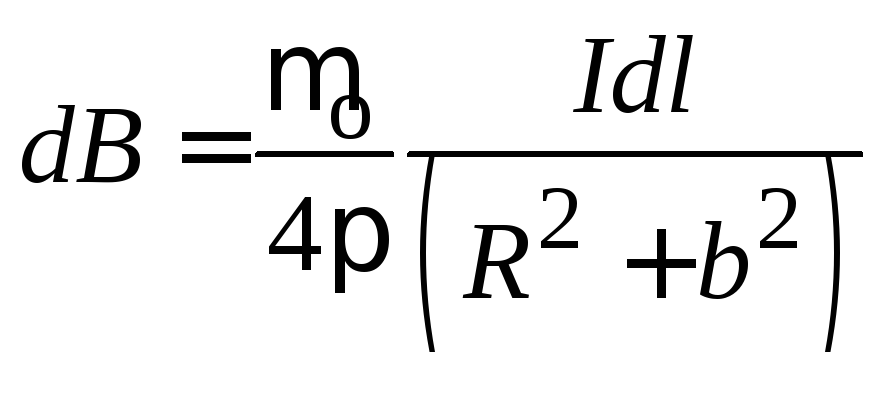Проинтегрировав
это выражение по всему контуру, получаем

.

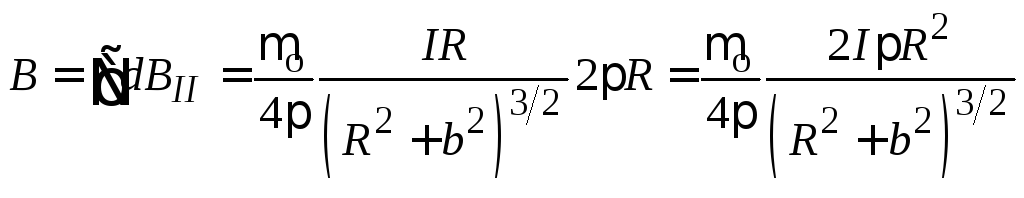Таким
образом, индукция магнитного поля на
оси кругового витка с током убывает
обратно пропорционально третьей степени
расстояния от центра витка до точки на
оси. Вектор магнитной индукции на оси
витка параллелен оси. Его направление
можно определить с помощью правого
винта: если направить правый винт
параллельно оси витка и вращать его по
направлению тока в витке, то направление
поступательного движения винта покажет
направление вектора магнитной индукции.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение.
Для решения задачи необходимы: μ₀ = 4∙π⋅10^-7 Гн/м − магнитная постоянная. 
Рассмотрим четыре участка, АВ, ВС, СД, ДА.
Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.

[ begin{align}
  & vec{B}={{{vec{B}}}_{AB}}+{{{vec{B}}}_{BC}}+{{{vec{B}}}_{CD}}+{{{vec{B}}}_{DA}},  \
 & Ox: B={{B}_{AB}}+{{B}_{BC}}+{{B}_{CD}}+{{B}_{DA}} (1). \
end{align}
 ]

Определим модуль вектора магнитной индукции на участке АВ.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био –  Савара –  Лапласа.

[ begin{align}
  & dB=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot sin alpha dalpha , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot intlimits_{{{alpha }_{1}}}^{{{alpha }_{2}}}{sin alpha dalpha ,} \
 & B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos {{alpha }_{1}}-cos {{alpha }_{2}}) (3). \
end{align} ]

Где: R – расстояние от т. О до проводника; – α₁ и α₂ углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
α₂ = 3∙π/4, α₁ =  π/ 4.

[ begin{align}
  & B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos frac{pi }{4}-cos frac{3cdot pi }{4}) , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (frac{sqrt{2}}{2}+frac{sqrt{2}}{2}) , \
 & {{B}_{BC}}={{B}_{DA}}={{B}_{CD}}={{B}_{AB}}=frac{sqrt{2}cdot {{mu }_{0}}cdot I}{4cdot pi cdot R} (5),R=frac{d}{2} (6), \
 & B=4cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{2cdot pi cdot d}, B=2cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{pi cdot d} (7). \
 & B=frac{2cdot sqrt{2}cdot 4cdot pi cdot {{10}^{-7}}cdot 5}{pi cdot 0,15}=37,6cdot {{10}^{-6}}. \
end{align}
 ]

Ответ 9,43 мкТ получается если бы квадрат был изготовлен из проволоки длиной 15 см.
Ответ: В = 37,6∙10^-6 Тл.

Популярное на сайте:

Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах. 

Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте. 

Как быстро и эффективно исправить почерк?  Люди часто предполагают, что каллиграфия и почерк являются синонимами, но это не так.

Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью. 

Свойством поля магнитного в любой его точке с позиции силы выступает вектор магнитной индукции [overrightarrow{mathrm{B}}].

Вектор индукции магнитного поля: главные понятия

Рассмотрим определение вектора индукции магнитного поля. Индукцию определяют как предел отношения F силы, воздействующий на магнитное поле, на ток [text { Idl }] к произведению элементарного тока [text { I }] со значением элемента проводника [text { dl }]. Другими словами, магнитная индукция действует по направлению перпендикулярно [perp] по направлению тока (или по-другому к элементу проводника [text { dl }Rightarrow] из (1), а также вектор магнитной индукции поля перпендикулярен [perp] к направлению силы, которая действует с магнитного поля.

Вектор магнитной индукции однородного поля и неоднородного

Если [overrightarrow{mathrm{B}}=mathrm{const}], то поле является однородным. Если оно не изменяется с течением времени, то про него говорят, что поле постоянное.

Вектор индукции магнитного поля: важные формулы

Важно!

Формула с векторами преобразуется в модульную форму, потому что векторы задают направление, а модульная форма — значения, которые необходимы для решения задачи.

Модуль вектора индукции магнитного поля: производные формулы

Есть еще формулы для определения модуля магнитной индукции. Она определяется как отношение силы в максимуме [mathrm{F}_{max }], которое реагирует на проводник длины (при этом L= 1 м) к силе элементарного тока [text { I }] в проводнике:

[B=frac{F_{max }}{I cdot L}]

В вакууме модуль индукции будет равен:

[mathrm{B}=mu 0 cdot mathrm{H}]

Чтобы найти вектор индукции через силу Лоренца, следует преобразовать формулу: [overrightarrow{mathrm{F}}=mathrm{q} cdot[overrightarrow{mathrm{V}} times overrightarrow{mathrm{B}}]] (Крестом обозначается произведение векторов)

[vec{F}=B cdot q cdot v cdot sin alpha]

[B=frac{F}{sin alpha cdot q v}]

В данном случае угол α — это угол между вектором индукции и скорости. Стоит отметить, что направление силы Лоренца [overrightarrow{mathrm{F}}] перпендикулярно [perp] каждому вектору, направлено по правилу Буравчика.  Под символом q подразумевается заряд в магнитном поле.

Как определяется направление вектора индукции магнитного поля?

За направление вектора индукции магнитного поля [overrightarrow{mathrm{B}}]  используют направление, в котором устанавливается под воздействием поля  утвердительного нормали к току с контору. Другими словами объясняют так: вектор идет в направление поступательного перемещения правого винта при вращении по направлению передвижения тока внутри контура.

Вектор индукции [overrightarrow{mathrm{B}}] обладает направлением, которое начинается со стрелки южного полюса [text { S }] (она свободна передвигается в поле) к полюсу северному [text { N }].

Магнитное поле возникает из-за электрических зарядов (элементарными токами), движущиеся в нем.

Для того чтобы определить направление вектора магнитной индукции в проводнике с элементарным током, используют правило правой руки (Буравчика). Они формулируются так:

• Для катушки с током: 4 согнутых пальца руки, которые обхватывают катушку, направляют по течению току. В это время оставленный большой палец на [90^{circ}] указывает на направление магнитной индукции [overrightarrow{mathrm{B}}] в середине катушки.

• Для прямого проводника с элементарным током: большой палец руки, который оставляется на [90^{circ}], направить по течению элементарного тока. В это время 4 согнутых пальца, которые держат проводник, показывают сторону, куда направлена индукция магнитного поля.

Задания по теме

Разберем примеры, в которых будет задействована данная формула и свойства.

Пример 1

Условие задачи:

Проводник представлен в квадратной форме. Каждая из сторон равна d. В данный момент по нему проходит элементарный ток силы I. Найдите индукцию магнитного поля в месте, где диагонали квадрата пересекаются.

Решение задачи следующее:

Сделаем рисунок, в котором плоскость совпадает с плоскостью проводника. Изобразим направление вектора индукции магнитного поля.

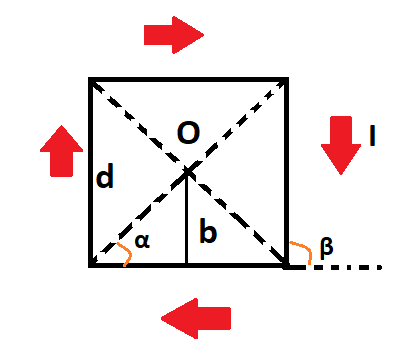
В данной точке О получаются проводники с элементарным током, которые расположены прямолинейно и вектор магнитной индукции поля перпендикулярен плоскости. Направления напряжености полей определяется в соответствием с правилом правого винта,то есть перпендикулярны плоскости изображения. Поэтому сумму векторов по принципу суперпозиции надо заменить на алгебраический вид. Получим следующее выражение: B=B₁+B₂+B₃+B₄ 

Из симметричности рисунка можно увидеть, что модули вектора индукции магнитного поля одинаковы. Получаем следующее: B=4B₁

В разделе физике «Электромагнетизм» использовали одну из формул, чтобы рассчитать модуль индукции прямолинейного проводника с элементарным током.

Чтобы формула подошла к данной задачи, ее применяют в следующем виде:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{4 mathrm{pi b}}(cos alpha-cos beta)]

углы α и β, которые отмечены на рисунке:

[beta=pi-alpha rightarrow cos beta=cos (pi-alpha)=-cos alpha]

Используем формулу [B_{1}=frac{I cdot mu_{0}}{4 pi b}(cos alpha-cos beta)] и преобразуем с применением тригонометрического свойства:

[mathrm{B}_{1}=frac{mathrm{I} cdot mu_{0}}{2 mathrm{pi b}} cdot cos alpha]

Поскольку у нас квадратная форма, то следует заметить следующее:

[mathrm{b}=mathrm{d} 2, alpha=frac{pi}{4} rightarrow cos alpha=frac{sqrt{2}}{2}]

Возьмем выведенные формулы и получим конечное выражение, то есть:

[mathrm{B}=4 cdot frac{mathrm{I} cdot mu_{0}}{pi mathrm{d}} cdot frac{sqrt{2}}{2}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Ответ: [mathrm{B}=frac{2 sqrt{2}}{pi mathrm{d}} cdot mathrm{I} cdot mu_{0}]

Пример 2

Условие задачи:

Бесконечно проводник с элементарным током (I) согнут под 90 градусов, который изображен на рисунке. Найдите вектор магнитной индукции однородного поля в точке А.

Решение задачи:

В точке А получается из двух частей проводника, то есть:

[overrightarrow{mathrm{B}}=mathrm{B}_{mathrm{II}}+mathrm{B}_{perp}]

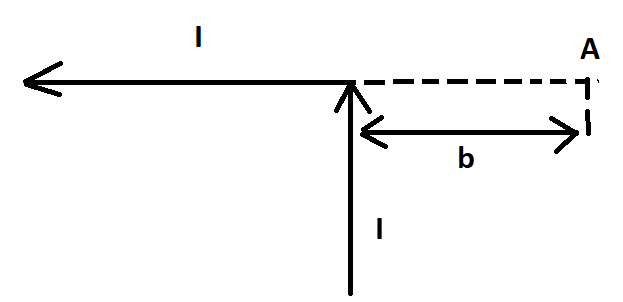
Теперь посмотрим горизонтальный участок, где расположена точка А. Данная область проводника с элементарным током формирует поле в этой точке. Вектор индукции магнитного поля [mathrm{B}_{mathrm{II}}] равен нулю, потому что в А все углы между с радиус-векторами и с элементарным током равны π.

Следовательно, произведение векторов [[mathrm{d} vec{ l } vec{r}]] и поток вектора индукции магнитного поля в законе Био-Савара-Лапласа будет равен нулю:

[overrightarrow{mathrm{B}}=frac{mu_{0}}{4 pi} oint frac{mathrm{I}[mathrm{d} vec{l} vec{r}]}{mathrm{r}^{3}}]

В этом случае [vec{r}] — радиус-вектор, который идет от элемента [mathrm{Idvec{l}}] к точке А, в которой находится индукция магнитного поля [overrightarrow{mathrm{B}}].

Индукция бесконечного проводника в точке А была бы равна:

[mathrm{B}^{prime}=frac{mu_{0}}{2 pi} frac{mathrm{I}}{mathrm{b}}]

Но так как полу бесконечный проводник, то следуя из принципа суперпозиции, получается следующее выражение для проводника магнитной индукций равна:

[mathrm{B}=mathrm{B}_{perp}=frac{1}{2} mathrm{~B}^{prime}=frac{mu_{0}}{Pi} frac{mathrm{I}}{mathrm{b}}]

Ответ: [mathrm{B}=frac{mu_{0}}{pi} frac{mathrm{I}}{mathrm{b}}]