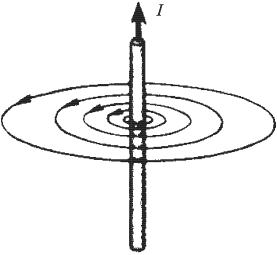
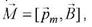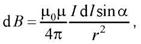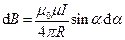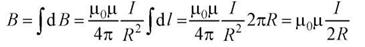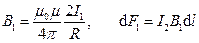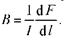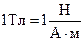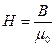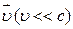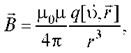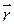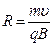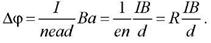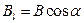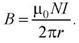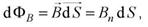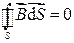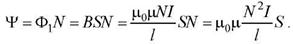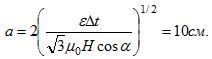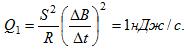Решение.
Для решения задачи необходимы: μ0 = 4∙π⋅10-7 Гн/м − магнитная постоянная.
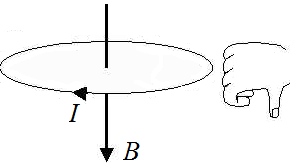
Рассмотрим четыре участка, АВ, ВС, СД, ДА.
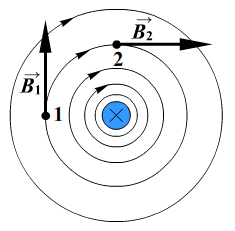
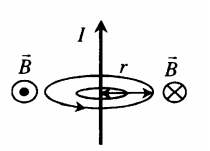
Направление вектора магнитной индукции на каждом участке определим по правилу буравчика. В точке О результирующий вектор магнитной индукции направлен от нас. Применим принцип суперпозиции.
[ begin{align}
& vec{B}={{{vec{B}}}_{AB}}+{{{vec{B}}}_{BC}}+{{{vec{B}}}_{CD}}+{{{vec{B}}}_{DA}}, \
& Ox: B={{B}_{AB}}+{{B}_{BC}}+{{B}_{CD}}+{{B}_{DA}} (1). \
end{align}
]
Определим модуль вектора магнитной индукции на участке АВ.
Индукция магнитного поля в произвольной точке О, созданного отрезком проводника с током конечной длины, определим используя закон Био – Савара – Лапласа.
[ begin{align}
& dB=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot sin alpha dalpha , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot intlimits_{{{alpha }_{1}}}^{{{alpha }_{2}}}{sin alpha dalpha ,} \
& B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos {{alpha }_{1}}-cos {{alpha }_{2}}) (3). \
end{align} ]
Где: R – расстояние от т. О до проводника; – α1 и α2 углы, образованные радиус-вектором, проведенном в т. О соответственно из начала и конца проводника, с направлением тока.
Определим модуль вектора магнитной индукции на каждом участке.
α2 = 3∙π/4, α1 = π/ 4.
[ begin{align}
& B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (cos frac{pi }{4}-cos frac{3cdot pi }{4}) , B=frac{{{mu }_{0}}cdot I}{4cdot pi cdot R}cdot (frac{sqrt{2}}{2}+frac{sqrt{2}}{2}) , \
& {{B}_{BC}}={{B}_{DA}}={{B}_{CD}}={{B}_{AB}}=frac{sqrt{2}cdot {{mu }_{0}}cdot I}{4cdot pi cdot R} (5),R=frac{d}{2} (6), \
& B=4cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{2cdot pi cdot d}, B=2cdot frac{sqrt{2}cdot {{mu }_{0}}cdot I}{pi cdot d} (7). \
& B=frac{2cdot sqrt{2}cdot 4cdot pi cdot {{10}^{-7}}cdot 5}{pi cdot 0,15}=37,6cdot {{10}^{-6}}. \
end{align}
]
Ответ 9,43 мкТ получается если бы квадрат был изготовлен из проволоки длиной 15 см.
Ответ: В = 37,6∙10-6 Тл.
Рамка с током. Направление магнитного поля.
Аналогично тому, как при исследовании электростатического поля использовался точечный пробный заряд, при исследовании магнитного поля используется замкнутый плоский контур с током (рамка с током), линейные размеры которого малы по сравнению с расстоянием до токов, образующих магнитное поле.
Ориентация контура в пространстве характеризуется направлением нормали n к контуру.

За положительное направление нормали принимается направление поступательного движения правого винта, головка которого вращается в направлении тока, текущего в рамке.
Магнитное поле оказывает на рамку с током ориентирующее действие, поворачивая её определенным образом. Это свойство используется для выбора направления магнитного поля.
За направление магнитного поля в данной точке принимается направление, вдоль которого располагается положительная нормаль к свободно подвешенной рамке с током, или направление, совпадающее с направлением силы, действующей на северный полюс (N) магнитной стрелки, помещенный в данную точку поля.
3. Вектор магнитной индукции.
Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств рамки с током и определяется векторным произведением



где α – угол между векторами 

Для плоского контура с током / магнитный момент определяется как
где 

Если в данную точку магнитного поля помещать рамки с различными магнитными моментами, то на них действуют различные вращающие моменты, но отношение 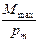
Аналогично тому, как силовая векторная характеристика электростатического поля – напряженность – определялась как сила, действующая на пробный заряд, силовая характеристика магнитного поля – магнитная индукция 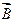
Графически магнитное поле, так же как электрическое, изображают с помощью линий магнитной индукции – линий, касательные к которым в каждой точке совпадают с направлением вектора
Линии магнитной индукции всегда замкнуты и охватывают проводники с током, в то время как линии электростатического поля – разомкнуты (они начинаются на положительных и заканчиваются на отрицательных зарядах).
4. Макротоки и микротоки.
В дальнейшем мы будем различать макроскопические токи, т.е. электрические токи, протекающие по проводникам в электрических цепях и микроскопические токи, обусловленных движением электронов в атомах и молекулах.
Намагниченность постоянных магнитов является следствием существованием в них микротоков.
Внешнее магнитное поле оказывает ориентирующее, упорядочивающее действие на эти микротоки. Например, если вблизи какого-то тела поместить проводник с током (макроток), то под действием его магнитного поля микротоки во всех атомах определенным образом ориентируются, создавая в теле дополнительное магнитное поле.
Вектор магнитной индукции 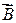
Поэтому, при одном и том же макротоке, вектор 
Магнитное поле макротока описывается вектором напряженности магнитного поля
В среде магнитное поле макротоков усиливается за счет поля микротоков среды.
5. Связь между 
Для однородной изотропной среды вектор магнитной индукции
где 

среды (п.39), безразмерная величина, показывающая, во сколько раз магнитное поле макротоков Н усиливается за счет поля микротоков среды.
6. Подобие векторных характеристик электростатического и магнитного полей.
Вектор магнитной индукции 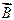

Аналогомвектора электрического смещения 

Для магнитного поля, как и для электрического, справедлив принцип суперпозиции: магнитная индукция результирующего поля, создаваемого несколькими токами или движущимися зарядами, равна векторной сумме магнитных индукций полей, создаваемых каждым током или движущимся зарядом.
7. Закон Био-Савара-Лапласа.



Где 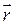

Направление 
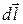



где α - угол между векторами 
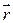
8. Магнитное поле прямого тока.

Из рисунка 
Следовательно
Угол α для всех элементов прямого провода
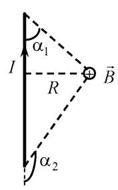

Если ток течет по отрезку провода (см. рисунок), то
Эта формула переходит в формулу для бесконечного длинного проводника при 
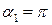
9. Магнитное поле в центре кругового тока.
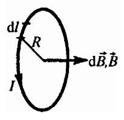
Можно показать, что на расстоянии r от центра витка вдоль оси витка магнитное поле будет равно
Напряженность магнитного поля, создаваемого круговым током, на большом расстоянии от витка стоком (r >> R)
где pm=IS – магнитный момент витка с током.

Очевидное подобие этих формул объясняет, почему часто говорят, что контур с током подобен “магнитному диполю”, имеющему равный с контуром магнитный момент.
10. Закон Ампера.



где 

Наглядно направление силы Ампера принято определять по правилу левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор 
11. Взаимодействие параллельных токов.
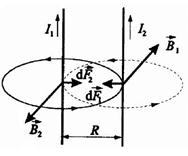
Два параллельных проводника с токами I1 и I2 находятся на расстоянии R друг от друга. Направление сил 


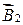
Отсюда: 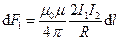

Проводники с токами одинакового направления притягиваются, с токами разного направления – отталкиваются.
12. Магнитная постоянная.
В системе СИ единица измерения силы тока – ампер – вместе с килограммом, метром и секундой является основной единицей. По определению “ампер есть сила неизменяющегося тока, который, проходя по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малого кругового сечения, расположенным на расстоянии 1 метра один от другого в вакууме, вызвал бы между этими проводниками силу, равную 2∙10 -7 ньютона на каждый метр длины”.
В вакууме (µ=1) сила взаимодействия на единицу длины проводника
При 
Отсюда
где генри (Гн) – единица индуктивности – будет определена позднее.
13. Единицы магнитной индукции и напряженности магнитного поля.
Пусть элемент проводника dl с током I перпендикулярен направлению магнитного поля. Закон Ампера dF = IBdl, откуда
Единица магнитной индукции В – тесла (Тл) – магнитная индукция такого однородного магнитного поля, которое действует с силой 1Н на каждый метр длины прямолинейного проводника, расположенного перпендикулярно направлению поля, если по этому проводнику проходит ток 1А:
Из формулы 
Единица напряженности магнитного поля Н – ампер на метр (А/м) –
напряженность такого поля, индукция которого в вакууме равна 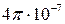
14. Магнитное поле свободно движущегося заряда.
Проводник с током создает вокруг себя магнитное поле. Электрический ток – это упорядоченное движение электрических зарядов. Магнитное поле 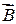
Где 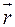
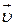
15. Сила Лоренца.
Так же как и на проводник с током, магнитное поле действует и на отдельный заряд, движущийся в магнитном поле.
Сила, действующая на электрический заряд q, движущийся в магнитном поле 

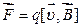
где α- угол между 
Сводная таблица.

Постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Движение заряда, на который кроме магнитного поля с индукцией 
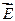
16. Движение заряженных частиц в магнитном поле.
Считаем, что магнитное поле однородно и на частицы не действуют электрические поля. Рассмотрим три возможных случая:
1. 
магнитной индукции (угол α между векторами 


2. 
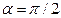
Сила Лоренца 
частицы. Частица будет двигаться по окружности радиуса R с центростремительным ускорением 

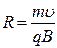
3.Заряженная частица движется под углом α к линиям магнитной
Движение частицы можно представить в виде суммы двух движений.
1)равномерного прямолинейного движения вдоль поля со скоростью
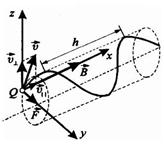
Суммарное движение будет движением по спирали, ось которой параллельна магнитному полю. Шаг винтовой линии 

Если магнитное поле неоднородно и заряженная частица движется под углом к линиям магнитного поля в направлении возрастания поля, то величины R и h уменьшаются с ростом 
17. Эффект Холла.
Эффект Холла – это возникновение электрического поля в проводнике или полупроводнике с током при помещении его в магнитное поле.
Эффект Холла – следствие влияния силы Лоренца на движение носителей тока. В магнитном поле 


Пусть, например, металлическая пластинка с током расположена в магнитном поле перпендикулярном току (см. рисунок). Сила Лоренца приводит к повышению концентрации носителей тока – электронов – у верхнего края пластинки.
При этом верхний край зарядится отрицательно, а нижний, соответственно – положительно. Стационарное распределение зарядов будет достигнуто, когда действие созданного таким образом электрического поля уравновесит силу Лоренца: 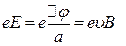


Поскольку сила тока 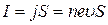

Знак постоянной Холла 
18. Теорема о циркуляции вектора

где 
составляющая вектора 


Теорема о циркуляции вектора 
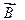

где n – число проводников с токами, охватываемых контуром L произвольной формы.
Эта теорема справедлива только для поля в вакууме, поскольку для поля в веществе надо учитывать молекулярные токи. Каждый ток учитывается столько раз, сколько он охватывается контуром. Положительным считается ток, направление которого связано с направлением обхода по контуру правилом правого винта.

В каждой точке этой окружности вектор 
отсюда
Сравним выражения для циркуляций векторов 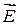
Принципиальное различие между этими формулами в том, что циркуляция вектора 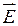

19. Магнитное поле соленоида.


На участках АВ и CD контур перпендикулярен линиям магнитной индукции, следовательно 
r 3 ). На участке DA контур совпадает с линией магнитной индукции, внутри соленоида поле однородно ( 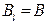
Магнитная индукция (бесконечного) соленоида в вакууме
20. Магнитное поле тороида в вакууме.
Тороидом – называется кольцевая катушка с витками, намотанными на сердечник, имеющий форму тора, по которой течет ток.
Магнитное поле отсутствует вне тороида, а внутри его оно является однородным.

В качестве контура выберем одну такую окружность радиуса r. По теореме о циркуляции 
21. Поток вектора магнитной индукции.
Потоком вектора магнитной индукции (магнитным потоком) через площадку dS называется скалярная физическая величина, равная
где 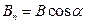
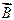
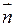
dS, α – угол между векторами 

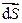
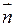
Поток вектора 
Поток вектора 
Поток вектора магнитной индукции через произвольную поверхность S
Если поле однородно и перпендикулярно ему расположена плоская поверхность с площадью S, то
Единица магнитного потока – вебер (Вб): 1В6 – магнитный поток, проходящий сквозь плоскую поверхность площадью 1м 2 , расположенную перпендикулярно однородному магнитному полю, индукция которого равна 1Тл (1 Вб=1 Тлм 2 ).
22. Теорема Гаусса для магнитного поля в вакууме
Поток вектора магнитной индукции сквозь любую замкнутую поверхность равен нулю
Эта теорема отражает факт отсутствия магнитных зарядов, вследствие чего линии магнитной индукции не имеют ни начала ни конца и являются замкнутыми.
Магнитный поток через поверхность, ограниченную замкнутым контуром, называется потокосцеплением 
Потокосцепление контура, обусловленное магнитным полем тока в самом этом контуре, называется потокосцеплением самоиндукции.
Например, найдем потокосцепление самоиндукции соленоида с сердечником с магнитной проницаемостью µ. Магнитный поток сквозь один
виток соленоида площадью S равен 
сцепленный со всеми витками соленоида равен
Потокосцепление контура, обусловленное магнитным полем тока, идущего в другом контуре, называется потокосцеплением взаимной индукции этих двух контуров.
24. Работа по перемещению проводника с током в магнитном поле.

Под ее действием проводник переместился из положения 1 в положение 2.
Работа, совершаемая магнитным полем:
dS = ldx – площадь, пересекаемая проводником при его перемещении в магнитном поле; BdS=dФ – поток вектора магнитной индукции, пронизывающий эту площадь. Таким образом,
Работа по перемещению проводника с током в магнитном поле равна произведению силы тока на магнитный поток, пересеченный движущимся проводником.
25. Работа по перемещению контура с током в магнитном поле.

сумме работ по перемещению проводников ABC (dAl) и CDA (dА2), т.е.
При перемещении участка CDA силы Ампера направлены в сторону перемещения (образуют с направлением перемещения острые углы), поэтому dА2 >0
Силы, действующие на участок ABC контура, направлены против перемещения (образуют с направлением перемещения тупые углы), поэтому dА1 > R0) ЭДС самоиндукции 

При замыкании цепи помимо внешней ЭДС 
Самоиндукции 

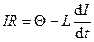

где 
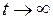
Таким образом, при включении источника тока сила тока возрастает по экспоненциальному закону (а не мгновенно).
34. Взаимная индукция

Рассмотрим два неподвижных контура 1 и 2 с токами I1 и I2, расположенных достаточно близко друг от друга. При протекании в контуре 1 тока I1 магнитный поток пронизывает второй контур
Коэффициенты пропорциональности L21 и L12 равны друг другу L12 = L2l = L и называются взаимной индуктивностью контуров.
При изменении силы тока в одном из контуров, в другом индуцируется
Взаимная индуктивность контуров зависит от геометрической формы, размеров, взаимного расположения контуров и от магнитной проницаемости окружающей контуры среды.
Для примера рассчитаем взаимную индуктивность двух катушек, намотанных на тороидальный сердечник.


где l – длина сердечника по средней линии. Тогда полный магнитный поток (потокосцепление) сквозь вторичную обмотку, содержащую N2 витков: 

Данное устройство является примером трансформатора.
Принцип действия трансформаторов, применяемых для повышения или понижения напряжения переменного тока, основан на явлении взаимной индукции. Переменный ток I1 создает в первичной обмотке переменное магнитное поле. Это вызывает во вторичной обмотке появление ЭДС взаимной индукции. При этом 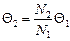
где jVj и N2 – число витков в первичной и вторичной обмотках, соответственно.
Отношение 
Если k> 1, то трансформатор – повышающий, если k 11 – удельный заряд электрона.
Кроме орбитальных моментов, электрон обладает собственным механическим моментом импульса Ls, называемый спином.
Спину электрона соответствует собственный (спиновый) магнитный момент 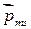

где 
единицей магнитного момента электрона.
Общий магнитный момент атома или молекулы равен векторной сумме магнитных моментов (орбитальных и спиновых) входящих в атом (молекулу) электронов
Магнитные моменты атомных ядер в тысячи раз меньше магнитных моментов электронов, поэтому ими как правило пренебрегают.
38.Диа- и парамагнетики.

На вращающийся по орбите электрон, как на замкнутый ток, в магнитном поле действует вращающий момент сил. В результате электрон получает дополнительное равномерное вращение, при котором вектор 
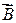
Теорема Лармора: действие магнитного поля на электронную орбиту можно свести ксообщению этой орбите прецессии с угловой скоростью
Прецессионное движение электронных орбит эквивалентно круговому микротоку. Так как этот микроток индуцирован внешним магнитным полем, то, согласно правилу Ленца, у атома появляется магнитный момент, направленный против внешнего поля.
Наведенные составляющие магнитных полей атомов складываются и образуют собственное магнитное поле вещества, ослабляющее внешнее магнитное поле. Этот эффект получил название диамагнитного эффекта, а вещества, намагничивающиеся во внешнем магнитном поле против направления поля, называются диамагнетиками (например, Ag, Au, Си. ).
Так как диамагнитный эффект обусловлен действием внешнего магнитного поля на электроны атомов вещества, то диамагнетизм свойствен всем веществам.
Наряду с диамагнитными веществами существуют и парамагнитные – вещества, намагничивающиеся во внешнем магнитном поле по направлению поля (пример: редкоземельные металлы, Pt, А1. ).
У парамагнитных веществ при отсутствии внешнего магнитного поля магнитные моменты электронов не компенсируют друг друга, и молекулы парамагнетиков всегда обладают магнитным моментом (такие молекулы называются полярными).
Вследствие теплового движения молекул их магнитные моменты ориентированы беспорядочно, поэтому, в отсутствие магнитного поля, парамагнитные вещества магнитными свойствами не обладают.
При внесении парамагнетика во внешнее магнитное поле устанавливается преимущественная ориентация магнитных моментов атомов (молекул) по полю (полной ориентации препятствует тепловое движение атомов).
Дата добавления: 2014-10-31 ; просмотров: 536 ; Нарушение авторских прав
Магнитное поле и его характеристики
теория по физике 🧲 магнетизм
Магнитное поле — особая форма материи, посредством которой осуществляется взаимодействие между движущимися электрическими частицами.
Основные свойства магнитного поля
- Магнитное поле порождается электрическим током (движущимися зарядами).
- Магнитное поле обнаруживается по действию на электрический ток (движущиеся заряды).
- Магнитное поле существует независимо от нас, от наших знаний о нем.
Вектор магнитной индукции
Вектор магнитной индукции — силовая характеристика магнитного поля. Она определяет, с какой силой магнитное поле действует на заряд, движущийся в поле с определенной скоростью. Обозначается как → B . Единица измерения — Тесла (Тл).
За единицу магнитной индукции можно принять магнитную индукцию однородного поля, котором на участок проводника длиной 1 м при силе тока в нем 1 А действует со стороны поля максимальная сила, равна 1 Н. 1 Н/(А∙м) = 1 Тл.
Модуль вектора магнитной индукции — физическая величина, равная отношению максимальной силы, действующей со стороны магнитного поля на отрезок проводника с током, к произведению силы тока и длины проводника:
B = F A m a x I l . .
За направление вектора магнитной индукции принимается направление от южного полюса S к северному N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Наглядную картину магнитного поля можно получить, если построить так называемые линии магнитной индукции. Линиями магнитной индукции называют линии, касательные к которым направлены так же, как и вектор магнитной индукции в данной точке поля.
Особенность линий магнитной индукции состоит в том, что они не имеют ни начала, ни конца. Они всегда замкнуты. Поля с замкнутыми силовыми линиями называют вихревыми. Поэтому магнитное поле — вихревое поле.
Замкнутость линий магнитной индукции представляет собой фундаментальное свойство магнитного поля. Оно заключается в том, что магнитное поле не имеет источников. Магнитных зарядов, подобным электрическим, в природе нет.
Напряженность магнитного поля
Вектор напряженности магнитного поля — характеристика магнитного поля, определяющая густоту силовых линий (линий магнитной индукции). Обозначается как → H . Единица измерения — А/м.
μ — магнитная проницаемость среды (у воздуха она равна 1), μ 0 — магнитная постоянная, равная 4 π · 10 − 7 Гн/м.
Внимание! Направление напряженности всегда совпадает с направлением вектора магнитной индукции: → H ↑↑ → B .
Направление вектора магнитной индукции и способы его определения
Чтобы определить направление вектора магнитной индукции, нужно:
- Расположить в магнитном поле компас.
- Дождаться, когда магнитная стрелка займет устойчивое положение.
- Принять за направление вектора магнитной индукции направление стрелки компаса «север».
В пространстве между полюсами постоянного магнита вектор магнитной индукции выходит из северного полюса:
При определении направления вектора магнитной индукции с помощью витка с током следует применять правило буравчика:
При вкручивании острия буравчика вдоль направления тока рукоятка будет вращаться по направлению вектора → B магнитной индукции.
Отсюда следует, что:
- Если по витку ток идет против часовой стрелки, то вектор магнитной индукции → B направлен вверх.
- Если по витку ток идет по часовой стрелке, то вектор магнитной индукции → B направлен вниз.
Способы обозначения направлений векторов:
- II. Объем и сроки выполнения задач в рамках проекта
- VII. Описание учебно-методического и материально-технического обеспечения образовательного процесса по предмету «Технология» (направление «Технический труд»).
- Алгоритм позиционирования товаров в рамках формирования товарной линии
- Анализ неоднородности магнитного поля над дефектом
- Аномалии магнитного поля Земли.
- Атеистическо-материалистическое направление философии французского Просвещения XVIII в.
- Биологическое действие СВЧ-поля.
- Быстропеременные региональные поля или (в других источниках литературы) переменные низкочастотные поля.
- В. Консервативное направление. Либеральное направление. Западники и славянофилы
- Взаимодействие электромагнитного поля и движущегося заряда.
| Вверх |  |
| Вниз |  |
| Влево |  |
| Вправо | 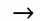 |
| На нас перпендикулярно плоскости чертежа |  |
| От нас перпендикулярно плоскости чертежа |  |
Пример №1. На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен (вверх, вниз, влево, вправо, от наблюдателя, к наблюдателю) вектор магнитной индукции в точке С?
Если мысленно начать вкручивать острие буравчика по направлению тока, то окажется, что вектор магнитной индукции в точке С будет направлен к нам — к наблюдателю.
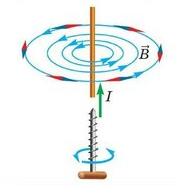
Магнитное поле прямолинейного тока
Линии магнитной индукции представляют собой концентрические окружности, лежащие в плоскости, перпендикулярной проводнику. Центр окружностей совпадает с осью проводника.
Если ток идет вверх, то силовые линии направлены против часовой стрелки. Если вниз, то они направлены по часовой стрелке. Их направление можно определить с помощью правила буравчика или правила правой руки:
Правило буравчика (правой руки)
Если большой палец правой руки, отклоненный на 90 градусов, направить в сторону тока в проводнике, то остальные 4 пальца покажут направление линий магнитной индукции.
Модуль вектора магнитной индукции на расстоянии r от оси проводника:
B = μ μ 0 I 2 π r . .
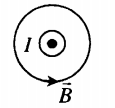
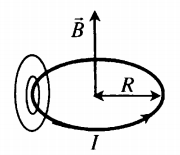
Магнитное поле кругового тока
Силовые линии представляют собой окружности, опоясывающие круговой ток. Вектор магнитной индукции в центре витка направлен вверх, если ток идет против часовой стрелки, и вниз, если по часовой стрелке.
Определить направление силовых линий магнитного поля витка с током можно также с помощью правила правой руки:
Если расположить четыре пальца правой руки по направлению тока в витке, то отклоненный на 90 градусов большой палец, покажет направление вектора магнитной индукции.
Модуль вектора магнитной индукции в центре витка, радиус которого равен R:
Модуль напряженности в центре витка:
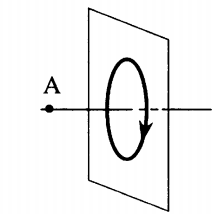
Пример №2. На рисунке изображен проволочный виток, по которому течет электрический ток в направлении, указанном стрелкой. Виток расположен в вертикальной плоскости. Точка А находится на горизонтальной прямой, проходящей через центр витка. Как направлен (вверх, вниз, влево, вправо) вектор магнитной индукции магнитного поля в точке А?
Если мысленно обхватить виток так, чтобы четыре пальца правой руки были бы направлены в сторону тока, то отклоненный на 90 градусов большой палец правой руки показал бы, что вектор магнитной индукции в точке А направлен вправо.
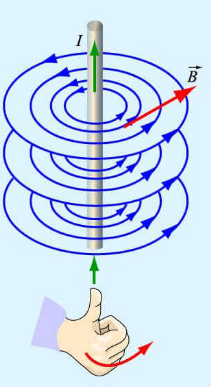
Магнитное поле электромагнита (соленоида)
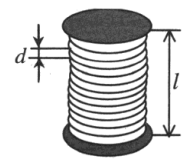
Соленоид — это катушка цилиндрической формы, витки которой намотаны вплотную, а длина значительно больше диаметра.
Число витков в соленоиде N определяется формулой:
l — длина соленоида, d — диаметр проволоки.
Линии магнитной индукции являются замкнутыми, причем внутри соленоида они располагаются параллельно друг другу. Поле внутри соленоида однородно.
Если ток по виткам соленоида идет против часовой стрелки, то вектор магнитной индукции → B внутри соленоида направлен вверх, если по часовой стрелке, то вниз. Для определения направления линий магнитной индукции можно воспользоваться правилом правой руки для витка с током.
Модуль вектора магнитной индукции в центральной области соленоида:
B = μ μ 0 I N l . . = μ μ 0 I d . .
Модуль напряженности магнитного поля в центральной части соленоида:
H = I N l . . = I d . .
Алгоритм определения полярности электромагнита
- Определить полярность источника.
- Указать на витках электромагнита условное направление тока (от «+» источника к «–»).
- Определить направление вектора магнитной индукции.
- Определить полюса электромагнита. Там, откуда выходят линии магнитной индукции, располагается северный полюс электромагнита (N, или «–». С противоположной стороны — южный (S, или «+»).
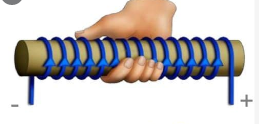
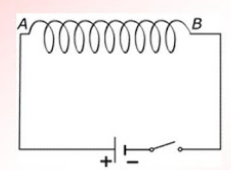
Пример №3. Через соленоид пропускают ток. Определите полюсы катушки.
Ток условно течет от положительного полюса источника тока к отрицательному. Следовательно, ток течет по виткам от точки А к точке В. Мысленно обхватив соленоид пальцами правой руки так, чтобы четыре пальца совпадали с направлением тока в витках соленоида, отставим большой палец на угол 90 градусов. Он покажет направление линий магнитной индукции внутри соленоида. Проделав это, увидим, что линии магнитной индукции направлены вправо. Следовательно, они выходят из В, который будет являться северным полюсом. Тогда А будет являться южным полюсом.
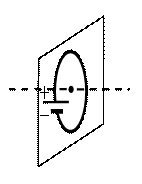
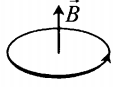
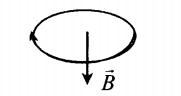
а) вертикально вверх в плоскости витка
б) вертикально вниз в плоскости витка
в) вправо перпендикулярно плоскости витка
г) влево перпендикулярно плоскости витка
Алгоритм решения
Решение
По условию задачи мы имеем дело с круглым проволочным витком. Поэтому для определения вектора → B магнитной индукции мы будем использовать правило правой руки.
Чтобы применить это правило, нам нужно знать направление течение тока в проводнике. Условно ток течет от положительного полюса источника к отрицательному. Следовательно, на рисунке ток течет по витку в направлении хода часовой стрелки.
Теперь можем применить правило правой руки. Для этого мысленно направим четыре пальца правой руки в направлении тока в проволочном витке. Теперь отставим на 90 градусов большой палец. Он показывает относительно рисунка влево. Это и есть направление вектора магнитной индукции.
pазбирался: Алиса Никитина | обсудить разбор | оценить
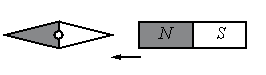
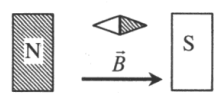
а) повернётся на 180°
б) повернётся на 90° по часовой стрелке
в) повернётся на 90° против часовой стрелки
г) останется в прежнем положении
Алгоритм решения
- Вспомнить, как взаимодействуют магниты.
- Определить исходное положение полюсов.
- Определить конечное положение полюсов и установить, как изменится положение магнитной стрелки.
Решение
Одноименные полюсы магнитов отталкиваются, а разноименные притягиваются. Изначально южный полюс магнитной стрелки находится справа, а северный — слева. Полосовой магнит подносят к ее южному полюсу северной стороной. Поскольку это разноименные полюса, положение магнитной стрелки не изменится.
pазбирался: Алиса Никитина | обсудить разбор | оценить
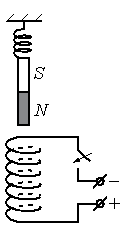
Алгоритм решения
- Определить направление тока в соленоиде.
- Определить полюса соленоида.
- Установить, как будет взаимодействовать соленоид с магнитом.
- Установить, как будет себя вести магнит после замыкания электрической цепи.
Решение
Чтобы определить направление тока в соленоиде, посмотрим на расположение полюсов источника тока. Ток условно направлен от положительного полюса к отрицательному. Следовательно, относительно рисунка ток в витках соленоида направлен по часовой стрелке.
Зная направление тока в соленоиде, можно определить его полюса. Северным будет тот полюс, из которого выходят линии магнитной индукции. Определить их направление поможет правило правой руки для соленоида. Мысленно обхватим соленоид так, чтобы направление четырех пальцев правой руки совпадало с направлением тока в витках соленоида. Теперь отставленный на 90 градусов большой палец покажет направление вектора магнитной индукции. Проделав все манипуляции, получим, что вектор магнитной индукции направлен вниз. Следовательно, внизу соленоида расположен северный полюс, а вверху — южный.
Известно, что одноименные полюса магнитов отталкиваются, а разноименные — притягиваются. Подвешенный полосовой магнит обращен к южному полюсу соленоида северным полюсом. А это значит, что при замыкании электрической цепи он будет растягивать пружину, притягиваясь к соленоиду (двигаться вниз).
pазбирался: Алиса Никитина | обсудить разбор | оценить
Физика. 11 класс
Конспект урока
Физика, 11 класс
Урок 3. Магнитная индукция. Действие магнитного поля на проводник и движущуюся заряжённую частицу
Перечень вопросов, рассматриваемых на уроке:
1) магнитное поле;
2) вектор магнитной индукции, линии магнитной индукции;
3) сила Ампера, сила Лоренца;
4) правило буравчика, правило левой руки.
Глоссарий по теме
Магнитная индукция – векторная величина, характеризующая величину и направление магнитного поля.
Сила Ампера – сила, действующая со стороны магнитного поля на проводник с током.
Сила Лоренца – сила, действующая со стороны магнитного поля на движущую частицу с зарядом.
Правило «буравчика» – правило для определения направления магнитного поля проводника с током.
Правило левой руки – правило для определения направления силы Ампера и силы Лоренца.
Соленоид – проволочная катушка.
Рамка с током – небольшой длины катушка с двумя выводами из скрученного гибкого проводника с током, способная поворачиваться вокруг оси, проходящей через диаметр катушки.
Основная и дополнительная литература по теме урока
Мякишев Г.Я., Буховцев Б.Б. Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций. М.: Просвещение, 2014. – С. 3 – 20
2. А.П. Рымкевич. Сборник задач по физике. 10-11 классы. – М: Дрофа, 2009. – С.109 – 112
Основное содержание урока
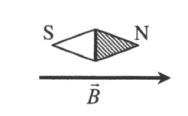
Магнитное поле – особый вид материи, которая создаётся электрическим током или постоянными магнитами. Для демонстрации действия и доказательства существования магнитного поля служат магнитная стрелка, способная вращаться на оси, или небольшая рамка (или катушка) с током, подвешенная на тонких скрученных гибких проводах.
Рамка с током и магнитная стрелка под действием магнитного поля поворачиваются так, что северный полюс (синяя часть) стрелки и положительная нормаль рамки указывают направление магнитного поля.
Магнитное поле, созданное постоянным магнитом или проводником с током, занимает всё пространство в окрестности этих тел. Магнитное поле принято (удобно) изображать в виде линий, которые называются линиями магнитного поля. Магнитные линии имеют вихревой характер, т.е. линии не имеют ни начала, ни конца, т.е. замкнуты. Направление касательной в каждой точке линии совпадает с направлением вектора магнитной индукции. Поля с замкнутыми линиями называются вихревыми.
Магнитное поле характеризуется векторной величиной, называемой магнитной индукцией. Магнитная индукция характеризует «силу» и направление магнитного поля – это количественная характеристика магнитного поля.
Она обозначается символом За направление вектора магнитной индукции принимают направление от южного полюса к северному магнитной стрелки, свободно установившейся в магнитном поле.
Направление магнитного поля устанавливают с помощью вектора магнитной индукции.
Направление вектора магнитной индукции прямого провода с током определяют по правилу буравчика (или правого винта).
Правило буравчика звучит следующим образом:
если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика совпадает с направлением линий магнитного поля тока.
Направление магнитного поля внутри соленоида определяют по правилу правой руки.
Определим модуль вектора магнитной индукции.
Наблюдения показывают, что максимальное значение силы, действующей на проводник, прямо пропорционально силе тока, длине проводника, находящегося в магнитном поле.
Тогда, зависимость силы от этих двух величин выглядит следующим образом
Отношение зависит только от магнитного поля и может быть принята за характеристику магнитного поля в данной точке.
Величина, численно равная отношению максимальной силы, действующей на проводник с током, на произведение силы тока и длины проводника, называется модулем вектора магнитной индукции:
Единицей измерения магнитной индукции является 1 тесла (Тл).
Сила, действующая на проводник с током в магнитном поле, равна произведению модуля магнитной индукции, силы тока, длины проводника и синуса угла между вектором магнитной индукции и направлением тока:
где α – угол между вектором B и направлением тока.
Направление силы Ампера определяется правилом левой руки:
Если ладонь левой руки развернуть так, чтобы линии магнитной индукции входили в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90 0 большой палец покажет направление силы Ампера.
Сила Ампера – сила, действующая на проводник с током со стороны магнитного поля.
Сила Лоренца – сила, действующая на движущуюся заряженную частицу со стороны магнитного поля. Её численное значение равно произведению заряда частицы на модули скорости и магнитной индукции и синус угла меду векторами скорости и магнитной индукции:
– заряд частицы;
– скорость частицы;
B – модуль магнитной индукции;
– угол между векторами скорости частицы и магнитной индукции.
Направление силы Лоренца также определяют по правилу левой руки:
Если четыре вытянутых пальца левой руки направлены вдоль вектора скорости заряженной частицы, а вектор магнитной индукции направлен в ладонь, то отведённый на 90 0 большой палец покажет направление силы Лоренца. Если частица имеет заряд отрицательного знака, то направление силы Лоренца противоположно тому направлению, которое имела бы положительная частица.
Получим формулы для радиуса окружности и периода вращения частицы, которая влетает в однородное магнитное поле перпендикулярно линиям магнитной индукции, применяя формулы второго закона Ньютона и центростремительного ускорения.
Согласно 2-му закону Ньютона
Время, за которое частица делает полный оборот (период обращения), равно:
Многим юным бывает досадно, что они не родились в старые времена, когда делались открытия. Им кажется, что теперь всё известно и никаких открытий на их долю не осталось.
Одной из нераскрытых тайн является механизм земного магнитного поля. Как же и чем вызывается магнитное поле Земли? Подумайте и может быть…
Одна из возможных гипотез.
Как известно, ядро Земли имеет высокую температуру
и высокую плотность. Судя по исследованиям, в самом центре содержится твёрдое ядро. При вращении Земли вокруг своей оси центр тяжести не совпадает с геометрическим центром из-за притяжения Солнца. В результате сместившееся из центра ядро вращаясь относительно оболочки Земли вызывает такое же движение жидкой расплавленной массы мантии, как чайная ложка, перемешивающая воду в стакане. Получается не что иное, как направленное движение зарядов. Есть электрический ток, а он, в свою очередь, создаёт магнитное поле.
Разбор тренировочных заданий
1. На рисунке изображён проводник с током, помещённый в магнитное поле. Стрелка указывает направление тока в проводнике. Вектор магнитной индукции направлен перпендикулярно плоскости рисунка к нам. Как направлена сила, действующая на проводник с током?
– точка означает, что магнитная индукция направлена на нас из глубины плоскости рисунка.
Используя правило левой руки, определяем направление силы Ампера:
Левую руку располагаем так, чтобы линии магнитной индукции входили в ладонь, 4 пальца направим вниз по направлению тока, тогда отогнутый на 90 0 большой палец покажет направление силы Ампера, т. е. она направлена влево.
2. По проводнику длиной 40 см протекает ток силой 10 А. Чему равна индукция магнитного поля, в которое помещён проводник, если на проводник действует сила 8 мН?
(Ответ выразите в мТл).
3. Определите модуль силы, действующей на проводник длиной 50 см при силе тока 10 А в магнитном поле с индукцией 0,15 Тл. (Ответ выразите в мН).
4. Протон в магнитном поле с индукцией 0,01 Тл описал окружность радиусом 10 см. Найдите скорость протона. (Ответ выразите в км/с, округлив до десятков)
5. С какой скоростью влетает электрон в однородное магнитное поле (индукция 1,8 Тл) перпендикулярно к линиям индукции, если магнитное поле действует на него с силой 3,6∙10 – ¹² Н? Ответ выразите в км/с.
6. Электрон движется в однородном магнитном поле с индукцией 3,14мТл. Чему равен период обращения электрона? (Ответ выразите в наносекундах, округлив до целых)
Запишем формулу модуля магнитной индукции:
B = 0,008 Н / ( 0,4м·10 A) = 0,002 Tл = 2 мTл.
Запишем формулу силы Ампера:
F = 0,l5 Tл· 10 A· 0,5 м = 0,75 Н = 750 мН
Заряд протона равен: q₀ = l,6·l0⁻ˡ⁹ Кл,
масса протона: m = l,67·l0⁻²⁷ кг.
Согласно 2-му закону Ньютона:
v = ( l,6·l0⁻ˡ⁹ Кл·0,l м·0,0l Tл) / l,67·l0⁻²⁷ кг ≈ 0,00096·l0⁸ м/с ≈ l00 км/с.
Ответ: v ≈ l00 км/с.
Найти:
Заряд электрона равен: q₀ = l,6·l0⁻ˡ⁹ Кл.
Используем формулу силы Лоренца:
.
Выразим из формулы силы скорость, учитывая, что sin90°=l,
v = 3,6·l0⁻¹² Н / (l,6·l0⁻ˡ⁹ Кл· l,8 Tл) = l,25·l0⁷м/с = l2500 км/с.
Ответ: v = l2500 км/с.
B = 3,l4 мТл = 3,l4·l0⁻³ Tл,
Масса электрона равна: m = 9,l·l0⁻³¹ кг.
Время, за которое частица делает полный оборот (период обращения), равно:
T = 2·3,l4·9,l·l0⁻³¹ кг/( l,6·l0⁻ˡ⁹ Кл·3,l4·l0⁻³ Tл) = ll,375·l0⁻⁹ с ≈ ll нс.
[spoiler title=”источники:”]
http://resh.edu.ru/subject/lesson/3806/conspect/
[/spoiler]
Решение:
На проводник действуют: две одинаковые силы натяжения нитей Т, сила тяжести mg и сила
со стороны магнитного поля, где α — угол между направлениями тока I и магнитной индукции (в нашем случае α = 90° и sinα = 1). Подразумевается, что направления тока и магнитной индукции таковы, что сила F направлена вниз (рис. 140). В противном случае силы натяжения нитей при пропускании тока не возрастают, а уменьшаются, и нити не оборвутся.
Если проводник находится в равновесии, то
отсюда
Для разрыва одной из нитей необходимо выполнение условия
или
6 На прямой проводник длины l=0,5 м, расположенный перпендикулярно к линиям индукции магнитного поля, действует сила F=0,15 Н. Найти ток I, протекающий в проводнике, если магнитная индукция B = 20 мТл.
Решение:
Если проводник расположен перпендикулярно к направлению магнитной индукции, то F=BIl, где I-ток в проводнике; отсюда I=F/Bl=15 А.
7 Между полюсами магнита подвешен горизонтально на двух невесомых нитях прямой проводник длины l=0,2 м и массы m=10 г. Индукция однородного магнитного поля B = 49 мТл и перпендикулярна к проводнику. На какой угол α от вертикали отклонятся нити, поддерживающие проводник, если по нему пропустить ток I=2 А?
Решение: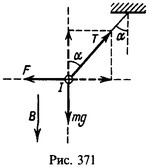
отсюда
8 Найти напряженность Н и индукцию B магнитного поля прямого тока в точке, находящейся на расстоянии r=4м от проводника, если ток I=100 А.
Решение:
9 ГОСТ 8.417—81 дает такое определение единицы силы тока — ампера: «Ампер равен силе неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожной малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 м один от другого, вызвал бы на каждом участке проводника длины 1 м силу взаимодействия, равную ». Исходя из этого определения, вычислить магнитную постоянную mo.
Решение:
Вокруг бесконечно длинного прямолинейного проводника, по которому течет ток I1 образуется магнитное поле, напряженность которого на расстоянии r от проводника
а индукция
При этом векторы Н и В направлены одинаково и лежат в плоскости, перпендикулярной к проводнику. На отрезок второго проводника длины l, по которому течет ток I2, магнитное поле действует с силой
где α — угол между направлениями отрезка проводника и магнитной индукции. Так как второй проводник параллелен первому, то α = 90° и sinα = 1. Таким образом,
Подставив значения
найдем
10 Индукция однородного магнитного поля B=0,5 Тл. Найти магнитный поток через площадку S=25 см2, расположенную перпендикулярно к линиям индукции. Чему будет равен магнитный поток, если площадку повернуть на угол α = 60° от первоначального положения?
Решение: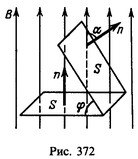
где α — угол между нормалью n к площадке и направлением магнитной индукции В. В первом случае
во втором случае α=φ (углы с взаимно перпендикулярными сторонами) и
11 Найти магнитную индукцию и магнитный поток через поперечное сечение никелевого сердечника соленоида (рис. 141), если напряженность однородного магнитного поля внутри соленоида H=25 кА/м. Площадь поперечного сечения сердечника S=20 см2, магнитная проницаемость никеля μ = 200.
Решение:
12 Магнитный поток через поперечное сечение катушки, имеющей n=1000 витков, изменился на величину ΔФ = 2 мВб в результате изменения тока в катушке от I1 = 4 А до I2 = 20А. Найти индуктивность L катушки.
Решение:
13 Виток площади S = 2 см2 расположен перпендикулярно к линиям индукции однородного магнитного поля. Найти индуцируемую в витке э.д.с, если за время Δt = 0,05 с магнитная индукция равномерно убывает от B1=0,5Тл до В2 = 0,1 Тл.
Решение:
14 Какой магнитный поток пронизывал каждый виток катушки, имеющей n =1000 витков, если при равномерном исчезновении магнитного поля в течение времени Δt = 0,1 с в катушке индуцируется э.д.с. ε = 10 В?
Решение:
15 Рамка в форме равностороннего треугольника помещена в однородное магнитное поле с напряженностью H=64кА/м. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 30°. Найти длину стороны рамки а, если в рамке при выключении поля в течение времени Δt = 0,03 с индуцируется э. д. с. ε = 10 мВ.
Решение:
Начальный магнитный поток через рамку
где
площадь рамки и B=µ0H-магнитная индукция. Конечный магнитный поток Ф2=0. Изменение магнитного потока
Э.д.с. индукции
отсюда
16 Квадратная рамка со стороной а=10см помещена в однородное магнитное поле. Нормаль к плоскости рамки составляет с линиями индукции магнитного поля угол α = 60°. Найти магнитную индукцию В этого поля, если в рамке при выключении поля в течение времени Δt = 0,01 с индуцируется э.д.с. ε = 50 мВ.
Решение:
17 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле перпендикулярно к линиям индукции. Сопротивление витка R=1 Ом. Какой ток I протечет по витку, если магнитная индукция поля будет убывать со скоростью ΔB/Δt = 0,01 Тл/с?
Решение:
18 Плоский виток площади S= 10 см2 помещен в однородное магнитное поле с напряженностью H=80 кА/м, перпендикулярное к линиям индукции. Сопротивление витка R = 1 Ом. Какой заряд протечет по витку, если поле будет исчезать с постоянной скоростью?
Решение:
19 Какова индуктивность катушки с железным сердечником, если за время Δt = 0,5 с ток в цепи изменился от I1 = 10 А до I2 = 5 А, а возникшая при этом э.д.с. самоиндукции ε = 25 В?
Решение:
Э.д.с. самоиндукции
отсюда
20 Проводник длины l=2 м движется в однородном магнитном поле со скоростью v = 5 м/с, перпендикулярной к проводнику и линиям индукции поля. Какая э. д. с. индуцируется в проводнике, если магнитная индукция B=0,1 Тл?
Решение: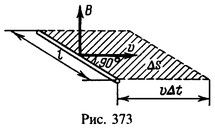
магнитный поток через площадь ΔS, «заметаемую» проводником за время Δt (рис. 373). Опуская знак минус, найдем
21 Самолет летит горизонтально со скоростью v = 900 км/ч. Найти разность потенциалов, возникающую между концами крыльев самолета, если вертикальная составляющая индукции земного магнитного поля Bo = 0,5 мкТл и размах крыльев самолета l=12 м.
Решение:
Крылья самолета за время Δt «заметают» площадь
Магнитный поток через эту площадь равен
где
вертикальная составляющая индукции земного магнитного поля (α — угол между вертикалью и направлением магнитной индукции). Разность потенциалов V между концами крыльев самолета равна э.д.с. ε, индуцируемой в металлических крыльях и корпусе самолета при его движении в магнитном поле Земли:
22 С какой скоростью должен двигаться проводник длины l=10 см перпендикулярно к линиям индукции однородного магнитного поля, чтобы между концами проводника возникла разность потенциалов V=0,01 В? Скорость проводника составляет с направлением самого проводника угол α = 30°. Линии индукции перпендикулярны к проводнику, индукция B = 0,2 Тл.
Решение: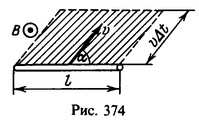
Магнитный поток через эту площадь
Разность потенциалов V между концами проводника равна э.д.с. ε, индуцируемой в этом проводнике:
23 Какой ток идет через гальванометр, присоединенный к железнодорожным рельсам, при приближении к нему поезда со скоростью v = 60 км/ч? Вертикальная составляющая индукции земного магнитного поля Bо=50 мкТл. Сопротивление гальванометра R=100 Ом. Расстояние между рельсами l=1,2 м; рельсы считать изолированными друг от друга и от земли.
Решение:
24 Квадратная рамка со стороной l=2 см помещена в однородное магнитное поле с индукцией B = 100 Тл. Плоскость рамки перпендикулярна к линиям индукции поля. Сопротивление рамки R=1 Ом. Какой ток протечет по рамке, если ее выдвигать из магнитного поля со скоростью ν = 1 см/с, перпендикулярной к линиям индукции? Поле имеет резко очерченные границы, и стороны рамки параллельны этим границам.
Решение: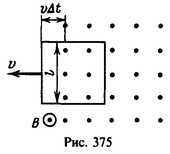
при движении рамки не изменяется. Поэтому э.д.с. индукции в рамке не возникает. После того как одна из сторон рамки вышла за границу поля (рис. 375), магнитный поток через поверхность, ограниченную рамкой, будет изменяться. За время Δt рамка перемещается на расстояние νΔt и часть площади рамки, которую пересекает магнитное поле, уменьшается на величину
Магнитный поток за это время изменяется на величину
Индуцируемая в рамке э.д.с.
и по рамке протечет ток
Когда рамка выйдет из области, где имеется магнитное поле, э.д.с. индукции снова станет равной нулю.
25 Проволочный виток площади S= 1 см2, имеющий сопротивление R = 1 мОм, пронизывается однородным магнитным полем, линии индукции которого перпендикулярны к плоскости витка. Магнитная индукция изменяется со скоростью ΔB/Δt = 0,01 Тл/с. Какое количество теплоты выделяется в витке за единицу времени?
Решение:
26 Прямоугольная рамка, подвижная сторона которой имеет длину l, помещена в однородное магнитное поле с индукцией B. Плоскость рамки перпендикулярна к линиям индукции магнитного поля. Подвижную сторону, которая вначале совпадает с противоположной ей неподвижной, начинают двигать равномерно со скоростью ν. Найти зависимость тока I в рамке от времени t. Сопротивление единицы длины проводника равно Rl.
Решение:
27 Два параллельных, замкнутых на одном конце провода, расстояние между которыми l=50 см, находятся в однородном магнитном поле с индукцией B = 5 мТл. Плоскость, в которой расположены провода, перпендикулярна к линиям индукции поля. На провода положен металлический мостик, который может скользить по проводам без трения. Мостик под действием силы F=0,1 мН движется со скоростью ν=10м/с. Найти сопротивление R мостика. Сопротивлением проводов пренебречь.
Решение:
28 Рамка из n = 1000 витков, имеющих площадь S = 5 см2, замкнута на гальванометр с сопротивлением R=10 кОм и помещена в однородное магнитное поле с индукцией B=10мТл, причем линии индукции поля перпендикулярны к ее плоскости. Какой заряд q протечет по цепи гальванометра, если направление индукции магнитного поля плавно изменить на обратное?
Решение:
При плавном изменении магнитной индукции в рамке индуцируется э.д.с.
где ΔФ-изменение магнитного потока, Δt — время, в течение которого происходило это изменение. Ток в рамке
Заряд, протекший по цепи за время Δt,
Начальный поток магнитной индукции
При изменении направления магнитного поля на обратное магнитный поток изменяет знак. Поэтому конечный магнитный поток
Изменение магнитного потока
Таким образом,
29 Замкнутая катушка диаметра D с числом витков n помещена в однородное магнитное поле с индукцией В. Плоскость катушки перпендикулярна к линиям индукции поля. Какой заряд q протечет по цепи катушки, если ее повернуть на 180? Проволока, из которой намотана катушка, имеет площадь сечения S и удельное сопротивление ρ.
Решение:
30 В цепь включены последовательно источник тока с э.д.с. ε = 1,2 В, реостат с сопротивлением R=1 Ом и катушка с индуктивностью L=1 Гн. В цепи протекал постоянный ток I0. С некоторого момента сопротивление реостата начинают менять так, чтобы ток уменьшался с постоянной скоростью ΔI/Δt = 0,2 А/с. Каково сопротивление R, цепи спустя время t = 2 с после начала изменения тока?
Решение:
Сумма э.д.с. источника тока и э.д.с, индуцируемой в цепи при равномерном изменении тока, равна
Ток изменяется
по закону
Сопротивление цепи в любой момент времени
В момент времени t= 2 с искомое сопротивление Rt= 1,75 0м.
31 Какой ток I покажет амперметр в схеме, изображенной на рис. 142, если индукция перпендикулярного к плоскости рисунка однородного магнитного поля меняется с течением времени по закону B = kt? Точки с и d лежат на концах диаметра проволочного кольца. Сопротивление единицы длины проволоки равно Rl; диаметр кольца равен D.
Рассчитаем
напряженность магнитного поля в центре
контура прямоугольной формы (рис.
16.4.1). Стороны прямоугольника равны a
и b,
сила тока в проводнике
I.
Разделим контур на четыре прямолинейных
отрезка конечной длины. Применяя правило
буравчика, убеждаемся, что напряженности
магнитных полей, созданных каждым
отрезком проводника в центре контура,
направлены одинаково (от нас).
В
соответствии с принципом суперпозиции
для них можно записать
.
Симметрия рамки
приводит к тому, что противоположные
стороны прямоугольного контура создают
одинаковые поля, поэтому в скалярной
форме получаем
.
(16.4.1)
Пусть отрезок
проводника MN
создает в т.О магнитное поле напряженностью
Н1,
для которого применим формулу напряженности
проводника конечной длины
.
Из чертежа для
прямоугольного треугольника MOF
получаем
,
где
гипотенуза треугольника МОF
с
= МО,
.
Разность косинусов
равна
=
.
Для напряженности
магнитного поля можно записать
.
Гипотенузу МО
треугольника MOF
определим, применив теорему Пифагора
=
.
Напряженность
магнитного поля, созданного отрезком
проводника MN,
равна
.
(16.4.2)
Аналогично
напряженность магнитного поля, созданного
отрезком проводника NL,
имеет следующий вид:
.
(16.4.3)
Подставляя формулы
(16.4.2) и (16.4.3) в формулу (16.4.1), получаем
.
После сокращения
напряженность магнитного поля в центре
прямоугольной рамки с током можно
записать в следующем виде:
.
(16.4.4)
Магнитная индукция
в центре рамки равна
.
(16.4.5)
Для контура
квадратной формы со стороной
в формулы (16.4.4.) и (16.4.5) необходимо
подставить условие равенства сторон
.
Напряженность магнитного поля в центре
контура квадратной формы определяется
выражением
,
(16.4.6)
а
магнитная индукция равна
.
(16.4.7)
Векторы индукции
и напряженности магнитного поля,
созданного в центре рамки с током,
имеющей прямоугольную (квадратную)
форму (рис. 16.4.1), направлены
перпендикулярно плоскости чертежа от
нас в соответствии с правилом правого
винта.
1 М 6.5. Закон полного тока
Циркуляцией
напряженности магнитного поля по
замкнутому контуру L
называется
интеграл
.
(16.5.1)
Р
ассмотрим
проводник бесконечной длины с током I,
расположенный перпендикулярно плоскости
чертежа (рис. 16.5.1). Пусть ток направлен
от нас. Замкнутый контур длиной L
выберем в виде окружности, проходящей
через точку М, находящуюся на расстоянии
r
от проводника. Проведем через эту точку
М линию напряженности, которая образует
окружность вокруг проводника с током
и совпадает с замкнутым контуром.
Вычислим циркуляцию вектора напряженности
по выбранному
замкнутому контуру L.
Для этого от точки М отложим элементарную
длину контура
.
Угол между вектором напряженности и
элементарной длиной равен нулю, тогда
.
Напряженность
магнитного поля бесконечно длинного
проводника одинакова во всех точках на
линии напряженности и определяется
выражением
(16.5.2)
Подставим
выражение (16.5.2) в формулу (16.5.1) и вынесем
напряженность из-под интеграла
.
(16.5.3)
Проинтегрируем
по длине контура
.
После сокращения
окончательно получаем
.
(16.5.4)
Данное
уравнение показывает, что циркуляция
вектора напряженности по замкнутому
контуру равна силе тока, охватываемого
этим контуром.
Если
замкнутый контур охватывает несколько
проводников с токами, то в правой части
формулы (16.5.4) получим алгебраическую
сумму токов.
.
(16.5.5)
Выражение
(16.5.5) является законом
полного тока или теоремой о циркуляции
напряженности магнитного поля: циркуляция
вектора напряженности магнитного поля
по замкнутому произвольному контуру
равна алгебраической сумме токов,
охватываемых этим контуром.
Если направление обхода контура совпадает
с направлением линии напряженности
магнитного поля, создаваемого проводником
с током, то силу тока в алгебраической
сумме берем со знаком плюс; если
направления противоположны, то сила
тока берется со знаком минус. Закон
полного тока позволяет определить
напряженность (индукцию) магнитного
поля, созданного проводниками с током
без применения закона Био-Савара-Лапласа,
в частности для расчета магнитного поля
соленоида.
Соседние файлы в предмете Физика
- #
- #
- #
Прежде чем изучать готовые решения задач по магнетизму, нужно знать теорию, поэтому для вас я подготовила краткую теорию по разделу «магнетизм в физике», и примеры решения в которых подробно решены задачи.
Эта страница подготовлена для школьников и студентов.
Если что-то непонятно — вы всегда можете написать мне в WhatsApp и я вам помогу!
Магнетизм. Определения, понятия и законы
Магнитное поле. Индукция магнитного поля (магнитная индукция)
Силовое поле, действующее на движущиеся электрические заряды, электрические токи и намагниченные тела (магниты), называется магнитным полем. В свою очередь, магнитное поле создается движущимися зарядами, токами и магнитами. Силовой характеристикой магнитного поля является вектор магнитной индукции 
Действие магнитного поля на рамку с током
На плоскую рамку с током, подвешенную на нити в однородном магнитном поле, действует момент сил, который стремится развернуть ее определенным образом.
Ориентирующее действие поля на рамку используется для выбора направления вектора магнитной индукции. С этой целью вводят понятие положительной нормали к рамке, которая определяется как единичный вектор, перпендикулярный плоскости рамки и направленный в сторону перемещения буравчика (винта), если вращать его по направлению тока в рамке (рис. 3.3.1). За направление вектора магнитной индукции в данной точке пространства принимается направление положительной нормали к рамке, свободно устанавливающейся в магнитном поле в окрестности данной точки. Это направление совпадает с направлением от южного полюса 

Замкнутый контур площадью 

Направление магнитного момента рамки с током, свободно устанавливающейся в магнитном поле, совпадает с направлением вектора магнитной индукции.
Линии магнитной индукции
Графически магнитное поле изображают с помощью линий магнитной индукции, которые представляют собой линии, касательные к которым направлены так же, как вектор 
Для вычисления магнитного поля электрического тока используют формулу Био-Савара-Лапласа. Согласно этой формуле, магнитная
индукция, создаваемая отрезком проводника длиной 

где 





Картины линий индукции магнитного поля прямого тока и соленоида
Формула (3.3.2) позволяет рассчитать магнитную индукцию 


Линии магнитной индукции представляют собой концентрические окружности в плоскостях, перпендикулярных проводнику (рис. 3.3.3). Направление магнитной индукции тока определяется правилом буравчика: если поступательное движение буравчика совпадает с направлением тока, то вращение рукоятки буравчика указывает направление магнитного поля.
Магнитное поле внутри длинного соленоида (катушки с током) вдали от его концов является однородным (рис. 3.3.4). Магнитная индукция внутри соленоида в точках, удаленных от его концов, равна
где 


определяется по правилу буравчика: если вращать рукоятку буравчика по току, то перемещение буравчика укажет направление линий магнитной индукции.
Понятие о магнитном поле Земли
Земной шар является естественным постоянным магнитом, вокруг которого существует магнитное поле. Средняя величина магнитной индукции вблизи земной поверхности равна 
Согласно современным представлениям, основная часть магнитного поля Земли (геомагнитного поля) имеет внутриземное происхождение. Это поле создается электрическими токами, протекающими в жидком металлическом ядре планеты. На расстояниях, не превышающих 


Магнитные полюса Земли смещены относительно географических, причем в северном полушарии находится южный магнитный полюс 
Незначительная часть (около 1 %) магнитного поля, окружающего Землю, создается электрическими токами, текущими в ионосфере — ионизованной части верхней атмосферы Земли.
На расстояниях, превышающих 

Магнитное поле Земли играет роль своеобразного «щита», защищающего все живое от потоков заряженных космических частиц (космических лучей). На больших расстояниях от Земли магнитное поле невелико, но захватывает громадные области пространства. Действуя на заряженные частицы длительное время, оно существенно изменяет их траектории, отклоняя потоки частиц от Земли. На расстояниях примерно от 500 до 60 000 км заряженные частицы движутся, навиваясь на линии индукции магнитного поля Земли (рис. 3.3.6). Они совершают колебания от одного магнитного полюса к другому с периодом от 0,1 до 1 с. Эта область космического пространства называется радиационным поясом Земли.
Лишь в полярных областях небольшая часть таких частиц вторгается в верхние слои атмосферы из радиационного пояса Земли и вызывает полярные сияния.
Сила, действующая на проводник с током в магнитном поле. Закон Ампера
На проводник с током, находящийся в магнитное поле, действует сила Ампера:
где 


между направлениями отрезка проводника и вектора магнитной индукции, 




Между двумя параллельно расположенными бесконечно длинными проводниками, по которым протекают постоянные токи (рис. 3.3.7), возникает сила взаимодействия, направление и величина которой могут быть найдены из закона Ампера. Поскольку проводник с током 




Действие магнитного поля на движущийся заряд. Сила Лоренца
На заряд 

где 
В однородном магнитном поле, вектор индукции которого перпендикулярен скорости заряженной частицы, она движется по окружности постоянного радиуса 
где 




Магнитные свойства вещества. Гипотеза Ампера
Магнитные взаимодействия зависят от свойств среды, в которой они происходят. Физическая величина, показывающая, во сколько раз индукция магнитного поля 

Согласно гипотезе Ампера магнитные свойства вещества определяются замкнутыми электрическими токами внутри него. В соответствии с современными представлениями, эти токи связаны с движением электронов в атомах вещества. Каждый электрон, движущийся в атоме вокруг ядра по замкнутой орбите, представляет собой элементарный электронный ток, магнитный момент которого, называемый орбитальным магнитным моментом, перпендикулярен плоскости орбиты.
Орбитальный магнитный момент атома равен векторной сумме орбитальных магнитных моментов его электронов. Если вещество состоит из молекул, то магнитный момент молекулы является векторной суммой орбитальных магнитных моментов ее атомов. Таким образом, атомы и молекулы в общем случае имеют магнитные моменты и могут создавать магнитное поле.
Магнетиками называются вещества, способные намагничиваться во внешнем магнитном поле, т.е. создавать собственное (внутреннее) магнитное поле самого вещества. По своим свойствам магнетики подразделяются на слабомагнитные и сильномагнитные вещества. К слабомагнитным веществам относятся диамагнетики и парамагнетики. Основную группу сильномагнитных веществ составляют ферромагнетики.
Диамагнетиками называются вещества, у которых атомы или молекулы в отсутствие внешнего магнитного поля не имеют магнитных моментов. Диамагнетиками являются инертные газы, ряд металлов (золото, серебро, ртуть, цинк, медь), вода, стекло, многие органические соединения. При внесении диамагнитного вещества в магнитное поле в каждом его атоме (или молекуле) индуцируется дополнительный атомный (или молекулярный) ток с некоторым магнитным моментом. Этот ток имеет такое направление, что создаваемое им магнитное поле противоположно внешнему полю. Вектор магнитной индукции внутреннего поля направлен против внешнего поля и ослабляет его. В этом и состоит намагничивание диамагнетиков, для которых 
Атомы (или молекулы), обладающие в отсутствие внешнего поля небольшим магнитным моментом, называются парамагнитными, а состоящие из них вещества — парамагнетиками. К парамагнетикам относятся кислород, окись азота, алюминий, платина, щелочные и щелочноземельные металлы и др. В отсутствие внешнего магнитного поля тепловое движение атомов (молекул) парамагнетика препятствует возникновению упорядоченного расположения магнитных моментов отдельных атомов (молекул), и собственного магнитного поля в веществе не возникает. При внесении парамагнетика во внешнее магнитное поле атомные (молекулярные) токи стремятся расположиться так, чтобы их магнитные моменты были параллельны вектору индукции внешнего поля. Совместное действие магнитного поля и теплового движения приводит к тому, что возникает преимущественная ориентация магнитных моментов атомов (молекул) по направлению внешнего поля. В парамагнитном веществе создается собственное (внутреннее) магнитное поле, вектор индукции которого направлен одинаково с вектором индукции внешнего поля. Для парамагнетиков 
Ферромагнетики
Ферромагнетиками называется группа веществ в твердом кристаллическом состоянии, обладающих магнитными свойствами, обусловленными особым взаимодействием атомных носителей магнетизма. К ферромагнетикам относятся железо, никель, кобальт, а также ряд сплавов. Ферромагнетизм объясняется квантовыми магнитными свойствами электронов. Дело в том, что электрон, независимо от его пребывания в какой-либо системе частиц (атом, молекула, кристалл), обладает собственным моментом импульса (спином) и связанным с ним собственным (спиновым) магнитным моментом. Важная особенность спина электрона состоит в том, что в магнитном поле (как внешнем, так и созданном атомными и молекулярными токами) спин может быть ориентирован так, чтобы его проекция на направление вектора магнитной индукции принимала только два значения, равные по модулю и противоположные по знаку.
В результате этого, в некоторых кристаллах, например в кристаллах железа, возникают условия для параллельной ориентации собственных магнитных моментов электронов группы атомов.
Внутри кристалла ферромагнетика образуются намагниченные области размером порядка 


При отключении внешнего магнитного поля значительная часть доменов в ферромагнитном образце сохраняет упорядоченную ориентацию — образец становится постоянным магнитом.
Упорядоченность ориентации доменов в ферромагнетике нарушается тепловыми колебаниями атомов в кристалле. Чем выше температура, тем интенсивнее разрушается порядок в ориентации доменов, в результате чего образец размагничивается. Температура, выше которой вещество теряет свойства ферромагнетика, называется температурой Кюри. Температура Кюри у железа 770 °C, у никеля 356 °C, у кобальта 1130 °C.
Указания по решению задач
Большинство задач данного раздела связано либо с равновесием, либо с движением тел под действием различных сил, включая силу Ампера и силу Лоренца. Поэтому, наряду с законами магнетизма и электромагнитной индукции, при решении задач необходимо использовать законы механики.
Примеры решения задач
Задача №3.3.1.
Частица массой 


Решение:
Со стороны магнитного поля на частицу действует сила Лоренца, перпендикулярная скорости частицы 

Под действием этой силы частица совершает движение по окружности радиусом 
где 
получаем ответ:
Задача №3.3.2.
Заряженная частица массой 







Решение:
Как только частица окажется в области, занимаемой магнитным полем, на нее начнет действовать сила Лоренца, направленная перпендикулярно скорости частицы. Под действием этой силы частица будет двигаться по дуге окружности радиусом R, который легко найти из уравнения движения (см. решение задачи 3.3.1): 
соотношением между радиусом дуги R и длиной L области, занимаемой магнитным полем. В частности, при R > L
Если 

При числовых данных из условия задачи 
Задача №3.3.3.
Квадратная проволочная рамка может свободно вращаться вокруг горизонтальной оси, совпадающей с одной из ее сторон. Рамка помещена в однородное магнитное поле с индукцией 





Решение:
Силы, действующие на отдельные отрезки рамки со стороны магнитного поля (силы Ампера 




Таким образом, рамка находится в равновесии под действием сил, изображенных на рисунке б, где 



Объединяя записанные выражения, после несложных преобразований получаем ответ:
Электромагнитная индукция. определения, понятия и законы
Опыты Фарадея. Явление электромагнитной индукции
Английский физик М. Фарадей в 1831 г. обнаружил, что при изменении магнитного поля, пронизывающего замкнутый проводящий контур, в нем возникает электрический ток. Этот ток был назван индукционным током. В своих опытах Фарадей наблюдал возникновение индукционного тока в катушке из металлической проволоки при вдвигании в нее и выдвигании из нее постоянного магнита, а также при изменении силы тока во второй катушке, магнитное поле которой пронизывает первую катушку.
Явление возникновения электрического тока в замкнутом проводящем контуре при изменениях магнитного поля, пронизывающего контур, называется электромагнитной индукцией.
Магнитный поток
Для количественного описания этого явления вводится понятие магнитного потока. Потоком магнитной индукции (магнитным потоком) через некоторую поверхность площадью 
где 


Поток магнитной индукции через контур с током будет положительным, если составляющая 


Для любого контура положительное направление нормали связано с положительным направлением обхода контура правилом буравчика: если рукоятку буравчика вращать по направлению обхода, то перемещение буравчика укажет положительное направление нормали.
Закон электромагнитной индукции. Правило Ленца
Появление электрического тока в замкнутом контуре при изменениях магнитного поля, пронизывающего контур, свидетельствует о действии в контуре сторонних сил неэлектрической природы, или о возникновении ЭДС индукции. Опыты показывают, что направление ЭДС индукции (и, следовательно, индукционного тока) зависит от того, возрастает или убывает магнитный поток через контур, а также от знака магнитного потока. Общее правило, позволяющее определить направление индукционного тока в контуре, было установлено в 1833 г. русским физиком Э.Х. Ленцем. Согласно правилу Ленца, возникающий в замкнутом контуре индукционный ток имеет такое направление, что созданный им магнитный поток через площадь, ограниченную контуром, стремится компенсировать то изменение магнитного потока, которым вызван данный ток.
Экспериментальные исследования зависимости ЭДС индукции от характера изменения магнитного потока привели к установлению закона электромагнитной индукции’. При изменении магнитного потока через поверхность, ограниченную замкнутым контуром, в нем возникает ЭДС индукции 
где 



В Международной системе единиц закон электромагнитной индукции используют для установления единицы магнитного потока.
Эту единицу называют вебером (Вб) и определяют следующим образом: магнитный поток через площадь, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции 1B: 1 Вб = 1 В • 1 с.
Единицу магнитной индукции устанавливают на основе соотношения (3.4.1). Если вектор 


ЭДС индукции возникает как в неподвижном контуре, помещенном в изменяющееся магнитное поле, так и в проводнике, движущемся в магнитном поле, которое может не меняться со временем. Значение ЭДС индукции в обоих случаях определяется законом (3.4.2), но происхождение ЭДС различно.
Если магнитное поле постоянно во времени, но магнитный поток через контур изменяется из-за движения отдельных проводников, образующих контур, то причиной возникновения ЭДС индукции является сила Лоренца, действующая на свободные заряды в движущемся проводнике. При использовании закона электромагнитной индукции в форме (3.4.2) нужно иметь в виду, что изменение магнитного потока связано с изменением площади контура. При движении незамкнутого проводника в магнитном поле, на концах проводника также возникает ЭДС индукции, величина которой определяется магнитным потоком через площадь, «заметаемую» проводником в единицу времени. В частности, при движении в магнитном поле прямолинейного проводника длиной 

где 

Вихревое электрическое поле
Физической причиной возникновения ЭДС индукции в неподвижном контуре является действие вихревого электрического поля, всегда возникающего в пространстве при изменении магнитного поля. Работа вихревого электрического поля по перемещению единичного заряда в проводнике и представляет собой ЭДС индукции.
Вихревое электрическое поле отличается от электростатического (кулоновского) поля тем, что оно создается не электрическими зарядами, а переменным магнитным полем, причем его силовые линии замкнуты сами на себя, а не начинаются и заканчиваются на зарядах, как в случае кулоновского поля. Работа вихревого электрического поля при перемещении заряда по замкнутой траектории отлична от нуля.
Самоиндукция. Индуктивность. ЭДС самоиндукции
Если магнитное поле вызвано током 


Единица индуктивности в СИ называется генри (Гн). Индуктивность контура равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции 1 В: 1 Гн = 1 В • 1 с/1 А.
Энергия магнитного поля
Для создания тока 


Собственная энергия тока сосредоточена в магнитном поле, созданном проводником с током, причем эта энергия распределена по всему пространству, где имеется магнитное поле. Энергия однородного магнитного поля, сосредоточенного в объеме 
Объемной плотностью энергии магнитного поля называется энергия, заключенная в единице объема поля
Это выражение справедливо не только для однородного поля, но и для произвольных, в том числе неоднородных в пространстве и переменных во времени магнитных полей.
Примеры решения задач
Задача №3.4.1.
Замкнутый проводник в виде прямоугольной трапеции находится в магнитном поле с индукцией 




Решение:
Для определения направления ЭДС индукции выберем нормаль к плоскости контура, совпадающую по направлению с магнитным полем (от нас). Тогда магнитный поток через контур будет положительным. Выбранной нормали соответствует направление обхода контура по часовой стрелке. Поскольку поле убывает со временем, изменение магнитного потока отрицательно: 
вытекает, что ЭДС индукции положительна, т.е. направлена по часовой стрелке. Туда же будет направлен и индукционный ток. Величина тока определяется отношением ЭДС индукции 




Ток течет по часовой стрелке.
Задача №3.4.2.
Катушка из 




Решение:
Магнитный поток, пронизывающий катушку в начальный момент, равен 






Задача №3.4.3.
При равномерном изменении силы тока через проволочную катушку в ней возникает ЭДС самоиндукции Е = 10 В. Катушка содержит N = 1000 витков. Какой заряд q протечет за время 
Решение:
Величина ЭДС самоиндукции равна 





Задача №3.4.4.
По двум вертикальным проводящим рейкам АВ и CD (см. рисунок), находящимся на расстоянии 




Решение:
Предоставленный самому себе проводник начнет под действием силы тяжести двигаться вниз. В результате этого возникнет изменение магнитного потока через контур, образованный рейками, резистором и проводником, и, как следствие, ЭДС индукции и индукционный 

Учитывая, что 



Движение проводника установится, т.е. ускорение проводника 

Задача №3.4.5.
В магнитном поле с индукцией 







Решение:
При движении стержня возникает ЭДС индукции 

Количество теплоты, выделяющееся в стержне за время 
Задача №3.4.6.
Прямоугольный контур .4ВСР перемещается поступательно с постоянной скоростью v в магнитном поле тока 

Решение:
Линии магнитной индукции, создаваемой током 
При движении контура со скоростью 
Очевидно, что 
Объединяя записанные выражения, получаем ответ:
Задача №3.4.7.
По двум металлическим параллельным рейкам, расположенным в горизонтальной плоскости к замкнутым на конденсатор 




Решение:
При движении проводника в контуре возникает ЭДС индукции Е, которая в каждый момент времени равна напряжению на конденсаторе 



Поскольку 


Задача №3.4.8.
Катушка индуктивностью 






Решение:
При замкнутом ключе через источник течет ток
Этот ток разветвляется на два тока 


Отсюда
После отключения источника (размыкания ключа) возникающая в катушке ЭДС самоиндукции 

При этом полная мощность 
Следовательно, мощность, выделяющаяся на резисторе, составляет от полной мощности, выделяющейся в этой цепи, следующую долю:
Поскольку данное отношение мощностей не зависит от времени, очевидно, что такую же долю составит и энергия, выделившаяся на резисторе за время существования ЭДС самоиндукции, от полной энергии, выделившейся в цепи. В свою очередь, полная выделившаяся энергия равна энергии 

Подставляя в это равенство найденный ранее ток через катушку, получаем ответ:
Возможно эти дополнительные страницы вам будут полезны:
- Предмет физика
- Готовые задачи по физике
- Решение задач по физической механике
- Заказать работу по физике
- Помощь по физике
- Решение задач по молекулярной физике
- Решение задач по электростатике и электродинамике
- Постоянный ток задачи с решением
- Электромагнитные колебания задачи с решением
- Задачи по оптике с решением
- Атом и атомное ядро решение задач