При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока. В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока. Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.
От чего зависит индуктивное сопротивление
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

Данная величина зависит от многих факторов. В первую очередь на нее оказывает влияние как значение тока не только в собственном проводнике, но и в соседних проводах. То есть увеличение сопротивления и потока рассеяния происходит по мере увеличения расстояния между фазными проводами. Одновременно снижается воздействие соседних проводов.
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
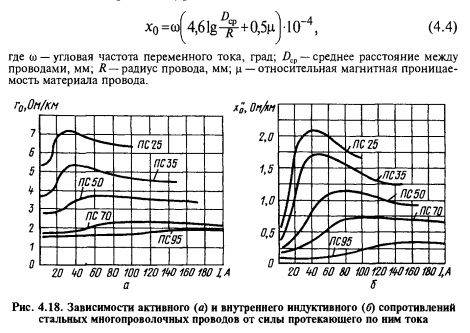
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
Индуктивное сопротивление в цепи переменного тока
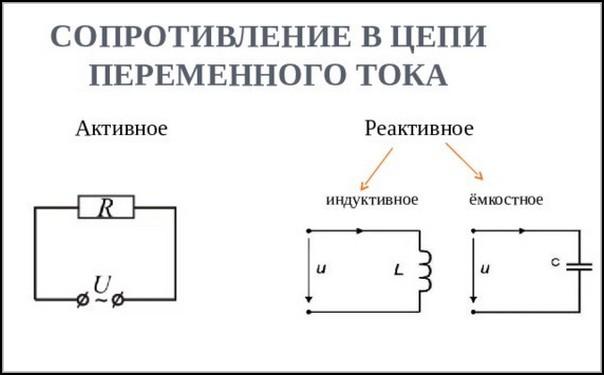
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
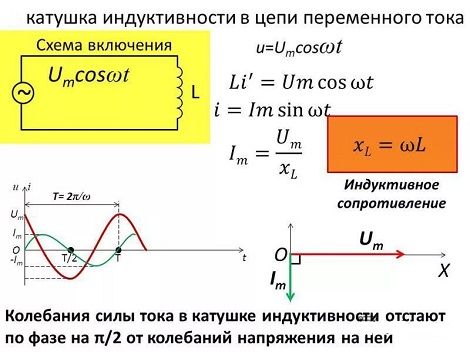
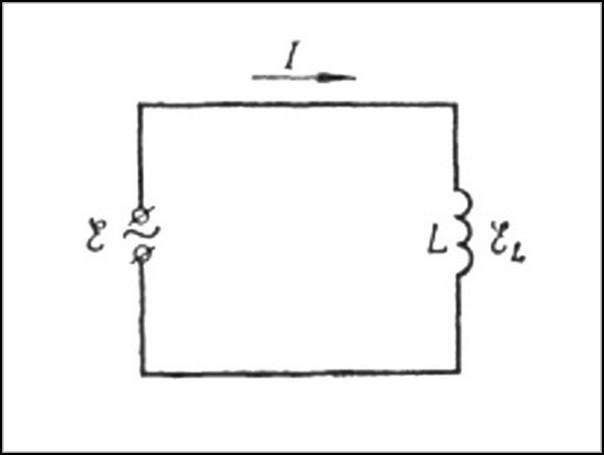
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Индуктивное сопротивление катушки
Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.
Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля. В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке. Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.
Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.
Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.
Индуктивное сопротивление
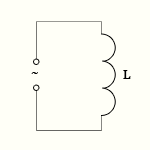
Индуктивность L в электрической цепи вызывает запаздывание тока (см Самоиндукция). Вследствие этого ток достигает максимального значения Im позже напряжения. Если R = 0, приложенное напряжение противоположно индуцированному напряжению:
[ u = L frac{di}{dt} = frac{d}{dt}(LI_{m} sin(ωt)) ]
отсюда
[ u = ωLI_{m} cos(ωt) ]
или
[ u = ωLI_{m} sin(ωt + frac{π}{2}) ]
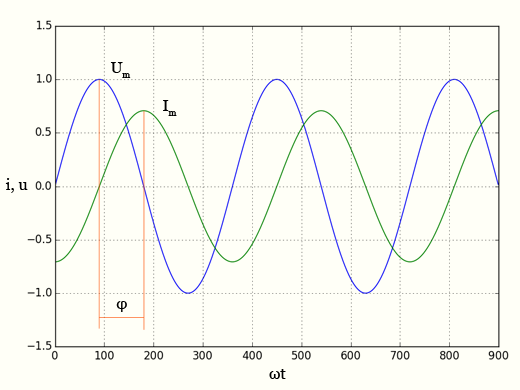
Индуктивное сопротивление — графики тока и напряжения
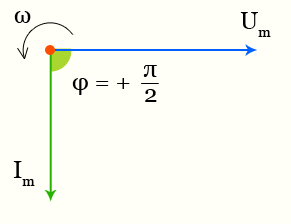
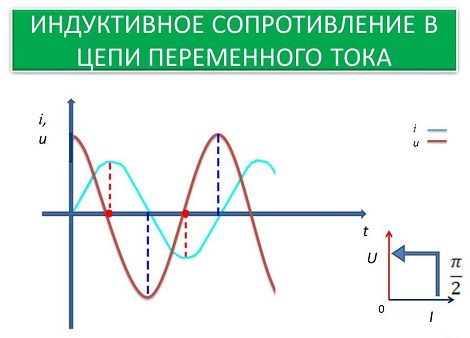
Между напряжением и током возникает разность фаз (сдвиг фаз) равная +π/2.
B цепи переменного тока, содержащей только индуктивность, напряжение опережает ток на π/2 (или Т/4).
Из написанного выше равенства следует, что амплитуда напряжения Um = ωLIm. Сопоставляя это выражение с законом Ома Um = RIm, мы видим, что величина ωL играет роль сопротивления.
Цепь переменного тока, содержащая индуктивность L, обладает сопротивлением переменному току; оно называется индуктивным сопротивлением XL.
Единица СИ индуктивного сопротивления: [XL] = Ом.
Если
| XL | индуктивное сопротивление цепи переменного тока, | Ом |
|---|---|---|
| L | индуктивность цепи, | Генри |
| ω = 2πf | круговая частота переменного тока, | Радиан/Секунда |
то имеем
[ X_{L} = ωL ]
При наличии в цепи только индуктивного сопротивления сила тока определяется выражением
[ I = frac{U}{ωL} ]
Вычислить, найти индуктивное сопротивление
Индуктивное сопротивление |
стр. 688 |
|---|
Что такое индуктивное сопротивление
Содержание
- 1 Виды сопротивления в электрической цепи
- 2 Что такое индуктивное сопротивление
- 3 Катушка индуктивности
- 4 Формула индуктивного сопротивления
- 5 Практическое использование
- 6 Видео по теме
В электрических цепях существует три вида сопротивления. Это активное, которое действует как при постоянном, так и при переменном токе, а также два вида реактивного — индуктивное и емкостное сопротивление. Умея их определять, можно посчитать полное сопротивление, которое также называют импедансом. От чего зависит индуктивное сопротивление и по какой формуле рассчитывается, будет рассмотрено в статье.

Виды сопротивления в электрической цепи
Если используется постоянный ток, то рассматривается только обычное сопротивление, которое также называется активным или омическим. При переменном существует не только активное, но и реактивное сопротивление. Последнее бывает индуктивным и емкостным. Его величина определяется по соответствующим формулам. Сопротивление называется реактивным потому что не вызывает безвозвратных потерь энергии.
В цепях переменного тока полное сопротивление представляет собой сумму омического, индуктивного и емкостного сопротивлений. Определить его можно по правилам векторного сложения слагаемых. Если рассматривать цепь, которая не содержит конденсаторов, то основную роль будет играть реактивное сопротивление катушки индуктивности.

Что такое индуктивное сопротивление
Когда по цепи течёт ток, то движущиеся заряды создают магнитное поле. При постоянном токе оно не будет меняться во времени. Если же происходит уменьшение или увеличение тока, то возникает явление самоиндукции. Она тормозит изменение электротока, тем самым уменьшая его. При этом сопротивление выражается через индуктивность.
Если имеется катушка, то индуктивное сопротивление в цепи создает она. Его значение зависит от частоты тока. Чем она больше, тем выше индуктивное сопротивление катушки.
Ещё одной особенностью является сдвиг фазы. Активное сопротивление не имеет смещения по отношению к питающему напряжению, емкостное запаздывает на 90 градусов, а индуктивное опережает напряжение на эту же величину.

Катушка индуктивности
Эта деталь обычно имеет сердечник цилиндрической или тороидальной формы, на который многократно намотан провод. Основной характеристикой катушки является индуктивность.
Как известно, магнитное поле создаётся движущимися электрическими зарядами. Даже если постоянный ток идёт по проводу, вокруг него создаётся магнитное поле. Оно создаёт препятствия для изменения тока в те моменты, когда меняется само, чему можно не удивляться, зная о существовании индуктивного сопротивления. Для постоянного тока это происходит в моменты включения и выключения.
Если питающее напряжение переменное, то изменения происходят непрерывно. Основная задача катушки индуктивности — увеличивать напряженность магнитного поля. Она имеет не только индуктивное, но и обычное сопротивление. Однако при расчётах его считают пренебрежимо малым.

Формула индуктивного сопротивления
Рассматриваемое сопротивление тем больше, чем выше частота тока и индуктивность. Эту зависимость легко объяснить. Большая частота подразумевает высокую скорость изменения магнитного поля, которая усиливает эффект самоиндукции. Увеличение индуктивности соответствует более сильному магнитному полю.
Индуктивное сопротивление обозначается как XL. Обозначение буквой Х используется для любого реактивного сопротивления. То, что оно индуктивное подтверждает буква L. Его единица измерения — Ом. Чтобы рассчитать значение, понадобится формула индуктивного сопротивления:

В этой формуле буквами F и L обозначаются частота переменного тока и индуктивность катушки соответственно. Индуктивность измеряется в Генри, сокращенно Гн.
Чтобы найти полное сопротивление в контуре, состоящем из резисторов и катушки, необходимо сложить активную и реактивную составляющую, воспользовавшись правилом прямоугольного треугольника. Один катет такого треугольника соответствует активному сопротивлению, а второй — реактивному. Гипотенуза — это полное сопротивление или импеданс. Его значение рассчитывается по теореме Пифагора.

- XL — это индуктивное сопротивление, которое определяется формулой, приведённой выше.
- R — активное сопротивление. Для его вычисления следует воспользоваться законом Ома.
Произведение 2πF в формуле сопротивления называют также круговой частотой. Ее обозначают буквой ω. С учетом этого формулу для определения индуктивного сопротивления можно записать так: XL = ω×L.

Практическое использование
Одним из распространённых применений индуктивного сопротивления катушки является создание фильтров. В сложных системах могут возникать шумы на высоких частотах, которые снижают качество передачи сигнала. Это может быть актуально, например, для акустических систем, зависящих от качества воспроизведения звуковых сигналов. В этом случае выручает то, что индуктивное сопротивление определяется частотой тока.
Электротоки разной частоты, проходящие через катушку, вызывают в ней разное индуктивное сопротивление. Оно тем больше, чем выше частота переменного тока. При нулевой частоте, то есть, установившемся постоянном ток, индуктивное сопротивление также равно нулю.

Сигналы пропускают через фильтр с индуктивным сопротивлением, препятствующим прохождению сигналов нежелательной частоты. Чтобы преградить путь низкочастотным звуковым сигналам, используют катушки со стальными сердечниками, высокочастотным — без сердечников. Такие катушки называются дросселями, соответственно, низкой и высокой частоты.
В рассматриваемой ситуации удобно одновременно использовать еще и ёмкостное сопротивление, зависящее также от частоты тока. Но оно с ее увеличением уменьшается. Таким образом, с помощью фильтров можно избавляться от нежелательных шумовых сигналов.

Ещё одно важное применение рассматриваемого явления — трансформатор. Та самая самоиндукция, которая тормозит прохождение тока, благодаря создаваемому сопротивлению в этом устройстве играет положительную роль.
В трансформаторе используется сердечник и две обмотки. На первичную обмотку поступает переменное напряжение питания, а на вторичной генерируется индукционный ток. Наличие индукционных токов определенной величины необходимо для работы многих электроприборов.
С помощью трансформатора можно, например, преобразовать 220 В сетевого питания в 12 В, которые необходимы для электропитания стереосистемы. Такая подстройка определяется соотношением количества витков на первичной и вторичной обмотках.
Катушка представляет собой источник ЭДС. Эту ее особенность используют в индукционных плитах. Электромагнитные волны, создаваемые катушкой, нагревают кухонную посуду и их содержимое. По такому же принципу работают и печи на сталелитейных заводах.
Зная, что собой представляет такое явление, как индуктивное сопротивление, его можно использовать для расчета параметров различного электротехнического и энергетического оборудования.
Видео по теме
Виды сопротивления и их особенности
Если в цепи постоянное напряжение, то, зная её сопротивление, можно узнать силу тока при помощи закона Ома. Он говорит о том, что сила тока пропорциональна напряжению, которое является его причиной. Коэффициент пропорциональности представляет обычное сопротивление. Его принято называть активным.
Если напряжение является постоянным, то сопротивление будет только активным. Его значение определяет, сколько энергии электрического поля преобразовано в тепло, то есть, безвозвратно утрачено. Поэтому при работе с кабелями СИП-3 1×50, СИП-2 3×70 и другими нужно помнить, что потери энергии из-за активного сопротивления могут быть значительными.

Более распространено использование переменного тока. Он возникает под воздействием напряжения, циклически изменяющегося по синусоидальному закону. Такой ток порождает реактивное сопротивление, которое дополняет действие активного. Существует две разновидности реактивного сопротивления различной природы — на основе индуктивности или емкости. Их отличительной особенностью является то, что они способствуют не трате электроэнергии, а преобразованию её в другую форму.
Нужно учитывать, что применение различных видов кабелей связано не только с наличием активного сопротивления, но и реактивного. Например, кабели СИП-3 1×50, СИП-2 3×70, АС-95 могут использоваться в электросетях и с активным, и индуктивным, и емкостным сопротивлениями.
Чтобы понять, что собой представляет индуктивное сопротивление, можно представить цепь, в которой имеется катушка, подключённая к источнику переменного тока. Как известно, напряжение меняется по синусоидальному закону. При этих изменениях катушка будет создавать магнитное поле, которое будет, в частности, влиять на текущий через него ток. Согласно природе магнитного поля, при уменьшении тока магнитное поле способствует его увеличению, а при усилении наблюдается противоположный эффект. Кроме того, цепь переменного тока с активным сопротивлением тратит энергию на выделение тепла.
На практике речь идёт о действии индуктивного сопротивления, обеспечивающего сдвиг фазы между током и напряжением. Движение зарядов создаёт поле, которое в свою очередь препятствует изменению тока. Такое сопротивление присутствует не только в катушках, но и, например, при использовании кабеля СИП-2 3×70.
Емкостное сопротивление имеет другую природу. Для объяснения следует рассмотреть цепь, состоящую из источника переменного тока и конденсатора. Последний представляет собой деталь, в которой две поверхности параллельны друг другу и не имеют непосредственного электрического контакта.
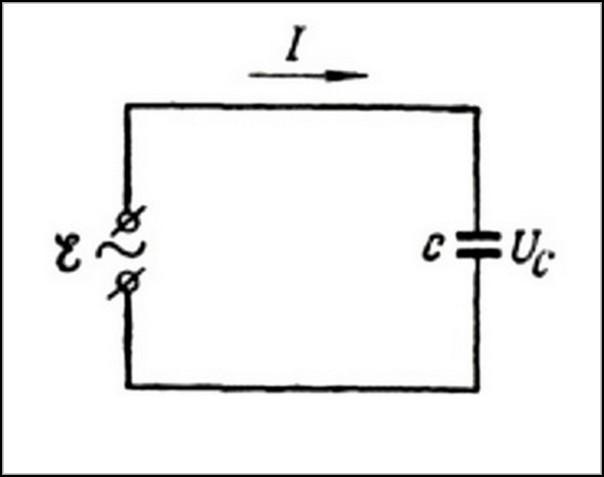
При использовании постоянного тока на обкладках конденсатора накапливаются заряды: на одной — положительный, а на второй — отрицательный. Электрополе за счет накопленного заряда представляет собой источник, противодействующий току. Поэтому конденсатор в цепи постоянного тока является бесконечно большим сопротивлением. Ток не проходит сквозь диэлектрик, разделяющий обкладки конденсатора.
В цепи переменного тока конденсатор циклически заряжается и разряжается, обеспечивая движение электрозарядов. Данный процесс в цепи переменного тока с активным и реактивным сопротивлением будет происходить с опозданием относительно синусоидального изменения напряжения. Таким образом, конденсатор представляет собой конечное сопротивление, получившее название емкостного.
Разница между емкостным и индуктивным сопротивлением заключается в том, что через индуктивную катушку постоянный ток протекает, а при использовании конденсатора пройти не может. Однако переменный ток в обеих цепях может течь без каких-либо проблем.

Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.
Схема для измерения
В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

Определение индуктивности
Принцип действия индуктивного сопротивления линий
Именно индуктивность признана главной характеристикой для катушек наряду с аналогичным показателем для их обмоток. R реактивного вида, проявляющееся под действием самоиндукционной ЭДС, растет в прямой пропорции с частотой тока.

Реактивная и активная составляющие обуславливают полное сопротивление, которое можно представить в виде суммы квадратов каждого показателя.
Оперативно справиться с поставленной задачей по расчету номинальных показателей помогут специальные таблицы. В них для самых распространенных проводников приведены все главные характеристики. Но на практике часто требуется узнать Х для участка с конкретной протяженностью. В этом случае главным инструментом является уже приводившееся выражение 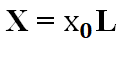
От каких факторов зависит сопротивление
Изменение силы тока создает электромагнитное поле переменной интенсивности. Результатом его воздействия на проводник является противодействие происходящему изменению тока.
Это противодействие называется реактивным сопротивлением. Существуют две его разновидности: индуктивная и емкостная. Первая создается при наличии в схеме индуктивного элемента, вторая — конденсатора.
В ситуации, когда в цепи присутствует катушка, ее реакция усиливается по мере увеличения частоты.
Цепь, в которой возникает индукция
В случае, когда ее индуктивность уменьшается, то противодействующая сила также становится меньше. При увеличении она возрастает.
Индуктивное сопротивление существенно связано с тем, какую форму принимает проводник. Оно имеется также и у отдельного провода, лежащего прямо. Однако если рядом будет еще один, то он будет оказывать воздействие дополнительно, что повлияет на рассматриваемую величину.
Рассматриваемую характеристику отдельного провода можно определять в зависимости от его толщины, но оно никак не связано с его сечением.
Принцип действия электродвижущей силы
Катушка индуктивности
Он представляет собой изолированный провод, многократно намотанный вокруг сердечника.
Обычно каркас имеет цилиндрическую или тороидальную форму.
Индуктивность рассматривается в качестве основной характеристики катушки. Это качество выражает способность элемента осуществлять преобразование переменного тока в магнитное поле.
Важно! Магнитные свойства существуют даже у одиночного провода, при условии, что изменяется проходящий через него ток. Воздействие поля направлено так, чтобы противодействовать его изменению. Если он будет увеличиться, поле будет его тормозить, а если ослабевать — усиливать.

Катушки индуктивности
Определение направления силовых линий подчиняется «правилу большого пальца»: если у сжатой в кулак руки большой палец указывает в направлении изменения силы тока, то сомкнутые пальцы подсказывают направление силовых линий поля.
Таким образом в том случае, если провод многократно намотан на цилиндрическое основание, то силовые линии от разных витков складываются и проходят через ось.
Для того, чтобы многократно увеличить индуктивность, в центр цилиндра помещают сердечник из ферромагнитного материала.
Калькулятор импеданса катушки индуктивности
Калькулятор определяет импеданс катушки индуктивности для заданной частоты синусоидального сигнала. Определяется также угловая частота.
Пример. Рассчитать импеданс катушки индуктивности 10 мкГн на частоте 25 МГц.
Входные данныеИндуктивность, Lгенри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)Частота, fгерц (Гц)миллигерц (мГц)килогерц (кГц)мегагерц (МГц)гигагерц (ГГц) Поделиться Поделиться ссылкой на этот калькулятор, включая входные параметры Twitter Facebook Google+ VK Закрыть Выходные данныеУгловая частотаω= рад/сИндуктивное реактивное сопротивлениеXL= Ом
Введите значения индуктивности и частоты, выберите единицы измерения и нажмите кнопку Рассчитать. Для ввода значения бесконечность наберите inf.
Отметим, что величина импеданса идеальной катушки индуктивности равна ее реактивному сопротивлению. Однако это не идентичные величины, так как между током и напряжением в индуктивной цепи существует фазовый сдвиг. Для расчетов используются указанная ниже формула:
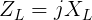
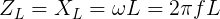
Здесь
XL — реактивное сопротивление катушки в омах (Ом),
ZL — импеданс катушки в омах (Ом),
ω = 2πf — угловая частота в рад/с,
f — частота в герцах (Гц),
L — индуктивность в генри (Гн),
j — мнимая единица.
Для расчета выберите единицы измерения и введите индуктивность и частоту. Импеданс катушки индуктивности будет показан в омах.
Катушка индуктивности представляет собой пассивный электрический элемент с двумя выводами, изготовленный, как правило, из изолированного провода в форме спирали, намотанного на магнитный сердечник или на оправку (без сердечника). Магнитный сердечник обычно изготовляется из ферромагнитного металла, например, железа или ферромагнитной керамики (феррита) и используется для усиления магнитного поля и, таким образом, для увеличения индуктивности катушки. Как и конденсаторы, катушки индуктивности используются для накопления и сохранения энергии. Однако, в отличие от конденсаторов, энергия в катушке хранится в форме окружающего ее магнитного поля. Катушки индуктивности применяются, в частности, в фильтрах для сглаживания постоянного тока или для предотвращения передачи высокочастотных помех по кабелям. Катушки индуктивности широко используются в колебательных контурах радиопередатчиков и радиоприемников, а также для изготовления трансформаторов.
Высокодобротная катушка индуктивности без сердечника, установленная в радиопередатчике
В отличие от конденсаторов, которые препятствуют изменению напряжения, приложенного к их обкладкам, катушки индуктивности препятствуют изменению текущего в них тока. В отличие от конденсаторов, которые не пропускают постоянный ток, катушки индуктивности пропускают его легко. Они препятствуют только прохождению переменного тока или иного изменяющегося тока и их способность препятствовать прохождению тока и называется индуктивностью. Индуктивность обозначается символом L в честь российского физика Эмиля Ленца и измеряется в генри — единицах, названных в честь американского ученого Джозефа Генри.
В отличие от резисторов, которые препятствуют прохождению электрического тока вследствие падения напряжения на них, пропорционального протекающему току, катушки индуктивности препятствуют изменению протекающего через них тока. На них создается падение напряжения, прямо пропорциональное скорости изменения тока. Полярность индуцированного напряжения всегда такова, что это напряжение поддерживает изменяющийся ток в его текущем состоянии. Например, если ток растет, то напряжение препятствует этому росту и старается уменьшить ток. В то же время, если ток через катушку уменьшается, напряжение мешает этому уменьшению и поддерживает более высокий ток. Чем выше скорость изменения тока, тем больше амплитуда этого обратного напряжения. В связи с указанным свойством, это напряжение часто называют индуктивными выбросами или обратным током. Для того, чтобы как-то отличить это свойство от сопротивления, используют понятие реактивного сопротивления. Если к катушке индуктивности приложено синусоидальное напряжение, то при бóльших частотах катушка оказывает току большее сопротивление, следовательно, ее реактивное сопротивление также увеличивается, как показано на графике.
График зависимости реактивного сопротивления катушки XL индуктивности и текущего через нее тока I от частоты f для нескольких величин индуктивности показывает прямую пропорциональную зависимость от частоты реактивного сопротивления и обратную зависимость от частоты протекающего через катушку тока
Полное сопротивление Z, как и реактивное сопротивление, измеряется в омах (Ом) и состоит из двух частей — действительной и мнимой. Первая из них представляет собой активное сопротивление R, которое затрудняет протекание тока в материале с плохой проводимостью и зависит от формы этого материала. Вторая часть — это рассмотренное выше реактивное сопротивление X. Оно также затрудняет протекание тока, но не вследствие свойств и формы проводящего материала, а из-за того, что протеканию тока мешает электрическое и магнитное поля.
Если реальная катушка индуктивности подключена к источнику постоянного напряжения, через нее протекает постоянный ток, ограниченный только сопротивлением провода, из которого намотана катушка. Когда катушка подключается к источнику постоянного напряжения, ток через нее медленно повышается от нуля до максимального значения, которое определяется внутренним сопротивлением источника и внутренним сопротивлением витков катушки. ЭДС самоиндукции, возникающая в катушке, препятствует резкому увеличению тока в ней. Эта ЭДС противодействует приложенному напряжению до тех пор, пока ток не достигнет максимального значения.
Если источник постоянного напряжения отключить от катушки, протекающий через нее ток постепенно падает до нуля. В этом случае опять возникает ЭДС самоиндукции, которая снова препятствует, на этот раз, уменьшению тока и которая старается поддержать ток в неизменном состоянии. В конце концов, ток постепенно уменьшается до нуля.
В чисто индуктивной цепи ток отстает от напряжения на π/2 радиан или 90°. 1 — в момент отрицательного максимума тока скорость его изменения нулевая и напряжение равно нулю; 2 — ток нулевой, скорость его изменения максимальная и напряжение равно положительному максимуму; 3 — ток положительный и максимальный, скорость его изменения нулевая и напряжение равно нулю; 4 — ток нулевой, скорость его изменения максимальная и напряжение равно отрицательному максимуму
Если к катушке индуктивности приложено переменное синусоидальное напряжение, ток отстает от напряжения на некоторый фазовый угол, как показано на графике. В идеальной катушке индуктивности этот угол будет равен точно 90° или четверти цикла. В точке (ωt = π/2), временнóй оси, где ток нулевой, напряжение на катушке достигает своего положительного максимума. Затем ток постепенно увеличивается и вокруг катушки создается магнитное поле, которое, в свою очередь, создает ЭДС самоиндукции, направленную противоположно току. Эта ЭДС является реакцией катушки на изменение протекающего через нее тока, и она максимальна, когда ток нулевой, так как в этой точке скорость изменения тока максимальная. Когда же ток достигает своего максимального значения (положительного или отрицательного), скорость изменения синусоидального тока становится нулевой и в этих точках максимумов ток ЭДС самоиндукции (определяемая этой скоростью) также равна нулю. Это приводит к тому, что синусоида напряжения не совпадает по фазе с током на угол 90° или π/2 радиан. То есть, напряжение опережает ток или ток отстает от напряжения.
Аналогичное явление можно наблюдать и в природе. Сравните: Солнце светит сильнее всего в астрономический полдень (солнечный свет — напряжение), однако самая жаркая часть дня обычно бывает через несколько часов после полудня (температура — ток). Или другой пример. День зимнего солнцестояния в северном полушарии (самый короткий день) — в конце декабря, однако самые холодные месяцы еще впереди. В зависимости от того, где вы живете, это будет январь или февраль. Вспомните поговорку «Солнце — на лето, зима — на мороз». Это как раз о поведении индуктивности, только в природной аналогии. Такой сезонный «сдвиг фаз» или отставание вызван поглощением энергии Солнца огромными массами воды в океанах. Они отдадут эту запасенную энергию, но позже — точно так же, как это делают катушки индуктивности.
День зимнего солнцестояния в северном полушарии — в конце декабря, однако самые холодные месяцы еще впереди. Именно так ведет себя ток в катушке индуктивности
Рассчитанный этим калькулятором импеданс представляет собой меру сопротивления катушки индуктивности протекающему через нее току на определенной частоте. Индуктивное реактивное сопротивление изменяется при изменении частоты приложенного переменного напряжения. Приведенные выше формула и график показывают, что реактивное сопротивление катушки индуктивности XL велико при высоких частотах и мало при низких частотах (конденсаторы ведут себя с точностью до наоборот). При высоких частотах индуктивное реактивное сопротивление становится очень большим и очень сильно противодействует протекающему току. С другой стороны, при очень низких частотах или при постоянном напряжении катушка индуктивности проводит очень хорошо — отсюда правило, которое мы выучили в школе: катушки индуктивности не пропускают переменный ток и пропускают постоянный. Если частота очень низкая, катушки индуктивности пропускают сигнал очень хорошо. Именно поэтому их устанавливают в фильтрах громкоговорителей (кроссоверах), чтобы высокие частоты не попадали на низкочастотные динамические головки.
Импеданс измеряется в омах, так же, как и сопротивление. Импеданс мешает прохождению электрического тока так же, как и сопротивление, и показывает как сильно катушка противодействует прохождению тока через нее. Но тогда возникает вопрос: в чем же разница между импедансом и сопротивлением? А разница заключается в зависимости импеданса от частоты приложенного сигнала. Сопротивление от частоты не зависит, а импеданс катушек индуктивности от частоты зависит. С увеличением частоты импеданс катушек уменьшается.
Этот калькулятор предназначен для расчета импеданса идеальных катушек индуктивности. Реальные катушки всегда имеют сопротивление, которое на эквивалентной схеме изображают включенным последовательно с индуктивностью. Для расчета импеданса реальных катушек индуктивности пользуйтесь калькулятором импеданса RL-цепей.
Катушки индуктивности в высокочастотном модуле телевизионного приемника
Формулы, зависимости и виды индуктивности
Электрическая индуктивность L – это величина, равная коэффициенту пропорциональности между током I, протекающим в замкнутом контуре, и создаваемым им магнитным потоком, иначе называемым потокосцеплением Y:
Y = LI.
Если к выводам катушки на некоторое время приложить напряжение, то в ней начнёт протекать ток I и формироваться магнитное поле. Чем меньше индуктивность L, тем быстрее протекает данный процесс. В итоге рассматриваемый двухполюсник накопит некоторое количество потенциальной энергии. При отключении питания он будет стремиться её вернуть. В результате на выводах катушки образуется ЭДС самоиндукции E, которая многократно превышает изначально приложенное напряжение. Подобная технология ранее использовалась в магнето систем зажигания ДВС, а сейчас широко встречается в повышающих DC-DC преобразователях.
Формула ЭДС самоиндукции, здесь t – это время, в течение которого ток I уменьшится до нуляПростой DC-DC повышающий преобразователь
Катушка (она же – дроссель) – это радиодеталь с ярко выраженной индуктивностью, ведь именно для этого её и создавали. Однако подобным свойством обладают в принципе все элементы. Например, конденсатор, резистор, кабель, просто кусок провода и даже тело человек также имеют некоторую индуктивность. В расчетах ВЧ схем это обязательно принимается во внимание.
Важно! Проводя измерение индуктивности специализированным прибором, стоит помнить, что нельзя держаться руками за оба его вывода. В противном случае показания могут измениться и будут неверными. Вызвано это включением в измеряемую цепь тела человека с его собственной индуктивностью.
Расчёт индуктивного сопротивления катушки
Любая индуктивность, в т.ч. катушка, оказывает переменному току некоторое сопротивление. Как его рассчитать, было описано выше. Из формулы XL=2pfL видно, что сопротивление дросселя в первую очередь зависит от частоты протекающего по нему тока и его индуктивности. При этом с обоими параметрами связь прямо пропорциональная.
Полное сопротивление
Частота – это характеристика внешней среды, индуктивность катушки зависит от ряда её геометрических свойств:
L=u0urN2S/l,
где:
- u0 – магнитная проницаемость вакуума — 4p*10-7 Гн/м;
- ur – относительная проницаемость сердечника;
- N – количество витков дросселя;
- S – его поперечное сечение в м2;
- l – длина катушки в метрах.
Располагая вышеописанными формулами и информацией о материале и размерах катушки, можно достаточно точно прикинуть её индуктивное сопротивление без каких-либо измерительных приборов.
Дополнительная информация. Некоторые цифровые мультиметры имеют режим замера индуктивности. Подобная функция встречается редко, однако иногда оказывается очень полезной. Поэтому при выборе прибора стоит обратить внимание на то, способен ли он измерять индуктивность.
Единицы индуктивного реактивного сопротивления | Единица СИ индуктивного реактивного сопротивления
Индуктивное реактивное сопротивление противодействует протеканию тока в цепи. Таким образом, единица измерения индуктивного сопротивления в системе СИ такая же, как и у сопротивления, то есть Ом.
Символ индуктивного сопротивления
Индуктивное сопротивление обозначается ?Lor XL.
Индуктивность в цепи постоянного тока
 Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.
Для лучшего понимания происходящих процессов в катушке, рассмотрим, что происходит в катушке при подаче на нее постоянного напряжения.
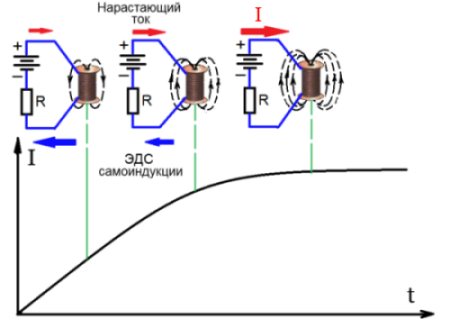
При подключении источника питания к катушке в ней начинает протекать ток, который создает вокруг неё магнитное поле.
Магнитные силовые линии поля распространяются через витки катушки наружу пересекая их, и образуют при этом ЭДС самоиндукции.
Эта ЭДС, согласно правилу Ленца, будет препятствовать мгновенному нарастанию тока в катушке. Нарастание тока происходит постепенно, по экспоненциальному закону.
Через небольшой промежуток времени переходной процесс заканчивается, и ток достигает своего нормального значения.
Продолжительность нарастания тока в секундах определяется по формуле:
t=3L/R,
где L – индуктивность катушки в генри, а R – общее сопротивление всей цепи в омах.
Если, к примеру, индуктивность катушки L=0,6 Г, а сопротивление цепи R=60 Ом, тогда длительность переходного процесса будет равна:
t=3•0,6/60=0,03 сек.
При отключении батареи от катушки индуктивность тоже происходит переходный процесс (такой опыт с первичной обмоткой трансформатора показан на странице “Электромагнетизм” рис.е).
В этом случае силовые магнитные линии будут приближаться к центру катушки опять пересекая ее витки. Создается ЭДС самоиндукции, которая уже направлена не против тока, а (опять же по правилу Ленца) совпадающая с направлением прерванного тока.
Если катушка имеет большую индуктивность (в нашем опыте катушкой является первичная обмотки трансформатора с большим количеством витков и значительным железным сердечником) и через нее протекал большой ток, то тогда ЭДС самоиндукции, появляющая на концах катушки индуктивности, может достигать величины во много раз больше напряжения источника питания.
Это объясняется тем, что при размыкании питающей сети энергия, запасенная в магнитном поле катушки, не исчезает, а превращается в ток.
Напряжение между концами катушки индуктивности может достигать таких значений, которое способно привести к пробою между обмотками, а так же выводу из строя полупроводниковых приборов. Это надо надо учитывать на практике при работе с приборами, имеющие катушки с большой индуктивностью через которые проходит значительный ток.
Индуктивность в цепи переменного тока
Для опытов с постоянным током катушка индуктивности намотана тонким проводом с большим количеством витков.
Это делается для того, чтобы при подаче на нее напряжения с мощного источника питания витки катушки не перегорели, т.к. при намотке витков толстым проводом сопротивление будет маленьким, а ток через нее большой (по закону Ома для постоянного тока I=U/R) и она может сгореть.
Сопротивление катушки индуктивности постоянному току (которое можно измерить мультиметром) называется активным сопротивлением.
Будет иначе, если в цепь катушки подать переменный ток.
При этом магнитное поле катушки индуктивности становится тоже переменным.
На рисунке показано, как меняется магнитное поле при синусоидальном токе. Во время периода магнитное поле меняет как свою силу, так и свое направление по синусоидальному закону. А это значит, что при этом возникает ЭДС самоиндукции, которая, согласно правилу Ленца, будет препятствовать приложенному извне напряжению.
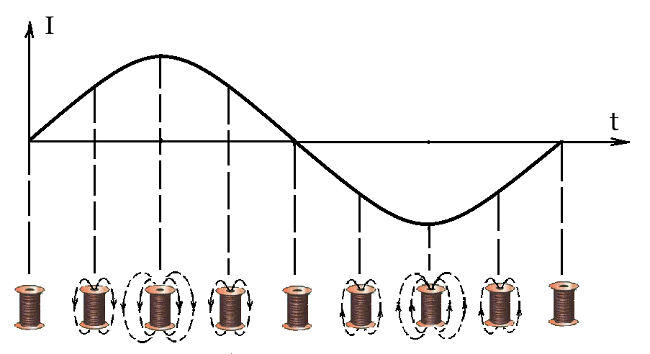
Рассмотрим график происходящих процессов в катушке индуктивности.
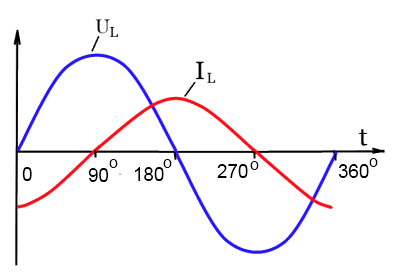
При включения катушки в цепь переменного тока в первую четверть периода ( 0º-90º) на катушку поступает нарастающее напряжение и ее магнитное поле “расширяется”, накапливая магнитную энергию. Ток, в этот момент, противодействующей ЭДС самоиндукции, максимальный и противоположный по знаку с напряжением на катушке.
За другую четверть периода (90º-180º), когда напряжение на катушке индуктивности уменьшается, магнитное поле “сворачивается”, индуцируя ЭДС самоиндукции, которое совпадает с направлением тока. Этот ток самоиндукции в катушке старается уже “помочь” уменьшающему переменному току сохранить достигнутый большой магнитный поток. В этот полупериод катушка индуктивности уже не потребляет, а отдает энергию обратно генератору.
Следовательно, происходит постоянный обмен энергий между генератором и катушкой. А это означает, что средняя мощность потребления катушки равна нулю.
Благодаря разнице фаз тока и напряжения в 90º, катушка индуктивности имеет реактивную мощность и, соответственно, реактивное сопротивление, как и конденсатор. Разница лишь в том, что в катушке индуктивности напряжение опережает ток, а в конденсаторе – наоборот.
Реактивное (индуктивное) сопротивление катушки, в отличии от ее активного сопротивления, не вызывает безвозвратных потерь энергии.
Допустим, возьмем идеальную катушку, в которой не учитываются сопротивления провода и другие потери.
Тогда катушка индуктивности окажет переменному напряжению индуктивное сопротивление XL,которое измеряется в омах и вычисляется по формуле:
![]()
где f – частота тока в герцах (Гц), а L – индуктивность катушки в генри (Г).
Отсюда видно, что величина индуктивного сопротивления катушки зависит от частоты и индуктивности. Чем выше частота тока и больше индуктивность катушки, тем больше индуктивное сопротивление.
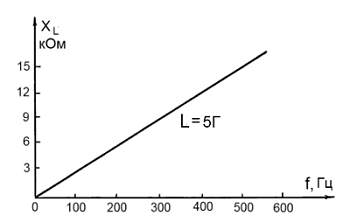
К примеру, найдем индуктивное сопротивление катушки индуктивностью 5Г на частоте 50Гц.
XL=2π•50•5=1570 Ом.
На частоте 1кГц эта катушка будет иметь индуктивное сопротивление 31кОм, а на 1МГц – 31МОм. На графике показана зависимость упомянутой катушки от частоты.
Теперь, зная значение индуктивного сопротивления, можно записать закон Ома при переменном токе через катушку:
![]()
Например,найдем ток, который протекает через идеальную катушку с индуктивностью L=500 мкГ, если ее подключить к переменному напряжению U=0,4 В и частотой f=500 кГц.
I= 0,4/2•3,14•5•103•500•10-6=0,25 мА
В реальной катушке нужно учитывать не только индуктивное сопротивление, но и сопротивление потерь Rпот.
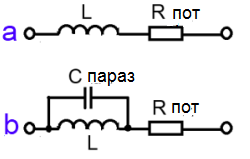
На низких частотах Rпот равно только сопротивлению провода катушки. При повышении частоты на катушке сопротивление потерь будет возрастать за счет появления других потерь (вихревые токи, поверхностный эффект проводника и т.д.) (рис.а).
Поэтому полное сопротивление катушки индуктивности переменному току на средних частотах равно:
![]()
и называется импедансом.
На высоких частотах начинает оказывать еще влияние cобственная (паразитная) емкость катушки Спараз, которая шунтирует индуктивность (рис.b).
Основными параметрами высокочастотных катушек индуктивности являются индуктивность, добротность и собственная емкость.
Индуктивность зависит от количества витков, размера катушки и наличия ферромагнитного сердечника. Чем больше намотано витков на катушке, тем больше ее индуктивность. А наличие сердечника увеличит индуктивность катушки.
Добротность определяет качество катушки индуктивности и равна отношению индукнивного сопротивления к сопротивлению потерь:
![]()
Чем больше добротность, тем качественнее катушка. Катушкой хорошего качества считается катушка с добротностью от 50 до 200.
Чтобы достигнуть такого качества используют следующие средства:
– применением сердечников, при которых увеличивается индуктивность при меньшем числе витков катушки (т.е. уменьшается сопротивление провода);
– увеличение толщины провода, что, правда, увеличит габариты катушки;
– в диапазоне длинных и средних волн применение провода литцендрат, который состоит из определенного количества проволочек изолированных друг от друга.
Собственная емкость катушки индуктивности обусловлена емкостью обмотки и является нежелательной. Для ее уменьшения применяются различные способы намотки катушки.
Одним из способов является перекрестная намотка типа “универсаль” (рис.c). Так же применяется намотка витков не плотно друг к другу, а на определенном расстоянии с принудительным шагом)(рис.d,e). 
Что называется индуктивным и емкостным сопротивлением?
Сопротивление индуктивное — величина, характеризующая сопротивление, оказываемое переменному току индуктивностью цепи (её участка), измеряется в омах. Ёмкостное сопротивление — величина, характеризующая сопротивление, оказываемое переменному току электрической ёмкостью цепи (или её участка).
Что такое емкостное сопротивление и как оно определяется?
— емкостное сопротивление — это проводник, включенный в цепь переменного тока и неимеющий заметного сопротивления и индуктивности, но имеющий заметную емкость С. — емкостное сопротивление проводника переменному току. — действующие значения силы тока и напряжения связаны соотношением, аналогичным закону Ома.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними
Мы с вами знаем формулировку закона Ома для цепей постоянного тока, которая гласит, что ток в такой цепи прямо пропорционален напряжению на элементе цепи и обратно пропорционален сопротивлению этого элемента постоянному току, протекающему через него.
Однако при изучении цепей переменного тока стало известно, что оказывается кроме элементов цепей с активным сопротивлением, есть элементы цепи с так называемым реактивным сопротивлением, то есть индуктивности и емкости (катушки и конденсаторы).
В цепи, содержащей только активное сопротивление, фаза тока всегда совпадает с фазой напряжения (рис 1.), т. е. сдвиг фаз тока и напряжения в цепи с чисто активным сопротивлением равен нулю.

Рисунок 1. Напряжение и ток в цепи с чисто активным сопротивлением. Сдвиг фаз между током и напряжение в цепи переменного тока с чисто активным сопротивлением всегда равен нулю
Отсюда следует, что угол между радиус-векторами тока и напряжения также равен нулю.
Тогда, падение напряжения на активном сопротивлении определяется по формуле:
| (1) |
- где, U-напряжение на элементе цепи,
- I – ток через элемент цепи
- R – активное сопротивление элемента
- Формула (1) применима как для амплитудных, так и для эффективных значений тока и напряжения:
 |
(2) |
- где, Um-амплитудное значение напряжения на элементе цепи,
- Im – амплитудное значение тока через элемент цепи
- R – активное сопротивление элемента
В цепи, содержащей чисто реактивное сопротивление — индуктивное или емкостное, — фазы тока и напряжения сдвинуты друг относительно друга на четверть периода, причем в чисто индуктивной цепи фаза тока отстает от фазы напряжения (рис. 2), а в чисто емкостной цепи фаза тока опережает фазу напряжения (рис. 3).

Рисунок 2. Напряжение и ток в цепи с чисто индуктивным сопротивлением. Фаза тока отстает от фазы напряжения на 90 градусов.

Рисунок 3. Напряжение и ток в цепи с чисто емкостным сопротивлением. Фаза тока опережает фазу напряжения на угол 90 градусов.
Отсюда следует, что в чисто реактивной цепи угол между радиус-векторами тока и напряжения всегда равен 90°, причем в чисто индуктивной цепи радиус-вектор тока при вращении движется позади радиус-вектора напряжения, а в чисто емкостной цепи он движется впереди радиус-вектора напряжения.
Падения напряжения на индуктивном и емкостном сопротивлениях определяются соответственно по формулам:
- где — UL-падение напряжение на чисто индуктивном сопротивлении ;
- UС—падение напряжения на чисто емкостном сопротивлении;
- I— значение тока в через реактивное сопротивление;
- L— индуктивность реактивного элемента;
- C— емкость реактивного элемента;
- ω— циклическая частота.
Эти формулы применимы как для амплитудных, так и для эффективных значений тока и напряжения синусоидальной формы. Однако здесь следует отметить, что они ни в коем случае не применимы для мгновенных значений тока и напряжения, а также и для несинусоидальных токов.
Приведенные выше формулы являются частными случаями закона Ома для переменного тока.
Следовательно, полный закон Ома для переменного тока будет иметь вид:
 |
(5) |
Где Z – полное сопротивление цепи переменного тока.
Теперь остается только вычистислить полное сопротивление цепи, а оно зависит непосредсвенно от какие активные и реактивные элементы присутсвуют в цепи и как они соединены.
Закон Ома для различных типовых цепей переменного тока
Давайте выясним, как будет выглядеть закон Ома для цепи переменного тока, состоящей из активного и индуктивного сопротивлений, соединенных последовательно (рис. 4.)

Рисунок 4. Цепь переменного тока с последовательным соединением активного и индуктивного сопротивления.
Закон Ома для переменного синусоидального тока в случае последовательного соединения активного и индуктивного сопротивлений выражается следующей формулой:
 |
(6) |
- где —эффективное значение силы тока в А;
- U—эффективное значение напряжения в В;
- R—активное сопротивление в Ом;
- ωL—индуктивное сопротивление в ом.
- Формула (6) будет также действительной, если в нее подставить амплитудные значения тока и напряжения.
В цепи, изображенной на рис. 5, соединены последовательно активное и емкостное сопротивления.
Рисунок 5. Цепь переменного тока с последовательным соединением активного и емкосного сопротивления.
А закон Ома для такой цепи принимает вид:
В общем случае, когда цепь содержит все три вида сопротивлений (рис. 6),
Рисунок 6. Цепь переменного тока с последовательным соединением активного, индуктивного и емкосного сопротивления.
Закон Ома при последовательном соединении активного, индуктивного и емкостного сопротивлений будет выглядеть так:
- где I-сила тока в А;
- U-напряжение в В;
- R-активное сопротивление в Ом;
- ωL-индуктивное сопротивление в Ом;
- 1/ωС-емкостное сопротивление в Ом.
- Формула (8) верна только для эффективных и амплитудных значений синусоидального тока и напряжения.
- Для того, что бы определить ток в цепях с параллельным соединением элементов (рисунок 7), то необходимо так же вычислить полное сопротивление цепи, как это делать можно прсмотреть здесь, зтем подставить значение полного сопротивления в общую формулу для закона Ома (5).
Рисунок 7. Полное сопротивление цепи при параллельном соединении активного и реактивных элементов. а) — параллельное соединение R и L; б) — параллельное соединение R и C.
Тоже самое касается и вычисления тока в колебательном контуре изображенном на рисунке 8.
Рисунок 8. Эквивалентная схема колебательного контура.
- Таким образом закон Ома для переменного тока можно сформулировать следующим образом.
- Значение тока в цепи переменного тока прямо пропорционально напряжению в цепи (или на участке цепи) и обратно пропорционально полному сопротивлению цепи (участка цепи)
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Источник: http://www.sxemotehnika.ru/zakon-oma-dlia-peremennogo-toka.html
Закон Ома для переменного тока

Когда-то люди жили без электричества. Потом научились делать батарейки, и так появился постоянный электрический ток. Есть у электриков шутка: «Что такое переменный ток? Это нет-нет, да шарахнет…» А вот тут возникает логичный вопрос: «Почему не остановились на постоянном токе, раз он безопаснее»? Исключительно с экономической точки зрения. Переменный ток гораздо удобнее и дешевле преобразовывать, то есть повышать или понижать. Точнее не сам ток, а напряжение. Когда протекает ток, он совершает работу, работа сопровождается выделением тепла. Мощность, это произведение тока и напряжения, а значит, повышая напряжение и понижая ток мы передадим ту же мощность, но с меньшим тепловыделением, а значит и с меньшими потерями. А ещё, чем выше напряжение, тем меньше сопротивление проводов, по которым протекает ток, это оказывает влияние на потери напряжения. Как-нибудь поговорим более подробно об этом. А пока обратимся к школьному курсу физики – ток протекает только по замкнутому контуру и возможен только при условии, что к этому контуру будет приложено напряжение и контур будет иметь какое-то сопротивление. Подробно об этом вы можете прочитать в статье Закон Ома для замкнутой цепи. А мы двинемся дальше.
Сейчас вы поймете, почему так важен и что даёт закон Ома для цепи переменного тока. В современной жизни без этого закона никак не обойтись. Поскольку ток, это работа, а работа есть выделение тепла, то существенная задача электротехники в том, чтобы соблюдался термический режим, проще говоря, чтобы не произошло перегрева электроцепей. Итак, закон Ома гласит, что:

Измерить напряжение довольно просто, для этого понадобится вольтметр, в нашем случае для переменного напряжения.
В цепях постоянного тока измерить сопротивление тоже не составляет сложности, для этого потребуется омметр.
Почему же возникают сложности с переменным током? А проблема, именно, в его переменности, а точнее понятиях емкости и индукции, которые ведут себя при переменном токе несколько иначе, нежели при постоянном.
Формула Закона Ома для переменного тока:

Кому-то эта формула может показаться неожиданной, потому что все привыкли видеть другую формулу:

Теперь давайте разберёмся, что такое полное сопротивление цепи и всё сразу встанет на свои места.
В цепях постоянного тока конденсаторы могут только накапливать заряд, а катушки индуктивности становятся обычным проводом, но в цепях переменного тока они становятся сопротивлениями.
Поэтому в переменном токе существует две составляющие: активный ток и реактивный. Как это происходит, сейчас увидите.
Ёмкостное сопротивление. При подаче напряжения на конденсатор сначала возникает сильный ток и потом поднимается напряжение, то есть в идеальных условиях ток опережает напряжение на угол 90.
Другими словами, ток совершает работу из-за наличия сопротивления в цепи, которое можно посчитать по формуле:

Таким образом, чем выше частота переменного тока и чем выше емкость конденсатора, тем меньше ёмкостное сопротивление.
Индуктивное сопротивление. Здесь все происходит наоборот, сначала возникает напряжение, затем запускается индукционный процесс который препятствует возрастанию тока. Подробнее об этом читайте в статьях про индукцию.

Поэтому здесь мы видим уже обратную картину – чем выше частота и чем больше индуктивность катушки, тем больше индуктивное сопротивление переменному току.
Почему эти понятия не встречаются в цепях постоянного тока? Ответ можно узнать, посмотрев на формулы. Если ток постоянный, то f=0.
То есть, емкостное сопротивление станет бесконечно большим, а это значит, что конденсатор в цепи постоянного тока становится похож на выключатель, который размыкает цепь и ток по ней не идёт, но при этом, конденсатор будет пропускать переменный ток.
А индуктивное сопротивление станет равно нулю, значит, у нас останется просто провод, который имеет свое собственное сопротивление, которое еще называется активным, и его можно измерить обычным омметром.
В отличие от конденсатора, у которого нет активного сопротивления, сопротивление катушки, если оно довольно большое, должно приниматься в расчёт. Как правило, активное сопротивление катушки очень маленькое по сравнению с индуктивным, поэтому его в расчёт не берут, но всё же правильно формула сопротивления катушки выглядит так:
![]()
- По такому принципу в электронике изготавливают фильтры, которые должны отсечь переменный ток от постоянного, то есть пропускать только переменный ток или наоборот заглушить переменный ток, оставив только постоянный, или даже заглушить токи какой-то одной или нескольких частот.
- А сейчас совсем вас запутаю… И катушка может иметь ёмкостные свойства и конденсатор – индуктивные, но как правило они слишком малы и носят паразитический характер.
- Ну а сейчас мы рассмотрим закон Ома для электрической цепи переменного тока наглядно.

Допустим, у нас есть цепь из последовательно включенных резистора (активное сопротивление), конденсатора (реактивное ёмкостное сопротивление) и катушка (активно-реактивное индуктивное сопротивление). Теперь, чтобы узнать силу тока в цепи нам нужно правильно посчитать полное сопротивление цепи.

Осталось применить всё изложенное выше.
Реактивное сопротивление Х это разница между индуктивным сопротивлением XL и ёмкостным сопротивлением XC. Ну а дальше векторным сложением можем узнать полное реактивное сопротивление

- следовательно:
- дальнейший расчет:
- или:
Что можно сказать в заключении. Как вы можете видеть, закон Ома для переменного тока точно такой же, как и для постоянного. Разница лишь в том, как считать сопротивление. Если в постоянном токе мы имеем только активное сопротивление, то в переменном токе добавляется еще и реактивное, а именно индуктивное и емкостное.
И, кстати говоря, реактивный ток – явление, с которым в электротехнике стараются бороться различными методами, поскольку эти токи паразитные и не несут полезной нагрузки. Об этом мы поговорим в других статьях.
Пока сообщу лишь, что идеальный вариант, к которому пока никто не смог приблизиться, чтобы нагрузка была исключительно активной.
Источник: https://uelektrika.ru/osnovy-yelektrotekhniki/zakon-oma-dlya-peremennogo-toka/
Закон Ома для переменного тока
После открытия в 1831 году Фарадеем электромагнитной индукции, появились первые генераторы постоянного, а после и переменного тока. Преимущество последних заключается в том, что переменный ток передается потребителю с меньшими потерями.
При увеличении напряжения в цепи, ток будет увеличиваться аналогично случаю с постоянным током. Но в цепи переменного тока сопротивление оказывается катушкой индуктивности и конденсатор. Основываясь на этом, запишем закон Ома для переменного тока: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

где
- I [А] – сила тока,
- U [В] – напряжение,
- Z [Ом] – полное сопротивление цепи.
Полное сопротивление цепи
В общем случае полное сопротивление цепи переменного тока (рис. 1) состоит из активного (R [Ом]), индуктивного, и емкостного сопротивлений. Иными словами, ток в цепи переменного тока зависит не только от активного омического сопротивления, но и от величины емкости (C [Ф]) и индуктивности (L [Гн]). Полное сопротивление цепи переменного тока можно вычислить по формуле:
 где
где
 — индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой.
— индуктивное сопротивление, оказываемое переменному току, обусловленное индуктивностью электрической цепи, создается катушкой. — емкостное сопротивление, создается конденсатором.
— емкостное сопротивление, создается конденсатором.
Полное сопротивление цепи переменного тока можно изобразить графически как гипотенузу прямоугольного треугольника, у которого катетами являются активное и индуктивное сопротивления.
Рис.1. Треугольник сопротивлений

Учитывая последние равенства, запишем формулу закона Ома для переменного тока:
 – амплитудное значение силы тока.
– амплитудное значение силы тока. 
Рис.2. Последовательная электрическая цепь из R, L, C элементов.
Из опыта можно определить, что в такой цепи колебания тока и напряжения не совпадают по фазе, а разность фаз между этими величинами зависит от индуктивности катушки и емкости конденсатора:

Цепь переменного тока состоит из последовательно соединенных конденсатора (емкостью С), катушки индуктивности (L) и активного сопротивления (R). На зажимы цепи подается действующее напряжение (U), частота которого ν. Чему равно действующее значение силы тока в цепи?
Дано:
Решение:
Источник: https://zakon-oma.ru/dlya-peremennogo-toka.php
Закон РћРјР° для цепей постоянного Рё переменного тока — теория Рё практика
- Онлайн расчёт электрических величин напряжения, тока и мощности для: участка цепи, полной цепи с резистивными, ёмкостными и индуктивными
- элементами.
— Рђ любите ли Р’С‹ закон РћРјР° так, как люблю его СЏ? — СЃРїСЂРѕСЃРёР» учитель физики стоящего СЂСЏРґРѕРј СЃ щитком Рё разглядывающего СЃРІРѕР№ обугленный палец электрика, — Всеми силами души Вашей, СЃРѕ всем энтузиазмом Рё исступлением, Рє которому только СЃРїРѕСЃРѕР±РЅР° пылкая молодость, — никак РЅРµ угомонялся РѕРЅ, сверкая РёР·-РїРѕРґ очков пытливым взглядом. — Мужик, ты что, дурак? – вежливо поинтересовался обиженный противоестественным РІРѕРїСЂРѕСЃРѕРј электрик Рё пошёл, насвистывая «РљР°Р»РёРЅРєСѓ-Малинку» РІ направлении ближайшего супермаркета — РЅРµ ради пьянства окаянного, Р° дабы залечить СЃРІРѕР№ увечный палец.
А тем временем, закон Ома является в электротехнике основным законом, который устанавливает связь силы электрического тока с сопротивлением и напряжением.
Формулировка закона Ома для участка цепи может быть представлена так: сила тока в проводнике прямо пропорциональна напряжению (разности потенциалов) на его концах и обратно пропорциональна сопротивлению этого проводника и записана в следующем виде:
I=U/R,  I – сила тока РІ РїСЂРѕРІРѕРґРЅРёРєРµ, измеряемая РІ амперах [Рђ]; U – электрическое напряжение (разность потенциалов), измеряемая РІ вольтах [Р’]; R – электрическое сопротивление РїСЂРѕРІРѕРґРЅРёРєР°, измеряемое РІ омах [РћРј].
I – сила тока в проводнике, измеряемая в амперах [А]; U – электрическое напряжение (разность потенциалов), измеряемая в вольтах [В]; R – электрическое сопротивление проводника, измеряемое в омах [Ом].
Производные РѕС‚ этой формулы приобретают такой же незамысловатый РІРёРґ: R=U/I Рё U=R×I.
Зная любые два из трёх приведённых параметров можно легко произвести расчёт и величины мощности, рассеиваемой на резисторе.
Мощность является функцией протекающего тока I(А) и приложенного напряжения U(В) и вычисляется по следующим формулам, также являющимся производными от основной формулы закона Ома:
P(Р’С‚) = U(Р’)Г—I(Рђ) = I2(Рђ)Г—R(РћРј) = U2(Р’)/R(РћРј) Можно, конечно, описывая закон РћРјР° обойтись Рё вообще без формул, Р° вместо РЅРёС… пользоваться словами или картинками: РЎ РґСЂСѓРіРѕР№ стороны, формулы настолько просты, что РЅРµ стоят выеденного яйца Рё, возможно, вообще РЅРµ заслуживают отдельной РєСЂСѓРїРЅРѕР№ статьи РЅР° страницах уважающего себя сайта. РќРµ заслуживают, так РЅРµ заслуживают. Калькулятор Вам РІ помощь, дамы Рё рыцари! Считайте, учитывайте размерность, РЅРµ стирайте РёР· памяти, что: 1Р’=1000РјР’=1000000РјРєР’; 1Рђ=1000РјРђ=1000000РјРєРђ; 1РћРј=0.001РєРћРј=0.000001РњРћРј; 1Р’С‚=1000РјР’С‚=100000РјРєР’С‚. РќСѓ Рё так, РЅР° РІСЃСЏРєРёР№ случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую РІ онлайн режиме проверить расчёты, связанные СЃРѕ знанием формул закона РћРјР°.
С другой стороны, формулы настолько просты, что не стоят выеденного яйца и, возможно, вообще не заслуживают отдельной крупной статьи на страницах уважающего себя сайта. Не заслуживают, так не заслуживают. Калькулятор Вам в помощь, дамы и рыцари! Считайте, учитывайте размерность, не стирайте из памяти, что: 1В=1000мВ=1000000мкВ; 1А=1000мА=1000000мкА; 1Ом=0.001кОм=0.000001МОм; 1Вт=1000мВт=100000мкВт. Ну и так, на всякий случай, чисто для проверки полученных результатов, приведём незамысловатую таблицу, позволяющую в онлайн режиме проверить расчёты, связанные со знанием формул закона Ома.
ТАБЛ�ЦА ДЛЯ ПРОВЕРК� РЕЗУЛЬТАТОВ РАСЧЁТОВ ЗАКОНА ОМА.
Вводить РІ таблицу нужно только РґРІР° имеющихся Сѓ Вас параметра, остальные посчитает таблица. Р’СЃРµ наши расчёты проводились РїСЂРё условии, что значение внешнего сопротивления R значительно превышает внутреннее сопротивление источника напряжения rвнутр. Если это условие РЅРµ соблюдается, то РїРѕРґ величиной R следует принять СЃСѓРјРјСѓ внешнего Рё внутреннего сопротивлений: R = Rвнешн + rвнутр , после чего закон приобретает солидное название — закон РћРјР° для полной цепи: I=U/(R+r) . Для многозвенных цепей возникает необходимость преобразования её Рє эквивалентному РІРёРґСѓ:
Значения последовательно соединённых резисторов просто суммируются, в то время как значения параллельно соединённых резисторов определяются исходя из формулы: 1/Rll = 1/R4+1/R5.
А онлайн калькулятор для расчёта величин сопротивлений при параллельном соединении нескольких проводников можно найти на странице ссылка на страницу.
Теперь, что касается закона Ома для переменного тока.
Если внешнее сопротивление у нас чисто активное (не содержит ёмкостей и индуктивностей), то формула, приведённая выше, остаётся в силе.
Единственное, что надо иметь РІ РІРёРґСѓ для правильной интерпретации закона РћРјР° для переменного тока — РїРѕРґ значением U следует понимать действующее (эффективное) значение амплитуды переменного сигнала.
Рђ что такое действующее значение Рё как РѕРЅРѕ связано СЃ амплитудой сигнала переменного тока? Приведём диаграммы для нескольких различных форм сигнала. Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал СЃРѕ скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя РЅР° СЂРёСЃСѓРЅРѕРє можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда РІ пределах положительной, или отрицательной (РІ наших случаях РѕРЅРё равны) полуволны. Рассчитываем действующее значение напряжение интересующей нас формы: Для СЃРёРЅСѓСЃР° U = UРґ = UР°/в€љ2; для треугольника Рё пилы U = UРґ = UР°/в€љ3; для меандра U = UРґ = UР°. РЎ этим разобрались!
Слева направо нарисованы диаграммы синусоидального сигнала, меандра (прямоугольный сигнал СЃРѕ скважностью, равной 2), сигнала треугольной формы, сигнала пилообразной формы. Глядя РЅР° СЂРёСЃСѓРЅРѕРє можно осмыслить, что амплитудное значение приведённых сигналов — это максимальное значение, которого достигает амплитуда РІ пределах положительной, или отрицательной (РІ наших случаях РѕРЅРё равны) полуволны. Рассчитываем действующее значение напряжение интересующей нас формы: Для СЃРёРЅСѓСЃР° U = UРґ = UР°/в€љ2; для треугольника Рё пилы U = UРґ = UР°/в€љ3; для меандра U = UРґ = UР°. РЎ этим разобрались!
Теперь посмотрим, как будет выглядеть формула закона Ома при наличии индуктивности или ёмкости в цепи переменного тока.
Р’ общем случае смотреться это будет так:
А формула остаётся прежней, просто в качестве сопротивления R выступает полное сопротивление цепи Z, состоящее из активного, ёмкостного и индуктивного сопротивлений.
Поскольку фазы протекающего через эти элементы тока РЅРµ одинаковы, то простым арифметическим сложением сопротивлений этих трёх элементов обойтись РЅРµ удаётся, Рё формула приобретает РІРёРґ:  Реактивные сопротивления конденсаторов Рё индуктивностей РјС‹ СЃ Вами уже рассчитывали РЅР° странице ссылка РЅР° страницу Рё знаем, что величины эти зависят РѕС‚ частоты, протекающего через РЅРёС… тока Рё описываются формулами: XC = 1/(2ПЂЖ’РЎ) , XL = 2ПЂЖ’L .
Реактивные сопротивления конденсаторов и индуктивностей мы с Вами уже рассчитывали на странице ссылка на страницу и знаем, что величины эти зависят от частоты, протекающего через них тока и описываются формулами: XC = 1/(2πƒС) , XL = 2πƒL .
Нарисуем таблицу для расчёта полного сопротивления цепи для переменного тока.
Количество вводимых элементов должно быть РЅРµ менее РѕРґРЅРѕРіРѕ, РїСЂРё наличии индуктивного или емкостного элемента — необходимо указать значение частоты f !
КАЛЬКУЛЯТОРДЛЯ ОНЛАЙН РАСЧЁТА ПОЛНОГО СОПРОТ�ВЛЕН�Я ЦЕП�.
Теперь давайте рассмотрим практический пример применения закона Ома в цепях переменного тока и рассчитаем простенький бестрансформаторный источник питания.
 Токозадающими цепями РІ данной схеме являются элементы R1 Рё РЎ1. Допустим, нас интересует выходное напряжение Uвых = 12 вольт РїСЂРё токе нагрузки 100 РјРђ. Выбираем стабилитрон Р”815Р” СЃ напряжением стабилизации 12Р’ Рё максимально допустимым током стабилизации 1,4Рђ. Зададимся током через стабилитрон СЃ некоторым запасом — 200РјРђ. РЎ учётом падения напряжения РЅР° стабилитроне, напряжение РЅР° токозадающей цепи равно 220РІ — 12РІ = 208РІ. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200РјРђ: Z = 208РІ/200РјРђ = 1,04РєРћРј. Резистор R1 является токоограничивающим Рё выбирается РІ пределах 10-100 РћРј РІ зависимости РѕС‚ максимального тока нагрузки. Зададимся номиналами R1 — 30 РћРј, РЎ1 — 1 РњРєС„, частотой сети f — 50 Гц Рё подставим РІСЃС‘ это хозяйство РІ таблицу. Получили полное сопротивление цепи, равное 3,183РєРћРј. Многовато будет — надо увеличивать ёмкость РЎ1. Поигрались туда-СЃСЋРґР°, нашли нужное значение ёмкости — 3,18 РњРєС„, РїСЂРё котором Z = 1,04РєРћРј. Р’СЃС‘ — закон РћРјР° выполнил СЃРІРѕСЋ функцию, расчёт закончен, всем спать полчаса!
Токозадающими цепями РІ данной схеме являются элементы R1 Рё РЎ1. Допустим, нас интересует выходное напряжение Uвых = 12 вольт РїСЂРё токе нагрузки 100 РјРђ. Выбираем стабилитрон Р”815Р” СЃ напряжением стабилизации 12Р’ Рё максимально допустимым током стабилизации 1,4Рђ. Зададимся током через стабилитрон СЃ некоторым запасом — 200РјРђ. РЎ учётом падения напряжения РЅР° стабилитроне, напряжение РЅР° токозадающей цепи равно 220РІ — 12РІ = 208РІ. Теперь рассчитаем сопротивление этой цепи Z для получения тока, равного 200РјРђ: Z = 208РІ/200РјРђ = 1,04РєРћРј. Резистор R1 является токоограничивающим Рё выбирается РІ пределах 10-100 РћРј РІ зависимости РѕС‚ максимального тока нагрузки. Зададимся номиналами R1 — 30 РћРј, РЎ1 — 1 РњРєС„, частотой сети f — 50 Гц Рё подставим РІСЃС‘ это хозяйство РІ таблицу. Получили полное сопротивление цепи, равное 3,183РєРћРј. Многовато будет — надо увеличивать ёмкость РЎ1. Поигрались туда-СЃСЋРґР°, нашли нужное значение ёмкости — 3,18 РњРєС„, РїСЂРё котором Z = 1,04РєРћРј. Р’СЃС‘ — закон РћРјР° выполнил СЃРІРѕСЋ функцию, расчёт закончен, всем спать полчаса!
Источник: https://vpayaem.ru/information11.html
Активное, емкостное и индуктивное сопротивление. Закон Ома для цепей переменного тока
Определение 1
Пусть источник переменного тока включен в цепь, в которой индуктивностью и емкостью можно пренебречь. Переменный ток изменяется в соответствии с законом:
[Ileft(t
ight)=I_m{sin left(omega t
ight) left(1
ight). }] 
- Рисунок 1.
- Тогда, если применить к участку цепи ($а R в$) (рис.1) закон Ома получим:
[U=IR=I_m{Rsin left(omega t
ight) left(2
ight), }]
где $U$ — напряжение на концах участка. Разность фаз между током и напряжением равна нулю. Амплитудное значение напряжения ($U_m$) равно:
[U_m=RI_mleft(3
ight),]
где коэффициент $R$ — называется активным сопротивлением. Наличие активного сопротивления в цепи всегда приводит к выделению тепла.
Допустим, что в участок цепи включен конденсатор емкости $С$, а $R=0$ и $L=0$. Будем считать силу тока ($I$) положительной, если она имеет направление, которое указано на рис. 2. Пусть заряд на конденсаторе равен $q$.

- Рисунок 2.
- Мы можем использовать следующие соотношения:

Ничего непонятно?
Попробуй обратиться за помощью к преподавателям
- Если $I(t)$ определена уравнением (1), то заряд выражен как:
- где $q_0$ произвольный постоянный заряд конденсатора, который не связан с колебаниями тока, поэтому можем допустить, что $q_0=0.$ Получим напряжение равно:
- Формула (6) показывает, что на конденсаторе колебания напряжения отстают от колебаний силы тока по фазе на $frac{pi }{2}.$ Амплитуда напряжения на емкости равна:
Величину $X_C=frac{1}{omega C}$ называют реактивным емкостным сопротивлением (емкостным сопротивлением, кажущимся сопротивлением емкости). Если ток постоянный, то $X_C=infty $.
Это значит, что постоянный ток не течет через конденсатор.
Из определения емкостного сопротивления видно, что при больших частотах колебаний, малые емкости являются небольшими сопротивлениями переменного тока.
Индуктивное сопротивление
Пусть участок цепи имеет только индуктивность (рис.3). Будем считать $I>0$, если ток направлен от $а$ к $в$.

- Рисунок 3.
- Если в катушке течет ток, то в индуктивности появляется ЭДС самоиндукции, следовательно, закон Ома примет вид:
- По условию $R=0. mathcal E$ самоиндукции можно выразить как:
- Из выражений (8), (9) следует, что:
- Амплитуда напряжения в данном случае равна:
- где $X_L- $индуктивное сопротивление (кажущееся сопротивление индуктивности).
Закон Ома для цепей переменного тока
Определение 2
Выражение вида:
[I_m=frac{U_m}{sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}}left(12
ight).]
где
[Z=sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}(13)]
называют полным электросопротивлением, или импедансом, иногда называют законом Ома для переменного тока. Однако необходимо помнить, что формула (12) относится к амплитудам тока и напряжения, а не мгновенным их значениям.
Пример 1
Задание: Чему равно действующее значение силы тока в цепи. Цепь переменного тока состоит из последовательно соединенных: конденсатора емкостью $C$, катушки индуктивности $L$, активного сопротивления $R$. На зажимы цепи подается напряжение действующее напряжение $U$ частота которого $
u$.
- Решение:
- Так как все элементы цепи соединены последовательно, то сила тока во всех элементах одинакова.
- Амплитудное значение силы тока выражается «законом Ома для переменного тока»:
- оно связано с действующим значением силы тока как:
- В условиях задачи мы имеем действующее значение напряжения $U$, нам в формуле (1.1) требуется амплитуда напряжения, используя формулу:
[I_m=frac{U_m}{sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}}left(1.1
ight)]
[I=frac{I_m}{sqrt{2}}left(1.2
ight).]
[U=frac{U_m}{sqrt{2}} o U_m=sqrt{2}Uleft(1.3
ight).]
Подставим в формулу (1.2) формулы (1.1) и (1.3), получим:
[I=frac{1}{sqrt{2}}frac{sqrt{2}U}{sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}}=frac{U}{sqrt{R^2+{left(omega L-frac{1}{omega C}
ight)}^2}}=frac{U}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}},]
где $omega =2pi
u .$
Ответ: $I=frac{U}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}}.$
Пример 2
- Задание: Используя условия задачи в первом примере, найдите действующие значения напряжений на катушке индуктивности ($U_L$), сопротивлении ($U_R$), конденсаторе ($U_C$).
- Решение:
- Используем результат примера 1. Напряжение на катушке индуктивности выражается формулой:
- Напряжение на активном сопротивлении ($U_R$) равно:
- Напряжение на конденсаторе ($U_C$) определяется как:
- Ответ: $U_L=2pi
u Lfrac{U}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}}, U_R=frac{UR}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}},U_C=frac{1}{C2pi
u }frac{U}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}}.$
[U_L=Iomega L=2 pi
u Lfrac{U}{sqrt{R^2+{left(2 pi
u L-frac{1}{2 pi
u C}
ight)}^2}}.]
[U_R=IR=frac{UR}{sqrt{R^2+{left(2pi
u L-frac{1}{2pi
u C}
ight)}^2}}.]
[U_C=frac{I}{C2 pi
u}=frac{1}{C2 pi
u}frac{U}{sqrt{R^2+{left(2 pi
u L-frac{1}{2 pi
u C}
ight)}^2}}.]
Источник: https://spravochnick.ru/fizika/peremennyy_sinusoidalnyy_tok/aktivnoe_emkostnoe_i_induktivnoe_soprotivlenie_zakon_oma_dlya_cepey_peremennogo_toka/
Закон Ома для переменного тока: формула
Закон Ома был открыт немецким физиком Георгом Омом в 1826 году и с тех пор начал широко применяться в электротехнической области в теории и на практике. Он выражается известной формулой, с посредством которой можно выполнить расчеты практически любой электрической цепи.
Тем не менее, закон Ома для переменного тока имеет свои особенности и отличия от подключений с постоянным током, определяемые наличием реактивных элементов.
Чтобы понять суть его работы, нужно пройти по всей цепочке, от простого к сложному, начиная с отдельного участка электрической цепи.
Закон ома для участка цепи
Закон Ома считается рабочим для различных вариантов электрических цепей. Более всего он известен по формуле I = U/R, применяемой в отношении отдельного отрезка цепи постоянного или переменного тока.
В ней присутствуют такие определения, как сила тока (I), измеряемая в амперах, напряжение (U), измеряемое в вольтах и сопротивление (R), измеряемое в Омах.  Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.
Широко распространенное определение этой формулы выражается известным понятием: сила тока прямо пропорциональна напряжению и обратно пропорциональна сопротивлению на конкретном отрезке цепи. Если увеличивается напряжение, то возрастает и сила тока, а рост сопротивления, наоборот, снижает ток. Сопротивление на этом отрезке может состоять не только из одного, но и из нескольких элементов, соединенных между собой последовательно или параллельно.
Формулу закона Ома для постоянного тока можно легко запомнить с помощью специального треугольника, изображенного на общем рисунке.
Он разделяется на три секции, в каждой из которых помещен отдельно взятый параметр. Такая подсказка дает возможность легко и быстро найти нужное значение.
Искомый показатель закрывается пальцем, а действия с оставшимися выполняются в зависимости от их положения относительно друг друга.
Если они расположены на одном уровне, то их нужно перемножить, а если на разных – верхний параметр делится на нижний. Данный способ поможет избежать путаницы в расчетах начинающим электротехникам.
Закон ома для полной цепи
Между отрезком и целой цепью существуют определенные различия. В качестве участка или отрезка рассматривается часть общей схемы, расположенная в самом источнике тока или напряжения. Она состоит из одного или нескольких элементов, соединенных с источником тока разными способами.
Система полной цепи представляет собой общую схему, состоящую из нескольких цепочек, включающую в себя батареи, разные виды нагрузок и соединяющие их провода. Она также работает по закону Ома и широко используется в практической деятельности, в том числе и для переменного тока.
Принцип действия закона Ома в полной цепи постоянного тока можно наглядно увидеть при выполнении несложного опыта.
Как показывает рисунок, для этого потребуется источник тока с напряжением U на его электродах, любое постоянное сопротивление R и соединительные провода. В качестве сопротивления можно взять обычную лампу накаливания.
Через ее нить будет протекать ток, создаваемый электронами, перемещающимися внутри металлического проводника, в соответствии с формулой I = U/R.
Система общей цепи будет состоять из внешнего участка, включающего в себя сопротивление, соединительные проводки и контакты батареи, и внутреннего отрезка, расположенного между электродами источника тока.
По внутреннему участку также будет протекать ток, образованный ионами с положительными и отрицательными зарядами.
Катод и анод станут накапливать заряды с плюсом и минусом, после чего среди них возникнет разность потенциалов.
Полноценное движение ионов будет затруднено внутренним сопротивлением батареи r, ограничивающим выход тока в наружную цепь, и понижающим его мощность до определенного предела.
Следовательно, ток в общей цепи проходит в пределах внутреннего и внешнего контуров, поочередно преодолевая общее сопротивление отрезков (R+r).
На размеры силы тока влияет такое понятие, как электродвижущая сила – ЭДС, прилагаемая к электродам, обозначенная символом Е.
Что такое трансформаторы тока
Значение ЭДС возможно измерить на выводах батареи с использованием вольтметра при отключенном внешнем контуре. После подключения нагрузки на вольтметре появится наличие напряжения U. Таким образом, при отключенной нагрузке U = E, в при подключении внешнего контура U < E.
ЭДС дает толчок движению зарядов в полной цепи и определяет силу тока I = E/(R+r). Данная формула отражает закон Ома для полной электрической цепи постоянного тока.
В ней хорошо просматриваются признаки внутреннего и наружного контуров. В случае отключения нагрузки внутри батареи все равно будут двигаться заряженные частицы.
Это явление называется током саморазряда, приводящее к ненужному расходу металлических частиц катода.
Под действием внутренней энергии источника питания сопротивление вызывает нагрев и его дальнейшее рассеивание снаружи элемента. Постепенно заряд батареи полностью исчезает без остатка.
Закон ома для цепи переменного тока
Для цепей переменного тока закон Ома будет выглядеть иначе. Если взять за основу формулу I = U/R, то кроме активного сопротивления R, в нее добавляются индуктивное XL и емкостное ХС сопротивления, относящиеся к реактивным. Подобные электрические схемы применяются значительно чаще, чем подключения с одним лишь активным сопротивлением и позволяют рассчитать любые варианты.
Сюда же включается параметр ω, представляющий собой циклическую частоту сети. Ее значение определяется формулой ω = 2πf, в которой f является частотой этой сети (Гц). При постоянном токе эта частота будет равной нулю, а емкость примет бесконечное значение. В данном случае электрическая цепь постоянного тока окажется разорванной, то есть реактивного сопротивления нет.
Цепь переменного тока ничем не отличается от постоянного, за исключением источника напряжения. Общая формула остается такой же, но при добавлении реактивных элементов ее содержание полностью изменится.
Параметр f уже не будет нулевым, что указывает на присутствие реактивного сопротивления. Оно тоже оказывает влияние на ток, протекающий в контуре и вызывает резонанс.
Для обозначения полного сопротивления контура используется символ Z.
Мощность короткого замыкания
Отмеченная величина не будет равной активному сопротивлению, то есть Z ≠ R. Закон Ома для переменного тока теперь будет выглядеть в виде формулы I = U/Z. Знание этих особенностей и правильное использование формул, помогут избежать неправильного решения электротехнических задач и предотвратить выход из строя отдельных элементов контура.
Источник: https://electric-220.ru/news/zakon_oma_dlja_peremennogo_toka/2018-03-02-1465
Цепь переменного тока с активным, индуктивным и емкостным сопротивлениями
По треугольнику сопротивлений можно также определить угол сдвига фаз между током и напряжением:
Пример. Активное сопротивление катушки составляет 5 ом, а ее полное сопротивление Z=30 ом. Определить угол сдвига фаз.
Решение.
При соs =0,25 угол =75°.
§ 56. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С АКТИВНЫМ, ИНДУКТИВНЫМ И ЕМКОСТНЫМ СОПРОТИВЛЕНИЯМИ
На рис. 57, а изображена цепь переменного тока, в которую включены последовательно активное сопротивление r, индуктивность L, обладающая индуктивным сопротивлением ХL, и емкость С, обладающая емкостным сопротивлением Хс.
Под действием переменного напряжения в этой цепи протекает переменный ток.
Выясним, чему равно общее напряжение на зажимах цепи. Построим векторную диаграмму тока и напряжений для рассматриваемой цепи (рис. 57, б).
Так как сопротивления соединены последовательно, то в них протекает одинаковый ток. Отложим по горизонтали, в выбранном масштабе вектор тока I.
В цепи с активным сопротивлением ток и напряжение совпадают по фазе, поэтому вектор напряжения Uа откладываем по вектору тока.
Напряжение на индуктивности опережает ток на угол = 90°. Поэтому вектор UL откладываем вверх
под углом 90° к вектору тока.
В цепи с емкостью, наоборот, напряжение отстает от тока на угол = 90°. Поэтому вектор Uc откладываем на диаграмме вниз под углом 90° к вектору тока.
Для определения общего напряжения, приложенного к зажимам цепи, сложим векторы UL и UС. Для этого отнимем от большего вектора UL вектор UС и получим вектор UL-UC, выражающий векторную сумму этих двух напряжений. Теперь сложим векторы (UL-UC) и Ua. Суммой этих векторов будет диагональ параллелограмма – вектор U, изображающий общее напряжение на зажимах цепи.
На основании теоремы Пифагора из треугольника напряжений АО Б следует, что
отсюда общее напряжение
Определим полное сопротивление цепи переменного тока, содержащей активное, индуктивное и емкостное сопротивления. Для этого разделим стороны треугольника напряжений АОБ на число I выражающее силу тока в цепи, и получим подобный треугольник сопротивлений А’О’Б’ (рис. 57, в). Его сторонами являются сопротивления r, (ХL — Хс) и полное сопротивление цепи Z.
Пользуясь теоремой Пифагора, можно написать, что
Отсюда полное сопротивление цепи
Силу тока в цепи с активным, индуктивным и емкостным сопротивлениями определяют по закону Ома:
На векторной диаграмме (рис. 57, б) видно, что в рассматриваемой цепи ток и напряжение генератора не совпадают по фазе. Из треугольника напряжений следует, что
- Из треугольника сопротивлений
- § 57. ЦЕПЬ ПЕРЕМЕННОГО ТОКА С ПАРАЛЛЕЛЬНО СОЕДИНЕННЫМИ СОПРОТИВЛЕНИЯМИ
На рис. 58 изображена цепь переменного тока, в которую включены параллельно две катушки. Каждая из этих катушек обладает соответственно активным сопротивлением r1 и r2 и индуктивным сопротивлением XL1 и XL2.
Полное сопротивление первой катушки
Полное сопротивление второй катушки
Напряжение на зажимах катушек равно напряжению генератора.
- Сила тока в каждой катушке определяется согласно закону Ома:
- Из этих равенств можно сделать вывод, что в такой цепи токи разветвляются обратно пропорционально полным сопротивлениям ветвей.
- Для определения угла сдвига фаз между напряжением и током
- в каждой катушке вычисляют и и по таблице тригонометрических функций находят значения углов 1 и 2.
- Чем больше угол сдвига фаз между напряжением и током, тем больше реактивный ток и меньше активный, тем хуже используется электрический ток в данной установке, ниже ее коэффициент мощности (cos ).
Так как первый закон Кирхгофа справедлив для цепей переменного тока, то в рассматриваемой цепи общий ток определяется геометрическим сложением векторов (рис. 58,6).
По горизонтали в выбранном масштабе отложим вектор напряжения U. Так как ток в цепи с индуктивностью отстает от напряжения, то вектор тока I1 выбранном масштабе отложим с помощью транспортира под углом 1 к вектору напряжения U, а вектор тока I2 и отложим под углом 2. Общий ток в цепи будет равен сумме векторов тока I1 и I2, который определяется с учетом выбранного масштаба.
- Чтобы найти общий ток, нужно воспользоваться тем, что активная составляющая общего тока — общий активный ток равен сумме активных токов ветвей:
- а общий реактивный ток — сумме реактивных токов ветвей (если все эти реактивные токи, отстающие по фазе или все опережающие):
- После чего определяют общий ток:
- Угол сдвига фаз между общим током и напряжением ср находят по векторной диаграмме.
Пример. Три катушки соединены параллельно и к ним подключено переменное напряжение U=100 в. Частота тока 50 гц. Активное сопротивление катушки r1=2 ом; r2=3 ом; r3=4 ом;
- Индуктивность катушек L1=0,04 гн; L2=0,03 гн; L3=0, 01 гн.
- Вычислить силу тока в каждой катушке и общий ток в цепи, а также угол сдвига фаз между током и напряжением.
- Решение. Индуктивное сопротивление катушек:
- Полное сопротивление катушек:
- Сила тока в катушках:
Источник: http://fiziku5.ru/uchebnye-materialy-po-fizike/cep-peremennogo-toka-s-aktivnym-induktivnym-i-emkostnym-soprotivleniyami
