Индуктивное сопротивление катушки
Так как самоиндукция препятствует всякому резкому изменению силы тока в цепи, то, следовательно, она представляет собой для переменного тока особого рода сопротивление, называемое индуктивным сопротивлением.
Чисто индуктивное сопротивление отличается от обычного (омического) сопротивления тем, что при прохождении через него переменного тока в нем не происходит потери мощности.
Под чисто индуктивным сопротивлением мы понимаем сопротивление, оказываемое переменному току катушкой, проводник которой не обладает вовсе омическим сопротивлением. В действительности же всякая катушка обладает некоторым омическим сопротивлением. Но если это сопротивление невелико по сравнению с индуктивным сопро¬тивлением, то им можно пренебречь.
При этом наблюдается следующее явление: в течение одной четверти периода, когда ток возрастает, магнитное поле потребляет энергию из цепи, а в течение следующей четверти периода, когда ток убывает, возвращает ее в цепь. Следовательно, в среднем за период в индуктивном сопротивлении мощность не затрачивается. Поэтому индуктивное сопротивление называется реактивным (прежде его неправильно называли безваттным).
Индуктивное сопротивление одной и той же катушки будет различным для токов различных частот. Чем выше частота переменного тока, тем большую роль играет индуктивность и тем больше будет индуктивное сопротивление данной катушки. Наоборот, чем ниже частота тока, тем индуктивное сопротивление катушки меньше. При частоте, равной нулю (установившийся постоянный ток), индуктивное сопротивление тоже равно нулю.
Рисунок 1. Зависимость индуктивного сопротивления катушки от частоты переменного тока. Реактивное сопротивление катушки возрастает с увеличением часторы тока.
Индуктивное сопротивление обозначается буквой XL и измеряется в омах.
Подсчет индуктивного сопротивления катушки для переменного тока данной частоты производится по формуле
XL=2π• f •L
где XL — индуктивное сопротивление в ом; f—частота переменного тока в гц; L — индуктивность катушки в гн
Как известно, величину 2π• f называют круговой частотой и обозначают буквой ω (омега). Поэтому приведенная выше формула может быть представлена так:
XL=ω•L
Отсюда следует, что для постоянного тока (ω = 0) индуктивное сопротивление равно нулю. Поэтому, когда, нужно пропустить по какой-либо цепи постоянный ток, задержав в то же время переменный, то в цепь включают последовательно катушку индуктивности.
Для преграждения пути токам низких звуковых частот ставят катушки с железным сердечником, так называемые дроссели низкой частоты, а для более высоких радиочастот — без железного сердечника, которые носят название дросселей высокой частоты.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Что зовется индуктивным сопротивлением
Когда на катушку подают переменное напряжение, ток, проходящий по ней, меняется согласно поданному напряжению. Это служит причиной изменения магнитного поля, создающего электродвижущую силу, препятствующую происходящему.

В такой цепи имеется зависимость электрических параметров от двух видов: обычного и индуктивного. Они обозначаются, соответственно, как R и XL.
На обычном происходит выделение мощности. Однако на реактивных элементах она является нулевой. Это связано с постоянным изменением направления переменного тока.
В течение одного периода колебаний энергия дважды закачивается в катушку и столько же раз возвращается в источник.

От чего зависит индуктивное сопротивление
При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока. В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока. Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.

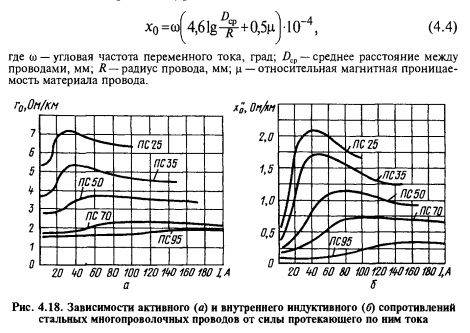
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
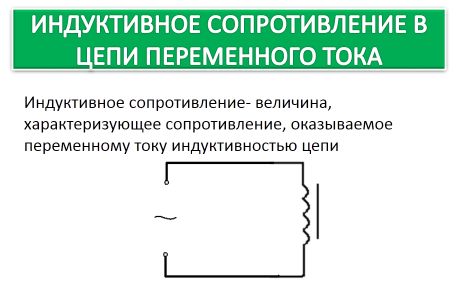
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Виды сопротивления в электрической цепи
Если используется постоянный ток, то рассматривается только обычное сопротивление, которое также называется активным или омическим. При переменном существует не только активное, но и реактивное сопротивление. Последнее бывает индуктивным и емкостным. Его величина определяется по соответствующим формулам. Сопротивление называется реактивным потому что не вызывает безвозвратных потерь энергии.
В цепях переменного тока полное сопротивление представляет собой сумму омического, индуктивного и емкостного сопротивлений. Определить его можно по правилам векторного сложения слагаемых. Если рассматривать цепь, которая не содержит конденсаторов, то основную роль будет играть реактивное сопротивление катушки индуктивности.
Катушка индуктивности
Эта деталь обычно имеет сердечник цилиндрической или тороидальной формы, на который многократно намотан провод. Основной характеристикой катушки является индуктивность.
Как известно, магнитное поле создаётся движущимися электрическими зарядами. Даже если постоянный ток идёт по проводу, вокруг него создаётся магнитное поле. Оно создаёт препятствия для изменения тока в те моменты, когда меняется само, чему можно не удивляться, зная о существовании индуктивного сопротивления. Для постоянного тока это происходит в моменты включения и выключения.
Если питающее напряжение переменное, то изменения происходят непрерывно. Основная задача катушки индуктивности — увеличивать напряженность магнитного поля. Она имеет не только индуктивное, но и обычное сопротивление. Однако при расчётах его считают пренебрежимо малым.
Формула индуктивного сопротивления
Рассматриваемое сопротивление тем больше, чем выше частота тока и индуктивность. Эту зависимость легко объяснить. Большая частота подразумевает высокую скорость изменения магнитного поля, которая усиливает эффект самоиндукции. Увеличение индуктивности соответствует более сильному магнитному полю.
Индуктивное сопротивление обозначается как XL. Обозначение буквой Х используется для любого реактивного сопротивления. То, что оно индуктивное подтверждает буква L. Его единица измерения — Ом. Чтобы рассчитать значение, понадобится формула индуктивного сопротивления:
В этой формуле буквами F и L обозначаются частота переменного тока и индуктивность катушки соответственно. Индуктивность измеряется в Генри, сокращенно Гн.
Чтобы найти полное сопротивление в контуре, состоящем из резисторов и катушки, необходимо сложить активную и реактивную составляющую, воспользовавшись правилом прямоугольного треугольника. Один катет такого треугольника соответствует активному сопротивлению, а второй — реактивному. Гипотенуза — это полное сопротивление или импеданс. Его значение рассчитывается по теореме Пифагора.
- XL — это индуктивное сопротивление, которое определяется формулой, приведённой выше.
- R — активное сопротивление. Для его вычисления следует воспользоваться законом Ома.
Произведение 2πF в формуле сопротивления называют также круговой частотой. Ее обозначают буквой ω. С учетом этого формулу для определения индуктивного сопротивления можно записать так: XL = ω×L.
В каких элементах возникает
Поскольку индуктивность – составляющая электрического тока, то она возникает в любых проводниках, по которым проходит переменный электрический ток. Особо выражено это в замкнутых контурах с сердечником из магнитопровода. Некоторая паразитная индуктивность присутствует в печатных платах и даже в микросхемах.
В каких единицах измеряется
Впервые индуктивность была вычислена американским ученым-физиком Джоном Генри и была названа в его честь – Генри, сокращенно Гн. Диапазон индуктивности очень широк, в приведенной ниже таблице видно, какие производные существуют:
| Кратные | Дольные | ||||||
| Величина | Название | Обозначение | Величина | Название | Обозначение | ||
| 101 | декагенри | даГн | daH | 10-1 | децигенри | дГн | dГн |
| 102 | гектогенри | гГн | hH | 10-2 | сантигенри | сГн | cГн |
| 103 | килогенри | кГн | kH | 10-3 | миллигенри | мГн | mГн |
| 106 | мегагенри | МГн | MH | 10-6 | микрогенри | мкГн | µГн |
| 109 | гигагенри | ГГн | GH | 10-9 | наногенри | нГн | nГн |
| 1012 | терагенри | ТГн | TH | 10-12 | пикогенри | пГн | pГн |
| 1015 | петагенри | ПГн | PH | 10-15 | фемтогенри | фГн | fГн |
| 1018 | эксагенри | ЭГн | EH | 10-18 | аттогенри | аГн | aГн |
| 1021 | зеттагенри | ЗГн | ZH | 10-21 | зептогенри | зГн | zГн |
| 1024 | иоттагенри | ИГн | YH | 10-24 | иоктогенри | иГн | yГн |
Первые две строчки производных в каждой части таблицы применять не рекомендуют, указывают либо в десятых или сотых долях генри, либо десятках и сотнях. В СИ используется указанное обозначение в других системах, таких как СГМС обозначение может отсутствовать, либо применяется статгенри ≈ 8,987552⋅1011 или абгенри.
Индуктивность, L — измеряется в Генри (Гн). Индуктивное сопротивление XL — измеряется в Омах (Ом)
Где применяется катушка (дроссель, индуктивность)
Дроссели имеют примитивную конструкцию: просто намотанный витками на каком-либо сердечнике проводник. В то же время в таком приборе нечему ломаться. Также у дросселей широчайший функционал и десятки применений. Из всего этого следует, что в какой бы точке города ни находился человек, в радиусе 1 км от него всегда будут тысячи катушек индуктивности, настолько они распространены.
Катушка как электромагнит
Самое простое применение катушки – это электромагнит. С подобным применением каждый сталкивается, заходя в подъезд. Сила, удерживающая дверь на месте и препятствующая несанкционированному доступу чужака, берётся из электромагнита. Он находится сверху.
Электрический ток, проходя по виткам катушки, создаёт вокруг неё переменное электромагнитное поле. Оно возбуждает в металлическом «бруске», расположенном на двери, вихревые токи, которые так же создают магнитное поле. В результате получаются два управляемых магнита. Они притягиваются друг к другу. Тем самым дверь надёжно удерживается на месте.
Другое применение электромагнитов в быту – индукционные плиты. Катушка наводит в металлической посуде переменный высокочастотный ток. Он, в свою очередь, своим тепловым действием разогревает кастрюлю. В промышленности нечто подобное используется для разогрева и плавки металлов. Только в таком случае применяются на порядки более высокие мощности и другие частоты тока.
Индуктивность как фильтр
Импульсные блоки питания, электрические двигатели и диммеры для регулировки яркости ламп накаливания выбрасывают в сеть большое количество искажений и помех. Вызвано это неравномерностью потребляемого тока. Для борьбы с подобными сетевыми шумами применяются специальные фильтры на основе конденсаторов и дросселей.
Данный узел представляет собой небольшую катушку из медного эмалированного провода диаметром 0,2-2 мм. Обмотка наматывается на ферритовый сердечник. Чаще всего он изготовлен в форме кольца, немного реже встречаются так называемые «гантельки».
Подобные фильтры имеются в компьютерных блоках питания, компактных люминесцентных лампах (иногда не ставят, экономят), на выходах сварочных инверторов.
Также фильтр может быть звуковым. Его задача – срезать определённый диапазон частот. Индуктивные свойства этого прибора таковы, что он хорошо проводит низкие частоты, а высокие – приглушает. Поэтому дроссели используют для того, чтобы до динамиков дошёл только бас. По факту ослаблено будут слышны и другие частоты. Для более эффективной работы фильтра нужны дополнительные детали: конденсаторы и операционные усилители.
Самодельный звуковой фильтр
Катушка как источник ЭДС
Китайская промышленность удивила школьников 2000-х новой игрушкой – вечным фонариком. Его не нужно было заряжать. Фонарик работал от катушки индуктивности, около которой под действием движения рук перемещался магнит. Он наводил в обмотке переменную ЭДС, которая питала осветительный прибор.
Подобное явление объясняется законом электромагнитной индукции. Если проводник (рамка) находится в переменном электромагнитном поле, то в нём начинает наводиться электродвижущая сила. Иными словами, появляется напряжение.
Закон этот совсем неигрушечный, ведь он используется в работе генераторов на подавляющем большинстве электростанций, в том числе любые ТЭЦ, ГЭС, АЭС и ветряки. По подобному принципу работают динамомашины, питающие фары велотранспорта.
Принцип работы генератора
Две катушки – трансформатор
Ещё одно распространённое применение – это электрический трансформатор. Конструктивно он состоит из двух и более катушек, расположенных на одном железном или ферритовом сердечнике. Подобный агрегат работает только с переменным напряжением. Если на первичную обмотку подать ток, то он создаст в сердечнике магнитный поток. Он, в свою очередь, наведёт ЭДС во вторичной обмотке. Напряжения во входной и выходной катушках прямо зависят от количества их витков.
Таким образом, можно трансформировать 220 В из розетки в 12 В, необходимых для питания небольшой стереосистемы, или преобразовать 10 000 вольт в 220 для передачи от подстанции к жилым домам. Подобным методом можно добиться и повышения напряжения, т.е. превратить 12 В обратно в 220.
Устройство трансформатора
Катушка индуктивности — элемент колебательного контура
Сейчас это уже редкость, но раньше для подстройки нужной радиостанции использовали колебательный контур. Он состоит из двух элементов, включенных параллельно: катушки индуктивности и переменного конденсатора. Работая в паре, они способны выделить из множества окружающих сигналов именно тот, который требуется. При попадании на антенну приёмника нужной частоты электромагнитных волн колебательный контур входит в резонанс. Процесс сопровождается лавинообразным увеличением ЭДС. Частота, на которой это происходит, зависит от индуктивности катушки и ёмкости конденсатора.
Катушка индуктивности – дроссель ДРЛ ламп
Несмотря на то, что освещение улиц и промышленных предприятий стремительно переходит на LED светильники, по СНГ всё ещё осталось огромное количество мест, где используются устаревшие дуговые ртутные люминесцентные лампы типа ДРЛ. Более всего они распространены в мелких городах и на второстепенных улицах. Их можно узнать по характерному холодно-белому свету и долгому розжигу.
ДРЛ лампы не способны работать без пускорегулирующего дросселя. Он обладает высоким индуктивным сопротивлением и призван ограничить пусковой ток осветительного прибора. Дроссели для ламп подбираются, исходя из их мощности. Наиболее распространённые номиналы – 250, 400 и 1000 Вт. Информация о мощности указывается на самом дросселе. Там же можно найти схемы включения.
Из вышесказанного можно подчеркнуть, что катушка индуктивности является консервативным и давно освоенным на практике электронным компонентом. Однако спрос на его применение по-прежнему не спадает. Поэтому знания, необходимые для расчета катушек и их правильного включения, необходимы каждому специалисту, имеющему дело с электроникой.
Активное сопротивление
Активное сопротивление – это сопротивление элемента или участка цепи электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы, например, механическую в электродвигателях или тепловую, когда речь идёт о нагреве чего-либо или просто потерях или другие виды энергии. Выражается в Омах и в формулах обозначается буквой R.
Активное сопротивление характерно для проводников, а его величина зависит от свойств этих самых проводников:
- Материал — обычно проводники выполняются из металла (или из графита, как щетки электрических машин) и у каждого проводника есть удельное сопротивление, оно измеряется в Ом·мм²/м.
- Длина и площадь поперечного сечения. Следует из предыдущего. Чем больше площадь поперечного сечения (мм²) – тем меньше сопротивление, или чем длиннее проводник – тем оно больше.
- Температура. Чем больше температура – тем больше сопротивление проводника.
Согласно закону Ома, сопротивление участка электрической цепи можно рассчитать, если известны ток и напряжение по формуле: R=U/I.
Таблица 1. Удельные электрические сопротивления некоторых веществ Таблица 1. Удельные электрические сопротивления некоторых веществ
Сопротивление проводника, определенной длины и сечения определяется по формуле: R=p*l/S,
где p (ро) – удельное сопротивление, l – длина, S – площадь поперечного сечения.
При протекании тока через активное сопротивление в любом случае происходят потери в виде тепла. По этой причине греются провода и кабельные линии под нагрузкой, трансформаторы, электродвигатели и так далее… Величина этих потерь определяется по формуле: P=U²/R. Кроме потерь в виде тепла на линии, а вернее сказать, на активном сопротивлении линии происходит падение напряжения (просадки), величина которых также рассчитывается по закону Ома: Uпад=I*Rл,
где Uпад – падение напряжение на линии, Rл – сопротивление линии.
Рисунок 1 — ток и напряжение в активном сопротивлении: а) схема условного с идеальным резистором, б) Синусоиды тока и напряжения, в) векторная диаграмма. Рисунок 1 — ток и напряжение в активном сопротивлении: а) схема условного с идеальным резистором, б) Синусоиды тока и напряжения, в) векторная диаграмма.
Напряжение и ток в активном сопротивлении совпадают по фазе, соответственно коэффициент мощности у активной нагрузки в идеальном случае равен 1. Это можно пронаблюдать на иллюстрации выше, как и то, что векторы U и I также совпадают по направлению, и между ними нет угла.
Под «идеальным случаем» понимается используемое в физике понятие «идеальный», то есть, когда объекту характерен какой-то единый набор свойств. Например, когда говорят «идеальный резистор» — это значит, такой резистор в котором есть только активное сопротивление, а реактивные составляющие отсутствуют. А «идеальная индуктивность» — это такая индуктивность, у которой нет активного сопротивления проводника, которым она намотана, а также паразитной ёмкости. То есть идеальная катушка, обладает только индуктивностью.
Подведем итоги — активное сопротивление характерно для нагрузки ток и напряжение в которой совпадают по фазе, это могут быть: провода, резисторы, ТЭНы и другие нагревательные элементы, лампы накаливания…
Реактивное сопротивление
Согласно энциклопедическому определению, реактивное сопротивление — это сопротивление элемента схемы, вызванное изменением тока или напряжения из-за индуктивности или ёмкости этого элемента. Отсюда следует, что реактивное сопротивление присуще только индуктивной или емкостной нагрузке. Измеряется оно также в Омах, но обозначается буквой X.
Также следует вспомнить законы коммутации:
- Ток на индуктивности не может изменяться скачком.
- Напряжение на ёмкости не может измениться мгновенно.
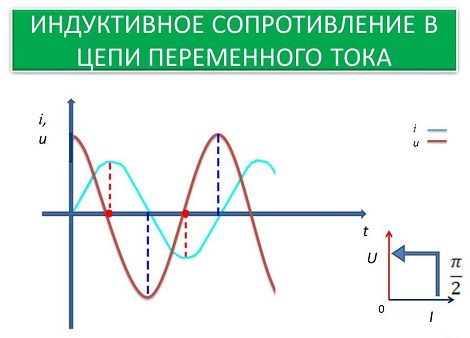
Другими словами, в индуктивности ток отстаёт от напряжения по фазе, а в ёмкости наоборот — ток опережает напряжение.
Реактивное сопротивление индуктивности
В цепи постоянного тока это вносит влияние в работу системы преимущественно при её коммутации (включении или отключении), а также при резком изменении режима работы и потребления тока и такого понятия как реактивное сопротивление для постоянного тока нет.
Но в цепи переменного тока реактивное сопротивление оказывает значительное влияние. При протекании переменного тока I в катушке, возникает магнитное поле. Оно создаёт в витках катушки ЭДС, которое в свою очередь препятствует изменению тока.
При увеличении тока, ЭДС отрицательна и препятствует нарастанию тока, при уменьшении — положительна и препятствует его убыванию, оказывая таким образом сопротивление изменению тока на протяжении всего периода.
Выше мы рассматривали график тока и напряжения в активном сопротивлении, и они совпадали по фазе, ниже приведен график тока и напряжения для катушки индуктивности.
Рисунок 2 — ток и напряжение в индуктивности: а) схема условного участка цепи с идеальной индуктивностью, б) синусоиды тока и напряжения, в) векторная диаграмма. Рисунок 2 — ток и напряжение в индуктивности: а) схема условного участка цепи с идеальной индуктивностью, б) синусоиды тока и напряжения, в) векторная диаграмма.
На рисунке 2.б видно, что ток и напряжение в индуктивности не совпадают по фазе. В идеальной индуктивности ток отстаёт от напряжения на 90 градусов, что более наглядно иллюстрирует векторная диаграмма на рисунке 2.в.
Сопротивление, которое индуктивность оказывает переменному току вычисляется по формуле: XL=ω*L=2*pi*f*L,
где ω — угловая частота (рад/с), L — индуктивность (Гн), pi – число пи (3.14), f — частота (Гц).
То есть чем больше частота переменного тока, тем большее сопротивление ему оказывает индуктивность.
Реактивное сопротивление ёмкости
В ёмкостной нагрузке дело обстоит также, но наоборот. На рисунке 3.б видно, что ток опережает напряжение, а на 3.в видно, что опережает на угол в 90˚.
Рисунок 3 — ток и напряжение в ёмкости: а) схема условного участка цепи с идеальным конденсатором (ёмкостью), б) синусоиды тока и напряжения, в) векторная диаграмма. Рисунок 3 — ток и напряжение в ёмкости: а) схема условного участка цепи с идеальным конденсатором (ёмкостью), б) синусоиды тока и напряжения, в) векторная диаграмма.
При протекании переменного тока в конденсаторе циклически происходят процессы заряда и разряда, или накопления и отдачи энергии электрическим полем между его обкладками. Конденсатор будет заряжаться до определённого максимального значения, пока ток не сменит направление на противоположное.
В момент когда напряжение достигнет амплитудного значения, ток будет равен нулю. Таким образом, напряжение на идеальном конденсаторе и ток всегда будут иметь расхождение во времени в четверть периода.
То есть емкостное сопротивление — это сопротивление изменению напряжения. Оно определяется по формуле: Xс=1/(ω*C)=1/(2*pi*f*c),
где ω — угловая частота (рад/с), C — ёмкость (Ф), pi – число пи (3.14), f — частота (Гц).
То есть чем меньше частота переменного тока, тем большее сопротивление оказывает ему ёмкость.
Но отклонение напряжения от тока по фазе на 90 градусов только в цепях с идеальной индуктивностью, на практике же такого нет.
Полное сопротивление
Так как и активное сопротивление, и индуктивность, и ёмкость влияют на токи и напряжения в электрической цепи по-своему, то при их соединении их сопротивления также складываются. Так, например полное реактивное сопротивление равно: X=XL-Xс
Таким образом реактивные сопротивления ёмкости и индуктивности приводятся к общему значению, то есть какое из них больше, такой характер и будет у цепи (индуктивный или емкостной).
В любой реальной цепи присутствуют все три составляющие: активная, емкостная и индуктивная. Тогда говорят о полном сопротивление цепи. Оно обозначается буквой Z и вычисляется по формуле:
где Z – полное сопротивление, r – активное, XL – индуктивное, Xc – емкостное.
Эта формула должна была вам напомнить теорему Пифагора, где квадрат гипотенузы равен сумме квадратов катетов. И это неспроста. Дело в том, что если на векторной диаграмме изобразить активное и полное реактивное сопротивление, то мы получим т.н. треугольник сопротивлений, где гипотенузой будет полное сопротивление цепи.
Угол Фи — это и есть угол, на который ток отстаёт от напряжения, а косинус этого угла (cosФ) называют коэффициентом мощности. Это опережение или отставание тока и напряжение приводит к тому, что этот ток возвращается обратно к источнику питания, а не выполняет какую-то работу в потребителе. Это приводит к излишней нагрузке на электросеть, то есть ток протекает полный, а работу выполняет только активная его часть.
Большая часть электрооборудования (электродвигатели, электромагниты и прочее) носит индуктивный характер, что приводит к значительному повышению нагрузки на электросеть и потребления реактивной мощности.
Чтобы бороться с этим явлением используются компенсаторы реактивной мощности — конденсаторные установки, синхронные двигатели, синхронные компенсаторы. То есть подключают какую-то нагрузку с емкостным характером, она нужна, чтобы уменьшить угол между током и напряжением и в итоге повысить коэффициент мощности.
Ну и напоследок ознакомьтесь с подборкой советских плакатов, которые иллюстрируют параметры электрических цепей со смешанной нагрузкой, а также их векторные диаграммы (треугольники сопротивлений, напряжения и мощности).
Последовательное соединение активного и индуктивного сопротивлений
Последовательное соединение активного и емкостного сопротивлений
Последовательное соединение индуктивности и ёмкости
Как определить полное сопротивление?
Полное сопротивление будет равно корню квадратному из суммы квадратов активного и реактивного сопротивлений, т. е.
Как влияет частота на индуктивное и емкостное сопротивление?
ЭДС самоиндукции — причина индуктивного сопротивления. В отличие от активного сопротивления, индуктивное не является характеристикой проводника, т. к. зависит от параметров цепи (частоты): чем больше частота переменного тока, тем больше сопротивление, которое ему оказывает катушка.
Источники
- https://ElectroInfo.net/raznoe/induktivnoe-soprotivlenie-osobennosti-induktivnogo-soprotivlenija.html
- https://electric-220.ru/news/formula_induktivnogo_soprotivlenija/2017-05-03-1254
- https://ProFazu.ru/knowledge/electrical/induktivnoe-soprotivlenie.html
- https://electricvdome.ru/osnovy-elektrotehniki/induktivnoe-soprotivlenie-katushki.html
- https://amperof.ru/teoriya/induktivnoe-soprotivlenie.html
- https://dzen.ru/a/Xvsq-VUfz2hUQAsy
- https://kmd-mk.ru/kak-vychislit-induktivnoe-soprotivlenie-katushki/
- https://kmd-mk.ru/chto-takoe-induktivnoe-i-emkostnoe-soprotivlenie/
Как вам статья?

Павел
Бакалавр “210400 Радиотехника” – ТУСУР. Томский государственный университет систем управления и радиоэлектроники
Написать
Пишите свои рекомендации и задавайте вопросы
При включении катушки индуктивности в цепь переменного тока, под действием непрерывно изменяющегося напряжения происходят изменения этого тока. В свою очередь, эти изменения вызывают генерацию магнитного поля, которое периодический возрастает или убывает. Под его влиянием в катушке индуцируется встречное напряжение, препятствующее изменениям тока. Таким образом, протекание тока происходит под непрерывным противодействием, получившим название индуктивного сопротивления.
От чего зависит индуктивное сопротивление
Данная величина связана напрямую с частотой приложенного напряжения (f) и значением индуктивности (L). Формула индуктивного сопротивления будет выглядеть следующим образом: XL = 2πfL. Прямая пропорциональная зависимость, в случае необходимости, позволяет путем преобразования основной формулы вычислить частоту или значение индуктивности.
Под действием переменного тока, проходящего по проводнику, вокруг этого проводника образуется переменное магнитное поле. Действие этого поля приводит к наведению в проводнике электродвижущей силы обратного направления, известной еще как ЭДС самоиндукции. Противодействие или сопротивление ЭДС переменному току получило название реактивного индуктивного сопротивления.
Данная величина зависит от многих факторов. В первую очередь на нее оказывает влияние как значение тока не только в собственном проводнике, но и в соседних проводах. То есть увеличение сопротивления и потока рассеяния происходит по мере увеличения расстояния между фазными проводами. Одновременно снижается воздействие соседних проводов.
Существует такое понятие, как погонное индуктивное сопротивление, которое вычисляется по формуле: X0 = ω x (4,61g x (Dср/Rпр) + 0,5μ) x 10-4 = X0’ + X0’’, в которой ω является угловой частотой, μ – магнитной проницаемостью, Dср – среднегеометрическим расстоянием между фазами ЛЭП, а Rпр – радиусом провода.
Величины X0’ и X0’’ представляют собой две составные части погонного индуктивного сопротивления. Первая из них X0’ представляет собой внешнее индуктивное сопротивление, зависящее только от внешнего магнитного поля и размеров ЛЭП. Другая величина – X0’’ является внутренним сопротивлением, зависящим от внутреннего магнитного поля и магнитной проницаемости μ.
На линиях электропередачи высокого напряжения от 330 кВ и более, проходящие фазы расщепляются на несколько отдельных проводов. Например, при напряжении 330 кВ фаза разделяется на два провода, что позволяет снизить индуктивное сопротивление примерно на 19%. Три провода используются при напряжении 500 кВ – индуктивное сопротивление удается снизить на 28%. Напряжение 750 кВ допускает разделение фаз на 4-6 проводников, что способствует снижению сопротивления примерно на 33%.
Погонное индуктивное сопротивление имеет величину в зависимости от радиуса провода и совершенно не зависит от сечения. Если радиус проводника будет увеличиваться, то значение погонного индуктивного сопротивления будет соответственно уменьшаться. Существенное влияние оказывают проводники, расположенные рядом.
Индуктивное сопротивление в цепи переменного тока
Одной из основных характеристик электрических цепей является сопротивление, которое может быть активным и реактивным. Типичными представителями активного сопротивления считаются обычные потребители – лампы, накаливания, резисторы, нагревательные спирали и другие элементы, в которых электрический ток совершает полезную работу.
К реактивному относятся индуктивное и емкостное сопротивления, находящиеся в промежуточных преобразователях электроэнергии – индуктивных катушках и конденсаторах. Эти параметры в обязательном порядке учитываются при выполнении различных расчетов. Например, для определения общего сопротивления участка цепи, складываются активная и реактивная составляющие. Сложение осуществляется геометрическим, то есть, векторным способом, путем построения прямоугольного треугольника. В нем оба катета являются обоими сопротивлениями, а гипотенуза – полным. Длина каждого катета соответствует действующему значению того или иного сопротивления.
В качестве примера можно рассмотреть характер индуктивного сопротивления в простейшей цепи переменного тока. В нее входит источник питания, обладающий ЭДС (Е), резистор, как активная составляющая (R) и катушка, обладающая индуктивностью (L). Возникновение индуктивного сопротивления происходит под действием ЭДС самоиндукции (Еси) в катушечных витках. Индуктивное сопротивление увеличивается в соответствии с ростом индуктивности цепи и значения тока, протекающего по контуру.
Таким образом, закон Ома для такой цепи переменного тока будет выглядеть в виде формулы: Е + Еси = I x R. Далее с помощью этой же формулы можно определить значение самоиндукции: Еси = -L x Iпр, где Iпр является производной тока от времени. Знак «минус» означает противоположное направление Еси по отношению к изменяющемуся значению тока. Поскольку в цепи переменного тока подобные изменения происходят постоянно, наблюдается существенное противодействие или сопротивление со стороны Еси. При постоянном токе данная зависимость отсутствует и все попытки подключения катушки в такую цепь привели бы к обычному короткому замыканию.
Для преодоления ЭДС самоиндукции, на выводах катушки источником питания должна создаваться такая разность потенциалов, чтобы она могла хотя-бы минимально компенсировать сопротивление Еси (Uкат = -Еси). Поскольку увеличение переменного тока в цепи приводит к возрастанию магнитного поля, происходит генерация вихревого поля, которое и вызывает рост противоположного тока в индуктивности. В результате, между током и напряжением происходит смещение фаз.
Индуктивное сопротивление катушки
Катушка индуктивности относится к категории пассивных компонентов, используемых в электронных схемах. Она способна сохранять электроэнергию, превращая ее в магнитное поле. В этом и состоит ее основная функция. Катушка индуктивности по своим характеристиками и свойствам напоминает конденсатор, сохраняющий энергию в виде электрического поля.
Индуктивность, измеряемая в Генри, заключается в появлении вокруг проводника с током магнитного поля. В свою очередь, связано с электродвижущей силой, которая противодействует приложенному переменному напряжению и силе тока в катушке. Данное свойство и есть индуктивное сопротивление, находящееся в противофазе с емкостным сопротивлением конденсатора. Индуктивность катушки возможно повысить за счет увеличения количества витков.
Для того чтобы выяснить, чему равно индуктивное сопротивление катушки, следует помнить, что оно, в первую очередь, противодействует переменному току. Как показывает практика, каждая индуктивная катушка сама по себе имеет определенное сопротивление.
Прохождение переменного синусоидального тока через катушку, приводит к возникновению переменного синусоидального напряжения или ЭДС. В результате, возникает индуктивное сопротивление, определяемое формулой: XL = ωL = 2πFL, в которой ω является угловой частотой, F – частотой в герцах, L – индуктивностью в генри.
Калькулятор индуктивного сопротивления катушки
При подключении катушки индуктивности в цепь переменного тока, под действием изменяющегося напряжения на обмотке,
происходят изменения этого тока с определенной частотой. Эти изменения вызывают генерацию магнитного поля, которое
периодический возрастает или убывает. В результате в катушке индуцируется встречное напряжение (ЭДС самоиндукции),
препятствующее изменениям тока. Величина ЭДС самоиндукции прямо пропорциональна скорости изменения тока.
Противодействие протеканию тока получило название индуктивного сопротивления XL.
XL — сопротивление, Ом;
f — частота, Гц;
I — индуктивность, Гн.
Электрическое сопротивление катушки индуктивности — это отношение действующих значений
напряжения и тока. Оно прямо пропорционально индуктивности и частоте изменения тока.
Фазы кривых тока и напряжения на катушке индуктивности смещены на 90 градусов,
при этом ток отстает от напряжения.
Расчет индуктивного сопротивления
Для расчета введите значение индуктивности расчетной катушки и частоту переменного тока
В калькуляторе активное сопротивление обмотки катушки принято как пренебрежимо малая величина по сравнению
с ее индуктивным сопротивлением.
Калькулятор вычисления действующих значений тока или напряжения на катушке индуктивности.
Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!
Для школьников.
В предыдущих статьях рассмотрены цепи переменного тока, содержащие только активное сопротивление и содержащие только емкостное сопротивление.
Сейчас рассмотрим случай, когда в цепи переменного тока находится только катушка индуктивности (индуктивное сопротивление), а активным и емкостным сопротивлениями цепи можно пренебречь.
Начнём с опыта, позволяющего понять, когда появляется и от чего зависит индуктивное сопротивление в цепи переменного тока.
Две маленькие одинаковые электрические лампочки подключались к источникам одинакового напряжения. Но одна (правая) подключалась к источнику постоянного тока (аккумуляторной батарее), а другая (левая) – к источнику переменного тока.
Лампочки светили одинаково, так как количество выделяющегося тепла не зависит от того, какой ток протекает по нитям лампочек (постоянный или переменный).
Затем к лампочкам последовательно подключили катушки индуктивности, сделанные из толстой медной проволоки, содержащей большое число витков. Внутри катушек находятся железные сердечники.
Катушками индуктивности называются катушки, имеющие большую индуктивность и малое активное сопротивление (изготовлены из толстой проволоки). Часто активным сопротивлением такой катушки можно пренебречь.
Опыт показал, что в случае постоянного тока лампочка горит ярко, а в случае переменного тока она светит тускло. Как это объяснить?
В случае постоянного тока лампочка горит ярко, потому что сопротивление катушки мало.
Но почему катушка индуктивности очень сильно ослабляет переменный ток? Продолжаем рассматривать опыт.
Если из катушки (рис. б) постепенно вытягивать железный сердечник, то нить лампочки будет накаляться всё сильнее. При полном вытягивании сердечника лампочка будет светить довольно ярко. Убрав железный сердечник, во много раз уменьшили индуктивность катушки, значит дело в индуктивности.
Так как сила переменного тока быстро меняется, то в катушке возникает ЭДС самоиндукции.
В цепи только с индуктивным сопротивлением приложенное к цепи напряжение в каждый момент времени равно и противоположно ЭДС самоиндукции.
ЭДС самоиндукции по правилу Ленца направлена так, что стремится препятствовать изменению тока, то есть оказывает току сопротивление. Чем больше индуктивность катушки, тем большая ЭДС самоиндукции в ней возникает, тем больше индуктивное сопротивление. Индуктивное сопротивление зависит ещё от частоты тока, чем больше частота, тем больше это сопротивление.
При нарастании тока ЭДС самоиндукции препятствует этому нарастанию, поэтому ток позже достигает максимума, чем в отсутствие самоиндукции.
При убывании тока ЭДС самоиндукции стремится поддерживать ток. Поэтому нулевые значения тока достигаются в более поздний момент, чем в отсутствие самоиндукции.
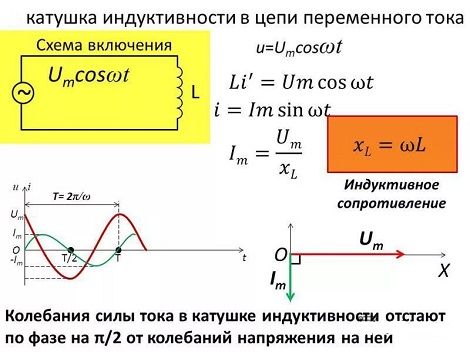
Таким образом, при наличие индуктивности ток отстаёт по фазе от тока в отсутствие индуктивности, а следовательно, отстаёт по фазе от своего напряжения.
Можно сказать так: из-за явления самоиндукции ток в катушке индуктивности не может меняться скачком и отстаёт от напряжения.
Чем больше частота тока, тем больше будет ЭДС самоиндукции, стремящейся противодействовать изменению тока и тем больше будет сопротивление переменному току.
Индуктивное сопротивление находится по формуле, которая получена теоретически и подтверждена опытом:
Напряжение на индуктивном сопротивлении (индуктивное напряжение) :
Ток в цепи, содержащей только индуктивность, равен отношению напряжения на зажимах источника к индуктивному сопротивлению цепи:
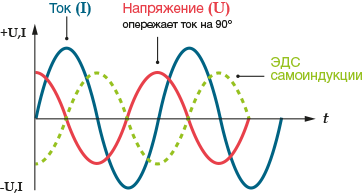
В цепи, содержащей только индуктивное сопротивление, напряжение опережает ток на четверть Т/4 периода (или ток отстаёт от напряжения на четверть периода):
Из рисунка видно, когда ток ещё только проходит через нулевое положение, напряжение уже проходит через максимум, то есть мгновенные значения напряжения и тока меняются согласно уравнениям:
Разность фаз между током и напряжением, равная “пи” пополам, величина отрицательная.
На следующем рисунке показано, как меняются во времени мгновенные значения тока, напряжения и мощности в цепи переменного тока, содержащей только индуктивное сопротивление:
Мгновенные значения мощности находятся через произведение мгновенных значений напряжения и тока, уравнения для которых записаны выше.
Видим, что мгновенная мощность в цепи, обладающей только индуктивностью, изменяется по синусоидальному закону с двойной частотой и имеет равные по модулю положительные и отрицательные значения.
В первую и третью части периода, когда ток в цепи растёт, мощность имеет положительное значение. В эти части периода магнитное поле вокруг электрической цепи усиливается за счёт энергии источника.
Убыванию тока соответствует отрицательное значение мощности. В эти части периода (второй и четвёртый) магнитное поле ослабевает, его энергия идёт обратно к источнику тока.
Таким образом, в цепи, содержащей только катушку индуктивности, происходит периодическая перекачка энергии от источника в энергию магнитного поля катушки индуктивности и возвращение её источнику.
Положительные и отрицательные значения мощности по модулю равны, поэтому средняя мощность за период в такой цепи равна нулю.
Эта мощность не расходуется во внешней части цепи, поэтому называется реактивной индуктивной мощностью:
Она образуется при работе электроприборов (трансформаторов, двигателей, электромагнитов и др., обладающих большой индуктивностью.)
Реактивная мощность в промышленных электрических цепях увеличивает нагрузку на провода и снижает коэффициент мощности цепи, поэтому реактивную нагрузку в электрической цепи на предприятиях снижают (об этом будет сказано в последующих статьях.)
Пример.
Катушка с индуктивностью 0,01 Гн включена в цепь переменного тока напряжением 120 В и частотой 50 Гц. Определить силу тока в катушке, индуктивное напряжение в ней и её реактивную мощность, если активным сопротивлением катушки можно пренебречь.
Используем формулы:
Ответ: 38,2 А; 120 В; 1460 Вт.
Из полученного ответа видим, что всё приложенное к катушке напряжение является индуктивным.
Итак, присутствие индуктивности в цепи переменного тока приводит к сдвигу фаз между током и напряжением в сети (колебания тока отстают от колебаний напряжения).
Емкостная мощность не совершает механической работы, не нагревает проводники.
Катушка индуктивности лишь периодически накапливает энергию магнитного поля и возвращает её обратно источнику тока.
К.В. Рулёва, к. ф.-м. н., доцент. Подписывайтесь на канал. Ставьте лайки. Спасибо.
Предыдущая запись : Конденсатор в цепи переменного тока. Емкостное сопротивление.
Следующая запись: Занятие 71. Последовательное соединение сопротивлений. Резонанс напряжений.
Ссылки на занятия до электростатики даны в Занятии 1 .
Ссылки на занятия (статьи), начиная с электростатики, даны в конце Занятия 45 .
Ссылки на занятия (статьи), начиная с теплового действия тока, даны в конце Занятия 58 .
Ссылки на занятия, начиная с переменного тока, даны в конце Занятия 70 .