Как найти индуктивное сопротивление трансформатора

При
расчете передачи с трансформаторами
сопротивления, напряжения и токи ли­ний
и трансформаторов приводятся к какому-то
одному напряжению. Чаще всего приведение
делается к входной стороне, т. е. при
понижающем трансформаторе к стороне
высшего напряжения.

Здесь
и в дальнейшем напряжение, к которому
производится приведение (в данном случае

)
будет обозначаться через
.

1. 3.2.1.
   Активные и индуктивные сопротивления
   трансформатора

Для
двухобмоточных трансформаторов активное
сопротивление:

(3.7)

Потери
короткого замыкания
даются в паспортных данных. Для
трехобмоточных трансформаторов заводами
да­ются потери короткого замыканиядля худшего случая, которым является
протекание тока по двум обмот­кам при
третьей разомкнутой. Сопротивление
трансформатора определяется как:

. (3.8)

Для
автотрансформаторов заводами даются
потери короткого замыкания для каждой
пары обмоток
,и.
Чтобы определить сопротивление каждого
луча, можно ориенти­ровочно принять:

,
(3.9)

. (3.10)

Аналогично
находятся и потери
.
Тогда:

,
,. (3.11)

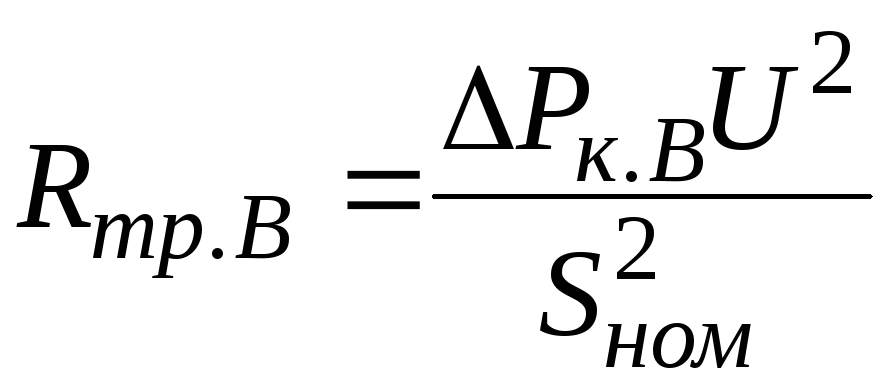
Индуктивное
сопротивление для двухобмоточного
трансформатора:

, (3.12)

где
— напряжение короткого замыкания в
процентах от номи­нального.

Для
трехобмоточных трансформаторов и
автотрансформаторов напряжения
ко­роткого замыкания даются заводами
для каждой пары обмоток в процентах от
номинального, поэтому индуктивное
сопротивление каждого луча, %, аналогично
(3.14) и (3.15):

. (3.13)

Откуда:

. (3.14)

Аналогично
рассчитываются
и.

Индуктивные
сопротивления мощных трансформаторов
и авто­трансформаторов в противоположность
кабельным линиям во много раз больше
активных.

3.2.2.
Активные и реактивные проводимости
трансформаторов

Активные
проводимости обусловлены перемагничиванием
и вихревыми токами и могут быть определены
как:

, (3.15)

где
– потери холостого хода, Вт.

Реактивные
проводимости обусловлены намагничивающей
мощностью, имеют индуктивный характер,
противоположный реактивной проводимости
линий и определя­ются как:

, (3.16)

где
— ток холостого хода в процентах от
номинального.

Полная проводимость
трансформатора:

. (3.17)

3.3.
Эквивалентное сопротивление элементов
системы

Чтобы определить
обобщенные постоянные всей линии
передачи, четырехполюсники соединяются
после­довательно, параллельно или
последовательно и параллельно в
зависимости от характера передачи (рис.
3). Для получения эквивалентного
сопротивления двухполюсников при
последовательном их соединении
складывают­ся сопротивления, а при
парал­лельном — проводимости. При
одинаковых параллельно соеди­ненных
четырехполюсни­ках сопротивления
делятся по­полам, а проводимости
умножа­ются на два.

Схема
четырехполюсников в общем виде может
быть представлена, как показано на рис.
4, а. Тогда обобщенные по­стоянные

параллельно включенных одинаковых
элементов (линий или трансформаторов)
запишутся как:

;
;

;

, (3.18)

где


– постоянные одного элемента.

Схема
принимает вид, показанный на рис. 4, б.
Два четы­рехполюсника этой схемы
можно соединить последовательно.
Окончательные значения обобщенных
постоянных

(рис. 4, в) можно представить в виде:

;

; (3.19)

;

.

Соседние файлы в папке ПЭТУ1

• #

  25.03.201658.27 Кб5Data009.tif

• #

  25.03.201649.08 Кб3Data010.tif

• #

  25.03.201665.6 Кб3Data011.tif
• #
• #

  25.03.201631.74 Кб3исходные_данные.xls

• #
• #
• #
• #

Содержание

• 1. Определение сопротивлений питающей энергосистемы
• 2. Определение сопротивлений трансформаторов
• 3. Определение сопротивлений кабелей
• 4. Определение сопротивлений шин и шинопроводов
• 5. Определение сопротивлений воздушных линии
• 6. Определение сопротивлений реакторов
• 7. Определение сопротивлений трансформаторов тока
• 8. Определение сопротивлений автоматических выключателей, рубильников, разъединителей
• 9. Определение сопротивлений контактных соединений кабелей и шинопроводов
• 10. Список литературы

Для того чтобы рассчитать токи КЗ в сети до 1000 В, следует первоначально составить схему замещения, которая состоит из всех сопротивлений цепи КЗ. Активные и индуктивные сопротивления всех элементов схемы замещения выражают в миллиомах (мОм).

Как определять сопротивления отдельных элементов схемы замещения, об этом вы и узнаете в этой статье.

1. Определение сопротивлений питающей энергосистемы

Активные и индуктивные сопротивления питающей энергосистемы рассчитывают на стороне ВН понижающего трансформатора и приводят к стороне НН по формуле 2-6 [Л3. с. 28].

На практике можно не учитывать активное сопротивление энергосистемы, а значение индуктивного сопротивления приравнивать как к полному сопротивлению энергосистемы (на точность расчетов это никак не скажется). В этом случае значение (в Омах) индуктивное (полное) сопротивление энергосистемы определяется по формуле 2-7 [Л3. с. 28].

После того как определили индуктивное сопротивление системы по формуле 2-7 [Л3. с. 28], данное сопротивление нужно привести к стороне НН по формуле 2-6 [Л3. с. 28].

Индуктивное сопротивление системы, также можно определить по формулам представленных в ГОСТ 28249-93:

Как мы видим формула 1 из ГОСТ 28249-93 соответствует формулам 2-6, 2-7 из [Л3. с. 28].

Пример

Определить сопротивление энергосистемы, учитывая, что ток КЗ со стороны энергосистемы на зажимах ВН трансформатора 6/0,4 кВ составляет в максимальном режиме – 19 кА, в минимальном – 13 кА.

Решение

Определяем индуктивное сопротивление энергосистемы по формулам 2-6, 2-7.

Сопротивление энергосистемы в максимальном режиме, приведенное к напряжению 0,4 кВ:

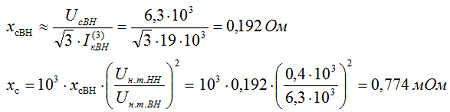
Сопротивление энергосистемы в минимальном режиме, приведенное к напряжению 0,4 кВ:

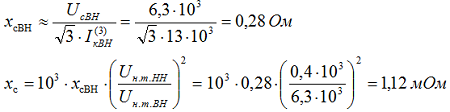
2. Определение сопротивлений трансформаторов

Значения (в мОм) полного (zт), активного (rт) и индуктивного (хт) сопротивления понижающего трансформатора приведенных к стороне НН определяются по формулам: 2-8, 2-9, 2-10 [Л3. с. 28].

На большинстве трансформаторов 10(6)/0,4 кВ имеется возможность регулирования напряжения путем переключения без возбуждения (ПБВ) при отключенном от сети трансформаторе как со стороны высшего так и низшего напряжения. Напряжение регулируется со стороны высшего напряжения на величину ±2х2,5% от номинального значения.

Для трансформаторов с пределом регулирования ПБВ ±2х2,5%, полное сопротивление будет изменятся в пределах:

Значения индуктивного и активного сопротивления трансформатора по ГОСТ 28249-93 определяются по формулам:

Как видно, формулы из ГОСТ 28249-93 совпадают с формулами приведенными в [Л3. с. 28].

Для упрощения расчета активного и индуктивного сопротивления тр-ра, можно использовать таблицу 2-4 [Л3. с. 29] для схем соединения обмоток трансформатора Y/Yo и ∆/Yo. Причем для схем соединения обмоток трансформатора ∆/Yo, значения активного (r0) и индуктивного (х0) сопротивления нулевой последовательности равны значениям активного и индуктивного сопротивления прямой последовательности: r0 = rт и х0 = хт.

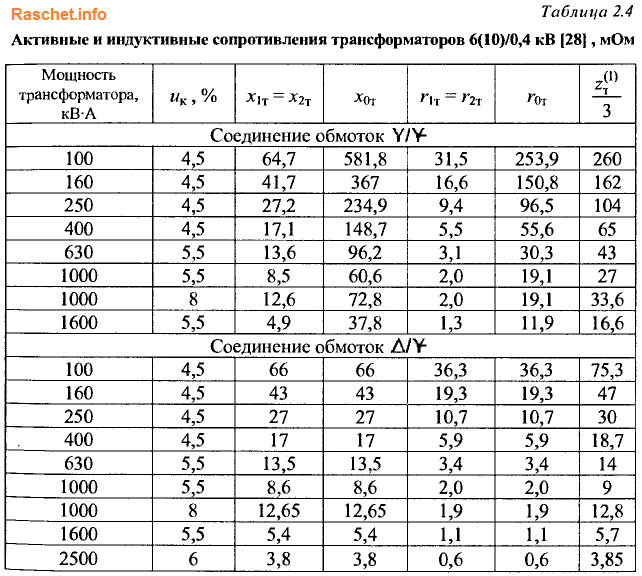
Пример

Определить сопротивление трансформатора ТМ 50/6 со схемой соединения обмоток ∆/Yо.

Решение

По справочным данным определяем технические данные трансформатора: Sном. = 50 кВА, Uном.ВН = 6,3 кВ, Uном.НН = 0,4 кВ, Uкз = 4%, ∆Ркз=1,1 кВт.

Определяем полное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-8:

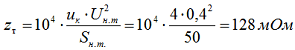
Определяем активное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-9:

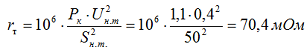
Определяем индуктивное сопротивление трансформатора для стороны 0,4 кВ по формуле 2-10:

3. Определение сопротивлений кабелей

Значения активного и индуктивного сопротивления кабелей определяются по формуле 2-11 [Л3. с. 29].

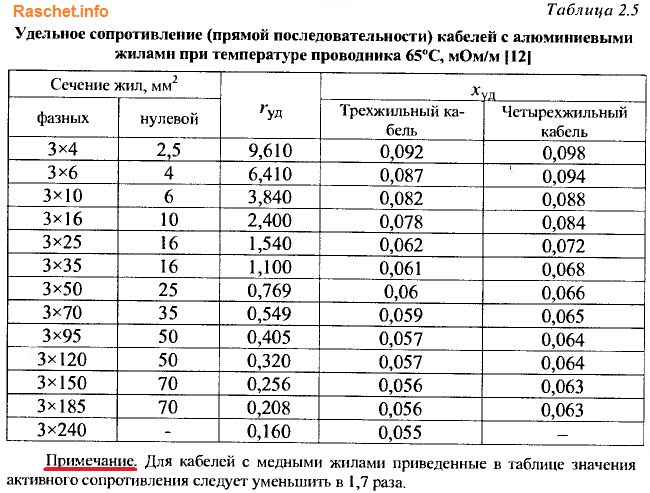
4. Определение сопротивлений шин и шинопроводов

Сопротивление шин и шинопроводов длиной 5м и меньше, можно не рассчитывать, так как они не влияют на значение токов КЗ.

Значения активного и индуктивного сопротивления шин и шинопроводов определяется аналогично кабелям.

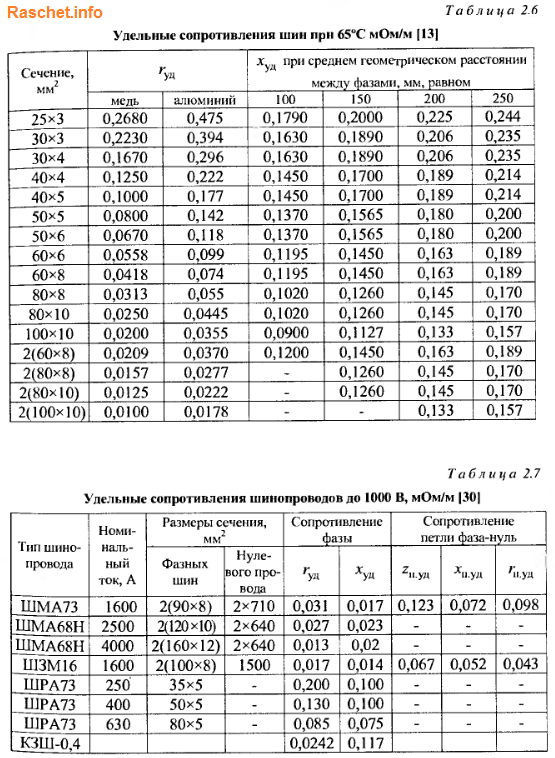
Зная расстояние между прямоугольными шинами, можно приближенно определить индуктивное сопротивление (мОм/м) по формуле 2-12 [Л3. с. 29].

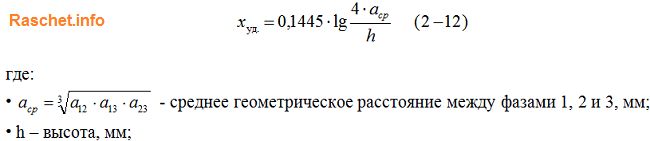
Пример

Определить активное и индуктивное сопротивление алюминиевых шин сечением 60х8 мм2 от трансформатора ТМ-630/6 до распределительного щита 0,4 кВ, общая длина проложенных от трансформатора до РП-0,4 кВ составляет 10 м. В данном примере определим сопротивление шин, когда шины находятся как в горизонтальном положении, так и в вертикальном.

Решение

4.1 Определим активное и индуктивное сопротивление шин при горизонтальном расположении.

По таблице 2.6 определяем погонное активное сопротивление r_уд. = 0,074 мОм/м, индуктивное сопротивление определяем по формуле 2-12 [Л3. с. 29].

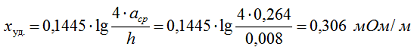
где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 60 + 200 = 460 мм, а среднегеометрическое расстояние:

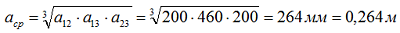
Сопротивление шин от тр-ра до РП-0,4 кВ:

4.2 Определим активное и индуктивное сопротивление шин при вертикальном расположении

При вертикальном расположении шин, активное сопротивление не изменяется, а индуктивное сопротивление составляет:

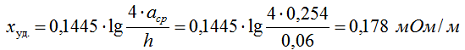
где: расстояние между шинами первой и второй фазы а₁₂ = 200 мм, между второй и третью а₂₃ = 200 мм, между первой и третью а₁₃ = 200 + 8 + 200 = 408 мм, а среднегеометрическое расстояние:

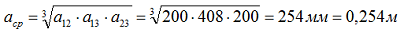
Сопротивление шин от тр-ра до РП-0,4 кВ:

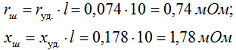
5. Определение сопротивлений воздушных линии

Активное и индуктивное сопротивления линий определяется по той же формуле 2-11 [Л3. с. 29], что и кабели.

Значение индуктивного сопротивления для проводов из цветных металлов можно приближенно принимать равным 0,3 мОм/м, активного по табл. 2.8.

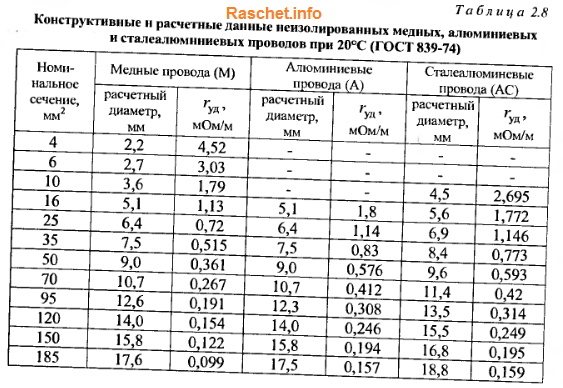
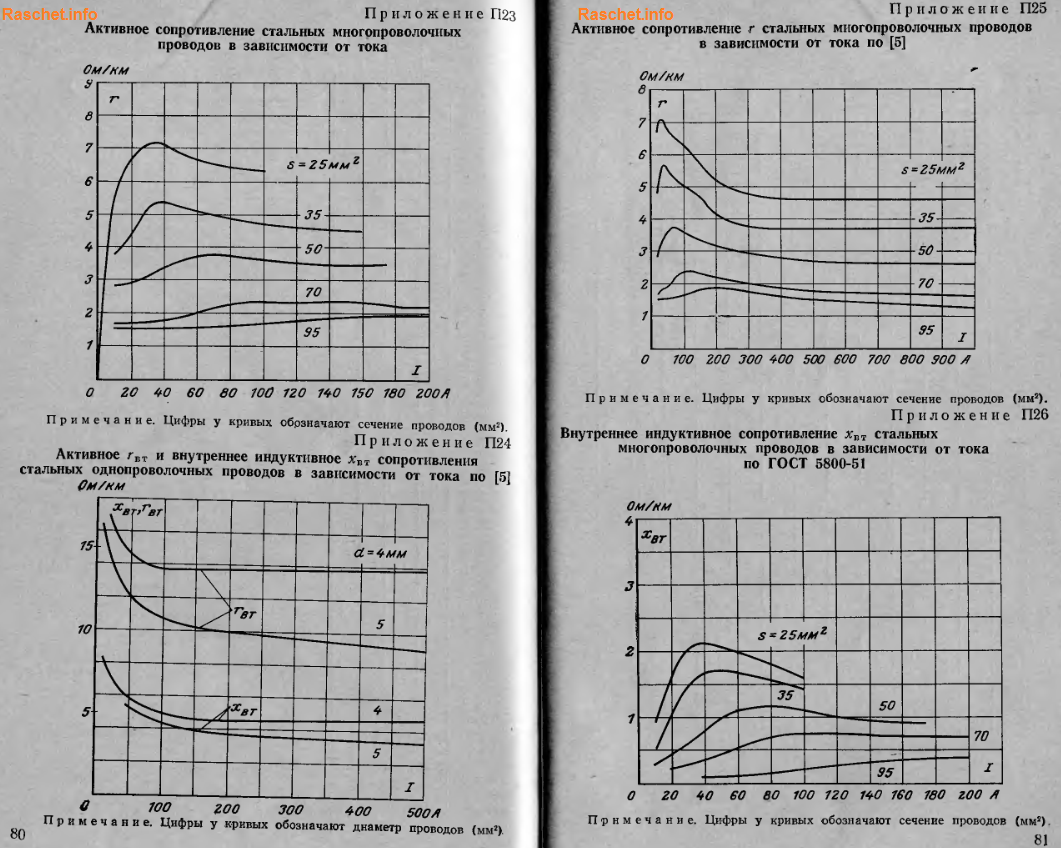
Для стальных проводов активное и индуктивное сопротивление определяется исходя из конструкции провода и значения протекающего по нему тока. Зависимость эта сложная и математическому расчету не поддается, из-за большого количества переменных (сечение провода, температура окружающего воздуха, которая постоянно меняется в течении года, времени суток; нагревом провода током КЗ), которые влияют на значение сопротивление стальных проводов.

Поэтому учесть все эти зависимости практически не возможно и на практике активное сопротивление условно принимают при температуре 20°С и определяют по кривым зависимости стальных проводов от проходящего по ним токам, представленных в приложениях П23-П27 [Л4. с. 80-82].

Активное и индуктивное сопротивление для проводов самонесущих изолированных (СИП) определяют по таблицам Б.1, Б.2 [Л5. с. 23-26].

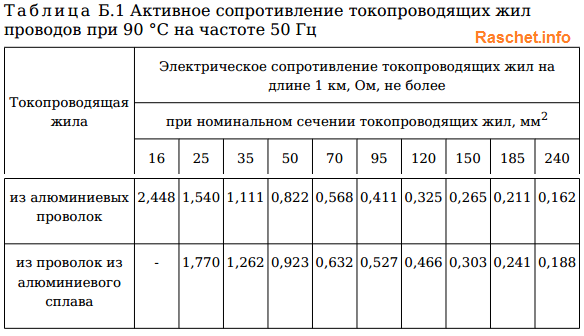
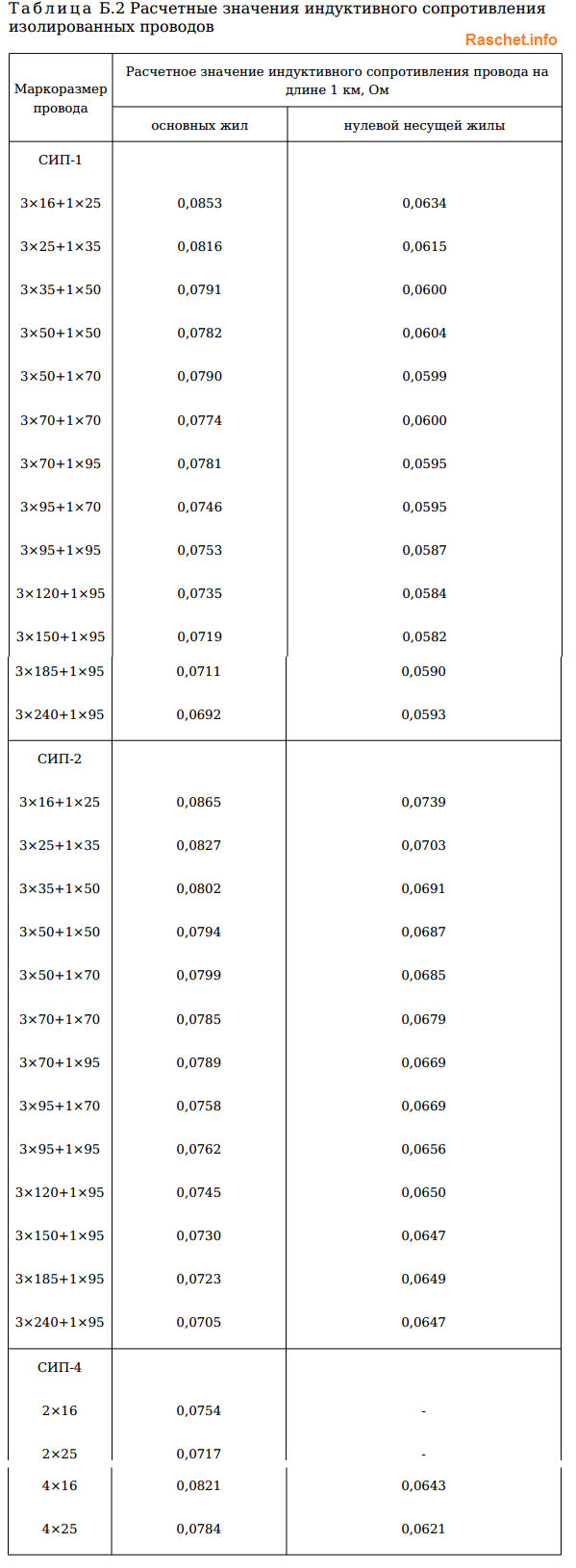
6. Определение сопротивлений реакторов

Номинальные параметры реактора уже заданы в обозначении самого реактора типа РТТ и РТСТ. Например у реактора типа РТТ-0,38-100-0,15:

• 0,38 – номинальное напряжение 380 В;
• 100 – номинальный ток 100 А;
• 0,15 – индуктивное сопротивление при частоте 50 Гц равно 150 мОм.

Активное сопротивление для исполнения У3 (алюминиевая обмотка) — 17 мОм, для исполнения Т3 (медная обмотка) – 16 мОм.

7. Определение сопротивлений трансформаторов тока

Значения активных и индуктивных сопротивлений трансформаторов тока принимаются по приложению 5 таблица 20 ГОСТ 28249-93. Активным и индуктивным сопротивлением одновитковых трансформаторов (на токи более 500 А) при расчетах токов КЗ можно пренебречь.

Согласно [Л3. с. 32] для упрощения расчетов, сопротивления трансформаторов тока не учитывают ввиду почти незаметного влияния на токи КЗ.

8. Определение сопротивлений автоматических выключателей, рубильников, разъединителей

Приближенные значения сопротивлений разъемных контактов коммутационных аппаратов напряжением до 1 кВ определяются по приложению 4 таблица 19 ГОСТ 28249-93. При приближенном учете сопротивление коммутационных аппаратов принимают — 1 мОм.

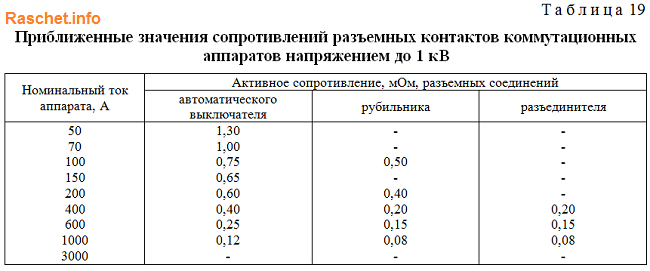
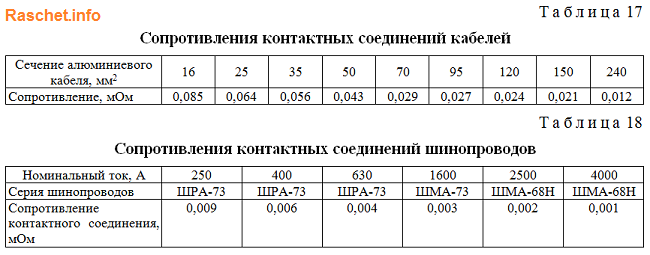
9. Определение сопротивлений контактных соединений кабелей и шинопроводов

Значения сопротивления контактных соединений кабелей и шинопроводов определяют по приложению 4 таблицы 17,18 ГОСТ 28249-93. Для упрощения расчетов, данными сопротивлениями можно пренебречь. При приближенном учете сопротивлений контактов принимают:
• rк = 0,1 мОм — для контактных соединений кабелей;
• rк = 0,01 мОм — для шинопроводов.

10. Список литературы

1. Рекомендации по расчету сопротивления цепи «фаза-нуль». Главэлектромонтаж. 1986 г.
2. ГОСТ 28249-93 – Методы расчета в электроустановках переменного тока напряжением до 1 кВ.
3. Беляев А.В. Выбор аппаратуры, защит и кабелей в сети 0,4 кВ. Учебное пособие. 2008 г.
4. Голубев М.Л. Расчет токов короткого замыкания в электросетях 0,4 — 35 кВ. 2-e изд. 1980 г.
5. ТУ 16-705.500-2006. Провода самонесущие изолированные и защищенные для воздушных линий электропередач.

Всего наилучшего! До новых встреч на сайте Raschet.info.

Трансформатор, как элемент радиотехники и электротехники, работает на основе электромагнитной индукции. Говоря об индуктивности трансформатора, имеют в виду индуктивность обмоток и взаимоиндукцию между ними.

Каждая из обмоток представляет некоторое количество витков провода, намотанных на ферромагнитный сердечник, то есть обыкновенную катушку индуктивности.

Трудность в определении параметров катушки заключается в том, что они изменяются в зависимости от нескольких параметров и их сочетания:

• токи в обмотках;
• уровень намагниченности магнитопровода;
• магнитные характеристики сердечника;
• взаимодействие между соседними обмотками;
• наличия постоянной составляющей тока.

Конструкция и принцип действия силового трансформатора

В основе конструкции любого трансформатора находятся следующие элементы:

1. Сердечник из ферромагнитного материала.
2. Первичная и вторичные обмотки. В случае автотрансформатора одна обмотка выполняет обе функции.

В сетях переменного тока промышленной частоты (50 или 60Гц) в качестве ферромагнитного материала используется сталь, обработанная по специальной технологии. На высоких частотах часто делаются трансформаторы без сердечника, поскольку для нормальной работы достаточно взаимосвязи межу катушками.

Принцип работы:

• в первичной обмотке, подключенной в цепь питания, создается переменное электрическое поле;
• под действием поля первичной катушки в сердечнике создается переменное магнитное поле;
• в силу электромагнитной индукции во всех обмотках наблюдается ЭДС индукции.

ЭДС индукции в первичной обмотке направлена противоположно поданному напряжению, поэтому они взаимно компенсируются. В результате, при отсутствии нагрузки через первичную обмотку протекает сравнительно небольшой ток холостого хода.

Наличие тока вторичной цепи аналогично вызывает дополнительный магнитный поток, а он – ЭДС самоиндукции в первичное катушке. В результате компенсация первичного напряжения снижается и растет ток в первичной цепи.

Физическое понятие индуктивности обмоток

Индуктивность представляет собой коэффициент пропорциональности между током, создаваемым замкнутым электрическим контуром, и магнитным потоком, который создается этим контуром.

Более понятной формулировкой будет та, которая говорит о величине ЭДС самоиндукции в замкнутом контуре, которая возникает при изменении силы тока за единицу времени. То есть, понятие индуктивности справедливо для изменяющегося тока.

При постоянном токе говорить об индуктивности бессмысленно.

В идеальном трансформаторе все электромагнитное поле, создаваемое обмотками, замкнуто в магнитном сердечнике. В реальных конструкциях существует поле рассеяния, величина которого зависит от способа выполнения катушки и конструктивных особенностей сердечника. Чем больше толщина намотки, тем большая часть электромагнитного поля замыкается вне магнитопровода.

Этому способствует также качество сборки магнитопровода. Зазоры между пластинами способствуют резкому увеличению рассеивания. В связи с этим наилучшими свойствами обладают О-образные сердечники.

Формулы и измерение

Формулы для расчета индуктивности катушек довольно сложны и имеет различный вид для различных типов исполнения обмоток:

• линейный проводник;
• одновитковая катушка;
• плоская катушка;
• соленоидальная обмотка;
• тороидальная форма.

Наибольшие сложности возникают при расчетах многовитковых многослойных катушек, то есть тех, которые составляют обмотку трансформаторов.

В подавляющем большинстве случаев точный расчет невозможен, поэтому приходится использовать примерные данные и уточнять их после проведения измерений.

Формулы  для расчета индуктивности трансформатора основаны на расчетах соленоида:

L=µ₀µN²S/l, где

µ0 – магнитная постоянная;

µ – магнитная проницаемость сердечника;

N – количество витков;

S – площадь одного витка;

l – длина обмотки.

Для измерения индуктивности существует несколько методик и приборов, созданных на их основе. В большинстве случаев измерение производится путем вычислений индуктивного сопротивления катушки при подаче образцового напряжения заданной частоты и измеренного значения тока через обмотку.

В специализированных приборах вычисления производятся автоматически, и пользователь только считывает показания шкалы прибора, выраженные в единицах индуктивности – Гн, мГн или мкГн.

Как измерить в домашних условиях

Приборы для непосредственного измерения индуктивности имеют высокую стоимость и редко используются в домашних условиях. С приемлемой точностью результаты можно получить, используя обычные приборы для измерения переменного тока: амперметр и вольтметр. Также необходим омметр.

Порядок действий следующий:

1. При помощи омметра определяют активное сопротивление обмотки R.
2. Подключают трансформатор последовательно с амперметром в сеть.
3. Параллельно обмотке подключают вольтметр.
4. По показаниям приборов определяют полное сопротивление трансформатора: Z=U/I
5. Индуктивное сопротивление находят, вычитая из полного сопротивления активное: X_L=Z-R
6. Индуктивность определяется по формуле: L=X_L/(2πf), где π – число пи 3.14, f – частота измерений.

Как правило, активное сопротивление намотки значительно (на несколько порядков) меньше индуктивного, поэтому можно его не учитывать. Именно поэтому, включение трансформатора в цепь постоянного напряжения вызывает короткое  замыкание. Ток обмотки при этом будет ограничиваться только активным сопротивлением.

Пример расчета

К примеру, требуется рассчитать индуктивность первичной обмотки трансформатора питания. Путем измерений определено:

1. Сопротивление обмотки 3 Ом.
2. Напряжение сети 220 В.
3. Частота питающего напряжения 50 Гц.
4. Ток холостого хода 05 А.

Полное сопротивление:

Z=U/I=220/0.05=4400 Ом

Активное сопротивление меньше полного в 10000 раз и его можно не учитывать.

Определяем индуктивность:

L=X_L/(2πf) =4400/ (2∙3.14∙50) =14 Гн.

В первой беседе мы коснулись переменного тока, – в цепях с активным сопротивлением переменный ток подчиняется всем законам которым подчиняется и постоянный ток, – однако, кроме активного сопротивления бывает еще и “реактивное”, – индуктивное.
1. – Индуктивное сопротивление.
Если в цепи присутствует кроме активного сопротивления еще и индуктивное, то оно будет оказывать дополнительное воздействие на переменный ток в цепи.
Прямой проводник обладает кроме омического, активного сопротивления еще и индуктивным, однако значение этого сопротивления крайне мало. Если же взять проводник и свернуть его в катушку то индуктивное сопротивление увеличится.
Индуктивное сопротивление катушки переменному току зависит от индуктивности самой катушки и частоты тока протекающего через эту катушку. Индуктивное сопротивление при увеличении частоты тока или увеличении количества витков катушки увеличивается!

Рассмотрим схему.

На схеме мы видим генератор “G” переменного тока с функцией изменения частоты. Генератор соединён с лампой накаливания через индуктивность катушки “L”, а так же измерительные приборы, – два вольтметра и амперметр.
Вольтметр Р1 измеряет напряжение на выходе генератора, вольтметр Р2 измеряет напряжение на нагрузке “Н” (лампа) и амперметр Р3 измеряющий ток в цепи.

Теперь давайте включим генератор и подадим в цепь переменный ток с частотой 500Гц. Лампа засветилась, вольтметр подключенный к генератору показывает 4В, вольтметр подключенный к лампе показывает 2,8В, а амперметр 380мА. Напряжение на лампе меньше чем на выходе генератора из за того, что индуктивность катушки оказывает сопротивление переменному току и чем выше частота, тем больше это сопротивление.

Давайте увеличим частоту генератора и посмотрим, что произойдет с напряжением на лампе и током в цепи.

Теперь частота генератора 2000Гц (музыкантов попрошу воздержаться….).

Теперь мы видим, что напряжение генератора не изменилось, что логично, а вот ток в цепи уменьшился до 140мА и напряжение на лампе упало практически до нуля.
Схема и параметры катушки не изменились, однако на более высокой частоте изменилось индуктивное сопротивление катушки.
Индуктивное сопротивление зависит от индуктивности катушки, единицей индуктивности является генри (Гн). Индуктивностью 1Гн обладает катушка у которой при изменении тока в ней на 1А в течении 1с развивается ЭДС самоиндукции равная 1В.
Катушки с индуктивностью в единицы Гн обычно больших размеров и применяются в устройствах с достаточно низкими частотами переменного тока, обычно в устройствах работающих на звуковых частотах.
Индуктивности в тысячных и миллионных долях Гн применяются в устройствах работающих с токами высоких частот, это всевозможные LC фильтры, колебательные контуры приёмников и дроссели импульсных источников питания. Тысячные доли Гн обозначаются как мГн (миллигенри), а миллионные мкГн (микрогенри).

Описанный опыт можно посмотреть в этом видеоролике.

2. – Трансформация переменного тока.
Переменный ток в энергетике выгоднее тем, что его легко трансформировать. Нужно это для передачи тока по линиям электропередач (ЛЭП) на большие расстояния, от электростанции к потребителю.
Из первой беседы нам известно, что от длины проводника зависит его сопротивление, а от сопротивления зависит ток в цепи, если мы попытаемся передать электроэнергию на большое расстояние, сотни или тысячи километров, используя при этом напряжение 230В как в бытовой сети то мы очень много энергии потеряем на нагреве провода. Например – если подключить к источнику напряжения 100В удлинитель с общим сопротивлением 50Ом и подключить на другом конце лампочку с рабочим током 1А то на проводе мы потеряем около 50В и 50Вт мощности. В итоге половину энергии мы потеряли. Но если напряжение повысить до 10 000В и предать его по этой же линии, а потом трансформировать обратно в 100В и запитать ту же лампочку то потери в линии составят всего 0,01Вт!!
Почему так? По тому, увеличивая напряжение в линии уменьшается ток, а из закона Ома известно, – чем меньше ток в цепи тем меньше падение напряжения на участке цепи (в нашем случае на проводах удлинителя).
Таким образом, увеличив напряжение и уменьшив ток – мы не меняя передаваемой мощности получаем меньше потерь.

Устройство трансформатора показано на рисунке ниже.

Трансформатор состоит из двух катушек на общем магнитопроводе, катушки называют обмотками и изображают на схемах как обычные катушки индуктивности, а магнитопровод – линией между ними. Действие трансформатора основано на явлении электромагнитной индукции. Переменный ток протекая в одной из обмоток трансформатора создает вокруг неё и в магнитопроводе переменное магнитное поле. Это поле пересекает витки второй обмотке и индуцирует в ней переменное напряжение той же частоты. Если к этой обмотке подключить нагрузку то в цепи потечет ток. Обмотку к которой подводится напряжение, называют первичной, а обмотку в которой индуцируется переменное напряжение – вторичной.
Напряжение которое получается на концах вторичной обмотки зависит от соотношения чисел витков в обмотках. При одинаковом количестве витков в обмотках, напряжение вторичной обмотки будет примерно равно напряжению подведенному к первичной, если во вторичной обмотке больше или меньше витков то и напряжение получаемое на её концах будет больше или соответственно меньше подведенного к первичной обмотке. В первом случае, трансформатор называют повышающим, во втором – понижающим.
Напряжение индуцируемое во вторичной обмотке, легко подсчитать по соотношению витков обмоток, – во сколько раз вторичная обмотка имеет больше или меньше витков чем в первичной, во столько же раз напряжение на ней будет больше или меньше чем подводимое к первичной обмотке. Если первичная обмотка имеет 1000 витков а вторичная 2000 витков, то, подведя к первичной обмотке 230В из розетки, на выходе вторичной мы получим 460В переменного напряжения. Если этот же трансформатор, подключить к розетке обмоткой содержащей 2000 витков, то, на концах обмотки содержащей 1000 витков мы получим 115В. В первом случае трансформатор был повышающим, во втором – понижающим.
Нужно понимать, что трансформация напряжения не изменяет мощность тока, если мы увеличиваем напряжение, то, неизбежно уменьшается ток, если напряжение уменьшается, то ток увеличивается в любом случае формула P=UI говорит нам, что мощность не изменилась.

Мощность трансформатора зависит от его габаритов, и сечения проводов обмоток, чем массивнее магнитопровод трансформатора, тем большую мощность он может обеспечить.
Магнитопроводы для трансформаторов работающих на низких частотах, выполняют из электротехнической стали, в виде пластин собранных в стопку.
На схемах низкочастотные трансформаторы обозначают буквой Т, а обмотки римскими цифрами – I, II, III, IV, и так далее.
Трансформаторы работающие на высоких частотах выполнены на магнитодиэлектрических магнитопроводах – например из феррита, могут вовсе не иметь магнитопровода или даже быть образованы двумя и более катушками на разных но расположенных рядом каркасах. На рисунке изображены ВЧ трансформаторы, – слева на общем каркасе, справа на разных.

В центре рисунка изображено схемное начертание ВЧ трансформатора.
Независимо от формы и конструкции магнитопровода высокочастотного трансформатора, на схемах он обозначается линией между обмотками, так же как и у низкочастотного трансформатора, а вот обмотки в отличии от низкочастотного трансформатора обозначаются так же как катушки индуктивности, – латинской L, L1, L2 и так далее.

Принцип работы высокочастотных трансформаторов не отличается от работы своих низкочастотных собратьев.
Трансформируется трансформатором только переменный ток, переменный ток может быть и пульсирующим и присутствовать в постоянном, то есть – если подключить к первичной обмотке трансформатора источник постоянного напряжения и изменять ток через обмотку, к примеру реостатом, то это изменение силы тока будет изменять и магнитное поле вокруг обмотки и в сердечнике трансформатора и это изменение будет неизбежно индуцировать ЭДС во вторичную обмотку. Вот тут есть задачка по этой теме, а вот тут правильный ответ на неё.

В следующей беседе поговорим о резисторах и конденсаторах.