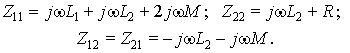Как найти индуктивность катушек соединенных параллельно

1 мГн = 0,001 Г. 1 мкГн = 0,000001 = 10⁻⁶ Гн. 1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.

Индуктивность характеризует способность электрического проводника преобразовывать электрический ток в изменение электрического потенциала в данном проводнике (самоиндукция) и в расположенных рядом проводниках (взаимоиндукция). Индуктивность обычно обозначается символом L в честь русского физика немецкого происхождения Эмилия Христиановича Ленца (Heinrich Lenz).

По определению самоиндукции напряжение v(t) и ток i(t) в катушке индуктивности связаны выражением

На всех соединенных параллельно катушках индуктивности имеется одно и то же напряжение V. В соответствии с правилом Кирхгофа для тока общий ток I равен сумме токов, протекающих через отдельные катушки:

Общая индуктивность L_eq соединенных параллельно трех катушек индуктивности, расположенных далеко друг от друга и не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям:

Или для n несвязанных катушек индуктивности:

Эта формула для L_eq используется для расчетов в этом калькуляторе. Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна

мкГн.

Отметим, что если одна или несколько величин индуктивности равны нулю, то L_eq стремится к нулю. Представьте себе очень короткий прямой проводник, шунтирующий катушку индуктивности — он и будет иметь почти нулевую индуктивность. Отметим также, что невозможно создать схему с нулевой индуктивностью.

Если параллельно соединены только две катушки индуктивности, имеем:

или

Эквивалентная индуктивность n одинаковых соединенных параллельно катушек индуктивности L равна

Отметим, что формула для расчета общей индуктивности нескольких катушек индуктивности, соединенных параллельно, используется и для расчета сопротивления группы резисторов, соединенных параллельно.

Отметим также, что для группы из любого количества соединенных параллельно катушек индуктивности эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивности, а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность группы.

Если индукторы расположены в магнитном поле друг друга, эти формулы работать не будут из-за явления взаимоиндукции (взаимной индукции), которое рассматривается в нашем калькуляторе взаимной индукции. Эффект взаимоиндукции может уменьшить или увеличить общую индуктивность катушек в зависимости от того как работает магнитная связь между катушками. Величина взаимной индукции зависит от расстояния между катушками и их ориентации. При этом взаимоиндукция может увеличивать или уменьшать общую индуктивность.

Если несколько катушек индуктивности соединены последовательно, их эквивалентная индуктивность определяется простым сложением индуктивностей отдельных катушек.

Для n соединенных последовательно катушек индуктивности имеем

Возможно, вы уже заметили, что катушки индуктивности ведут себя точно так же, как резисторы: если катушки соединены последовательно, их эквивалентные индуктивности всегда будет выше, чем индуктивности отдельных катушек, соединенных последовательно, а при параллельном соединении эквивалентная индуктивность всегда будет меньше индуктивностей отдельных катушек.

Зачем соединять катушки последовательно, если можно просто намотать большую катушку индуктивности? Вот один из примеров.

В микроэлектронике для реализации довольно больших индуктивностей на единицу площади интегральной микросхемы используется комбинирование спиральных катушек в нескольких слоях металлизации. Для этой цели используется многослойная пакетная конфигурация катушек индуктивности. Несколько слоев металлизации со спиральными катушками располагают точно один над другим. Катушки соединяют последовательно, чтобы индуктивности складывались для получения одной большой катушки индуктивности. Без такого пакетного расположения при использовании планарной технологии было бы невозможно создать большие индуктивности. Благодаря такому пакетному расположению коэффициент связи катушек k ≈ 1.

В этом калькуляторе мы рассматриваем только идеальные катушки индуктивности. Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.

Соединение катушек

Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.

Последовательное соединение катушек индуктивности.

Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.

Рисунок 1. Последовательное соединение катушект индуктивности.

Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:

где L1, L2 и L3 — индуктивности отдельных катушек.

Параллельное соединение катушек индуктивности.

Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же усло­вия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:

Рисунок 2. Параллельное соединение катушек индуктивности.

Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:

Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или парал­лельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопро­тивления цепи при последовательном и параллельном соеди­нении резисторов.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, распо­ложены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше фор­мула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

1. Магнитные потоки обеих катушек имеют одинаковые на­правления
2. Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений то­ков в них.

Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответство­вать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направ­лены в одну сторону. Очевидно, при этих условиях витки каж­дой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в дру­гой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых состав­лена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по фор­муле:

В первом случае ставится знак + (плюс), а во втором слу­чае знак — (минус).

Величина М, называемая коэффициентом взаим­ной индукции, представляет собой добавочную индук­тивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство варио­метров. Вариометр состоит из двух катушек, общая индуктив­ность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передат­чиков.

Калькулятор параллельных индуктивностей

Параллельные и последовательные схемы соединения катушек индуктивности часто используются для получения
требуемой индуктивности. Для этого используются стандартные катушки с фиксированным значением индуктивности.

Если параллельно соединены только две катушки индуктивности, имеем:

Расчет индуктивности

Расчет эквивалентной индуктивности
Расчет при известном эквивалентном значении

Обнаружили ошибку или неточность в работе калькулятора? Сообщите нам об этом.
Соблюдайте технику безопасности во время работы с электронными компонентами!

Соединение катушек индуктивности

Соединение катушек индуктивности при отсутствии взаимного влияния магнитных полей катушек.

Последовательное соединение катушек индуктивности.

Суммарная индуктивность двух или нескольких катушек, соединенных последовательно и расположенных на таком расстоянии друг от друга, что магнитное поле одной катушки не пересекает витков другой (рисунок 1), равна сумме их индуктивностей.

Рисунок 1. Последовательное соединение катушек индуктивности.

Цепь, изображенная на рисунке 1, обладает общей индуктивностью L, которая выражается так:

где L1, L2 и L3 — индуктивности отдельных катушек.

Параллельное соединение катушек индуктивности.

Индуктивность цепи, составленной из тех же катушек при параллельном их соединении (рисунок 2) и при соблюдении того же усло­вия относительно их расположения (отсутствие магнитного взаимодействия), подсчитывается по следующей формуле:

Рисунок 2. Параллельное соединение катушек индуктивности.

Индуктивность двух катушек, соединенных параллельно, определяется по следующей формуле:

Как видим, формулы для подсчета результирующих индуктивностей катушек, соединенных последовательно или парал­лельно и не взаимодействующих между собой, совершенно тождественны с формулами для подсчета омического сопро­тивления цепи при последовательном и параллельном соеди­нении резисторов.

Соединение катушек при наличии взаимного влияния их магнитных полей.

Если катушки, включенные в цепь последовательно, распо­ложены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь (рисунок 3а), то для определения их общей индуктивности приведенная выше фор­мула будет уже непригодна. При таком расположении катушек могут быть два случая, а именно:

1. Магнитные потоки обеих катушек имеют одинаковые на­правления
2. Магнитные потоки обеих катушек направлены навстречу друг другу

Тот или другой случай будет иметь место в зависимости от направления витков обмотки катушек и от направлений то­ков в них.

Рисунок 3. Соединение катушек индуктивности: а)суммарная индуктивность увеличивается за счет взаимной индукции б)суммарная индуктивность уменьшается за счет взаимной индукции.

Если обе катушки намотаны в одну сторону и токи в них текут в одном направлении, то это будет соответство­вать первому случаю; если же токи текут в противоположных направлениях (рисунок 3б), то будет иметь место второй случай.

Разберем первый случай, когда магнитные потоки направ­лены в одну сторону. Очевидно, при этих условиях витки каж­дой катушки будут пронизываться своим потоком и частью потока другой катушки, т. е. магнитные потоки в той и в дру­гой катушке будут больше по сравнению с тем случаем, когда между катушками нет индуктивной связи. Увеличение магнитного потока, пронизывающего витки той или иной катушки, равносильно увеличению ее индуктивности. Поэтому общая индуктивность цепи в рассматриваемом случае будет больше суммы индуктивностей отдельных катушек, из которых состав­лена цепь.

Рассуждая таким же образом, мы придем к выводу, что для второго случая, когда потоки направлены навстречу друг другу, общая индуктивность цепи будет меньше суммы индуктивностей отдельных катушек.

Подсчет величины индуктивности цепи, составленной из двух соединенных последовательно катушек индуктивности L1 и L2 при наличии между ними индуктивной связи, производится по фор­муле:

В первом случае ставится знак + (плюс), а во втором слу­чае знак — (минус).

Величина М, называемаякоэффициентом взаим­ной индукции, представляет собой добавочную индук­тивность, обусловленную частью магнитного потока, общей для обеих катушек.

На явлении взаимоиндукции основано устройство варио­метров. Вариометр состоит из двух катушек, общая индуктив­ность которых может, по желанию, плавно изменяться в некоторых пределах. В радиотехнике вариометры применяются для настройки колебательных контуров приемников и передат­чиков.

Основой
расчета являются уравнения цепи
(Кирхгофа, контурные или узловые),
составленные с учетом взаимного влияния
индуктивно связанных элементов.

Для
анализа последовательного соединения
двух связанных катушек используем
уравнения Кирхгофа. При этом маркированные
зажимы последовательно включенных
катушек могут быть соединены по-разному.
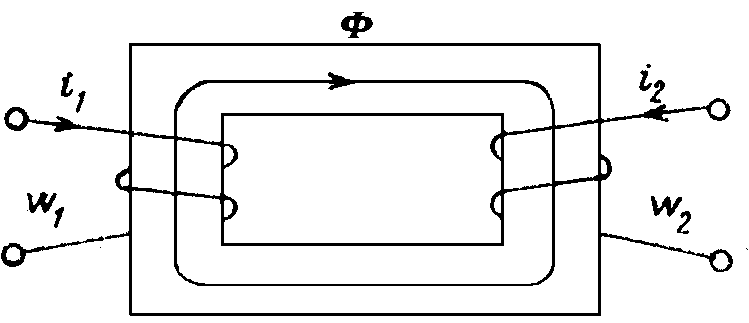
Суммарное напряжение согласно включенных
катушек (рис. 9.4, а)
равно

Величина L_э = (L₁ + L₂ + 2M)
в этом случае представляет собой эквивалентную
индуктивность.

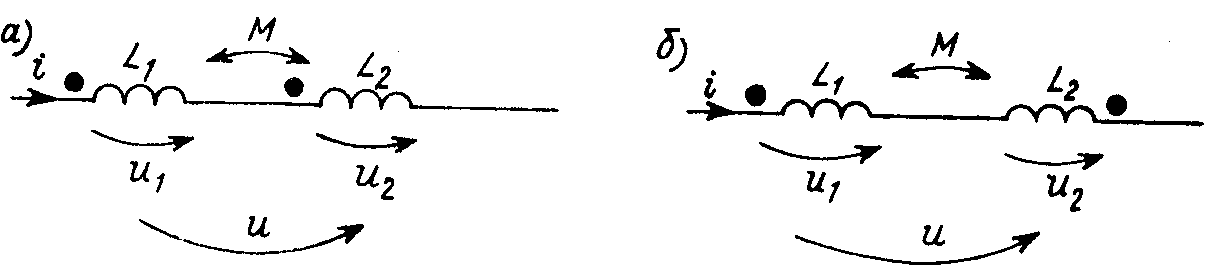
Рис.
9.4

Для
встречного включения (рис. 9.4, б)
имеем

и
эквивалентная индуктивность
равна L_э = (L₁ + L₂ – 2M).

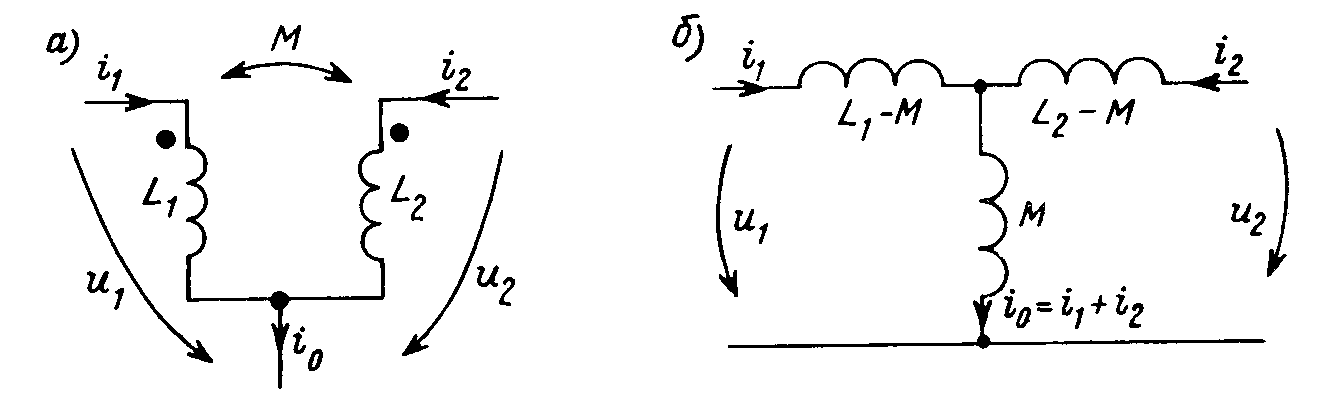
Рис.
9.5

Если
две индуктивно связанные катушки (рис.
9.5, а)
имеют общую точку (пусть, например, их
немаркированные зажимы соединены друг
с другом), то, переписав соотношения для
напряжений (9.1)
в форме:

получаем
возможность заменить их Т-образной
схемой замещения, не содержащей
индуктивных связей (рис. 9.5, б).

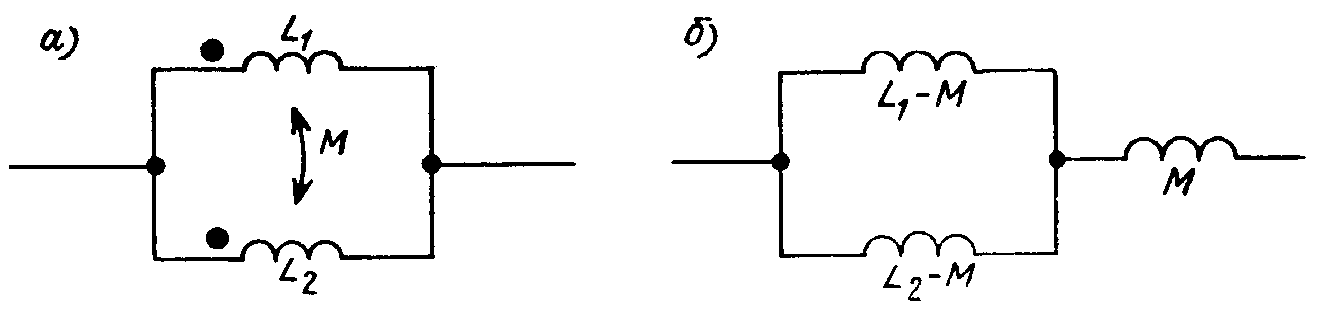
Рис.
9.6

Для
определения эквивалентной индуктивности
параллельно соединенных катушек (рис.
9.6, а),
преобразуем эту схему в изображенную
на рис. 9.6, б.
Поскольку индуктивности при последовательном
и параллельном соединениях суммируются
по тем же правилам, что и сопротивления,
для эквивалентной индуктивности
параллельного соединения имеем:

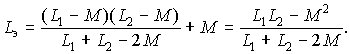
Так
как соединенные произвольным образом
катушки сохраняют индуктивный характер,
то эквивалентная индуктивность при
встречном и параллельном соединениях
имеет положительное значение, несмотря
на наличие отрицательных слагаемых в
полученных выражениях. Это означает,
что значения L₁, L₂ и M двух
катушек не независимы друг от друга, а
связаны неравенствами: L₁L₂  M²; L₁ + L₂ 2M.
Возведением второго из неравенств в
квадрат можно убедиться, что оно является
более сильным, чем первое неравенство,
т. е. условие L₁L₂   M² обеспечивает
выполнение и второго неравенства.

Величина  — коэффициент
связи обмоток —
характеризует степень взаимного влияния
обмоток друг на друга. При k = 1
или  имеем
совершенную связь обмоток —

 первой
обмотки L₁ = w₁Φ/i₁ = /R_м (R_м —
магнитное сопротивление сердечника).
Аналогично L₂ = /R_м; M = w₁w₂/R_м и k = 1.
В системе произвольного числа индуктивно
связанных обмоток для любой пары
выполняется условиеи
матрица взаимных индуктивностей М является
при отсутствии совершенных связей (k_pq<
1) положительно определенной.

При
сильной связи обмоток (k  1)
одна из индуктивностей в Т-образной
схеме замещения (рис. 9.5, б)
может оказаться отрицательной. Так,
при L₁> M > L₂ имеем L₂ – M < 0.
Поэтому эквивалентную схему с взаимной
индуктивностью (рис. 9.5, а)
можно использовать для моделирования
цепей с отрицательной индуктивностью.

Для
расчета разветвленных цепей с индуктивно
связанными элементами (рис. 9.8) используем
метод контурных токов.

Рис.
9.8

Контурные
уравнения в комплексной форме имеют
общий вид:

Выбор
независимых контуров указан стрелками
на схеме.

При
записи собственных и общих сопротивлений
запишем по уже известным правилам
сначала члены, не связанные с взаимной
индуктивностью. Далее учтем члены,
отражающие индуктивные связи. В
собственных сопротивлениях контуров
слагаемые + j2ωM появляются,
если обе индуктивно связанные катушки
входят в данный контур и их маркировка
соответствует согласному включению в
этом контуре. Если при обходе контура,
включающего две связанные катушки, одна
из катушек обтекается контурным током
в положительном, а другая – в
отрицательном направлении, то член в
соответствующем собственном сопротивлении
будет иметь знак “минус”, т. е. – j2ωM.

При
записи общего сопротивления двух
контуров учитывается их взаимное
индуктивное влияние друг на друга. Здесь
член jωM имеет
знак “плюс”, если положительные
направления обоих контурных токов
ориентированы одинаково относительно
маркированных зажимов катушек, и оба
тока протекают по ним либо в положительном,
либо в отрицательном направлении. Если
же один из влияющих друг на друга токов
протекает в положительном, а другой –
в отрицательном направлении, в общем
сопротивлении контуров учитывают член
– jωM.
С учетом сформулированных правил получим
для контурных сопротивлений цепи (см.
рис. 9.8):