Если по катушке идет переменный ток, то магнитный поток, пронизывающий катушку, меняется. Поэтому возникает ЭДС индукции в том же самом проводнике, по которому идет переменный ток. Это явление называют самоиндукцией.
При самоиндукции проводящий контур выполняет двойную роль. С одной стороны, переменный ток в проводнике вызывает появление магнитного потока через поверхность, ограниченную контуром. А так как магнитный поток изменяется со временем, появляется ЭДС индукции εis. По правилу Ленца в момент нарастания тока напряженность вихревого электрического поля направлена против тока. Следовательно, в этот момент вихревое поле препятствует нарастанию тока. Наоборот, в момент уменьшения тока вихревое поле поддерживает его.
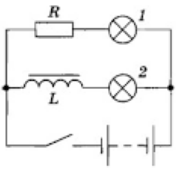
Явление самоиндукции можно наблюдать в простых опытах. На рисунке представлена схема параллельного соединения двух одинаковых ламп. Одну из них подключают к источнику через резистор R, а другую — последовательно с катушкой L, снабженной железным сердечником.
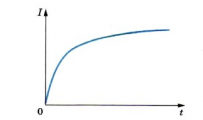
При замыкании ключа первая лампа вспыхивает практически сразу, а вторая — с заметным запозданием. ЭДС самоиндукции в цепи этой лампы велика, и сила тока не сразу достигает своего максимального значения (см. график ниже).
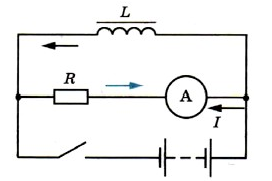
Появление ЭДС самоиндукции при размыкании можно наблюдать в опыте с цепью, схематически показанной на следующем рисунке. При размыкании ключа в катушке L возникает ЭДС самоиндукции, поддерживающая первоначальный ток. В результате в момент размыкания через гальванометр идет ток (цветная стрелка), направленный против начального тока до размыкания (черная стрелка). Сила тока при размыкании цепи может превышать силу тока, проходящего через гальванометр при замкнутом ключе. Это означает, что ЭДС самоиндукции εis больше ЭДС ε батареи элементов.
Самоиндукция и инерция
Явление самоиндукции проще понять, проведя аналогию с инерцией в механике. Инерция приводит к тому, что под действием силы тело не мгновенно приобретает скорость, а постепенно. Тело нельзя мгновенно затормозить, как бы велика ни была тормозящая сила. Точно так же за счет самоиндукции при замыкании цепи сила тока не сразу приобретает определенное значение, а нарастает постепенно. Выключая источник, мы не прекращаем ток сразу. Самоиндукция его поддерживает некоторое время, несмотря на сопротивление цепи.
Чтобы увеличить скорость тела, согласно законам механики нужно совершить работу. При торможении тело само совершает работу. Точно так же для создания тока нужно совершить работу против вихревого электрического поля, а при исчезновении тока это поле совершает положительную работу.
Индуктивность
Модуль вектора индукции В магнитного поля, создаваемого током, пропорционален силе тока. Так как магнитный поток Ф пропорционален В, то Ф ~ В~ I. Это дает право утверждать, что:
Φ=LI
L — коэффициент пропорциональности между током в проводящем контуре и магнитным потоком, пронизывающим этот контур. Эту величину также называют индуктивностью контура, или его коэффициентом самоиндукции.
Применив закон электромагнитной индукции, а также считая, что форма контура остается неизменной, и поток меняется только за счет изменения силы тока, получим:
εis=−ΔΦΔt=−LΔIΔt
Эта формула позволяет дать такую формулировку L, которая точно отражает суть этой величины.
Определение
Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.
Единица измерения индуктивности — генри (Гн). Индуктивность проводника равна 1 Гн, если в нем при изменении силы тока на 1 А за 1 с возникает ЭДС самоиндукции в 1 В.
Индуктивность подобна электроемкости. Она зависит от геометрических факторов: размеров проводника и его формы, но не зависит непосредственно от силы тока в проводнике. Кроме геометрии проводника, индуктивность зависит от магнитных свойств среды, в которой находится проводник.
Пример №1. При равномерном изменении силы тока в катушке на 10 А за 0,02 с в ней возникает ЭДС самоиндукции, равная 200 В. Чему равна индуктивность катушки?
Выразим индуктивность из формулы для ЭДС самоиндукции:
L=−ΔtεisΔI=0,02·20010=−0,4 (Гн)
Знак «минус» означает, что ЭДС самоиндукции действует так, что индукционный ток препятствует изменению магнитного потока. Поэтому само значение индуктивности мы можем принять за модуль полученного результата — 0,4 Гн.
Задание EF17686
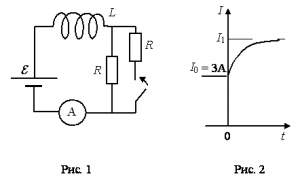
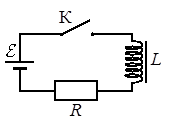
Катушка, обладающая индуктивностью L, соединена с источником питания с ЭДС ε и двумя одинаковыми резисторами R. Электрическая схема соединения показана на рис. 1. В начальный момент ключ в цепи разомкнут.
В момент времени t=0 ключ замыкают, что приводит к изменениям силы тока, регистрируемым амперметром, как показано на рис. 2. Основываясь на известных физических законах, объясните, почему при замыкании ключа сила тока плавно увеличивается до некоторого нового значения – I1. Определите значение силы тока I1. Внутренним сопротивлением источника тока пренебречь.
Алгоритм решения
1.Установить, какими физическими законами можно описать эксперимент.
2.Описать, что происходит до замыкания ключа.
3.Определить, что произойдет после замыкания ключа.
4.Вычислить силу тока в катушке.
Решение
На рисунке 1 изображена схема, в которой катушка индуктивности подключена последовательно к двум параллельно соединенным резистором и источнику тока. Амперметр тоже соединен с катушкой последовательно, следовательно, он определяет силу тока, проходящую через нее.
Для описания процесса можно подходит закон Ома для полной цепи и формула ЭДС самоиндукции, которая будет возникать при изменении силы тока в цепи:
IRобщ=ε+εis
εis=−LΔIΔt
До замыкания ключа общее сопротивление цепи равно сопротивлению одного резистора — R. Так как ток в этом случае постоянный, ЭДС самоиндукции отсутствует. Тогда закон Ома принимает вид:
I0=εR
Когда ключ замыкается, сопротивление в цепи уменьшается вдвое, так как подключается второй резистор:
1Rобщ=1R+1R=2R
Rобщ=0,5R
Изменение сопротивления в цепи вызывает изменение силы тока. В результате возникает ЭДС самоиндукции. Она препятствует изменению силы тока через катушку в соответствии с правилом Ленца. Поэтому сила тока через катушку при замыкании ключа не претерпевает скачка.
Постепенно ЭДС самоиндукции уменьшается до нуля, а сила тока через катушку плавно возрастает до значения:
I1=ε0,5R=2I0
На рисунке 2 начальная сила тока равна 3 А. Следовательно:
I1=3·2=6 (А)
Ответ: 6
pазбирался: Алиса Никитина | обсудить разбор
Задание EF17724
В электрической цепи, показанной на рисунке, ЭДС и внутреннее сопротивление источника тока соответственно равны 12 В и 1 Ом, ёмкость конденсатора 2 мФ, индуктивность катушки 36 мГн и сопротивление лампы 5 Ом. В начальный момент времени ключ К замкнут. Какая энергия выделится в лампе после размыкания ключа? Сопротивлением катушки и проводов пренебречь. Ответ записать в мДж.
Алгоритм решения
1.Записать исходные данные и перевести единицы измерения в СИ.
2.Установить величину электромагнитного поля катушки и электрического поля конденсатора.
3.Выполнить решение задачи в общем виде.
4.Подставить неизвестные данные и вычислить искомую величину.
Решение
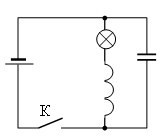
Запишем исходные данные:
• ЭДС источника тока: ε = 12 В.
• Сопротивление источника тока: r = 1 Ом.
• Емкость конденсатора: C = 2 мФ.
• Индуктивность катушки: L = 36 мГн.
• Сопротивление лампы: R = 5 Ом.
2 мФ = 2∙10–3 Ф
36 мГн = 36∙10–3 Гн
Пока ключ замкнут, через катушку L течёт ток определяемый внутренним сопротивлением источника и сопротивлением лампочки. Его можно вычислить, используя закон Ома для полной цепи:
I=εR+r
При этом конденсатор будет заряжен до напряжения U, которое определяется законом Ома для участка цепи:
U=IR
Подставив в это выражение закон Ома для полной цепи, получим:
U=εRR+r
Энергия электрического поля в конденсаторе определяется формулой:
Wкон=CU22=C2(εRR+r)2
Энергия электромагнитного поля в катушке определяется формулой:
Wкат=LI22=L2(εR+r)2
После размыкания ключа начинаются затухающие электромагнитные колебания, и вся энергия, запасённая в конденсаторе и катушке, выделится на лампе:
E=Wкон+Wкат=C2(εRR+r)2+L2(εR+r)2
Ответ: 172
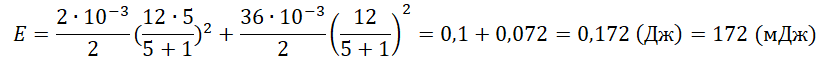
pазбирался: Алиса Никитина | обсудить разбор
Задание EF18478
Катушка индуктивности подключена к источнику тока с пренебрежимо малым внутренним сопротивлением через резистор Ом (см. рисунок). В момент ключ К замыкают. Значения силы тока в цепи, измеренные в последовательные моменты времени
с точностью 0,01 А, представлены в таблице.
Выберите два верных утверждения о процессах, происходящих в цепи.
Ответ:
- Напряжение на резисторе в момент времени t= 1,0 c равно 1,9 В.
- Энергия катушки максимальна в момент времени t= 0 c.
- ЭДС источника тока равна 18 В.
- Напряжение на катушке максимально в момент времени t= 6,0 c.
- Модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В.
Алгоритм решения
1.Проверить истинность каждого утверждения.
2.Выбрать 2 верных утверждения.
Решение
Согласно утверждению 1, напряжение на резисторе в момент времени t = 1,0 c равно 1,9 В. Так как сила тока еще не установилась, а сопротивление источника тока пренебрежимо мало, вычислить напряжение на резисторе можно с помощью закона Ома для полной цепи:
I=ε−εisR
U=ε−εis=IR=0,19·60=11,4 (В)
Следовательно, утверждение 1 — неверно.
Согласно утверждению 2, энергия катушки максимальна в момент времени t = 0 c. Энергия катушки определяется формулой:
Wкат=LI22
Так как сила тока в начальный момент времени равна нулю, то энергия катушки в это время тоже нулевая.
Следовательно, утверждение 2 — неверно.
Согласно утверждению 3, ЭДС источника тока равна 18 В. Вычислить ЭДС источника тока можно, используя закон Ома для полной цепи в момент, когда сила тока в цепи достигнет максимального значения. В этом случае ЭДС самоиндукции будет равна 0. Тогда:
I=εR
ε=IR=0,3·60=18 (В).
Это действительно так. Следовательно, утверждение 3 — верно.
Согласно утверждению 4, напряжение на катушке максимально в момент времени t = 6,0 c. Напряжение на катушке равно разности напряжения ЭДС источника тока и напряжения на резисторе (так как они соединены последовательно):
U=ε−IR
Так как значение силы тока в момент времени t = 6,0 с максимально, то напряжение на катушке. Следовательно, утверждение 4 — неверно.
Согласно утверждению 5, модуль ЭДС самоиндукции катушки в момент времени t = 2,0 с равен 2,4В. Проверяя истинность утверждения 3, мы выяснили, что ЭДС источника тока равна 18 В. Следовательно, ЭДС самоиндукции равна:
εis=ε−IR
Для вычислений используем значения из таблицы для момента времени t = 2,0 с:
εis=18−0,26·60=2,4 (В)
Следовательно, утверждение 5 — верно.
Ответ: 35
pазбирался: Алиса Никитина | обсудить разбор
Алиса Никитина | Просмотров: 4.2k
Явление электромагнитной индукции очень часто наблюдается в электротехнике. Взаимное влияние электрических и магнитных полей иногда приводит к интересным результатам. Самоиндукция – частный случай электромагнитной индукции.
Общеизвестно, что причиной порождения электрического тока является переменное магнитное поле. Именно этот принцип реализован в конструкциях современных генераторов. Природа самоиндукции также связана с электромагнетизмом, но это явление проявляется она по-другому.
Определение
Рассмотрим схему катушки, по обмоткам которой протекает электрический ток (рис. 1). Так как вокруг проводника, который находится под током, всегда существует связанное с ним магнитное поле, то силовые линии этого поля пронизывают плоскости витков. В результате такого взаимодействия соленоиды образуют собственное магнитное поле, магнитные линии которого замыкаются за его пределами.
Частным случаем катушки является замкнутый контур (один виток). В нём, как и в катушке, образуется собственное магнитное поле (см. рис. 2). Если ток постоянный, то в контуре никаких изменений не происходит.
Но при изменении параметров, например, в результате размыкания цепи, изменяется магнитный поток, создаваемый электрическим полем, что является причиной возникновения ЭДС индукции. Аналогичное изменение произойдёт и в случае замыкания цепи.
Изменение параметров магнитного поля вызывает появление вихревого электрического поля, что в свою очередь приводит к возбуждению индуктивной электродвижущей силы. Возникновение ЭДС индукции, в результате изменения ток в замкнутом контуре, называется самоиндукцией.
Магнитный поток, ограниченный поверхностью контура, меняется прямо пропорционально изменению тока, циркулирующего в нём.
Направление вектора ЭДС самоиндукции не совпадает с направлением тока в период его возрастания (при замыкании цепи), но он сонаправлен с ним в период убывания (разъединения цепи). Такое действие проявляется в замедлении появления тока в соленоиде при замыкания цепи, или в его задержке на какое-то время после разрыва цепи.
Описанное явление можно наблюдать на опыте с лампочками, одна из которых подключена последовательно с индуктивностью (см. рис. 3).
Как видно на рисунке слева, ток от источника питания, проходящий через лампочку 2, при замыкании контактов встретит сопротивление вихревых токов, поскольку они противоположно направлены. Поэтому зажигание этой лампочки произойдёт с задержкой.
На время включения лампочки 1 вихревые токи повлияют, но сила тока в её цепи уменьшится после зажигания лампы 2. При отключении цепи от источника питания произойдёт обратный процесс: лампочка в цепи индуктивности некоторое время будет медленно угасать, а вторая лампа потухнет сразу после разъединения контактов.
График на рисунке 4 красноречиво объясняет эффект задержки.
Обратите внимание на нелинейность изменения силы тока по времени.
Аналогичные процессы происходят в цепи, состоящей из одной катушки. На рисунке 5 изображена такая схема и график изменения силы тока.
Остаётся добавить, что скорость изменение величины ЭДС зависит от количества витков соленоида. Чем больше витков, тем больше влияние вихревых токов, на параметры цепи.
В случае с переменным током амплитуда ЭДС самоиндукции пропорциональна амплитуде синусоиды питания, её частоте и индуктивности катушки.
Синусоидальный ток, проходя через катушку индуктивности, сдвигается по фазе на величину π/2. Именно этот сдвиг является причиной отставания собственного тока катушки от тока, вырабатываемого источником питания.
Формулы
Собственный магнитный поток контура (Ф) связан прямо пропорциональной зависимостью с индуктивностью (L) этого контура и величиной тока в нём (i). Данная зависимость выражается формулой: Ф = L×i. Коэффициент пропорциональности L принято называть коэффициентом самоиндукции или же просто индуктивностью контура.
При этом индуктивность контура пребывает в зависимости от его геометрии, площади плоскости ограниченной витком и магнитной проницаемости окружающей среды. Но этот коэффициент не зависит от силы тока в контуре. Если же форма, линейные размеры и магнитная проницаемость не изменяются, то для определения величины индуктивной ЭДС применяется формула:
где Eсамоинд. – ЭДС самоиндукции, Δi – изменение силы тока за время Δt.
Индуктивность
Выше мы отметили, что индуктивность контура зависит от его геометрии и размеров, а также от магнитной проницаемости среды. Если речь идёт о катушке, то эти утверждения справедливы и для неё. На индуктивность катушки влияет её диаметр и количество витков. Индуктивность существенно повышается, если в катушку добавить ферромагнитный сердечник.
Магнитные поля отдельных витков катушки складываются. Если витков достаточно много, то ток, протекающий через катушку, образует вокруг неё сильное магнитное поле, реагирующее на изменения электрического поля. Индуктивность является той величиной, которая характеризует то, насколько сильно проводник, из которого состоят витки, противодействует электрическому току.
Чем больше индуктивность катушки и чем выше скорость прерывания её цепи, тем больший всплеск ЭДС произойдёт в цепи. При этом полярность вихревых токов на выводах катушки противоположна направлению тока источника питания.
Индуктивность (то есть коэффициент пропорциональности) является важной характеристикой катушек, дросселей и других контурных элементов. Этот параметр можно сравнить с ёмкостью конденсаторов. Тем более что действие катушки индуктивности и конденсатора в электрических цепях очень похожи. RL и RC цепочки часто используют для сглаживания всплесков напряжений в различных фильтрах.
Единицей измерения индуктивности в международной системе СИ является генри. Величина размеров в 1 Гн – это такая индуктивность, при которой ЭДС составляет 1 В, при скорости изменения тока на 1 А за секунду.
Индуктивность определяет количество энергии, выделяющейся в результате действия собственного магнитного поля при самоиндукции. Эту энергию легко рассчитать по формуле: Wм = LI2/2.
Собственная энергия катушки численно равна работе, которую необходимо выполнить источником питания при преодолении ЭДС самоиндукции.
Важно знать, что в результате резкого разрыва цепи с большой индуктивностью, энергия высвобождается в виде искры или даже с образованием дугового разряда.
Примеры использования на практике
Явление самоиндукции нашло широкое практическое применение. Автолюбители прекрасно знают, что такое катушка зажигания. Без неё карбюраторный двигатель не запустится.
Работает этот важный узел следующим образом:
- На катушку с большой индуктивностью подаётся бортовое напряжение 12 В.
- Электрическая цепь резко обрывается специальным прерывателем.
- Накопленная энергия самоиндукции поступает по высоковольтным проводам на свечу и образует на её электродах мощную искру.
- Искровой разряд зажигает топливную смесь, приводя в движение поршень.
В современных автомобилях разрыв цепи выполняет электроника, но суть от этого не меняется – для образования искры по-прежнему используется энергия самоиндукции.
Мы уже упоминали о сетевых фильтрах, в которых используется явление самоиндукции. RL цепочка реагирует на любое изменение параметров. При его возрастании она задерживает во времени пиковые скачки и заполняет собственными вихревыми токами провалы. Таким образом, происходит сглаживание напряжения в электрически цепях.
В блоках питания электронной аппаратуры таким же способом убирают:
- шумы:
- пульсации;
- нежелательные частоты.
Самоиндукция дросселей используется в люминесцентных лампах для розжига электродов. После срабатывания стартера происходит разрыв контактов, в результате чего в дросселе наводится ЭДС самоиндукции. Энергия дросселя разжигает дугу на электродах, и люминесцентная лампа начинает светиться.
Перечисленные примеры демонстрируют полезное применение самоиндукции. Однако, как это всегда бывает, индуктивная ЭДС может наносить вред. При разъединении контактов выключателей, нагрузкой которых являются цепи с большой индуктивностью, возможны дуговые разряды. Они разрушают контакты, замедляют время защиты и т.п. С целью снижения риска от негативных влияний самоиндукции автоматические выключатели оборудуют дугогасительными камерами.
В таких случаях приходится принимать меры для нейтрализации энергии ЭДС самоиндукции. Ещё большая потребность в рассеянии энергии самоиндукции возникает в полупроводниковых ключах, чувствительных к пробоям.
В промышленности и энергетике самоиндукция является серьёзной проблемой. При отключении нагруженных линий ЭДС самоиндукции может достигать опасных для жизни величин. Это требует дополнительных затрат на принятие мер предосторожности. В частности, необходимо устанавливать на линиях устройства, препятствующие молниеносному размыканию цепи.
Видео в помощь
Тема : Самоиндукция. Эдс самоиндукции. Индуктивность. Энергия магнитного поля.
-
Самоиндукция. Эдс самоиндукции.
При изменении
силы тока в катушке происходит изменение
магнитного потока, создаваемого этим
током. Изменение магнитного потока,
пронизывающего катушку, вызывает
появление ЭДС индукции в катушке,
называемой ЭДС самоиндукции. Под
действием ЭДС самоиндукции в катушке
появляется ток самоиндукции, который
противодействует изменению основного
тока в цепи, вызывающего это явление
называемое самоиндукцией.
Явление
возникновения ЭДС в электрической цепи
в результате изменения силы тока в этой
же цепи называется самоиндукцией.
Согласно правилу Ленца ЭДС самоиндукции
противодействует изменению тока в цепи,
вследствие чего величина силы тока в
цепи не может изменяться мгновенно.
ЭДС самоиндукции
в цепи прямопророрциональна скорости
изменения силы тока в этой цепи.
.
-
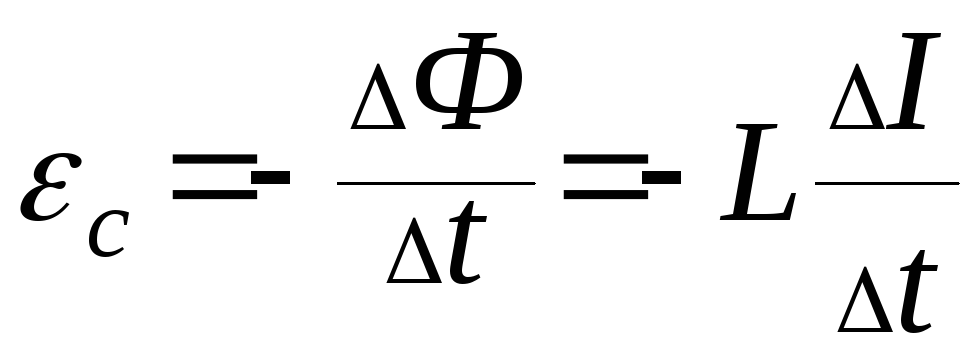
Индуктивность соленоида (катушки).
Магнитный поток
внутри проводящего контура зависит от
силы тока, проходящего по контуру, формы,
размеров контура и магнитных свойств
окружающей среды.
Величина,
влияющая на магнитный поток, создаваемый
током в проводящем контуре, называется
индуктивностью контура и обозначается
L.
При этом справедливо
соотношение
– магнитный поток самоиндукции контура.
За единицу
индуктивности контура в СИ принимается
Генри (Гн) – индуктивность такого
контура, который создает магнитный
поток в 1Вб при силе тока в нем 1А.
Согласно закону
электромагнитной индукции
.
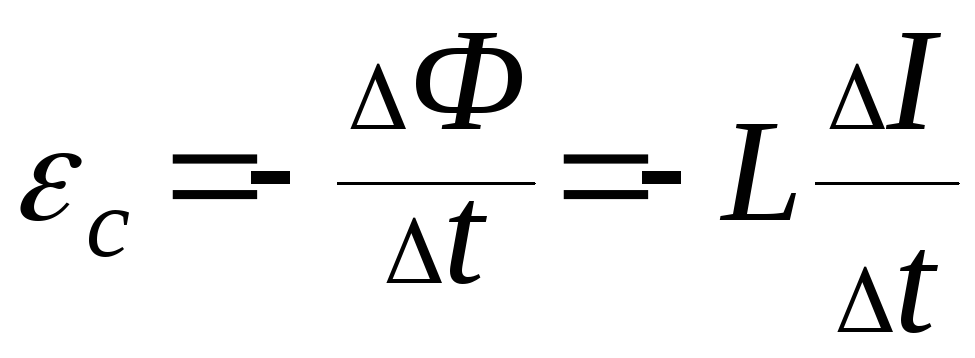
Формула для
определения индуктивности катушки
,
где n
– число витков в катушке,
– магнитная постоянная,
– магнитная проницаемость среды, в
которой находится катушка, S
– площадь витка,
l
– длина катушки.
Индуктивность
контура является мерой его «инертности»
по отношению к изменению силы тока в
контуре (то есть L
является аналогом инертной массы в
механике).
-
Энергия магнитного поля тока.
Пользуясь формулой
для вычисления работы по перемещению
проводника с током в магнитном поле
и формулой изменения магнитного потока
при изменении тока в контуре
,
получим значение энергии магнитного
тока
.
Для создания тока
в контуре необходимо совершить работу
по преодолению ЭДС самоиндукции, то
есть затратить некоторую энергию. Эта
энергия «запасается» в магнитном поле
контура с током. Она выделяется после
размыкания цепи.
-
Энергия электромагнитного поля.
Если в формулу
энергии магнитного поля подставим
значение индуктивности катушки
и значение
силы тока из формулы индукции магнитного
поля
,
то получим
.
Появление
электромагнитных полей зависит от
выбора системы отсчета, поэтому в одних
случаях проявляются электрические
свойства, в других – магнитные, а в
третьих – электромагнитные свойства
поля.
Электромагнитное
поле обладает энергией, которая равна
сумме энергий электрического и магнитного
полей
-
Общая характеристика Солнца.
Солнце –это
раскаленный плазменный шар.
m=2
кг,
r=
тыс.км,
температура
фотосферы 5770К, в центре – около15млнК,
ускорение свободного падения q=274
,
постоянный объем Солнца обусловлен
равновесным состоянием сил гравитации
и сил давления газов.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Самоиндукция. Индуктивность. Энергия магнитного поля тока
- Подробности
- Обновлено 13.08.2018 23:14
- Просмотров: 791
Самоиндукция
Каждый проводник, по которому протекает эл.ток, находится в собственном магнитном поле.
При изменении силы тока в проводнике меняется м.поле, т.е. изменяется магнитный поток, создаваемый этим током. Изменение магнитного потока ведет в возникновению вихревого эл.поля и в цепи появляется ЭДС индукции.
Это явление называется самоиндукцией.
Самоиндукция – явление возникновения ЭДС индукции в эл.цепи в результате изменения силы тока.
Возникающая при этом ЭДС называется ЭДС самоиндукции
Проявление явления самоиндукции
Замыкание цепи
При замыкании в эл.цепи нарастает ток, что вызывает в катушке увеличение магнитного потока, возникает вихревое эл.поле, направленное против тока, т.е. в катушке возникает ЭДС самоиндукции, препятствующая нарастанию тока в цепи (вихревое поле тормозит электроны).
В результате Л1 загорается позже, чем Л2.
Размыкание цепи
При размыкании эл.цепи ток убывает, возникает уменьшение м.потока в катушке, возникает вихревое эл.поле, направленное как ток (стремящееся сохранить прежнюю силу тока) , т.е. в катушке возникает ЭДС самоиндукции, поддерживающая ток в цепи.
В результате Л при выключении ярко вспыхивает.
Вывод:
в электротехнике явление самоиндукции проявляется при замыкании цепи (электрический ток нарастает постепенно) и при размыкании цепи (электрический ток пропадает не сразу).
ИНДУКТИВНОСТЬ
От чего зависит ЭДС самоиндукции?
Электрический ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф ~ B), индукция пропорциональна силе тока в проводнике
(B ~ I), следовательно магнитный поток пропорционален силе тока (Ф ~ I).
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника (размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность – физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф – магнитный поток через контур, I – сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от:
числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды ( возможен сердечник).
ЭДС САМОИНДУКЦИИ
ЭДС самоиндукции препятствует нарастанию силы тока при включении цепи и убыванию силы тока при размыкании цепи.
ЭНЕРГИЯ МАГНИТНОГО ПОЛЯ ТОКА
Вокруг проводника с током существует магнитное поле, которое обладает энергией.
Откуда она берется? Источник тока, включенный в эл.цепь, обладает запасом энергии.
В момент замыкания эл.цепи источник тока расходует часть своей энергии на преодоление действия возникающей ЭДС самоиндукции. Эта часть энергии, называемая собственной энергией тока, и идет на образование магнитного поля.
Энергия магнитного поля равна собственной энергии тока.
Собственная энергия тока численно равна работе, которую должен совершить источник тока для преодоления ЭДС самоиндукции, чтобы создать ток в цепи.
Энергия магнитного поля, созданного током, прямо пропорциональна квадрату силы тока.
Куда пропадает энергия магнитного поля после прекращения тока? – выделяется ( при размыкании цепи с достаточно большой силой тока возможно возникновение искры или дуги)
ВОПРОСЫ К ПРОВЕРОЧНОЙ РАБОТЕ
по теме “Электромагнитная индукция”
1. Перечислить 6 способов получения индукционного тока.
2. Явление электромагнитной индукции (определение).
3. Правило Ленца.
4. Магнитный поток ( определение, чертеж, формула, входящие величины, их ед. измерения).
5. Закон электромагнитной индукции (определение, формула).
6. Свойства вихревого электрического поля.
7. ЭДС индукции проводника, движущегося в однородном магнитном поле ( причина появления, чертеж, формула, входящие величины, их ед. измерения).
8. Самоиндукция (кратко проявление в электротехнике, определение).
9. ЭДС самоиндукции (ее действие и формула).
10. Индуктивность (определение, формулы, ед. измерения).
11. Энергия магнитного поля тока (формула, откуда появляется энергия м. поля тока, куда пропадает при прекращении тока).
Электромагнитное поле – Класс!ная физика
Взаимодействие токов. Магнитное поле. Вектор магнитной индукции. Сила Ампера —
Действие магнитного поля на движущийся заряд.Магнитные свойства вещества —
Явление электромагнитной индукции. Магнитный поток. Направление индукционного тока. Правило Ленца —
ЭДС электромагнитной индукции. Вихревое электрическое поле —
ЭДС индукции в движущихся проводниках
—
Самоиндукция. Индуктивность. Энергия магнитного поля. Вопросы к пр/работе
«Искусство
экспериментатора состоит в том,
чтобы
уметь задавать природе
вопросы
и понимать её ответы».
Майкл
Фарадей
Задача
1.
В результате убывания тока в контуре от 8 А до 2 А за 12 мс, в контуре возникла
ЭДС самоиндукции 25 мВ. Найдите индуктивность данного контура.
|
ДАНО: |
СИ |
РЕШЕНИЕ ЭДС самоиндукции Изменение силы тока равно Выразим индуктивность из |
|
|
Ответ:
50 мкГн.
Задача
2.
Через площадь контура проходит магнитный поток 2 мВб, создаваемый протекающим
по контуру током силой 5 А. В течение 50 мс ток равномерно уменьшается до 3 А.
Найдите ЭДС самоиндукции.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем закон самоиндукции Индуктивность – это В задаче указан магнитный С учетом последних формул ЭДС самоиндукции равно |
|
|
Ответ:
16 мВ.
Задача
3.
К источнику тока с ЭДС 12 В и внутренним сопротивлением 1 Ом подключен реостат,
сопротивление которого за 0,5 с равномерно увеличивают от 10 Ом до 15 Ом. При
этом в реостате возникает ЭДС самоиндукции 0,03 В. Найдите индуктивность
реостата.
|
ДАНО: |
РЕШЕНИЕ Запишем закон самоиндукции Запишем закон Ома для полной цепи Найдём выражения для Тогда изменение тока равно Выразим индуктивность из закона самоиндукции |
|
|
Ответ:
44 мГн.
Задача
4.
В магнитное поле с индукцией 200 мТл помещена рамка, площадь которой равна
40 см2. Изначально магнитный поток, пронизывающий рамку равен
нулю. После этого рамку поворачивают на 30º. Найдите ЭДС самоиндукции,
которая возникнет в рамке, когда её перестанут вращать, предполагая, что время
остановки занимает 1 мс.
|
ДАНО: |
СИ |
РЕШЕНИЕ Магнитный поток определяется по формуле Если Рамку поворачивают на 30º. Запишем закон самоиндукции Пока рамку поворачивали, в Тогда индуктивность равна ЭДС самоиндукции Второй способ решения Магнитный поток рассчитывается по формуле Закон электромагнитной индукции ЭДС самоиндукции Изменение тока равно всему Магнитный поток определяется по выражению Т.к. |
|
|
Ответ:
0,4 В.
Задача
5.
На рисунке изображён соленоид, радиус которого равен 10 см, и он содержит 500
витков проволоки. Индукция магнитного поля соленоида равна 600 мкТл. Найдите
ЭДС самоиндукции, которая возникнет в соленоиде при исчезновении тока в нём за
0,1 с.
|
ДАНО: |
СИ |
РЕШЕНИЕ Запишем закон самоиндукции Изменение тока равно тому Магнитное поле соленоида Индуктивность соленоида определяется по формуле С учётом последних формул закон самоиндукции примет вид Объём цилиндра определяется по формуле Тогда ЭДС самоиндукции |
|
|
Ответ:
47 В.
