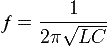Как найти индуктивность колебательного контура если

Расчёт индуктивности колебательного контура

Расчёт индуктивности колебательного контура  (L,C)

Колебательный контур —  простейшая система, в которой могут происходить свободные электромагнитные колебания.

Колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

Формула расчета индуктивности колебательного контура

•   L = 1/(4π²F²C)

Где:

•     F – Резонансная частота, Гц)
•     L – Индуктивность, (Гн)
•     C – Ёмкость, (Ф)

Онлайн-калькулятор для расчёта индуктивности колебательного контура.

Индуктивность для колебательного контура LC

Ёмкость:

Частота :

Индуктивность:

Поделиться в соц сетях:

Популярные сообщения из этого блога

Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:

Ф (1)

• где

Рис. 1. Соленоид

В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:

(1)

• где

Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда . Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда  и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.

Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:

• при параллельном подключении:

(2)

В случае двух элементов, соединённых параллельно:

(3)

• при последовательном подключении:

(4)

Федеральное
агентство по образованию

Государственное
образовательное учреждение

высшего
профессионального образования

САМАРСКИЙ
ГОСУДАРСТВЕННЫЙ

АЭРОКОСМИЧЕСКИЙ
УНИВЕРСИТЕТ

имени академика
С.П. Королёва ( СГАУ )

Факультет инженеров
воздушного транспорта

Кафедра электронных
систем и устройств

Расчет катушки индуктивности колебательного контура и обоснование выбора материалов.

Выполнил
студентка: Воробьёва А.Ю.

Группа
№ 3203

Вариант
№ 33

Проверил
преподаватель:

Макарычев
Ю.И.

Самара
2011

Содержание

1 Задание для расчета	3
2 Расчет	3
2.1 Нахождение индуктивности Lк	3
2.2 Выбор материала каркаса	4
2.3 Выбор размеров каркаса	4
2.4 Расчет индуктивности катушки с учетом сердечника.	5
2.5 Определение числа витков	6
2.6 Определение оптимального диаметра провода	7
2.7 Учет влияния экрана	9
2.8 Расчет собственной емкости катушки.	10
2.9 Расчет добротности	11
3 Расчет ТКИ и ТКЧ	12
4 Выбор конденсатора контура	13
5 Итог	15
Список используемой литературы	16

1 Задание.

Рассчитать индуктивность колебательного
контура на резонансной частоте

.При
условии, что емкость конденсатора

.
Тип и материалы сердечников,

,

и другие необходимые данные для расчета
приведены

Материал экрана: алюминий.

Тип и материал сердечника: СЦР-1,Р-20.

Выбрать материал и размеры каркаса, тип
намотки. Определить число витков и
оптимальный диаметр провода. Вычислить
собственную емкость, добротность,
температурный коэффициент индуктивности
и температурный коэффициент частоты.

Рисунок 1.Колебательный контур.

где С_к – емкость контура;

L_к – индуктивность
контура.

2 Расчет

2.1 Нахождение индуктивности контура.

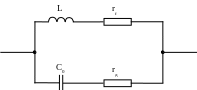
Рисунок 2. Схема замещения катушки
идеальными элементами.

где L – идеальная
индуктивность катушки;

С₀ – собственная емкость
катушки;

r_f
– сопротивление обмотки катушки;

r_д – сопротивление
диэлектрика каркаса за счет поляризации.

Определим индуктивность исходя из
формулы

определим L.

,

2.2 Выбор материала каркаса.

Каркас катушки в значительной степени
определяет ее стоимость и
электрические параметры.

Каркас должен быть
удобным для намотки и крепления в
приборе,
обеспечивать устройство (распайку)
выводов обмотки и надежную фиксацию
положения построечного элемента.
Материал каркаса должен
допускать применение прогрессивных
технологических методов
изготовления, быть дешевым, механически
прочным, вносить малые потери,
обладать необходимой теплостойкостью,
малой влагостойкостью
и небольшим коэффициентом линейного
расширения и, в
ряде случаев, малым значением температурного
коэффициента диэлектрической
проницаемости.

В достаточной степени
этим требованиям отвечают каркасы из
полистирола, фенопластов, пресс-материалов
типов АГ-4С, ДСВ-2Р-2М и им подобных. На
пониженных частотах может оказаться
целесообразным
применение более дешевых каркасов из
бакелизированных
трубок.

Для каркасов катушек
с высокой стабильностью применяют
радиокерамику
типа В, радиофарфор, ультрафарфор и
высокочастотный
стеатитит.

Исходя из заданных параметров наиболее
подходящим материалом является

высокочастотный стеатитит.

2.3 Выбор размеров каркаса.

Прежде чем
приступить к дальнейшим вычислениям,
для удобства, приведем чертеж катушки:

Рисунок 3. Чертеж катушки индуктивности.

где l_c
– длина сердечника;

l_к – длина намотки;

D_c –
диаметр сердечника;

D_к – диаметр катушки;

d – диаметр провода без
изоляции.

По сводным таблицам для СЦР – 1 можно
найти D_c=0,6см,
l_c=0,9см.

Для цилиндрических сердечников D_k=0,9см
и предварительно возьмем l_к=0,9см.

2.4 Расчет индуктивности катушки с учетом
сердечника.

где

–
необходимая величина расчетной
индуктивности;

–
действующая магнитная проницаемость
сердечника.

где

–
начальная магнитная проницаемость
материала сердечника;

– коэффициент использования магнитных
свойств;

-поправочный
коэффициент.

определяем по графику

=f(l_k/
D_c),

определяем по графику

=f(l_c/
D_c)

(l_k/
D_c)=0,9/0,6=1,5;

=0,28.

(l_c/
D_c)=0,9/0,6=1,5;

=0,9.

определяем по таблице, исходя из того,
что задана марка магнитного материала
Р-20.

=10.

Таким образом

2.5 Определение числа витков и типа
намотки.

Применяемые виды
намотки можно разделить на однослойные
и многослойные.

При однослойной
намотке витки
располагаются на цилиндрической
поверхности каркаса в один слой. При
плотном расположении
витков, разделяемых лишь изоляцией
провода, получается
сплошная однослойная намотка при
расположении витков на некотором
расстоянии друг от друга — намотка с
шагом.

Однослойные катушки
с шагом отличаются высокой добротностью
(150 -400) и
стабильностью; они в основном применяются
в контурах KB
и УКВ.

Для повышения
точности намотки провода применяются
нарезные каркасы,
т. е. каркасы, на поверхности которых
сделана неглубокая (0,2 — 0,3d)
спиральная канавка. Однако погружение
провода в диэлектрик
каркаса несколько понижает добротность
и стабильность катушки.

Для высокостабильных
катушек применяются специальные способы
изготовления намоток – тугая, горячая
и осажденная или нанесенная
намотки.

Катушки без каркаса
могут быть практически выполнены при
числе витков
не более трех. Они отличаются несколько
более высокой добротностью,
но, имеют малую механическую жесткость
и пониженную
стабильность.

Для катушек
индуктивностью выше 15—20
мкГн применяют
сплошную
однослойную намотку. Целесообразность
перехода на сплошную намотку определяется
диаметром катушки: чем больше диаметр
катушки, тем большая индуктивность
может быть получена при
применении намотки с шагом.

Катушки со сплошной
намоткой также отличаются высокой
добротностью (150—250) и стабильностью и
широко используются в контурах
для коротких, промежуточных и средних
волн, если требуется
индуктивность не выше 200—500 мкГн.

Для изготовления
катушек с индуктивностью выше 200—500
мкГн применяют
многослойные намотки.

Целесообразность
перехода на многослойную намотку
определяется
диаметром катушки. Чем больше диаметр
катушки, тем при
большей индуктивности следует переходить
на многослойную
намотку.

Многослойные намотки
могут быть разделены на простые и
сложные.

Широкое применение
имеют сложные многослойные намотки,
например
универсальные.

Катушки, предназначенные
для работы в диапазоне частот до 500 кГц,
имеют многослойную обмотку. Применяют
рядовую многослойную
или универсальную намотки, а также
намотку «внавал».
Катушки для частот выше 1—2 МГц имеют
однослойную намотку.

Для намотки катушек
применяют провода в эмалевой изоляции
марок ПЭЛ, ПЭ,
ПЭВ, комбинированной изоляции марок
ПШО, ПШД, ПЭЛШО,
ПЭШД, а также литцендрат ЛЭШО И ЛЭШД.

Для многослойных
катушек с универсальной намоткой
применяют обычно
провода с волокнистой изоляцией, так
как волок­нистая
изоляция обеспечивает большее сцепление
витков.

Для катушек с шагом
применяется неизолированный провод
МГМ, покрытый
слоем серебра.

В данной работе целесообразно применить
однослойную намотку из ПЭЛ.

Для определения числа витков однослойной
катушки воспользуемся формулой:

Значение L₀ определяем
по графику, L₀=f(l_k/
D_к)

(l_k/
D_к)=1; L₀
=7

Откуда

2.6 Определение оптимального диаметра
провода.

Между сопротивлением провода катушки
и его диаметром существует сложная
зависимость, так как при этом изменяется
проявление поверхностного эффекта и
эффекта близости.

Рассмотрим вопрос о влиянии диаметра
провода на сопротивление катушки. В
случае прямолинейного провода увеличение
диаметра вызывает увеличение его
периметра, а, следовательно, уменьшение
сопротивления току высокой частоты.
Зависимость сопротивления отрезка
прямолинейного провода от диаметра при
некоторой частоте выражается кривой L
на рис. 4 (кривая I представляет
собой зависимость сопротивления току
высокой частоты от диаметра). При
свертывании провода в спираль возникает
эффект близости, который проявляется
тем сильнее, чем больше диаметр провода.
Увеличение сопротивления за счет эффекта
близости примерно пропорционально
диаметру провода и изображается прямой
II. Сложив величины,
характеризуемые кривыми I
и II, получим изменение
полного активного сопротивления провода
катушки в зависимости от его диаметра;
эта зависимость выражается кривой III.
Ход кривой III показывает,
что при вполне определенном диаметре
провода сопротивление катушки имеет
минимальное значение. Можно показать,
что при этом сопротивление провода
катушки (с учетом поверхностного эффекта)
равно увеличению сопротивления за счет
эффекта близости.

Рис. 4

Оптимальный диаметр провода катушки
рассчитывают при помощи вспомогательного
коэффициента:

где

– вспомогательный параметр;

-поправочный
коэффициент.

D_к – диаметр катушки;

N –число витков намотки;

где f ₀ – резонансная
частота.

к=f(l/D)

к=4

,т.к.

,
то

;

0,065см,
в целях экономии меди возьмем d_опт
= 0,69мм

Используя эмалевую изоляцию провода
типа ПЭЛ принимаем диаметр провода
равным 0,35

Проведем проверку подобранного диаметра
провода:

,
следовательно, выбор параметров каркаса
сделан правильно.

2.7 Учет влияния экрана.

Для устранения
паразитных связей, обусловленных внешним
электромагнитным
полем катушки, и для устранения влияния
внешних полей
катушка экранируется, то есть располагается
внутри замкнутого,
металлического заземленного экрана.

Экранирующее действие
характеризуется отношением напряженности
внешнего поля катушки при наличии экрана
к напряженности
поля при его отсутствии. Для экрана
среднего качества,
выполненного, например, в виде алюминиевого
стакана, это отношение равно приблизительно
0,01 — 0,05, что бывает достаточно для
большинства практических случаев. Для
усиления экранирующего действия
применяются двойные и даже тройные
экраны.

Под влиянием экрана
изменяются основные электрические
параметры
катушки; уменьшается ее индуктивность,
а также увеличиваются
сопротивление и собственная емкость.
Добротность экранированной катушки
оказывается ниже добротности той же
катушки при отсутствии экрана. Изменение
параметров катушки зависит
от соотношения между ее размерами и
размерами экрана.

Для того чтобы индуктивность и добротность
падали не более чем на 10%:, рекомендуются
следующие соотношения м.д. диаметрами
экрана и катушки:[3]

;

где

– диаметр экрана.

Выберем диаметр экрана равным 2,3см,
высоту равную 1,8см;

При помещении катушки в экран ее
индуктивность и добротность уменьшаются.
Индуктивность экранированной катушки
составляет:

где

–
индуктивность неэкранированной катушки;

к – коэффициент связи м.д. экраном и
катушкой.

Для однослойных катушек:

где

– коэффициент зависящий от отношения
длины катушки к ее диаметру.

;

Определяем индуктивность экранированной
катушки:

Т.к

и высота между катушкой и экраном равна
высоте катушки, то потери вносимые
экраном в К.И. можно определить по
формуле:[3]

Где латуни

2.8 Расчет собственной емкости катушки.

В катушке, между
отдельными витками и между витками и
ближайшими
металлическими телами—экранами, шасси
прибора и т. п.,
всегда существует разность потенциалов,
которая создает электрическое
поле. Влияние этого поля подобно влиянию
некоторой емкости, включенной параллельно
катушке; эту емкость называют собственной
(или распределенной) емкостью катушки.
Ее величина зависит
от размеров катушки, конструкции обмотки,
близости расположения
витков со значительной разностью
потенциалов, удаленности
их от экранов, диэлектрической
проницаемости изоляции провода
и каркаса, а также ряда других конструктивных
факторов. Чем
больше диаметр катушки, чем ближе друг
к другу расположены витки со значительной
разностью потенциалов, чем выше
диэлек­трическая проницаемость
изоляции провода и материала каркаса,
тем больше
собственная емкость катушки индуктивности.

Наименьшей собственной
емкостью (1—2 пФ) обладают однослойные
катушки, намотанные с шагом. Многослойные
катушки обладают
большей емкостью,- величина которой
зависит от способа намотки.
Например, емкость катушек с простой
универсальной намоткой составляет 5 —
10 пФ, с перекрестной универсальной
намоткой 15 – 30
пФ.

Расчет собственной
емкости однослойных катушек удобнее
производить по
эмпирической формуле:

где

определяется
по графикам.

Тогда

.

2.9 Расчет добротности.

Добротность контура зависит не только
от его параметров, но также и от параметров
внешней цепи — внутреннего сопротивления
источника и сопротивления нагрузки.

Добротность контура определяют по
формуле:

Сопротивление току высокой частоты.

Для катушек, работающих на частотах
выше 10МГц, сопротивление

вычисляется
по формуле:

где d – диаметр провода
без изоляции;

N – число витков катушки;

D – диаметр катушки;

Ом

Потери вносимые сердечником.

Потери вносимые сердечником могут быть
найдены по следующей формуле:

Предположим, что катушка находится в
радиоприемнике, тогда Н=0, и тогда

Ом.

Потери в диэлектрике.

Диэлектрические
потери возникают в поле собственной
емкости катушки
через диэлектрик С_ол
и зависят от величины этой емкости,
качества tgδ
материала
каркаса и частоты. Потери в диэлектрике
обусловлены тем, что между соседними
витками катушки существует емкость,
имеющая две составляющих — емкость
через воздух С_ов
и емкость
через диэлектрик С_ол.

рис.5

Сопротивление, вносимое диэлектрическими
потерями, можно представить включенным
параллельно собственной емкости катушки.
Величина этого сопротивления равна:[3]

.

Пересчитывая это сопротивление на
последовательное, получаем:

Откуда

,
поэтому добротность контура равна:

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Колебательный контур LC

Колебательный контур — электрическая цепь, в которой могут возникать колебания с частотой, определяемой параметрами цепи.

Простейший колебательный контур состоит из конденсатора и катушки индуктивности, соединенных параллельно или последовательно.

– Конденсатор C – реактивный элемент. Обладает способностью накапливать и отдавать электрическую энергию.
– Катушка индуктивности L – реактивный элемент. Обладает способностью накапливать и отдавать магнитную энергию.

Рассмотрим, как возникают и поддерживаются свободные электрические колебания в параллельном контуре LC.

Основные свойства индуктивности

– Ток, протекающий в катушке индуктивности, создаёт магнитное поле с энергией .
– Изменение тока в катушке вызывает изменение магнитного потока в её витках, создавая в них ЭДС, препятствующую изменению тока и магнитного потока.

Природа электромагнитных колебаний в контуре

Период свободных колебаний контура LC можно описать следующим образом:

Если конденсатор ёмкостью C заряжен до напряжения U, потенциальная энергия его заряда составит.
Если параллельно заряженному конденсатору подключить катушку индуктивности L, в цепи пойдёт ток разряда конденсатора, создавая магнитное поле в катушке.

Внешний магнитный поток создаст ЭДС в направлении противоположном току в катушке, что будет препятствовать нарастанию тока в каждом витке, поэтому конденсатор разрядится не мгновенно, а через время t₁,
которое определяется индуктивностью катушки и ёмкостью конденсатора из расчёта t₁ = .
По истечении времени t₁, когда конденсатор разрядится до нуля, ток в катушке и магнитная энергия будут максимальны.
Накопленная катушкой магнитная энергия в этот момент составит.
В идеальном рассмотрении, при полном отсутствии потерь в контуре, E_C будет равна E_L.
Таким образом, электрическая энергия конденсатора перейдёт в магнитную энергию катушки.

Далее изменение (уменьшение от максимума) магнитного потока накопленной энергии катушки будет создавать в ней ЭДС,
которая продолжит ток в том же направлении и начнётся процесс заряда конденсатора индукционным током. Уменьшаясь от максимума до нуля в течении времени t₂ = t₁, он перезарядит конденсатор от нулевого до максимального отрицательного значения (-U).
Так магнитная энергия катушки перейдёт в электрическую энергию конденсатора.

Описанные интервалы t₁ и t₂ составят половину периода полного колебания в контуре.
Во второй половине процессы аналогичны, только конденсатор будет разряжаться от отрицательного значения, а ток и магнитный поток сменят направление.
Магнитная энергия вновь будет накапливаться в катушке в течении времени t₃, сменив полярность полюсов.

В течении заключительного этапа колебания (t₄),
накопленная магнитная энергия катушки зарядит конденсатор до первоначального значения U
(в случае отсутствия потерь) и процесс колебания повторится.

В реальности, при наличии потерь энергии на активном сопротивлении проводников,
фазовых и магнитных потерь, колебания будут затухающими по амплитуде.
Время t₁ + t₂ + t₃ + t₄ составит период колебаний .
Частота свободных колебаний контура ƒ = 1 / T

Частота свободных колебаний является частотой резонанса контура,
на которой реактивное сопротивление индуктивности X_L=2πfL равно реактивному сопротивлению ёмкости X_C=1/(2πfC).

---

Расчёт частоты резонанса LC-контура:

Предлагается простой онлайн-калькулятор для расчёта резонансной частоты колебательного контура.

Необходимо вписать значения и кликнуть мышкой в таблице.
При переключении множителей автоматически происходит пересчёт результата.

---

Похожие страницы с расчётами:

Рассчитать импеданс.

Рассчитать реактивное сопротивление.

Рассчитать реактивную мощность и компенсацию.

---