Как найти индуктивность на фазе

Переменный электрический ток:

До сих пор рассматривались электрические цепи, содержащие в различных сочетаниях резисторы, конденсаторы и катушки, с источником постоянного тока либо без него. Теперь рассмотрим подключение таких цепей к источнику переменного тока.

Пусть источник тока создает переменное гармоническое напряжение (рис. 194)

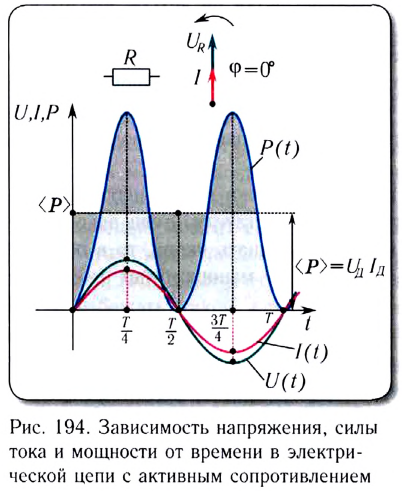
Согласно закону Ома сила тока на участке цепи, содержащем только резистор сопротивлением R, подключенный к этому источнику, изменяется со временем также по синусоидальному закону:

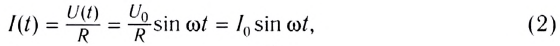
где 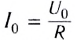— амплитудное значение силы тока в цепи.

Как видно, сила тока в такой цепи также меняется с течением времени по синусоидальному закону.

Величины 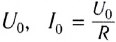  называются амплитудными значениями напряжения и силы тока. Значения напряжения U(t) и силы тока I(t), зависящие от времени, называют мгновенными.

Зная мгновенные значения U(t) и I(t), можно вычислить мгновенную мощность 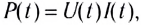которая, в отличие от цепей постоянного тока, изменяется с течением времени.

С учетом зависимости силы тока от времени в цепи перепишем выражение для мгновенной тепловой мощности на резисторе в виде

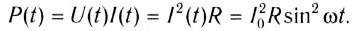
Поскольку мгновенная мощность меняется со временем, то использовать эту величину в качестве характеристики длительно протекающих процессов на практике крайне неудобно.

Перепишем формулу для мощности по-другому:

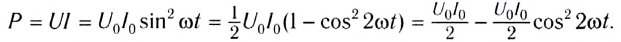
Первое слагаемое не зависит от времени. Второе слагаемое — переменная составляющая — функция косинуса двойного угла и ее среднее значение за период колебаний равно нулю (см. рис. 194).

Поэтому среднее значение мощности переменного электрического тока за длительный промежуток времени можно найти по формуле

Это выражение позволяет ввести действующие (эффективные) значения силы тока и напряжения, которые используются в качестве основных характеристик переменного тока.

Действующим (эффективным) значением силы переменного тока называется сила такого постоянного тока, который, проходя по цепи, выделяет в единицу времени такое же количество теплоты, что и данный переменный ток.
Поскольку для постоянного тока 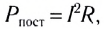то с учетом ранее полученного выражения для среднего значения мощности переменного тока действующее значение силы тока  

Аналогично можно ввести действующее значение и для напряжения

Таким образом, выражения для расчета мощности, потребляемой в цепях постоянного тока, остаются справедливыми и для переменного тока, если использовать в них действующие значения силы тока и напряжения:

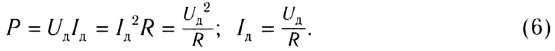
Необходимо отметить, что закон Ома для цепи переменного тока, содержащей только резистор сопротивлением R, выполняется как для амплитудных и действующих, так и для мгновенных значений напряжения и силы тока, вследствие того, что их колебания совпадают по фазе (см. рис. 194).
Таким образом, резисторы оказывают сопротивление как постоянному, так и переменному току, при этом в обоих случаях в них происходит превращение электрической энергии во внутреннюю. Вследствие этого сопротивление резисторов R получило название активного или омического сопротивления.

Катушка индуктивности в цепях переменного тока

Реальный соленоид (катушка индуктивности) обладает активным сопротивлением R и индуктивностью L. В цепях постоянного тока главную роль играет его сопротивление R, тогда как в цепях переменного тока — его индуктивность L.

Рассмотрим физические процессы, происходящие в идеальной катушке, у которой отсутствует активное сопротивление (R=0), при включении ее в цепь переменного тока.

В катушке индуктивностью L переменный ток 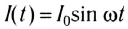вызывает появление ЭДС самоиндукции:
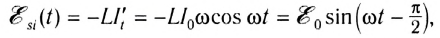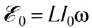где — амплитудное значение ЭДС самоиндукции (рис. 195).

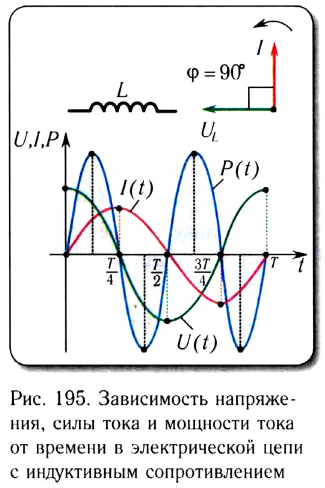
При возрастании силы тока ЭДС самоиндукции согласно правилу Ленца будет препятствовать его увеличению. Для идеальной катушки, активное сопротивление которой равно нулю (R=0), согласно закону Ома для полной цепи 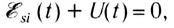где U(t) напряжение на концах катушки.

Следовательно, в любой момент времени внешнее напряжение на концах катушки равно по модулю и противоположно по знаку ЭДС самоиндукции в катушке:

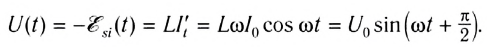
Сравнивая выражения для мгновенных значений силы тока I(t) и напряжения U(t), видим, что для их амплитудных значений можно записать закон Ома в виде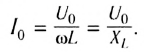

Величину 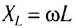называют индуктивным сопротивлением катушки. Оно пропорционально индуктивности катушки и частоте переменного тока в цепи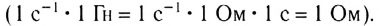  

Обратите внимание на то, что фазы колебаний силы тока и напряжения не совпадают. Наличие сдвига фаз означает, что мгновенное значение напряжения U на катушке индуктивности опережает мгновенное значение силы I переменного тока по фазе на 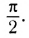 Такой сдвиг фаз между колебаниями силы тока и напряжения характерен в целом для цепей переменного тока, содержащих элементы, обладающие индуктивностью.
Закон Ома для цепи переменного тока, содержащей только катушку индуктивности, выполняется и для действующих значении силы тока 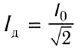и напряжения 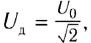так как 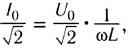тогда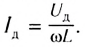

Таким образом, если в цепь переменного тока включена катушка индуктивности, то закон Ома выполняется для амплитудных и действующих значений силы тока и напряжения, но не выполняется для их мгновенных значений, так как мгновенные значения силы тока и напряжения не совпадают по фазе (см. рис. 195).

Мгновенная мощность, потребляемая катушкой индуктивности от источника переменного тока, определяется по формуле

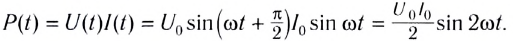
Поскольку среднее за период значение функции 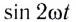равно нулю, то и средняя мощность за период также равна нулю:

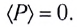
Как видно из рисунка 195, цепь с идеальной катушкой индуктивности в течение первой и третьей четвертей периода работает в режиме потребителя, запасая энергию магнитного поля 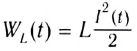в катушке, а в течение второй и четвертой — в режиме генератора, возвращая источнику запасенную энергию.

Поскольку потерь энергии в этом случае не происходит, то индуктивное сопротивление называют реактивным.

Главная >> Поддержка >> Словарь >>

Определение индуктивности фазы обмотки статора электродвигателя

В качестве примера рассмотрим трехфазный асинхронный двигатель с короткозамкнутым ротором.

Число пар полюсов: 2p = 4

Номинальный ток фазы статора I = 350 А.

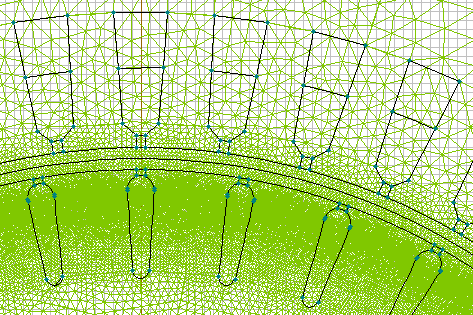
Для выполнения данной задачи воспользуемся модулем Магнитное поле переменных синусоидальных токов.

На практике величина индуктивности фазы обмотки статора L_s определяется расчетным путем, исходя из заранее известных паспортных данных электродвигателя и параметров Г-образной или Т-образной схемы замещения, или опытным путем.

Для определения индуктивности фазы обмотки статора с помощью пакета ELCUT, необходимо запитать одну исследуемую фазу электродвигателя и вычислить величину магнитного потока. Контур интегрирования необходимо построить таким образом, чтобы силовые линии магнитного поля пересекали контур только в одну сторону.

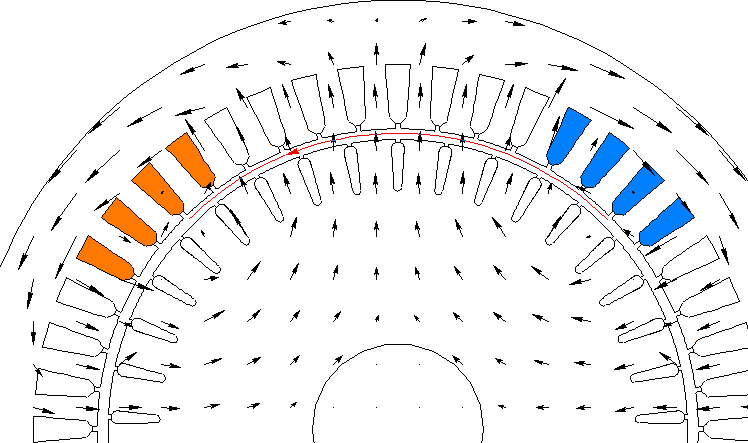
Аналогичным образом вычисляется магнитный поток, создаваемый другими полюсами. В данном случае необходимо отдельно производить расчет для двух полюсов, так как зубчатость может вызвать несимметрию распределения потока по полюсам.

L = (Ф1 + Ф2) / I

Загрузить файлы задачи phase_winding_inductance.zip

Как ведет себя катушка индуктивности в цепи постоянного и переменного тока?

Катушка индуктивности в цепи постоянного тока

Итак, для этого опыта нам понадобится блок питания, который выдает постоянное напряжение, лампочка накаливания и собственно сама катушка индуктивности.

Чтобы сделать катушку индуктивности с хорошей индуктивностью, нам надо взять ферритовый сердечник:

Намотать на него лакированного медного провода и зачистить выводы:

Замеряем индуктивность нашей катушки с помощью LC метра:

132 микрогенри.

Теперь собираем все это вот по такой схеме:

где

L — катушка индуктивности

La — лампочка накаливания на напряжение 12 Вольт

Bat — блок питания, с выставленным напряжением 12 Вольт

Лампочка засветилась!

Как вы помните из прошлой статьи, конденсатор у нас не пропускал  постоянный электрический ток:

Делаем вывод: постоянный электрический ток почти беспрепятственно течет через катушку индуктивности. Сопротивлением обладает только сам  провод, из которого намотана катушка.

Катушка индуктивности в цепи переменного тока

Для того, чтобы узнать, как ведет себя катушка индуктивности в цепи переменного тока, нам понадобится осциллограф, генератор частоты, собственно сама катушка индуктивности и резистор на 100 Ом.  Чем больше сопротивление, тем меньше будет проседать напряжение с моего генератора частоты, поэтому я взял резистор на 100 Ом.Он у меня будет в качестве шунта. Падение напряжения на этом резисторе будет зависеть от тока, протекающего через него

Собираем все это дело по такой схеме:

Получилось как то так:

Сразу договоримся, что у нас первый канал будет красным цветом, а второй канал — желтым. Следовательно, красная синусоида — это частота, которую нам выдает генератор частоты, а желтая синусоида — это сигнал, который снимается с резистора.

Мы с вами узнали, что при нулевой частоте (постоянный ток), катушка почти беспрепятственно пропускает через себя электрический ток. В нашем опыте мы будем подавать с генератора частоты синусоидальный сигнал с разной частотой и смотреть, меняется ли напряжение на резисторе.

Опыт N1

Для начала подаем сигнал  с частотой  в 1 Килогерц.

Давайте разберемся, что есть что. В зеленой рамочке я вывел автоматические замеры, которые делает осциллограф

Красный кружок с цифрой «1» — это замеры «красного»канала. Как мы видим, F (частота) =1 Килогерц, а Ма (амплитуда) = 1,96 Вольт. Ну грубо скажем 2 Вольта. Смотрим на кружочек с цифрой «2». F=1 Килогерц, а Ма=1,96 Вольт. То есть можно сказать, что сигнал на выходе точно такой же, как и на входе.

Увеличиваем частоту до 10 Килогерц

Амплитуда не уменьшилась. Сигнал какой есть, такой и остался.

Увеличиваем до 100 Килогерц

Заметили разницу? Амплитуда желтого сигнала стала меньше, да еще и график желтого сигнала сдвигается вправо, то есть запаздывает, или научным языком, появляется сдвиг фаз. Красный сигнал никуда не сдвигается, запаздывает именно желтый. Это имейте ввиду.

Сдвиг фаз — это разность между начальными фазами двух измеряемых величин. В данном случае напряжения. Для того, чтобы произвести замер сдвига фаз, должно быть условие, что у этих сигналов одна и та же частота. Амплитуда может быть любой. Ниже на рисунке приведен этот самый сдвиг фаз или, как еще его называют, разность фаз:

Увеличиваем частоту до 200 Килогерц

На частоте 200 Килогерц амплитуда упала вдвое, да и разность фаз стала больше.

Увеличиваем частоту до 300 Килогерц.

Амплитуда  желтого сигнала упала уже до 720 милливольт. Разность фаз стала еще больше.

Увеличиваем частоту до 500 Килогерц

Амплитуда уменьшилась до 480 милливольт.

Добавляем еще частоту до 1 Мегагерц

Амплитуда желтого канала  стала 280 милливольт.

Ну и добавляем частоту до предела, который позволяет выдать генератор частоты: 2 Мегагерца

Амплитуда «желтого» сигнала стала настолько маленькой, что мне пришлось ее даже увеличить в 5 раз.

И можно сказать, что сдвиг фаз стал почти 90 градусов или π/2.

Но станет ли сдвиг фаз больше, чем 90 градусов, если подать очень-очень большую частоту? Эксперименты говорят, что нет. Если сказать просто, то при бесконечной частоте сдвиг фаз будет равняться 90 градусов. Если совместить наши графики на бесконечной частоте, то можно увидеть примерно вот такой рисунок:

Так какой вывод можно сделать?

С увеличением частоты сопротивление катушки растет,  а также увеличивается сдвиг фаз. И чем больше частота, тем больше будет сдвиг фазы, но не более, чем 90 градусов.

Опыт N2

Давайте же уменьшим индуктивность катушки. Прогоним еще раз по тем же самым частотам. Я убрал половину витков и сделал витки на край феррита, тем самым уменьшил индуктивность до 33 микрогенри.

Смотрите формулу катушки индуктивности.

Итак, прогоняем все по тем же значениям частоты

При  частоте в 1 Килогерц у  нас значение почти не изменилось.

10 Килогерц

Здесь тоже  ничего не изменилось.

100 Килогерц

Тоже почти ничего не изменилось, кроме того, что желтый сигнал стал тихонько сдвигаться.

200 Килогерц

Здесь уже видим, что амплитуда на желтом сигнале начинает проседать и сдвиг фаз наращивает обороты.

300 Килогерц

Сдвиг фаз стал больше и амплитуда просела еще больше

500 Килогерц

Сдвиг стал еще больше и амплитуда желтого сигнала тоже просела.

1 Мегагерц

Амплитуда желтого сигнала падает, сдвиг фаз прибавляется. 😉

2 Мегагерца, предел моего генератор частоты

Сдвиг фаз стал почти равен 90 градусов, а амплитуда стала даже меньше, чем пол Вольта.

Обратите внимание на амплитуду в Вольтах  на тех же самых частотах. В первом случае у нас индуктивность была больше, чем во втором случае, но амплитуда желтого сигнала во втором случае больше, чем в первом.

Отсюда вывод напрашивается сам собой:

При уменьшении индуктивности, сопротивление катушки индуктивности также уменьшается.

Реактивное сопротивление катушки индуктивности

С помощью нехитрых умозаключений, физиками была выведена формула:

где

Х_L —  реактивное сопротивление катушки, Ом

П — постоянная и равна  приблизительно 3,14

F — частота, Гц

L — индуктивность, Гн

В данном опыте мы с вами получили фильтр низких частот (ФНЧ). Как вы видели сами, на низких частотах катушка индуктивности почти не оказывает сопротивление напряжению, следовательно амплитуда  и мощность  на выходе такого фильтра будет почти такой же, как и на входе. Но с увеличением частоты у нас амплитуда гасится. Применив такой фильтр на динамик, можно с уверенностью сказать, что будет усиливаться только бас, то есть низкая частота звука.

Видео про катушку индуктивности:

Заключение

Постоянный ток протекает через катушку индуктивности без каких-либо проблем. Сопротивлением обладает только сам провод, из которого намотана катушка.

Сопротивление катушки зависит от частоты протекающего через нее тока и выражается формулой:

Индуктивность трёхфазной линии.

Векторный потенциал
в системе из трех проводов с параллельными
и одинаково направленными токами в
любой точке равен:

,

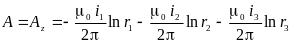
причём сумма всех
токов равна нулю (i₁+
i₂+i₃=
0) даже при
отсутствии симметрии в системе токов.

Векторный потенциал
в различных точках около проводов имеет
различную начальную фазу. В связи с
этим магнитные потоки, сцепленные с
отдельными проводами трёхфазной линии,
не совпадают по фазе с токами в этих
проводах, что приводит к перераспределению
нагрузки между проводами и к переносу
мощности между ними.

Покажем это,
рассматривая уравнения трёхфазной
линии в комплексной форме:

.

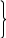
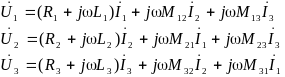
В симметричной
системе токов прямой последовательности
токи сдвинуты на 120⁰:

;

;

,

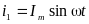
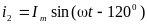
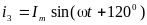
Учитывая симметрию
системы токов:

;

,
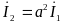
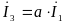
получим:

I₁

.

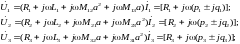
I₃
I₂

Вещественные
слагаемые в скобках различны, что
свидетельствует о различных значениях
активной мощности, потребляемой в разных
проводах линии.

При использовании
транспозиции проводов трёхфазная линия
становится симметричной, потому: M₁₂
= M₁₃
= M₂₃
= M,
L₁
= L₂
= L₃
= L
и R
₁
= R
₂
= R
₃ = R.
В этом случае уравнения для различных
фаз становятся идентичными:

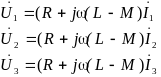
В любом проводе
сдвиг фаз между током и напряжением
одинаков, что позволяет исключить
перенос мощности между проводами линии.

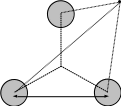
Рассмотрим
трёхфазную линию, провода которой
расположены в вершинах равностороннего
треугольника (рис.10–8): При таком
расположении проводов линия симметрична
без их транспозиции, если вблизи нет
ферромагнитных поверхностей.

1 r₁
m

r₃
r₂

r₀

r₀
r₀

D

2
3

Рисунок 10–8

В рассматриваемой
системе векторный потенциал равен нулю
в бесконечности (при r_k
-> )
и в центре симметрии ( r_k
= r₀),
так как сумма токов в скобках равна
нулю:

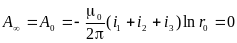
Векторный потенциал
на поверхности провода первой фазы,
учитывая симметрию системы токов (i₂
+ i₃
= – i₁),
равен:

.

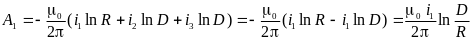
Определим внешний
магнитный поток первой фазы, а затем
индуктивность первой фазы, равную
(из-за симметрии системы) индуктивности
любой фазы:

;

.

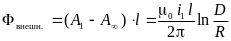
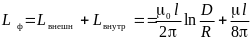
Лекция 11 Переменное электромагнитное поле в диэлектрике

В переменном
электромагнитном поле наблюдаются
одновременно обе, рассмотренные ранее
нами в отдельности, его стороны. Связь
между ними дают первое и второе уравнения
Максвелла – закон полного тока и закон
электромагнитной индукции:

,
.

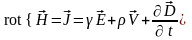
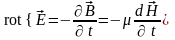
Анализируя
переменное электромагнитное поле в
диэлектрике, считаем диэлектрик
идеальным (=0)
и предполагаем отсутствие в нем объёмных
зарядов (=0).
Тогда:

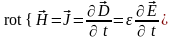
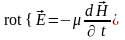
Запишем оба
уравнения в проекциях на оси декартовой
системы координат:

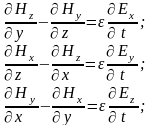
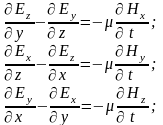
Рассмотрим случай
плоско
поляризованной электромагнитной волны,
в которой все характеризующие её величины
зависят только от одной из координат
(z),
а от остальных
координат (x,
y)
не зависят. Такой характер имеют
электромагнитные волны, излучаемые
антенной, на больших (z>>)
расстояниях от антенны, где 
– длина электромагнитной волны в
диэлектрике. Часто такую волну называют
плоской.

В плоской
электромагнитной волне производные от
любых проекций векторов поля по
координатам x
и y
равны нулю,
поэтому система уравнений упрощается
и принимает вид:

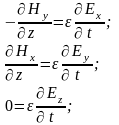
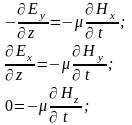
Из последних
уравнений каждой системы ввиду равенства
нулю производных получаем, что проекции
векторов E_z
и
H_z
не зависят от времени: E_z=const
и H_z=const.
Принимаем их равными нулю, так как
переменное поле, излучённое антенной,
не содержит постоянных составляющих.
Кроме того, мы уже рассматривали ранее
постоянные электрические и магнитные
поля, и в случае необходимости можем,
если потребуется учесть их вместе с
переменным полем, применив принцип
наложения.

Рассматривая
оставшиеся четыре уравнения для проекций,
направим ось x
декартовой
системы координат вдоль вектора
напряжённости электрического поля
(E_y=0).
В этом случае остаётся единственная
составляющая вектора напряжённости
электрического поля:
E=E_x.
В этом случае уравнения ещё больше
упрощаются:

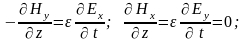
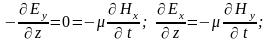
Из полученных
уравнений следует, что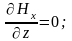

,
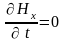
т.е.

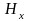
=const=0,

и при выбранном
направлении осей координат, вектор
напряжённости магнитного поля имеет
лишь единственную составляющую,
направленную вдоль оси y:
H=H_y.
Это означает, что в
плоско поляризованной электромагнитной
волне в диэлектрике в любой точке векторы
напряжённости электрического и магнитного
поля расположены взаимно перпендикулярно.

Н
айдём
решение системы двух оставшихся
уравнений:

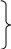
Дифференцируя
первое уравнение по времени, а второе
по координате z,
получим:

;
,
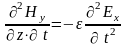
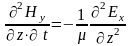
откуда:

,
и обозначив

,
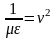
запишем уравнение для вектора напряжённости
электрического поля, которое называется
волновым уравнением:

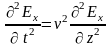
При рассмотрении
режимов в цепях с распределёнными
параметрами нами были получены аналогичные
уравнения для напряжения в произвольной
точке линии без потерь, в которой
координата x
отсчитывается от начала линии:

.

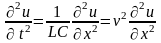
Решение для
волнового уравнения в линии мы получили
в виде суммы прямой и обратной бегущих
волн напряжения:

u
= u_
+ u_
= u^/(x-vt)
+ u^//(x+vt).

Решение для
напряжённости электрического поля
запишем по аналогии:

E_x
= E^/(z-vt)
+ E^//(z+vt).

Коэффициенты

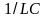
и

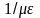
в обоих уравнениях имеют одинаковые
размерности, так как в цепях с
распределёнными параметрами эти
параметры задаются на единицу длины
линии:

[L]
= []
= Гн/м; [C]
= []=
Ф/м

Выражение для волн
тока в линии мы получали с помощью
волнового сопротивления:

,

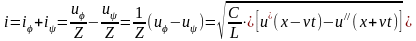
здесь через Z
обозначено
волновое сопротивление линии без потерь,
которое по аналогии эквивалентно
волновому сопротивлению идеального
диэлектрика для электромагнитных волн:

.

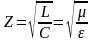
Применив аналогичное
преобразование для решения волнового
уравнения относительно напряжённости
электрического поля, получим решения
для напряжённости магнитного поля:

.

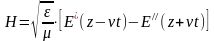
Полученные
решения означают, что векторы E
и
H
в любой
точке переменного электромагнитного
поля взаимно перпендикулярны, связаны
между собой через волновое сопротивление,
а электромагнитные волны распространяются
в диэлектрике со скоростью v,
которая
называется скоростью света и в пустоте
равна:

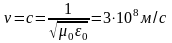
В любых диэлектриках
≥₀
и ≥₀,
поэтому скорость распространения
электромагнитных волн в них меньше или
равна скорости света в пустоте vc.

Волновое
сопротивление, связывающее между собой
напряжённости электрического и магнитного
поля в прямой и обратной волнах:

,

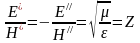
также зависит от
свойств диэлектрика и для пустоты равно:

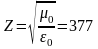
Ом

Для прямой (или
обратной) волны в отдельности можем
записать соотношение:

;
;
.

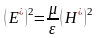
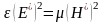
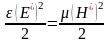
Это означает, что
плотности энергии электрического и
магнитного поля в любой точке для прямой
(или обратной) электромагнитной волны
равны друг другу:

.

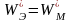
Для электромагнитных
волн в идеальном диэлектрике можно
использовать по аналогии все ранее
полученные соотношения для бегущих
волн в однородной линии без потерь. В
частности, справедливы формулы для
определения отражённой и преломлённой
волн на границе диэлектриков с различными
волновыми сопротивлениями. При этом
соблюдаются все граничные условия для
составляющих векторов напряжённости
электрического и магнитного поля.
Вообще, решение волнового уравнения
может быть получено, если заданы граничные
и начальные условия для векторов.

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #