Всем доброго времени суток. В прошлых статьях (часть 1, часть 2, часть 3) я рассказал о расчёте индуктивности индуктивных элементов без сердечников. Однако их применение ограниченно, вследствие, больших габаритных размеров. Поэтому для увеличения индуктивности и уменьшения размеров и улучшения других показателей индуктивные элементы устанавливают на сердечники из материалов с различными магнитными свойствами.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Особенности расчёта индуктивных элементов с сердечниками
В отличие от индуктивных элементов без сердечников, при расчёте которых учитывался магнитный поток пронизывающий только проводник с током, магнитный поток индуктивных элементов с сердечниками практически полностью замыкается на сердечники. Поэтому при расчёте индуктивности таких элементов необходимо учитывать размеры сердечника и материал, из которого он изготовлен, то есть его магнитную проницаемость.
Обобщённую формулу для расчёта индуктивных элементов с сердечниками можно выразит с помощью следующего выражения
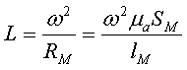
где ω – количество витков катушки,
RM – сопротивление магнитной цепи,
μа – абсолютная магнитная проницаемость вещества, из которого изготовлен сердечник,
SM – площадь поперечного сечения сердечника,
lM – длина средней магнитной силовой линии,
Таким образом, зная размеры сердечника можно достаточно просто вычислить индуктивность. Однако в связи с такой простотой выражения и разбросом магнитной проницаемости материала сердечника, погрешность в расчёте индуктивности составит 25 %.
Для сердечников, имеющих сложную конструктивную конфигурацию, вводится понятие эффективных (эквивалентных) размеров, которые учитывают особенности формы сердечников: эффективный путь магнитной линии le и эффективная площадь поперечного сечения Se сердечника. Тогда индуктивность катушки с сердечником будет вычисляться по формуле
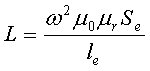
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
Se – эффективная площадь поперечного сечения сердечника,
le – эффективный путь магнитной линии сердечника.
Таким образом, расчёт индуктивности индуктивных элементов с сердечниками сводится к нахождению эффективных размеров сердечника. Для упрощения нахождения данных размеров сердечника ввели вспомогательные величины, называемые постоянные сердечников:
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника, измеряется в мм-1;
С2 – вторая постоянная сердечника, которая равна сумме отношений длин однородных по сечению участков сердечника к квадрату своего сечения, измеряется в мм-3;
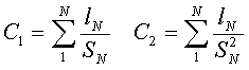
где N – количество разнородных участков сердечника,
lN – длина N – го участка сердечника,
SN – площадь N – го участка сердечника.
Тогда величины Se и le определятся из следующих выражений
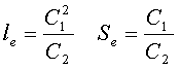
Кроме индуктивности с помощью постоянных С1 и С2 определяют эффективный объём Ve, который требуется для определения параметоров силовых индуктивных элементов – трансформаторов и дросселей. Если же есть необходимость рассчитать только индуктивность L, то используют только постоянную С1 по следующему выражению
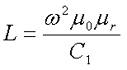
где ω – количество витков катушки,
μ0 – магнитная постоянная, μ0 = 4π*10-7,
μr – относительная магнитная проницаемость вещества,
С1 – первая постоянная сердечника, которая равна сумме отношений длины однородных по сечению участков сердечника к поперечного сечения сердечника.
Несмотря на довольно сложные формулировки и формулы, вычисление индуктивности по ним достаточно простое.
Выпускается достаточно много типов сердечников, которые обладают различными конструктивными особенностями и свойствами, рассмотрим некоторые из них.
Расчёт катушки с тороидальным сердечником
Тороидальные (кольцевые) сердечники, благодаря своей простоте изготовления находят широкое применение в различных импульсных трансформаторах, фильтрах и дросселях и обеспечивают небольшую потребляемую мощность при минимальных потерях.
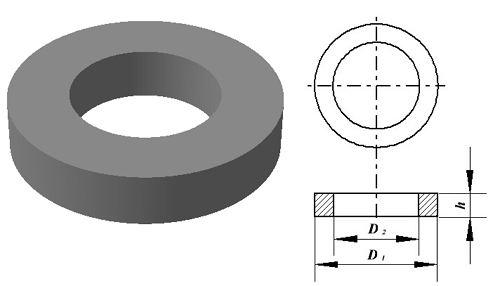
Тороидальный сердечник.
Для расчёта индуктивности достаточно знать три конструктивных параметра такого магнитопровода: D1 – внешний диаметр, D2 – внутренний диаметр, h – высота сердечника.
Расчёт эффективных параметров сердечника, как сказано выше, основан на двух величинах С1 и С2, которые составляют
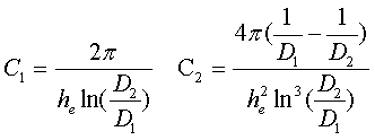
где he – эффективная высота сердечника,
D1 – внешний диаметр сердечника,
D2 – внутренний диаметр сердечника.
Расчёт эффективной высоты he сердечника зависит от конструктивных особенностей.
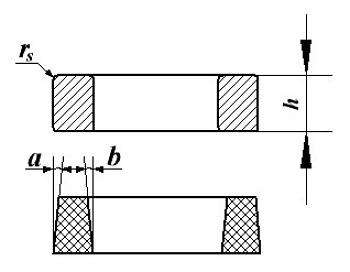
Расчёт эквивалентной высоты тороидального сердечника: прямоугольное сечение (вверху) и трапецеидальное сечение (снизу).
Рассмотрим несколько случаев:
а) прямоугольное поперечное сечение с острыми кромками
![]()
б) прямоугольное поперечное сечение со скруглёнными кромками и радиусом скругления rs
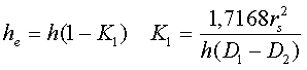
в) трапецеидальное поперечное сечение с острыми кромками
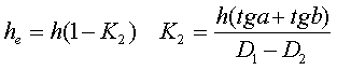
г) трапецеидальное поперечное сечение со скруглёнными кромками
![]()
Пример. В качестве примера рассчитаем индуктивность тороидальной катушки, имеющий ω = 50 витков, намотанных на равномерно на магнитопровод со следующими размерами D1 = 20 мм, D2 = 10 мм, h = 7 мм, сечение магнитопровода прямоугольное со скруглёнными кромками, радиус скругления rs = 0,5 мм, относительная магнитная проницаемость материала сердечника μr = 1000.
Так как рассчитываем только индуктивность, то в расчёте коэффициента С2 нет необходимости
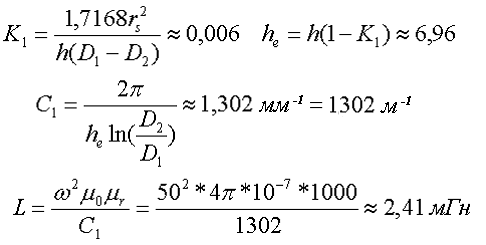
Расчёт катушки с П–образным сердечником прямоугольного сечения
В отличие от тороидальных сердечников, П – образные сердечники выполняются разборными и состоят из двух частей. Существует две модификации таких сердечников: состоящие из двух П – образных частей и из П – образной и прямоугольной замыкающей пластины.
Такие сердечники применяются в импульсных трансформаторах и трансформаторах строчной развертки и, обладая большой магнитной проницаемостью, обеспечивают малую потребляемую мощность.
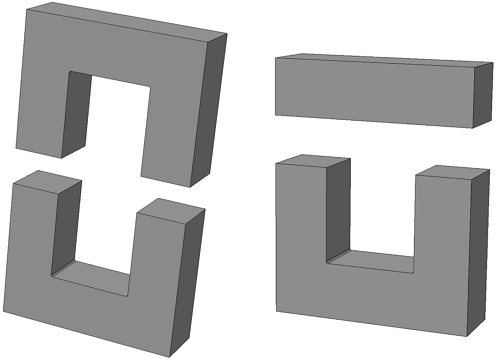
П-образный сердечник с прямоугольным сечением: из двух П-образных частей (слева) и П-образной части с замыкающей прямоугольной пластиной (справа).
Для расчёта параметров сердечника рассмотрим сечение замкнутого П-образного сердечника
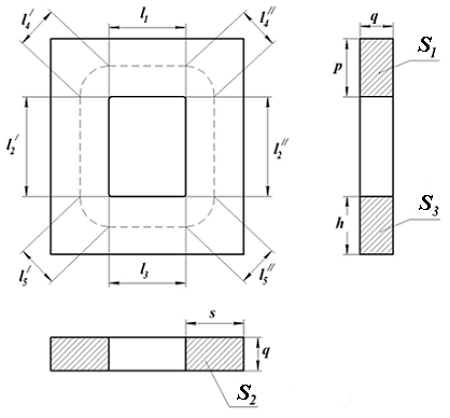
Сечение П-образного прямоугольного сердечника.
Данный сердечник состоит из нескольких участков l1, l2, l3, l4, l5 имеющих различное сечение S1, S2, S3, S4, S5,. Тогда коэффициенты С1 и С2 составят
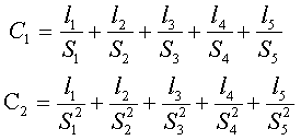
Неизвестные величины можно найти следующим образом
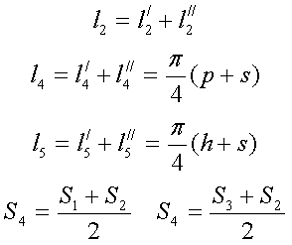
Пример. Необходимо рассчитать индуктивность обмотки трансформатора, выполненного на П-образном сердечнике фирмы Epcos типа UU93/152/16, выполненного из двух П-образных половинок, материал сердечника N87 μr = 1950, количество витков ω = 150.
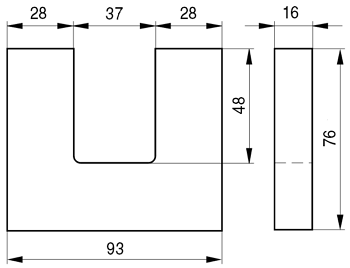
Сердечник Epcos U93/76/16.
Таким образом, расчётные параметры сердечника составят
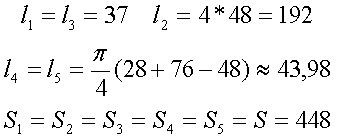
Таким образом коэффициент С1 и индуктивность L составят
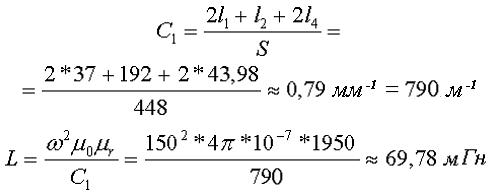
Расчёт катушки с П-образным сердечником круглого сечения
Кроме П-образных катушек с прямоугольным сечение, широко применяются П-образные катушки с круговым сечением. Они также состоят из двух П-образных частей

П-образный сердечник с круговым сечением.
Для расчёта рассмотрим сечение замкнутого сердечника состоящего из двух пловинок.
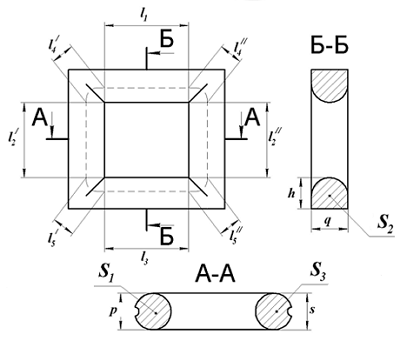
Сечение П-образного сердечника с круговым сечением.
Аналогично сердечнику с прямоугольным сечением выделим пять участков длины сердечника с различным сечением и расчёт соответственно тоже. Площадь круговых участков считается по известной формуле для площади круга, влиянием технологических пазов и отверстий можно пренебречь
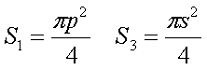
Пример. В качестве примера рассчитаем индуктивность катушки, выполненной на сердечнике. Сердечник из двух частей типа SDMR 40 UY20 (μr = 2500), количество витков ω = 60.
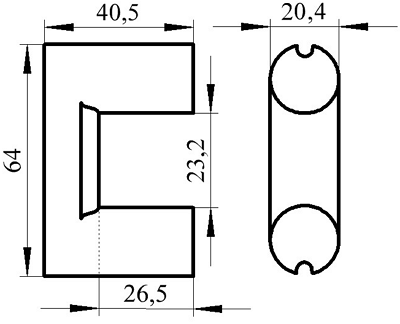
Сердечник типа SDMR 40 UY20.
Параметры сердечника для расчёта составят
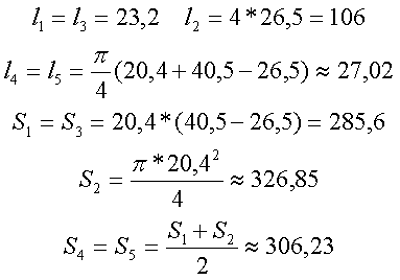
Таким образом коэффициент С1 и индуктивность L составят
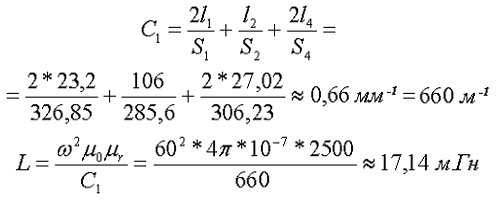
На сегодня всё. Продолжение смотри в следующей статье.
Определение индуктивности основные соотношения
Катушка индуктивности, дроссель или просто индуктивность – элемент, название которого происходит от слова
inductio – навожу, вызываю. Классически и упрощенно индуктивность можно представить как несколько витков,
обмотанные вокруг ферромагнитного сердечника. При этом, поскольку витки расположены рядом (и к тому же на
одном ферромагнитном сердечнике) то они связаны индуктивно и изменение тока в одном витке вызывает
(индуктирует) противоток и противо-ЭДС в другом и рост тока замедляется. Так как в катушке индуктивности все
витки соединены последовательно, то они взаимонаводят противоток, препятствующий росту тока. И напротив,
если катушку отключить от источника то витки будут наводить друг в друге ЭДС, чтобы ток через индуктивность
не изменился. Классический аналог индуктивности есть инерция массы. Более распространенное название катушки
индуктивности – дроссель.
Скорость роста тока через индуктивность пропорциональна приложенному к нему напряжению и обратно
пропорциональна величине самой индуктивности:
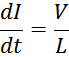
В случае если напряжение на дросселе постоянно ток возрастает по линейному закону:
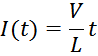
Конструктивно индуктивность обычно состоит из двух основных элементов, определяющих её свойства: обмотки и
ферромагнитного сердечника.
С увеличением тока дросселя индукция в магнитопроводе увеличивается и после достижения индукции насыщения,
определяемой материалом магнитопровода индуктивность дросселя резко падает. Если к дросселю еще приложено
напряжение, то ток через него резко возрастает. Максимальное значение тока, соответствующего индукции
насыщения является максимальным рабочим током дросселя. Этот параметр указывается в справочных листках на
серийно выпускаемые дроссели.
Обмотка характеризуется рядом параметров:
- числом витков;
- тип и параметры провода;
- средней площадью сечения витка;
- длиной обмотки;
- типом обмотки (однослойная, многослойная, тип многослойной намотки и т.д.).
Сердечник характеризуется следующими параметрами:
- тип сердечника (форма магнитопровода);
- материал сердечника;
- наличие и величина немагнитного зазора;
- площадь сечения магнитопровода;
- длина средней линии магнитопровода;
- площадь окна магнитопровода.
Единица измерения индуктивности – Генри. В честь американского ученого Джозефа Генри.
Условное обозначение дросселя:
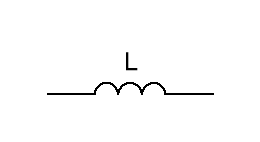
Рисунок L.1 – Условное обозначение дросселя (без магнитопровода)
Основные параметры дросселя
Характеристики обмотки и сердечника характеризуют основные параметры дросселя:
- индуктивность L;
- омическое сопротивление R;
- максимальный ток через дроссель (без перехода сердечника в насыщение);
- эквивалентная паразитная емкость обмотки C;
- максимальная рабочая частота (характеризуется материалом сердечника);
- масса и габариты.
Функции индуктивности в силовой электронике
В устройствах силовой электроники индуктивность играет ряд функций:
- функцию накопителя энергии (в импульсных стабилизаторах и родственных им обратноходовых
преобразователях); - в составе LC-фильтров;
- в составе резонансных LC-контуров.
Типы индуктивностей
Существует несколько типов индуктивностей используемых в силовой электронике:
- выводные индуктивности;
- SMD-индуктивности;
- индуктивности на ферритовых стандартных каркасах.
Выводные и SMD-индуктивности, как правило, имеют небольшие значения тока и величины индуктивности и могут
быть использованы в маломощных импульсных стабилизаторах и фильтрах. Конкретный тип дросселя выбирается
согласно рассчитанным параметрам: рабочему номиналу индуктивности, максимально допустимому току, рабочей
частоте. Кроме этого важно учитывать наличие или отсутствие электромагнитной экранировки корпуса дросселя,
что сказывается на уровне излучаемых им электромагнитных помех.
Для стабилизаторов мощностью более 20 Вт целесообразно использование мощных дросселей выполняемых на
стандартных сердечниках.
Эквивалентная схема дросселя
Эквивалентная электрическая схема дросселя, содержащая все основные паразитные элементы, представлена на
рисунке L.2.
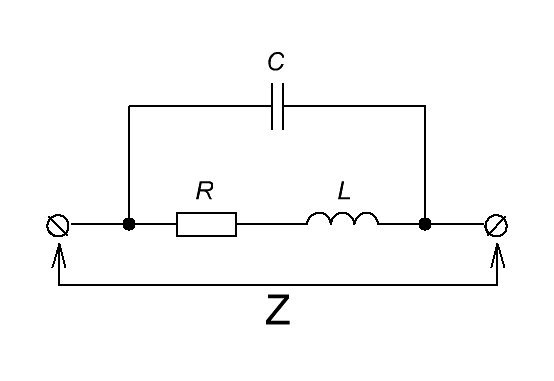
Рисунок L.2 – Эквивалентная схема дросселя
Последовательное сопротивление дросселя R зависит от длины и сечения провода, из которого выполнена обмотка.
Кроме того при большой толщине провода на высоких частотах проявляется скин-эффект, значительно
увеличивающий последовательное сопротивление. Подробнее влияние скин-эффекта и методика количественного
расчета описана в части «Влияние скин-эффекта на сопротивление обмоток при высоких частотах» раздела
«Трансформатор».
Паразитная емкость дросселя C существенно зависит от геометрии магнитопровода и способа намотки. Так меньшим
значением паразитной емкости обладают дроссели с однорядовой и N-образной обмоткой (подробнее – часть
«Обмотки» раздела «Трансформатор»).
Если в емкости энергия запасается в электрическом поле между обкладками, то энергия индуктивности запасается
в магнитном поле. Интересно, что если магнитопровод не является замкнутым, то энергия дросселя «размещается»
вокруг дросселя, вызывая существенные наводки на близкорасположенные контуры.
Расчет индуктивности дросселя
Общее соотношение для определения индуктивности того или иного дросселя с замкнутым магнитопроводом имеет
вид:
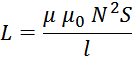
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала сердечника (эффективное значение магнитной проницаемости
сердечника);
S – площадь сечения магнитопровода;
l – длина магнитопровода;
N – число витков.
Это соотношение имеет достаточно общий характер. На практике индуктивность дросселя с магнитопроводом
является индуктивностью лишь в определенном диапазоне токов. Основным лимитирующим процессом является
насыщение магнитопровода. Об этом подробнее – ниже.
Процесс насыщения магнитопровода, рабочий диапазон изменения индукции
Для понимания процесса насыщения важно понимание причинно-следственной связи. Магнитная индукция в
магнитопроводе B является следствием напряженности магнитного поля H (ампер-витки), создаваемой током
обмотки I:
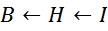
Упрощенно можно сказать, что индукция магнитного поля определяется напряженностью магнитного поля через
коэффициент пропорциональности µ0µ (упрощенно – потому, что зависимость имеет форму гистерезиса):
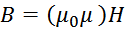
Изменение тока через индуктивность приводит к изменению напряжённости поля и соответственно изменению
индукции магнитного поля. Материал магнитопровода определяет рамки изменения магнитной индукции – индукция
ограничена сверху индукцией насыщения Bsat. Пока изменение магнитной индукции происходит в
пределах [- Bsat … + Bsat] дроссель сохраняет свои индуктивные свойства и заданный
уровень индуктивности. В двухтактных преобразователях может быть использован весь размах допустимого
изменения индукции. В однотактных стабилизаторах и преобразователях (когда прикладываемое напряжение
однополярное) этот рабочий диапазон изменения индукции в магнитопроводе уменьшается до [+Br … + Bsat].
Здесь Br – остаточная индукция (remanence) – индукция, которая остается в материале
магнитопровода при снижении напряжённости внешнего магнитного поля до нуля. То есть начало нового рабочего
цикла начнется с роста B не от нуля, а с некоторого значения Br .
Для увеличения размаха индукции ΔB рабочего цикла магнитопровода необходимо уменьшать величину остаточной
индукции магнитного поля, поскольку гистерезисный цикл магнитопровода однотактного устройства
(трансформатора обратноходового преобразователя, силовые дроссели) лежит лишь в одном сегменте полной
гистерезисной петли. То есть размах магнитной индукции ограничен с одой стороны индукцией насыщения, а с
другой стороны – остаточной магнитной индукцией. Индукция насыщения является параметром неизменным,
индивидуальным для ферромагнитного материала, а вот уровень остаточной индукции может быть уменьшен.
Из соотношения, связывающего индукцию магнитного поля с напряженностью магнитного поля следует, что,
допустимый диапазон изменения напряженности магнитного поля определяется двумя факторами: с одной стороны, –
диапазоном возможного изменения индукции в магнитопроводе ΔB, с другой, – коэффициентом пропорциональности,
определяемым магнитной проницаемостью:
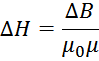
Существует теорема о циркуляции вектора напряженности магнитного поля. Эта теорема гласит «Циркуляция вектора
напряженности магнитного поля по некоторому контуру равна алгебраической сумме микроскопических токов
охватываемых этим контуром»:
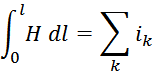
Согласно теореме о циркуляции вектора напряженности магнитного поля (в базе – теорема о циркуляции магнитного
поля) для случая дросселя с замкнутым магнитопроводом диапазон изменения тока (от нуля) определяется
диапазоном изменения напряженности магнитного поля:
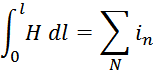
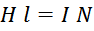
Заменяя абсолютные значения на изменения величин ΔI и ΔH получаем:
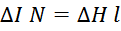
где:
ΔI – максимальное изменение тока обмотки дросселя;
N – число витков в дросселе;
ΔH – допустимый диапазон изменения напряженности магнитного поля в материале магнитопроводе (от нулевого
значения);
l – длина магнитной линии магнитопровода.
Подставляя выражение для напряженности магнитного поля в выражение теоремы о циркуляции вектора напряженности
магнитного поля получаем выражение для определения максимальной амплитуды тока дросселя:
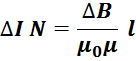
Отсюда следует, что максимальные ампер-витки, которые можно получить при сохранении индуктивных свойств
дросселя (без насыщения) определяются диапазоном возможного изменения индукции в магнитопроводе ΔB, с
другой, – коэффициентом пропорциональности, определяемым магнитной проницаемостью μ.
Для увеличения ампер-витков можно использовать, во-первых, снижение остаточной индукции Br,
во-вторых, – уменьшение эффективной магнитной проницаемости μ. Все это обеспечивается за счет введения в
магнитопровод индуктивного элемента немагнитного зазора.
Немагнитный зазор – основные соотношения
Введение немагнитного зазора является одним из способов снижения остаточной индукции магнитного поля и
уменьшение эффективной магнитной проницаемости сердечника. Ниже подробно рассмотрено как введение зазора
влияет на конкретные рабочие параметры индуктивного элемента.
Влияние на остаточную индукцию магнитного поля Br
Введение немагнитного зазора длиной lg приводит к «перераспределению» напряженности магнитного
поля между магнитопроводом и зазором. При этом в соответствии с законом полного тока [Вдовин С. С.
Проектирование импульсных трансформаторов. – 2-е изд., перераб. и доп. — Л.: Энергоатомиздат. Ленингр.
отд-ние, 1991. — 208 с: ил.]:
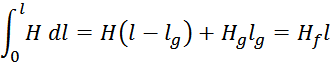
где:
l – общая длина промежутка вместе с зазором;
lg – длина немагнитного зазора;
H – напряженность поля в материале магнитопроводе;
Hg – напряженность поля в немагнитном зазоре;
Hf – напряженность внешнего (эквивалентного) магнитного поля.
Смысл данного выражения заключается в том, что произведение эквивалентной напряженности поля Hf
на общую длину промежутка с зазором (эдакое магнитное напряжение) складывается из произведения напряженности
поля в магнитопроводе H на длину магнитопровода (l-lg) и произведения напряженности поля в зазоре
Hg на длину зазора lg. То есть магнитный зазор фактически берет на себя часть
суммарного «магнитного напряжения» и эффективная напряженность внешнего (эквивалентного) магнитного поля
увеличивается. Напомним, что напряженность поля по сути есть ампер·витки.
В соответствии с принципом непрерывности магнитного потока магнитные поток в зазоре Φg равен
магнитному потоку в магнитопроводе Φ0:
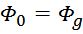
Поскольку размеры зазора достаточно малы по сравнению с шириной магнитопровода, то можно считать, что поле в
зазоре однородно, площадь внутри зазора равна площади поперечного сечения магнитопровода и соответственно
индукция магнитного поля в зазоре Bgравна индукции магнитного поля в магнитопроводе B0:
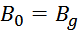
Отсюда следует, что выражение для «перераспределения» напряженности магнитного поля между магнитопроводом и
зазором можно преобразовать:
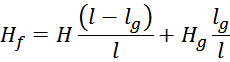
И поскольку длина немагнитного зазора много меньше длины промежутка:
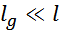
то:
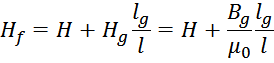
И поскольку B0 = Bg то:
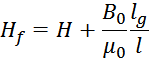
Или с учетом выражения для напряженности магнитного поля получаем выражение, связывающее эквивалентную
напряженность магнитного поля Hf с индукцией магнитного поля при наличии немагнитного зазора
lg:
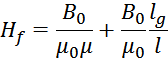
Если бы зазора не было, то выражение имело бы вид:
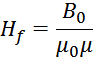
Сопоставление формул «с зазором» и «без зазора» наглядно показывает, что при одном и том же значении индукции
B0 достигается большее значение напряженности, то есть большие ампер-витки. При этом увеличение
напряженности магнитного поля на происходит на величину:
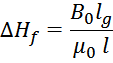
Графические, введение зазора вытягивает гистерезисный цикл вдоль оси H (рисунок L.3). Эквивалентный
гистерезисный цикл может быть построен смещением точек нормального гистерезисного цикла B = f (H) вправо
(при положительных значениях H) и влево (при отрицательных значениях H) на «расстояние»:
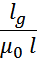
Или, размышляя по другому, при одних и тех же ампер-витках, но с введенным зазором индукция магнитного поля в
магнитопроводе уменьшается.
Определим величину остаточной индукции Br. Значение Br можно вычислить, зная величину
коэрцитивной силы Hc и величину магнитной проницаемости на начальном участке гистерезиса
(геометрия расчетов показана на рисунке L.3):
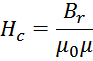
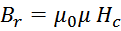
При введении зазора эта величина уменьшается пропорционально уменьшению эффективной магнитной
проницаемости:
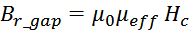
где:
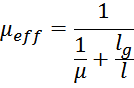
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора.
Обоснование формулы для расчета эффективной магнитной проницаемости μeffпредставлено в следующем
разделе.
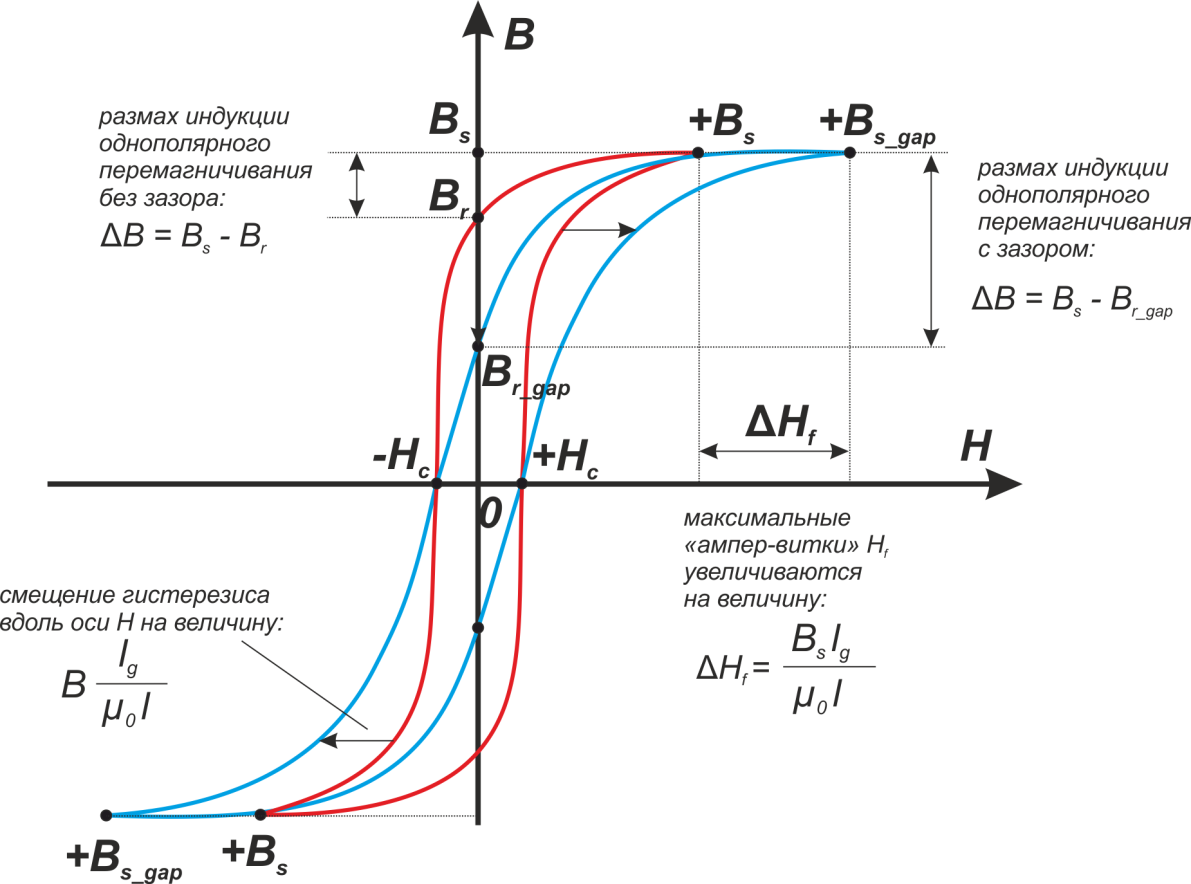
Рисунок L.3 – Эквивалентный гистерезисный цикл для магнитопровода с зазором
Из сопоставления эквивалентного гистерезисного цикла магнитопровода с зазором и нормального гистерезисного
цикла магнитопровода (без зазора) следует, что остаточная магнитная индукция гистерезисного цикла
магнитопровода с зазором существенно меньше остаточной индукции в случае без зазора. Таким образом, ведение
зазора является эффективным способом уменьшения остаточной индукции магнитного поля.
Влияние зазора на эффективную магнитную проницаемость сердечника μeff
Выражение, связывающее эквивалентную напряженность магнитного поля Hf с индукцией магнитного поля
при наличии немагнитного зазора lg:
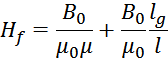
Можно привести к традиционному виду:
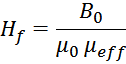
где:
μeff – эффективная магнитная проницаемость материала сердечника с зазором.
Выразим μeff:
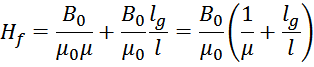
где:
Отсюда получаем, что при введении немагнитного зазора в магнитопровод эффективная магнитная проницаемость
материала сердечника с зазором μeff уменьшается и вычисляется по соотношению:
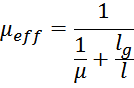
где:
μ – магнитная проницаемость материала сердечника;
lg – длина магнитного зазора.
Влияние зазора на индуктивность
Общее соотношение для определения индуктивности того или иного дросселя с замкнутым магнитопроводом имеет
вид:
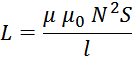
где:
µ0 – магнитная постоянная;
µ – магнитная проницаемость материала сердечника;
S – площадь сечения магнитопровода;
l – длина магнитопровода;
N – число витков.
При введении немагнитного зазора в вышеприведенном соотношении расчета индуктивности магнитная проницаемость
материала сердечника µ заменяется на эффективную магнитная проницаемость материала сердечника с зазором
μeff вычисляемая по выше приведенному соотношению. Подставляя μeff в формулу для
индуктивности, получаем выражение для индуктивности дросселя с зазором:
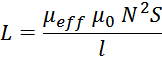
где:
μeff – эффективная магнитная проницаемость материала сердечника с зазором.
Таким образом, введение зазора является эффективным способом увеличения индуктивности «за счет меди» то есть
при увеличении числа витков.
Влияние немагнитного зазора на максимальный ток
При введении немагнитного зазора в вышеприведенном соотношении расчета индуктивности используется эффективная
магнитная проницаемость материала сердечника с зазором μeff вычисляемая по соотношению:
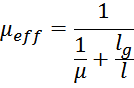
где:
μ – магнитная проницаемость материала сердечника;
lg – длина немагнитного зазора.
Подставляя, получаем выражение для индуктивности дросселя с зазором:
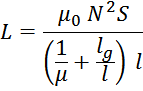
Максимальный ток, до которого дроссель работает в линейном режиме без насыщения определяется индукцией
насыщения. Найдем соотношение для расчета максимального тока дросселя:
В соответствии с теоремой о циркуляции вектора напряженности магнитного поля (циркуляция вектора
напряженности магнитного поля по некоторому контуру равна алгебраической сумме токов, охватываемых этим
контуром) произведение тока в единичном витке на количество витков в дросселе численно равно произведению
напряженности магнитного поля в магнитопроводе на его длину (типа «магнитному напряжению»):
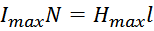
Напряженность магнитного поля связана с индукцией магнитного поля:
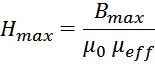
Подставляя, получаем:
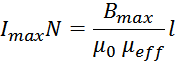
Или:
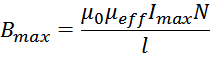
Или:
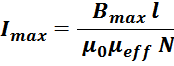
Подставляя выражение для эффективной магнитной проницаемости μeff, получаем:
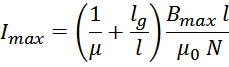
Из полученного соотношения видно, что максимальный ток дросселя возрастает с ростом немагнитного зазора,
эффективной длины магнитопровода, максимально допустимой индукции материала, обратно пропорционально числу
витков. Кажущийся очевидный парадокс заключается в том, что максимальный ток дросселя не зависит от площади
сечения магнитопровода. Физически парадокс объясняется тем, что ферромагнитный сердечник является хорошим
проводником магнитного поля и все падение напряженности магнитного поля приходится на немагнитный зазор.
Тем не менее, существует два основных способа увеличения максимального тока дросселя без насыщения
магнитопровода – или «за счет феррита» или «за счет меди»:
Способ увеличения номинального тока дросселя при сохранении «за счет феррита» состоит в уменьшении числа
витков N при одновременном увеличении площади сечения магнитопровода S, с тем чтобы индуктивность дросселя L
оставалась постоянной;
Способ увеличения номинального тока дросселя «за счет меди» заключается во введении в магнитопровод
магнитного зазора lg и увеличении числа витков N с тем чтобы компенсировать уменьшение
индуктивности.
На практике задача проектирования дросселя всегда является задачей оптимизации и поиска компромиссов с целью
нахождения оптимальных массо-, габаритно-, экономично-, технологично-, -«и т.д.» параметров. Важно при этом
обеспечить два условия:
тепловой режим дросселя должен находиться в разумных пределах (не более 80-100 °С);
окно магнитопровода должно быть максимально заполнено медью. При этом достигаются оптимальные массогабаритные
параметры и из магнитопровода выжимается «экономический максимум».
Для создания немагнитного зазора используют термостойкие и не хладотекучие материалы – например, плотную
бумагу, электрокартон, стеклотекстолит, полиимид (он же термоскотч). Фторопласт, полиэтилен, ПВХ не
подходит, так как со временем они проявляют свойства хладотекучести и размягчаются под действием нагрева
магнитопровода и зазор уменьшается.
Влияние немагнитного зазора на максимальную энергию дросселя
Подставляя полученные выражения учитывающие зазор в формулу для максимальной энергии, запасаемой дросселем,
получаем:
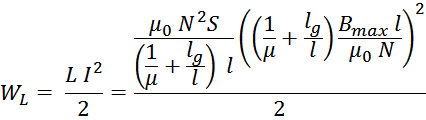
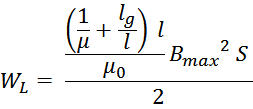
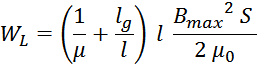
Из данных соотношений видно, что энергия, которую можно запасти в дросселе с зазором увеличивается (на
величину обратно пропорциональную уменьшению эффективной магнитной проницаемости).
Расчет числа витков в обмотке с учетом зазора
Для дросселей с зазором в магнитопроводе индуктивность определяется по формуле:
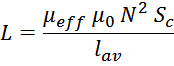
где:
μ0 – магнитная постоянная, 1,25663 · 10-6 Гн/м;
N – число витков обмотки;
Sc – сечение магнитопровода;
lav – эффективная длина средней линии магнитопровода;
μeff – магнитная проницаемость материала сердечника с зазором.
Отсюда можно получить выражение для расчета числа витков:
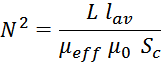
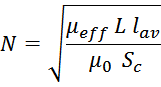
В случае использования магнитопровода с интегрированным зазором для расчета числа витков целесообразно
использовать значение индуктивности единичного витка для данного магнитопровода AL величина
которой указывается в справочных листках.
В этом случае число витков соответственно:
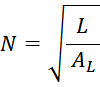
где:
AL – индуктивность единичного витка;
L – требуемая величина индуктивности.
Величина индукции в магнитопроводе с введенным зазором равна:
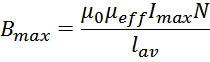
где:
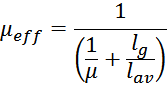
Расчет по соотношению:
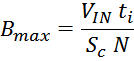
дает аналогичный результат.
В datasheet-ах [Ferrites and Accessories – EPCOS Data Book 2013. EPCOS AG.
ferrites-and-accessories-data-book-130501.pdf], как правило, указывают индивидуальные для каждого
магнитопровода коэффициенты K1 и K2 используя которые можно вычислить необходимую величину зазора для
получения нужной величины индуктивности единичного витка AL:
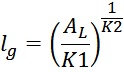
где:
K1 и K2 – коэффициенты, индивидуальные для каждого магнитопровода;
AL – индуктивность единичного витка.
Явление «выпучивания» поля из немагнитного зазора
Как было показано выше введение немагнитного зазора приводит к уменьшению эффективной магнитной
проницаемости. Физически это обусловлено тем, что в магнитную цепь магнитопровода обладающего малым
«магнитным сопротивляемся» вносится участок с большим магнитным сопротивлением – немагнитный зазор.
Добавляем в бочку меда ложку дегтя J. Во всех приведенных выше соотношениях принято допущение, что магнитное
сопротивление зазора линейно возрастает с увеличением его длины. На практике это не совсем так. Дело в том,
что с ростом длины немагнитного зазора линии магнитного поля «выпучиваются» (fringing) наружу и эффективная
площадь магнитного поля зазора становится больше площади поперечного сечения магнитопровода (рисунок
L.4).
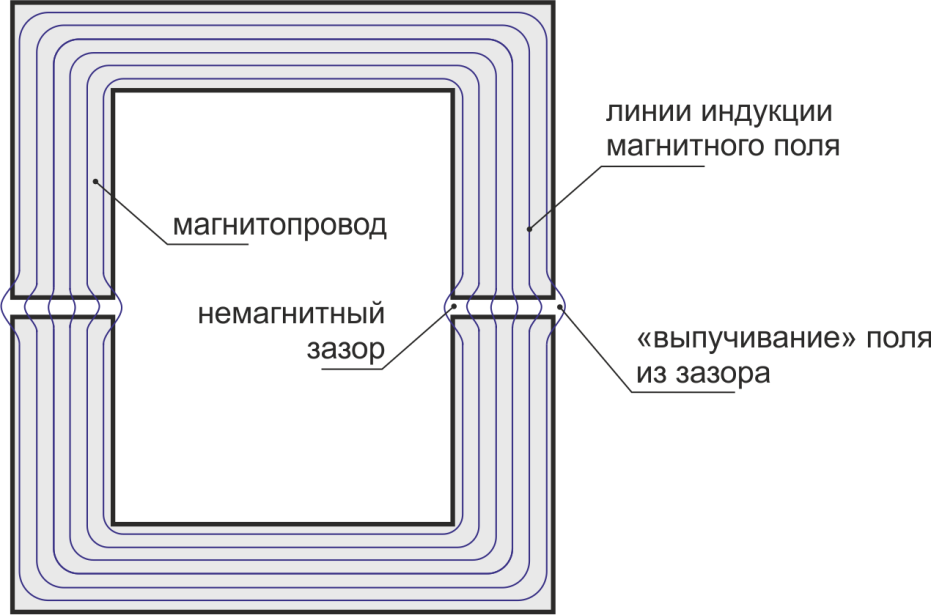
Рисунок L.4 – «Выпучивание» линий магнитного поля из немагнитного зазора
В соответствии с [Magnetics Design Handbook from TI by Lloyd H. Dixon. Section 5. Inductor and Flyback.
Transformer Design. Texas Instruments. 2001. http://www.ti.com/lit/ml/slup127/slup127.pdf] эффективная
площадь магнитного полявычисляется:
Для магнитопроводов с прямоугольным сечением:
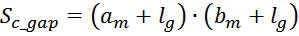
где:
Sc_gap – эффективная площадь охватываемая линями магнитного поля зазора;
am, bm – геометрические размеры магнитопровода вблизи зазора (ширина, глубина);
lg – длина немагнитного зазора.
И с учетом, что площадь сечения магнитопровода определяется как:
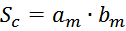
Можно ввести так называемый корректирующий фактор:
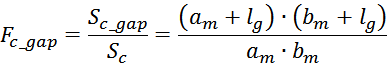
Для магнитопроводов с круглым сечением:
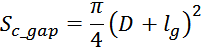
где:
Sc_gap – эффективная площадь охватываемая линями магнитного поля зазора;
D – диаметр поперечного сечения магнитопровода вблизи зазора;
lg – длина немагнитного зазора.
И с учетом, что площадь сечения магнитопровода определяется как:
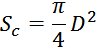
И корректирующий фактор определяется выражением:
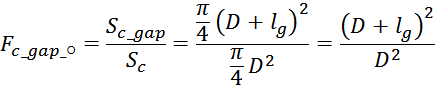
В случае если в магнитную линию магнитопровода введено два зазора, что характерно для магнитопроводов
состоящих из двух половинок (Ш-, П- чашеобразные) то:
используемое в расчетах значение немагнитного зазора делится на два:
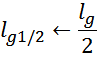
результирующее значение корректирующего фактора рассчитывается как произведение корректирующих факторов от
каждого из зазоров:
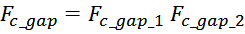
В работе [Colonel Wm. T. McLyman. Transformer and Inductor Design Handbook, Third Edition. CRC Press. 2004.
Chapter 13. Flyback Converter, Transformer Design] корректирующий факторпредлагается вычислить по
соотношению:
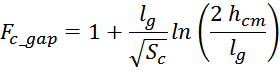
где:
Sc – площадь сечения магнитопровода;
lg – длина немагнитного зазора (используется значение lg даже если зазор разделен на
два);
hcm – высота каркаса магнитопровода.
Расчеты по данной формуле в целом хорошо коррелируют с результатами расчетов по приведенной выше
методике.
Поскольку в магнитопроводе с зазором эффективная площадь поперечного сечения в зазоре увеличивается, то это
приводит к увеличению индуктивности дросселя L на коэффициент Fc_gap:
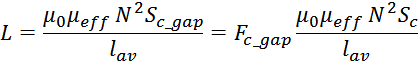
Это можно представить как увеличение эффективной магнитной проницаемости на коэффициент Fc_gap при
прочих равных и неизменных параметрах.
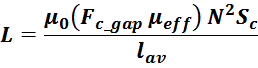
Увеличение эффективной магнитной проницаемости приводит к снижению максимального тока:
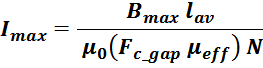
Резюме: явление «выпучивания» магнитного поля с одной стороны приводит к увеличению индуктивности дросселя по
сравнению с рассчитанным значением, с другой стороны приводит к уменьшению максимального тока. При расчетах
дросселя с большими величинами немагнитного зазора необходимо обязательно учитывать явление выпучивания поля
и вносить поправки в расчет. Методика коррекции расчета немагнитного зазора следующая:
рассчитывается целевое значение эффективной магнитной проницаемости µeff ;
рассчитывается величина немагнитного зазора lg на основе целевого значения µeff ;
рассчитывается величина корректирующего фактора Fc_gap для полученного ранее значения немагнитного
зазора lg;
осуществляется итерационный выбор величины немагнитного зазора lg<* с целью достижения заданной
величины магнитной проницаемости µeff:
в качестве первого приближения используется произведение рассчитанной величины немагнитного зазора
lg и корректирующего фактора Fc_gap:
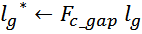
на основании полученного lg* рассчитывается новая величина корректирующего
фактораFc_gap*:
на основании полученного lg* рассчитывается новое значение эффективной магнитной
проницаемости µeff*:
вычисляется произведение полученных величин Fc_gap* и µeff* и
сравнивается с целевым значением магнитной проницаемости µeff:
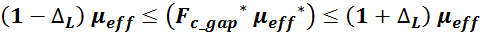
где:
∆L – допустимая погрешность отклонения от заданной величины индуктивности (5%, 10%, 20 % и т.д.).
Если полученное произведение укладывается в рамки допустимого отклонения ∆L, то соответствующее
значение lg* принимается в качестве конструктивного параметра реально вводимого
немагнитного зазора, если нет – изменяют в ту или иную сторону lg* и повторяют
действия, начиная со второго. Так итерационно подбирают значение lg* для обеспечения
заданного значения эффективной магнитной проницаемости.
Если полученное значение Fc_gap превышает 2, то рекомендуется выбрать магнитопровод
больших габаритов и повторить расчет, поскольку, во первых начинает появляться сильная нелинейность
зависимости Sc_gap от lg, во вторых при больших величинах зазора часть витков обмотки
не полностью охватывается магнитным потоком, в третьих значительно возрастает уровень электромагнитных помех
вблизи дросселя, что ухудшает проблемы электромагнитной совместимости.
Представленная выше методика хоть и является достаточно универсальной, но она требует достаточно большого
числа вычислений. При использовании стандартных магнитопроводов лучше и точнее использовать данные в
datasheet-ах аппроксиационные соотношения, связывающие «индуктивность на виток» AL – и величину
введенного немагнитного зазора lg.
В datasheet-ах [Ferrites and Accessories – EPCOS Data Book 2013. EPCOS AG.
ferrites-and-accessories-data-book-130501.pdf], как правило, указывают индивидуальные для каждого
магнитопровода коэффициенты K1 и K2 используя которые можно вычислить необходимую величину зазора для
получения нужной величины индуктивности единичного витка AL:
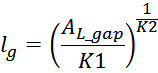
где:
K1 и K2 – коэффициенты, индивидуальные для каждого магнитопровода;
lg – (мм) длина немагнитного зазора (суммарное значение если зазора два);
AL_gap – (нГн) индуктивность единичного витка магнитопровода с зазором.
Индивидуальные для каждого типа магнитопровода коэффициенты K1 и K2 уже учитывают явление «выпучивания»
магнитного потока. Поэтому данным соотношением целесообразно пользоваться.
При практических расчетах необходимо вычислить величину вводимого немагнитного зазора lg на основе
заданного значения эффективной магнитной проницаемости μeff. Выведем соотношение для данных
вычислений.
Выражение для индуктивности единичного витка ALмагнитопровода без зазора имеет вид:
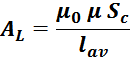
где:
μ – магнитная проницаемость магнитопровода без зазора.
Выражение для индуктивности единичного витка AL_gap магнитопровода с зазоромимеет вид:
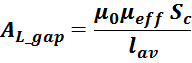
где:
μeff – эффективная магнитная проницаемость магнитопровода с зазором.
Отношение представленных индуктивностей единичного витка равно отношению магнитных проницаемостей:
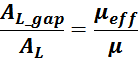
Отсюда можно вывести выражение связывающее индуктивность единичного витка AL_gapмагнитопровода с
зазором с эффективной магнитная проницаемостью данного магнитопровода:
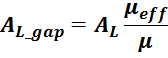
Методика расчета параметров дросселя
Исходные данные
Исходными данными для расчета параметров дросселя являются:
величина индуктивности L;
максимальный рабочий ток Imax;
среднеквадратичное значение тока Irms (максимальное значение);
рабочая частота f;
допустимый суммарный уровень тепловых потерь Ptotal_loss ;
максимальное омическое сопротивление обмотки R.
Индуктивность дросселя
Индуктивность дросселя, зависит от квадрата числа витков, площади сечения сердечника, длины сердечника и
немагнитного зазора:
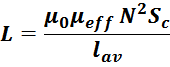
где:
µ0 – магнитная постоянная;
µeff – эффективная магнитная проницаемость сердечника с зазором;
S – площадь сечения магнитопровода;
lav – эффективная длина магнитопровода;
N – число витков.
В справочных листках на магнитопроводы кроме габаритных параметров (Ae – площадь поперечного
сечения сердечника, Amin – площадь окна магнитопровода, le – длина магнитопровода)
часто приводят параметр AL – индуктивность единичного витка.
Если в справочном листке на магнитопровод дана информация об индуктивности единичного витка, то индуктивность
дросселя рассчитывается по простой формуле:
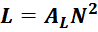
где:
AL – индуктивность единичного витка;
N – число витков в обмотке.
Практически важным для расчетов является значение AL для магнитопроводов с интегрированным
зазором.
Соответственно для расчета числа витков N необходимых для получения заданной величины индуктивности L на
магнитопроводе с известной индуктивностью единичного витка ALиспользуют соотношение:
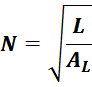
Максимальное значение тока
В соответствии с теоремой о циркуляции вектора напряженности магнитного поля (циркуляция вектора
напряженности магнитного поля по некоторому контуру равна алгебраической сумме токов, охватываемых этим
контуром) произведение тока в единичном витке на количество витков в дросселе численно равно произведению
напряженности магнитного поля в магнитопроводе на его длину (типа «магнитному напряжению»):
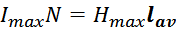
Напряженность магнитного поля связана с индукцией магнитного поля:
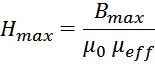
Подставляя, получаем:
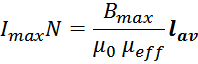
Откуда следует выражение для максимального рабочего тока дросселя:
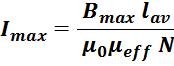
где:
Bmax – максимальная индукция в магнитопроводе;
µ0 – магнитная постоянная;
µeff – эффективная магнитная проницаемость сердечника с зазором;
lav – эффективная длина магнитопровода;
N – число витков.
Оптимальное проектирование силового дросселя
Оптимальное проектирование по критерию максимального использования магнитопровода заключается в том, чтобы
спроектировать дроссель таким образом, чтобы обеспечить максимальное использование возможностей содержания
(«феррита» магнитопровода) при одновременно максимальном использовании возможностей формы (геометрии
магнитопровода). Наглядно эту философию иллюстрирует рисунок L.5.
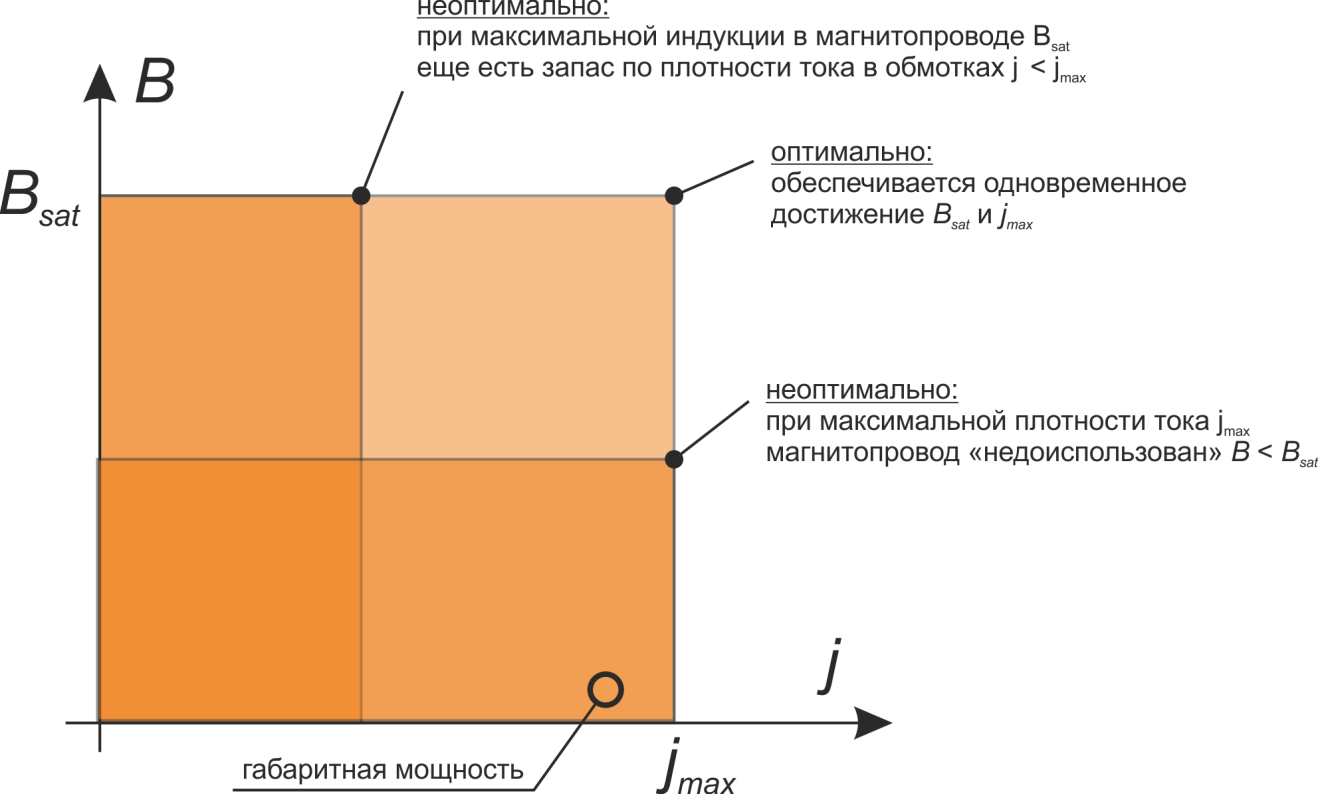
Рисунок L.5 – К определению критерия максимального использования магнитопровода
Максимальные возможности «феррита» магнитопровода определяются либо потерями, которые
характеризуются энергоовыделением в магнитопроводе, либо индукцией насыщения Bsat. Потери зависят
от размаха индукции ΔB и частоты f. В работе [Magnetics Design Handbook from TI by Lloyd H. Dixon. Section
5. Inductor and Flyback. Transformer Design. Texas Instruments. 2001.
http://www.ti.com/lit/ml/slup127/slup127.pdf] принято, что максимальный уровень потерь в магнитопроводе
составляет 0,1 Вт/см3. Индукция насыщения Bsatбольшинства ферритов не превышает 0,3
Тл.
Максимальные возможности геометрии магнитопровода прежде всего определяются возможностями
размещения в окне магнитопровода проводников обмотки. Условие максимального использования окна состоит в
максимально полной «набивке» окна магнитопровода при выполнении условия максимальной плотности тока в
обмотке. В той жеработе [Magnetics Design Handbook from TI by Lloyd H. Dixon. Section 5. Inductor and
Flyback. Transformer Design. Texas Instruments. 2001. http://www.ti.com/lit/ml/slup127/slup127.pdf] принято,
что максимальный уровень плотности тока для условий конвективного охлаждения составляет 4,2 А/см2.
На практике, необходимо просчитывать каждый конкретный случай геометрии и условий охлаждения сердечника. При
этом критерий максимального использования магнитопровода не всегда является оптимальным экономически, но это
весьма хорошее приближение.
При проектировании силового дросселя важно помнить, что потери в ферритовом сердечнике растут с увеличением
размаха индукции ΔB нелинейно. То есть если размах индукции ΔB возрастает в 2 раза то потери могут вырасти,
к примеру, в 10 раз. Таким образом, для уменьшения потерь в магнитопроводе не стоит гнаться за достижением
максимально допустимого ΔB. С другой стороны при увеличении площади заполнения окна магнитопровода обмоткой
при увеличении числа витков и одновременном увеличении немагнитного зазора (чтобы L не изменилась) потери
возрастают линейно. Это означает, что зачастую целесообразно использовать «под завязку» все окно
магнитопровода и ввести такой немагнитный зазор, какой необходимо для обеспечения заданного значения
индуктивности L. При таком подходе потери будут уменьшены, но стоимость изделия возрастет.
Подробное описание методики выбора конструктивных элементов дросселя – магнитопровода, обмоток (типы и
сравнительная характеристика геометрии магнитопроводов, типы и характеристики ферритов для импульсных
источников питания, конструктивные особенности обмоток) даны в разделе «Трансформатор»).
Габаритный параметр силового дросселя. Вывод соотношения
Для определения «масштаба бедствия», то есть ориентировочных габаритов необходимого магнитопровода необходимо
рассчитать габаритный параметр дросселя – произведение ширины окна и сечения магнитопровода
S0SС. Выведем соотношение для расчета S0SС.
Площадь окна магнитопровода S0
Площадь окна магнитопровода, занимаемая медью обмоток составляет:
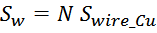
где:
N – число витков в обмотке;
Swire_Cu – площадь сечения провода обмотки «по меди».
Плотность тока в проводнике обмотки определяется как отношение тока I в нем к площади сечения:
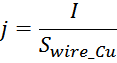
Максимальное значение плотности тока в обмотке ограничивается её омическим нагревом, величина которого
определяется среднеквадратичным значением тока через обмотку Irms:
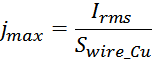
Отсюда можно выразить площадь сечения провода через отношение тока через провод к максимальной плотности тока
jmax в нем:
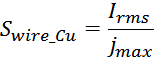
Подставляя это выражение в выражение для площади окна магнитопровода занимаемой медью, получаем соотношение
для площади, занимаемой медью обмоток:
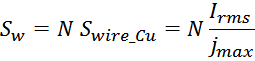
Среднеквадратичное значение тока определяется формой импульсов тока через обмотку.
Отношение площади занимаемой проводниками обмоток к общей площади окна магнитопровода называют коэффициентом
заполнения окна k0 :
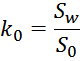
где:
S0 – общая площадь окна сердечника;
Sw – часть площади окна сердечника заполненную проводниками обмоток.
Таким образом, можно получить выражение для общей площади окна, в которой размещена обмотка дросселя:
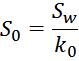
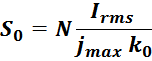
Из выражения также следует соотношение для максимального числа витков Nmax, которые физически
можно «втиснуть» в окно манитопровода:
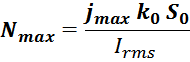
где:
S0 – общая площадь окна сердечника;
k0 – коэффициентом заполнения окна;
jmax – максимальная плотность тока (значение на постоянном токе);
Irms – среднеквадратичное значение тока, которое определяет тепловые потери.
Площадь сечения магнитопровода SС
По определению индуктивность есть коэффициент пропорциональность между потокосцеплением (суммой магнитных
потоков всех витков) и током:
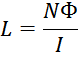
Магнитный поток витка есть произведение магнитной индукции на площадь поперечного сечения магнитопровода:
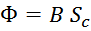
Отсюда:
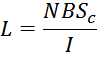
Откуда следует выражение для площади сечения магнитопровода SС:
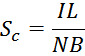
В перечисленных соотношениях соотношении подразумевается одномоментное значение тока. При этом максимальное
значение тока Imax будет соответствовать максимальному значению индукции в магнитопроводе Bmax:
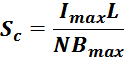
где:
Imax – максимальное значение тока обмотки дросселя.
L – индуктивность дросселя;
Bmax – максимальная индукция в магнитопроводе;
N – число витков.
Габаритный параметр дросселя S0SС
Перемножая соотношения для S0 и SС, получаем:
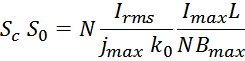
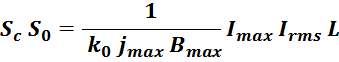
где:
k0 – коэффициент заполнения окна магнитопровода равный отношению площади занимаемой проводниками
обмоток к общей площади окна магнитопровода.
jmax – максимальное значение плотности тока в проводнике;
Bmax – максимальное значение индукции в магнитопроводе;
Imax – максимальное значение тока через дроссель;
L – индуктивность дросселя.
Система из четырех уравнений – «четыре кита» для расчета силового дросселя
Итого для расчета дросселя мы имеем систему из четырех уравнений с пятью неизвестными:
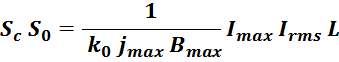
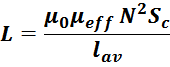
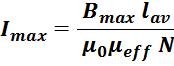
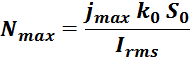
Эта система имеет бесконечное число взаимозависимых решений. В реальности решения «квантованы», что
определяется прежде всего фиксированными размерами магнитопровода. Непосредственный расчет конструкции
дросселя осуществляется с использованием данных уравнений в строгой последовательности.
На основе расcчитанного значения габаритного параметра ScS0 можно определить конкретный
трансформатор с конкретными Sc, S0, l, µ. Вопрос в том какой должна быть эффективная
магнитная проницаемость магнитопровода µeff, на основании значения которой рассчитывается
вводимый зазор и каким должно быть число витков N. С одной стороны эффективная магнитная проницаемость
µeff и число витков N входят в формулу для индуктивности дросселя, с другой – в соотношение для
его максимального тока. Выразим из данных соотношений µeff :
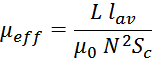
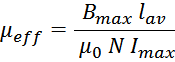
Приравнивая полученные выражения:
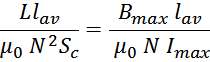
Получим выражение для числа витков дросселя:
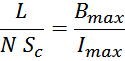
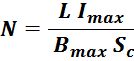
Если полученное значение для числа витков N меньше значения максимального числа витков Nmax
умещаемых в окне магнитопровода:
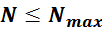
то расчет можно продолжить. Если нет, то нужно выбрать магнитопровод покрупнее.
Эффективную магнитную проницаемость магнитопровода µeff можно найти, подставляя полученное число
витков в полученное выше выражение:
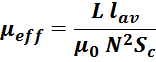
Основные соотношения расчета конструкции силового дросселя
Конструктивный расчет является важной составляющей всего расчета дросселя, так как только после выполнения
расчета конструкции можно корректно рассчитать все паразитные параметры трансформатора, определить его
тепловой режим и в конечном итоге спроектировать надежный источник питания.
Расчет конструктивных особенностей силового дросселя во многом определяется типом магнитопровода. Порядок
расчета значительным образом отличается для магнитопровода с цилиндрической обмоткой (Ш-, П-образный,
чашкообразный) и обмоткой тороидальной (тор, кольцо).
Параметры обмоточного провода
Площадь поперечного сечения провода обмотки Swire_Cu рассчитывается по соотношению, связывающему
заданную максимальную плотность тока в обмотке jmax и максимальное значение тока Imax:
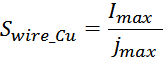
Более корректно было бы учитывать не максимальное, а среднеквадратичное значение, но на практике в
большинстве случаев такое упрощение не существенно влияет на результат. Тем более, что плотность тока
выбирается ориентировочно. В дальнейшем выполняется точное вычисление рассеиваемой мощности и по
необходимости вносятся коррективы в конструкцию.
Исходя из вычисленного значения площади Swire_Cu рассчитывают диаметр проводов обмотки (по меди)
исходя их соотношения, связывающего площадь с диаметром:
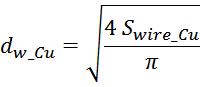
Однако полученное значение почти наверняка точно не совпадет с характеристиками выпускаемых обмоточных
проводов. Поэтому на основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода
(по меди) из номенклатуры диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в
большую сторону.
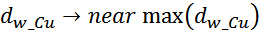
В соответствии со справочным листком на моточные провода определяется диаметр с изоляцией выбранного типа
обмоточного провода dw_ins :
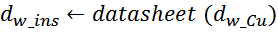
Диаметр провода в изоляции, является одним из базовых параметров и учитывается при расчете числа витков в
одном слое, проверки условия размещения обмоток в окне магнитопровода и т.д.
Средняя длина витка обмотки дросселя
Средняя длина витка обмотки lw_t_av определяется исходя из геометрических соображений как среднее
арифметическое между длинами первого lw_first, и последнего витка lw_last обмотки:
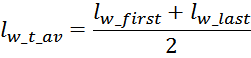
Ниже представлены соотношения для расчета средней длины витка для различных типов магнитопроводов.
Ш- и П- образные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредняя длина
витка оценивается исходя из конфигурации магнитопровода (рисунок L.6).
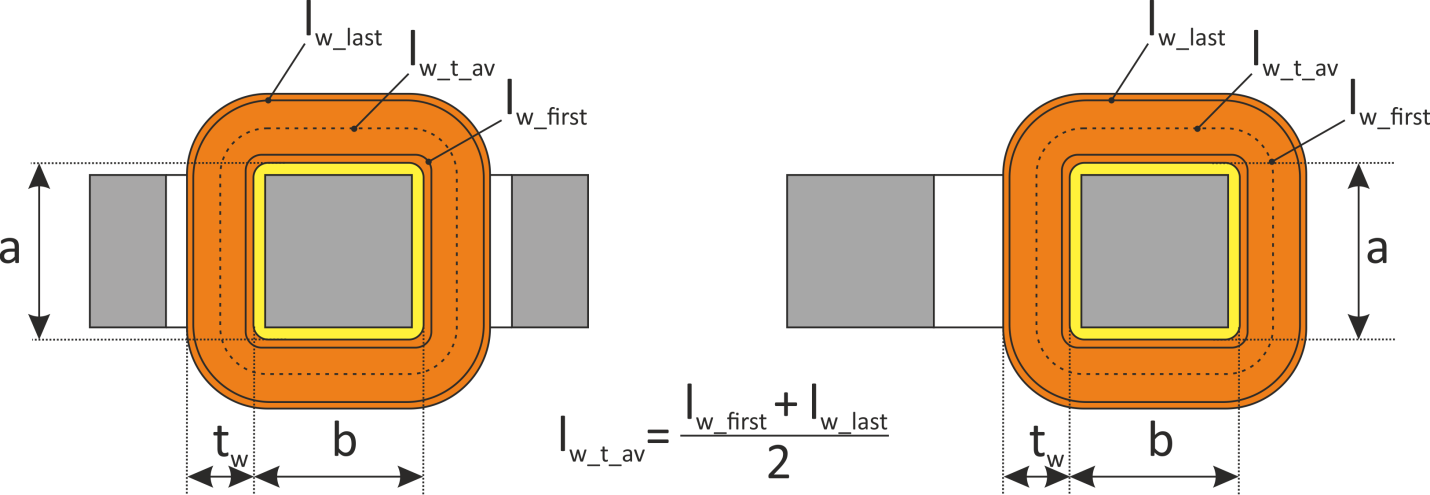
Рисунок L.6 К определению средней длины витка для Ш- и П- образных магнитопроводов
Длина внешнего витка обмотки lw_last (без учета закруглений) равна:
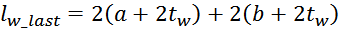
Или, упрощая:
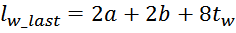
Длина внутреннего витка обмотки lw_first равна:
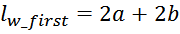
Здесь:
a, b – геометрические параметры, характеризующие сечение каркаса магнитопровода;
tw – толщина обмотки.
В первом приближении толщину обмотки tw можно посчитать исходя из соотношения учитывающее число
слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность намотки):
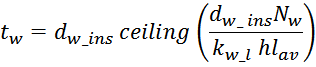
где:
ceiling – функция округления до большего целого;
hlav – средняя ширина намоточного слоя, для Ш- и П- образных магнитопроводовопределяется высотой
каркаса магнитопровода hcm.
Nw – число витков в обмотке;
kw_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода (таблица L.1).
Таблица L.1 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
Итого, объединяя, получаем:
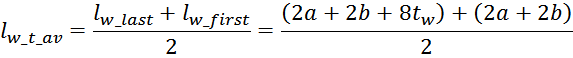
Итоговое выражение для средней длины витка обмотки:
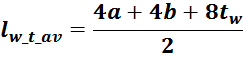
где толщина обмотки:
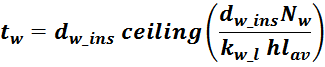
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка оценивается следующим образом:
Длина внутреннего витка lw_first равна:
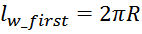
где:
R – внутренний радиус каркаса магнитопровода.
Длина внешнего витка lw_last равна:
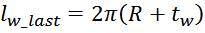
где:
tw – толщина обмотки.
В первом приближении толщину первичной обмотки t1 можно посчитать исходя из соотношения
учитывающее число слоев и толщину провода (здесь не учитывается межслоевая изоляция и плотность намотки):
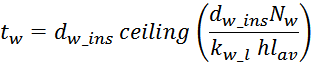
Итого, объединяя, получаем:
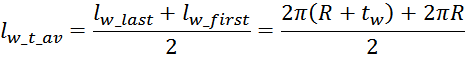
Итоговое выражение для средней длины витка обмотки:
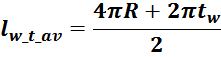
где:
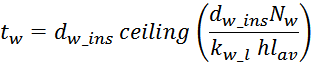
Тороидальные магнитопроводы
Для тороидальных магнитопроводов расчет среднего витка несколько сложнее. Это обусловлено тем, что толщина
внутреннего слоя обмотки будет выше плотности намотки внешнего слоя вследствие того что длина внутреннего
кольца тора меньше длины внешнего кольца.
Внешний виток обмотки на тороидальных магнитопроводах представляет собой трапецию со скругленными углами
(рисунок L.7). Разобьём внешний виток обмотки на 8 частей: четыре сектора по четверти окружности, два из
которых имеют радиус равный толщине внешнего tw_ext, а два – внутреннего tw_int слоев
обмотки, две высоты магнитопровода hm и два сегмента (боковые стороны трапеции) длина которых
определяется из теоремы Пифагора для прямоугольного треугольника (из ширины магнитопровода wm, и
разницы высот внутреннего tw_ext и внешнего tw_int витков).
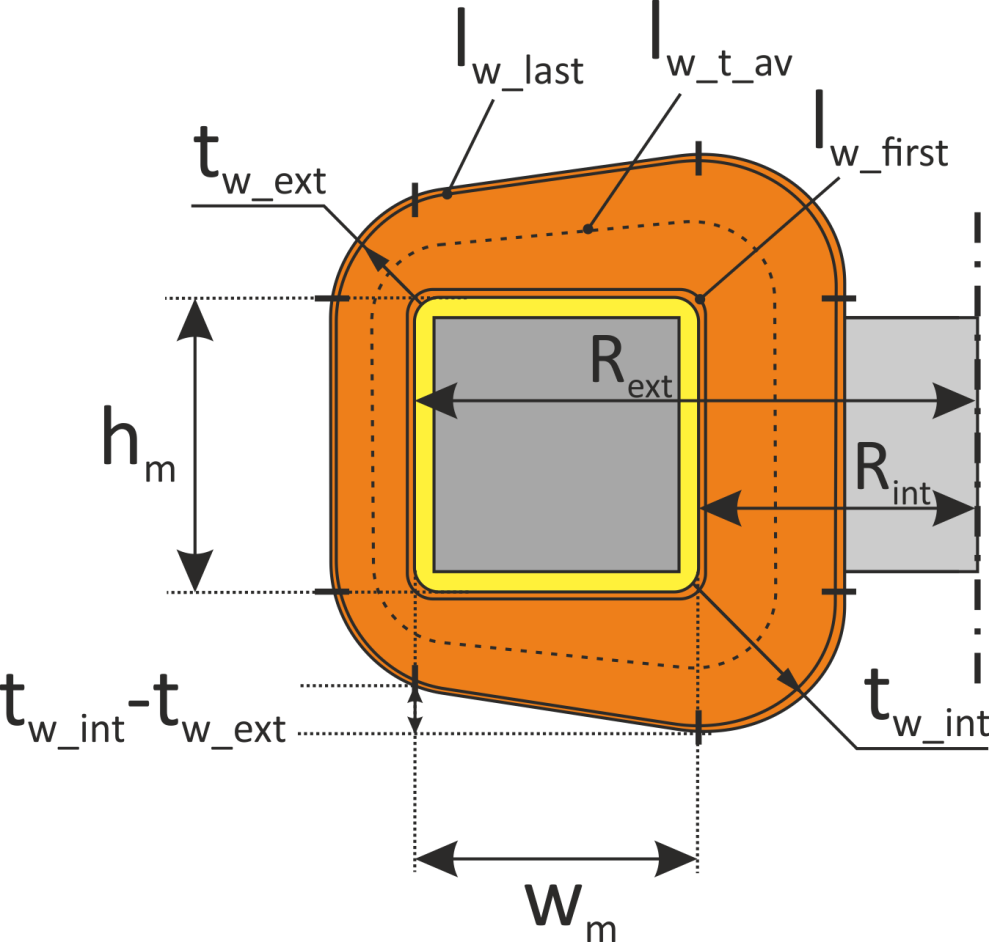
Рисунок L.7 – К определению средней длины витка тороидальных магнитопроводов
Итого общая длина внешнего витка первичной обмотки с учетом закруглений равна:
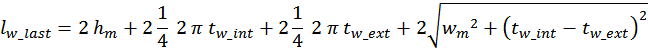
Или:
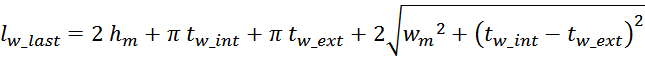
Общая длина внутреннего витка обмотки при условии прямоугольного сечения магнитопровода равна:
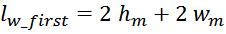
Плотность намотки и соответственно толщина внутреннего слоя обмотки будет выше плотности намотки внешнего
слоя. В первом приближении коэффициент пропорциональности равен отношению длин окружностей внешнего и
внутреннего радиусов тора. Можно считать, что толщины внешнего tw_ext и внутреннего
tw_int слоев обмотки связаны этим коэффициентом пропорциональности. Таким образом:
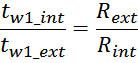
Rext – внешний радиус тора;
Rint – внутренний радиус тора.
Аналогично случаю с Ш- и П- образными магнитопроводами можно в первом приближении найти толщину
tw_int внутреннего слоя обмотки исходя их соотношения учитывающее число слоев и толщину провода
(здесь не учитывается межслоевая изоляция и плотность намотки). Только в качестве высоты обмотки используем
длину внутренней окружности тора:
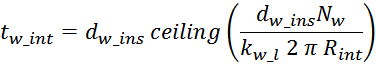
где:
функция (ceiling) – округление до большего целого;
dw_ins – диаметр обмоточного провода с изоляцией;
Rint – внутренний радиус тора;
Nw – число витков в обмотке;
kw_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода (таблица L.1).
На основании оценочного значения толщины внутреннего слоя tw_int можно воспользовавшись пропорцией
определить толщину внешнего слоя tw_ext:
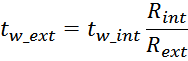
Итого, объединяя, получаем:
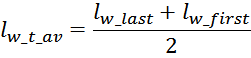
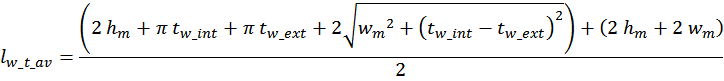
Итоговое выражение для средней длины витка обмотки имеет вид:
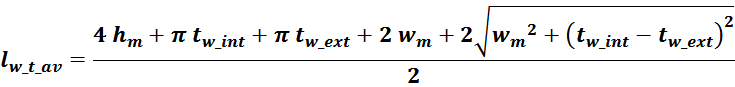
где:
tw_int – толщина внутреннего слоя обмотки:
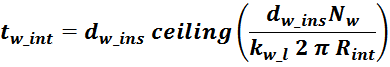
tw_ext – толщина внешнего слоя обмотки:
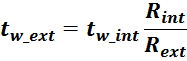
Определение длины обмотки
Длина обмотки lw определяется как произведение средней длины витка на число витков Nw:
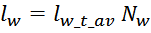
Полученная величина определяет, сколько провода нужно отмерить на обмотку дросселя и используется при расчете
омического сопротивления обмотки.
Фактическая проверка возможности размещения обмотки дросселя
Несмотря на то, что в начале проектирования дросселя задается коэффициент заполнения окна магнитопровода
k0, исходя из типа магнитопровода, по окончании расчета необходимо выполнить окончательную
проверку возможности размещения обмотки. Дело в том, что коэффициент заполнения окна магнитопровода
k0 является оценочным параметром, на основе которого определяется габаритный параметр дросселя. В
зависимости от выбранного типа магнитопровода, типа и толщины обмоточного провода, толщины межслоевой
изоляции реальный коэффициент k0 может существенно изменяться. Поэтому после всех расчетов
необходимо проверить факт реального размещения обмотки в окне магнитопровода. Кроме этого, может быть
неоптимальное использование окна магнитопровода, если останется слишком много свободного места в окне
обмотки.
Расчет структуры дросселя существенным образом различается для различных типов магнитопровода. Ниже приведен
расчет для наиболее распространенных геометрий магнитопровода:
Ш- и П- образные и чашеобразные магнитопроводы
Для конструктивного расчета структуры цилиндрической обмотки дросселя определяется средняя ширина намоточного
слоя hlav. Она равна высоте каркаса магнитопровода hcm (рисунок L.8):
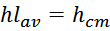
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
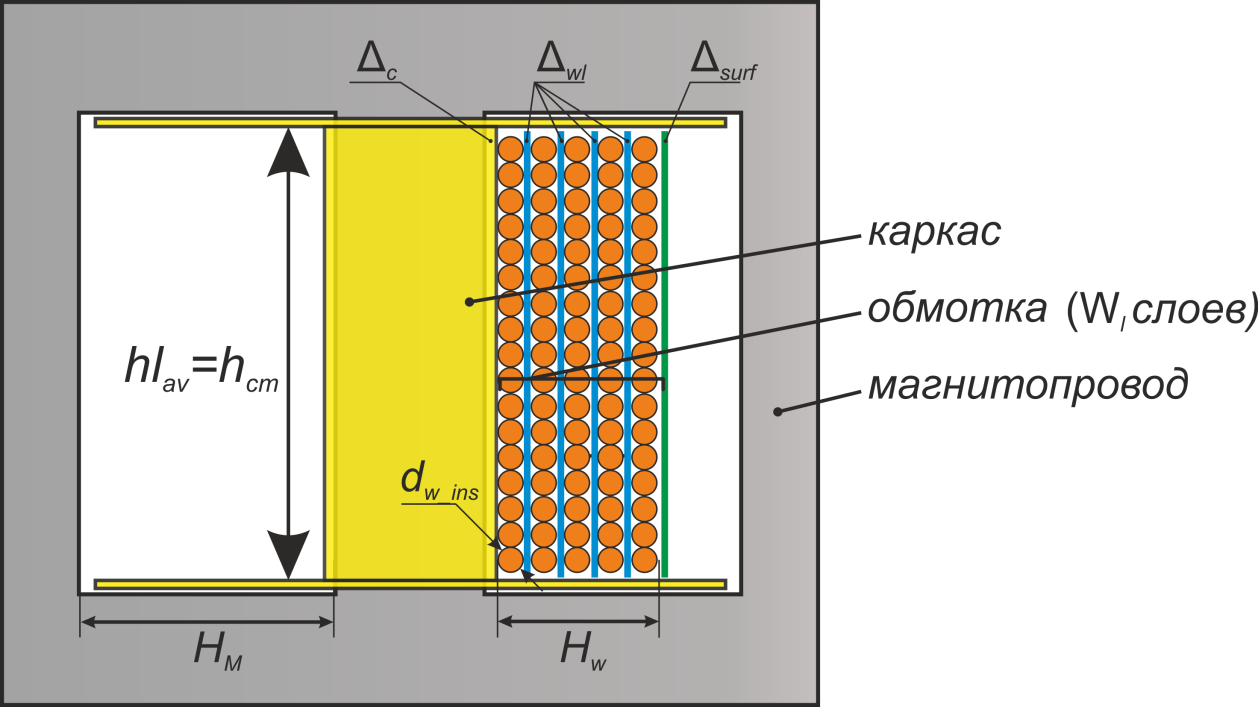
Рисунок L.8 – К расчету конструкции обмотки дросселя
Исходя из полученной величины hlav и известной величины диаметра проводника обмотки с изоляцией
dw ins определяется число витков в одном слое обмотки Nl. Число витков в одном слое
рассчитывается как произведение коэффициента укладки kl и меньшего целого (floor) от отношения
hcm(определяет hlav) к диаметру проводника обмотки с изоляцией dw_ins:
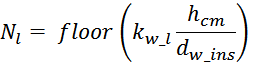
где:
floor – операция округления до меньшего целого;
hcm – высота каркаса магнитопровода;
dw_ins – диаметр проводника обмотки с изоляцией;
kw_l – коэффициент укладки (laying), зависящий от толщины провода (таблица L.1).
Таблица L.1 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.].
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
На основе числа витков в одном слое Nl рассчитывается общее число слоев обмотки. Число слоев в
обмотке дросселя Wl определяется как отношение числа витков в обмотке к числу витков в единичном
слое с округлением до большего целого (ceiling):
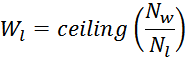
где:
Nw – число витков в обмотке;
Nl – число витков в одном слое обмотки;
ceiling – функция округления до большего целого.
Теперь, когда известно число слоев можно рассчитать толщину обмотки. Толщина обмотки дросселя Hw
рассчитывается по соотношению, учитывающему толщину межслоевой изоляции [Сетевые блоки питания с
высокочастотными преобразователями. О.А. Эраносян. Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
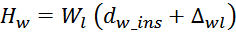
где:
Δwl – толщина межслоевой изоляции обмотки;
Wl – число слоев в обмотке;
dw_ins – диаметр провода обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величина Δwl принимается равно нулю (в
реальности, при плотно намотке за счет укладывания витков следующего слоя в пазы слоя предыдущего толщина
обмотки может быть несколько меньше).
«Пирог» обмотки кроме собственно самой обмотки проводом включает в себя каркас, определяющий расстояние между
поверхностью каркаса и магнитопроводом и слой внешней изоляции обмотки. Суммарная толщина «пирога» намотки HΣ
составляет:
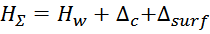
где:
Hw – толщина обмотки дросселя;
Δc – толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом);
Δsurf – толщина слоя внешней изоляции обмотки.
Складывая все составляющие проверяем условие фактического размещения всех конструктивных элементов обмотки в
окне магнитопровода:
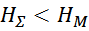
где:
HΣ – суммарная толщина «пирога» намотки;
HM – ширина окна магнитопровода.
Тороидальные магнитопроводы
Особенностью использования тороидальных (кольцевых) магнитопроводов является то, что по мере выполнения
обмотки ширина намоточного слоя hl (высота обмотки) которая определяется внутренней окружностью уменьшается.
То есть число витков в последующем слое обмотке будет меньше, чем в предыдущем. Эта нелинейность вносит
существенные коррективы в расчет конструкции трансформаторов и дросселей, выполненных на тороидальных
магнитопроводах.
Итак, для первого слоя обмотки ширина намоточного слоя hl1 определяется выражением:
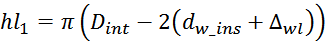
где:
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δwl – толщина межслоевой изоляции обмотки;
dins – диаметр провода обмотки с изоляцией.
Исходным внутренним диаметром для выполнения первого слоя обмотки является величина внутреннего диаметра тора
магнитопровода с учетом изоляции Dint. Далее при выполнении обмотки от слоя к слою внутренний
диаметр уменьшается на величину равную удвоенной толщине проводника обмотки с межслоевой изоляцией 2(dw_ins
+ Δwl).
Для 2-го слоя ширина обмотки будет равна:
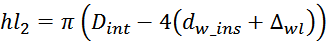
Для 3-го слоя:
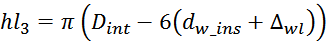
Для n-го слоя:
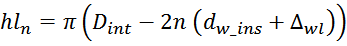
То есть мы получаем убывающую арифметическую прогрессию.
С учетом конструктивной необходимости должен оставаться некоторый остаточный диаметр магнитопровода
D0. При этом обеспечивается условие:
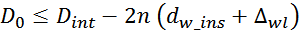
где:
D0 – остаточный диаметр магнитопровода.
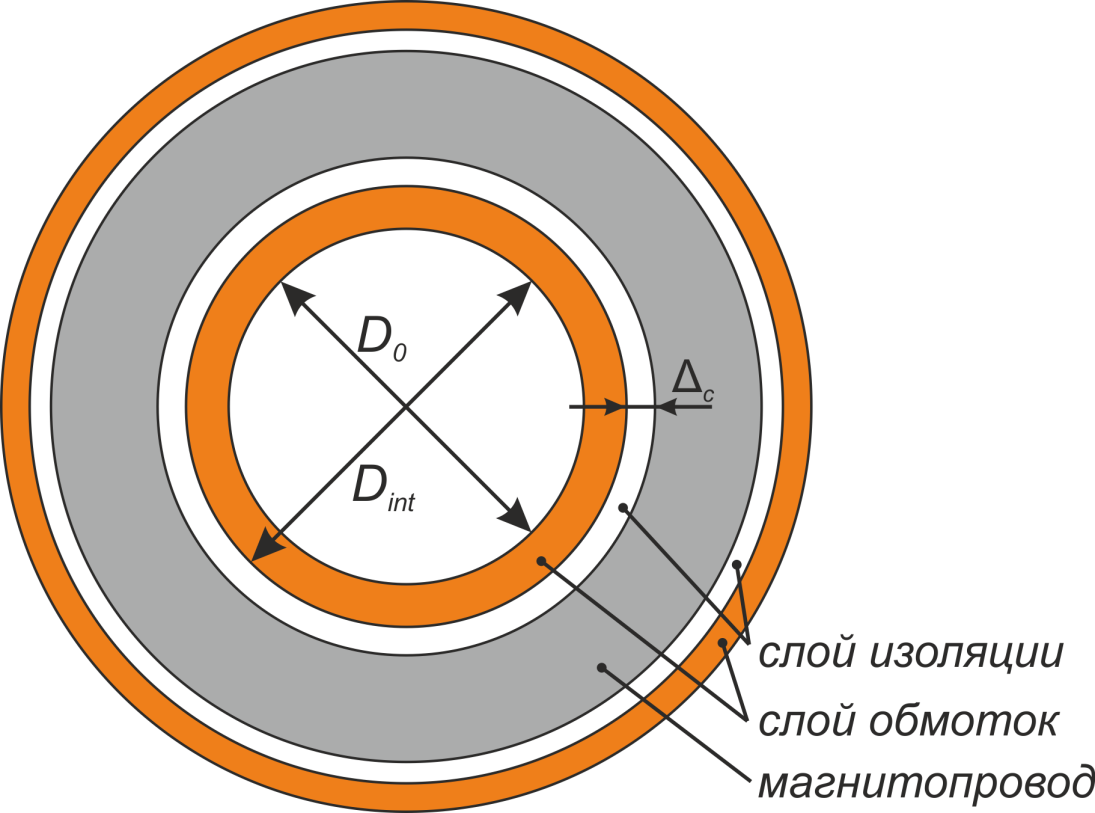
Рисунок L.9 – К расчету конструкции обмоток тороидального дросселя: Dint – внутренний диаметр
тора магнитопровода с учетом слоя изоляции, D0 – остаточный технологический диаметр.
Используя знак равенства в предыдущем выражении получаем выражение для числа слоев обмотки Wl:
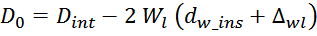
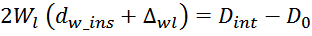
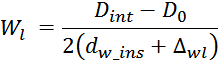
Уменьшение ширины намоточного слоя при переходе от слоя к слою определяется выражением:
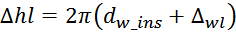
Уменьшение числа витков от слоя к слою определяется выражением:
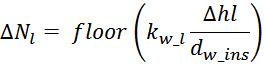
где:
операция (floor) – округление до меньшего целого;
Δhl – уменьшение ширины намоточного слоя от слоя к слою;
dw_ins – диаметр проводника обмотки с изоляцией;
kw_l – коэффициент укладки обмотки, зависящий от толщины провода (таблица L.1).
Таблица L.1 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.].
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
С учетом того, что число витков от слоя к слою уменьшается в соответствии с законом арифметической
прогрессии, то сумма всех витков Nw определяется соотношением:
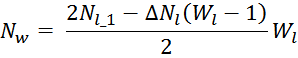
где:
ΔNl – уменьшение числа витков от слоя к слою;
Wl – число слоев обмотки;
Nl_1 – число витков первого слоя обмотки, определяемое из выражения:
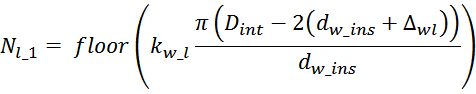
Практический интерес представляет обратная задача – нахождение числа слоев при заданном числе витков в
обмотке. Преобразуем предыдущее выражение суммы арифметической прогрессии к виду:
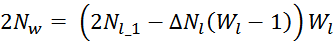
И проводя ряд преобразований:
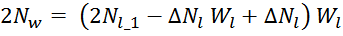
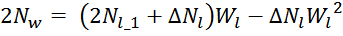
Получаем квадратное уравнение:
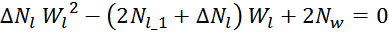
Решая это квадратное уравнение, и отбрасывая корень, не имеющий физического смысла, получаем выражение для
числа слоев обмотки Wl:
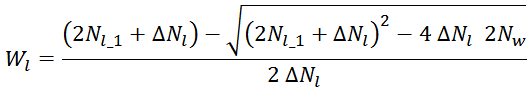
Полученное значение, как правило, будет дробным, и число слоев обмотки Wlопределяется округлением
полученного числа до большего целого (ceiling):
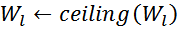
Толщина обмотки Hw рассчитывается по соотношению, учитывающему толщину межслоевой изоляции
[Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян. Энергоатомиздат. Ленингр.
отд-ние, 1991, 176 с.]:
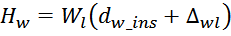
где:
Δwl – толщина межслоевой изоляции обмотки;
Wl – число слоев в первичной обмотке;
dw_ins – диаметр провода обмотки с изоляцией.
Далее необходима проверка условия фактического размещения обмотки в окне магнитопровода. Суммарная толщина
«пирога» намотки составляет:
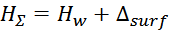
где:
Hw – толщина обмотки;
Δsurf – толщина слоя внешней изоляции обмотки.
Должно выполняться условие размещения всех конструктивных элементов обмотки в окне магнитопровода:
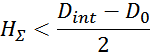
где:
HΣ – суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 – остаточный диаметр внутри тороидального дросселя (технологический).
Последовательность расчета силового дросселя
Входными данными для расчета силового дросселя являются:
величина заданной индуктивности дросселя L;
максимальное значение тока через дроссель Imax;
среднеквадратичное значение тока через дроссель Irms;
рабочая частота f .
Среднеквадратичное значение тока Irms, протекающего через силовой дроссель зависит от формы тока
протекающего через дроссель, которая определяется режимом работы дросселя.
1. Определение типа дросселя, расчет среднеквадратичного значения тока
Задача расчета силового дросселя по сути, сводится к задаче расчета конструкции дросселя для получения
заданной L с максимальным током Imax и обеспечивающем протекание тока с заданным
среднеквадратичным значением Irms при условии минимальных габаритов дросселя.
Перед началом расчетов необходимо определить тип силового дросселя, то есть то в каком преобразователе или
стабилизаторе дроссель будет использоваться. Это накладывает определенные особенности на токовый режим и
предопределяет последовательность дальнейших расчетов.
Ниже перечислены основные типы силовых дросселей:
силовой дроссель выходного фильтра преобразователей напряжения (прямоходовый преобразователь, преобразователь
«косой полумост», полумостовой, мостовой преобразователи, преобразователь «пуш-пул»). Этот тип дросселя
работает в непрерывном режиме.
силовой дроссель стабилизаторов напряжения – понижающего, повышающего и инвертирующего стабилизаторов. Этот
тип дросселя может работать как непрерывном так и в прерывистом режиме.
Определяем среднеквадратичное значение тока Irms, протекающего через силовой дроссель. Оно
различно для прерывистых и непрерывных токов:
– для силовых дросселей выходного фильтра преобразователей напряжения и силовых дросселей понижающего, повышающего и инвертирующего стабилизаторов работающих в режиме непрерывных токов.
В режиме непрерывных токов характерной является форма импульсов тока дросселя изображенная на рисунке L.10
(раздел «Резисторы»).
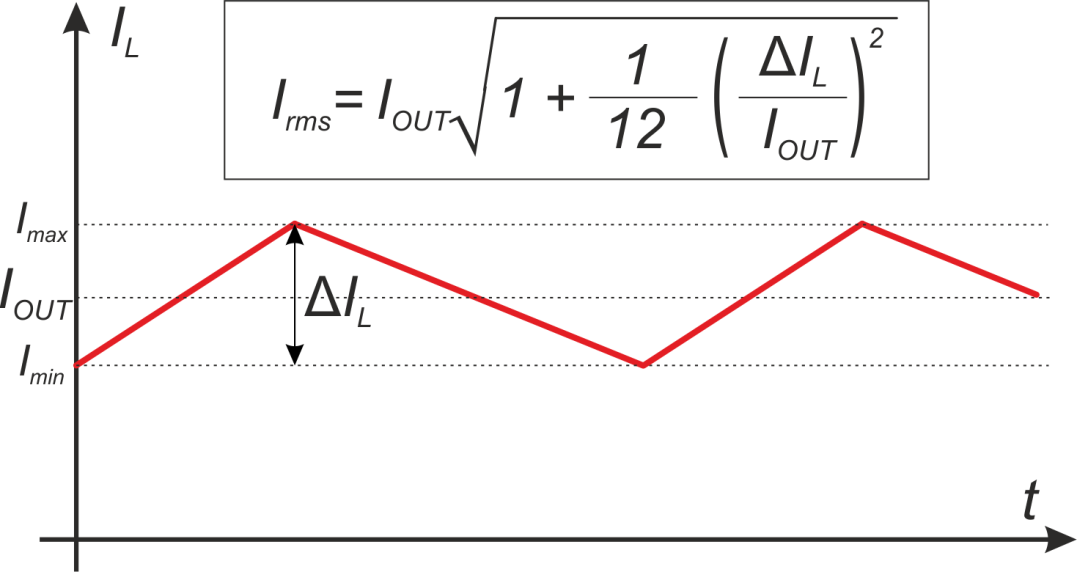
Рисунок L.10 – К расчету среднеквадратичного значения тока при треугольной форме импульсов и непрерывном
токе
Среднеквадратичное значение тока Irms определяется из соотношения:
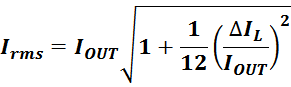
где:
IOUT – выходной ток (максимальное значение);
ΔIL – величина пульсаций тока дросселя (размах импульсов – разница между минимальным и
максимальным значениями).
– для дросселей понижающего, повышающего и инвертирующего стабилизаторов работающих в режиме прерывистных токов (или в пограничном режиме).
В режиме прерывистых токов характерной является форма импульсов тока дросселя изображенная на рисунке L.11
(раздел «Резисторы»).
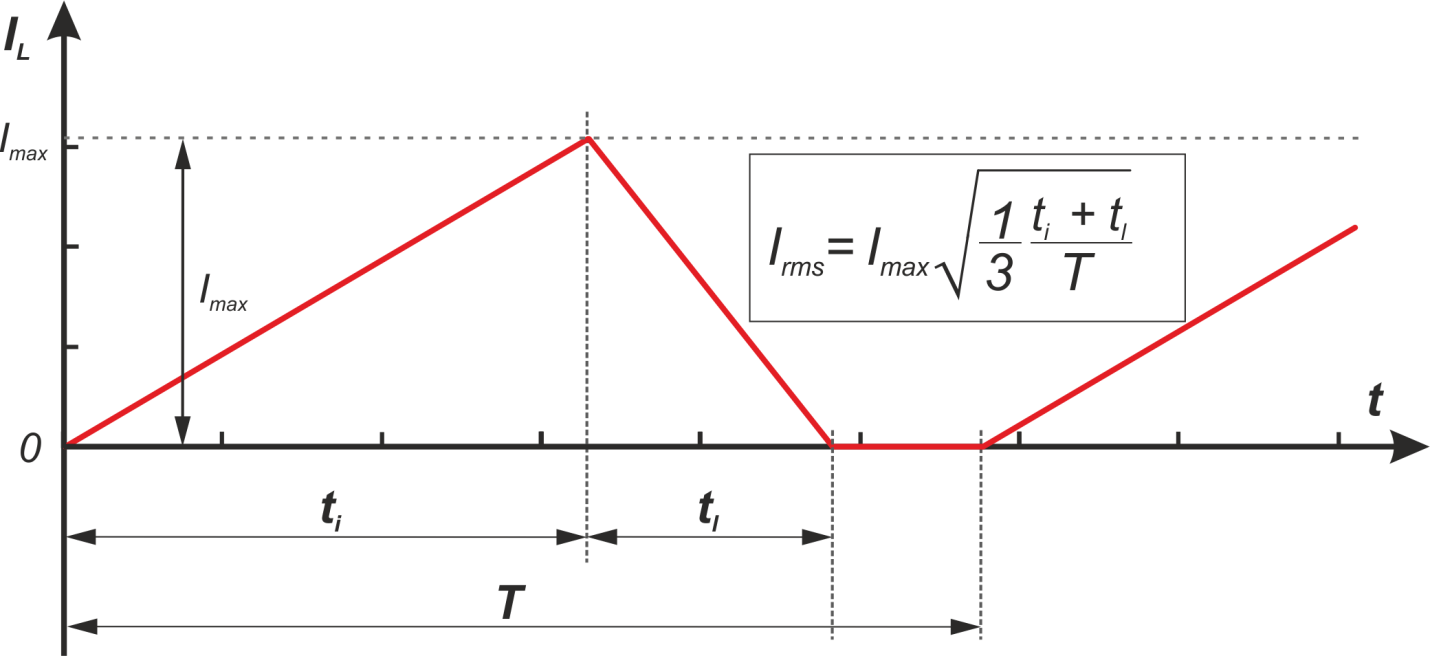
Рисунок L.11 – К расчету среднеквадратичного значения тока при треугольной форме импульсов и прерывистом
токе – к расчету дросселей понижающего стабилизатора работающего в режиме прерывистных токов (или в
пограничном режиме)
Среднеквадратичное значение тока Irms определяется из соотношения:
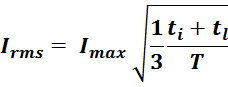
где:
Imax – максимальное значение (амплитуда импульсов);
ti – длительность переднего фронта импульса (рост);
tl – длительность заднего фронта импульса (спад).
T – период повторения импульсов.
В пограничном режиме рост ti и спад тока tl занимают весь период и выражение для Irmsможет
быть упрощено:
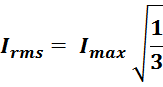
2. Определение габаритного параметра дросселя SCS0
Определяем габаритный параметр дросселя SCS0:
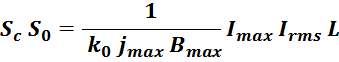
где:
k0 – коэффициент заполнения окна магнитопровода равный отношению площади занимаемой проводниками
обмоток к общей площади окна магнитопровода;
jmax – максимальное значение плотности тока в проводнике;
Bmax – максимальное значение индукции в магнитопроводе;
Imax – максимальное значение тока через дроссель;
Irms – среднеквадратичное значение тока через дроссель;
L – индуктивность дросселя;
S0 – площадь окна сердечника дросселя;
SС – площадь поперечного сечения сердечника дросселя.
Ниже даны рекомендации по выбору параметров, входящих в соотношение габаритного параметра дросселя:
k0 – коэффициент заполнения окна магнитопровода выбирается в зависимости от типа
используемого магнитопровода:
для Ш-образного магнитопровода [Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян.
Энергоатомиздат. Ленингр. отд-ние, 1991, 176 с.]:
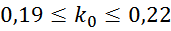
(в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника дросселя уже с
учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 – [McLyman C.
Transformer and inductor design handbook.2004]).
для кольцевого магнитопровода [Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет.
Учебное пособие. — М.: СОЛОН-ПРЕСС, 2008. — 448 с. – 57 стр.]:
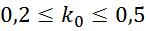
jmax – максимальное значение плотности тока в проводнике выбирается в пределах 4-8
А/мм2. Чем больше «прокачиваемая» мощность, тем меньше выбирается значение плотности тока.
Bmax – максимальное значение индукции в магнитопроводе определяется исходя из
параметров используемого феррита и рабочей частоты. Для определения данного параметра необходимо, хотя бы
предварительно, выбрать тип феррита. В первом приближении и в типовом случае принимается в пределах 0,15-0,2
Тл;
Imax – максимальное значение тока через дроссель является входным параметром для
расчета;
Irms – среднеквадратичное значение тока через дроссель рассчитывается в зависимости
от формы протекающего тока по соотношениям приведенным в разделе «Резисторы».
3. Выбор магнитопровода
В соответствии с рассчитанным параметром ScS0 и желаемыми конструктивными особенностями
(формфактор, технологичность намотки, электромагнитная совместимость, экономика и т.д.) выбираем в первом
приближении конкретный тип магнитопровода и феррита, из которого он изготовлен.
Для силовых дросселей повышающего и инвертирующего стабилизаторов которые работают в режиме прерывистых токов
целесообразно выбирать магнитопровод в который можно и удобно вводить зазор. Это может быть, например
Ш-образный магнитопровод.
Для силовых дросселей понижающего стабилизатора работающего в режиме непрерывных токов можно использовать и
магнитопроводы с замкнутым сердечником, например кольца.
Согласно datasheet на выбранный типоразмер сердечника находим:
S0 – площадь окна сердечника дросселя (в datasheet обозначается как Acw –
Cross-sectional winding area of core или если указаны данные на каркас – AN);
SС – площадь поперечного сечения сердечника дросселя (в datasheet обозначается как Ae–
Effective cross-sectional area);
lav – средняя длина магнитной линии выбранного магнитопровода (в datasheetобозначается как
le – effective magnetic path length);
Геометрические параметры сечения магнитопровода вблизи каждого вводимого в магнитопровод немагнитного зазора:
для части магнитопровода с прямоугольным сечением – am, bm – (ширина и глубина
магнитопровода в месте зазора); для части магнитопровода с круглым сечением – D – диаметр поперечного
сечения магнитопровода вблизи зазора;
Геометрические параметры, характеризующие сечение каркаса магнитопровода: для части магнитопровода с
прямоугольным сечением каркаса – a, b – (ширина и глубина); для части магнитопровода с круглым сечением – R
– радиус каркаса магнитопровода;
Геометрические параметры тороидальных магнитопроводов: wm – ширина магнитопровода; hm –
высота магнитопровода; Rint – внутренний радиус тора; Rext – внешний радиус тора.
hcm –высота каркаса магнитопровода;
HM – ширина окна магнитопровода;
ST – суммарная эффективная площадь охлаждения дросселя (в datasheet как правило не приводится и
потому вычисляется в каждом случае индивидуально как суммарная «внешняя» площадь охлаждения дросселя).
Согласно выбранному типу феррита из datasheet на него находим:
µ – магнитная проницаемость материала магнитопровода;
Pvferrit – мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Для удобства поиска можно воспользоваться онлайн-утилитами, например: https://tools.tdk-electronics.tdk.com/mdt/core_data
Важная ремарка: выбирать типоразмер магнитопровода «впритык» по габаритному параметру дросселя SCS0
настоятельно не рекомендуется. Во первых могут возникнуть проблемы с конструктивным размещением зазора и
обмотки, во вторых это почти всегда подразумевает работу в области больших значений индукции магнитного
поля, что приводит к максимальным потерям в магнитопроводе.
4. Расчет максимального числа витков в обмотке
Далее определяем максимальное число витков в обмотке Nmax :
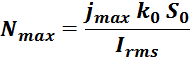
Необходимо отметить, что в данном математическом соотношении считается, что проводники обмотки занимают всю
площадь окна магнитопровода с учетом заранее определенного коэффициента заполнения k0.
5. Расчёт минимального числа витков дросселя
Рассчитываем число витков дросселя Nmin, обеспечивающее заданное значение индуктивности L и
максимального тока Imaxпри условии достижения максимального значения Bmax в
магнитопроводе:
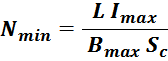
6. Проверка первичного условия размещения обмотки и определение числа витков в обмотке N
Проверяем условие размещения рассчитанного числа витков в окне магнитопровода: рассчитанное витков N должно
быть меньше максимально возможного числа витков Nmax:
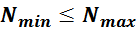
Если условие пройдено, то расчет можно продолжить. Если нет, то нужно выбрать другой магнитопровод. И
выполнить расчеты по пунктам 3-6.
Если значение Nmax будет более чем на 15-20% больше рассчитанного значения Nmin, то
есть остается еще много места в окне магнитопровода то целесообразно использовать большее число витков. Это
обеспечит выполнение условий оптимального проектирования магнитопровода, когда площадь окна магнитопровода
будет использована полностью, а значение индукции в магнитопроводе будет снижено.
Таким образом, выбираем число витков N из диапазона от Nmin до Nmax :
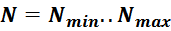
7. Расчет эффективной магнитной проницаемости магнитопровода дросселя µeff
Определяем необходимое значение эффективной магнитной проницаемости магнитопровода дросселя µeff
для получения заданной индуктивности дросселя:
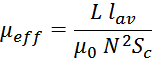
где:
lav – средняя длина магнитной линии выбранного магнитопровода;
L – заданная индуктивность дросселя;
µ0 – магнитная постоянная;
SС – площадь сечения выбранного магнитопровода.
Важная ремарка: как правило в datasheet на магнитопровод приведены данные для готовых магнитопроводов с
введенным зазором «Gapped». Величины эффективной магнитной проницаемости могут дать нижнюю границу диапазона
нижнего значения µeff , а также характерные значения величины зазоров.
Также можно выбрать готовый магнитопровод с зазором со значением эффективной магнитной проницаемости µeff
максимально близкой к рассчитанному. В этом случае потребуется корректировка числа витков обмотки:
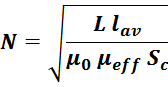
где:
μeff – эффективная магнитная проницаемость серийно выпускаемого магнитопровода с зазором.
При выборе готового магнитопровода с зазором шаги расчета 8-10 пропускаются
8. Расчет немагнитного зазора lg
В большинстве случаев для стандартных магнитопроводов в datasheet-ах [Ferrites and Accessories – EPCOS Data
Book 2013. EPCOS AG. ferrites-and-accessories-data-book-130501.pdf] даны индивидуальные для каждого
магнитопровода коэффициенты K1 и K2 предназначенные для вычисления необходимой величины немагнитного зазора
для получения нужной величины индуктивности единичного витка AL_gap:
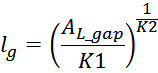
где:
K1 и K2 – коэффициенты, индивидуальные для каждого магнитопровода;
lg – (мм) длина немагнитного зазора (суммарное значение если в магнитопроводе два зазора);
AL_gap – (нГн) индуктивность единичного витка магнитопровода с зазором, рассчитываемая по
выражению:
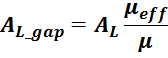
где:
AL – (нГн) индуктивность единичного витка магнитопровода без зазора;
µ – магнитная проницаемость магнитопровода без зазора.
Индивидуальные для каждого типа магнитопровода коэффициенты K1 и K2 уже учитывают явление «выпучивания»
магнитного потока и поэтому при после вычисления lgкорректировка не требуется и далее
осуществляется переход к шагу 11 «Расчет конструкции дросселя».
В случае если расчет lg по приведенной выше методике выполнить нельзя, то в соответствии с
рассчитанным μeff вычисляем величину вводимого немагнитного зазора lg по соотношению:
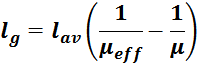
µ – магнитная проницаемость магнитопровода.
Важно понимать, что полученная величина зазора не учитывает явление «выпирания» магнитного потока и нуждается
в коррекции. Для коррекции выполняется расчет корректирующего фактора описанный в следующем пункте.
9. Расчет корректирующего фактора Fc_gap
Рассчитываем корректирующий фактор Fc_gap (см. пункт «Явление «выпучивания» поля из немагнитного
зазора» данного раздела), равный отношению эффективной площади поперечного сечения магнитного потока в
зазоре к площади поперечного сечения магнитопровода.
В случае если магнитопровод будет иметь два эффективных зазора на длине магнитной линии, что характерно для
магнитопроводов состоящих из двух половинок (Ш-, П-, чашеобразные) то:
– используемое в расчетах значение немагнитного зазора делится на два и в расчетахкорректирующий фактора
используется другое значение :
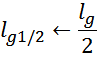
– значение корректирующего фактора вычисляется отдельно для каждого из зазоров, поскольку они, как правило,
имеют разую геометрию (например это все Ш-образные);
– результирующее значение корректирующего фактора рассчитывается как произведение корректирующих факторов
каждого из зазоров:
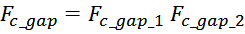
Для зазора магнитопровода с прямоугольным сечением:
Согласно datasheet определяем геометрические размеры «прямоугольника» зазора: ширина магнитопровода вблизи
зазора am, и глубина магнитопровода вблизи зазора bm;
Вычисляем корректирующий фактор:
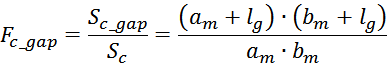
где:
am, bm – геометрические размеры магнитопровода вблизи зазора (ширина, глубина);
lg – длина немагнитного зазора (или значение lg1/2 если зазора два);
Sc_gap – эффективная площадь, охватываемая линями магнитного поля зазора;
Sc – площадь поперечного сечения магнитопровода.
Для зазора магнитопровода с круглым сечением корректирующий фактор вычисляется по выражению:
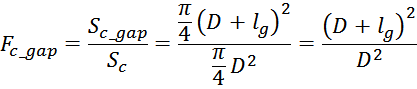
где:
D – диаметр поперечного сечения магнитопровода вблизи зазора;
lg – длина немагнитного зазора (или значение lg1/2 если зазора два).
Далее, в случае если в магнитопровод введено два зазора, вычисляем результирующее значение корректирующего
фактора как произведение корректирующих факторов каждого из зазоров:
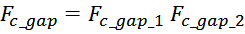
10. Корректировка величины немагнитного зазора lg
Корректируем величину немагнитного зазора lg в соответствии с рассчитанным Fc_gap.
В зависимости от полученной величины корректирующего фактора Fc_gap возможно несколько вариантов:
– если Fc_gap меньше единицы плюс допустимая погрешность величины индуктивности ∆L
(то есть, увеличение индуктивности не превышает установленную погрешность):
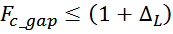
где:
∆L – допустимая погрешность отклонения от заданной величины индуктивности (5%, 10%, 20% и т.д.).
Для большинства практических случаев оптимальным является выбор ∆L на уровне 10%.
то рассчитанная величина немагнитного зазора lg принимается как конструктивная величина вводимого
зазора;
– если Fc_gapgap больше единицы плюс допустимая погрешность величины индуктивности ∆L и меньше 2 :
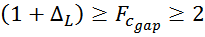
то необходима коррекция немагнитного зазора то осуществляется итерационный выбор величины немагнитного зазора
lg* с целью достижения заданной величины магнитной проницаемости µeff:
в качестве первого приближения используется произведение рассчитанной немагнитного зазора lgи
величины корректирующего фактора Fc_gap:
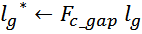
– на основании полученного нового значения lg* рассчитывается новая величина
корректирующего фактора Fc_gap* представленным выше формулам для расчета
Fc_gap;
– вычисляется новое значение эффективной магнитной проницаемости определяемое новым зазором
lg* . Произведение Fc_gap* и магнитной проницаемости с новым
зазором сравнивается с целевым значением магнитной проницаемости µeff:
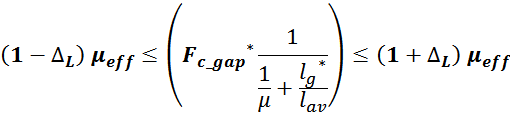
где:
∆L – допустимая погрешность отклонения от заданной величины индуктивности (5%, 10%, 20% и т.д.).
µeff – целевое значение эффективной магнитной проницаемости материала сердечника;
lav – средняя длина магнитной линии магнитопровода;
lg*– корректированное значение величины немагнитного зазора.
Если полученное произведение укладывается в рамки допустимого отклонения ∆L, то соответствующее
значение lg* принимается в качестве конструктивного параметра реально вводимого
немагнитного зазора, если нет – изменяют в ту или иную сторону lg* и повторяют
действия, начиная со второго. Так итерационно подбирают значение lg* для обеспечения
заданного значения эффективной магнитной проницаемости.
– если Fc_gapgap больше 2, то рекомендуется выбрать магнитопровод больших
габаритов и повторить расчет, начиная с пункта 2.
11. Расчет конструкции дросселя
В результате выполненного последовательного расчета по шагам 1-9 мы получаем следующие параметры:
конкретный тип магнитопровода c конкретными геометрическими параметрами;
число витков N;
величина немагнитного зазора lg;
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже. При расчете использованы соотношения, представленные в разделе
«Трансформатор»).
11.1 Расчёт параметров провода обмотки
Минимальная площадь поперечного сечения провода обмотки Swire_Cu рассчитывается по соотношению:
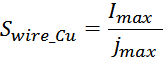
Далее вычисляется диаметр провода (по меди) для выполнения обмотки:
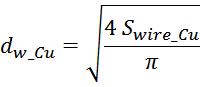
11.2 Выбор типа провода обмотки и определение диаметра и площади поперечного сечения проводника с
изоляцией
На основании вычисленного диаметра провода (по меди) dw_Cu выбирается ближайший диаметр провода из
номенклатуры диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую
сторону:
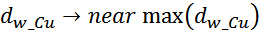
Пересчитывается реальная площадь поперечного сечения выбранного типа провода по меди Swire_Cu по
формуле:
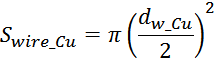
Далее в соответствии со справочным листком на выбранный провод определяется его диаметр с изоляцией dw
ins.
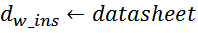
11.3 Расчёт средней длины витка
Ш- и П- образные магнитопроводы
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредняя длина
витка lw_t_av рассчитывается по соотношениям:
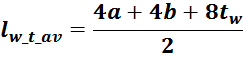
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок L.6);
tw – толщина обмотки, вычисляемая по соотношению:
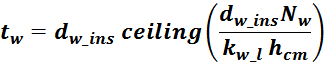
где:
функция ceiling – округление до большего целого;
hcm – высота каркаса магнитопровода, определяющая среднюю ширину намоточного слоя hlav;
Nw – число витков в обмотке;
kw_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода (таблица L.1).
Таблица L.1 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
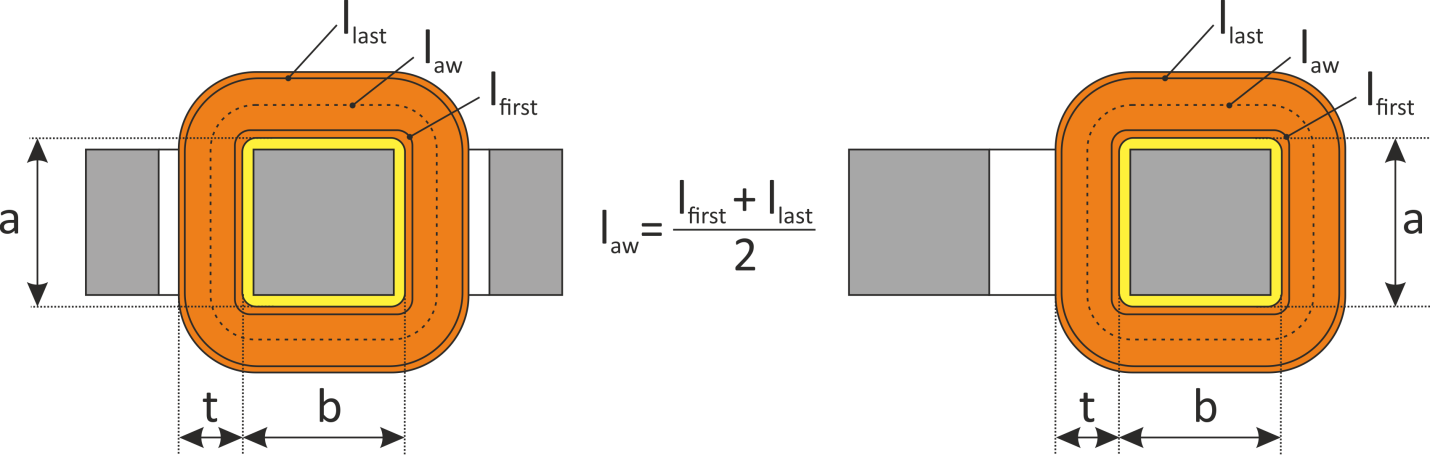
Рисунок L.6 – К определению средней длины витка для Ш- и П- образных магнитопроводов
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по соотношению:
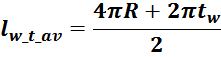
где:
R – внутренний радиус каркаса магнитопровода;
tw – толщина обмотки, вычисляемая по соотношению:
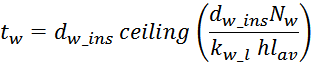
где:
функция (ceiling) – округление до большего целого;
hcm – высота каркаса магнитопровода, определяющая среднюю ширину намоточного слоя hlav;
Nw – число витков в обмотке;
kw_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода (таблица L.1).
Тороидальные магнитопроводы
Для тороидальных магнитопроводов (рисунок L.7) расчет среднего витка осуществляется по соотношению:
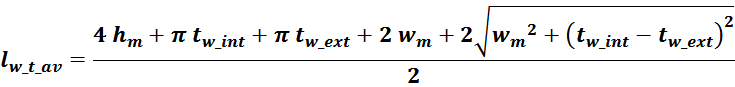
где:
wm – ширина магнитопровода;
hm – высота магнитопровода;
tw_int – толщина внутреннего слоя;
tw_ext – толщина внешнего слоя.
tw_int и tw_ext определяются по соотношениям:
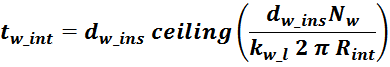
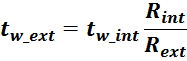
где:
функция ceiling – округление до большего целого;
Rint – внутренний радиус тора;
Rext – внешний радиус тора;
dw_ins – диаметр обмоточного провода с изоляцией;
Nw – число витков в обмотке;
kw_l – коэффициент укладки (laying) обмотки, зависящий от толщины провода (таблица L.1).
Ширина магнитопровода wm определяется согласно datasheet на магнитопровод по соотношению:
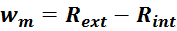

Рисунок L.7 – К определению средней длины витка тороидальных магнитопроводов.
11.4 Определение длины обмотки
Длина обмотки определяется как произведение средней длины витка на число витков:
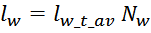
Полученная величина определяет, сколько провода нужно отмерить на обмотку дросселя.
11.5 Конструктивный расчет структуры обмотки дросселя, фактическая проверка возможности
размещения обмотки
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для выполнения конструктивного расчета необходим выбор материалов и определение толщин слоев изоляции
«пирога» обмоток:
Δwl – толщина межслоевой изоляции обмотки (если межслоевой изоляции обмотки не предусмотрено, то
величина Δwl принимается равной нулю);
Δsurf – толщина слоя внешней изоляции обмотки.
Для конструктивного расчета структуры обмотки дросселя выполняется следующая последовательность действий:
Ш- и П- образные и чашеобразные магнитопроводы
– определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода
hcm (рисунок L.8):
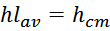
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
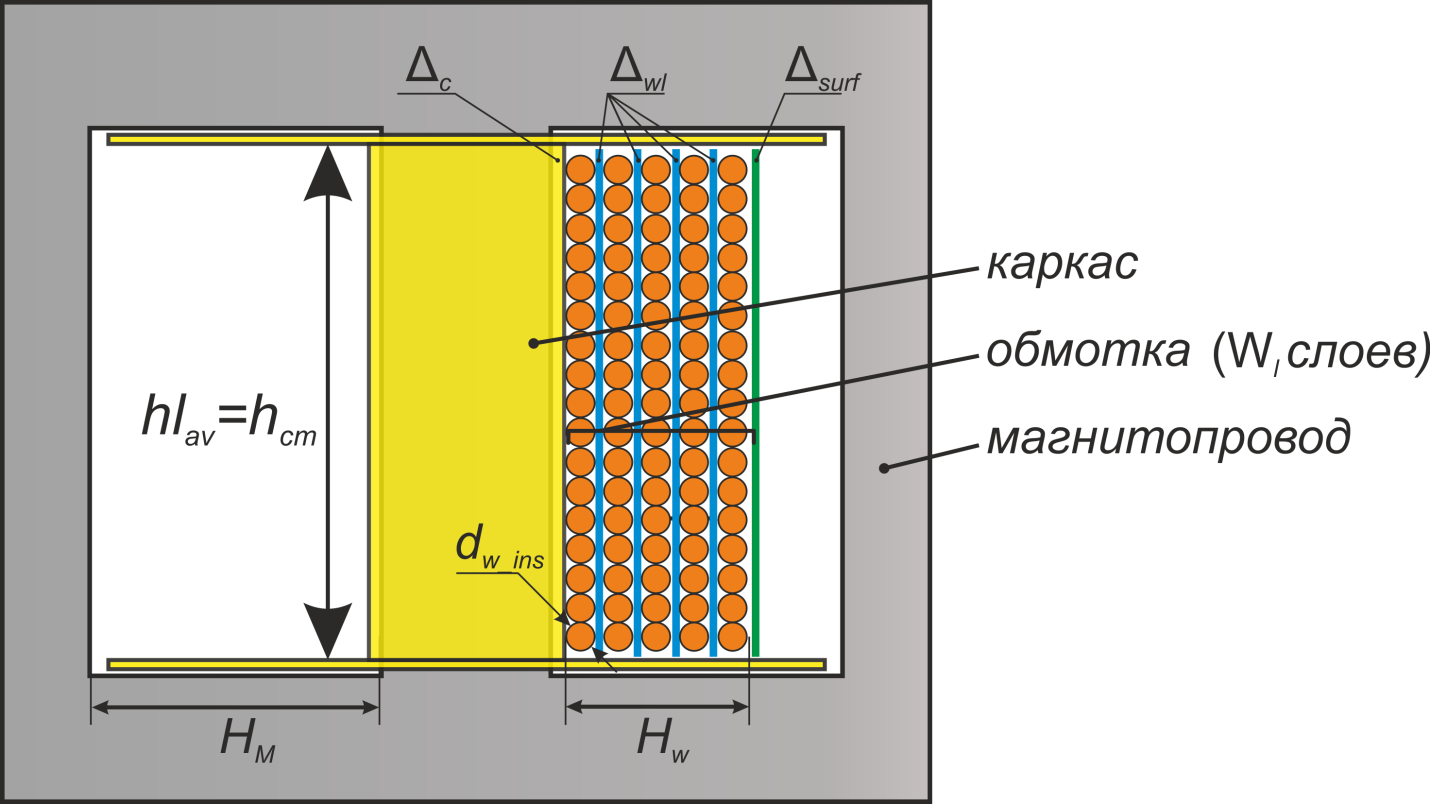
Рисунок L.8 – К расчету конструкции обмотки дросселя
определяется число витков в одном слое обмотки Nl:
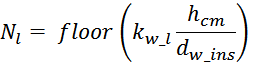
где:
hcm – высота каркаса магнитопровода;
dw_ins – диаметр проводника обмотки с изоляцией;
kw_l – коэффициент укладки (laying), зависящий от толщины провода (таблица L.1).
-рассчитывается общее число слоев обмотки Wl :
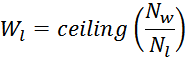
где:
ceiling – округление до большего целого;
Nw – число витков в обмотке;
Nl – число витков в одном слое обмотки.
– рассчитывается толщина обмотки Hw:
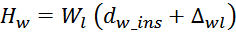
где:
Δwl – толщина межслоевой изоляции обмотки;
Wl – число слоев в обмотке;
dw_ins – диаметр провода обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величина Δwl принимается равной нулю.
рассчитывается общая толщина «пирога» обмотки HΣ:
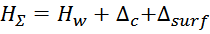
где:
Δc – толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом). В случае если
используется стандартный каркас, и все расчеты ведутся на основе его известных размеров и Δc не
учитывается;
Δsurf – толщина слоя внешней изоляции обмотки.
проверяется условие фактического размещения всех конструктивных элементов обмотки в окне магнитопровода:
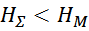
где:
HΣ – суммарная толщина «пирога» намотки;
HM – ширина окна магнитопровода.
Тороидальные магнитопроводы
В случае тороидальных магнитопроводов ширина намоточного слоя hl уменьшается по мере намотки. Поэтому все
сложнее.
Рассчитывается число витков первого слоя Nl_1 обмотки согласно выражению:
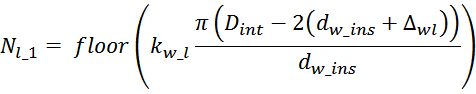
где:
floor – округление до меньшего целого;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции);
Δwl – толщина межслоевой изоляции обмотки;
dw_ins – диаметр провода обмотки с изоляцией.
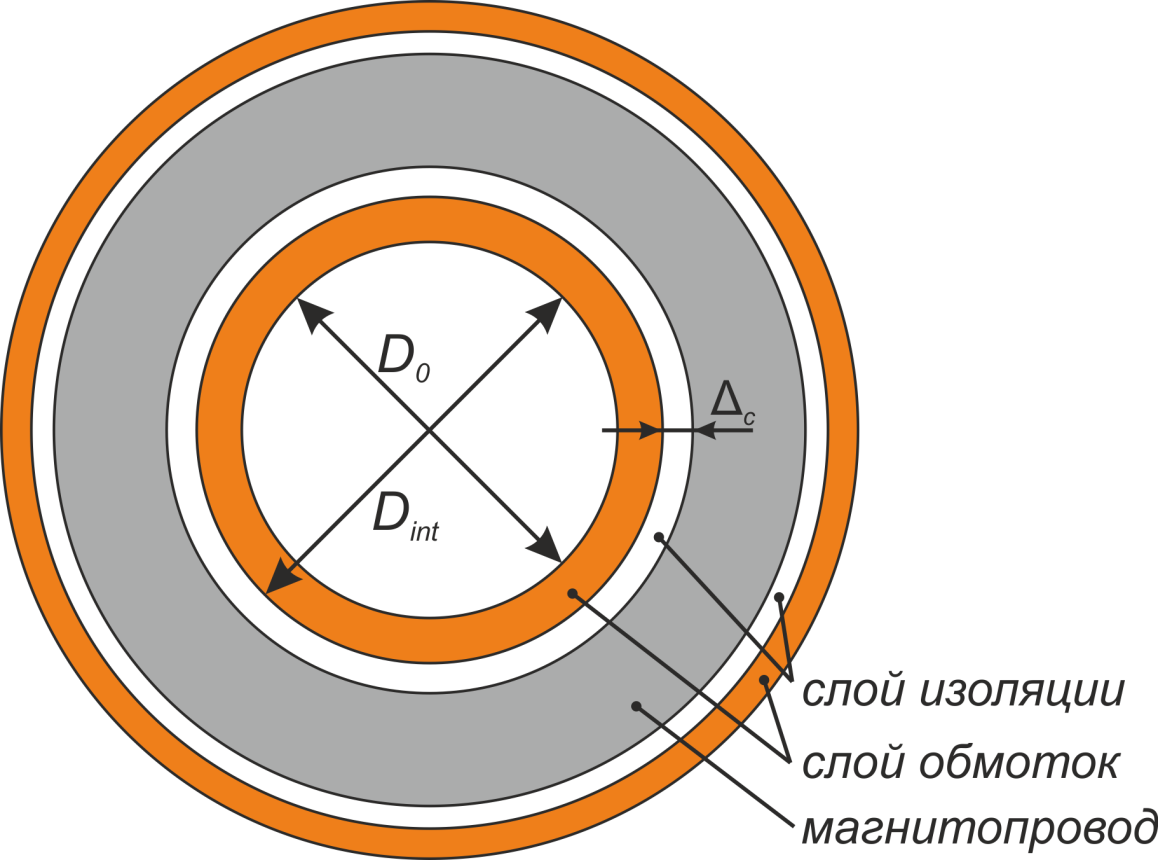
Рисунок L.9 – К расчету конструкции обмоток тороидального дросселя: Dint – внутренний диаметр
тора магнитопровода с учетом слоя изоляции, D0 – остаточный технологический диаметр
Рассчитывается уменьшение ширины намоточного слоя при переходе от слоя к слою Δhl:
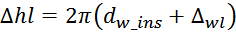
Рассчитывается уменьшение числа витков от слоя к слою ΔNl:
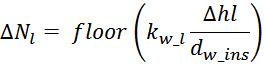
где:
kw_l – коэффициент укладки (laying), зависящий от толщины провода (таблица L.1).
Рассчитывается число слоев обмотки Wl :
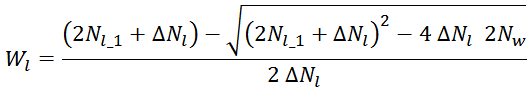
где:
Nw – число витков в обмотке;
Округляем полученное Wl до большего целого (ceiling):
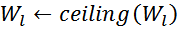
Рассчитывается толщина обмотки Hw :
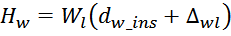
где:
Δwl – толщина межслоевой изоляции обмотки;
Wl – число слоев в первичной обмотке;
dw_ins – диаметр провода первичной обмотки с изоляцией.
Рассчитывается суммарная толщина «пирога» намотки:
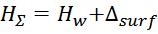
где:
Hw – толщина обмотки;
Δsurf – толщина слоя внешней изоляции обмотки.
Проверяется условие размещения всех конструктивных элементов обмотки в окне магнитопровода:
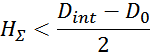
где:
HΣ – суммарная толщина «пирога» намотки;
Dint – внутренний диаметр тора магнитопровода (с учетом изоляции) который фактически определяет
ширину окна магнитопровода;
D0 – остаточный диаметр внутри тороидального трансформатора (технологический).
12. Расчет сопротивления обмотки дросселя Rw
Электрическое сопротивление обмотки дросселя Rw рассчитывается по формуле для расчета омического
сопротивления протяженного проводника:
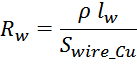
где
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1 );
lw – длина обмотки;
Swire_Cu – площадь поперечного сечения выбранного типа провода (по меди).
13. Расчет омических потерь в обмотке дросселя
Суммарные потери на омическом сопротивлении обмотки Pwindingопределяются по формуле:
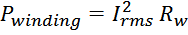
Rw – сопротивление обмотки;
Irms – среднеквадратичное значение тока в обмотке.
NB: При высоких рабочих температурах дросселя необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. пункт «Влияние скин-эффекта на сопротивление
обмоток при высоких частотах» раздела «Трансформатор»).
14. Оценка уровня потерь в магнитопроводе
Рассчитываем максимальную индукцию в магнитопроводе :
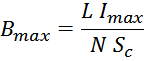
где:
L – заданное значение индуктивности дросселя;
Imax – максимальное значение тока дросселя;
N – число витков обмотки дросселя;
Sc – площадь сечения магнитопровода.
На основании полученного значения максимальной индукции в магнитопроводе рассчитываем уровень потерь.
Существуют три способа определения потерь в магнитопроводе:
рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
определить по графику из datasheet на выбранный тип феррита;
определить по уровню максимальных потерь из datasheet на магнитопровод;
определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя – частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum design of a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
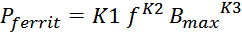
где:
f – частота;
Bmax – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения мощности потерь в магнитопроводе можно использовать соотношение:
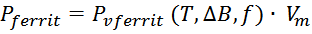
где:
Pvferrit – мощность потерь на единицу объема, являющейся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода (L.12);
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.
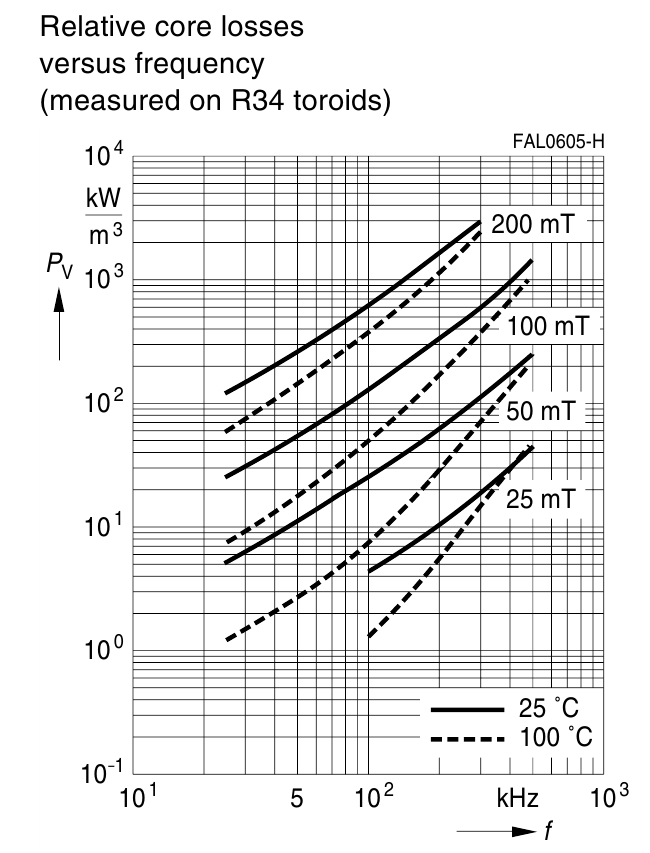
Рисунок L.12 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRIT material N87, EPCOS AG 2006]
Данный способ расчета потерь в магнитопроводе является наиболее точным.
Определение по уровню максимальных потерь из datasheet на магнитопровод
Максимальный уровень потерь в магнитопроводе соответствует крайним режимам эксплуатации магнитопровода.
Уровень максимальных потерь часто приводится в datasheet на конкретный тип магнитопровода при различных
условиях (индукция магнитного поля, частота, температура). Уровень максимальных потерь обозначается как
PV (W/set).
В этом случае мощности потерь в магнитопроводе Pferrit приравнивается к уровню максимальных потерь
PV представленном в datasheet для наиболее близких условий эксплуатации:
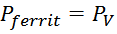
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
15. Расчет суммарных потерь
Суммарные потери дросселя Ptotal_loss складываются из омических потерь обмотки и потерь
магнитопровода:
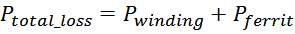
где:
Pwinding – омические потери в обмотке;
Pferrit – потери в магнитопроводе.
Соотношение потерь в обмотке и магнитопроводе является критерием оптимального проектирования. Если эти потери
приблизительно равны, то данный индуктор спроектирован самым оптимальным образом. Вообще чем ближе Pwinding
и Pferrit по величине тем лучше, поскольку при этом, как правило, достигается минимум потерь при
минимуме материала.
Если эти параметры отличаются более чем в 3-5 раз, то имеет смысл пересчитать дроссель по пунктам 3-15
используя другой магнитопровод.
16. Расчет температурного режима дросселя и оптимизация
Установившаяся температура перегрева дросселя относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
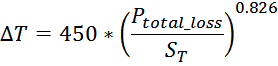
где:
Ptotal loss – мощность суммарных потерь в дросселе;
ST – суммарная эффективная площадь охлаждения дросселя (в см2).
Полученное ∆T (дельта перегрева) складывается с температурой эксплуатации дросселя и рассчитывается его
максимальная рабочая температура. Если полученное значение температуры нагрева дросселя лежит в пределах
50-80°С, то расчет дросселя можно считать законченным. Если полученное значение превышает 80°С, то имеет
смысл использовать магнитопровод большего размера. Эмпирически установленным критерием допустимой области
работы является 0,2 Вт/см2 – максимальная величина мощности, рассеиваемой единицей поверхности
индуктора или трансформатора.
Если в результате расчета уровень перегрева дросселя ΔT будет значительно меньше максимально допустимого:
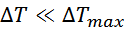
то имеет смысл использовать оптимизировать конструкцию дросселя с целью уменьшения стоимости и
массогабаритных показателей – уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева дросселя получится, что мощность, выделяемая на активном
сопротивлении обмотки существенно меньше, чем в феррите магнитопровода:
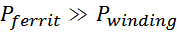
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
3-16.
Необходимо понимать, что оптимизация расчета дросселя проводится с учетом целевых приоритетов:
Приоритет 1 – Малые массогабаритные параметры дросселя и, соответственно, стоимость. В этом случае необходимо
провести расчет всех параметров дросселя с целью обеспечения (но не превышения) заданного уровня перегрева и
минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах индукции итерационно
увеличиваются;
Приоритет 2 – Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры дросселя (индукция, плотность тока и т.д.) провести расчет всех параметров
дросселя с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции итерационно
уменьшаются.
Для дросселей больших габаритов (с рассеваемой площадью более 1000 см2) установившаяся температура
нагрева дросселя относительно окружающей среды ∆T (дельта перегрева) оценивается по соотношению [В.Е.
Китаев, А.А. Бокуняев. Проектирование источников электропитания устройств связи. Учеб. пособие.- М.:
Связь,1972.- 200 с.]:
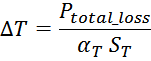
где:
Ptotal loss – мощность суммарных потерь в дросселе;
αT – коэффициент теплоотдачи, зависящий от множества факторов (материал трансформатора,
конструктивное исполнение, температуры окружающей среды и т.д.). Для практических расчетов принимается
равным: 11-13 Вт/м2 °С;
ST – суммарная эффективная площадь охлаждения дросселя.
Частные случаи. Расчет индуктивных элементов с накоплением энергии: силовые дроссели понижающего,
повышающего и инвертирующего стабилизаторов, трансформатор обратноходового преобразователя.
Теоретические рассуждения и предпосылкиs
В результате расчета различных индуктивных элементов работающих в режиме накопления энергии мы получаем
входные параметры для проектирования конструкции дросселя «в железе». Как правило, входные данные к
проектированию это:
– для силовых дросселей: индуктивность L, максимальный ток Imax, плюс форма импульсов тока и
возможно сопротивление обмотки R.
для трансформатора обратноходового преобразователя: индуктивности обмоток L1, L2, … Ln, максимальные токи
обмоток I1, I2, … In, форма импульсов тока, и, возможно, сопротивления обмоток R1, R2, … Rn.
Таким образом, в сути все сводится к задаче – нужно получить заданную L с максимальным рабочим током Imax
при условии минимальных габаритов дросселя и допустимом уровне тепловых потерь.
Небольшое отступление: Задача не простая, не так ли? Пробуем решить задачу «в лоб» и рассмотрим
типовой случай заблуждения. Используем обычный «беззазорный» магнитопровод и рассчитываем обмотку с
требуемой индуктивностью. По расчетам получаем сравнительно небольшое число витков, и действительно, по
факту обмотка занимает сравнительно немного места в окне магнитопровода. Однако в процессе испытаний
оказывается, что получившийся дроссель впадает в глубокое насыщение еще далеко до нужного максимального
тока. Что же делать? Опять пробуем «в лоб»: взять магнитопровод потолще, с большей площадью сечения и
уменьшить число витков. Вроде бы получается, и заданная индуктивность и работает без насыщения, только вот
весит этот магнитопровод за полкило. Нерационально… Так что бараний подход «в лоб» тут не работает.
Что делают: вводят в магнитопровод зазор, ухудшая эффективную магнитную проницаемость, а потерю в
индуктивности «добирают» увеличивая число витков. Это вкратце. Ниже дано подробное описание.
Силовые дроссели понижающего, повышающего и инвертирующего стабилизаторов
Расчет силовых дросселей понижающего, повышающего и инвертирующего стабилизаторов осуществляется с
использованием алгоритма приведенного выше в разделе «Последовательность расчета силового дросселя».
После расчета сопротивления обмотки выполняется оценка потерь и тепловой расчет дросселя (пункты 11-15
раздела). В результате расчетов может получиться, что дросселя будет слишком горячий или слишком холодный. В
этом случае необходимо выполнить оптимизацию конструкции дросселя (использовать другой магнитопровод,
феррит) и выполнить расчеты по пунктам 3-15 снова.
Трансформатор обратноходового преобразователя
Как уже было сказано ранее трансформатор обратноходового преобразователя, по сути, представляет собой
многообмоточный дроссель.
Габаритный параметр обычного дросселя с одной обмоткой определяется выражением:
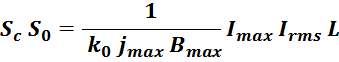
Трансформатор обратноходового преобразователя содержит как минимум две обмотки. Выведем соотношение для
габаритного параметра трансформатора обратноходового преобразователя.
Вывод соотношения для габаритного параметра трансформатора обратноходового
преобразователя
Для определения габаритного параметра трансформатора обратноходового преобразователя воспользуемся
аналогичными выкладками для нахождения габаритного параметра дросселя – произведение ширины окна и сечения
магнитопровода S0SС. Выведем соотношение для расчета S0SС
трансформатора, содержащего две обмотки – первичную и вторичную.
Площадь окна магнитопровода S0
Площадь окна магнитопровода, занимаемая медью обмоток составляет:
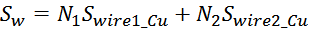
где:
N1, N2 – число витков в первичной и вторичной обмотках;
Swire1_Cu , Swire2_Cu – площадь сечения провода «по меди» для первичной и вторичной
обмоток соответственно.
Плотность тока в проводнике обмотки определяется как отношение тока в нем к площади сечения :
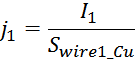
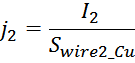
Максимальное значение плотности тока в обмотке ограничивается её омическим нагревом, величина которого
определяется среднеквадратичным значением тока через обмотку Irms. Будем считать, что
максимальное значение тока плотности тока одинаково для всех обмоток:
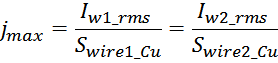
Поскольку площадь сечения провода можно выразить через отношение тока через провод к плотности тока в
нем:
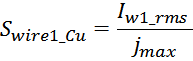
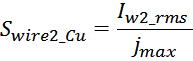
То, подставляя это выражение в выражение для площади окна магнитопровода, занимаемой медью обмоток,
получаем:
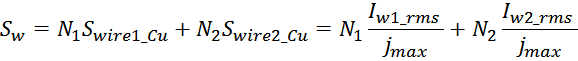
или
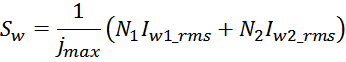
С учетом того, что среднеквадратичные значения токов обмоток связаны с максимальными значениями по
соотношениям (раздел «Резисторы»):
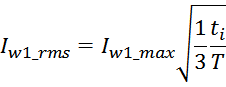
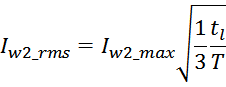
где:
ti – длительность интервала накопления энергии;
tl – длительность интервала передачи энергии;
Iw1_max – максимальное значение тока первичной обмотки;
Iw2_max – максимальное значение тока вторичной обмотки.
Подставляя эти значения, получаем:
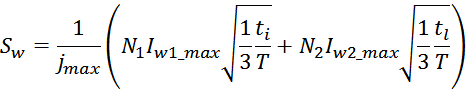
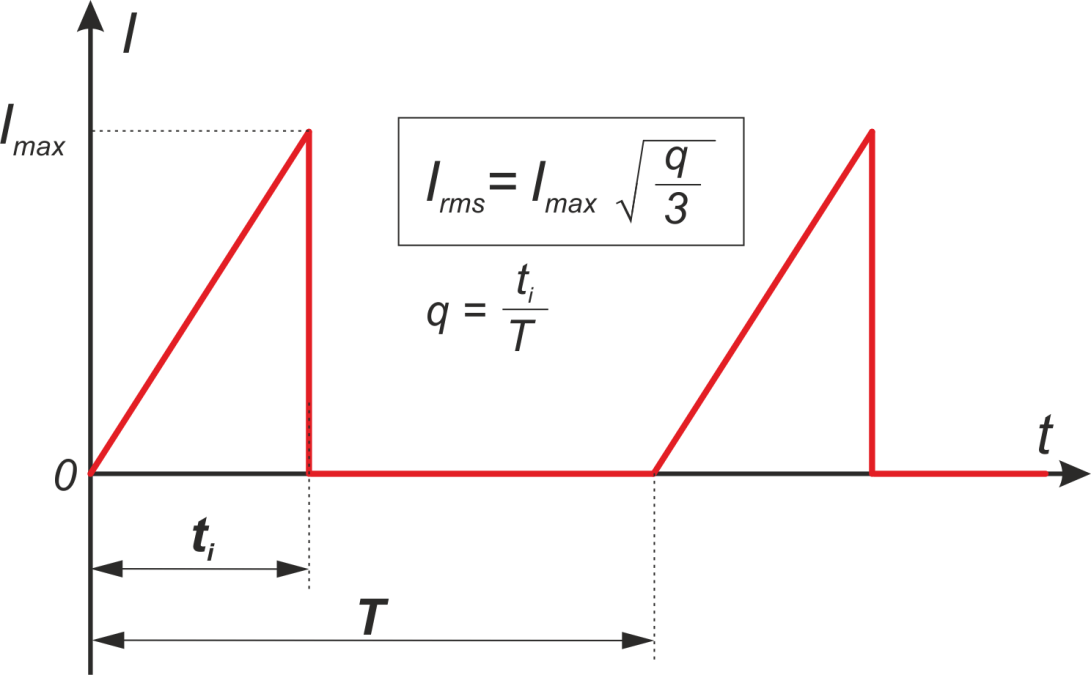
Рисунок L.13 – Расчет среднеквадратичного значения тока при треугольной форме импульсов – к расчету
трансформатора обратноходового преобразователя работающего в режиме прерывистых токов
Из физики работы обратноходового преобразователя известно, что отношение максимальных значений токов
первичной и вторичной обмоток определяется отношением числа витков в них (см. раздел «Обратноходовый
преобразователь»):
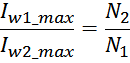
Из этого соотношения можно выразить ток вторичной обмотки:
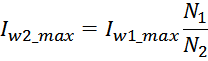
С учетом этого выражение принимает вид:
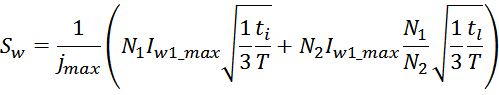
Сокращая множитель получаем:
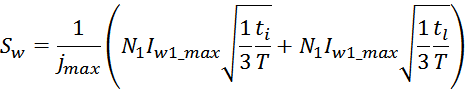
В этом соотношении площадь, занимаемая вторичной обмоткой, приведена к площади занимаемой первичной
обмоткой.
Вынося общий множитель за скобки, получаем:
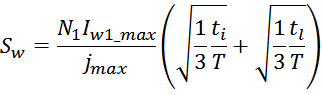
На практике основным режимом работы обратноходового преобразователя является прерывистый режим (раздел
«Обратноходовый преобразователь»). Для вывода соотношения габаритной мощности рассмотрим пограничный режим
работы преобразователя, который и соответствует максимальной выходной мощности. В этом режиме длительности
накопления ti и передачи tl энергии занимают весь период (это понятно и подробно
изложено в разделе «Обратноходовый преобразователь»):
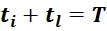
С учетом этого можно упростить выражение в скобках. Выражая длительность импульса спада tl :
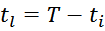
Получаем:
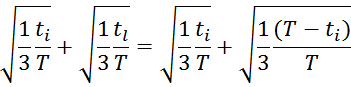
Вынося за скобки общий множитель получаем:
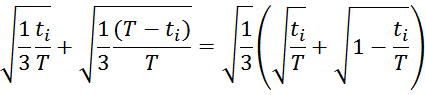
Функция в скобках от аргумента ti/T имеем максимум при ti/T равном 0,5. Таким образом,
максимальное значение суммы равно:
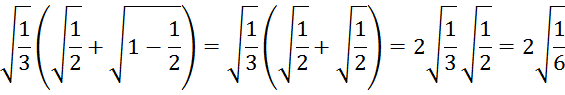
С учетом этого получаем выражение для площади окна:
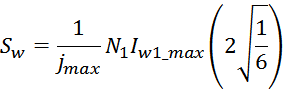
Перегруппируя которое выводим соотношение для площади, занимаемой медью обмоток:
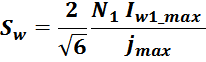
Отношение площади занимаемой проводниками обмоток к общей площади окна магнитопровода называют коэффициентом
заполнения окна k0 :
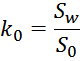
где:
S0 – общая площадь окна сердечника;
Sw – часть площади окна сердечника заполненную проводниками обмоток.
Таким образом, можно получить выражение для общей площади окна, в которой размещена обмотка
трансформатора:
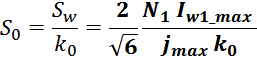
Из выражения также следует соотношение для числа витков первичной обмотки:
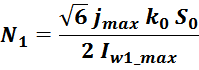
Площадь сечения магнитопровода SС
По определению индуктивность есть коэффициент пропорциональность между потокосцепленем (суммой магнитных
потоков всех витков) и током:
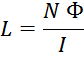
Магнитный поток витка есть произведение магнитной индукции на площадь поперечного сечения магнитопровода:
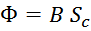
Отсюда:
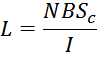
Откуда следует выражение для площади сечения магнитопровода SС:
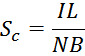
В перечисленных соотношениях соотношении подразумевается одномоментное значение тока. При этом максимальное
значение тока будет соответствовать максимальному значению индукции, в магнитопроводе. В данном соотношении
применительно к обратноходовому трансформатору может быть использована как индуктивность первичной так и
вторичной обмотки. Но поскольку соотношение для площади окна приведено к первичной обмотке то и это
выражение выполним для первичной обмотки :
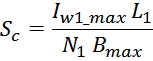
Габаритный параметр обратноходового трансформатора S0SС
Перемножая соотношения для S0 и SС, получаем габаритный параметр обратноходового
трансформатора:
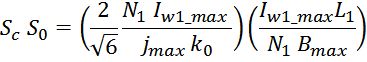
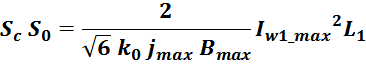
где:
k0 – коэффициент заполнения окна магнитопровода равный отношению площади занимаемой проводниками
обмоток к общей площади окна магнитопровода.
jmax – максимальное значение плотности тока в проводнике;
Bmax – максимальное значение индукции в магнитопроводе;
Iw1_max – максимальное значение тока через первичную обмотку трансформатора;
L1 – индуктивность первичной обмотки трансформатора.
Поскольку рассматриваемый обратноходовой преобразователь работает в режиме прерывистых токов то
энергия, запасаемая и отдаваемая индуктивностью за один период работы (преобразователя) равна:
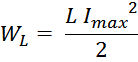
С другой стороны эта энергия связана с номинальной мощностью через рабочую частоту f:
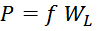
Поскольку в выражение габаритного параметра входит произведение LI2 то можно его выразить через
мощность и частоту и получить:
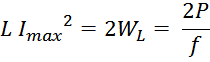
Подставляя это выражение в соотношение для габаритного параметра получаем:
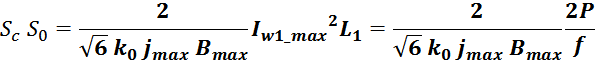
где:
P – расчетная мощность обратноходового преобразователя;
f – рабочая частота преобразователя.
Последовательность расчета трансформатора обратноходового преобразователя
Входными данными для расчета трансформатора обратноходового преобразователя являются:
величина индуктивности первичной обмотки L1 ;
максимальный ток первичной обмотки Iw1_max;
максимальный ток вторичной обмотки Iw2_max;
максимальная входная мощность преобразователя PIN_max;
рабочая частота f;
коэффициент трансформации k;
максимальный коэффициент заполнения qmax .
1. Определение габаритного параметра трансформатора SCS0
Определяем габаритный параметр обратноходового трансформатора S0S:
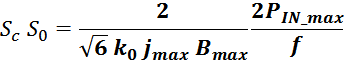
где:
PIN_max – максимальная входная мощность преобразователя;
k0 – коэффициент заполнения окна магнитопровода для Ш-образного магнитопровода
[Сетевые блоки питания с высокочастотными преобразователями. О.А. Эраносян. Энергоатомиздат. Ленингр.
отд-ние, 1991, 176 с.] выбирается в следующих пределах:
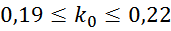
(в ряде случаев, в особенности, когда S0 представляет собой площадь окна сердечника трансформатора
уже с учетом каркаса магнитопровода, то может быть выбран k0 вплоть до 0,28-0,4 – [McLyman C.
Transformer and inductor design handbook.2004]). Для определения коэффициента заполнения окна k0
необходимо, хотя бы предварительно, выбрать тип магнитопровода. Как правило, для построения обратноходовых
преобразователей используют Ш-образные магнитопроводы имеющие минимальную индуктивность рассеяния.
jmax – максимальное значение плотности тока в проводнике выбирается в пределах 4-8
А/мм2. Чем больше «прокачиваемая» мощность, тем меньше выбирается значение плотности тока.
Bmax – максимальное значение индукции в магнитопроводе. Для определения данного
параметра необходимо, хотя бы предварительно, выбрать тип феррита. Величина Bmaxопределяется
исходя из параметров выбранного типа феррита и рабочей частоты. В первом приближении и в типовом случае
принимается в пределах 0,15-0,2 Тл;
f – рабочая частота преобразователя.
2. Выбор магнитопровода
Выбираем тип магнитопровода в соответствии с рассчитанным параметром ScS0, желаемыми
конструктивными особенностями (формфактор, технологичность намотки, электромагнитная совместимость,
экономика и т.д.) и типом феррита.
Для трансформатора обратноходового преобразователя работающего в режиме прерывистых токов целесообразно
выбирать магнитопровод в который можно и удобно вводить зазор. Это может быть, например Ш-образный
магнитопровод.
Ниже дана таблица для оценочного определения типа магнитопровода в зависимости от мощности
стабилизатора/преобразователя [HIGH-FREQUENCY POWER TRANSFORMERS. Design a high-frequency power transformer
based on flyback topology. DINESH KUMAR. ELECTRONICS FOR YOU. March 2004].
Таблица L.2 – Соответствие типоразмера магнитопровода и мощности flyback-преобразователя [HIGH-FREQUENCY
POWER TRANSFORMERS. Design a high-frequency power transformer based on flyback topology. DINESH KUMAR.
ELECTRONICS FOR YOU. March 2004]
|
Мощность |
Тип магнитопровода |
Мощность |
Тип магнитопровода |
|
0-10 Вт |
EFD15 SEE16 EF16 EPC17 EE19 EF(D)20 EPC25 EF(D)25 |
30-50 Вт |
EI28 EER28(L) ETD29 EF(D)30 EER35 |
|
10-20 Вт |
EE19 EPC19 EF(D)20 EPC25 EF(D)25 |
50-70 Вт |
EER28L ETD34 EER35 ETD39 |
|
20-30 Вт |
EL25 EF(D)25 EPC25 EPC30 EF(D)30 ETD29 EER28(L) |
70-100 Вт |
ETD34 EER35 ETD39 EER40 E21 |
Для дальнейших расчетов потребуются следующие параметры выбранного типа магнитопровода:
S0 – площадь окна сердечника трансформатора (в datasheet часто обозначается как AN);
Sc – эффективная площадь поперечного сечения выбранного магнитопровода (в datasheetчасто
обозначается как Ae);
lav – средняя длина магнитной линии выбранного магнитопровода (в datasheetобозначается как
le – effective magnetic path length).
геометрические параметры сечения магнитопровода вблизи каждого вводимого в магнитопровод немагнитного зазора:
для части магнитопровода с прямоугольным сечением – am, bm – (ширина и глубина
магнитопровода в месте зазора); для части магнитопровода с круглым сечением – D – диаметр поперечного
сечения магнитопровода вблизи зазора;
геометрические параметры, характеризующие сечение каркаса магнитопровода: для части магнитопровода с
прямоугольным сечением каркаса – a, b – (ширина и глубина); для части магнитопровода с круглым сечением – R
– радиус каркаса магнитопровода;
hcm –высота каркаса магнитопровода;
HM – ширина окна магнитопровода;
ST – суммарная эффективная площадь охлаждения трансформатора (в datasheet как правило не
приводится и потому вычисляется в каждом случае индивидуально как суммарная «внешняя» площадь охлаждения
трансформатора).
Согласно выбранному типу феррита из datasheet на него находим:
µ – магнитная проницаемость материала магнитопровода;
Pvferrit – мощность потерь на единицу объема, являющаяся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Для удобства поиска можно воспользоваться онлайн-утилитами, например: https://tools.tdk-electronics.tdk.com/mdt/core_data
Важная ремарка: выбирать типоразмер магнитопровода «впритык» по габаритному параметру трансформатора
SCS0 настоятельно не рекомендуется. Во первых могут возникнуть проблемы с
конструктивным размещением зазора и обмотки, во вторых это почти всегда подразумевает работу в области
больших значений индукции магнитного поля, что приводит к максимальным потерям в магнитопроводе.
3. Расчет максимального числа витков в первичной и вторичной обмотках
Далее определяем максимальное число витков в первичной и вторичной обмотках Nw1_max и Nw2_max :
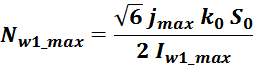
где:
S0 – площадь окна сердечника трансформатора (в datasheet часто обозначается как AN);
Iw1_max – максимальное значение тока первичной обмотки.
Необходимо отметить, что в данном математическом соотношении считается, что проводники обмоток занимают всю
площадь окна магнитопровода с учетом заранее определенного коэффициента заполнения k0. При этом
«отводятся» равные площади окна под первичную и вторичную обмотки. Каждой по половине окна.
В соответствии с заданным коэффициентом трансформации определяем максимальное число витков во вторичной
обмотке Nw2_max (про коэффициент трансформации – см. раздел «Трансформатор»).
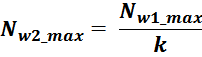
где:
k – коэффициент трансформации трансформатора.
4. Расчёт минимального числа витков первичной обмотки
Рассчитываем минимальное число витков первичной обмотки Nw1_min обеспечивающее заданное значение
индуктивности первичной обмотки L1 и максимального тока Iw1_max :
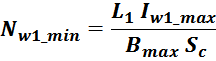
где:
L1 – индуктивность первичной обмотки трансформатора;
Sc – эффективная площадь поперечного сечения выбранного магнитопровода (в datasheetчасто
обозначается как Ae).
5. Проверка первичного условия размещения обмоток и определение числа витков в первичной обмотке
N1
Проверяем условие размещения рассчитанного числа витков в окне магнитопровода: рассчитанное минимальное число
витков Nw1_min должно быть меньше максимально «умещаемого» числа витков Nw1_max:
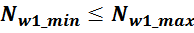
Если условие пройдено, то расчет можно продолжить. Если нет, то нужно выбрать другой магнитопровод. И
выполнить расчеты по пунктам 2-5.
Если значение Nw1_max будет более чем на 15-20% больше рассчитанного значения Nw1_min,
то есть остается еще много места в окне магнитопровода то целесообразно использовать большее число витков.
Это обеспечит выполнение условий оптимального проектирования магнитопровода, когда площадь окна
магнитопровода будет использована полностью, а значение индукции в магнитопроводе будет снижено.
Таким образом, выбираем число витков N1 из диапазона от Nw1_min до Nw1_max :
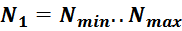
6. Расчет эффективной магнитной проницаемости магнитопровода µeff
Определяем необходимое значение эффективной магнитной проницаемости магнитопровода трансформатора
µeff для получения заданной индуктивности первичной обмотки:
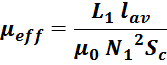
где:
lav – средняя длина магнитной линии выбранного магнитопровода;
L1 – заданная индуктивность первичной обмотки трансформатора;
µ0 – магнитная постоянная;
N1 – число витков в первичной обмотке;
SС – площадь сечения выбранного магнитопровода.
Полученное значение μeff не должно превышать собственную проницаемость феррита μ.
Также можно выбрать готовый магнитопровод с зазором со значением эффективной магнитной проницаемости µeff
максимально близкой к рассчитанному. В этом случае потребуется корректировка числа витков первичной обмотки:
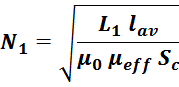
где:
μeff – эффективная магнитная проницаемость серийно выпускаемого магнитопровода с зазором.
При выборе готового магнитопровода с зазором шаги расчета 8-10 пропускаются.
7. Расчёт числа витков вторичной обмотки N2
Рассчитываем число витков во вторичной обмотке N2 в соответствии с заданным коэффициентом
трансформации k:
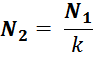
8. Расчет немагнитного зазора lg
В большинстве случаев для стандартных магнитопроводов в datasheet-ах [Ferrites and Accessories – EPCOS Data
Book 2013. EPCOS AG. ferrites-and-accessories-data-book-130501.pdf] даны индивидуальные для каждого
магнитопровода коэффициенты K1 и K2 предназначенные для вычисления необходимой величины немагнитного зазора
для получения нужной величины индуктивности единичного витка AL_gap:
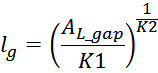
где:
K1 и K2 – коэффициенты, индивидуальные для каждого магнитопровода;
lg – (мм) длина немагнитного зазора (суммарное значение если зазора два);
AL_gap – (нГн) индуктивность единичного витка магнитопровода с зазором, рассчитываемая по
выражению:
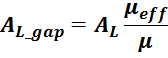
где:
AL – (нГн) индуктивность единичного витка магнитопровода без зазора;
µ – магнитная проницаемость магнитопровода без зазора.
Индивидуальные для каждого типа магнитопровода коэффициенты K1 и K2 уже учитывают явление «выпучивания»
магнитного потока и поэтому при после вычисления lgкорректировка не требуется и далее
осуществляется переход к шагу 11 «Расчет среднеквадратичных значений токов обмоток».
В случае если расчет lg по приведенной выше методике выполнить нельзя, то в соответствии с
рассчитанным μeff вычисляем величину вводимого немагнитного зазора lg по соотношению:
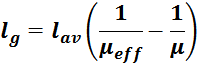
µ – магнитная проницаемость магнитопровода.
Важно понимать, что полученная величина зазора не учитывает явление «выпирания» магнитного потока и нуждается
в коррекции (шаги расчета 9 и 10).
9. Расчет корректирующего фактора Fc_gap
Рассчитываем корректирующий фактор Fc_gap (см. пункт «Явление «выпучивания» поля из немагнитного
зазора» настоящего раздела), равный отношению эффективной площади поперечного сечения магнитного потока в
зазоре к площади поперечного сечения магнитопровода.
В случае если магнитопровод будет иметь два зазора (или три для Ш-образного), что характерно для
магнитопроводов состоящих из двух половинок (Ш-, П- чашеобразные) то:
– используемое в расчетах значение немагнитного зазора делится на два:
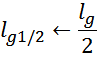
– результирующее значение корректирующего фактора рассчитывается как произведение корректирующих факторов от
каждого из зазоров:
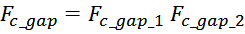
Для магнитопроводов с прямоугольным сечением: корректирующий фактор равен:
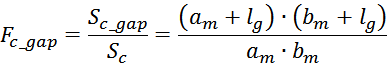
где:
am, bm – геометрические размеры магнитопровода вблизи зазора (ширина, глубина);
lg – длина немагнитного зазора;
Sc_gap – эффективная площадь, охватываемая линями магнитного поля зазора;
Sc – площадь поперечного сечения магнитопровода.
Для магнитопроводов с круглым сечением корректирующий фактор вычисляется по выражению:
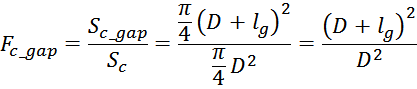
где:
D – диаметр поперечного сечения магнитопровода вблизи зазора;
lg – длина немагнитного зазора.
В случае если в магнитопровод введено два зазора, что характерно для магнитопроводов состоящих из двух
половинок (Ш-, П- чашеобразные) то результирующее значение корректирующего фактора рассчитывается как
произведение корректирующих факторов от каждого из зазоров:
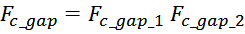
10. Корректировка величины немагнитного зазора lg
Корректируем величину немагнитного зазора lg в соответствии с рассчитанным Fc_gap.
В зависимости от полученной величины корректирующего фактора Fc_gap возможно несколько вариантов:
– если Fc_gap меньше единицы плюс допустимая погрешность величины индуктивности ∆L
(то есть, увеличение индуктивности не превышает установленную погрешность):
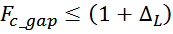
где:
∆L – допустимая погрешность отклонения от заданной величины индуктивности (5%, 10%, 20% и т.д.).
Для большинства практических случаев оптимальным является выбор ∆L на уровне 10%.
то рассчитанная величина немагнитного зазора lg принимается как конструктивная величина вводимого
зазора;
– если Fc_gapgap больше единицы плюс допустимая погрешность величины индуктивности ∆L и меньше 2 :
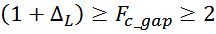
то необходима коррекция немагнитного зазора то осуществляется итерационный выбор величины немагнитного зазора
lg* с целью достижения заданной величины магнитной проницаемости µeff:
– в качестве первого приближения используется произведение рассчитанной немагнитного зазора и величины lg
и корректирующего фактора Fc_gap:
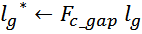
на основании полученного lg* рассчитывается новая величина корректирующего
фактораFc_gap* представленным выше формулам для расчета Fc_gap;
– вычисляется новое значение эффективной магнитной проницаемости определяемое новым зазором
lg* . Произведение Fc_gap* и магнитной проницаемости с новым
зазором сравнивается с целевым значением магнитной проницаемости µeff:
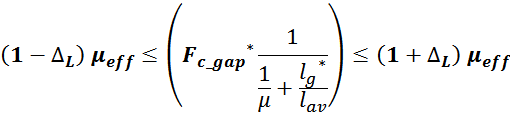
где:
∆L – допустимая погрешность отклонения от заданной величины индуктивности (5%, 10%, 20% и т.д.).
µeff – целевое значение эффективной магнитной проницаемости материала сердечника;
lav – средняя длина магнитной линии магнитопровода;
lg* – корректированное значение величины немагнитного зазора.
Если полученное произведение укладывается в рамки допустимого отклонения∆L, то соответствующее
значение lg* принимается в качестве конструктивного параметра реально вводимого
немагнитного зазора, если нет – изменяют в ту или иную сторону lg* и повторяют
действия, начиная со второго. Так итерационно подбирают значение lg* для обеспечения
заданного значения эффективной магнитной проницаемости.
– если Fc_gapgap больше 2, то рекомендуется выбрать магнитопровод больших
габаритов и повторить расчет, начиная с пункта 2.
11. Расчет среднеквадратичных значений токов обмоток
Рассчитываем среднеквадратичные значения токов обмоток (их максимальные значения):
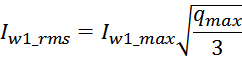
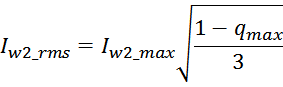
где:
qmax– максимальный коэффициент заполнения;
Iw1_max – максимальное значение тока первичной обмотки;
Iw2_max – максимальное значение тока вторичной обмотки.
12. Расчет конструкции трансформатора обратноходового преобразователя
Конструкция трансформатора обратноходового преобразователя имеет существенные отличия от конструкции обычного
дросселя в связи с этим ниже отдельно представлен порядок расчета конструкции трансформатора обратноходового
преобразователя.
В результате выполненного последовательного расчета по шагам 1-6 мы получаем следующие параметры:
конкретный тип магнитопровода c конкретными геометрическими параметрами;
число витков первичной и вторичной обмоток N1 и N2;
величину немагнитного зазора lg (или был выбран магнитопровод с зазором).
Далее после получения этих базовых параметров выполняется детальный конструктивный расчет. Последовательность
расчета представлена ниже. При расчете использованы соотношения, представленные в разделе
«Трансформатор»).
12.1 Расчёт параметров проводов обмоток
Минимальная площадь поперечного сечения обмоток рассчитывается по соотношениям:
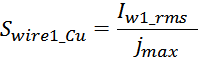
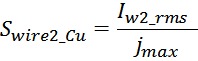
Swire1_Cu – площадь поперечного сечения проводника первичной обмотки по меди;
Swire2_Cu – площадь поперечного сечения проводника вторичной обмотки по меди.
Для однотактных трансформаторов, в отличие от двухтактных, при расчете сечения провода необходимо
использовать именно среднеквадратичное (в крайнем случае – среднее) значение тока. Упрощенный расчет с
использованием максимального значения приведет к значительной ошибке.
Далее вычисляется диаметр проводов (по меди) для выполнения обмоток:
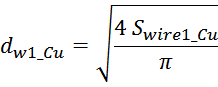
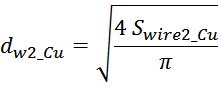
12.2 Выбор типа провода обмоток и определение диаметра и площади поперечного сечения проводников
с изоляцией
На основании вычисленного диаметра провода (по меди) выбирается ближайший диаметр провода из номенклатуры
диаметров выбранного типа провода (ПЭЛ, ПЭТВ и т.д.). Округление производится в большую сторону.
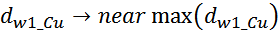
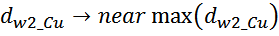
В соответствии с выбранным типом провода пересчитывается площади поперечного сечения выбранного типа провода
по меди по формулам:
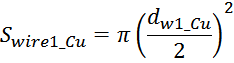
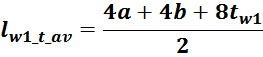
Далее в соответствии со справочным листком на выбранный тип обмоточного провода для первичной и вторичной
обмоток определяется его диаметр с изоляцией dw1_ins и dw2_ins. Диаметр провода в
изоляции учитывается при расчете числа витков в одном слое, проверки условия размещения обмоток в окне
магнитопровода и т.д.
12.3 Расчёт средней длины витка обмоток трансформатора
Традиционно для создания трансформаторов обратноходовых преобразователей используются Ш- и П- образные
магнитопроводы. Ниже представлены соотношения для расчета средней длины витка для данных магнитопроводов
(аналогичные соотношения представлены в разделе «Трансформатор»).
Для Ш- и П- образных магнитопроводов с прямоугольным сечением магнитопроводасредние длины
витков рассчитываются по соотношениям:
для первичной обмотки:
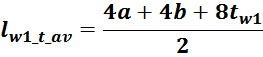
где:
a, b – геометрические параметры характеризующие сечение каркаса магнитопровода (см. рисунок L.6);
tw1 – толщина обмотки, вычисляемая по соотношению:
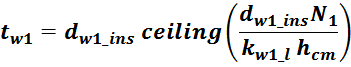
здесь:
функция ceiling – округление до большего целого;
hcm –высота каркаса магнитопровода;
N1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины провода (таблица
L.1).
Таблица L.1 – Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
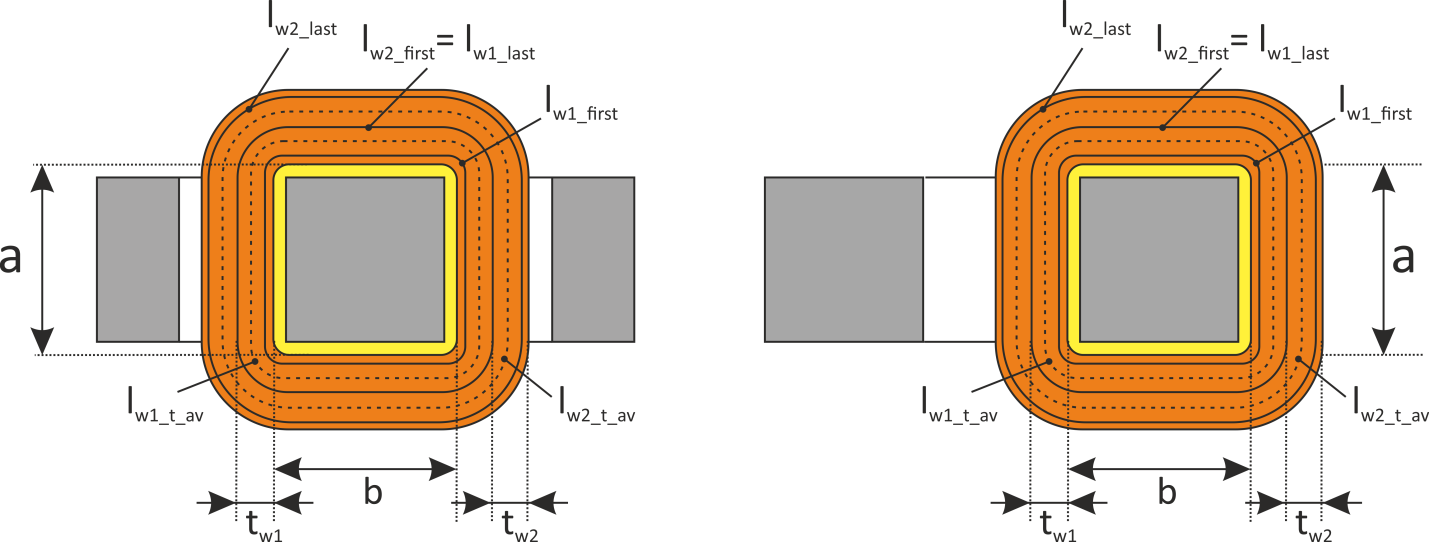
Рисунок L.6 – К определению средней длины витка для Ш- и П- образных магнитопроводов
для вторичной обмотки:
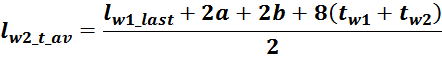
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по соотношению:
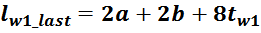
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
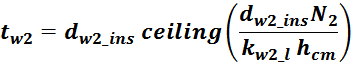
здесь:
N2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины провода (таблица
L.1).
Для Ш- и П- образных, чашеобразных и других магнитопроводов с круглым сечением центрального стержня
магнитопровода средняя длина витка рассчитывается по следующим соотношениям:
для первичной обмотки:
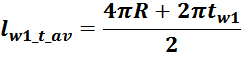
где:
R – радиус каркаса магнитопровода;
tw1 – толщина первичной обмотки, вычисляемая по соотношению:
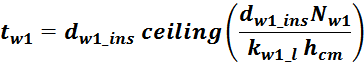
где:
функция ceiling – округление до большего целого;
hcm – высота обмотки, определяется высотой каркаса магнитопровода;
N1 – число витков в первичной обмотке;
kw1_l – коэффициент укладки (laying) первичной обмотки, зависящий от толщины провода (таблица
L.1).
для вторичной обмотки:
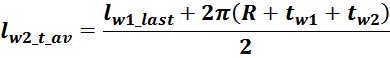
где:
lw1_last – длина внешнего витка первичной обмотки, вычисляемая по соотношению:
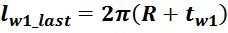
tw2 – толщина вторичной обмотки, вычисляемая по соотношению:
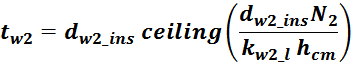
здесь:
N2 – число витков в вторичной обмотке;
kw2_l – коэффициент укладки (laying) вторичной обмотки, зависящий от толщины провода (таблица
L.1).
12.4 Определение длин обмоток
Длина обмоток определяется как произведение средней длины витка на число витков:
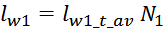
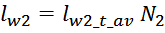
Полученная величина определяет, сколько провода нужно отмерить на обмотку трансформатора.
12.5 Конструктивный расчет структуры обмоток трансформатора, фактическая проверка возможности
размещения обмоток
Использование некоторой предопределенной величины коэффициента заполнения окна не дает однозначной гарантии
размещения обмотки в окне магнитопровода. Поэтому необходима проверка конструктивного условия размещения
обмотки в окне магнитопровода. Кроме этого, может быть неоптимальное использование окна магнитопровода, если
останется слишком много свободного места в окне обмотки.
Для выполнения конструктивного расчета необходим выбор материалов и определение толщин слоев изоляции
«пирога» обмоток:
Δw1l – толщина межслоевой изоляции первичной обмотки (если межслоевой изоляции обмотки не
предусмотрено, то величина Δw1l принимается равной нулю);
Δw2l – толщина межслоевой изоляции вторичной обмотки (если межслоевой изоляции обмотки не
предусмотрено, то величина Δw2l принимается равной нулю);
Δ(1-2)l – толщина межобмоточной изоляции;
Δsurf – толщина слоя внешней изоляции обмотки.
Для конструктивного расчета структуры обмотки трансформатора выполняется следующая последовательность
действий:
Ш- и П- образные и чашеобразные магнитопроводы
определяется средняя ширина намоточного слоя hlav. Она равна высоте каркаса магнитопровода hcm (рисунок
L.14):
Высота каркаса магнитопровода hcm определяется из справочных данных (datasheet) на магнитопровод.
В ряде случаев, например при использовании секционирования обмотки, в качестве высоты каркаса hcm
используется высота секции.
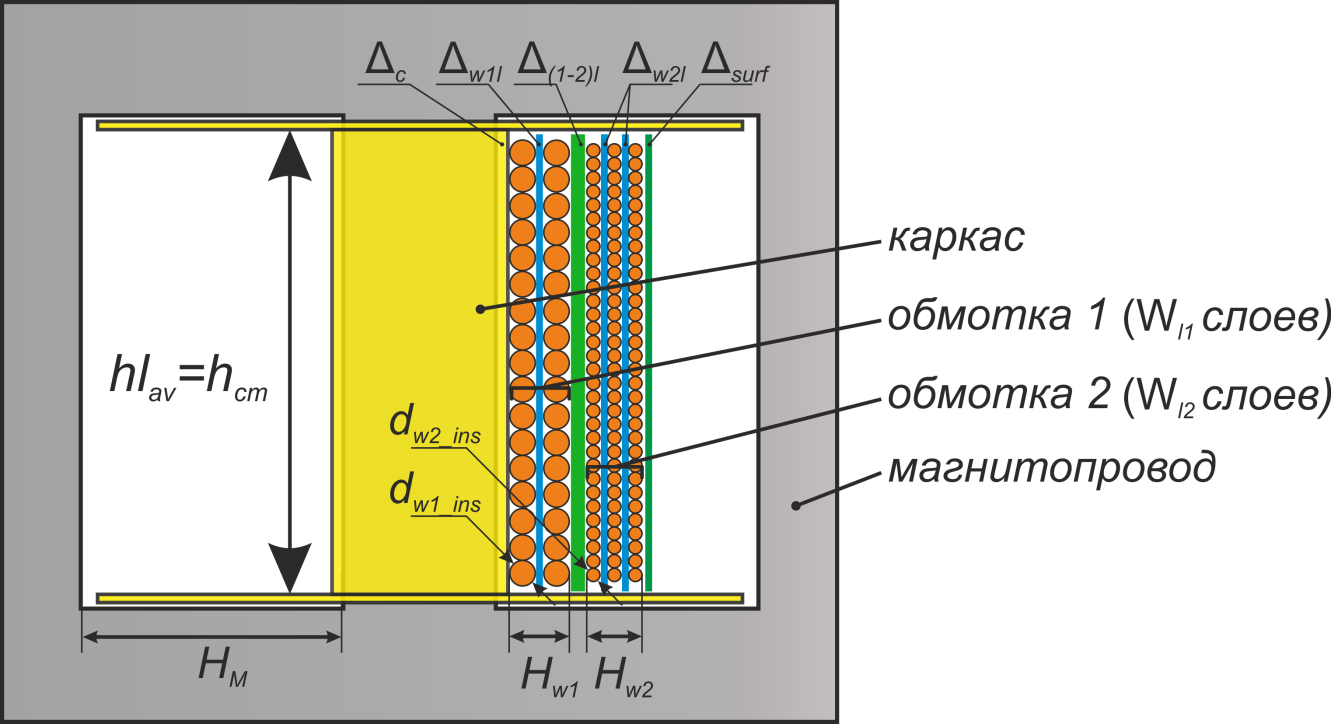
Рисунок L.14 – К расчету конструкции обмотки трансформатора обратноходового преобразователя
– определяется число витков в одном слое для первичной и вторичной обмоток Nw1_l и
Nw2_l :
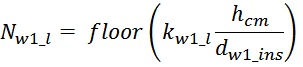
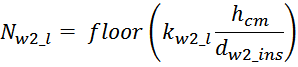
где:
hcm – высота каркаса магнитопровода;
dw1_ins , dw2_ins – диаметры проводников обмоток с изоляцией;
kw1_l , kw2_l – коэффициенты укладки (laying), зависящие от толщины провода (таблица
L.1).
Таблица L.1 Коэффициент укладки в зависимости от диаметра провода для трансформаторов кольцевой конструкции
[Гейтенко Е.Н. Источники вторичного электропитания. Схемотехника и расчет. Учебное пособие. — М.:
СОЛОН-ПРЕСС, 2008. — 448 с.]
|
Диаметр провода с изоляцией, мм |
0,08 – 0,31 |
0,31-0,5 |
0,5-2,1 |
|
Коэффициент укладки |
0,8-0,75 |
0,75-0,7 |
0,65-0,6 |
Рассчитывается общее число слоев для первичной и вторичной обмоток Wl1 , Wl2 как
отношение числа витков в обмотке к числу витков в единичном слое с округлением до большего целого (ceiling)
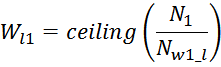
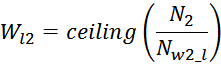
где:
(ceiling) – округление до большего целого;
N1, N2 – число витков в первичной и вторично обмотках, соответственно;
Nw1_l , Nw2_l – число витков в одном слое первичной и вторичной обмоток,
соответственно.
Рассчитываются толщины обмоток трансформатора Hw1 , Hw2 :
для первичной обмотки:
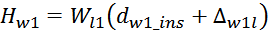
где:
Δw1l – толщина межслоевой изоляции первичной обмотки;
Wl1 – число слоев в первичной обмотке;
dw1_ins – диаметр провода первичной обмотки с изоляцией.
для вторичной обмотки:
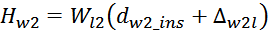
где:
Δw2l – толщина межслоевой изоляции вторичной обмотки;
Wl2 – число слоев в вторичной обмотке;
dw2_ins – диаметр провода вторичной обмотки с изоляцией.
В случае если межслоевой изоляции не предусмотрено, то величины Δw1l и Δw2lпринимаются
равными нулю (в реальности, при плотно намотке за счет укладывания витков следующего слоя в пазы слоя
предыдущего толщина обмотки может быть несколько меньше).
Рассчитывается общая толщина «пирога» обмотки HΣ. В случае намотки обмоток трансформатора одна
поверх другой (типично для обратноходового преобразователя) общая толщина обмоток складывается из толщин
каждой из обмоток, толщины межобмоточной изоляции Δ(1-2)l и толщины каркаса Δc
(расстояния между поверхностью каркаса и магнитопроводом) и толщины слоя внешней изоляции обмотки
Δsurf:
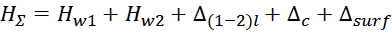
где:
Δ(1-2)l – толщина межобмоточной изоляции;
Δc – толщина каркаса (расстояние между поверхностью каркаса и магнитопроводом). В случае если
ширина окна магнитопровода HM принимается уже с учетом толщины каркаса, то Δc в данной
формуле не учитывается;
Δsurf – толщина слоя внешней изоляции обмотки;
Hw1 , Hw2 – толщины обмоток трансформатора.
Проверяется условие фактического размещения всех конструктивных элементов «пирога» обмоток в окне
магнитопровода:
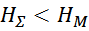
где:
HΣ – суммарная толщина «пирога» обмоток;
HM – ширина окна магнитопровода.
В случае невыполнения данного условия необходимо использовать другой магнитопровод и повторить процедуру
расчета (пункты 2 – 12).
13. Расчет сопротивления обмоток трансформатора
Электрическое сопротивление обмоток трансформатора Rw1 и Rw2 рассчитывается по формуле
для расчета омического сопротивления протяженного проводника:
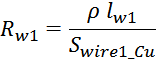
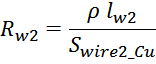
где:
ρ – удельное сопротивление материала провода (для меди – 0,0175 Ом·мм2 м-1 );
lw1 , lw2 – длины проводов первичной и вторичной обмоток соответственно;
Swire1_Cu , Swire2_Cu – площади поперечного сечения выбранного типа провода (по меди).
14. Расчет омических потерь в обмотках
Суммарные потери на омическом сопротивлении обмоток определяются по формулам:
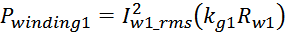
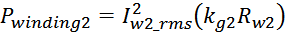
где:
Rw1 , Rw2 – сопротивление первичной и вторичной обмоток на постоянном токе;
kg1 , kg2 – коэффициент добавочных потерь за счет скин-эффекта и эффекта близости в
первичной и вторичной обмотках соответственно;
Iw1_rms , Iw2_rms – среднеквадратичное значение тока в первичной и вторичной обмотках
соответственно.
NB: При высоких рабочих температурах трансформатора необходимо учитывать влияние температуры на удельное
сопротивление проводников обмоток. При высоких частотах необходимо оценить увеличение эффективного
сопротивления обмоток в результате действия скин-эффекта (см. раздел «Трансформатор»).
15. Оценка уровня потерь в магнитопроводе
Рассчитываем максимальную индукцию в магнитопроводе:
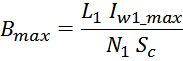
где:
L1 – заданное значение индуктивности первичной обмотки трансформатора;
Iw1_max – максимальное значение тока первичной обмотки трансформатора;
N1 – число витков первичной обмотки трансформатора;
Sc – площадь сечения магнитопровода.
На основании полученного значения максимальной индукции в магнитопроводе рассчитываем уровень потерь.
Существуют три способа определения потерь в магнитопроводе:
рассчитать по формуле (при наличии аппроксимацонных коэффициентов);
определить по графику из datasheet;
определить экспериментально.
Расчёт по аппроксимацонным коэффициентам
Тепловая энергия, выделяемая в магнитопроводе определяется режимом работы дросселя – частотой работы f и
уровнем магнитной индукции Bmax. Для расчета потерь в магнитопроводе Pferrit
используют следующее аппроксимирующее выражение [Optimum design of a high-power, high-frequency transformer.
R. Petkov. IEEE Transactions on Power Electronics (Volume: 11, Issue: 1, Jan 1996)]:
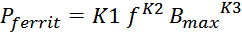
где
f – частота;
Bmax – индукция;
K1, K2, K3 – аппроксимационные коэффициенты, определенные для каждого конкретного типа феррита.
Определение по графику относительных потерь из datasheet
Для определения потерь в магнитопроводе можно использовать соотношение:
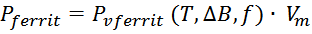
где:
Pvferrit – мощность потерь на единицу объема, являющаяся функцией температуры, магнитной индукции
и частоты. Графики данной зависимости представлены в справочных листах (datasheet) на каждый ферромагнитный
материал магнитопровода;
Vm – объем магнитопровода (приводится в справочных листах (datasheet).
Мощность потерь на единицу объема определяется типом феррита и приводится в справочных данных на конкретный
тип магнитного материала.

Рисунок L.12 – Зависимость мощности потерь от частоты при различных значениях индукции магнитного поля и
температуре для феррита N87 [Ferrites and accessories. SIFERRIT material N87, EPCOS AG 2006]
Данный способ расчета потерь в магнитопроводе является наиболее точным.
Определение по уровню максимальных потерь из datasheet на магнитопровод
Максимальный уровень потерь в магнитопроводе соответствует крайним режимам эксплуатации магнитопровода.
Уровень максимальных потерь часто приводится в datasheet на конкретный тип магнитопровода при различных
условиях (индукция магнитного поля, частота, температура). Уровень максимальных потерь обозначается как
PV (W/set).
В этом случае мощности потерь в магнитопроводе Pferrit приравнивается к уровню максимальных потерь
PV представленном в datasheet для наиболее близких условий эксплуатации:
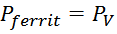
Экспериментальное определение
В случае отсутствия данных для расчета остается путь экспериментального определения потерь.
16. Расчет суммарных потерь
Суммарные потери дросселя складываются из омических потерь обмотки и потерь магнитопровода:
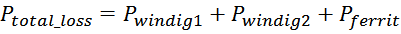
где:
Pwinding1, Pwinding2 – омические потери в первичной и вторичной обмотке
соответственно;
Pferrit – потери в магнитопроводе.
Соотношение потерь в обмотке и магнитопроводе является критерием оптимального проектирования. Если эти потери
приблизительно равны, то данный трансформатор обратноходового преобразователя спроектирован самым
оптимальным образом. Чем ближе Pwinding и Pferrit по величине тем лучше, поскольку при
этом, как правило, достигается минимум потерь при минимуме материала.
Если эти параметры отличаются более чем в 3-5 раз, то имеет смысл пересчитать трансформатор по пунктам 3-15
используя другой магнитопровод.
17. Расчет температурного режима трансформатора и оптимизация
Установившаяся температура перегрева трансформатора относительно окружающей среды ∆T (дельта перегрева)
приблизительно оценивается по соотношению [McLyman C. Transformer and inductor design handbook.2004]:
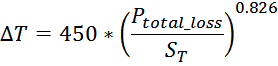
где:
Ptotal loss – мощность суммарных потерь в трансформаторе;
ST – суммарная эффективная площадь охлаждения трансформатора (в см2).
Полученное ∆T (дельта перегрева) складывается с температурой эксплуатации трансформатора и рассчитывается его
максимальная рабочая температура. Если полученное значение температуры нагрева трансформатора лежит в
пределах 50-80°С, то расчет трансформатора можно считать законченным. Если полученное значение превышает
80°С, то имеет смысл использовать магнитопровод большего размера.
Если в результате расчета уровень перегрева трансформатора ΔT будет значительно меньше максимально
допустимого:
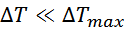
то имеет смысл использовать оптимизировать конструкцию трансформатора с целью уменьшения стоимости и
массогабаритных показателей – уменьшить формфактор магнитопровода и варьировать плотность тока, размах
индукции (можно делать одновременно с повышением частоты).
Кроме того, если при допустимом уровне нагрева трансформатора получится, что мощность, выделяемая на активном
сопротивлении обмотки существенно меньше, чем в феррите магнитопровода:
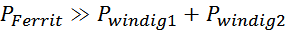
то имеет смысл использовать большую плотность тока, протекающего через обмотки и повторить расчет по пунктам
1-12.
Необходимо понимать, что оптимизация расчета трансформатора проводится с учетом целевых приоритетов:
Приоритет 1 – Малые массогабаритные параметры трансформатора и, соответственно, стоимость. В этом случае
необходимо провести расчет всех параметров трансформатора с целью обеспечения (но не превышения) заданного
уровня перегрева и минимальной стоимости/массогабаритных параметров. В этом случае плотность тока, размах
индукции итерационно увеличиваются;
Приоритет 2 – Высокий КПД. В этом случае необходимо задаться максимальными массогабаритными параметрами и с
учетом этого варьируя параметры трансформатора (индукция, плотность тока и т.д.) провести расчет всех
параметров трансформатора с целью минимизации мощности потерь. В этом случае плотность тока, размах индукции
итерационно уменьшаются;
18. Расчет величины паразитной индуктивности рассеяния первичной обмотки Lw1_leak
Индуктивность рассеяния первичной обмотки зависит от взаимного расположения первичной и вторичной обмоток и
структуры и расположения их слоев.
Для типовой конструкции трансформатора, состоящей из двух единых обмоток, когда вторичная обмотка расположена
поверх первичной (рисунок L.15) индуктивность рассеяния оценивается по формуле [McLyman C. Transformer and
inductor design handbook.2004]:
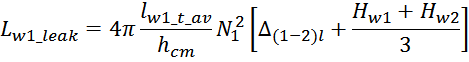
где:
lw1_t_av – средняя длина витка первичной обмотки;
hcm – высота каркаса магнитопровода (определяет высоту обмотки);
Δ(1-2)l – толщина межобмоточной изоляции;
Hw1 , Hw2 – толщины первичной и вторичной обмоток.
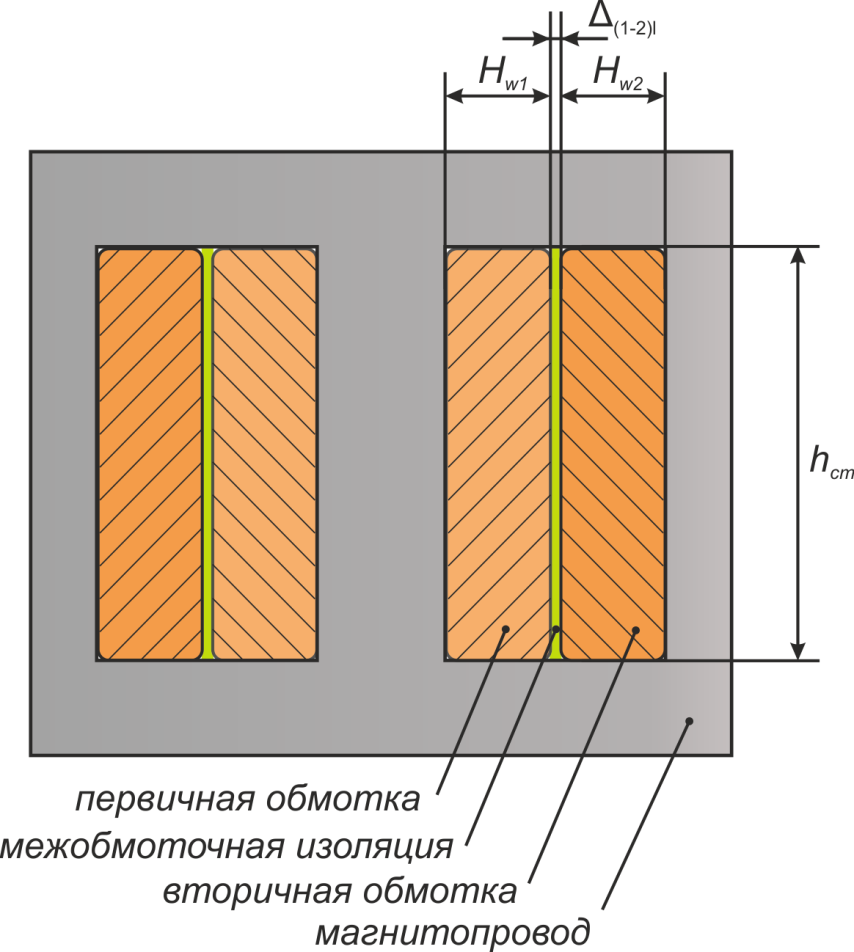
Рисунок L.15 – Типовое расположение обмоток трансформатора, состоящего из двух единых обмоток, при этом
вторичная обмотка расположена поверх первичной
Для конструкции трансформатора с чередованием обмоток, когда вторичная обмотка разбивается на две равные
части, между которыми располагается первичная обмотка (рисунок L.16) индуктивность рассеяния оценивается по
формуле [McLyman C. Transformer and inductor design handbook.2004]:
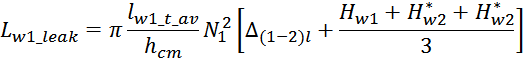
где:
lw1_t_av – средняя длина витка первичной обмотки;
hcm – высота каркаса магнитопровода (определяет высоту обмотки);
Δ(1-2)l – толщина межобмоточной изоляции;
Hw1 – толщина первичной обмотки;
Hw2* – толщина секции половины вторичной обмотки.
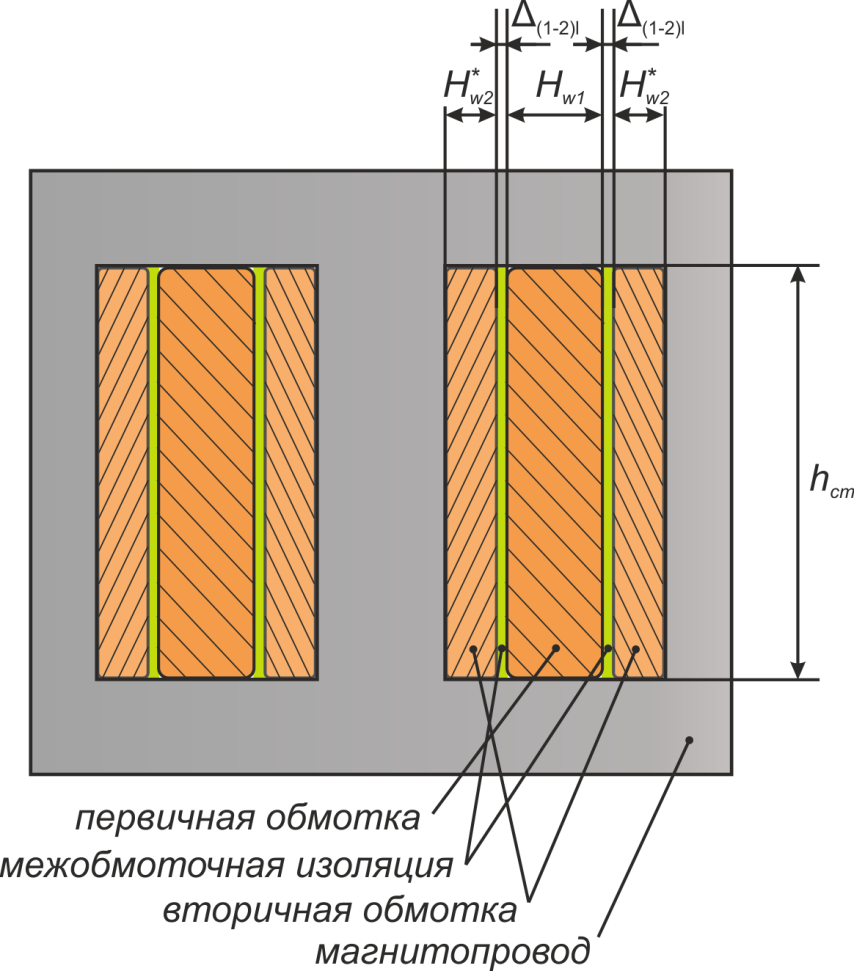
Рисунок L.16 – Типовое расположение обмоток трансформатора, состоящего из двух единых обмоток, при этом
вторичная обмотка расположена поверх первичной.
В соответствии с [Flyback Converter snubber Design. Switching Power Magazine. 2005] для грубой оценки
индуктивности рассеяния можно считать, что она составляет величину порядка 1% от индуктивности
намагничивания.
В результате выполненного последовательного расчета мы получаем следующие параметры:
конкретный тип магнитопровода c конкретными геометрическими параметрами;
число витков первичной N1 и вторичной N2 обмоток;
величину немагнитного зазора lg;
омическое сопротивление первичной Rw1 и вторичной Rw2 обмоток;
потери на омическом сопротивлении обмоток Pwinding1 и Pwinding2;
потери в магнитопроводе Pferrit ;
суммарная мощность потерь в трансформаторе Ptotal_loss;
уровень перегрева трансформатора ΔT;
индуктивность рассеяния первичной обмотки Lw1_leak .
-
Методики расчета индуктивности катушек
Основным
элементом катушек индуктивности является
токовод. Величина индуктивности
определяется конструкцией токовода и
его размерами.
Полная
индуктивность медного провода круглого
сечения длиной lПРи диаметромd0равна
![]() (3.1)
(3.1)
Из
(3.1) следует, что индуктивность провода
уменьшается с ростом его диаметра. Это
свойство широко используют в УКВ
аппаратуре для уменьшения индуктивности
соединительных проводов за счет
увеличения их диаметра.
Если
одиночный проводник согнуть, например,
в кольцо, то его индуктивность уменьшится
из-за встречного направления токов в
соседних частях кольца. Однако, для
круглого кольца индуктивность будет
наибольшей по сравнению с индуктивностью
витка любой другой конфигурации,
поскольку круглый виток охватывает
наибольшую площадь, обеспечивая
наибольшее потокосцепление.
Индуктивность
круглого плоского витка диаметром Dиз провода круглого сечения длинойlПРи диаметромdПРравна
![]() (3.2)
(3.2)
При
сворачивании проводника в несколько
витков wодинакового
диаметра образуется катушка, индуктивность
которой можно определить как суммарную
индуктивность всех витков с учетом
взаимоиндукцииMмежду
ними:
![]() (3.3)
(3.3)
Индексы при Муказывают на взаимную индуктивность
между первым и вторым, вторым и третьим,
первым и третьим витками и т.д. Если
известен коэффициент связи, который
определяется равенством
![]() ,
,
(3.4)
то индуктивность
катушки с произвольным числом витков
определяется из
![]() . (3.5)
. (3.5)
Коэффициент связи
между витками, расположенными на
расстоянии τ, в однослойной катушке
определяется выражением
 (3.6)
(3.6)
Для сплошной намотки
τ=d0.
Индуктивность
многослойной катушки незначительно
зависит от диаметра провода, так как
определяется в основном взаимоиндукцией
между витками.
Из-за трудности
определения коэффициента связи выражение
(3.5) обычно применяют для расчета катушек
индуктивности с небольшим числом витков
(обычно не более шести).
Для катушек с однородным
замкнутым магнитопроводом (с тороидальным
сердечником) выражение для определения
индуктивности принимает вид
![]() , (3.7)
, (3.7)
где μ– начальная магнитная
проницаемость сердечника (μ=1 для
диэлектрического каркаса или воздуха);
μ0=4π·10-7Гн/м – магнитная постоянная;
w– число витков обмотки;
S
– площадь поперечного сечения катушки;
![]() – длина намотки катушки;
– длина намотки катушки;
Таким
образом, увеличение индуктивности
катушки может быть достигнуто за счет
увеличения числа витков, магнитной
проницаемости сердечника, площади
поперечного сечения магнитопровода, а
также уменьшения длины намотки.
В
высокочастотных катушках замкнутый
магнитопровод как правило отсутствует,
поэтому индуктивность катушки будет
меньше, рассчитанной по (3.7). Для учета
рассеивания магнитного потока на краях
катушки вводится поправочный коэффициент
k, который зависит от
отношения диаметра катушки к длине
намотки
 (3.8)
(3.8)
Для
практических расчетов однослойных
цилиндрических катушек, намотанных
виток к витку (рис.3.2 а),используют
выражение
 , (3.9)
, (3.9)
где
 – коэффициент формы катушки, учитывающий
– коэффициент формы катушки, учитывающий
краевые эффекты;
μ– начальная магнитная
проницаемость сердечника (μ=1 для
катушек без магнитного сердечника);
μ0=4π·10-7Гн/м –
магнитная постоянная;
w– число витков обмотки;
![]() – площадь поперечного сечения круглой
– площадь поперечного сечения круглой
катушки;
D– диаметр катушки;
![]() – длина намотки.
– длина намотки.
Для
практических расчетов однослойных
цилиндрических катушек без сердечника,
намотанных с принудительным шагом τ(рис.3.2 б),индуктивн ость
ость
рассчитывают по (3.9), но полученный
результат уменьшают на поправкуΔL
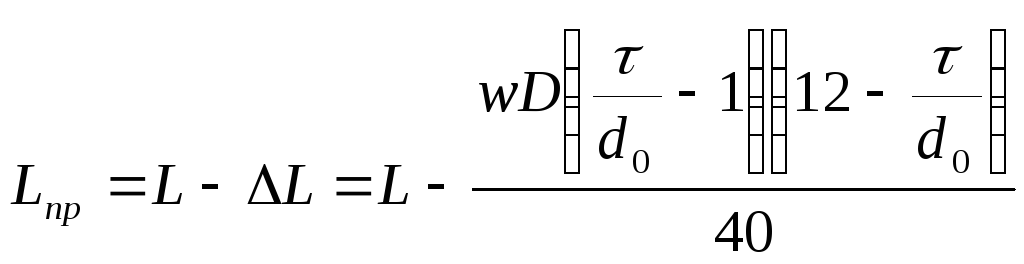 , (3.10)
, (3.10)
где τ– шаг намотки;
L–
индуктивность катушки, определенная
по (3.9) приμ=1.
Для
практических расчетов индуктивности
тороидальной однослойной катушки,
намотанной сплошным слоем на круглом
магнитном сердечнике прямоугольного
сечения (рис.3.2 в), используют
выражение
![]() , (3.11)
, (3.11)
где
![]() – площадь поперечного сечения сердечника
– площадь поперечного сечения сердечника
тороида;
![]() – средняя длина сердечника тороида;
– средняя длина сердечника тороида;
D– внешний диаметр сердечника тороида;
d– внутренний диаметр сердечника тороида;
h– высота сердечника тороида.
Для практических
расчетов многослойных катушек без
сердечника(рис.3.2 г) используют
выражение
 , (3.12)
, (3.12)
г деDCP
деDCP
– средний диаметр катушки;
t– толщина катушки;
l– длина катушки.
Для
практических расчетов многослойных
секционированных катушек без сердечника
(рис.3.2 д) используют выражение
![]() , (3.13)
, (3.13)
где LC
– индуктивность одной секции катушки;
n– число секций;
kCB– коэффициент связи между смежными
секциями, зависящий от отношения![]() (рис.3.3);
(рис.3.3);
b
– расстояние между секциями.
Для
практических расчетов плоских круглых
спиральных катушек (рис.3.2 е) используют
выражение
![]() , (3.14)
, (3.14)
где DBH,DH –внутренний и наружный диаметры
катушки, соответственно.
Для
практических расчетов плоских
квадратных спиральных катушек (рис.3.2
ж) используют выражение
![]() , (3.15)
, (3.15)
где АBH,АH
–внутренняя и наружная стороны
катушки, соответственно.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
10.02.20165.15 Mб192.doc
- #
- #
- #
- #
- #
- #
Если у вас имеется катушка индуктивности с воздушным сердечником и необходимо рассчитать её индуктивность, то вам поможет онлайн калькулятор. Достаточно ввести основные параметры катушки и вы сразу получите результат.
Найти индуктивность катушки с воздушным сердечником проще простого. Введите в калькулятор диаметр и длину катушки, а также количество витков. Останется только нажать кнопку «расчет» и вы узнаете индуктивность такой катушки.
Формула индуктивности катушки с воздушным сердечником
Расчет однослойной катушки индуктивности без сердечника производится по формуле:
L = (D2 * n2) / (45 * D + 100 * l) , где
L — индуктивность катушки в мкГн,
D — диаметр катушки в см,
n — число витков в шт,
l — длина намотки в см.
Формула конечно не сложная, но лучше всего индуктивность катушки с воздушным сердечником рассчитывать на нашем онлайн калькуляторе. Это как минимум убережёт вас от ошибок и сэкономит максимум времени.
Единицы измерения индуктивности
Единицей измерения индуктивности является Генри (Гн). В таблице ниже приводим зависимости между разными величинами.
| Название | Обозначение | Международное | Перевод единиц |
|---|---|---|---|
| Генри | Гн | H | — |
| Килогенри | кГн | kH | 1 кГн = 103 Гн |
| Миллигенри | мГн | mH | 1 мГн = 10-3 Гн |
| Микрогенри | мкГн | µH | 1 мкГн = 10-6 Гн |
| Наногенри | нГн | nH | 1 нГн = 10-9 Гн |
| Пикогенри | пГн | pH | 1 пГн = 10-12 Гн |
Пример расчета индуктивности однослойной катушки с воздушным сердечником
Давайте рассмотрим пример расчета индуктивности однослойной катушки на 1/4 волны с воздушным сердечником. Допустим у нас катушка диаметром 10 мм, длиной 50 мм и с количеством витков 200 штук. Подставим имеющиеся значения в формулу:
L = (12 * 2002) / (45 * 1 + 100 * 5) = 73,394 мкГн.
Надо помнить что эта формула эмпирическая и подходит для простого частного случая. Она не учитывает ни диаметр проволоки ни рабочую частоту на которой будет работать катушка. Для более сложных расчетов нужен будет другой калькулятор индуктивности.
Вот мы и рассмотрели как считается катушка индуктивности с воздушным сердечником. Эти знания вам обязательно пригодятся.
Было полезно? Поделитесь с друзьями!
На рисунке выше показана однослойная катушка индуктивности: Dc — диаметр катушки, D — диаметр оправки или каркаса катушки, p — шаг намотки катушки, d — диаметр провода без изоляции и di — диаметр провода с изоляцией
Для расчета индуктивности LS применяется приведенная ниже формула из статьи Р. Уивера (R. Weaver) Численные методы расчета индуктивности:

Здесь
D — диаметр оправки или каркаса катушки в см,
l — длина катушки в см,
N — число витков и
L — индуктивность в мкГн.
Эта формула справедлива только для соленоида, намотанного плоским проводом. Это означает, что катушка намотана очень тонкой лентой без зазора между соседними витками. Она является хорошим приближением для катушек с большим количеством витков, намотанных проводом круглого сечения с минимальным зазором между витками. Американский физик Эдвард Беннетт Роса (Edward Bennett Rosa, 1873–1921) работавший в Национального бюро стандартов США (NBS, сейчас называется Национальное бюро стандартов и технологий (NIST) разработал так называемые корректирующие коэффициенты для приведенной выше формулы в форме (см. формула 10.1 в статье Дэвида Найта, David W. Knight):

Здесь LS — индуктивность плоской спирали, описанная выше, и

где ks — безразмерный корректирующий коэффициент, учитывающий разницу между самоиндукцией витка из круглого провода и витка из плоской ленты; km — безразмерный корректирующий коэффициент, учитывающий разницу в полной взаимоиндукции витков из круглого провода по сравнению с витками из плоской ленты; Dc — диаметр катушки в см, измеренный между центрами проводов и N — число витков.
Величина коэффициента Роса km определяется по формуле 10.18 в упомянутой выше статье Дэвида Найта:

Коэффициент Роса ks, учитывающий различие в самоиндукции, определяется по формуле 10.4 в статье Д. Найта:

Здесь p — шаг намотки (расстояние между витками, измеренное по центрам проводов) и d — диаметр провода. Отметим, что отношение p/d всегда больше единицы, так как толщина изоляции провода конечна, а минимально возможное расстояние между двумя соседними витками с очень тонкой изоляцией, расположенными без зазора, равна диаметру провода d.
Факторы, влияющие на индуктивность катушки
На индуктивность катушки влияют несколько факторов.
- Количество витков. Катушка с большим количеством витков имеет бóльшую индуктивность по сравнению с катушкой с меньшим количеством витков.
- Длина намотки. Две катушки с одинаковым количеством витков, но разной длиной намотки имеют разную индуктивность. Более длинная катушка имеет меньшую индуктивность. Это связано с тем, что магнитное поле менее компактной катушки более слабое и оно не может хорошо концентрироваться в растянутой катушке.
- Диаметр катушки. Две плотно намотанные катушки с одинаковым количеством витков и разными диаметрами имеют разную индуктивность. Катушка с бóльшим диаметром имеет бóльшую индуктивность.
- Сердечник. Для увеличения индуктивности в катушку часто вставляется сердечник из материала с высокой магнитной проницаемостью. Сердечники с более высокой магнитной проницаемостью позволяют получить более высокую индуктивность. Сердечники, изготовленные из магнитной керамики — феррита, часто используются в катушках и трансформаторах различных электронных устройств, так как у них очень низкие потери на вихревые токи.





Упрощенная эквивалентная схема реальной катушки индуктивности: Rw — сопротивление обмотки и ее выводов; L — индуктивность идеальной катушки; Rl — сопротивление вследствие потерь в сердечнике; и Cw — паразитная емкость катушки и ее выводов.
Эквивалентная схема реальной катушки индуктивности
В этом калькуляторе мы рассматривали идеальную катушку индуктивности. В то же время, в реальной жизни таких катушке не бывает. Катушки обычно конструируются с минимальными размерами таким образом, чтобы они помещались в миниатюрное устройство. Любую реальную катушку индуктивности можно представить в виде идеальной индуктивности, к которой параллельно подключены емкость и сопротивление, а еще одно сопротивление подключено последовательно. Параллельное сопротивление учитывает потери на гистерезис и вихревые токи в магнитном сердечнике. Это параллельное сопротивление зависит от материала сердечника, рабочей частоты и магнитного потока в сердечнике.
Паразитная емкость появляется в связи с тем, что витки катушки находятся близко друг к другу. Любые два витка провода можно рассмотреть как две обкладки маленького конденсатора. Витки разделяются изолятором, таким как воздух, изоляционный лак, лента или иной изоляционный материал. Относительная диэлектрическая проницаемость материалов, используемых для изоляции, увеличивает емкость обмотки. Чем выше эта проницаемость, тем выше емкость. В некоторых случаях дополнительная емкость может появиться также между катушкой и противовесом, если катушка расположена над ним. На высоких частотах реактивное сопротивление паразитной емкости может быть весьма высоким и игнорировать его нельзя. Для уменьшения паразитной емкости используются различные методы намотки катушек.

Для уменьшения паразитной емкости катушки с высокой добротностью для радиопередатчиков наматывают так, чтобы было достаточно большое расстояние между витками
Если индуктивность большая, то сопротивление обмотки (Rw на схеме) игнорировать уже нельзя. Тем не менее, оно мало по сравнению с реактивным сопротивлением больших катушке на высоких частотах. Однако, на низких частотах и на постоянном токе это сопротивление необходимо учитывать, так как в этих условиях через катушку могут протекать значительные токи.

Катушки индуктивности и обмотки в различных устройствах
