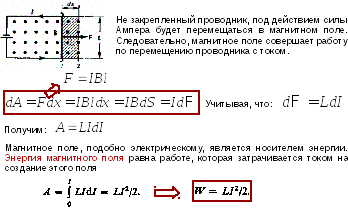
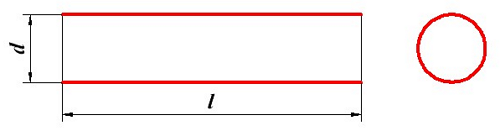
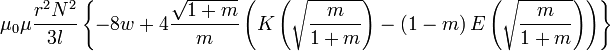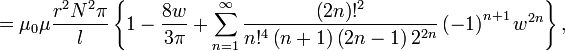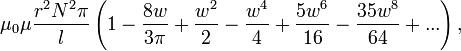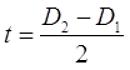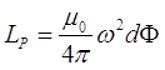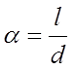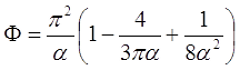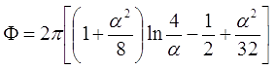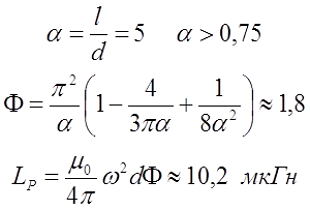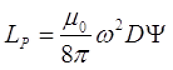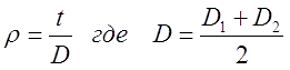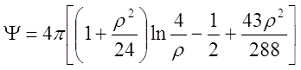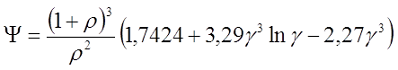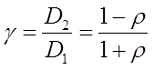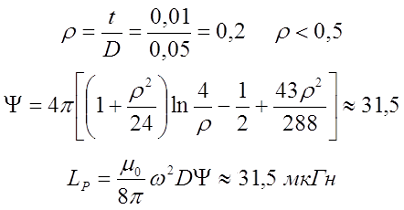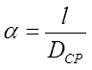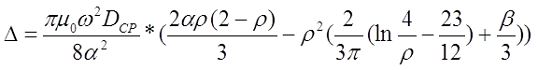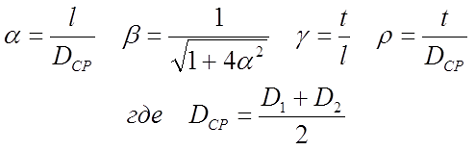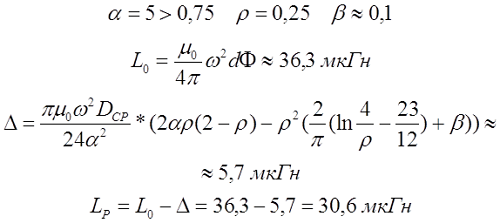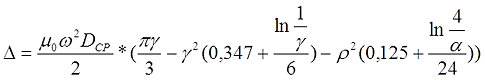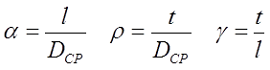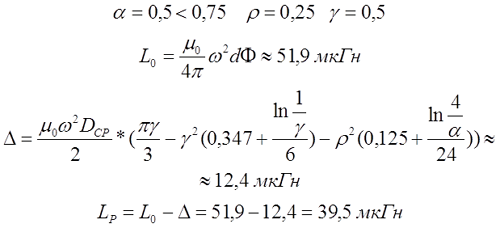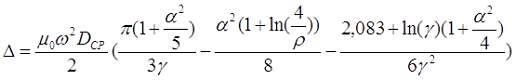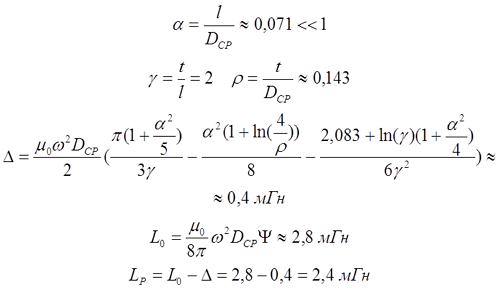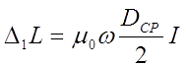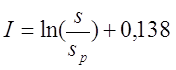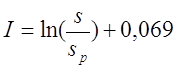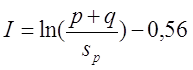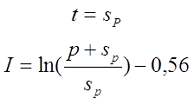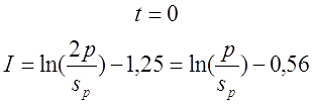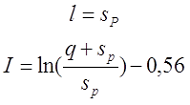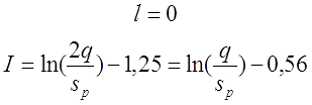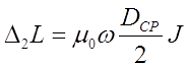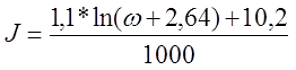Индуктивность соленоида
Соленоид —
длинная, тонкая катушка, то есть катушка,
длина которой намного больше, чем её
диаметр (также в дальнейших выкладках
здесь подразумевается, что толщина
обмотки намного меньше, чем диаметр
катушки). При этих условиях и без
использования магнитного материала
плотность магнитного потока внутри
катушки является фактически постоянной
и (приближенно) равна
где − магнитная
постоянная, −
число витков, −
ток и −
длина катушки. Пренебрегая краевыми
эффектами на концах соленоида, получим[16],
что потокосцепление через катушку равно
плотности потока ,
умноженному на площадь поперечного
сечения и
число витков :
Отсюда
следует формула для индуктивности
соленоида (без сердечника):
Если
катушка внутри полностью заполнена
магнитным материалом (сердечником), то
индуктивность отличается на
множитель — относительную
магнитную проницаемость[17]сердечника:
В
случае, когда ,
можно (следует) под S понимать
площадь сечения сердечника и пользоваться
данной формулой даже при толстой намотке,
если только полная площадь сечения
катушки не превосходит площади сечения
сердечника во много раз.
Более точные формулы для соленоида конечного размера
Для
однослойного (с очень тонкой намоткой)
соленоида конечных размеров (не бесконечно
длинного) существуют более точные, хотя
и более сложные формулы[18]:
где
–
количество витков,
–
радиус цилиндра,
–
длина его образующей,
,
,
– Эллиптические
интегралы.
Это
дает
-
для
-
для
-
Трансформатор.
Энергия магнитного поля. Основы теории
Максвелла. Уравнения Максвелла в
интегральной форме.
-
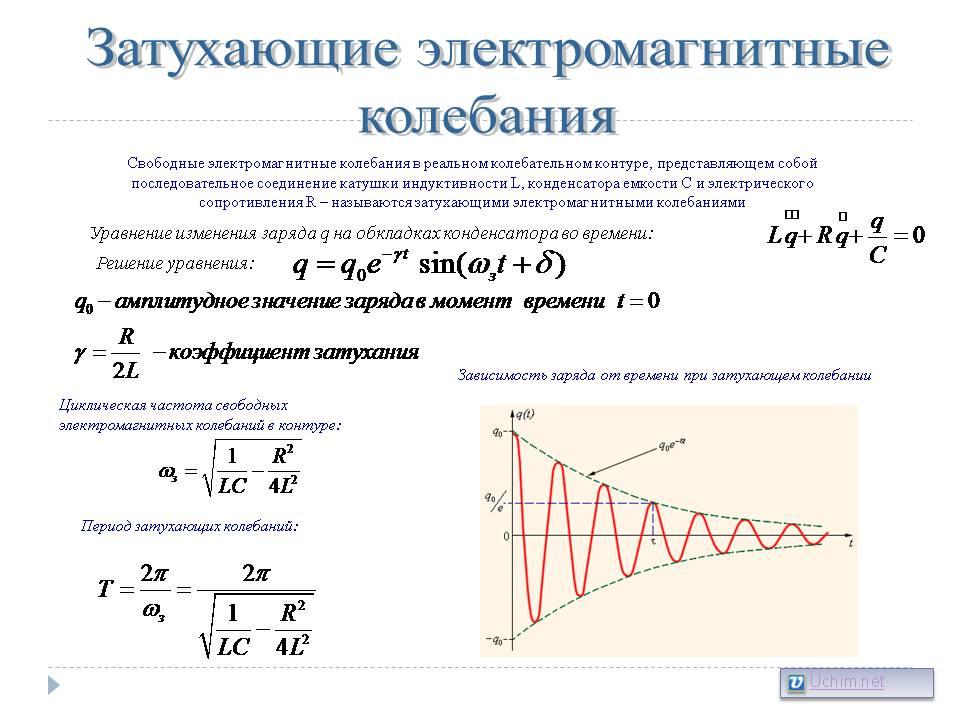
Электрический
колебательный контур. Затухающие
электромагнитные колебания. Вынужденные
электромагнитные колебания. Явление
резонанса
Колебательный
контур — осциллятор,
представляющий собой электрическую
цепь,
содержащую соединённые катушку
индуктивности и конденсатор.
В такой цепи могут
возбуждаться колебания тока (и напряжения).
Колебательный
контур — простейшая система, в которой
могут происходить свободные электромагнитные колебания
Резонансная
частота контура
определяется так называемой формулой
Томсона:
Принцип действия
Пусть
конденсатор ёмкостью C заряжен
до напряжения . Энергия,
запасённая в конденсаторе составляет
При
соединении конденсатора с катушкой
индуктивности, в цепи потечёт ток ,
что вызовет в катушке электродвижущую
силу (ЭДС) самоиндукции,
направленную на уменьшение тока в цепи.
Ток, вызванный этой ЭДС (при отсутствии
потерь в индуктивности) в начальный
момент будет равен току разряда
конденсатора, то есть результирующий
ток будет равен нулю. Магнитная энергия
катушки в этот (начальный) момент равна
нулю.
Затем
результирующий ток в цепи будет
возрастать, а энергия из конденсатора
будет переходить в катушку до полного
разряда конденсатора. В этот момент
электрическая энергия конденсатора .
Магнитная же энергия, сосредоточенная
в катушке, напротив, максимальна и равна
,
где — индуктивность катушки,
—
максимальное значение тока.
После
этого начнётся перезарядка конденсатора,
то есть заряд конденсатора напряжением
другой полярности. Перезарядка будет
проходить до тех пор, пока магнитная
энергия катушки не перейдёт в электрическую
энергию конденсатора. Конденсатор, в
этом случае, снова будет заряжен до
напряжения .
В
результате в цепи возникают колебания,
длительность которых будет обратно
пропорциональна потерям энергии в
контуре.
В
общем, описанные выше процессы в
параллельном колебательном контуре
называются резонанс
токов,
что означает, что
через индуктивность и ёмкость протекают
токи, больше тока проходящего через
весь контур, причем эти токи больше в
определённое число раз, которое
называется добротностью.
Эти большие токи не покидают пределов
контура, так как они противофазны и сами
себя компенсируют. Стоит также заметить,
что сопротивление параллельного
колебательного контура на резонансной
частоте стремится к бесконечности (в
отличие от последовательного колебательного
контура, сопротивление которого на
резонансной частоте стремится к нулю),
а это делает его незаменимым фильтром.
Стоит
заметить, что помимо простого колебательного
контура, есть ещё колебательные контуры
первого, второго и третьего рода, что
учитывают потери и имеют другие
особенности.
Вынужденными
электромагнитными колебаниями называют
периодические изменения силы тока и
напряжения в электрической цепи,
происходящие под действием переменной
ЭДС от внешнего источника. Внешним
источником ЭДС в электрических цепях
являются генераторы переменного тока,
работающие на электростанциях.
Принцип
действия генератора переменного тока
легко показать при рассмотрении
вращающейся рамки провода в магнитном
поле.
В
однородное магнитное поле с индукцией
В помещаем прямоугольную рамку,
образованную проводниками (abсd).
Пусть
плоскость рамки перпендикулярна индукции
магнитного поля В и ее площадь равна S.
Магнитный
поток в момент времени t0 =
0 будет равен Ф = В*8.
При
равномерном вращении рамки вокруг оси
OO1 с
угловой скоростью w магнитный поток,
пронизывающий рамку, будет изменяться
с течением времени по закону:
Изменение
магнитного потока возбуждает в рамке
ЭДС индукцию, равную
где
Е0=
ВSw – амплитуда ЭДС.
Если
с помощью контактных колец и скользящих
по ним щеток соединить концы рамки с
электрической цепью, то под действием
ЭДС индукции, изменяющейся со временем
по гармоническому закону, в электрической
цепи возникнут вынужденные гармонические
колебания силы тока – переменный
ток.
На
практике синусоидальная ЭДС возбуждается
не путем вращения рамки в магнитном
поле, а путем вращения магнита или
электромагнита (ротора) внутри статора
– неподвижных обмоток, навитых на
сердечники из магнитомягкого материала.
В этих обмотках находится переменная
ЭДС, что позволяет избежать снятия
напряжения с помощью контактных колец.
Явление
резонанса
относится к наиболее важным с практической
точки зрения свойствам электрических
цепей. Оно заключается в том, что
электрическая
цепь, имеющая реактивные элементы
обладает чисто резистивным сопротивлением.
Общее
условие резонанса
для любого двухполюсника можно
сформулировать в виде Im[Z]=0
или Im[Y]=0,
где Z
и Y
комплексное сопротивление и проводимость
двухполюсника. Следовательно, режим
резонанса полностью определяется
параметрами электрической цепи и не
зависит от внешнего воздействия на нее
со стороны источников электрической
энергии.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
68. Индуктивность соленоида и тороида
Индуктивность соленоида будем определять
по формуле
.
Магнитный поток, охватывающий все витки
соленоида выражается в виде
, где
поток, пронизывающий один виток, N – число витков соленоида. Поскольку


Сравнив это выражение с вышеприведенным ,
получим формулу для индуктивности соленоида.

(54)
Эта формула справедлива и для тороида, для него l длина средней линии тороида, равная l=2πr
Из формулы, выражающей индуктивность
соленоида легко получить единицу измерения магнитной постоянной 
Если внутрь соленоида или тороида
вставить сердечник из какого-либо магнитного материала, то индуктивность
возрастет μ раз

Всем доброго времени суток. Сегодняшняя статья является продолжением предыдущей. Здесь продолжим рассматривать расчёт индуктивностей индуктивных элементов без сердечников. В прошлой статье я рассказал, как рассчитать индуктивность прямого провода и провода свёрнутого в кольцо (виток), в данной статье будем рассчитывать индуктивность круговых катушек, то есть поперечный профиль, которых представляет собой окружности.
Для сборки радиоэлектронного устройства можно преобрески DIY KIT набор по ссылке.
Виды катушек индуктивности
Круговые катушки индуктивности являются, наверное, самыми распространёнными. В тоже время из-за разнообразия их форм существует некоторая трудность в расчёте индуктивности. Для некоторого упрощения расчёта катушки индуктивности делятся на несколько видов. Рассмотрим основные конструктивные особенности круговых катушек индуктивности
Расчёт индуктивности катушки.
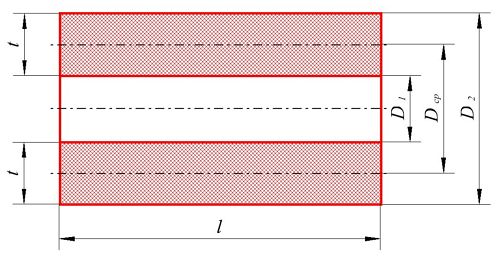
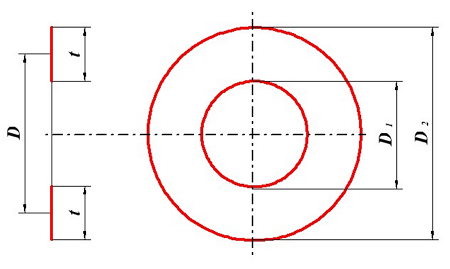
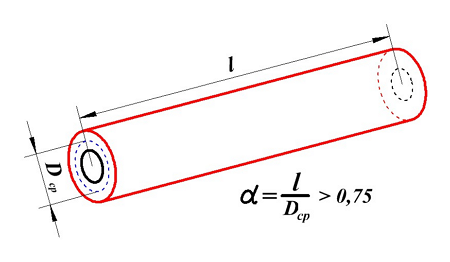
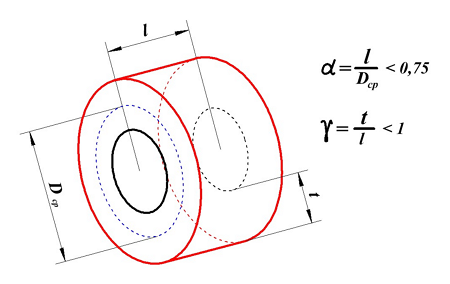
Для расчёта индуктивности круговой катушки необходимо знать следующие размеры:
D1 – внутренний диаметр, D2 – внешний диаметр, Dср – средний диаметр, l – длина катушки (аксиальный размер), t – толщина обмотки (радиальный размер), где t можно вычислить
Поэтому, в зависимости от соотношения между этими размерами различают следующие катушки индуктивности:
если l > Dср – длинная катушка,
если l < Dср – короткая катушка,
если l << Dср – очень короткая катушка,
если l = 0 – плоская катушка,
если t ≈ Dср – толстая катушка,
если t << Dср – тонкая катушка,
если t = 0 – соленоид.
Особенности расчёта катушек индуктивности
Кроме конструктивных параметров, на индуктивность влияет также параметры обмоточного провода (диаметр, толщина изоляции, шаг намотки), хотя в большинстве случаев влияние их незначительно, но в некоторых случаях, например, при большом шаге намотки их следует учитывать. Поэтому общая индуктивность катушки можно представить следующим выражением
где LР – расчётная индуктивность;
∆L – поправка на «изоляцию», ∆L = ∆1L + ∆2L;
∆1L – поправка учитывающая влияние индуктивности витков;
∆2L – поправка учитывающая влияние взаимной индуктивности витков.
В большинстве случаев, например, при плотной намотке «виток к витку» поправка ∆L составляет несколько процентов от расчётной индуктивности LР, поэтому если нет необходимости в точном значении общей индуктивности L, поправку на изоляцию ∆L можно не учитывать.
Особенности расчёта круговых катушек индуктивности состоят в следующем:
1. При определении расчётной индуктивности LP, средний диаметр принимается равным среднему диаметру реальной катушки;
2. Длина намотки l и толщина намотки t принимается равными шагу обмотки (p – шаг по длине катушки, q – шаг по толщине намотки) умноженному на количество слоёв ω в том или ином направлении
3. Если у катушки в каком-либо направлении (по длине намотки l или по толщине намотки t) имеется только один ряд (или слой), то в этом направлении размер l или t можно принять равным нулю, то есть расчёт ведётся как для соленоида или плоской катушки.
4. В некоторых случаях, при большом диаметре провода или шаге намотки у однослойных катушках размер l или t принимается равным диаметру голого провода d.
5. Так как величина поправки на взаимную индуктивность ∆2L в несколько раз меньше, чем поправка на индуктивность витков ∆1L, то при расчётах можно учитывать только ∆1L.
Приступим к расчётным выражениям, в начале рассчитаем простейшие круговые катушки – соленоид и плоскую катушку.
Расчёт индуктивности соленоида
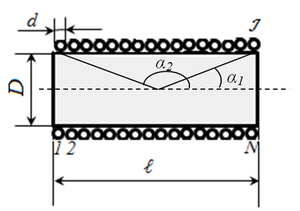
Определение индуктивности соленоида, d – диаметр соленоида, l – длина соленоида.
Соленоид представляет собой катушку, намотанную на каркас в один слой, поэтому толщину слоя можно принять равной нулю t = 0, а расчётная формула индуктивности будет иметь вид
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
d – диаметр соленоида, м;
Φ – коэффициент, который зависит от отношения α = l/D;
l – длина соленоида, м;
Поправочный коэффициент Φ зависит от отношения длины соленоида l к его диаметру d
Для длинного соленоида, то есть α > 0,75, поправочный коэффициент составит
Для короткого соленоида, то есть α < 0,75, поправочный коэффициент составит
Пример. Необходимо рассчитать соленоид диаметром d = 1 см и длиной l = 5 см, который имеет ω = 75 витков.
Стоит отметить, что формула расчёта соленоида подходит для большинства однослойных катушек с точностью в несколько процентов.
Online расчёт индуктивности соленоида
Индуктивность плоской катушки
Определение индуктивности плоской катушки, D1 – внутренний диаметр, D2 – внешний диаметр, D – средний диаметр, t – толщина намотки.
В данном случае в качестве плоской катушки представлена идеализированная катушка, длина намотки которой приняли равной нулю l = 0, тогда индуктивность такой катушки можно вычислить по следующей формуле
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
D – средний диаметр катушки, м;
Ψ – коэффициент, который зависит от отношения ρ = t/D;
t – толщина намотки катушки.
Коэффициент Ψ зависит от соотношения толщины намотки t и среднего диаметра катушки D
При небольшой толщине намотки, когда ρ < 0,5
При большой толщине намотки, когда ρ > 0,5
где γ – коэффициент учитывающий соотношение внешнего и внутреннего диаметров обмотки катушки
Пример. Рассчитаем плоскую катушку со средним диаметром D = 5 см и толщиной намотки t = 1 см, состоящую из ω = 20 витков.
Выражения для индуктивности тонкой катушки позволяют рассчитать индуктивность и большинства катушек с малой длиной и большой толщиной обмоток.
Online расчёт индуктивности плоской катушки.
Индуктивность круговой катушки прямоугольного сечения
Теперь перейдём от идеализированных катушек к реальным, которые в своем сечении представляют собой прямоугольник
Индуктивность прямоугольной катушки.
Катушку прямоугольного сечения можно представить в виде соленоида с ненулевой толщиной обмотки t ≠ 0, либо в виде плоской катушки с ненулевой длиной l ≠ 0, поэтому рассчитать необходимую катушку можно либо как соленоид, либо как плоскую катушку, а затем внести поправку.
Таким образом, индуктивность прямоугольной катушки можно вычислить по следующей формуле
где L0 – индуктивность идеальной катушки (соленоида или плоской катушки) в зависимости от α = l/Dcp;
l – длина катушки, м;
Dcp – средний диаметр катушки, м;
∆ — поправка на форму катушки.
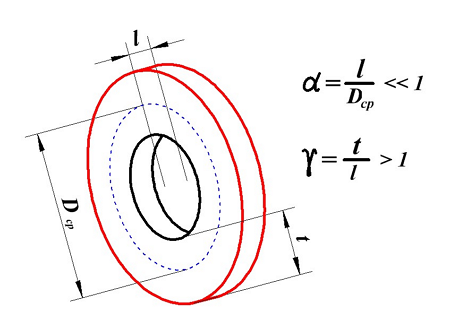
В принципе реальную катушку индуктивности, в зависимости от отношения длины намотки l к среднему диаметру Dcp, можно разделить на несколько типов:
1. Длинная катушка, у которой α > 0,75.
2. Короткая катушка, имеющая α < 0,75 и γ < 1.
3. Очень короткая катушка, имеет α << 1 и γ > 1.
где
Рассмотрим каждый случай по отдельности.
Индуктивность длинной катушки
Длинная катушка.
Для длинной катушки (α > 0,75) величина L0 рассчитывается также как для длинного соленоида, где l – длина соленоида, Dcp – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
где D1 – внутренний диаметр, D2 – внешний диаметр.
Пример. Рассчитаем индуктивность катушки длиной l = 10 см, средним диаметром DCP = 2 см, количеством витков ω = 100 и толщиной намотки t = 5 мм.
Индуктивность короткой катушки
Короткая катушка.
Для короткой катушки (α < 0,75, t < l) величина L0 рассчитывается также как для короткого соленоида, где l – длина соленоида, DСР – средний диаметр соленоида, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l;
Пример. Рассчитаем индуктивность катушки длиной l = 1 см, средним диаметром DСР = 2 см, толщиной намотки t = 5 мм, количеством витков ω = 50.
Индуктивность очень короткой катушки
Очень короткая катушка.
Для очень короткой катушки (α << 1, t > l) величина L0 рассчитывается также как для плоской катушки, где t – толщина намотки, Dcp – средний диаметр катушки, а значение поправки ∆ вычисляется по следующему выражению
где α – коэффициент, учитывающий отношение длины катушки l к её среднему диаметру DCP;
γ – коэффициент, учитывающий отношение толщины намотки t к длине намотки l, γ < 1;
ρ – коэффициент, учитывающий отношение толщины намотки t к её среднему диаметру DCP.
Пример. Рассчитаем индуктивность катушки длиной l = 5 мм, средним диаметром DCP = 7 см, намотка толщиной t = 1 см, количество витков ω = 150.
Online расчёт индуктивности круговой катушки прямоугольного сечения.
Расчёт поправки на собственную индуктивность витков
Как я писал в начале статьи, полная индуктивность катушки L состоит из расчётной индуктивности LP и поправки на изоляцию ∆L, которая в свои очередь состоит из поправки на собственную индуктивность витков ∆1L и поправки на взаимную индуктивность витков ∆2L
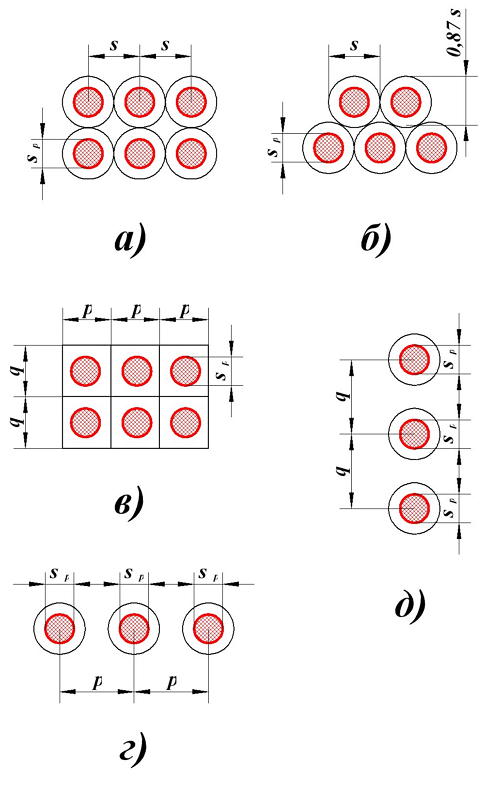
Данные поправки зависят от взаимного расположения витков в катушке. Для провода круглого сечения возможны следующие варианты заполнения катушки
Расположение провода круглого сечения в катушке индуктивности. s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции), p – шаг намотки по длине катушки, q – шаг намотки по толщине катушки.
В общем случае поправка на собственную индуктивность витков рассчитывается по следующему выражению
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
I – коэффициент, зависящий от расположения витков катушки.
Коэффициент I определяется в зависимости от расположения провода, варианты которого изображены на рисунке выше.
Для варианта а), провод намотан с небольшим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта б), провод намотан с большим коэффициентом заполнения
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта в), провод намотан с шагом p по длине катушки и с шагом q по толщине катушки
где s – диаметр провода с изоляцией, sp – диаметр голого провода (без изоляции).
Для варианта г), провод намотан в один слой по длине катушки с шагом p. В зависимости от способа вычисления расчётной индуктивности LP
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP толщина намотки t принята равной нулю (расcчитывалась как соленоид), то коэффициент I будет равен
где p – шаг намотки по длине катушки, sp – диаметр голого провода (без изоляции).
Для варианта д), провод намотан в один слой по толщине намотки с шагом q, также возможно два случая
— если при вычислении расчётной индуктивности LP длина намотки l принята равной диаметру голого провода sP, то коэффициент I будет равен
— если при вычислении расчётной индуктивности LP длина намотки l принята равной нулю (рассчитывалась как плоская катушка), то коэффициент I будет равен
где q – шаг намотки по толщине катушки, sp – диаметр голого провода (без изоляции).
Расчёт поправки на взаимную индуктивность витков
В общем случае поправка на взаимную индуктивность витков ∆2L катушки определяется выражением
где μ0 – магнитная постоянная, μ0 = 4π•10-7 Гн/м;
ω – число витков соленоида;
DСР – средний диаметр катушки, м;
J – коэффициент, зависящий формы катушки и от числа витков катушки.
1. Для катушки выполненной в один слой по длине катушки (соленоид):
а) при определении расчётной индуктивности LP толщина намотки t принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP толщина намотки t принята равной нулю (рассчитывается как соленоид), то коэффициент J составит
где ω – количество витков катушки.
2. Для катушки, выполненной в один слой по толщине намотки (плоская катушка):
а) при определении расчётной индуктивности LP длина катушки l принята равной шагу намотки р, то коэффициент J составит
где ω – количество витков катушки.
б) при определении расчётной индуктивности LP длина катушки l принята равной нулю (рассчитывается как плоская катушка), то коэффициент J составит
где ω – количество витков катушки.
На сегодня всё. В следующей статье я закончу с индуктивными элементами без сердечников.
Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:
Ф (1)
- где
Рис. 1. Соленоид
В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:
(1)
- где
Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда
. Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда
и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.
Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:
- при параллельном подключении:
(2)
В случае двух элементов, соединённых параллельно:
(3)
- при последовательном подключении:
(4)
Индуктивность контура — теоретические основы
Индуктивностью называется идеализированный элемент, приближающийся по своим свойствам к индуктивной катушке, в котором накапливается энергия магнитного поля.
Условное обозначение индуктивности и положительные направления тока, ЭДС самоиндукции и напряжения:
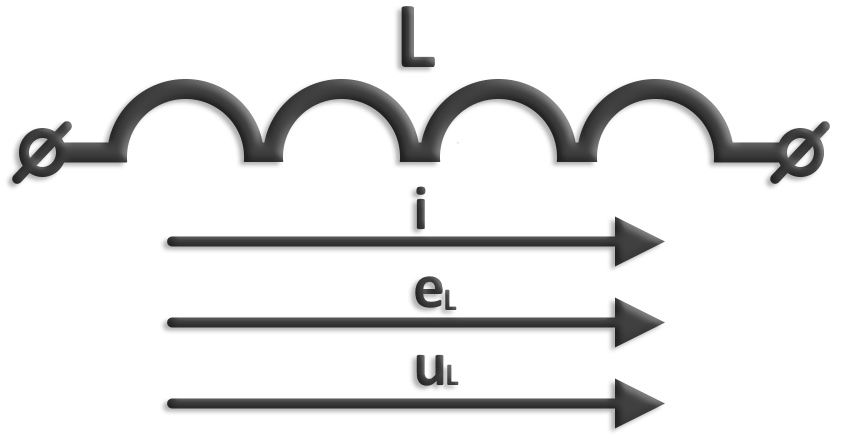
Если по проводнику пропустить ток, то вокруг него создается магнитный поток Φ. Суммарный магнитный поток (поток сцепления) катушки индуктивности равен Ψ= w×Φ, где Φ — магнитный поток, создаваемый одним витком; w — число витков.
По определению собственная индуктивность (или просто индуктивность) равна коэффициенту пропорциональности между потокосцеплением и током
катушки L=Ψ/i.
Индуктивность измеряется в генри 1 Гн = 1 Вб / 1 А. Символ L, используемый для обозначения индуктивности, был принят в честь Эмилия Христиановича Ленца (Heinrich Friedrich Emil Lenz). Единица измерения индуктивности названа в честь Джозефа Генри(Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Поток сцепления катушки индуктивности равен Ψ=L×i.
В соответствии с законом электромагнитной индукции при изменении магнитного потока в катушке наводится ЭДС самоиндукции eL=-dΨ/dt. Знак «-» ставится потому, что ЭДС имеет такое направление, что образуемый ею ток своим магнитным полем препятствует изменению магнитного потока, вызывающего данную ЭДС.
Напряжение на индуктивности уравновешивает ЭДС и может быть записано в
виде uL=-eL=dΨ/dt=L×di/dt.
Мгновенная мощность, поступающая в катушку индуктивности равна p=uL×i=L×i×di/dt.
Энергия, запасаемая в катушке индуктивности равна wM=∫(0^t)ptd=∫(0^t)L×i×dt×di/dt=(L×i²)/2.
Взаимная индуктивность характеризует свойство одного элемента с током i1 создавать магнитное поле, частично сцепляющиеся с витками w2 другого элемента.
Коэффициент взаимной индуктивности определяется по формуле M=Ψ12/i2=Ψ21/i1, где Ψ12 — поток сцепления первого контура, вызванный током второго контура (аналогично Ψ21). Измеряется в Гн.
Электрическая цепь и индуктивность контура
Индуктивность характеризует электромагнитные свойства электроцепей. В более узком понятии, это элемент или участок цепи, обладающий большой величиной самоиндукции.
Таким элементом может считаться один, несколько или даже часть витка проводника, на высоких частотах также прямой отрезок провода любой длины.
Электромагнитная индукция
Электромагнитная индукция — явление возникновения тока в замкнутом проводящем контуре при изменении магнитного потока, пронизывающего его.
Явление электромагнитной индукции открыл Майкл Фарадей в ходе серии опытов.
Опыт раз. На одну непроводящую основу намотали две катушки таким образом, что витки одной катушки были расположены между витками второй. Витки первой катушки были замкнуты на гальванометр, а второй — подключены к источнику тока.
При замыкании ключа и протекании тока по второй катушке в первой возникал импульс тока. При размыкании ключа также наблюдался импульс тока, но ток через гальванометр тек в противоположном направлении.
Опыт два. Первую катушку подключили к источнику тока, а вторую — к гальванометру. При этом вторая катушка перемещалась относительно первой. При приближении или удалении катушки фиксировался ток.
Опыт три. Катушку замкнули на гальванометр, а магнит передвигали относительно катушки.
Вот что показали эти опыты:
-
- Индукционный ток возникает только при изменении линий магнитной индукции.
-
- Направление тока различается при увеличении числа линий и при их уменьшении.
- Сила индукционного тока зависит от скорости изменения магнитного потока. При этом как само поле может изменяться, так и контур может перемещаться в неоднородном магнитном поле.
Почему возникает индукционный ток?
Ток в цепи может существовать, когда на свободные заряды действуют сторонние силы. Работа этих сил по перемещению единичного положительного заряда вдоль замкнутого контура равна электродвижущей силе (ЭДС).
Значит, при изменении числа магнитных линий через поверхность, ограниченную контуром, в нем появляется ЭДС, которую называют ЭДС индукции.
Самоиндукция и измерение индуктивности
Индуктивность проводника
При изменении тока, который протекает в замкнутом электрическом контуре, меняется создаваемый им магнитный поток. Вследствие этого наводится ЭДС, которая называется ЭДС самоиндукции.
Напряжение ЭДС определяется формулой расчета индукции:
Ꜫ=-L∙di/dt.
То есть ЭДС прямо пропорциональна величине скорости изменения тока с некоторым коэффициентом L, который и называется «индуктивность».
Как найти индуктивность контура
Формула, которая является простейшей для нахождения величины, следующая:
- L = F : I,
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
- Ei = -L х dI : dt.
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
- W = L I2 : 2.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
- L= µ0n2V,
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
- L = µ0N2S : l,
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Обозначение и единицы измерения
Сопротивление тока: формула
В честь Ленца, единица измерения индуктивности получила обозначение символом «L». Выражается в Генри, сокращенно Гн (в англоязычной литературе Н), в честь известного американского физика.

Джозеф Генри
Если при изменении тока в один ампер за каждую секунду ЭДС самоиндукции составляет 1 вольт, то индуктивность цепи будет измеряться в 1 генри.
Как может обозначаться индуктивность в других системах:
- В системе СГС, СГСМ – в сантиметрах. Для отличия от единицы длины обозначается абгенри;
- В системе СГСЭ – в статгенри.
Свойства
Имеет следующие свойства:
- Зависит от количества витков контура, его геометрических размеров и магнитных свойств сердечника;
- Не может быть отрицательной;
- Исходя из определения, скорость изменения тока в контуре, ограничена значением его индуктивности;
- При увеличении частоты тока реактивное сопротивление катушки увеличивается;
- Обладает свойством запасать энергию – при отключении тока запасенная энергия стремится компенсировать падение тока.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π2f2LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
- Lk = Lp + Lm + Lb,
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Чтобы снизить индуктивность устройства, необходимо токоведущие части конденсатора расположить так, чтобы взаимно компенсировались их магнитные поля. Иными словами, токоведущие части с одинаковым движением тока нужно удалять друг от друга как можно дальше, а с противоположным направлением сближать. При совмещении токоотводов с уменьшением толщины диэлектрика можно снизить индуктивность секции. Этого можно достигнуть еще путем деления одной секции с большим объемом на несколько с более мелкой емкостью.
“Катушка ниток”
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
- I = U : R,
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь “катушка – источник тока”, то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN2R2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N2R2 :2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.
- Значение индуктивности зависит от “витков в квадрате”.
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Применение катушек индуктивности
Индуктивности широко используются в аналоговых схемах и схемах обработки сигналов. Они в сочетании с конденсаторами и другими радиокомпонентами образуют специальные схемы, которые могут усилить или отфильтровать сигналы определенной частоты.
Катушки индуктивности получили широкое применение начиная от больших катушек индуктивности, таких как дроссели в источниках питания, которые в сочетании с конденсаторами фильтра устраняют остаточные помехи и другие колебания на выходе источника питания, и до столь малых индуктивностей, которые располагаются внутри интегральных микросхем.
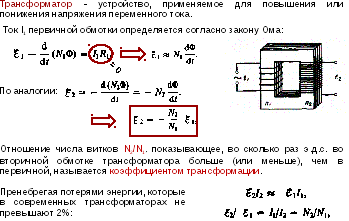
Две (или более) катушки индуктивности, которые соединены единым магнитным потоком, образуют трансформатор, являющимся основным компонентом схем работающих с электрической сетью электроснабжения. Эффективность трансформатора возрастает с увеличением частоты напряжения.
По этой причине, в самолетах используется переменное напряжение с частотой 400 герц вместо обычных 50 или 60 герц, что в свою очередь позволяет значительно сэкономить на массе используемых трансформаторов в электроснабжении самолета.
Так же индуктивности используются в качестве устройства для хранения энергии в импульсных стабилизаторах напряжения, в высоковольтных электрических системах передачи электроэнергии для преднамеренного снижения системного напряжения или ограничения ток короткого замыкания.
Общие сведения
Для того чтобы понять, от чего зависит индуктивность катушки, необходимо подробно изучить всю информацию об этой физической величине. Первым делом следует рассмотреть принятое международное обозначение параметра, его назначение, характеристики и единицы измерения.
Само понятие индуктивности было предложено известным английским физиком Оливером Хевисайдом, который занимался её изучением. Этот учёный подарил миру и другие известные термины — электропроводимость, магнитная проницаемость и сопротивление, а также ЭДС (электродвижущая сила).

Первая буква фамилии другого знаменитого физика — Эмилия Ленца — была взята в качестве обозначения индуктивности в формулах и при проведении расчётов. В наше время символ L продолжает использоваться при упоминании этого параметра.
Выдающийся американский физик Джозеф Генри первым обнаружил явление индуктивности. В его честь физики назвали единицу измерения в международной СИ, которая чаще всего используется в расчётах. В других системах (гауссова и СГС) индуктивность измеряют в сантиметрах. Для упрощения вычислений было принято соотношение, в котором 1 см равняется 1 наногенри. Очень редко используемая система СГСЭ оставляет коэффициент самоиндукции без каких-либо единиц измерения или использует величину статгенри. Она зависит от нескольких параметров и приблизительно равняется 89875520000 генри.
Среди основных свойств индуктивности выделяются:
- Величина параметра никогда не может быть меньше нуля.
- Показатель зависит только от магнитных свойств сердечника катушки, а также от геометрических размеров контура.
Способы расчёта
Существует несколько основных способов определить индуктивность катушки. Все формулы, которые будут использоваться в расчётах, легко можно найти в справочной литературе или интернете. Весь процесс вычисления довольно простой и не составит труда для людей, имеющих элементарные математические и физические знания.
Через силу тока
Этот расчёт считается самым простым способом определения индуктивности катушки. Формула через силу тока вытекает из самого термина. Какова индуктивность катушки — можно определить по формуле: L=Ф/I, где:
- L — индуктивность контура (в генри);
- Ф — величина магнитного потока, измеряемого в веберах;
- I — сила тока в катушке (в амперах).
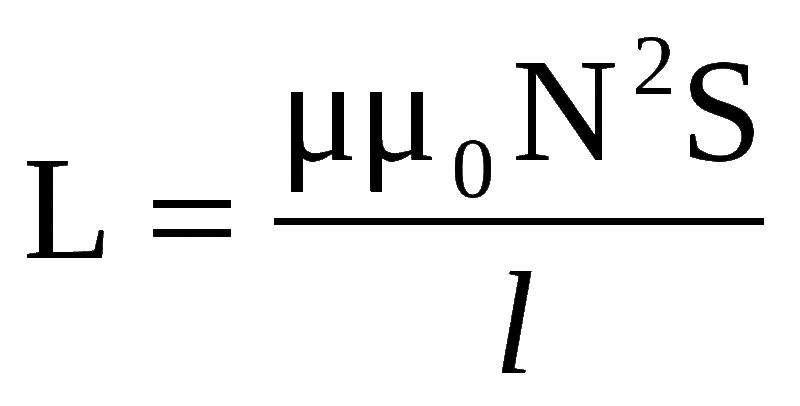
Такая формула подходит только для одновиткового контура. Если катушка состоит из нескольких витков, то вместо величины магнитного потока используется полный поток (суммарное значение). Когда же через все витки проходит одинаковый магнитный поток, то для определения суммарного значения достаточно умножить величину одного из них на общее количество.
Соленоид конечной длины
Соленоид представляет собой тонкую длинную катушку, где толщина обмотки значительно меньше диаметра. В этом случае расчёты ведутся по той же формуле, что и через силу тока, только величина магнитного потока будет определяться следующим образом: Ф=µ0NS/l, где:
-
µ0 — магнитная проницаемость среды, определяющаяся по справочным таблицам (для воздуха, который принимается по умолчанию в большинстве расчётов, она равна 0,00000126 генри/метр); - N — количество витков в катушке;
- S — площадь поперечного сечения витка, измеряемая в квадратных метрах;
- l — длина соленоида в метрах.
Коэффициент самоиндукции соленоида можно рассчитать и исходя из способа определения энергии магнитного потока поля. Это более простой вариант, но он требует наличия некоторых величин. Формула для нахождения индуктивности — L=2W/I 2 , где:
- W — энергия магнитного потока, измеряемая в джоулях;
- I — сила тока в амперах.
Катушка с тороидальным сердечником
большинстве случаев тороидальная катушка наматывается на сердечник, изготовленный из материала, обладающего большой магнитной проницаемостью. В этом случае для расчётов индуктивности можно использовать формулу для прямого соленоида бесконечной длины. Она имеет такой вид: L=N µ0 µS/2 πr, где:
- N — число витков катушки;
- µ — относительная магнитная проницаемость;
- µ0 — магнитная постоянная;
- S — площадь сечения сердечника;
- π — математическая постоянная, равная 3,14;
- r — средний радиус тора.

Длинный проводник
Большинство таких квазилинейных проводников имеет круглое сечение. В этом случае величина коэффициента самоиндукции будет определяться по стандартной формуле для приближённых расчётов: L= µ0l (µelnl/r+ µi/4)/2 π. Здесь используются следующие обозначения:
-
l — длина проводника в метрах; - r — радиус сечения провода, измеряемый в метрах;
- µ0 — магнитная постоянная;
- µi — относительная магнитная проницаемость, характерная для материала, из которого изготовлен проводник;
- µe — относительная магнитная проницаемость внешней среды (чаще всего принимается значение для вакуума, которое равняется 1);
- π — число Пи;
- ln — обозначение логарифма.
Графический вывод формулы
Существует возможность получить записанную формулу, используя графический метод. Для этого отобразим на графике зависимость магнитного потока Φ(I) от тока I (рис. 1.21.2). Полное количество выделившейся теплоты, которое равно изначальному запасу энергии магнитного поля, определится как площадь получившегося на рис. 1.21.2 треугольника:
Рисунок 1.21.2. Вычисление энергии магнитного поля.
В итоге формула энергии Wм магнитного поля катушки с индуктивностью L, создаваемого током I, будет записана в виде формулы:
Wм=ΦI2=LI22=Φ22L
Используем выражение, которое мы получили, для энергии катушки к длинному соленоиду с магнитным сердечником. Применяя указанные выше формулы для коэффициента самоиндукции Lμ соленоида и для магнитного поля B, создаваемого током I, получим запись:
Wм=μ0·μ·n2·I22V=B22μ0·μV
В этой формуле V является объемом соленоида. Полученное выражение демонстрирует нам, что магнитная энергия имеет локализацию не в витках катушки, по которым проходит ток, а распределена по всему объему, в котором возникло магнитное поле.
Определение 4
Объёмная плотность магнитной энергии – это физическая величина, которая равна энергии магнитного поля в единице объема: Wм=B22μ·μ.
В свое время Максвелл продемонстрировал, что указанная формула (в нашем случае выведенная для длинного соленоида) верна для любых магнитных полей.
Об индуктивности простыми словами
Индуктивностью является физическая величина, которая была введена с целью оценки способности электрического проводника противодействовать току. Т.е. индуктивность, или как ее еще называют – коэффициент самоиндукции, показывает зависимость Ɛ от свойств проводника и от магнитной проницаемости среды, в которой он находится. Единицей измерения величины является генри (Гн).
Если рассмотреть величину на примере катушки индуктивности, то можно понять, что ее показатели будут изменяться в зависимости от числа витков катушки, а также ее размеров и формы. Чем больше количество витков, тем больше индуктивность. Данная величина также будет увеличена, если внутрь катушки будет помещен сердечник, так как изменится относительная магнитная проницаемость среды, в которой находится проводник. Данную зависимость можно увидеть на схеме.
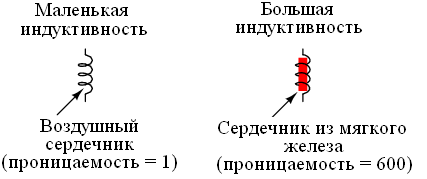
Если посмотреть на формулу зависимости ЭДС от индуктивности, то можно понять, что чем больше будет величина, тем заметнее будет электродвижущая сила, что говорит о их прямой пропорциональности. Следуя из этого, можно сделать вывод, что индуктивность выступает неким «хранилищем» энергии, которое открывается в момент изменения тока.
Ɛ=- L(dI/dt), где:
- Ɛ – ЭДС самоиндукции;
- L-индуктивность;
- I – сила тока;
- t – время.
При этом L равно магнитному полю (Ф) деленному на силу тока (I).
Польза и вред
Такое явление, как самоиндукция, большинство людей наблюдают ежедневно, даже не осознавая этого. Так, например, принцип работы люминесцентных трубчатых ламп основан именно на явлении самоиндукции. Также данное явление можно наблюдать в цепи зажигания транспортных средств, работающих на бензине. Это возможно благодаря наличию катушки индуктивности и прерывателя. Так, в момент, когда через катушку проходит ток, прерыватель разрывает цепь питания катушки, в результате чего и образуется ЭДС, которая далее приводит к тому, что импульс более 10 кВ поступает на свечи зажигания.
Явление самоиндукции также приносит пользу, убирая лишнюю пульсацию, частоты или различные шумы в музыкальных колонках или другой аудиотехнике. Именно на ней основано работа различных «шумовых» фильтров.
Однако самоиндукция способна приносить не только пользу, но и заметный вред. Особенно часто она вредит различным выключателям, рубильникам, розеткам и другим устройствам, размыкающим электрическую цепь. Ее негативное воздействие на электроприборы можно заметить невооруженным глазом: искра в розетке в момент вытаскивания вилки, работающего фена и есть проявление сопротивления изменению силы тока.
Именно поэтому лампочки чаще всего перегорают именно в момент выключения света, а не наоборот. Это связано с тем, что сопротивление приводит к выгоранию контактов и накоплению цепей с токами в различных электроприборах, что в свою очередь представляет собой довольно серьезную техническую проблему.
Индуктивность и самоиндукция – незнакомые многим термины, с которыми люди встречаются ежедневно. И если первый термин является физической величиной, обозначающей способность проводника препятствовать изменению напряжения, то второй объясняет появление ЭДС индукции в том же проводнике.
Предыдущая
РазноеЧто такое фазное и линейное напряжение?
Следующая
РазноеБлуждающие токи и способы борьбы с ними