Как найти индуктивность в треугольнике

Схема соединения “Треугольник”

Автор: Евгений Живоглядов.
Дата публикации: 17 июля 2013 .
Категория: Статьи.

Соединение в треугольник трехфазного генератора или вторичной обмотки трансформатора.

Соединим конец x обмотки ax с началом b обмотки by, конец y обмотки by с началом c обмотки cz, конец z обмотки cz с началом a обмотки ax так, как показано на рисунке 1. Такое соединение по виду напоминает треугольник, откуда и происходит его название. Линейные провода присоединены в вершинах треугольника.

Рисунок 1. Соединение в треугольник генератора.

Основные соотношения:
1. При соединении в треугольник линейные и фазные напряжения равны потому, что каждые два линейных провода (как видно из рисунка 1) присоединены к началу и концу одной из фазных обмоток, а все фазные обмотки одинаковы.
2. Линейные токи I_л больше фазных I_ф в √3 = 1,73 раза.

Как доказать, что I_л = 1,73 × I_ф? Воспользуемся для этого векторной диаграммой рисунка 2.

Рисунок 2. Определение линейных токов при соединении в треугольник.

Фазные токи I_ab, I_bc, I_ca в трех электроприемниках ЭП (рисунок 2, а) изображаются векторной диаграммой (рисунок 2, б), которая получена путем перенесения параллельно самим себе векторов с рисунка 2, а. Вершины треугольника нагрузок a, b и c являются узловыми точками. Поэтому согласно первому закону Кирхгофа справедливы равенства

Понятно, что эти равенства геометрические, поэтому вычитание нужно выполнять по правилам вычитания векторов, что и сделано на рисунке 2, б. Непосредственное измерение длин векторов или вычисления по правилам геометрии показывают, что линейные токи I_a, I_b и I_c больше фазных токов I_ab, I_bc и I_ca в √3 = 1,73 раза.

На рисунке 2, б также видно, что векторная диаграмма симметричных линейных токов I_a, I_b и I_c сдвинута на 30° в сторону, обратную вращению векторов, относительно диаграммы фазных токов I_ab, I_bc и I_ca. Иными словами, ток I_a отстает на 30° от тока I_ab. Ток I_b отстает на 30° от тока I_bc, ток I_c отстает на 30° от тока I_ca.
Порядок индексов в обозначении фазных токов указывает на порядок вращения фаз. В нашем примере порядок следования (вращения) фаз: a, b, c.

На рисунке 2, в показано соединение в треугольник обмоток генератора или вторичных обмоток трансформатора. Векторы токов I_ba, I_ac, I_cb, проходящих в обмотках генератора (вторичных обмотках трансформатора), и векторы токов в нагрузке (I_ab, I_ca, I_bc) соответственно параллельны, но повернуты на 180°. Причина такого расположения векторов станет ясна, если совместить рисунок 2, в с правой частью рисунка 2, а, что и выполнено на рисунке 2, г.

Обращается внимание на то, что все три обмотки внутри генератора (трансформатора) соединены последовательно и образуют замкнутую цепь. Подобное соединение в установках постоянного тока привело бы к короткому замыканию. В установках трехфазного тока в силу того, что электродвижущие силы (э. д. с.) сдвинуты по фазе на 120°, ток в этом замкнутом контуре отсутствует, так как в каждый момент сумма э. д. с. трех обмоток равна нулю 1 .

Необходимо здесь же заметить, что для отсутствия тока в контуре обмоток генератора (трансформатора) необходимо, чтобы обмотки имели одинаковые числа витков, были сдвинуты на 120 электрических градусов и имели э. д. с. строго синусоидальные или во всяком случае не содержащие гармоник, кратных трем (смотрите статью “Понятие о магнитном равновесии трансформатора”).

Генераторы практически никогда не соединяют в треугольник. В трансформаторах такие соединения не только распространены, но иногда выполняются с целью получения внутри трансформатора токов третьих гармоник. Зачем? Понятно не затем, чтобы создавать в трансформаторе дополнительные потери. Причины здесь гораздо сложнее, смотрите статью “Понятие о магнитном равновесии трансформатора”.

Соединение в треугольник обмоток трансформаторов в двух вариантах показано на рисунке 3. Подробно вопрос о соединениях обмоток трансформаторов рассмотрен в статье “Группы соединения трансформаторов”.

Рисунок 3. Соединение в треугольник трансформаторов.

Соединение в треугольник электроприемников и конденсаторных батарей.

Соединение в треугольник обмоток электродвигателей показано на рисунках 4, а – в. При этом на рисунке 4, а обмотки и соединены и расположены треугольником; на рисунке 4, б обмотки соединены треугольником, но расположены произвольно; на рисунке 4, в обмотки расположены звездой, но соединены в треугольник. На рисунке 4, г обмотки расположены треугольником, но соединены в звезду.

Рисунок 4. Соединение в треугольник электроприемников.

Все эти рисунки подчеркивают, что дело отнюдь не в том, как расположены изображения электроприемников на чертежах (хотя их часто удобно располагать в соответствии с видом соединения), а в том, что с чем соединено: концы (начала) всех обмоток между собой или конец одной обмотки с началом другой. В первом случае получается соединение в звезду, во втором – в треугольник.

Соединение в треугольник конденсаторных батарей показано на рисунке 4, д.

На рисунке 4, е показано соединение в треугольник ламп. Хотя лампы территориально разбросаны по разным квартирам, но они объединены сначала в группы в пределах каждой квартиры, затем в группы по стоякам 2 и, наконец, эти группы соединены в треугольник на вводном щите 1. Заметьте: до вводного щита нагрузка трехфазная, после вводного щита (в стояках и квартирах) однофазная, хотя она и включена между двумя фазами.

На каком основании нагрузка, питающаяся от двух фаз названа однофазной? На том основании, что изменения тока в обоих проводах, к которым присоединена нагрузка, происходят одинаково, то есть в каждый момент ток проходит через одни и те же фазы.

Видео 1. Соединение треугольником

1 Отсутствие тока в замкнутом контуре еще не означает, что в фазных обмотках нет тока. Токи в фазных обмотках соответствуют их нагрузкам.

Источник: Каминский Е. А., “Звезда, треугольник, зигзаг” – 4-е издание, переработанное – Москва: Энергия, 1977 – 104с.

Трехфазные цепи

Содержание:

Трехфазные цепи:

Многофазной системой называется совокупность электрических цепей, называемых фазами, в которой действуют синусоидальные напряжения одной частоты, отличающиеся друг от друга по фазе. Чаще всего применяются симметричные многофазные системы, напряжения которых равны по величине и сдвинуты по фазе на угол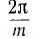

Трехфазная система

Наибольшее распространение имеет трехфазная система, созданная русским ученым М. О. Доливо-Добровольским (1891 г.); он изобрел и разработал все звенья этой системы — генераторы, трансформаторы, линии передачи и двигатели трехфазного тока.

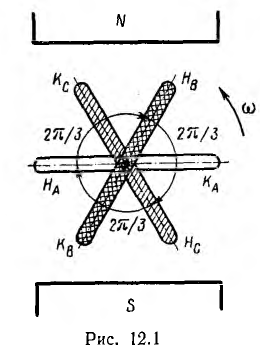
Простейший трехфазный генератор (рис. 12.1) подобен рассмотренному в источнику однофазного напряжения; он состоит из трех одинаковых плоских витков или катушек, называемых фазами генератора, вращающихся в однородном магнитном поле с равномерной угловой скоростью ω вокруг оси, перпендикулярной к направлению магнитных линий. В каждой фазе следует различать начало и конец. Считая, что все катушки намотаны в одном направлении, например по часовой стрелке, можно принять за начало начальный зажим катушки или, наоборот, конечный, но принятое условие должно быть одинаковым для всех фаз. Цепи нагрузки подключаются к генератору с помощью щеток, наложенных на кольца, соединенные с катушками аналогично рис. 6.1 (на рис. 12.1 они не показаны).

Три фазы трехфазного генератора расположены под углом 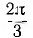друг к другу; первой, или фазой А, можно назвать любую из трех фаз, второй — фазу В, начало которой H_B сдвинуто в пространстве относительно начала первой Н_А на угол 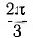против направления вращения, третьей — фазу С, начало которой Н_c сдвинуто относительно начала второй H_B также на 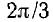в том же направлении.

При вращении в фазах будут индуктироваться э. д. с.; период Т этих э. д. с. обороту. Катушки одинаковы, поэтому (амплитуды) э. д. с. фаз будут также одинаковы. Так как фазы сдвинуты друг относительно друга в пространстве на угол 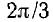, т. е. на 1/3 полного оборота, их э. д. с. будут сдвинуты во времени на Т/3 — треть периода, что соответствует фазному сдвигу, равному:

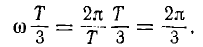
Если за начальный взять момент времени, когда плоскость первой катушки перпендикулярна линиям магнитной индукции (см. рис. 12.1), э. д. с. (отсчитываемая, например, от конца к началу)

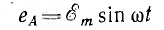
и э. д. с. двух других катушек (отсчитываемые в том же направлении), отставая по фазе на углы 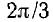и 2•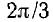, будут равны:

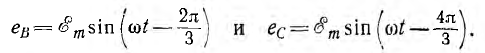
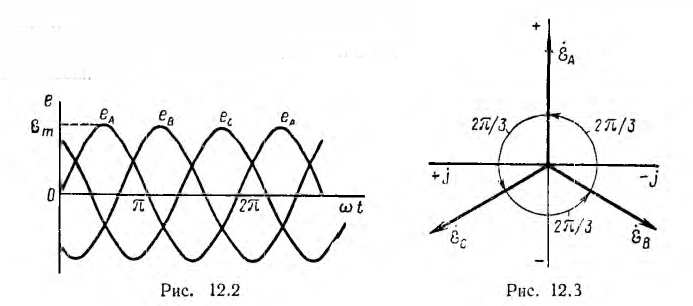
Временная диаграмма э. д. с. изображена на рис. 12.2. Если вектор э. д. с. первой фазы направить по оси вещественных комплексной плоскости (рис. 12.3), комплексы э. д. с. симметричной системы будут иметь вид:

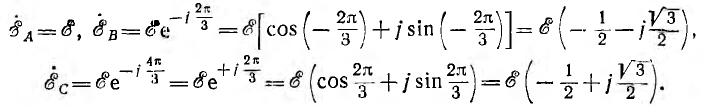
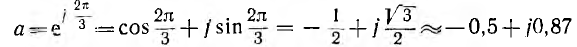
является оператором поворота вектора на угол 2π/3 в положительном направлении. Тогда

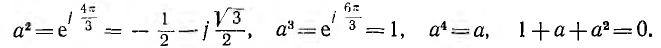
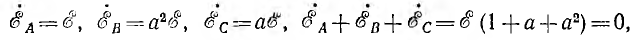
т. е. сумма векторов симметричной системы равна нулю. Это значит, что равна нулю в любой момент времени и алгебраическая сумма мгновенных значений, что можно видеть и из рис. 12.2, если взять сумму ординат трех синусоид для любой абсциссы.

Если в цепь каждой фазы генератора включить одинаковые по величине и характеру сопротивления (рис. 12.4), то токи фаз будут равны по величине и сдвинуты по фазе относительно своих напряжений на один и тот же угол ϕ:

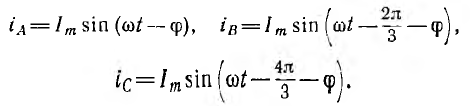
Они также образуют трехфазную симметричную систему векторов.

При неодинаковой нагрузке фаз максимальные значения токов и фазные сдвиги будут различны, и система токов будет несимметричной.

В электроизмерительной технике и автоматике применяется также двухфазная система, векторная диаграмма э д. с. которой показана на рис. 12.5. Хотя э. д. с. 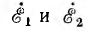по величине равны, двухфазная система несимметрична, так как сумма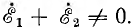

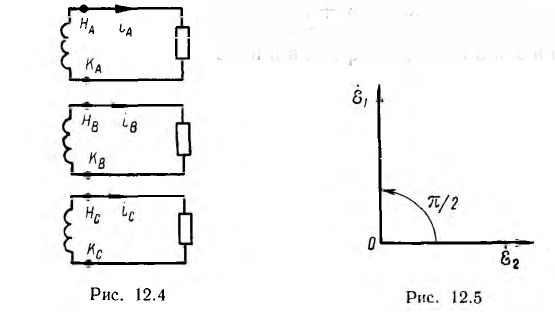
Показанная на рис. 12.4 несвязанная трехфазная система, при которой отдельные фазы не соединены между собой, на практике не применяется — генераторы и приемники связывают или в звезду, или в треугольник.

Соединение звездой

При соединении генератора звездой вместе соединяются концы фаз, образуя нулевую (нейтральную) точку 0. К началам фаз генератора с помощью трехпроводной линии передачи присоединяется приемник. Если последний также соединен звездой, нулевые точки генератора и приемника могут быть соединены нулевым (нейтральным) проводом (рис. 12.6).

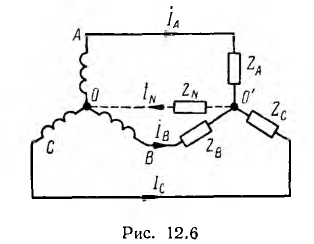
Различают величины, относящиеся к фазам генератора и приемника — фазные напряжения и токи, и к линейным проводам — линейные напряжения и токи. Так как линейные провода соединены последовательно с фазами генератора и приемника, линейные токи в звезде равны соответствующим фазным токам.

Для получения симметричных соотношений между величинами следует выбирать положительные направления токов во всех фазах единообразно; обычно направляют токи от генератора к приемнику (см. рис. 12.6), т. е. в сторону движения энергии. В соответствии с аналогом закона Ома 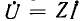положительные направления фазных напряжений совпадают с направлением токов. Положительные направления линейных напряжений могут быть выбраны произвольно, а также единообразно. Произволен также выбор направления тока на нулевом проводе.

Если выбрать направление тока в нулевом проводе от нулевой очки приемника к нулевой точке генератора (см. рис. 12.6), мгновенное значение i_N и комплекс I_N этого тока в общем случае будут:

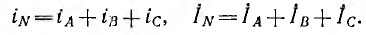
На рис. 12.7, а изображена диаграмма фазных напряжений на фиемнике в соответствии с принятым на рис. 12.6 направлением гоков, сходящихся в нулевой точке О’ приемника.

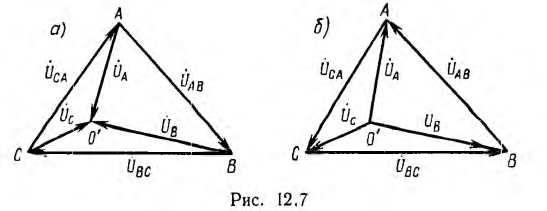
Эта диаграмма называется топографической, так как ее точкам А, В, С, О’ соответствуют одноименные точки цепи. Векторы и комплексные линейные напряжения 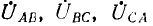направлены, как это обычно принято, от точки, соответствующей первому индексу, к точке, соответствующей второму индексу; линейные напряжения равны разности соответствующих фазных напряжений:

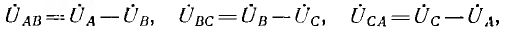
а их мгновенные значения

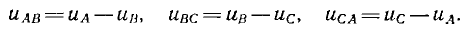
Из этих соотношений вытекает, что сумма линейных напряжений равна нулю.

Топографическая векторная диаграмма рис. 12.7, а, в которой векторы фазных напряжений сходятся в одной точке, соответствующей нулевой точке приемника, обычно заменяется диаграммой рис. 12.7, б, где эти векторы выходят из этой же точки; так как при этом все векторы фазных и линейных напряжений изменяют свои направления на обратные, приведенные выше соотношения между напряжениями сохраняются.

При симметричной системе фазных напряжений векторы линейных напряжений образуют равносторонний треугольник; нулевая точка совпадает с его центром тяжести (рис. 12.8) и линейное напряжение

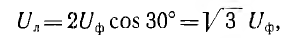
г. е. по абсолютной величине линейные напряжения в 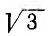раз больше разных.

Далее сначала рассматриваются цепи без взаимной индукции между фазами и между фазами и нулевым проводом.

В звезде с нулевым проводом (см. рис. 12.6), если пренебречь его сопротивлением (Z_N = 0), а также сопротивлением, линейных проводов, фазные напряжения приемника будут, очевидно равны фазным напряжениям генератора; их векторные диаграммы совпадут (см. рис. 12.7, б). Следовательно, фазные комплексные токи будут определяться фазными комплексными напряжениями генератора и комплексными сопротивлениями или проводимостями тех же фаз приемника:

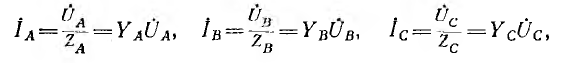
т. е. соединение звездой с нулевым проводом без сопротивления обеспечивает независимую работу фаз.

При симметричной системе фазных напряжений и одинаковой нагрузке фаз система фазных токов будет симметричной и ток I_N нулевого провода, равный сумме токов, будет также равен нулю независимо от величины сопротивления этого провода.

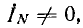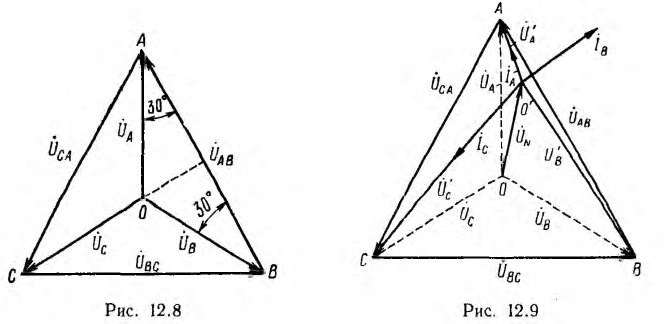
В звезде с нулевым проводом, имеющим сопротивление Z_N в общем случае, когда между нулевыми точками генератора и приемника возникает узловое напряжение 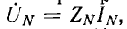что вызывает на векторной диаграмме (рис. 12.9) смещение точки О’, соответствующей нулевой точке приемника, относительно точки 0, соответствующей нулевой точке генератора. То, что вектор 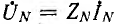на рис. 12.9 направлен от 0 к О’, т. е. против направления I_N, объясняется указанным выше изменением направления векторов всех напряжений (см. рис. 12.7, а и б). В соответствии с методом узловых напряжений

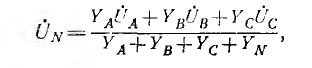
где 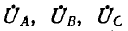—фазные напряжения генератора; 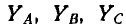— проводимости фаз, Y_N — проводимость нулевого провода.

В звезде без нулевого провода Y_N =0 и

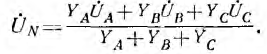
Фазные напряжения на приемнике и токи (см. рис. 12.9):

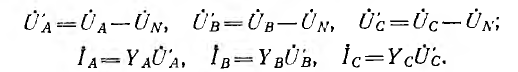
Выражения для узлового напряжения показывают, что 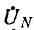будет изменяться при изменении нагрузки в любой фазе; вместе с 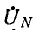будут изменяться напряжения всех фаз приемника, а следовательно, и все токи. Таким образом, звезда без нулевого провода, а также звезда с нулевым проводом, имеющим сопротивление, не обеспечивает независимой работы фаз.

В случае звезды без нулевого провода фазные напряжения на приемнике могут быть выражены через линейные напряжения:

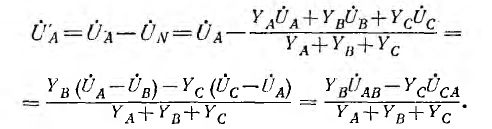
Выражения для 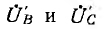можно получить, пользуясь круговой перестановкой индексов:

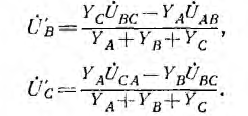
Приведенный вывод выражений для фазных напряжений на приемнике через фазные или линейные напряжения генератора справедлив для общего случая несимметричных систем фазных и линейных напряжений.

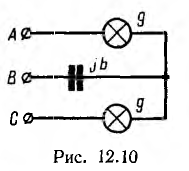
Примером неодинаковой нагрузки фаз может служить прибор для определения порядка следования фаз (рис. 12.10). Он представляет собой три одинаковые по величине проводимости, соединенные в звезду, — две лампы накаливания и конденсатор; тогда, считая, что проводимости ламп линейны,

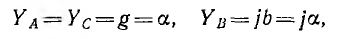
где а — абсолютное значение проводимостей. При симметричной системе фазных напряжений генератора, если вектор U_А направлен по оси вещественных величин (U_A = U), узловое напряжение

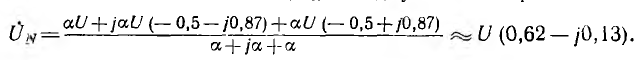
Тогда комплексные напряжения на лампах будут:

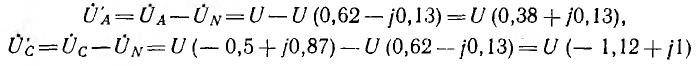
На рис. 12.9 показана векторная диаграмма для рассматриваемой цепи. Векторы токов 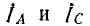совпадают по фазе с напряжениями 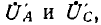ток I_B опережает напряжение U_в по фазе на π/2.

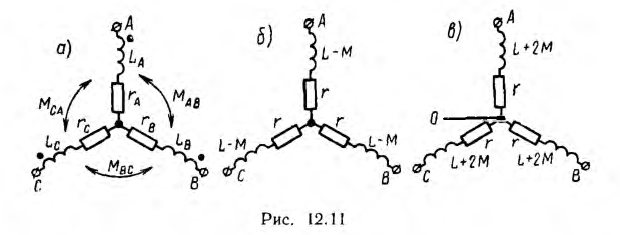
Действующие значения напряжений на лампах и их отношение будут:

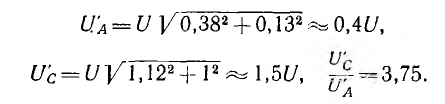
Поэтому лампа, включенная в фазу С, будет светиться ярче лампы, включенной в фазу А, т. е. фазы следуют друг за другом в следующем порядке: яркая лампа, тусклая лампа, конденсатор.

При индуктивных связях между фазами приемника и между его фазами и нулевым проводом должны быть учтены э. д. с. взаимной индукции. Так, например, для соединения звездой с нулевым проводом или без него по схеме рис. 12.11, а при взаимной индукции только между фазами уравнение по второму закону Кирхгофа для фазы А приемника будет иметь вид:

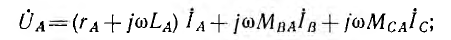
уравнения для второй и третьей фаз можно получить путем круговой перестановки индексов А, В, С.

Если нагрузка фаз одинакова, т. е.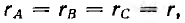

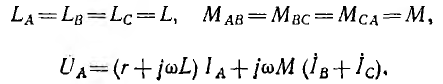(12.1)

Если, кроме того, нулевой провод отсутствует или при его наличии система фазных напряжений симметрична, то сумма токов 1_А + 1_в + 1_С=0, и уравнение (12.1) получит вид:

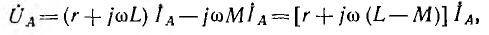
г. е. в этом случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, б без индуктивных связей, но с индуктивностью фаз приемника, равной L — М.

Для дальнейшего представляет интерес случай, когда есть нулевой провод, а все фазные напряжения генератора равны между собой и совпадают по фазе: 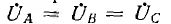(так называемая нулевая система); тогда, очевидно, все токи также будут равны между собой:

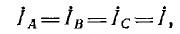
и уравнение (12.1) получит вид:

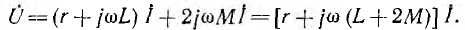
Это значит, что в данном случае цепь рис. 12.11, а эквивалентна схеме рис. 12.11, в без индуктивной связи, но с индуктивностью фаз приемника, равной L + 2М. Ток нулевого провода будет, очевидно, равен 3I.

Соединение треугольником

Чтобы соединить генератор в треугольник, нужно связать конец каждой фазы с началом следующей; в результате фазы генератора образуют замкнутый контур. При таком соединении симметричного генератора с отключенной нагрузкой (рис. 12.12) ток внутри него не возникает, так как сумма его э. д. c., образующих симметричную систему, равна нулю.

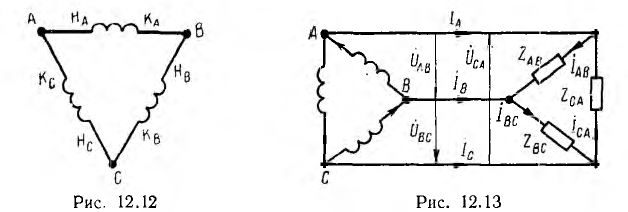
Соединив приемник также в треугольник (рис. 12.13), можно видеть, что фазные напряжения генератора и приемника одновременно являются и линейными, линейные же токи 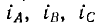— отличны от фазных токов 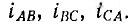Для получения симметричных соотношений между линейными и фазными токами следует выбирать их положительные направления единообразно. Для всех линейных токов обычно выбирается направление от генератора к приемнику, для фазных — по направлению обхода контура, например, против часовой стрелки для приемника (рис. 12.13). Тогда по первому закону Кирхгофа для приемника получаются следующие соотношения для мгно венных значений и комплексных токов:

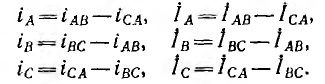
Для генератора соотношения между линейными и фазными токами аналогичны. Таким образом, линейные токи равны разностям соответствующих фазных токов.

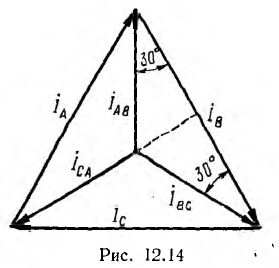
Из полученных соотношений видно, что сумма линейных токов равна нулю:

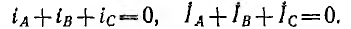
Для симметричной системы фазных токов (рис. 12.14)

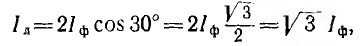
т. е. по абсолютной величине линейные токи в 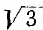раз больше фазных.

Токи в фазах приемника будут определяться линейными напряжениями и сопротивлениями или прово-димостями фаз приемника:

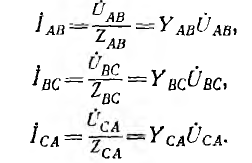
По приведенным соотношениям фазных токов могут быть определены линейные токи.

Если пренебречь сопротивлением проводов, напряжения генератора будут равны напряжениям приемника и фазы будут работать независимо друг от друга: всякое изменение сопротивления какой-либо фазы приемника вызовет изменение тока этой фазы и токов двух примыкающих к этой фазе линейных проводов, но никак не отразится на токах других фаз.

Если сопротивление линейных проводов не равно нулю (рис. 12.15, а), то из-за падения напряжения в них треугольник не обеспечивает независимой работы фаз. Изменение, например, сопротивления фазы АВ вызовет изменение фазного тока I_AB, а следовательно, и линейных токов I_А и I_B. При этом изменятся падения напряжения в линейных проводах А и В, что при неизменных линейных напряжениях на зажимах генератора вызовет изменение напряжений на всех трех фазах приемника; следовательно, должны измениться также токи 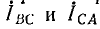тех фаз, сопротивление которых оставалось неизменным.

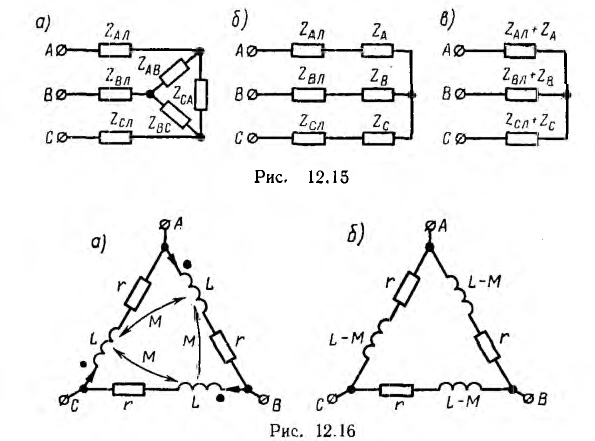
Для расчета цепи рис. 12.15, а при заданных линейных напряжениях, помимо методов уравнений Кирхгофа, наложения, контурных токов и узловых напряжений, при отсутствии взаимной индукции можно применить метод преобразования. Треугольник Z_AB, Z_BC. Z_CA преобразуют в эквивалентную звезду Z_A, Z_B, Z_c по формулам, соответствующим (рис. 12.15, б):

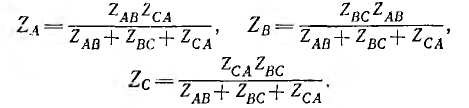
Объединяя в каждой фазе сопротивление линии и приемника, приводят схему к звезде (рис. 12.15, в), после определения токов которой возвращаются к цепи рис. 12.15, б, находя фазные и линейные напряжения на звезде Z_A, Z_B, Z_c, а затем — к исходному треугольнику (см. рис. 12.15, а), чтобы найти его фазные токи.

Приведенные выше выражения для расчета соединения треугольником справедливы для общего случая несимметричной системы напряжений генератора.

При наличии взаимной индукции, одинаковой нагрузке фаз и симметричной системе напряжений (рис. 12.16, а) система фазных токов будет также симметричной, тогда

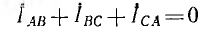
и уравнение по второму закону Кирхгофа примет вид:

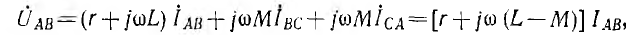
т. е. в этом случае цепь рис. 12.16, а эквивалентна схеме рис. 12.16, б без индуктивной связи, но с индуктивностью фаз приемника, равной L – М.

Мощность трехфазных систем и ее измерение

Мгновенная мощность трехфазной системы, как и всякой сложной цепи, равна сумме мощностей отдельных приемников, т. е. сумме мощностей фаз. Мгновенная мощность симметричной и одинакова нагруженной трехфазной системы

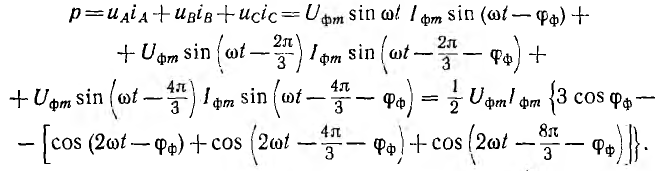
Сумма трех косинусоид, сдвинутых по фазе на угол 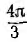равна нулю, в чем можно убедиться, построив и сложив векторы, изображающие эти функции. Следовательно,

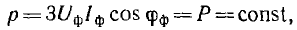
т. е. мгновенная мощность симметричной одинаково нагруженной трехфазной системы постоянна, тогда как мощность однофазной системы изменяется во времени с двойной частотой по сравнению с частотой напряжения и тока.

Многофазная система, мгновенная мощность которой постоянна, называется уравновешенной. Интересно отметить, что несимметричная двухфазная система с равными напряжениями (см. рис. 12.5) в случае одинаковой нагрузки фаз также является уравновешенной:

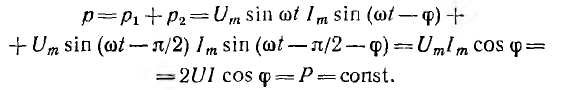
Из-за уравновешенности трехфазные и двухфазные двигатели имеют постоянный вращающий момент, тогда как момент однофазных двигателей пульсирует с двойной частотой.

Выражение для мощности уравновешенной трехфазной системы может быть преобразовано. В симметричной звезде

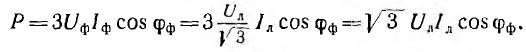
В симметричном треугольнике

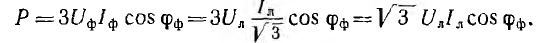
В обоих случаях выражения для мощности получились одинаковыми.

Для измерения мощности трехфазной симметричной и одинаково нагруженной системы достаточен один ваттметр, включенный в одну из фаз и измеряющий ее мощность. Аналогично включается однофазный счетчик электрической энергии, Для получения мощности и, соответственно, энергии трехфазной системы показания этих приборов следует утроить.

В общем случае несимметричной системы и неодинаковой нагрузки мгновенная мощность р есть величина переменная, т. е. такая система является неуравновешенной. Средняя мощность этой системы равна сумме средних мощностей отдельных фаз:

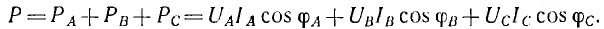
Следовательно, средняя мощность в данном случае может быть измерена тремя ваттметрами, включенными в каждую фазу, как это показано на рис. 12.17, а, для звезды с нулевым проводом (точками обозначены условные «начала» параллельных и последовательных цепей ваттметров).

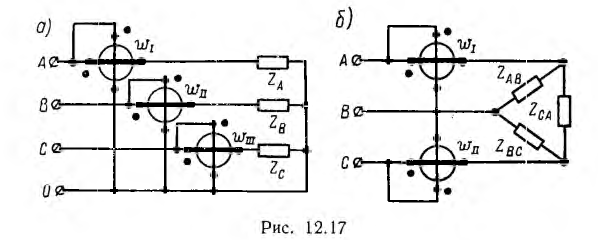
В случае трех проводной системы можно ограничиться двумя ваттметрами, включенными так, как показано на рис. 12.17, б для измерения средней мощности трехфазной системы, соединенной треугольником. Мгновенные мощности, усредняемые первым и вторым ваттметрами, соответственно равны:

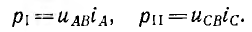
Так как 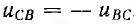сумма этих мощностей

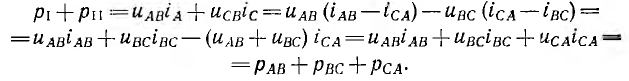
При переходе к средним мощностям получается, что сумма показаний ваттметров

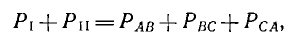
т. е. равна мощности системы. Вывод справедлив и для звезды без нулевого провода, так как она может быть заменена эквивалентным треугольником.

Реактивная и полная мощности симметричной и одинаково нагруженной трехфазной системы равны суммам соответствующих мощностей всех фаз:

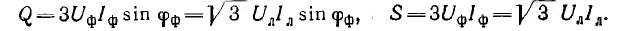
В общем случае несимметричной и неодинаково нагруженной трехфазной системы суммирование реактивных и полных мощностей фаз не дает величин, характерных для нагрузки генератора в целом, как это было в однофазной цепи с одним источником энергии. Предлагаемые в литературе определения реактивной и полной мощностей трехфазной несимметричной и неодинаково нагруженной системы чисто условны и потому здесь не рассматриваются.

Сравнение трехфазных и однофазной cиcтем

Сопротивление линейных и нулевого проводов, соединяющих генератор и приемник, обычно мало по сравнению с сопротивлением фаз приемника, и выводы, сделанные по поводу независимости работы фаз при соединении звездой и треугольником, можно обобщить следующим образом:

1. в звезде с нулевым проводом и в треугольнике токи фаз практически мало зависят друг от друга и поэтому эти схемы следует применять при неодинаковой нагрузке фаз;
2. звезда без нулевого провода может применяться только при одинаковой нагрузке фаз.

Необходимо отметить, что схема соединений генератора и приемника может быть различной, и один из них может быть соединен треугольником, другой — звездой без нулевого провода.

Представляет интерес сравнение расхода металла с удельным сопротивлением р на провода однофазной и трехфазной линий передачи (рис. 12.18) той же мощности Р на то же расстояние l при одинаковом cosϕ и том же к. п. д., т. е. тех же потерях в линии Р_л = kP, где k — относительная потеря мощности, и одинаковом линейном напряжении U.

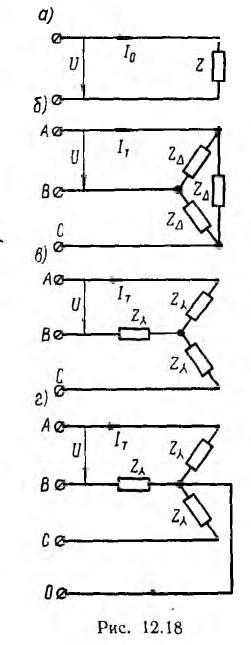
Для однофазной двухпроводной линии (рис. 12.18, а) Р = UI₀ cosϕ; отсюда ток I₀, потери Р_л и сопротивление r₀ одного провода:

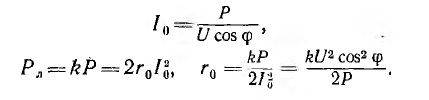
Следовательно, сечение s₀ и объем V₀ проводов соответственно равны:

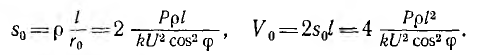
Отсюда видно, что формула для сечения двухпроводной линии переменного тока отличается от аналогичной формулы для линии постоянного тока наличием множителя 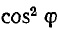в знаменателе, приводящему к тем большему увеличению расхода металла, чем ниже коэффициент мощности .

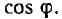Для трехфазной трехпроводной линии (рис. 12.18, б и в) 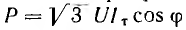и аналогично

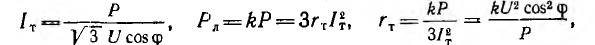
а сечение s_T и объем V_T проводов:

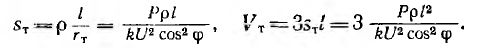
В знаменателе этих выражений также присутствует множитель .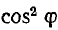

Из формул для s₀ и s_T видна эффективность высокого напряжения и большого коэффициента мощности — сечения обратно пропорциональны квадратам этих величин. Вместе с тем очевидно, что стоимость изоляции проводов растет с ростом напряжения. В результате экономически оптимальное напряжение U оказывается тем выше, чем больше передаваемая мощность Р и длина l линии.

Соотношение объемов металла линий: однофазной двухпроводной V₀ и трехфазных —- трехпроводной V_r и четырехпроводной с нулевым проводом половинного сечения 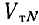(рис. 12.18, г) будет

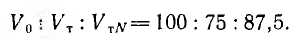
Таким образом, при одинаковом линейном напряжении звезда без нулевого провода и треугольник, очевидно, дают одинаковый расход металла на линию передачи и экономию в 25% по сравнению с однофазной линией, а нулевой провод половинного сечения вызывает перерасход металла, но все же система остается легче однофазной на 12,5%.

Соединение звездой с нулевым проводом имеет важное преимущество: помимо трехфазных приемников, рассчитанных на линейное напряжение, оно позволяет включать однофазные приемники и на линейное, и на фазное напряжение.

Если приемники работают при одинаковом фазном напряжении, линейное напряжение звезды будет в 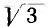раз больше, чем треугольника, что уменьшит расход металла в 3 раза.

Основным преимуществом трехфазной системы по сравнению с однофазной является возможность легко создавать вращающееся магнитное поле, используемое, в частности, в трехфазных асинхронных двигателях, наиболее простых по конструкции и в эксплуатации.

Пульсирующее и вращающееся магнитные поля

Электрические индуктивные машины переменного тока в большинстве случаев имеют магнитопровод в виде двух коаксиальных цилиндров, набранных из стальных листов и разделенных воздушным зазором (рис. 12 19). Внешний цилиндр S является статором, внутренний R — ротором.

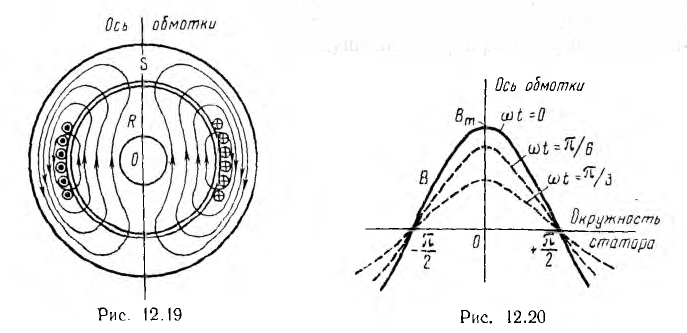
Если по обмотке статора, уложенной в его пазы н распределенной на части, например одной трети его окружности (рис. 12.19), будет проходить постоянный ток, магнитный поток, замыкающийся через статор, воздушный зазор и ротор будет постоянным. Приближенно магнитную индукцию можно считать распределенной по окружности статора по синусоидальному закону (сплошная линия на рис. 12.20); она имеет максимальные значения В_m по оси обмотки и равна нулю на нейтральной линии, перпендикулярной к оси обмотки. Такое синусоидально распределенное в зазоре машины поле можно условно изобразить постоянным вектором В_m (рис. 12.21), аналогично тому, как ранее это было сделано для величин, изменяющихся по синусоиде во времени.

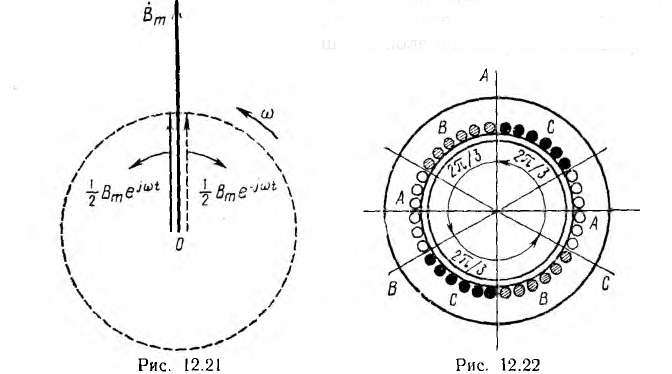
Если по обмотке статора пропускать переменный ток, синусоидальное распределение магнитного поля сохранится, но поле будет пульсирующим, т. е. изменяющимся во времени по синусоидальному закону (см. рис. 12.20). Принимая за начало счета времени момент, когда индукция по оси обмотки максимальна, пульсирующее поле можно условно изобразить вектором 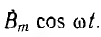Согласно формуле Эйлера,

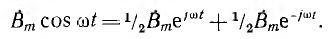(12.2)

Это значит, что пульсирующее синусоидально распределенное поле может быть представлено в виде суммы двух также синусоидально распределенных полей 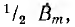, постоянных во времени, но вращающихся с угловой скоростью ω в разные стороны; последнее видно из противоположных знаков показателей степени множителей вращения. Поле 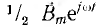, вращающееся в положительном направлении вращения векторов, называется прямым, поле 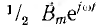— обратным. Вращающиеся векторы, условно изображающие эти поля, на рис. 12.21 показаны для момента начала счета времени.

Разложение пульсирующего поля на два вращающихся используется, например, в однофазных двигателях, где прямое поле, воздействуя на ротор, приводит его во вращение, а обратное поле экранируется.

В трехфазных машинах на статор наложены три обмотки, показанные в разрезе на рис. 12.22, занимающие каждая треть его окружности; следовательно, эти обмотки и их оси сдвинуты в пространстве на угол 2π/3. Обмотки обтекаются токами, векторы которых образуют симметричную трехфазную систему. Тогда выражение для поля первой фазы А совпадает с выражением (12.2) при том же начале счета времени

Пусть обмотка, обтекаемая током второй фазы В, т. е. током, отстающим от тока первой фазы на угол 2π/3, сдвинута в пространстве вперед по направлению вращения прямого поля на тот же угол, что учитывается множителем 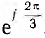. Тогда выражение для поля фазы В получает вид:

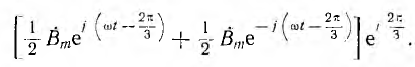
Аналогично записывается поле третьей фазы С, но так как она обтекается током, опережающим по фазе ток фазы А на угол 2π/3, и сдвинута в пространстве на тот же угол назад, знаки всех углов 2π/3 изменяются на обратные.

Результирующее поле определяется наложением полей всех трех фаз:

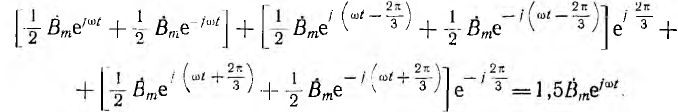
Отсюда видно, что все прямые поля трех обмоток арифметически складываются, тогда как обратные поля в сумме дают нуль и в машине возникает вращающееся поле, постоянное во времени. Амплитуда вращающегося поля в полтора раза превышает амплитуду пульсирующего поля отдельных обмоток, а фаза совпадает с фазой прямого поля обмотки первой фазы А.

В трехфазных двигателях вращающееся поле также используется для приведения во вращение ротора; из-за постоянства мощности в трехфазных системах и, следовательно, вращающего момента, а также отсутствия обратного поля эти двигатели имеют значительное преимущество перед однофазными.

Основы метода симметричных составляющих

Метод симметричных составляющих, предложенный Фортескью, позволяет сравнительно просто рассчитывать несимметричные, в частности, аварийные режимы в трехфазных системах и машинах. До предложения этого метода для таких расчетов надо было решать дифференциальные уравнения с переменными коэффициентами или оперировать с сопротивлениями, зависящими от токов.

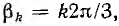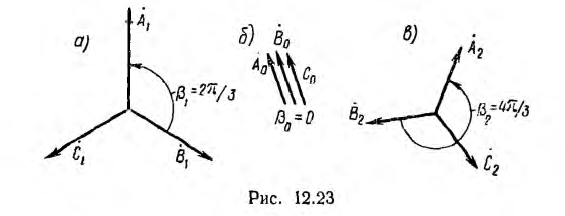
В общем случае симметричной трехфазной системой векторов называется система, состоящая из трех равных по величине векторов, причем каждый вслед идущий вектор сдвинут относительно предыдущего на угол где k — любое целое число. Система 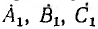(рис. 12.23, a), у которой угол сдвига между вслед идущими векторами 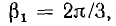имеет прямой порядок следования фаз в направлении вращения векторов и называется прямой системой.

Симметричные системы линейных и фазных напряжений и токов, рассмотренные выше, были именно прямыми системами. Система 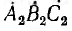(рис. 12.13, в), в которой угол сдвига между вслед идущими векторами 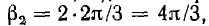имеет обратный порядок следования фаз и называется обратной системой. Система векторов 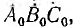совпадающих по фазе (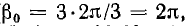т. е. β = 0) называется нулевой системой (рис. 12.23, б).

Система векторов, сдвинутых по фазе на угол 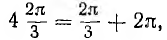является также прямой системой и т. д. Таким образом, все многообразие симметричных трехфазных систем сводится к трем системам, изображенным на рис. 12.23.

Пользуясь оператором 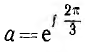поворота вектора на угол 2π/3 в положительном направлении и приняв за основные вектор A₁ прямой системы, вектор A₂ обратной системы и вектор A₀ нулевой системы, через них можно выразить остальные векторы:

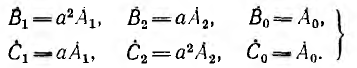(12.3)

Пусть задана несимметричная система трех векторов А, В, С. Далее доказывается, что каждый вектор этой системы может быть представлен в виде суммы трех векторов, являющихся составляющими прямой, обратной и нулевой систем:

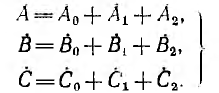(12.4)

Подстановка уравнений (12.3) в уравнения (12.4) дает:

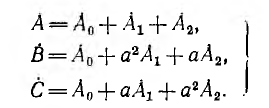(12.5)

Система уравнений (12.5) решается относительно А₀, А₁, A₂ однозначно:

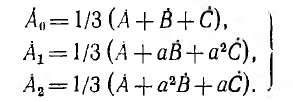(12.6)

Отсюда и следует, что несимметричную систему векторов можно разложить на три симметричные системы.

Из первого уравнения системы (12.6) видно, что если сумма векторов несимметричной системы равна нулю, будут равны нулю и векторы нулевой системы. Следовательно, несимметричные системы линейных напряжений и линейных токов при отсутствии нулевого провода содержат только прямую и обратную составляющие.

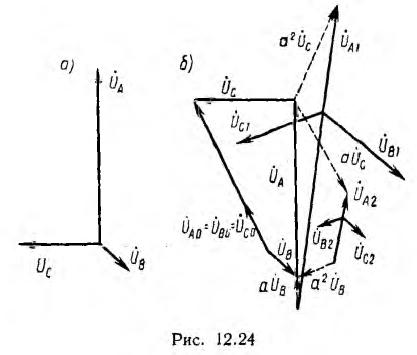
Определение симметричных составляющих несимметричной системы векторов по выражениям (12.6) может быть выполнено также графически. Пусть задана несимметричная система векторов фазных напряжений 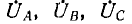(рис. 12.24, а). Во все три суммы напряжений (см. систему 12.6) вектор U_А входит без изменений, а векторы U_в и U_с во второй и третьей суммах повернуты на угол 2π/3 или 4π/3. Следует начертить вектор U_B, из его конца (т. е. стрелки) — вектор U_A, а из конца U_А — вектор U_с (рис. 12.24, б). Если вектор U в повернуть на угол 2π/3 и 4π/3 вокруг его конца, примыкающего к началу вектора U_А, а вектор U_с — вокруг начала, совпадающего с концом вектора U_А, суммы векторов по выражениям (12.6) будут равны утроенным искомым векторам:

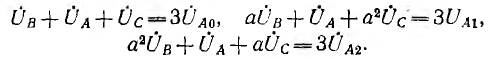
Далее очевидным построением определяются все векторы трех симметричных систем.

Аналогично производится разложение несимметричной системы токов.

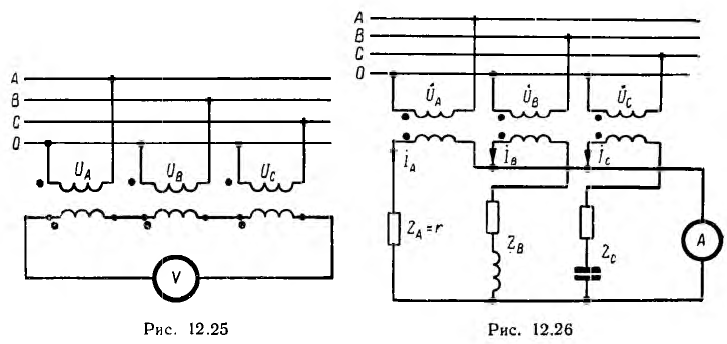
Симметричные составляющие несимметричной трехфазной системы напряжений и токов могут быть определены экспериментально. Например, для измерения нулевой составляющей системы фазных напряжений надо однообразно включить на фазные напряжения трансформаторы малой мощности, вторичные обмотки которых и вольтметр соединяются последовательно (рис. 12.25). Тогда, считая для простоты, что у трансформаторов коэффициент трансформации напряжения равен единице, суммарное напряжение, измеряемое вольтметром,

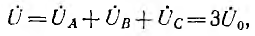
т. е. пропорционально напряжению нулевой системы.

Для измерения напряжения прямой последовательности (рис. 12.26) трансформаторы включаются на одинаковые по величине полные сопротивления z — трансформатор фазы А на активное сопротивление Z_A=r, фазы В на активно-индуктивное сопротивление 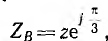, фазы С — на активно-емкостное сопротивление 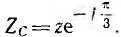. Чтобы вторичные токи трансформаторов В и С были сдвинуты по фазе относительно напряжений 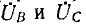на дополнительные до π углы — соответственно 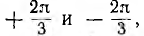, что соответствует умножению на операторы 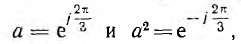вторичные обмотки этих трансформаторов включаются так, как показано на рис. 12.26.

Цепи нагрузок всех трех трансформаторов соединяются параллельно и замыкаются на амперметр. Последний измеряет суммарный ток

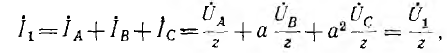
пропорциональный напряжению U₁ системы прямой последовательности.

Если поменять местами нагрузки фаз В и С, суммарный ток

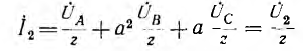
будет пропорционален напряжению U₂ системы обратной последовательности.

Рассмотренные схемы называются фильтрами симметричных составляющих. Они применяются в схемах защиты трехфазных энергетических систем от аварийных режимов, вызывающих несимметрию токов и напряжений отдельных фаз.

Разложение на симметричные составляющие позволяет весьма просто решать задачи на расчет трехфазных цепей при одинаковой нагрузке фаз с взаимной индукцией между ними при несимметричной системе напряжений, что широко используется в теории электрических машин. Система напряжений разлагается на симметричные составляющие, для каждой из них находят токи фаз и применяют метод наложения. При этом сопротивление фаз приемника для каждой составляющей может быть различным. Например, для цепи рис. 12.11, соединенной в звезду с нулевым проводом, сопротивление фаз для нулевой системы напряжений:

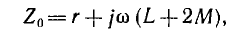
а для прямой и обратной составляющих, являющихся симметричными трехфазными системами, сопротивления

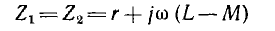
только для статических устройств, например для трансформаторов. Во вращающихся машинах прямая система токов создает магнитное поле, вращающееся в одном направлении с ротором, а обратная система токов — в противоположном; это приведет к неравенству 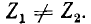. Таким образом, в общем случае

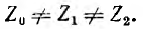
После определения комплексных токов каждой составляющей они пофазно суммируются и дают систему действительных токов фаз.

При неодинаковой нагрузке фаз приемника расчет усложняется, так как тогда каждая из симметричных составляющих системы такое зависит от всех составляющих систем напряжений. Эти задачи рассматриваются в литературе, посвященной расчету аварийных режимов в трехфазных электрических сетях и системах.

Можно показать, что в самом общем случае несимметрии средняя мощность всей цепи равна сумме средних мощностей нулевой, прямой и обратной составляющих:

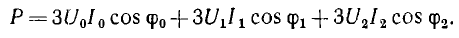
Трехфазные цепи

Трехфазная система ЭДС:

Производство, передача и распределение электрической энергии осуществляется в основном трехфазным током в трехфазных цепях. Широкое распространение в качестве нагрузки в трехфазных цепях получили трехфазные потребители. В трехфазных цепях используются трехфазные трансформаторы. Электрическую энергию в трехфазных цепях производят трехфазные генераторы, создающие синусоидальные ЭДС одинаковой частоты, в трехфазных системах.

Трехфазной называется система трех ЭДС одинаковой частоты, Вдвинутых друг относительно друга по фазе так, что сумма углов сдвига равна 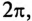или 360°.

Трехфазная система ЭДС называется симметричной, если ЭДС трех фаз сдвинуты друг относительно друга на угол 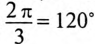и амплитуды этих трех ЭДС одинаковы по величине:

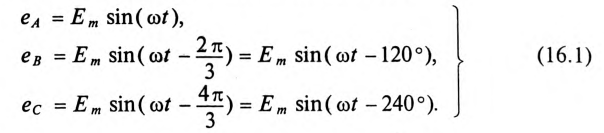
Комплексы этих ЭДС

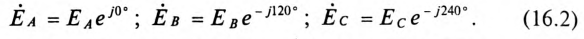
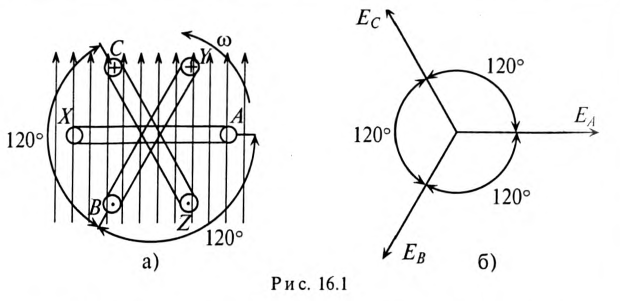
Получение симметричной трехфазной системы ЭДС осуществляется в трехфазном электромашинном генераторе (рис. 16.1а), в Котором три жестко скрепленные под углом 120° обмотки пересекают магнитное поле с частотой 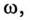вращаясь (в данном случае) против часовой стрелки.

Начала обмоток трехфазного генератора обозначаются прописными буквами 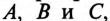а концы их соответственно 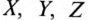(т.е. в трехфазном генераторе имеется три обмотк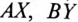и: и 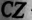рис. 16.1а).

Таким образом, при вращении в магнитном поле жестко скрепленных обмоток в них индуктируются одинаковые ЭДС 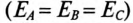одинаковой частоты 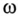и сдвинутые на 120°.

Векторная диаграмма такой симметричной системы ЭДС изображена на рис. 16.1б. Как видно из векторной диаграммы, мгновенное значение ЭДС в обмотке CZ можно записать в виде

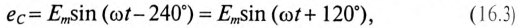
а комплекс этой ЭДС

т. е. логично, чтобы начальная фаза 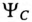превышала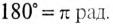

К каждой обмотке трехфазного генератора может быть подключена нагрузка с сопротивлениями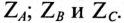

Если при этом три обмотки генератора электрически не соединены (рис. 16.2а), то такая трехфазная система называется несвязанной. Несвязанная трехфазная система практического применения не нашла.

Практическое применение нашла связанная трехфазная система (рис. 16.2б). Эта система экономически и энергетически более рациональна, так как используется три или четыре соединительных провода вместо шести и получить можно два различных напряжения, фазное и линейное, вместо одного.

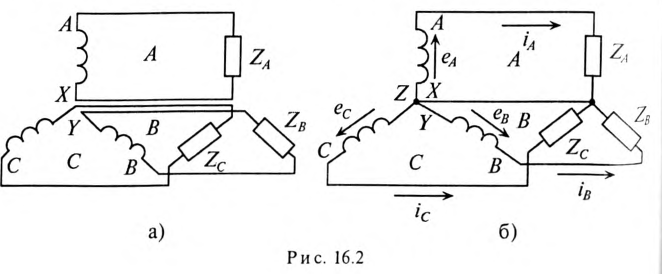
Каждая обмотка трехфазного генератора со своей нагрузкой и соединительными проводами называется фазой (рис. 16.2). В трехфазной системе различают три фазы А, В и С (международные обозначения — прописные буквы).

Положительное направление ЭДС и токов в каждой фазе на рис. 16.26 указаны стрелками.

В связанных трехфазных системах применяется соединение обмоток генератора и потребителя звездой F или треугольником Е.

Соединение обмоток генератора звездой

При соединении обмоток генератора звездой концы обмоток X, Yи Z элeктpичecки соединяются в одну точку 0 (рис. 16.3а), которая называется нулевой, или нейтральной. При этом генератор с потребителем соединяется тремя или четырьмя проводами.

Провода, подключенные к началам обмоток генератора (А, В и С, называют линейными проводами, а провод, подключенный к нулевой точке 0, называется нулевым, или нейтральным.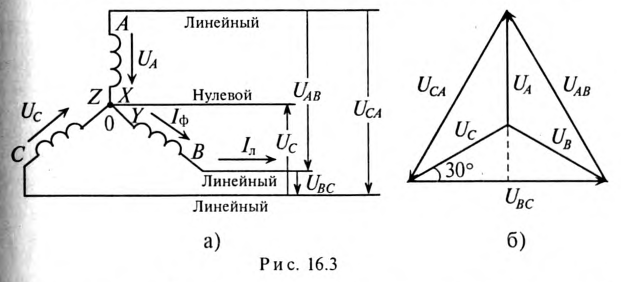

В связанных трехфазных системах различают фазные и линейные напряжения и токи.

Фазным называется напряжение между началом и концом обмотки генератора или между нулевым и линейным проводом. Обозначаются фазные напряжения прописными буквами с индексами фаз 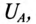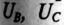(рис. 16.3а). Так как сопротивление обмоток генератора мало, то фазные напряжения практически не отличаются от ЭДС в обмотках генератора.

Линейным называется напряжение между началами обмоток генератора или между линейными проводами. Обозначаются линейные напряжения 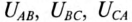(рис. 16.3а).

Можно определить зависимость между линейными и фазными напряжениями при соединении обмоток генератора звездой.

Мгновенные значения фазных напряжений равны разностям потенциалов между началами и концами соответствующих обмоток, т.е:

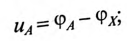
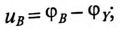
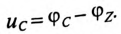
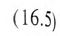
Мгновенные значения, линейных напряжений равны разностям потенциалов между началами соответствуют: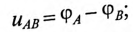

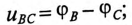
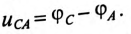
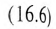
Потенциалы концов обмоток одинаковы 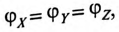так как все они соединены электрически в одну точку.

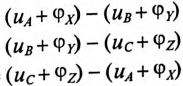
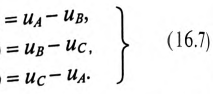
То есть мгновенное значение линейных напряжений определяется разностью мгновенных значений двух соответствующих фазных напряжений.

При соединении обмоток генератора звездой действующее значение линейного напряжения определяется геометрической разностью двух соответствующих фазных напряжений. На этом основании построена векторная диаграмма напряжений (рис. 16.3б) для соединения обмоток генератора звездой. К такому же результат) приводит определение комплексов линейных напряжений символическим методом:

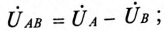
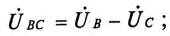
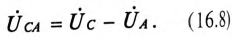
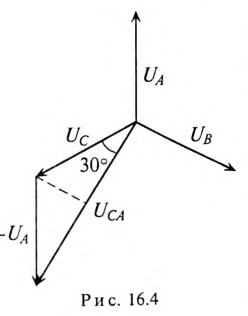
При симметричной системе ЭДС фазные напряжения равны по величине 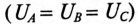и сдвинуты по фазе на угол 120°. По векторной диаграмме (рис. 16.3б) определяется линейное напряжение (рис. 16.4).

Линейное напряжение 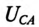при симметричной системе ЭДС трехфазного генератора определяется равенством

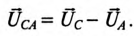
Из диаграммы (рис. 16.4) определяется вектор (комплекс)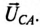

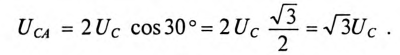
При симметричной системе ЭДС линейное напряжение трехфазного генератора, обмотки которого соединены звездой, в 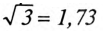раза больше фазного напряжения:

Если говорят о напряжении генератора 127/220 В, то имеется в виду, что фазное напряжение в трехфазной цепи 127 В, а линейное — 220 В. В сети с напряжением 220/380 В фазное напряжение 220 В, а линейное — 380 В. Очевидно, что обмотки генератора такой симметричной цепи соединены звездой и отношение напряжений получится равным

В связанных трехфазных системах фазным называется ток, провидящий по обмотке (фазе) генератора 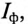а линейным считается ток, проходящий по линейному проводу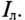

Как видно на рис. 16.3а, при соединении обмоток генератора звездой линейный ток 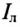равен фазному току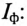

Соединение обмоток генератора треугольником

При соединении обмоток генератора треугольником (рис. 16.5а) конец обмотки фазы А соединяется с началом обмотки фазы В, конец обмотки фазы В соединяется к началом обмотки фазы С, конец обмотки фазы С соединяется с началом обмотки фазы А и к точкам соединения подключаются линейные провода.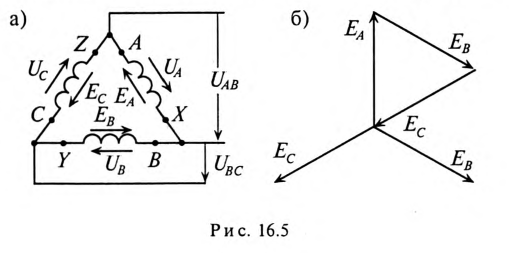

При соединении обмоток генератора треугольником (рис. 16.5а) трехфазная цепь трехпроводная.

Как следует из схемы соединения обмоток треугольником (рис. 16.5а), линейное напряжение 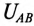равно фазному напряжению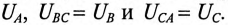

То есть

Из схемы (рис. 16.5а) следует, что три обмотки генератора, соединенные треугольником, образуют замкнутый контур, ток в котором при отсутствии нагрузки (холостой ход) определяется выражением

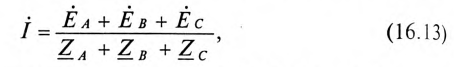
где 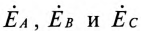– комплексы (векторы) ЭДС фаз генератора; 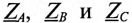— комплексы сопротивлений обмоток генератора 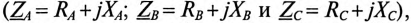т.е. каждая обмотка обладает активным R и индуктивным X сопротивлениями.

Так как сопротивления обмоток малы, падением напряжения на них можно пренебречь и считать, что напряжение на каждой обмотке генератора равно ее ЭДС.

При симметричной системе ЭДС и правильном соединении обмоток генератора треугольником (рис. 16.5а) геометрическая сумма ЭДС (комплексов) обмоток генератора, образующих замкнутый контур, равна нулю (рис. 16.5б). Следовательно, и ток в замкнутом контуре обмоток, соединенных треугольником, также равен нулю 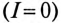при холостом ходе независимо от величины внутреннего сопротивления обмоток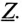

Если обмотки симметричного генератора соединены «неправильным» треугольником, т. е. неправильно подключить начало и конец хотя бы одной из обмоток, например 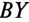(рис. 16.5’а), то геометрическая сумма ЭДС в замкнутом контуре обмоток будет равна удвоенному значению ЭДС одной фазы (рис. 1б.5’б). С учетом малого внутреннего сопротивления обмоток генератора ток в замкнутом контуре достигает катастрофической величины даже при отсутствии нагрузки (холостой ход). Таким образом, соединена, обмоток трехфазного генератора «неправильным» треугольником равносильно короткому замыканию в замкнутом контуре обмоток.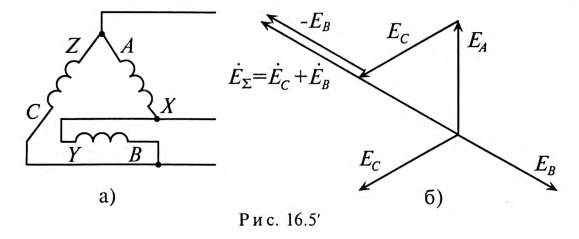

Соединение потребителей звездой

При соединении звездой потребителя и генератора (рис. 16.6) трехфазная система представляет собой сложную цепь с двумя узловыми точками 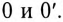Точка 0 — нейтральная точка генератора, а 0′ — нейтральная точка потребителя. Напряжение между этими узловыми точками 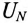называется напряжением смещения нейтрали.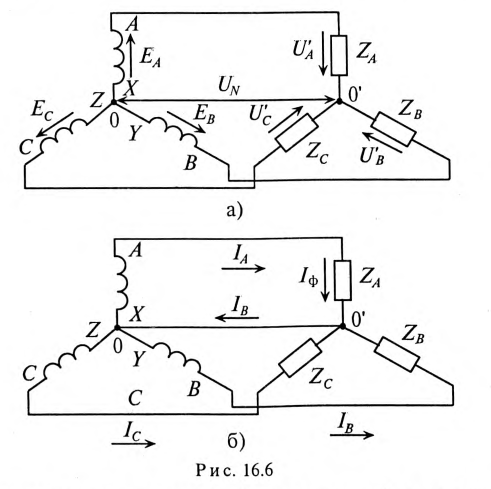

Соединение генератора и потребителя звездой может быть с нулевым проводом (рис. 16.6б), т.е. четырехпроводная цепь, и без нулевого провода (рис. 16.6а), т.е. трехпроводная цепь.

Величину напряжения смещения нейтрали 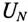определяют методом узлового напряжения (см. (4.9)) в символической (геометрической) форме:

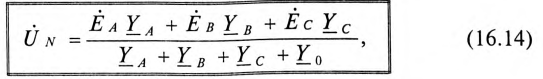
где 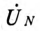– комплекс (вектор) напряжения смещения нейтрали; 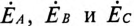комплексы (векторы) ЭДС в обмотках соответствующих фаз генератора; 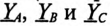– комплексы проводимостей соответствующих фаз:

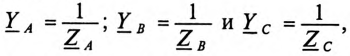
где 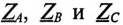– комплексы сопротивлений фаз потребителя, включая внутреннее сопротивление обмоток генератора и сопротивление соединительных проводов; 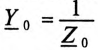— комплекс проводимости нулевого провода, a 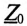— комплекс его сопротивления.

Напряжение U’ на каждой фазе потребителя, соединенного звездой (рис. 16.6а), с учетом напряжения смещения нейтрали, определяют следующим образом:

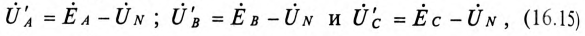
где 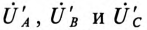— комплексы (векторы) напряжений на фазах потребителей.

На основании (16.15) строится векторная диаграмма напряжений (рис. 16.7), на которой вектор напряжения смещения нейтрали взят произвольно. Из векторной диаграммы (рис. 16.7) следует, что при наличии напряжения смещения нейтрали напряжения на фазах потребителя, соединенного звездой, различны по величине и по начальной фазе даже при симметричной системе ЭДС в обмотках генератора.

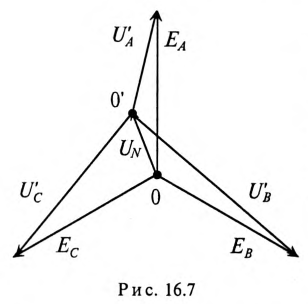
Очевидно (рис. 16.7), что напряжения на фазах потребителя, соединенного звездой, будут одинаковыми по величине 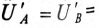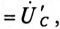если напряжение смещения нейтрали отсутствует, т.е. 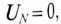при симметричной системе ЭДС генератора.

Напряжение смещения нейтрали отсутствует, т. е. 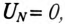при равномерной (симметричной) нагрузке фаз или при наличии нулевого провода.

Рассмотрим эти условия:

1. Равномерная нагрузка фаз.

Равномерной называют нагрузку, при которой комплексы сопротивлений фаз равны между собой.

То есть

или

Тогда 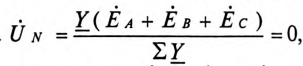так как при симметричной системе ЭДС сумма 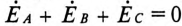(см. рис. 16.5б).

Так как комплекс сопротивления фазы 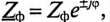то равномерной считается нагрузка, при которой сопротивления фаз одинаковы по величине 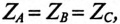по характеру (активный, индуктивный или емкостной) и имеют одинаковый угол сдвига фаз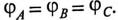

2. Наличие нулевого провода.

При наличии нулевого провода, соединяющего нейтральные точки 0 и 0′ (рис. 16.6б),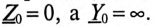

Тогда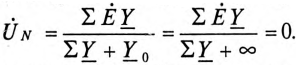

В обоих случаях (1 и 2) напряжения на фазах потребителя, подключенного к трехфазному генератору с симметричной системой ЭДС, одинаковы по величине. При этом величина напряжения 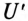на каждой фазе потребителя, соединенного звездой, в 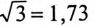раза меньше линейного напряжения, т. е.

Ток в нулевом проводе 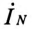(рис. 16.66) при соединении потребителей звездой определяется геометрической суммой токов в фазах потребителя:

Токи в фазах потребителя определяются по формулам

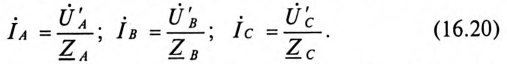
Очевидно, что при равномерной нагрузке фаз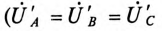 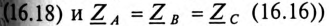токи в фазах равны по величине «сдвинуты, как и напряжения, по фазе на 120°. Следовательно, их геометрическая сумма 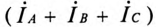равна нулю, т.е. 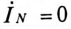(см. рис. 16.5б, где вместо 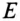подставить ).

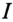Таким образом, при равномерной нагрузке фаз нулевой провод не нужен.

При неравномерной нагрузке фаз отсутствие нулевого провода приводит к неодинаковым по величине напряжениям на каждой фазе потребителя (рис. 16.7). При этом на фазе с большим сопротивлением Z будет большее напряжение U’.

Так как отсутствие нулевого провода при неравномерной нагрузке фаз потребителя, соединенного звездой, нарушает режим работы потребителей U’, то предохранитель в нулевой провод не ставят.

Следовательно, нулевой провод служит для выравнивания напряжений на фазах потребителя при неравномерной нагрузке фаз.

При соединении потребителей звездой ток каждой фазы потребителя 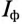(рис. 16.16) равен линейному току трехфазной цепи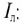

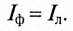
Соединение потребителей треугольником

При соединении потребителя треугольником (рис. 16.8) к каждой фазе потребителя приложено линейное напряжение трехфазной цепи

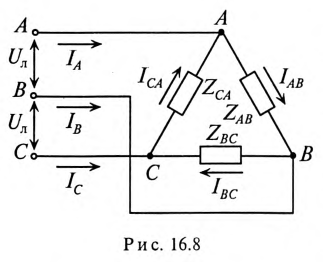
Так как при симметричной системе ЭДС все линейные напряжения равны по величине и сдвинуты на угол 120° по фазе, то и напряжения на каждой фазе потребителя, соединенного треугольником, равны по величине 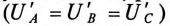и сдвинуты по фазе на угол 120°, независимо от характера нагрузки.

При соединении потребителей треугольником линейные токи обозначаются прописными буквами с индексами фаз, т. е. 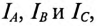а токи в фазах потребителя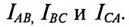

Воспользовавшись первым законом Кирхгофа, линейные токи можно определить выражениями (рис. 16.8)

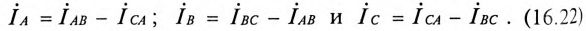
Линейный ток при соединении потребителей треугольником определяется геометрической разностью двух фазных токов, сходящихся с линейным в одной узловой точке (рис. 16.8).

Фазные токи потребителя, соединенного треугольником, определяются:

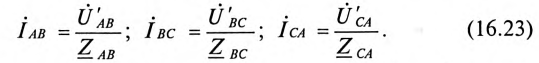
При симметричной системе ЭДС генератора 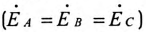и равномерной нагрузке фаз потребителя 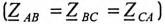токи в фазах потребителя равны между собой по величине 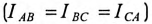и, так лее как напряжения на фазах потребителя, сдвинуты друг относительно друга по фазе на угол 120° (рис. 16.9).

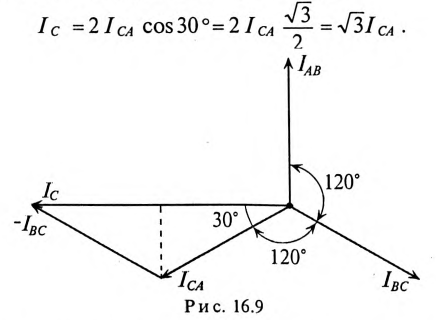
Таким образом, при равномерной нагрузке фаз и симметричной системе ЭДС при соединении потребителей треугольником линейный ток в трехфазной цепи в 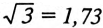раза больше фазного тока:

Мощность трехфазного тока

Активная мощность, отдаваемая трехфазным генератором и потребляемая трехфазным потребителем, определяется суммой активных мощностей каждой фазы потребителя:

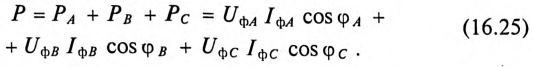
Аналогичное определение можно отнести и к реактивной мощности трехфазного тока, т. е.

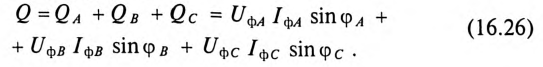
Полная, или кажущаяся, мощность трехфазного потребителя равна

=

Очевидно, что при равномерной нагрузке фаз 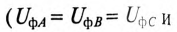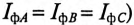активная мощность трехфазного тока равна утроенному значению активной мощности каждой фазы

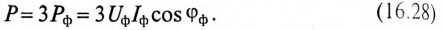
Однако на практике удобней оперировать линейными величинами, так как доступными являются линейные провода, а не обмотки генератора или двигателя.

При соединении потребителя звездой при равномерной нагрузке фаз

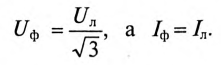
Тогда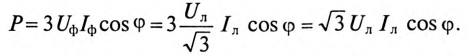

При соединении потребителей треугольником при равномерной нагрузке фаз

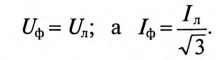
Тогда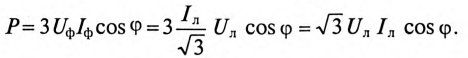

Таким образом, при равномерной нагрузке фаз при соединении потребителей звездой и треугольником мощности трехфазного тока определяются выражениями:

При неравномерной нагрузке фаз полная, или кажущаяся, мощность трехфазного тока может быть определена суммой полных мощностей каждой фазы, выраженной в комплексной форме, а именно

Равномерную нагрузку в трехфазных цепях обеспечивают электрические двигатели трехфазного тока, обмотки которых могут гь соединены или звездой, или треугольником.

Топографическая диаграмма

Напряжение между отдельными точками трехфазной цепи можно найти графически путем построения так называемой топографической диаграммы.

Топографическая диаграмма — это векторная диаграмма, поенная так, чтобы каждой точке цепи соответствовала определенная точка на диаграмме и чтобы вектор, проведенный в эту точку из начала координат, выражал по величине и фазе потенциал соответствующей точки цепи. Отрезок, соединяющий любые две точки на этой диаграмме, определяет напряжение между соответствующими точками цепи. Если топографическая диаграмма встроена в определенном масштабе, то по ней можно определить искомое напряжение и ток по величине и по фазе.

При построении топографической диаграммы для трехфазной цепи удобно принять за точку с нулевым потенциалом нулевую, или нейтральную, точку генератора. Этой точке генератора соответствует начало координат топографической диаграммы.

Топографическая диаграмма для трехфазной цепи, изображенной на рис. 16.6, построена при условии, что точка 0 на диаграмме (рис. 16.10) соответствует нулевой точке генератора, потенциал которой равен нулю, т. е.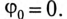

Из точки 0 откладываются в определенном масштабе напряжений 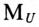векторы фазных ЭДС 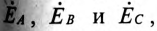в результате чего получаются точки А, В и С на топографической диаграмме. Эти точки на диаграмме соответствуют началам обмоток генератора, Соединенного звездой точками А, В и С цепи.

Отрезок 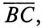равный разности векторов 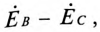представляет собой линейное напряжение 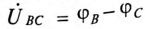(падением напряжения на внутреннем сопротивлении обмотки генератора пренебрегаем, т.е. 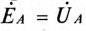). Аналогично отрезки 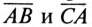на топографической диаграмме изображают линейные напряжения 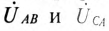соответственно.

Отложив из точки 0 (начало координат) вектор напряжения смещения нейтрали 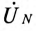(отрезок 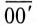), определяют потенциал нулевой точки потребителя 0′ на диаграмме. Тогда отрезки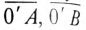 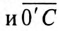выражают напряжение на фазах потребителя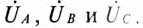

Если напряжение смешения нейтрали 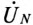отсутствует 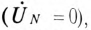то точка 0′ (нулевая точка потребителя) на топографической диаграмме совпадет с точкой 0 (нулевой точкой генератора). Тогда векторы напряжений на фазах потребителя 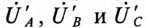равны по величине и по фазе векторам ЭДС генератора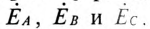

Применение топографической диаграммы для расчета трехфазной цепи рассмотрено в примере 16.1 настоящей главы.

Пример 16.1

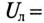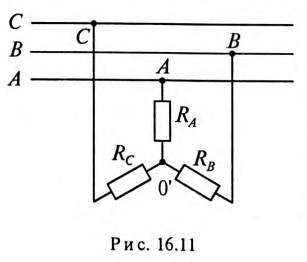
К трехфазной трехпроводной сети с линейным напряжением 220 В подключен потребитель, соединенный звездой, с сопротивлениями 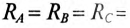10 Ом (рис. 16.11).

Определить напряжение и ток каждой фазы потребителя в каждом из трех режимов:

1. Потребители соединены звездой, как показано на рис. 16.11.

2. Обрыв в фазе А, т. е.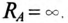

3. Короткое замыкание в фазе А, т. е.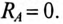

Решение

Решение этой задачи производится с помощью построения топографической диаграммы для каждого режима.

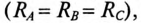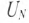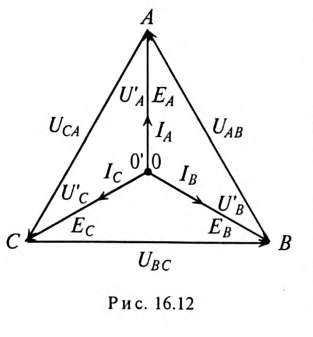
1. Так как в данном режиме имеет место равномерная нагрузка фаз следовательно, напряжение смещения нейтрали равно нулю 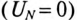и точка 0′ на топографической диаграмме совпадает с точкой 0 (рис. 16.12).

Пренебрегая внутренним сопротивлением обмоток генератора 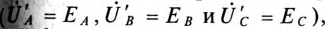определяют напряжение на каждой фазе потребителя при симметричной системе ЭДС:

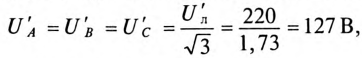
так как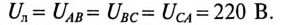

Toк каждой фазы потребителя будет равен

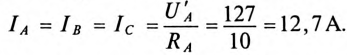
Линейные токи в каждом линейном проводе также равны между собой и равны фазным токам каждой фазы, т.е.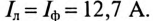

2. При обрыве в фазе А схема трехфазной цепи обретает следующий вид (рис. 16.13а), а топографическая диаграмма показана на рис. 16.13б.

Таким образом, точка 0′ на топографической диаграмме при обрыве в фазе А как бы опустилась на вектор линейного напряжения 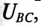разделив его величину поровну между 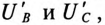т. е.

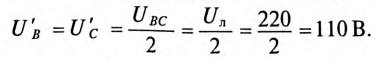
Напряжение на оборванной фазе А, т. е. напряжение между точками 0′ и А в схеме, как следует из топографической диаграммы рис. 16.13б), будет равно

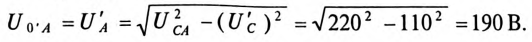
Токи в фазах: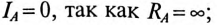

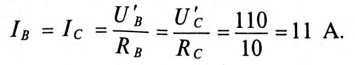
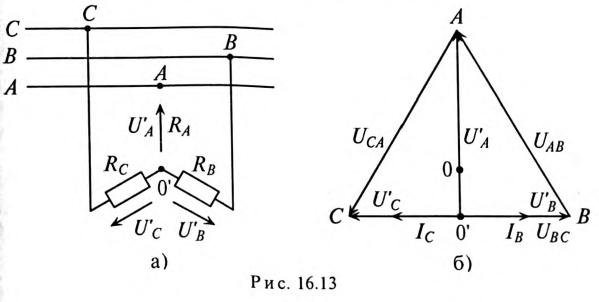
Токи в линейных проводах:

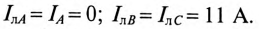
3. При коротком замыкании фазы А схема трехфазной цепи показана на рис. 16.14а, топографическая диаграмма на рис. 16.14б.

Таким образом, точка 0′ на топографической диаграмме при коротком замыкании фазы как бы поднялась в точку А 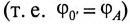и фазные напряжения 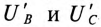совпали с векторами линейных напряжений 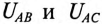соответственно и стали равными им по величине, т.е.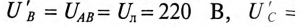

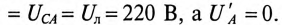
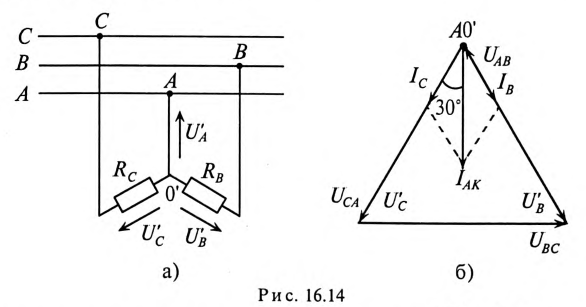
Токи в фазах будут равны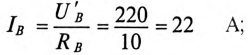
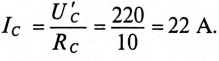
Ток в коротко замкнутой фазе 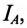т. е. ток в проводе, соединяющем точку 0′ и А, определяется геометрической суммой токов 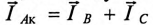(рис. 16.14б), т.е.

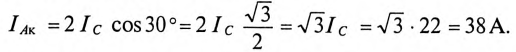
Напряжение 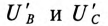и токи 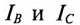в режимах 2 и 3 легко определить из схем рис. 16.13а и 16.14а, не прибегая к топографическим диаграммам.

Пример 16.2

К соединенному звездой генератору с фазным напряжением 127 В подключен потребитель, соединенный треугольником. Активное сопротивление каждой фазы потребителя R = 8 Ом, индуктивное 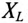= 6 Ом (рис. 16.15а).

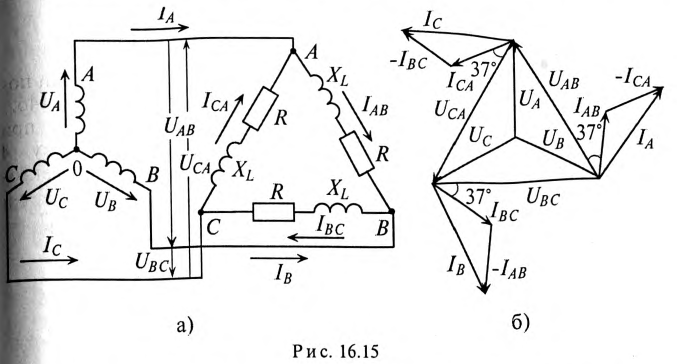
Определить ток в каждой фазе генератора, отдаваемую им мощность и построить векторную диаграмму.

Решение

Эту задачу можно решить, не прибегая к символическому методу и построению топографической диаграммы.

Напряжение на каждой фазе потребителя 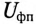равно линейному напряжению генератора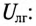

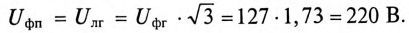
Сопротивление каждой фазы потребителя равно

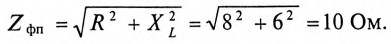
Ток каждой фазы потребителя (нагрузка равномерная):

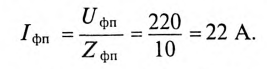
В каждой фазе генератора проходит линейный ток потребителя, единенного треугольником, т.е. (см. рис. 16.15а)

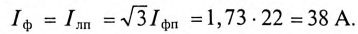
Отдаваемая генератором мощность (активная мощность) равна

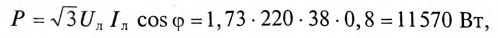
Так как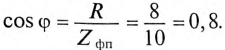

Угол 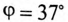(Приложение 10).

Таким образом, ток фазы потребителя отстает от напряжения на угол 37°, так как нагрузка индуктивного характера.

Вычисленные величины легли в основу построения векторной диаграммы (рис. 16.15б).

Пример 16.3

Параметры трехфазного потребителя, соединенного звездой, имеют следующие значения: 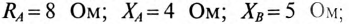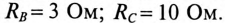Линейное напряжение сети симметричной системы ЭДС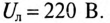

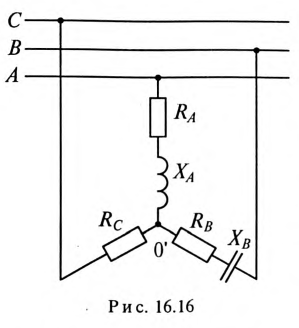
1) напряжение на каждой фазе потребителя;

2) токи каждой фазы потребителя;

3) мощности 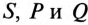цепи. Построить векторную диаграмму.

Решение

Допустим, что обмотки генератора соединены звездой, тогда напряжение каждой фазы генератора (при симметричной системе ЭДС)

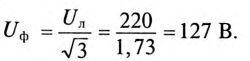
Напряжение на каждой обмотке генератора в комплексной форме:

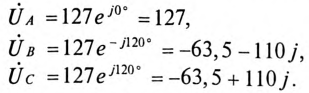
Сопротивление 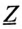каждой фазы потребителя:

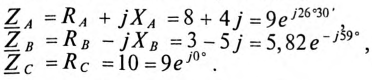
Проводимости 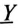каждой фазы потребителя:

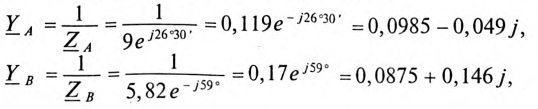
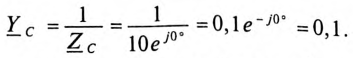
Напряжение смещения нейтрали 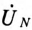при отсутствии нулевого провода, т. е. при 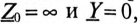будет равно

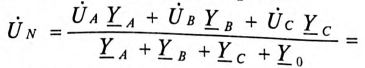
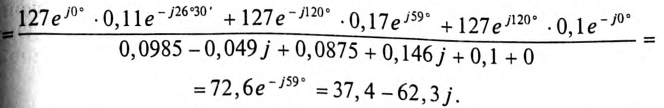
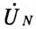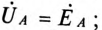
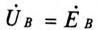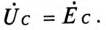При вычислении принято: и Напряжение на каждой фазе потребителя (16.15):

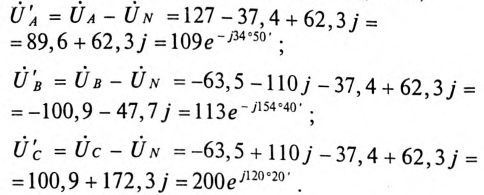
Токи в каждой фазе потребителя: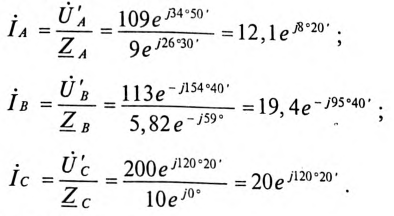

Мощности каждой фазы потребителя:

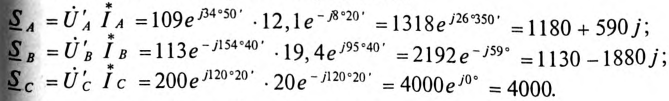
Мощность всей трехфазной нагрузки:

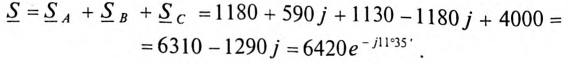
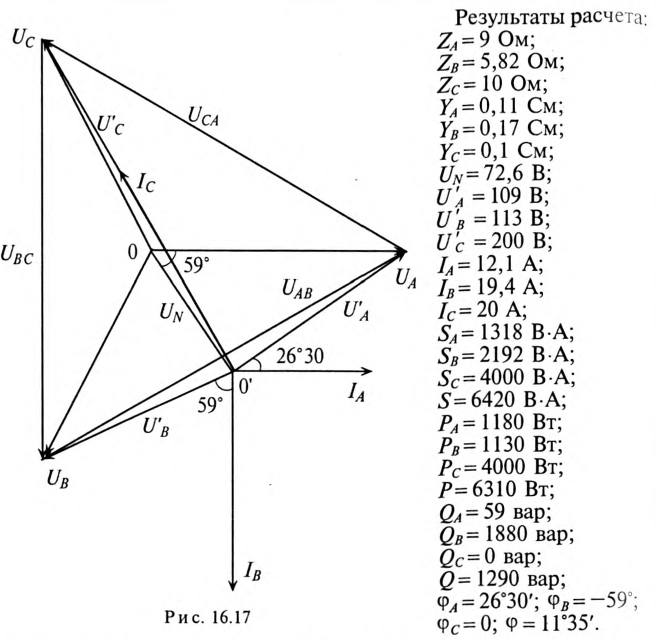
Векторная диаграмма рассматриваемой цепи изображена на рис. 16.17.

Пример 16.4

К трехфазной сети с линейным напряжением 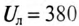подключены двигатель Д и однофазные силовые потребители (рис. 16.18).

Обмотки трехфазного двигателя мощностью 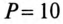кВт и 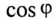= 0,76 соединены треугольником. Однофазные силовые потребители с параметрами: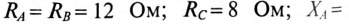 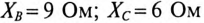— соединены звездой.

Определить: показания амперметров 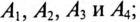мощность Р, потребляемую всей нагрузкой; показания вольтметров.

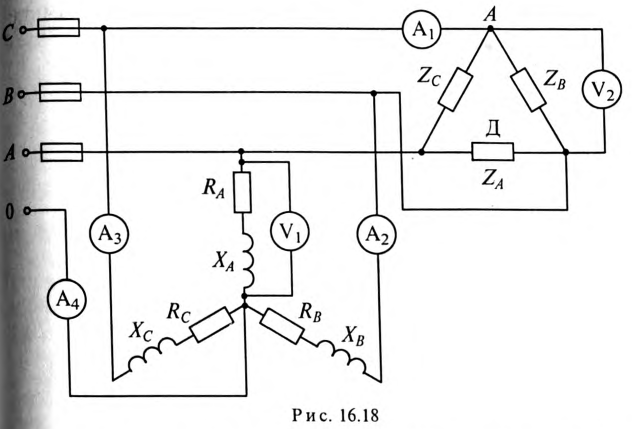
В линейном проводе С сгорел предохранитель (обрыв линейного провода С). Как при этом изменится показание вольтметpa 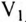, если оборвется и нулевой провод? Как изменится показание вольтметра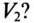

Решение

Расчет трехфазной цепи (рис. 16.18) можно осуществить, не прибегая к символическому методу и построению топографической диаграммы.

Амперметр 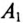включен в линейный провод С, подводящий 1ние к двигателю, обмотки которого соединены треугольником и представляют равномерную нагрузку фаз; следовательно (см. (16.29))

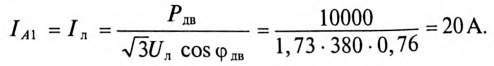
Амперметр 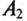измеряет ток в фазе В силового потребителя, соединенного звездой. При наличии нулевого провода напряжение на каждой фазе потребителя 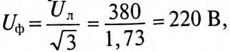тогда ток в фазе В будет равен

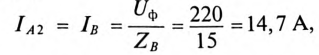
так как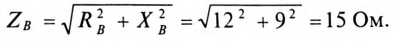

Показания амперметра 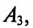включенного в фазу С силового потребителя:

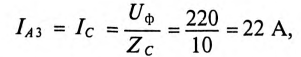
так как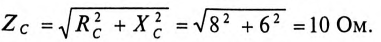

Амперметр 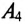включен в нулевой провод, ток в котором 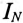определяется геометрической суммой токов в фазах силового потребителя, соединенного звездой (см. (16.19) и рис. 16.19).

Для вычисления геометрической суммы токов фаз необходимо построить векторную диаграмму токов (рис. 16.19).

При наличии нулевого провода напряжения на фазах сдвинуты на угол 120°. Угол сдвига фаз между током и напряжением, исходя из условий, для всех трех фаз одинаков (это видно из заданных параметров силового потребителя):

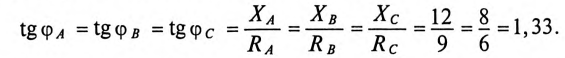
Следовательно, фазные токи сдвинуты так же, как и напряжения, на угол 120°. Величины токов определены: 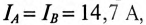На основании этих данных можно построить векторную диаграмму токов (рис. 16.19).

На векторной диаграмме складываются геометрически 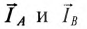и получается суммарный ток, равный 14,7 А.

Поскольку этот суммарный ток находится в противофазе с током 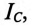то ток в нулевом проводе 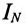равен 7,3 А:

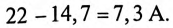
Следовательно, амперметр 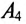покажет ток 7,3 А.

Для расчета мощности Р, потребляемой всей нагрузкой, вычисляется активная мощность каждого силового потребителя:

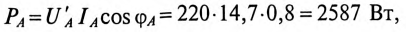
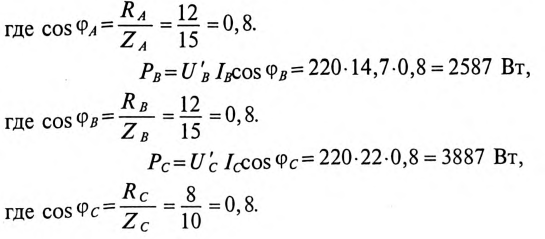
Тогда активная мощность, потребляемая всей нагрузкой, будет равна

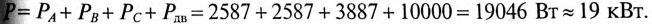
При обрыве линейного провода С и нулевого провода две фазы силового потребителя А и В кажутся соединенными последовательно и подключенными к личному напряжению 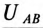=380 В. Так как сопротивления этих фаз равны по величине, то это линейное напряжение распределится между ними поровну, т.е.

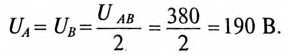
Таким образом, вольтметр 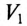покажет напряжение 190 В вместо 220 В, которое он показывал до обрыва.

При обрыве линейного провода С фазы В и С двигателя окажутся соединенными последовательно и подключенными к линейному напряжению 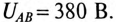Так как сопротивления обмоток двигателя равны между собой, то линейное напряжение 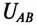распределится поровну между обмотками В и С двигателя, т.е.

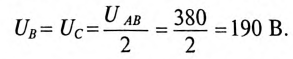
Таким образом, вольтметр 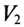покажет напряжение 190 В вместо 380 В, которое он показывал до обрыва.

Вращающееся магнитное поле двухфазного тока

Двухфазным током называется совокупность двух однофазных токов, сдвинутых по фазе на угол 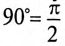друг относительно друга (рис. 17.3б):

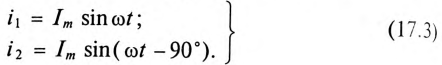
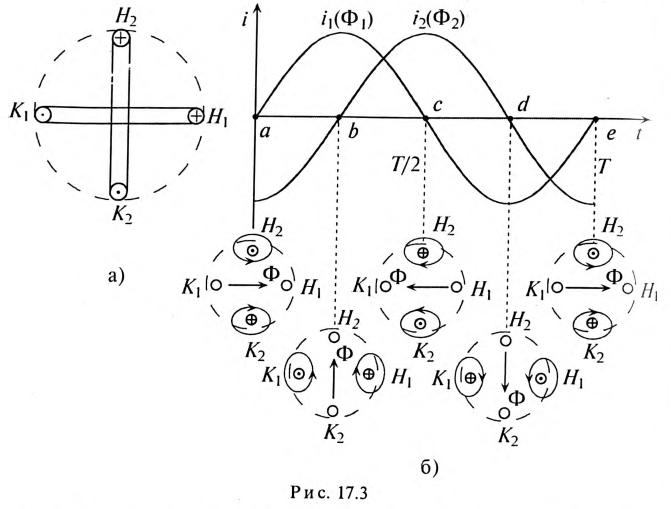
Эти токи создают в обмотках переменные магнитные потоки, сдвинутые по фазе также на угол 90°:

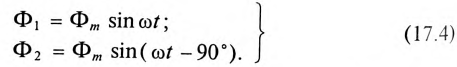
Таким образом, если по двум неподвижно скрепленным под углом 90° обмоткам пропустить двухфазный ток, то внутри этих обмоток (рис. 17.3а) создается вращающееся магнитное поле двухфазного тока.

Как видно (рис. 17.3б), постоянный магнитный поток 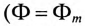одной фазы) вращается против часовой стрелки, если при указанном расположении обмоток первый ток 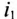опережает второй ток 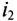по фазе.

Нетрудно убедиться в том, что если бы второй ток 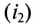опережал первый 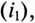то магнитное поле вращалось бы в обратную сторону. Вращающееся магнитное поле двухфазного тока широко применяется для пуска и работы однофазных машин переменного тока.

Пульсирующее магнитное поле

Если по неподвижной катушке (обмотке) машины пропустить синусоидальный ток 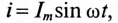то внутри этой катушки создается пульсирующее магнитное поле, т. е. поле, изменяющееся по величине и направлению, но расположенное в одной плоскости (рис. 17.4).

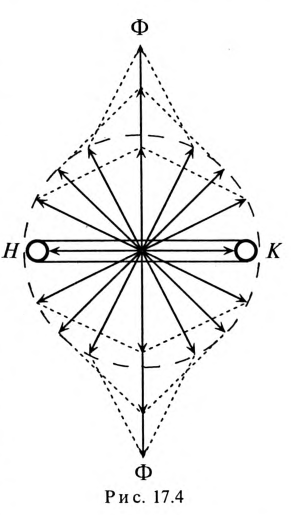
Пульсирующее магнитное поле, к видно из рис. 17.4, можно рассматривать как два магнитных поля, вращающихся в разные стогны. Поэтому в машинах, в которых используется пульсирующее магнитное поле, отсутствует пусковой момент. Для работы таких машин его необходимо создать. Пусковой момент в таких машинах создают или механически, или за счет пусковой обмотки, по которой в момент пуска пропускают импульс тока, сдвинутого по фазе относительно основного синусоидального тока, проходящего по катушке (обмотке) машины (аналогично двухфазному току).

Определение трёхфазных цепей

Наряду с однофазными источниками существуют источники энергии, содержащие две, три, четыре и т.д., характеризуемые тем, что их ЭДС, имея одинаковую частоту, сдвинуты друг относительно друга на некоторый угол. Такие генераторы называются многофазными, а электрические цепи с такими источниками – многофазными.

Трёхфазный генератор

Трёхфазные цепи получили наибольшее практическое применение. В связи с этим основные исследования многофазных цепей будем проводить на примере трёхфазных. Рассмотрим вопрос реализации трёхфазного источника, которым является трёхфазный генератор (рис. 4.1).

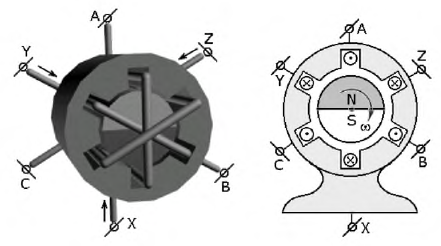
Рис. 4.1. Трёхфазный генератор

Для упрощения понимания принципа работы генератора обмотки (фазы) представлены одним витком. В качестве ротора генератора выбран постоянный магнит. Каждая из обмоток имеет начало – клеммы 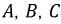и конец – 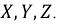Обмотки в пространстве сдвинуты друг относительно друга на 120°, из чего следует, что максимумы ЭДС в них достигаются в разные моменты времени, отстоящие друг от друга на одну треть периода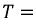 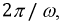где 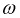— угловая частота вращения ротора.

Последовательность, в которой ЭДС достигают максимума в соответствующих фазах, носит название порядка чередования фаз. Прямым порядком чередования фаз называют последовательность 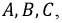при которой фаза 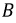отстает от фазы 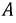на 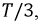и фаза 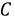отстает от фазы 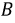на 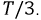На рис. 4.2 изображен график мгновенных значений ЭДС для прямого порядка чередования фаз. Изменение направления вращения ротора трёхфазного генератора на противоположное меняет эту последовательность чередования фаз, и она станет уже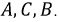

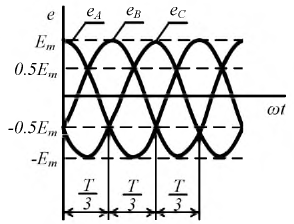
Рис. 4.2. Графики мгновенных значений ЭДС фаз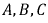

Запишем мгновенные значения ЭДС, индуктируемые в фазах при вращении ротора генератора:

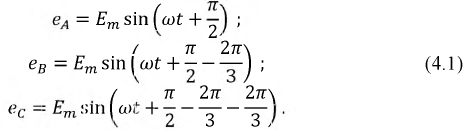
Поскольку ЭДС каждой фазы генератора синусоидальна, то их можно изобразить на комплексной плоскости в виде векторов соответствующих фазных ЭДС: 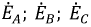(рис. 4.3).

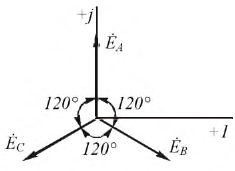
Рис. 4.3. Векторная диаграмма фазных ЭДС

Важным обстоятельством является то, что система векторов фазных ЭДС генератора на комплексной плоскости образует симметричную трехлучевую звезду и сумма этих векторов в любой момент времени равна нулю.

При подключении к каждой из фаз генератора нагрузки по ней будет протекать ток. Таким образом, реализуется трёхфазная система.

Способы соединения фаз генератора и нагрузки

Соединение фаз генератора и нагрузки четырехпроводной звездой:

При соединении фаз генератора звездой все концы или начала соединяют в одну общую точку. На рис. 4.4.а показана несвязанная трёхфазная система, в которой каждая фаза генератора и приемника образует отдельную электрическую цепь и поэтому для связи генератора и приемника требуется 6 проводов.

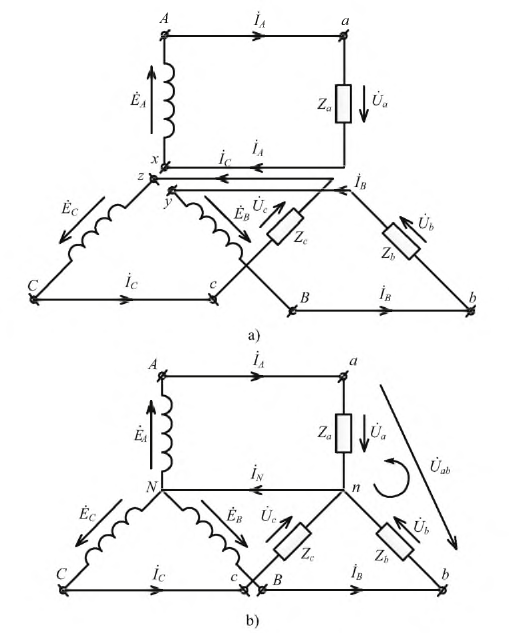
Рис. 4.4. Соединение звездой а) несвязанная трёхфазная система, b) четырехпроводная звезда

При соединении звездой количество проводов уменьшится до 4-х. Причем провод, соединяющий общие (нейтральные или нулевые) точки фаз генератора 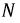и приемника называется нейтральным или нулевым. Остальные провода, соединяющие фазы генератора и приемника – линейные.

Токи, протекающие по фазам генератора или приемника, называются фазными токами, токи, протекающие по проводам, соединяющим фазы генератора и приемника, – линейными токам, ток, протекающий по нейтральному проводу – нейтральным.

Напряжение между началом и концом фазы генератора или приемника называется фазным, напряжение между двумя фазами или линиями – линейным.

Для этого способа соединения между линейными и фазными параметрами цепи существуют следующие соотношения:

Установим взаимосвязь между комплексами линейных и фазных напряжений источника (рис. 4.5).

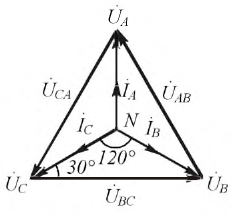
Рис. 4.5. Векторно-топографическая диаграмма трёхфазной цепи при соединении приёмников звездой при симметричной активной нагрузке

В дальнейших рассуждениях фазные ЭДС заменим напряжениями на фазах источника:

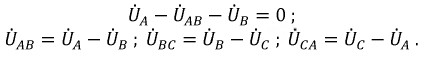
Выберем любой равнобедренный треугольник, образованный двумя фазными и линейным напряжениями и опустим перпендикуляр из вершины 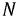на основание. Перпендикуляр является медианой и биссектрисой.

Из любого прямоугольного треугольника получим:

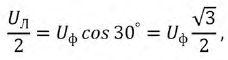
Это второе важное соотношение для соединения звездой.

Частным случаем такого соединения является соединение «звезда-звезда» без нулевого провода.

Соединение фаз генератора и нагрузки треугольником

Вторым базовым способом соединения фаз генератора и нагрузки является соединение типа «треугольник-треугольник» (рис. 4.6).

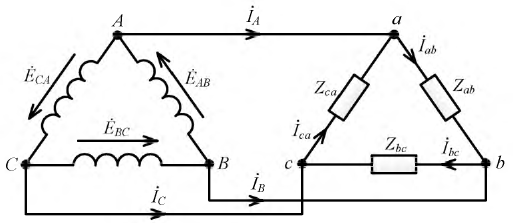
Рис. 4.6. Соединение «треугольник-треугольник»

При соединении треугольником существует следующее соотношение:

Установим взаимосвязь между фазными и линейными токами:

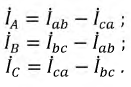
Построим векторную диаграмму токов и напряжений приемника (рис. 4.7) для данного способа соединения.

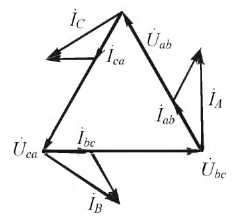
Рис. 4.7. Векторно-топографическая диаграмма трёхфазной цепи при соединении

Рассмотрев любой треугольник токов, можно, аналогично напряжениям при соединении звездой, сделать вывод (только для симметричной нагрузки):

Помимо вышеназванных существуют и комбинированные способы соединения: «звезда-треугольник», «треугольник-звезда».

Режимы работы трёхфазных цепей

Различают симметричный и несимметричный режимы работы трехфазной цепи. При. симметричном режиме сопротивления трех фаз одинаковы и ЭДС образуют трехфазную. симметричную систему. В этом случае токи фаз а, в, с будут равны по величине и сдвинуты по угол 120 градусов.

Соединение «звезда-звезда» с нулевым проводом и без нулевого провода

Поскольку трёхфазные цепи являются совокупностью однофазных цепей, то для их расчета используются все ранее рассмотренные специальные методы, в том числе и комплексный метод расчета. Следовательно, расчет трёхфазных цепей можно иллюстрировать построением векторных диаграмм токов нагрузки и топографических диаграмм напряжений.

Наиболее рациональным методом расчета такой цепи может считаться метод двух узлов. Для выбранных положительных направлений напряжений и токов на схеме (рис. 4.8) составим соответствующую систему уравнений для расчета токов. приемников треугольником и симметричной активной нагрузке

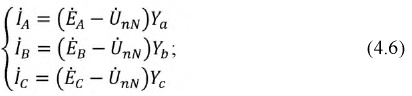
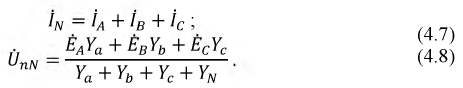
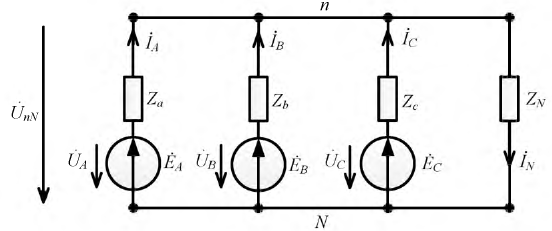
Рис. 4.8. Соединение фаз генератора и приемника по схеме «четырехпроводная звезда»

1. Симметричная нагрузка.

Нагрузка считается симметричной, если комплексные сопротивления ее фаз равны:

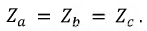
Для простоты в качестве потребителей фаз нагрузки будем рассматривать активные сопротивления 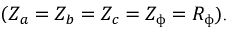Наличие нулевого провода делает одинаковыми потенциалы узлов 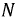и 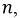если сопротивлением нулевого провода можно пренебречь 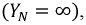значит 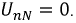При этом фазные токи равны, а фазные напряжения на нагрузке будут полностью повторять фазные напряжения генератора. Для фазы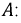

Аналогично для фаз и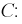

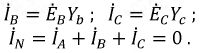
Исходя из сказанного, построим топографическую диаграмму фазных напряжений и векторную диаграмму токов (рис. 4.9).

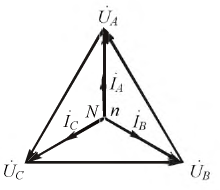
Рис. 4.9. Векторно-топографическая диаграмма для симметричной нагрузки в трех- и четырехпроводной системах

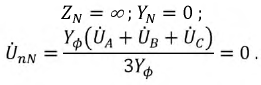
При симметричной нагрузке, как и в четырехпроводной схеме, фазы приемника работают независимо друг от друга и нулевой провод не нужен. Диаграмма в данном случае будет абсолютно той же, что и для четырехпроводной звезды.

2. Несимметричная нагрузка.

Пусть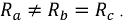

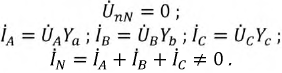
На векторно-топографической диаграмме токов и напряжений (рис. 4.10) показано суммирование фазных токов.

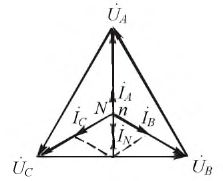
Рис. 4.10. Векторно-топографическая диаграмма для несимметричной нагрузки

Пусть 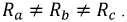Из-за неравенства проводимостей ветвей 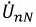не равно нулю, то есть между точкам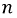и и 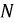появляется разность потенциалов – смещение нейтрали. При этом фазные напряжения на нагрузках уже не будут повторять систему фазных напряжений генератора. Поэтому задача сводится к расчету положения точки 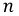на комплексной плоскости относительно 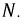Для его определения можно воспользоваться формулой узлового напряжения и теоретически ее рассчитать. Однако это можно сделать, основываясь на экспериментальных данных, суть которых состоит в следующем: производят измерения напряжений на фазах нагрузки; в выбранном масштабе для напряжений проводят дуги окружностей радиусами, равными измеренным фазным напряжениям из точек Точка пересечения этих трех дуг и даст искомое местоположение точки внутри треугольника, ограниченного линейными напряжениями (рис. 4.11).

Рис. 4.11. Определение смещения нулевой точки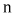

Соединив точк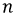и и отрезком, получим смещение нейтрали. По найденным фазным напряжениям приемника направляем векторы токов. Должно выполняться равенство:

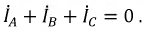
По результатам выполненных построений можно сделать главный вывод: если заведомо известно, что нагрузка несимметрична или может таковою стать, необходимо использовать четырехпроводную схему.

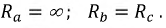
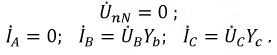
Векторная диаграмма (рис. 4.12) иллюстрирует работу четырехпроводной системы.

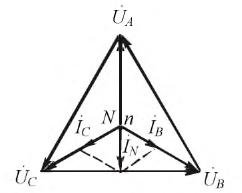
Рис. 4.12. Векторно-топографическая диаграмма для обрыва фазы в четырехпроводной системе

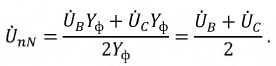
Напряжение смещения 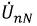можно также определить методом засечек, как это показано на рис. 4.13.

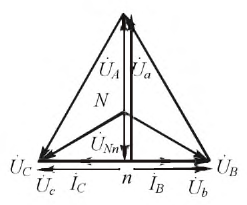
Рис. 4.13. Векторно-топографическая диаграмма для обрыва фазы в трехпроводной системе

По первому закону Кирхгофа:

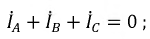
Поскольку 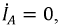то

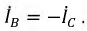
Токи в фазах 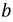и 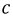должны находиться в противофазе.

4. Короткое замыкание фазы.

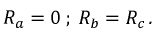
В четырехпроводной системе при коротком замыкании фазы приемника получаем короткое замыкание фазы источника.

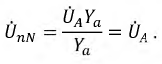
Фазные напряжения приемника:

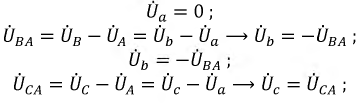
т.е. фазные напряжения увеличились до линейных напряжений, соответственно, токи в фазах:

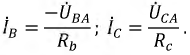
возросли в 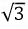раз. Ток в закороченной фазе определится по первому закону Кирхгофа:

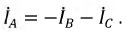
Построение векторно-топографической диаграммы для короткого замыкания показано на рис. 4.14.

5. Разнородная нагрузка.

Общий принцип построения векторных диаграмм токов и топографических диаграмм напряжений остается тем же. Единственное отличие будет состоять в появлении фазовых сдвигов между токами и напряжениями на фазах нагрузки в зависимости от ее характера.

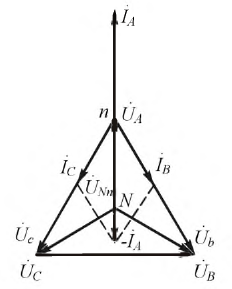
Рис. 4.14. Векторно-топографическая диаграмма для короткого замыкания фазы 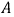в трехпроводной системе

По схеме трехпроводной звезды включают трёхфазные симметричные приемники, например, трёхфазные асинхронные и синхронные двигатели.

Соединение потребителей треугольником

Рассмотрим различные режимы работы приемника при соединении его фаз треугольником (рис. 4.15).

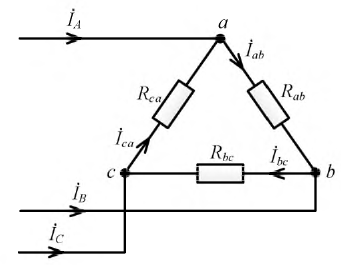
Рис. 4.15. Соединение фаз приемника треугольником

Вновь будем считать, что в качестве потребителей в фазах включены активные сопротивления (для простоты построений).

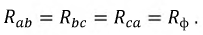
На рис. 4.7 построена векторная диаграмма для симметричной нагрузки при соединении фаз приемника треугольником.

Токи равны по модулю и отличаются только по фазе:

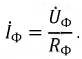
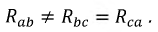
Фазы по-прежнему работают независимо друг от друга и поэтому токи будут:

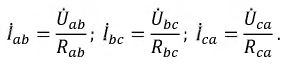
Линейные токи определяются соответственно по формулам (4.9). Векторная диаграмма представлена на рис. 4.16.

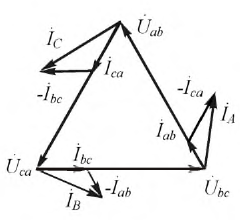
Рис. 4.16. Векторно-топографическая диаграмма для несимметричной нагрузки приемников, соединенных треугольником

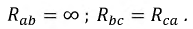
На рис. 4.17 построена векторная диаграмма при соединении приемников треугольником для обрыва фазы.

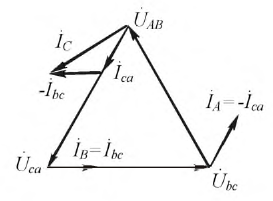
Рис. 4.17. Векторно-топографическая диаграмма для обрыва фазы при соединении приемников треугольником

Соотношения для токов:

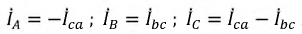
При разнородной нагрузке методика расчета не меняется.

Расчет мощности в трёхфазных цепях

Рассмотрим расчет мощности при соединении приемников по схеме четырехпроводной звезды и допустим, что нагрузка несимметрична. Если учесть, что сопротивление нейтрального провода не равно нулю и активное, имеем:

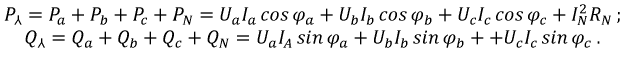
При симметричной нагрузке для трех- и четырехпроводной системы получим:

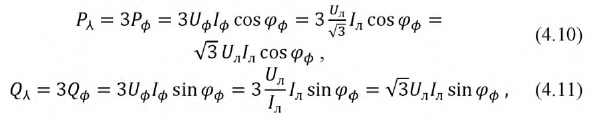
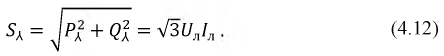
При соединении фаз приемника треугольником и несимметричной нагрузке имеем:

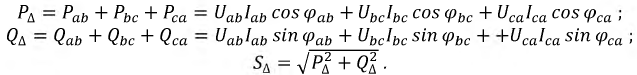
При симметричной нагрузке:

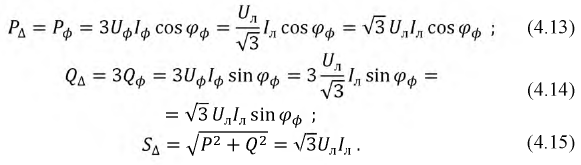
При этом необходимо учесть, что одинаковые формулы для расчета мощности при разном способе соединения фаз нагрузки (4.10-4.12) и (4.13- 4.15) не означают одинаковые численные значения.

Пример. Пусть трёхфазный приемник с сопротивлением фазы 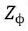соединен «звездой», тогда активная мощность будет:

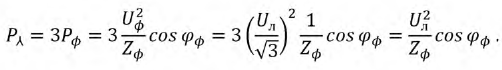
Теперь фазы того же приемника соединим «треугольником» и подключим к тому же трёхфазному источнику:

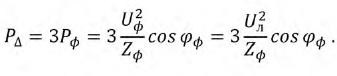
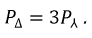
Измерение мощности в трёхфазных цепях

Для измерения активной мощности в симметричной трехфазной цепи достаточно одного ваттметра, включенного на измерение мощности одной из фаз.

Соединение приемников по схеме четырехпроводной звезды

В схеме (рис. 4.18) однофазные ваттметры включаются в каждую фазу, причем через токовые катушки протекают линейные токи, а катушки напряжения ваттметров включены между нулевым проводом и соответствующими линейными проводами.

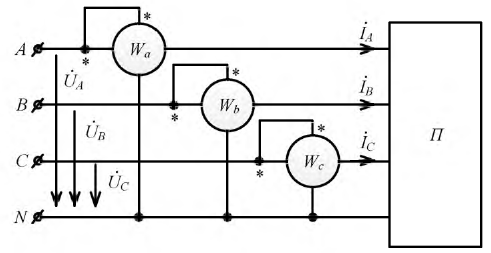
Рис. 4.18. Схема включения ваттметров для измерения мощности в четырехпроводной системе

Так как активная мощность – это вещественная часть полной мощности:

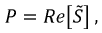
то суммарная мощность трех ваттметров может быть представлена выражением:

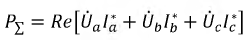
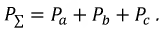
В случае симметричной нагрузки для измерения мощности, потребляемой ею, достаточно воспользоваться одним ваттметром, показание которого нужно утроить.

Соединение приемников по схеме трехпроводной звезды или треугольником

В этом случае измерить мощность трёхфазного приемника можно с помощью двух ваттметров (рис. 4.19).

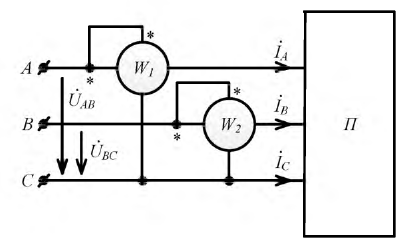
Рис. 4.19. Схема измерения активной мощности двумя ваттметрами

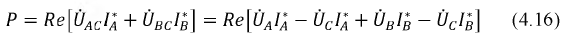
Если учесть, что:

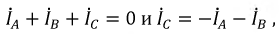
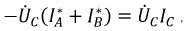
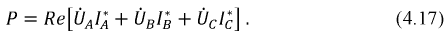
Оба ваттметра выполняются в одном корпусе, и прибор имеет две пары выводов для токовых катушек и две пары выводов – для катушек напряжения. Включают трёхфазный ваттметр по приведенной на рис. 4.19 схеме или по любой схеме с циклической заменой фаз.

Метод симметричных составляющих

Любую несимметричную трёхфазную систему можно разложить на три симметричные трёхфазные системы: прямой, обратной и нулевой последовательностей фаз. Такое разложение широко применяется при анализе работы трёхфазных машин и, в особенности, при расчете токов короткого замыкания в трёхфазных системах.

Пусть дана несимметричная трёхфазная система векторов 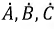(рис. 4.20).

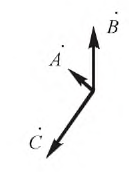
Рис. 4.20. Несимметричная трёхфазная система векторов

Каждый из векторов этой системы можно представить в виде суммы трех составляющих:

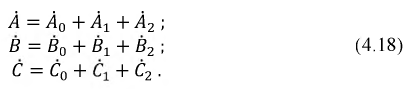
На рис. 4.21 изображены системы указанных выше последовательностей.

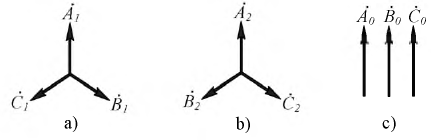
Рис. 4.21. Симметричные системы векторов прямой (a), обратной (b) и нулевой (с) последовательностей

Векторы прямой, обратной и нулевой последовательностей подчиняются следующим соотношениям:

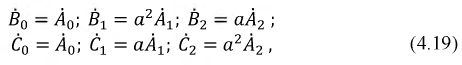
где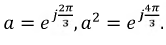

Коэффициент 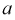называется поворотным множителем

Подставим соотношения (4.19) в систему уравнений (4.18). Тогда получим:

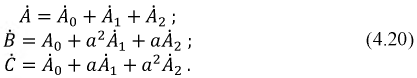
Решение системы уравнений (4.20) относительно 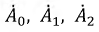дает:

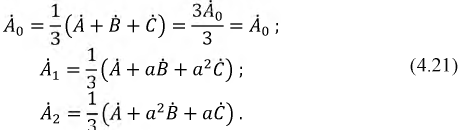
Симметричные составляющие можно определить графически, если на векторной диаграмме несимметричной системы векторов выполнить построения в соответствии с системой уравнений (4.21).

Фильтры симметричных составляющих

Симметричные составляющие несимметричных систем можно определить не только аналитически или графически, но и при помощи электрических схем, называемых фильтрами симметричных составляющих.

Эти фильтры применяются в схемах, защищающих электрические установки. Степень асимметрии системы токов и напряжений не должна превосходить известные пределы, т.е. составляющие нулевой и обратной последовательностей системы напряжений и токов при нормальных режимах должны быть меньше некоторых наперед заданных величин, определяемых для каждой конкретной установки индивидуально.

Возможность выделить при помощи электрических схем отдельные симметричные составляющие позволяет осуществить воздействие любой из них на приборы, защищающие установку, которые, будучи соответствующим образом отрегулированы, отключат или всю установку, или её часть, как только величина соответствующей составляющей превысит допустимый предел.

В качестве примера на рис. 4.22 приведены схемы фильтров нулевой последовательности линейных токов и фазных напряжений.

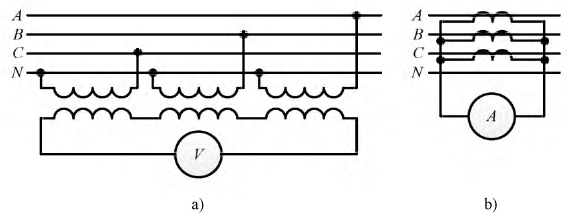
Рис. 4.22. Схемы фильтров нулевой последовательности

В схеме (рис. 4.22,a) вторичные обмотки трансформаторов напряжения включены последовательно и поэтому вольтметр определяет сумму фазных напряжений, т.е. утроенную составляющую нулевой последовательности системы фазных напряжений.

В схеме (рис. 4.22,b) вторичные обмотки трансформаторов тока включены параллельно и поэтому амперметр измеряет сумму линейных токов, то есть утроенную составляющую нулевой последовательности линейных токов.

Рекомендую подробно изучить предметы:

Электротехника Основы теории цепей

Ещё лекции с примерами решения и объяснением:

• Периодические несинусоидальные напряжения и токи в линейных цепях
• Нелинейные цепи переменного тока
• Переходные процессы
• Переходные процессы в линейных цепях
• Четырехполюсники
• Линейные диаграммы
• Круговые диаграммы
• Цепи с взаимной индукцией

При копировании любых материалов с сайта evkova.org обязательна активная ссылка на сайт www.evkova.org

Сайт создан коллективом преподавателей на некоммерческой основе для дополнительного образования молодежи

Сайт пишется, поддерживается и управляется коллективом преподавателей

Whatsapp и логотип whatsapp являются товарными знаками корпорации WhatsApp LLC.

Cайт носит информационный характер и ни при каких условиях не является публичной офертой, которая определяется положениями статьи 437 Гражданского кодекса РФ. Анна Евкова не оказывает никаких услуг.

§61. Схема соединения «треугольником»

При соединении фазных обмоток источника трехфазного тока «треугольником» (рис. 211, а) конец первой фазы АВ соединяется с началом второй фазы ВС, конец второй фазы соединяется с началом третьей фазы СА и конец третьей фазы — с началом первой АВ. Три линейных провода 1, 2 и 3, идущих к приемникам электрической энергии, присоединяются к началам А, В и С этих фаз. Точно так же могут соединяться и отдельные группы приемников Z_AB, Z_BC, Z_CA (фазы нагрузки). При этом каждая фаза нагрузки присоединяется к двум линейным проводам, идущим от источника, т. е. включается на линейное напряжение, которое одновременно будет и фазным напряжением. Таким образом, в схеме «треугольник» фазные напряжения Uф равны линейным Uл и не зависят от сопротивлений Z_AB, Z_BC, Z_CA фаз нагрузки.

Как следует из формулы (77), при соединении «треугольником» трех фазных обмоток генератора или другого источника переменного тока сумма э. д. с, действующая в замкнутом контуре, образованном этими обмотками, равна нулю. Поэтому в этом контуре при отсутствии нагрузки не возникает тока. Но каждая из фазных э. д. с. может создавать ток в цепи своей фазы.
Линейные токи в схеме «треугольник» согласно первому закону Кирхгофа для узлов А, В и С соответственно:

Переходя от мгновенных значений токов к их векторам, получим:

Следовательно, линейный ток равен векторной разности соответствующих фазных токов.

По полученным векторным уравнениям можно для равномерной нагрузки фаз построить векторную диаграмму (рис. 211,б), которую можно преобразовать в диаграмму (рис. 211, в), из которой

Рис. 211. Схема «треугольник» (а) и векторные диаграммы токов для этой схемы при равномерной нагрузке (б и в)

видно, что при равномерной нагрузке фаз векторы линейных токов ?_А, ?_B, ?_C образуют равносторонний треугольник ABC, внутри которого расположена трехлучевая звезда векторов фазных токов ?_АВ, ?_BC и ?_СА. Отсюда по аналогии с диаграммой рис. 207,б следует, что

т. е. при равномерной нагрузке фаз в схеме «треугольник» линейный ток больше фазного тока в ?3 раз.

Следовательно, при переключении приемников со «звезды» на «треугольник» фазные токи возрастают в ?3 раз, а линейные токи — в 3 раза. Возможность включения одних и тех же приемников по схеме «звезда» или «треугольник» расширяет область их применения. Например, если приемник рассчитан на фазное напряжение 220 В, то при соединении по схеме «треугольник» он может быть включен в сеть с линейным напряжением 220 В, а при соединении по схеме «звезда» — в сеть с линейным напряжением 220?3 = 380 В. Приемники, рассчитанные на фазное напряжение 127 В, могут работать в сетях с линейными напряжениями 127 и 127?3= 220 В.

Особенности подвода трехфазного тока к приемникам. В трех-проводной трехфазной сети (при схемах «звезда без нулевого провода» и «треугольник») алгебраическая сумма мгновенных значений линейных токов в любой момент времени равна нулю, поэтому такие токи совместно не создают магнитного поля. Это позволяет прокладывать три линейных провода в одной общей металлической трубе или в кабеле с металлической оболочкой без опасности образования вихревых токов. Не допускается прокладка линейных проводов по отдельности в металлических трубах, так как возникающие вихревые токи вызывали бы сильный нагрев металла. То же самое происходило бы при прокладке в кабеле с металлической оболочкой или в трубе трех линейных проводов при схеме «звезда с нулевым проводом», так как сумма токов в них не равна нулю.

[spoiler title=”источники:”]

http://www.evkova.org/trehfaznyie-tsepi

[/spoiler]

П

Рис. 3. 11. 3.12.

ри соединении треугольником (рис.
4.11.) каждая фаза приемника подключена
к двум линейным проводам, поэтому каждое
фазное напряжение равно соответствующему
линейному напряжению.

Таким образом,
соединение треугольником следует
применять тогда, когда каждая фаза
трехфазного приемника рассчитана на
напряжение, равное номинальному линейному
напряжению сети.

Рис. 4.11.

Фазные токи
,,в общем случае не равны линейным токам,,и могут быть найдены по следующим
соотношениям:

,
,.

Линейные токи
,,могут быть определены через значения
фазных токов. Из первого закона Кирхгофа
запишем:

,
,.

Использую указанные
соотношения и имея векторы фазных токов,
можно построить векторную диаграмму
линейных токов (рис. 4.12.).

При симметричной
нагрузке соединением «треугольник»
равны в отдельности активные и полные
реактивные сопротивления всех фаз
,

Однако, как правило,
однофазные приемники подключаются не
одновременно. Нагрузку можно считать
симметричной лишь тогда, когда включены
все приемники. Для каждой фазы могут
быть использованы все методы расчета,
рассмотренные ранее применительно к
однофазной цепи с одним источником.
Зная, например, фазные напряжения и
сопротивления, можно по закону Ома найти
фазные токи по формулам
,,

При симметричной
нагрузке,
,-фазные токи равны друг другу и сдвинуты
по фазе относительно соответствующих
фазных напряжений на одинаковые углы.

В

Рис. 3. 13.

екторная диаграмма фазных напряжений
и токов на рис. 4.13. показывает, что при
симметричной нагрузке векторы фазных
токов равны по величине и сдвинуты по
фазе относительно друг друга на угол.

Векторы линейных
токов
изображают результирующими векторов
фазных токов, как показано на рис. 4.13.
Из векторной диаграммы следует, что_.

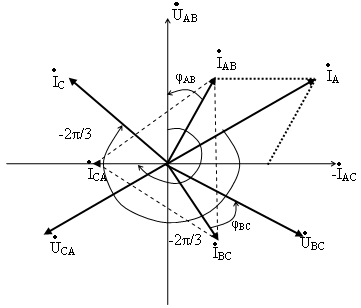
Рис. 4.13.

Такое же соотношение
существует между любыми другими фазными
и линейными токами. Поэтому можно
написать, что при симметричной нагрузке

_.

Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы АВ будут равны

Таким же путем
находим мощности фаз ВС и СА. В силу
равенства напряжений, токов, углов
сдвига фаз и сопротивлений при симметричной
нагрузке
,,.

При симметричной
нагрузке активная Р,
реактивная Q
и полная S
мощности трехфазного приемника
,,

.

В качестве
номинальных напряжений и токов трехфазных
приемников указываются обычно линейные
напряжения и токи. Учитывая это, мощности
трехфазных приемников желательно также
выражать через линейные напряжения и
токи
,,_.

4.6. Несимметричные нагрузки при соединении треугольником

Несимметричной
нагрузкой считают такую, при которой
активное или реактивное сопротивление
хотя бы одной из фаз не равно сопротивлениям
других фаз (рис. 4.14.) r_AB
= r_BC
= r_C;
X_AB=X_BC≠X
_CA.
В таком
случае при несимметричной нагрузке Z_AB
≠ Z_BC
≠ Z_CA.

Фазные токи, углы
сдвига фаз между фазными напряжениями
и токами, а также мощности могут быть
определены по формулам

,
,

Так как,
а при несимметричной нагрузкеZ_AB
≠ Z_BC
≠ Z_CA,
то.

Рис. 4.14.

Углы сдвига фаз
между фазными токами и напряжениями
зависят от величины и характера
сопротивлений фаз и могут быть определены
следующим образом
;;.

Т.о., при несимметричной
нагрузке фазные токи, углы сдвига фаз
и фазные мощности в общем случае
различные.

Зная фазные
напряжения, токи и углы сдвига фаз между
ними, либо токи и сопротивления, можно
найти фазные мощности. Например, мощности
фазы AB

Активные и реактивные
мощности приемника
;
.

Векторная диаграмма
при несимметричной нагрузке для случая,
когда в фазе AB
имеется активное сопротивление, в фазе
BC
– активное и индуктивное сопротивления,
фазе CA
– активное и емкостное сопротивления,
приведена на рис. 4.15. Построение векторов
линейных токов произведено в соответствии
с выражениями
,
,.

Если
кроме фазных токов, требуется определить
линейные токи, то их можно так же
определить по векторной диаграмме, не
прибегая к решению задачи в комплексной
форме.

Рис. 4.15.

О

Рис. 3. 15.

тключение нагрузки одной из фаз
можно считать частным случаем
несимметричной нагрузки, при которой
сопротивление отключенной фазы равно
бесконечности. Так при отключении фазыCA
сопротивление Z
_CA
= ∞. При этом, ток
;
фазные токи,
а также углыφ_AB,
φ _BC
не изменятся, а линейные токи
уменьшатся и будут равны
,
_.

Пример 20. Расчет потребителя при соединении в треугольник

Три одинаковых лампы накаливания включены треугольником. Сопротивление каждой лампы 484 Ом. Вольтметр показывает напряжение 220 вольт. Определить фазные и линейные токи в схеме. Найти мощность, потребляемую всей схемой.

Рис. 88. Схема к примеру 20.

Соединение ламп накаливания в треугольник

Вольтметр подключён между линейными проводами и показывает линейное напряжение. Оно в треугольнике равно фазному и равно 220В.

Сопротивление каждой фазы потребителя R_ф равно сопротивлению лампы R_л. Фазные токи можно найти по закону Ома:

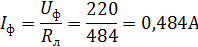
Линейный ток в каждой фазе найдём по формуле:

I_л= I_ф=1,73*0,484=1,15А.

Общая мощность, потребляемая схемой, равна утроенной мощности одной фазы, т.к. нагрузка равномерная:

42. Формулы для определения активной мощности трёхфазной системы при равномерной и неравномерной нагрузке.

Мощность в трёхфазной системе

Активную мощность, потребляемую одной фазой трёхфазного потребителя, можно найти по формуле, рассмотренной при изучении темы «однофазный переменный ток»

В случае равномерной нагрузки мощность всех фаз одинакова, поэтому общая мощность можно найти, утроив мощность одной фазы

Если же нагрузка неравномерная, придётся вычислить мощность каждой фазы отдельно и, затем, найти сумму мощностей всех фаз

Для случая активной нагрузки (рис. 80), коэффициент мощности (cosφ) равен единице. Если же в фазе потребителя включена цепочка RLили RC, то коэффициент мощности можно найти по формуле

cosφ=R/Z, гдеZ =

Пример 18. Расчёт мощности потребителя при соединении звездой

По данным примера17 определить мощность, потребляемую всеми тремя лампами

В любой электрической схеме, в том числе в трехфазной системе, общая мощность равна сумме мощностей, потребляемых элементами схемы. Поскольку мощность каждой из ламп известна, общая мощность трёхфазной системы

Пример 19. Расчёт тока, потребляемого трёхфазным электродвигателем, по его параметрам

Трёхфазный электродвигатель, обмотки которого соединены звездой, подключён к стандартной трёхфазной сети с линейным напряжением U_л =380 В. Частота тока в сети — 50 Гц.

Известны паспортные данные двигателя: механическая мощность двигателя 4,2 КВт, КПД=h=0,72 (72%), коэффициент мощности – cosj =0,85.

Определить: а) фазные токи, потребляемые двигателем; б) параметры обмотки двигателя.

А) Найдем ток, потребляемый каждой обмоткой двигателя.

На статоре трёхфазного двигателя уложено три обмотки. Каждая обмотка представляет собой реальную катушку индуктивности и изображена на схеме в виде цепочки RL, т.е. как последовательное соединение активного сопротивления и индуктивности.

Рис. 86. Схема включения обмоток двигателя к примеру 19.

В паспортных данных двигателя указана механическая мощность P₂ (мощность на валу двигателя). Для расчёта электрических параметров двигателя необходимо знать электрическую мощность P₁, потребляемую двигателем от трёхфазной питающей сети.

Механическая (полезная) мощность P₂ всегда меньше, чем электрическая мощность P₁, потребляемая от сети. По формуле КПД найдем электрическую мощность, потребляемую двигателем.

Р_эл= Р_мех /h =4200 / 0,72 = 5833 Вт.

По формуле мощности трёхфазной системы найдём ток, потребляемый одной фазой двигателя:

Фазное напряжение U_ф, необходимое для расчётанайдено, зная соотношение между линейным и фазным напряжением, по формуле:

U_ф = U_л / =220 В.

Б) Находим параметры обмотки двигателя: её активное сопротивление и индуктивность.

Полное сопротивление фазы двигателя, т.е. полное сопротивление такой катушки можно найти из закона Ома для реальной катушки, зная напряжение на фазе и ток фазы:

Зная соотношения для реальной катушкииндуктивности, найдём активную и реактивную составляющие полного сопротивления фазы двигателя:

R_ф = Z_ф* cosj =21,15 * 0,85 = 18 Ом.

X_L =

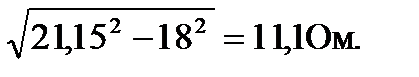
Из формулы индуктивного сопротивления катушки найдём индуктивность фазы двигателя:

L = X_L/ 2pf = 11,1 / 2*3.14*50 = 0,035 Гн.

Источник

Расчёт трёхфазного потребителя по схеме «треугольник»

Соединение приемников треугольником. При соединении трехфазного по-

требителя по схеме «треугольник» начало одной фазы потребителя соединяют

с концом другой.

При соединении приемника треугольником фазные напряжения равны линей-

ным U_Л =U_Ф , а линейные токи определяют по первому закону Кирхгофа:

Фазные токи рассчитывают по за закону Ома:

Топографическая диаграмма фазных и линейных напряжений представляет со-

бой замкнутый треугольник. Векторную диаграмму токов совмещают с топо-

графической диаграммой напряжений.

При симметричной нагрузке токи во всех фазах одинаковы и связаны с линейными токами по формуле:

3) Работа и мощность электрического тока. Энергетический баланс в электрических цепях. В электротехнике существует понятие мощности источника и мощности потребителя. Мощность источника – это скорость, с которой неэлектрическая энергия в источнике преобразуется в электрическую Рист. = А/t = ЕIt/t = EI

Мощность потребителя (приемника) – это скорость, с которой в приемнике

электрическая энергия переходит в неэлектрическую.

Рпот.= А/t = U I t/t =U I = I 2 R В любой электрической цепи должен соблюдаться энергетический баланс – алгебраическая сумма мощностей всех источников должна быть равна арифметической сумме мощностей всех потребителей энергии: Это равенство называют балансом мощности электрической цепи:

Если направление ЭДС источника совпадает с направлением тока, то он работает в режиме генератора, т.е. поставляет электрическую энергию в цепь. Его ЭДС имеет знак плюс. Если направление ЭДС противоположно направлению тока, то он работает в режиме потребителя, т.е. потребляет электрическую энергию. Его ЭДС имеет знак минус. В

уравнении баланса мощности нужно учитывать знак ЭДС источника.

2) Режимы работы источников питания. Различают четыре режима работы источников питания.

Режим холостого хода.хх.В режиме холостого хода выводы источника разомкнуты: (Rх= ∞). Этот режим используют для измерения ЭДС источника. Параметры

режима холостого хода:

Iхх = 0; Rхх = ∞; Uхх = E ; (Uхх =E-Ir; r = 0; Uхх = E )

Режим короткого замыкания. К.з. В режиме короткого замыкания выводы источника замкнуты сами на себя: ( Rк.з= 0). ;

Номинальный режим. Это режим работы источника питания при номинальных значениях тока и напряжения. Номинальные значения тока и напряжения

приводятся в паспорте источника питания.

Согласованный режим. Это режим работы источника питания с максимальной мощностью Р=Р mах. При условии R=R Формула мощности для согласованного режима: P_max= I 2 R = E 2 / 4R.

9) Рассмотрим цепь с последовательно соединенными активным сопротивлением — R , индуктивностью –L и емко-

стью – С. Для векторов действующих напряжений .

запишем второй закон Кирхгофа:

Складывая эти вектора графически и, учитывая, что вектор напряжения на

Ū_R совпадает по фазе с вектором тока, вектор на-

пряжения на индуктивности — Ū_L опережает ток на угол π/2, а вектор напряжения на емкости — Ū_C отстает от вектора тока на угол π/2, получим прямоугольный треугольник напряжений, гипотенуза которого равна полному напряжению — U , а катеты равны активному напряжению — Ū_R и реактивному

Из треугольника напряжений видно, что:

U = Если разделить все стороны прямоугольного треугольника напряжений на общий ток I , то получим подобный ему треугольник сопротивлений, гипотенуза

которого равна полному сопротивлению цепи — Z , а катеты — активному и ре-

активному сопротивлению цепи — R и ( X_L — X_C) :

Из этого треугольника можно найти полное сопротивление цепи

и записать закон Ома для цепи переменного синусоидального тока:

1)Эквивалентные преобразования электрических цепей.

Последовательное соединение элементов. При последовательном соединении

элементов через все элементы протекает один и тот же ток; напряжение на

входе цепи равно сумме напряжений на элементах. Последовательное соединение элементов можно заменить одним эквивалентным сопротивлением.

Напряжение на сопротивлениях распределяется прямо пропорционально этим

Параллельное соединение. При параллельном соединении все участки цепи соединяются к одной паре узлов и находятся под воздействием одного и того

же напряжения. Ток на входе цепи равен сумме токов на параллельных участках цепи. Параллельное соединение элементов можно заменить одним эквивалентным

При параллельном соединении элементов токи в них распределяются обратно

пропорционально их сопротивлениям:

Смешанное соединение. Это сочетание последовательного и параллельного

Эквивалентное сопротивление для последовательно-параллельного соединения

Сложное соединение. Это соединение, имеющее три и более узлов. В сложных цепях встречаются соединения сопротивлений в виде звезды и треугольника.

Формулы преобразования треугольника сопротивлений в эквивалентную трех-

лучевую звезду имеют вид:

Формулы обратного преобразования ветвей трехлучевой звезды в эквивалент-

Источник

Соединение потребителей электрической энергии в треугольник

При соединении фаз электроприемников в треугольник каждая фаза будет подключена к двум линейным проводам, как показано на рисунке ниже:

Поэтому при таком типе соединения, обратно звезде, независимо от характера и значения сопротивления приемника каждое фазное напряжение будет равно линейному, то есть U_Ф = U_Л. Если не брать во внимание сопротивления фазных проводов, то можно предположить, что напряжения источника и приемника электрической энергии равны.

На основании приведенной выше схемы и формулы можно сделать вывод, что соединение фаз приемников электрической энергии в треугольник следует применять тогда, когда каждая фаза трехфазного или двухфазного потребителя электрической энергии рассчитана на линейное напряжение сети.

В отличии от соединения звездой, где фазные и линейные токи равны, при соединении треугольником они равны не будут. Применив первый закон Кирхгофа к узловым точкам a, b, c получим соотношение между фазными и линейными токами:

Имея векторы фазных токов, используя данное соотношение, не трудно построить векторы линейных токов.

Симметричная нагрузка при соединении приемников треугольником

В отношении любой фазы можно применять формулы, которые справедливы для однофазных цепей:

Очевидно, что при симметричной нагрузке:

Векторная диаграмма фазных (линейных) напряжений и токов при активно-индуктивной симметричной нагрузке показана ниже:

В соответствии с формулой (1) были построены векторы линейных токов. Также стоит обратить внимание на то, что при построении векторных диаграмм для соединения треугольник вектор линейного напряжения U_ab принято направлять вертикально вверх.

Векторы линейных токов часто изображают соединяющими векторы фазных токов, как это показано на рисунке b):

На основании данной векторной диаграммы можно записать: . Такое же соотношение справедливо и для других фаз. Исходя из этого, можно вывести формулу зависимости между фазным и линейным током для соединения фаз потребителей треугольником при симметричной нагрузке .

Пример

Трехфазная сеть имеет линейное напряжение U_Л = 220 В. К ней необходимо подключить трехфазный электроприемник с фазным напряжением в 220 В и содержащим последовательно подключенные активное r_ф = 8,65 Ом и индуктивное x_ф = 5 Ом сопротивления.

Решение

Поскольку линейные и фазные напряжения в этом случае будут равны, то выбираем способ соединения обмоток потребителя в треугольник.

Линейные и фазные токи, а также полные сопротивления фаз будут равны:

Активная, реактивная и полная мощности электроприемника любой фазы будут равны:

Векторные диаграммы приведены выше.

Несимметричная нагрузка при соединении приемников треугольником

В случае несимметричного сопротивления фаз, как и при соединении в звезду, для подключения к сети электроприемники разбивают на три примерно одинаковые по мощности группы. Подключение каждой группы производится к двум фазным проводом, у которых есть отличия по фазе:

В пределах каждой группы подключение приемников производится параллельно.

После замены сопротивления нескольких приемников в одной фазе на одно эквивалентное получим такую схему:

Углы сдвига между напряжением и током, мощности и фазные токи можно найти из формулы (2). В случае несимметричной нагрузки (в нашем случае схема выше) фазные мощности, токи, а также углы сдвига (cos φ) не будут равны. Векторная диаграмма для случая, когда фаза ab имеет активную нагрузку, bc – активно-индуктивную, ca – активно-емкостную, показана ниже:

Для определения суммарной мощности всех фаз нужно применять выражение:

Пример

Дана несимметричная электрическая цепь, включенная по схеме выше, с параметрами: U_Л = 220 В, r_ab = 40 Ом, x_Lbc = 10 Ом, r_bс = 17,3 Ом, x_cа = 5 Ом, r_Ccа = 8,65 Ом. Нужно определить линейные и фазные токи, а также мощности.

Решение

Воспользовавшись выражением для определения комплексных значений получим:

Комплексные значения полных сопротивлений фаз: Z_ab = 40 Ом, Z_bс = 17,3 + j10 Ом, Z_bс = 8,65 – j5 Ом.

Комплексные и действующие значения линейных и фазных токов:

Дольше можно проводить расчеты, не прибегая к комплексному методу:

Общие активные и реактивные мощности:

Углы сдвига между токами и напряжениями:

Векторная диаграмма для несимметричного треугольника приводилась выше.

Источник

Расчет мощности трехфазной сети

Количество потребленной энергии в сети однофазного тока определяется простейшими расчетами, это не вызывает затруднений. Расчет мощности трехфазной сети сопряжен с некоторыми трудностями:

• Наличие трех фаз вместо одной;
• Различные схемы соединения потребителей – «звезда» или «треугольник»;
• Симметрия или ее отсутствие при распределении нагрузки по фазам.

Как узнать свою схему

Для правильного определения и расчета мощности требуется знание нескольких факторов:

• Количества фаз питания;
• Способа соединения потребителей.

При однофазном подключении используется два провода:

• Фазный провод;
• Нулевой провод.

Для трехфазной сети характерно наличие трех или четырех проводников (подключение с заземленной нейтралью). При этом используется две различных схемы включения:

• «Треугольник». Каждая нагрузка подсоединяется с двумя соседними. Напряжение каждой фазы подводится к точкам соединения потребителей.
• «Звезда». Все три потребителя соединяются в одной точке. Ко вторым концам подключаются фазы питания. Это схема с изолированной нейтралью. В схеме с заземленной нейтралью точка соединения потребителей подключается к нулевому проводнику.

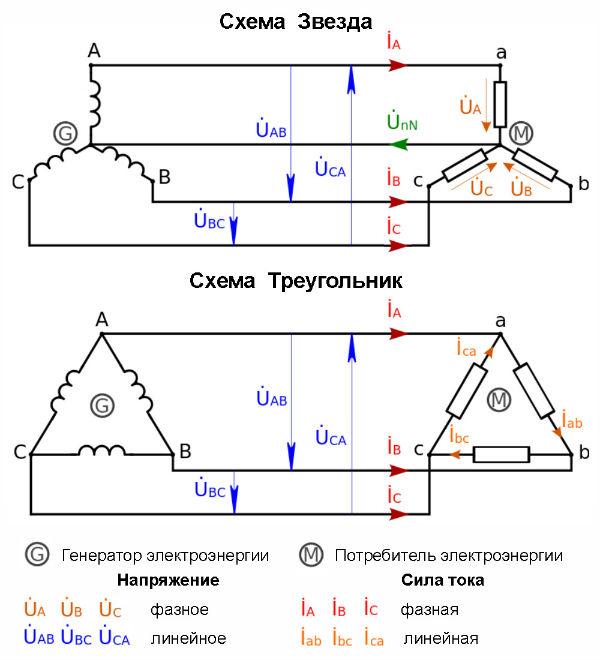
Трёхфазное или однофазное подключение

В зависимости от того, какой тип подключения используют, определение потребляемой мощности производится по-разному.

В однофазной сети потребляемая энергия считается по простейшей формуле:

где cosϕ – коэффициент мощности, характеризующий сдвиг фаз между током и напряжением в реактивной нагрузке.

Мощность 3 х фазной сети является суммой потребления по каждой фазе в отдельности. Формула мощности 3 х фазного тока имеет следующий вид:

Pобщ=Uа∙Iа∙cosϕа+ Ub∙Ib∙cosϕb+ Uc∙Ic∙cosϕc,

где U, I, cosϕ – напряжение, сила тока и коэффициент мощности в каждой фазе, соответственно.

К сведению. Видно, что в общем случае трехфазное соединение требует большее количество приборов учета.

Иногда посчитать потребление энергии можно по упрощенному варианту. При симметричном потреблении, например, при подключении асинхронного двигателя, токи потребления одинаковы, и формула принимает следующий вид:

где:

• Uф, Iф – фазные напряжение и ток;
• Uл, Iл – линейные напряжение и ток.

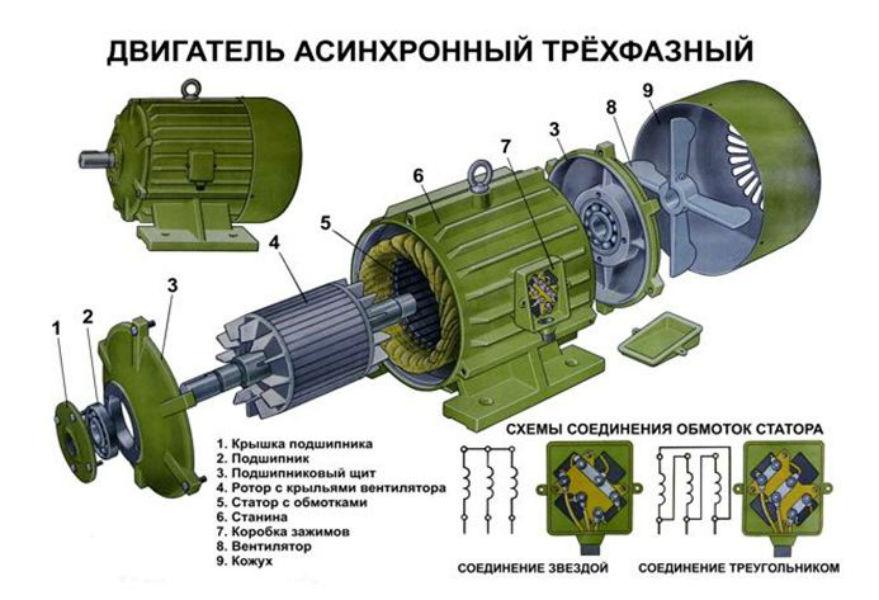
Характеристики трехфазной системы

Трехфазная система электропитания характеризуется несколькими значениями напряжения и тока. Все зависит от того, между какими точками схемы производятся измерения:

• между фазным проводом и нейтралью – фазное напряжение Uф;
• между отдельными фазами – линейное Uл.

Соотношение между данными параметрами:

При симметричном распределении нагрузки токи во всех проводах равны. В четырехпроводной схеме (с заземленным нулем) ток в нулевом проводнике отсутствует, поэтому даже при обрыве нуля сеть продолжает нормально функционировать.

В том случае, когда потребление энергии по фазам различается, в нейтральном проводе протекает некоторый ток. Полный обрыв нейтрального проводника вызывает перекос фаз, поэтому напряжение на проводах может измениться в диапазоне от нуля до линейного.

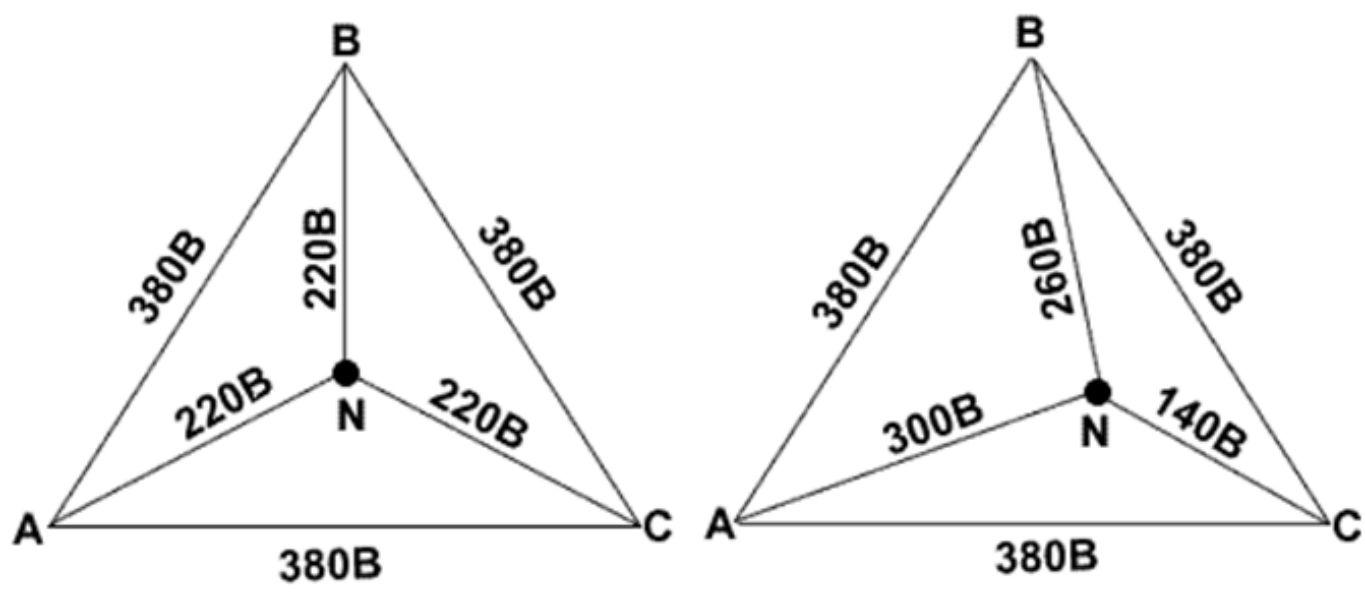
Реактивный характер нагрузки учитывается коэффициентом мощности cosϕ. Данная величина пришла из теории комплексных чисел, которые используются, когда необходимо рассчитать параметры цепей переменного тока. В случае активной нагрузки cosϕ=1, но, чем более реактивный характер имеют потребители, тем больше коэффициент уменьшается, показывая, как снижается реальная мощность относительно полной.

Важно! Поэтому для правильного расчета и уменьшения нагрузки на генераторное оборудование в реактивных цепях устанавливают корректоры коэффициента мощности. Цепи с корректором приближают коэффициент cosϕ к единице.

Пример расчёта мощностных показателей

Наиболее простым примером может считаться расчет потребления энергии симметричной нагрузкой. Сколько будет потреблять электроэнергии трехфазный асинхронный двигатель, подключенный в сеть с линейным напряжением 380 В, и потребляющий ток 10 А по каждой фазе? Коэффициент мощности cosϕ=0.76. Тогда потребляемая мощность равна:

Более сложный расчет бытовой сети:

• Фазное напряжение – 220 В;
• Потребление по линиям – 10 А, 5 А, 2 А;
• Первые две фазы подключены к активной нагрузке (электроплита, чайник);
• Третья нагружена на люминесцентные светильники с cosϕ=0,5.

Pобщ=Uа∙Iа∙cosϕа+ Ub∙Ib∙cosϕb+ Uc∙Ic∙cosϕc=220∙10+220∙5+220∙2∙0,5=3520 ВА.

Используя онлайн калькулятор расчетов, можно избавиться от большинства ошибок и сократить время вычислений. Требуется лишь правильно ввести данные по текущим параметрам

Измерение мощности ваттметром

Мощность потребления трехфазного тока измеряют, используя ваттметры. Это может быть специальный ваттметр, для 3-х фазной сети, либо однофазный, включенный по определенной схеме. Современные приборы учета электроэнергии часто выполняются по цифровой схемотехнике. Такие конструкции отличаются высокой точностью измерений, большими возможностями оперирования с входными и выходными данными.

Варианты измерений:

• Соединение «звезда» с нулевым проводником и симметричная нагрузка – измерительный прибор подключается к одной из линий, считанные показания умножаются на три.
• Несимметричное потребление тока в соединении «звезда» – три ваттметра в цепи каждой фазы. Показания ваттметров суммируются;
• Любая нагрузка и соединение «треугольник» – два ваттметра, подключенных в цепь любых двух нагрузок. Показания ваттметров также суммируются.

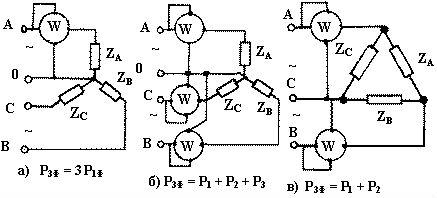
На практике всегда стараются выполнить нагрузку симметричной. Это, во-первых, улучшает параметры сети, во-вторых, упрощает учет электрической энергии.

Видео

Источник

Содержание:

Индуктивность и ее расчет:

Основным соотношением для магнитного поля является принцип непрерывности магнитного потока: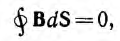

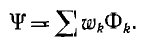
На рис. 1.12, а и б проиллюстрировано различие между потоком и
потокосцеплением, причем число линий в условном масштабе равно
величине потока.

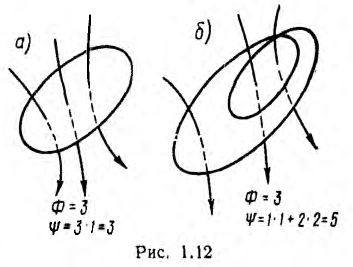
Индукция измеряется в тесла (тл), магнитный поток и потокосцепление — в веберах (вб).
Индуктивность уединенного контура, равная отношению потокосцепления к току:

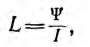
пропорциональна магнитной проницаемости среды, в которой он находится, и определяется конфигурацией контура. Единицей индуктивности является генри (гн).
Для расчета индуктивности контура необходимо предварительно рассчитать его магнитное поле по основному соотношению — закону полного тока:

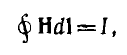
устанавливающему связь между напряженностью магнитного поля 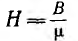и полным током I — алгебраической суммой токов, сцепляющихся с путем интегрирования. При этом положительное направление тока I связано с направлением dI обхода правилом правого винта.
Напряженность магнитного поля измеряется в а/м, магнитная проницаемость — в гн/м.
Если потокосцепление контура изменяется во времени, то в контуре появляется э. д. с. индукции е, величина и направление которой определяется законом электромагнитной индукции:

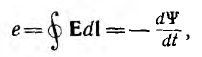
где Е — вектор напряженности наведенного в контуре электрического поля.
Таким образом, закон электромагнитной индукции связывает между собой изменение магнитного поля с возникающим электрическим полем.
Максвеллом было постулировано обобщение этого закона, заключающееся в том, что электрическое поле возникает при изменении магнитного поля в любой среде, а не только в проводящем контуре.

Закон электромагнитной индукции, открытый Фарадеем в 1831 г., был дополнен Ленцем в 1832— 1834 гг. Им было установлено общее правило: з. д. с. индукции всегда стремится создать ток, направленный так, чтобы препятствовать изменению потока, сцепляющегося с контуром.
При изменении тока в контуре изменяется потокосцепление ψ_L созданное этим током, и в контуре наводится э. д. с. самоиндукции

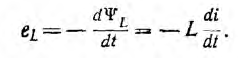
Индуктивность тороида и соленоида

Если на кольцевой сердечник — тороид, выполненный из материала проницаемостью µ > µ₀, нанести обмотку не по всей его длине (рис. 1.13), то только часть потока проходит по сердечнику, остальная часть — поток рассеяния — замыкается в воздухе. Тороид же, содержащий витки, плотно и равномерно распределенные по всей длине сердечника (рис. 1.14), замечателен тем, что практически весь магнитный поток сосредоточивается в сердечнике, т. е. потока рассеяния нет. Линии вектора напряженности поля представляют собой окружности, сцепляющиеся со всеми витками. Ввиду симметрии напряженность поля в каждой точке окружности по величине постоянна; по направлению она совпадает с касательной к окружности.

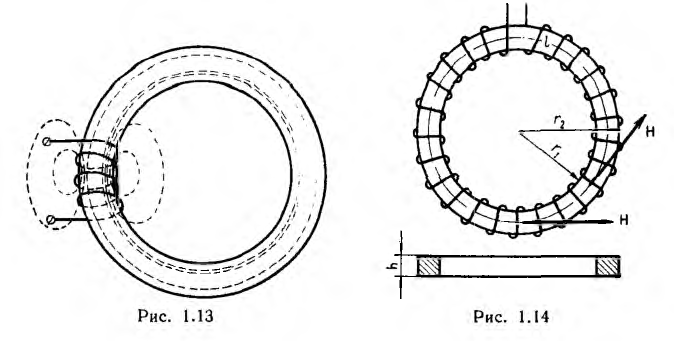
Тороиды широко применяются в трансформаторах, магнитных усилителях и электроизмерительных приборах.

Пусть тороид имеет прямоугольное сечение высотой Н, с радиусами г₁ и г₂, магнитная проницаемость материала µ.

По закону полного тока для окружности с радиусом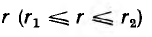

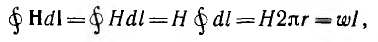
откуда

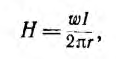
т. е. напряженность поля убывает по мере приближения к наружному краю тороида. Это в равной мере относится и к индукции

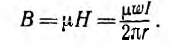
Поток в сердечнике тороида

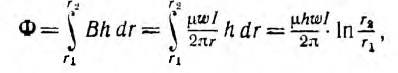
а потокосцепление

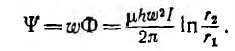
Отсюда индуктивность тороида

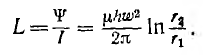
Если расчет вести для средней линии I и приближенно считать поле в тороиде распределенным равномерно, то напряженность

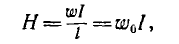
где w₀ — число витков на единицу длины, а магнитный поток и индуктивность, соответственно,

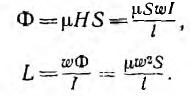
Обычно в реальных тороидах отношение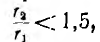 что приводит при этих приближенных формулах к погрешности, не превышающей 1,2 %. Последняя формула для индуктивности может быть применена и к длинному соленоиду, рассматриваемому как часть тороида бесконечно большого радиуса. Для соленоида конечной длины µ=µ₀

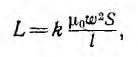
где k < 1 — коэффициент, учитывающий, что в таком соленоиде не весь поток пронизывает все витки.

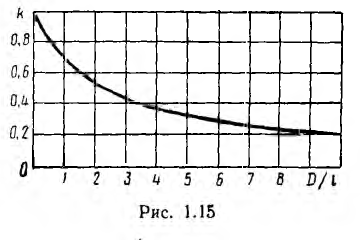
Как показывает точный расчет, этот коэффициент зависит от отношения диаметра D катушки к ее длине I (рис. 1.15). При 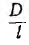= 0,1 коэффициент k — 0,96, поэтому при 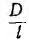< 0 ,1 приближенно принимают k = 1.

Индуктивность двухпроводной линии

Двухпроводная линия (рис. 1.16, а) состоит из двух параллельных проводов одинакового радиуса г₀, имеющих большую длину I по сравнению с расстоянием d между ними. Магнитная проницаемость материала проводов (г, окружающей среды — µ₀. Токи I в прямом и обратном проводах отличаются лишь направлением; начало координат взято в центре сечения левого провода.

Для отдельного провода ввиду его осевой симметрии, при пренебрежении искажением поля у его концов, применение закона полного тока к окружности радиуса 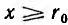дает:

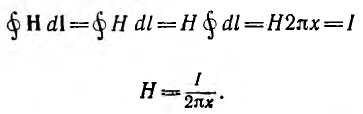
При интегрировании по окружности, лежащей внутри отдельного провода 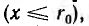охватывается лишь часть L_Х всего тока, протекающая внутри круга радиуса х, равная при равномерном распределении тока по сечению

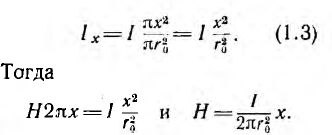
В воздухе между проводами на линии, соединяющей центры их сечений 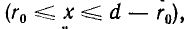направления полей, создаваемых обоими токами согласно правилу правого винта, совпадают и напряженности поля и индукции складываются:

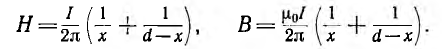
Эти же формулы справедливы и для 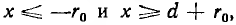т. е. снаружи линии, но здесь они дают разность полей.

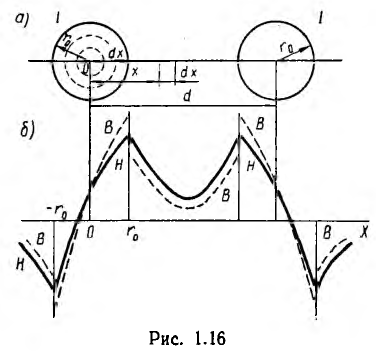
Внутри левого провода линии напряженность поля и индукция от обоих проводов будут:

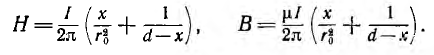
Внутри правого провода 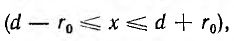соответственно,

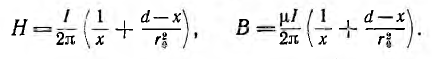
На рис. 1.16, б представлено распределение напряженности поля и индукции вдоль оси х для магнитной проницаемости материала проводов µ > µ₀. Посередине между проводами поле минимально, но в нуль не обращается. Поле также не равно нулю на осях проводов.

На внутренней стороне проводов напряженность поля и индукция больше, чем на внешней. В отличие от напряженности поля индукция имеет разрыв у поверхности проводов. Для вычисления индуктивности линии необходимо найти потокосцепление. Элементарный поток, проходящий через площадку Idx в воздухе между проводами,

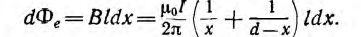
Весь поток между проводами – внешний поток

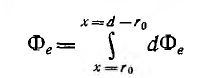
одновременно является внешним потокосцеплением, так как сцепляется с контуром один раз. Поэтому

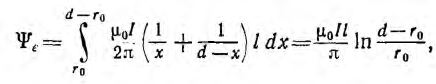
а соответствующая ему внешняя индуктивность

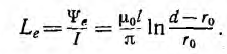
Для большинства линий расстояние d между проводами значительно превышает радиус r₀ проводов. В этом случае

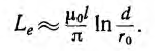
Для определения внутренней индуктивности, соответствующей внутреннему потоку, при d > r₀ поле внутри провода линии может вычисляться как поле уединенного провода, так как поле, создаваемое вторым проводом внутри первого, по сравнению с полем первого, пренебрежимо мало. Тогда элементарный поток внутри провода

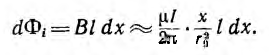
Так как поток dФ_i охватывает не весь ток, а только его часть [см. формулу (1.3)], элементарное потокосцепление

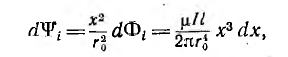
Весь поток между проводами — внешний поток

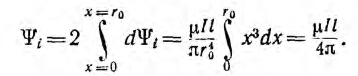
Соответственно, внутренняя индуктивность

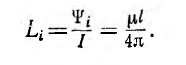
Суммарная индуктивность линии

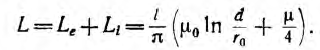
При медных или алюминиевых проводах (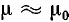) в большинстве случаев вторым членом можно пренебречь по сравнению с первым и тогда

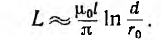
Для стальных проводов (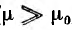) основной частью потока является
внутренний поток и индуктивность

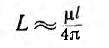
практически не будет зависеть от расстояния между проводами.

Взаимоиндуктивность и ее расчет

Для двух контуров, имеющих w₁ и w₂ витков с токами I₁ и I₂ (рис. 1.17), поток первого контура, определяемый током этого контура, — поток самоиндукции Ф_1l—может быть разложен на поток рассеяния Ф_1s, пронизывающий только этот контур, и поток взаимоиндукции Ф_1m, пронизывающий также и второй контур:

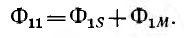
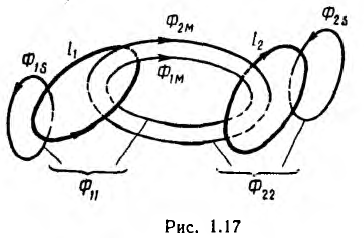
Потокосцепление, соответствующее потоку Ф₁₁ (при условии, что этот поток пронизывает все витки первого контура, равно

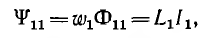
а потокосцепление рассеяния

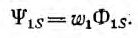
Аналогично для второго контура

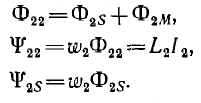
Потокосцепление второго контура, определяемое током первого,

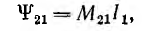
а потокосцепление первого контура, определяемое током второго,

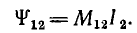
Можно показать, что

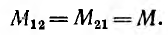
Величина M называется взаимоиндуктивностью и определяется конфигурацией контуров, их взаимным расположением и магнитной проницаемостью среды. Взаимоиндуктивность также измеряется в генри (гн).
Суммарный поток, пронизывающий первый контур,

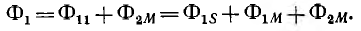
Суммарное потокосцепление первого контура

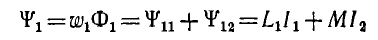
и соответственно для второго контура

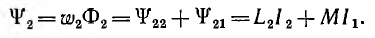
В этих алгебраических суммах первый член всегда положителен, а знак перед вторым членом определяется направлением токов в контурах; положительный знак соответствует случаю совпадения направлений потоков Ф_1м и Ф_2м (см. рис. 1.17).
Из изложенного видно, что

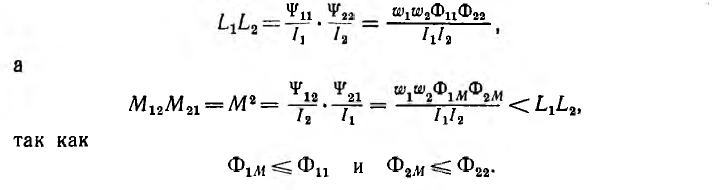
Таким образом, взаимоиндуктивность и индуктивности всегда удовлетворяют неравенству

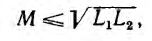
а используемый в технических расчетах коэффициент связи двух контуров

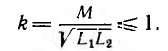
Аналогично, в системе многих контуров потокосцепление контура определяется токами всех контуров:

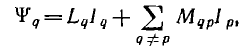
где L_q — индуктивность q-то контура, М_qp = М_рq — взаимоиндуктивность q- и р-го контуров. Общий прием расчета взаимоиндуктивности контуров заключается
в нахождении потокосцепления, пронизывающего контур q, но созданного током р-го контура, и делении его на этот ток.

Взаимоиндуктивность двух параллельных двухпроводных линий

Пусть две параллельные двухпроводные линии расположены симметрично так, как это было показано на рис. 1.4. При условии d> г₀ внутренним потоком в проводах по сравнению с внешним можно пренебречь.
Магнитный поток, пронизывающий первую линию и созданный током I₂ второй, может быть найден как сумма потоков, создаваемых каждым из проводов второй линии в отдельности.
Тогда магнитный поток, пронизывающий первую линию,

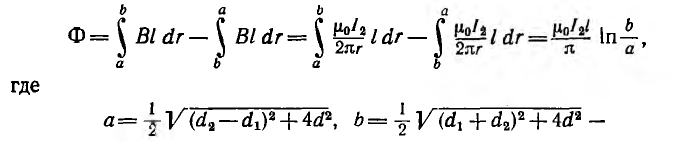
расстояния от провода линии 1 до проводов линии 2 .

Магнитный поток Ф одновременно является потокосцеплением 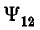первой линии, так как сцепляется с ней один раз; поэтому

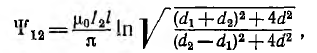
а взаимоиндуктивность

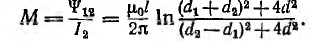
Для уменьшения коэффициента связи между линиями связи l и передачи 2 применяют транспозицию линии связи, заключающуюся в перекрещивании проводов линии связи через равные расстояния; тогда суммарное потокосцепление 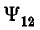будет равно нулю.

Линейные и нелинейные катушки индуктивности

У линейных материалов магнитная проницаемость µ, не зависит от напряженности поля и характеристика 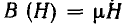для них изображается прямой линией (рис. 1.18, а). Магнитная проницаемость пропорциональна тангенсу угла а наклона этой прямой:

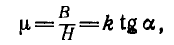
где k — масштабный коэффициент.

К нелинейным материалам относятся ферромагнетик и — железо, никель, кобальт и гадолиний. Важное значение в электротехнике имеют первые три элемента, главным образом в виде сплавов. У нелинейных материалов магнитная проницаемость очень велика 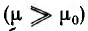и зависит от напряженности поля.

Подобно нелинейным диэлектрикам по кривой первоначальногo намагничивания В (Н) (рис. 1.18, б) могут быть определены статическая магнитная проницаемость

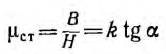
и дифференциальная, а при быстрых изменениях поля — динамическая магнитная проницаемость

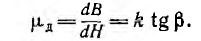
На рис. 1.18, б эти проницаемости представлены в функции напряженности поля. Максимальные значения магнитной проницаемости в очень чистом железе и в некоторых сплавах, например в пермаллое (сплав железа и-никеля с различными присадками), в сотни тысяч раз превышают магнитную постоянную равную

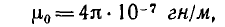
магнитной проницаемости вакуума.

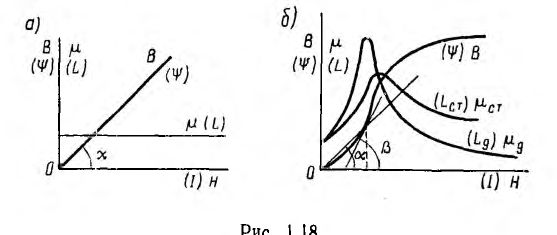
В переменных магнитных полях в ферромагнетиках имеет место явление магнитного гистерезиса (рис. 1.19), заключающееся в несовпадении кривой В (Н) при возрастании напряженности поля с кривой при убывании поля.

Кривая, соединяющая вершины петель гистерезиса, называется основной кривой намагничивания и практически совпадает с кривой первоначального намагничивания, Ферромагнитные свойства зависят от температуры и проявляются лишь в определенном ее интервале.

Для тороида 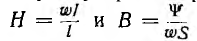и веберамперные характеристики ψ (I) в соответствующем масштабе совпадают с кривыми В (H); поэтому прямая и кривые на рис. 1.18 а и б соответствуют также веберамперным характеристикам при величинах, указанных в скобках.

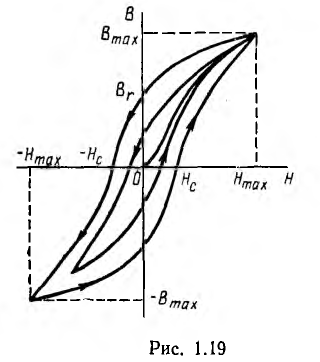
Для нелинейных тороидов вводятся понятия статической индуктивности

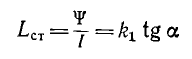
и дифференциальной, а также динамической индуктивности

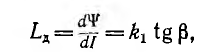
являющихся функциями тока (см. рис. 1.18, б); для линейных тороидов эти индуктивности совпадают.

Аналогично индуктивностям в нелинейных системах контуров вводятся статическая взаимоиндуктивность

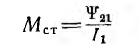
и дифференциальная, взаимоиндуктивность, а также динамическая

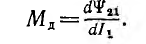
Индуктивность нелинейного тороида

Расчет нелинейного тороида может быть произведен, если задана зависимость В (H) или µ(H). Так как эти зависимости теоретически не выводятся, то для приближенного решения подбирают по кривой В(H) аппроксимирующую функцию.

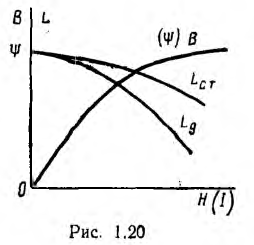
Пусть аппроксимирующая функция для характеристики В (H) (рис. 1.20)
материала сердечника тороида будет

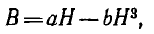
где а и b — постоянные.

Так как для тороида с ферромагнитным однородным cердечником напряженность поля по-прежнему определяется формулой 

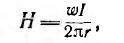
то индукция будет равна

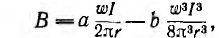
а потокосцепление

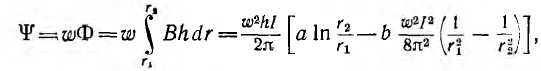
откуда статическая индуктивность

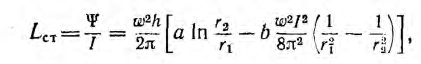
а дифференциальная индуктивность

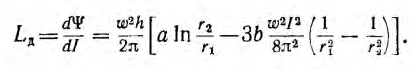
Кривые зависимости этих индуктивностей от тока представлены
на рис. 1.20.

Реальная катушка в отличии от идеальной имеет не только индуктивность, но и активное сопротивление, поэтому при протекании переменного тока в ней сопровождается не только изменением энергии в магнитном поле, но и преобразованием электрической энергии в другой вид. В частности, в проводе катушки электрическая энергия преобразуется в тепло в соответствии с законом Ленца — Джоуля.

Ранее было выяснено, что в цепи переменного тока процесс преобразования электрической энергии в другой вид характеризуется активной мощностью цепи Р, а изменение энергии в магнитном поле — реактивной мощностью Q.

В реальной катушке имеют место оба процесса, т. е. ее активная и реактивная мощности отличны от нуля. Поэтому одна реальная катушка в схеме замещения должна быть представлена активным и реактивным элементами.

Схема замещения катушки с последовательным соединением элементов

В схеме с последовательным соединением элементов реальная катушка характеризуется активным сопротивлением R и индуктивностью L.

Активное сопротивление определяется величиной мощности потерь

R = P/I²

а индуктивность — конструкцией катушки. Предположим, что ток в катушке (рис. 13.9, а) выражается уравнением i = I_msinωt. Требуется определить напряжение в цепи и мощность.
При переменном токе в катушке возникает э. д. с. самоиндукции e_L поэтому ток зависит от действия приложенного напряжения и эдс e_L. Уравнение электрического равновесия цепи, составленное по второму закону Кирхгофа, имеет вид:

Приложенное к катушке напряжение состоит из двух слагаемых,одно из которых u_R равно падению напряжения в активном сопротивлении, а другое u_L уравновешивает эдс самоиндукции.

В соответствии с этим катушку в схеме замещения можно представить активным и индуктивным сопротивлениями, соединенными последовательно (рис. 13.9, б).
Дополнительно заметим, что оба слагаемых в правой части равенства (13.12) являются синусоидальными функциями времени. Согласно выводам полученных в этих предыдущих двух (первая, вторая) статьях получим — u_R совпадает по фазе с током, U_L опережает ток на 90°.

Поэтому:

u = R*I_msinωt  + ωLI_msin(ωt+π/2).

Векторная диаграмма реальной катушки и полное её сопротивление

Несовпадение по фазе слагаемых в выражении (13.12) затрудняет определение амплитуды и действующей величины приложенного к цепи напряжения U. Поэтому воспользуемся векторным способом сложения синусоидальных величин. Амплитуды составляющих общего напряжения

U_mR = RI_m;       U_mL = ωLI_m ,

а действующие величины

U_R = RI; U_L = X_LI .

Вектор общего напряжения

U = U_R + U_L

Для того чтобы найти величину вектора U, построим векторную диаграмму (рис. 13.10, а), предварительно выбрав масштабы тока Mi и напряжения Мu.

За исходный вектор диаграммы принимаем вектор тока I. Направление этого вектора совпадает с положительным направлением оси, от которой отсчитываются фазовые углы (начальная фаза заданного тока Ψi =0). Как и ранее, эту ось удобно (но не обязательно) направить по горизонтали.

Вектор U_R по направлению совпадает с вектором тока I, а вектор U_L направлен перпендикулярно вектору I с положительным углом.

Из диаграммы видно, что вектор тока I общего напряжения U отражает вектор тока I на угол φ>0, но φ<90°, а по величине равен гипотенузе прямоугольного треугольника, катетами которого являются векторы падений напряжения в активном и индуктивном сопротивлениях U_R и U_L :

U_R = Ucosφ 

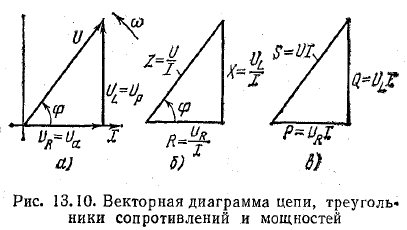
Проекция вектора напряжения U на направление вектора тока называется активной составляющей вектора напряжения и обозначается U_a. Для катушки по схеме рис. 13.9 при U_a = U_R

U = Usinφ                                                        (13.14)

Проекция вектора напряжения U на направление, перпендикулярное вектору тока, называется реактивной составляющей вектора напряжения и обозначается U_p. Для катушки U_p = U_L

При токе i = Imsinωt уравнение напряжения можно записать на основании векторной диаграммы в виде

U = U_msin(ωt+φ)

Стороны треугольника напряжений, выраженные в единицах напряжения, разделим на ток I. Получим подобный треугольник сопротивлений (рис. 13.10, б), катетами которого являются активное R = U_R/I и индуктивное X_L = U_L/I, сопротивления, а гипотенузой величина Z = U/I.

Отношение действующего напряжения к действующему току данной цепи называется полным сопротивлением цепи.
Стороны треугольника сопротивлений нельзя считать векторами, так как сопротивления не являются функциями времени.
Из треугольника сопротивлений следует

Понятие о полном сопротивлении цепи Z позволяет выразить связь между действующими величинами напряжения и тока формулой, подобной формуле Ома:

Из треугольников сопротивления и напряжения определяются

cosφ = U_R/U = R/Z;    sinφ = U_L/U = X_L/Z;    tgφ = U_L/U_R = X_L/R. (13.18)

Мощность реальной катушки

Мгновенная мощность катушки

p = ui = U_msin(ωt+φ) * I_msinωt

Из графика мгновенной мощности (рис. 13.11) видно, что в течение периода мощность четыре раза меняет знак; следовательно, направление потока энергии и в данном случае в течение периода меняется. Относительно некоторой оси t’, сдвинутой параллельно оси t на величину Р, график мгновенно мощности является синусоидальной функцией двойной частоты.
При положительном значении мощности энергия переходит от источника в приемник, а при отрицательном — наоборот. Нетрудно заметить, что количество энергии, поступившей в приемник (положительная площадь), больше возвращенной обратно (отрицательная площадь).

Следовательно, в цепи с активным сопротивлением и индуктивностью часть энергии, поступающей от генератора, необратимо превращается в другой вид энергии, но некоторая часть возвращается обратно. Этот процесс повторяется в каждый период тока, поэтому в цепи наряду с непрерывным превращением электрической энергии в другой вид энергии (активная энергия) часть ее совершает колебания между источником и приемником (реактивная энергия).

Скорость необратимого процесса преобразования энергии оценивается средней мощностью за период, или активной мощностью Р, скорость обменного процесса характеризуется реактивной мощностью Q.

Согласно выводам полученных в этих предыдущих  (первая, вторая) статьях — в активном сопротивлении P = U_RI   Q = 0;  а в индуктивном Р = 0; Q = U_LI. 

Активная мощность всей цепи равна активной мощности в сопротивлении R, а реактивная — реактивной мощности в индуктивном сопротивлении X_L. Подставляя значения U_R = Ucosφ и U_L = Usinφ, определяемые из треугольника напряжений по формулам (13.18), получим:

                   P = UIcosφ                                (13.19)

                    Q = UIsinφ                                (13.20)

Кроме активной и реактивной мощностей пользуются понятием полной мощности S, которая определяется произведением действующих величин напряжения и тока цепи;

                   S = UI = I²Z                                (13.21)

Величину полной мощности можно получить из выражения (13.22), которое легко доказать на основании формул (13.19) и (13.20):

                        (13.22)                         

Мощности S, Р, Q графически можно выразить сторонами прямоугольного треугольника (см. рис. 13.10, в). Треугольник мощностей получается из треугольника напряжений, если стороны последнего, выраженные в единицах напряжения, умножить на ток. Из треугольника мощностей можно определить

cosφ = P/S;       sinφ = Q/S;     tgφ = Q/P.             (13.23)

Полная мощность имеет ту же размерность, что Р и Q, но для различия единицу полной мощности называют вольт-ампер (В · А).

Активная мощность Р меньше или равна полной мощности цепи.
Отношение активной мощности цепи к ее полной мощности P/S =
= cosφ называют коэффициентом мощности.

Назначение приемников электрической энергии — преобразование
ее в другие виды энергии. Поэтому колебания энергии в цепи не только
бесполезны, но и вредны, так как при этом в приемнике не совершается
полного преобразования электрической энергии в работу или тепло,
а в соединительных проводах она теряется.

Схема замещения реальной катушки с параллельным соединением элементов

Для реальной катушки можно составить и другую расчетную схему — с параллельным соединением двух ветвей: с активной G и индуктивной B_L проводимостями. На рис. 13.12, б эта схема показана в сравнении со схемой последовательного соединения активного и индуктивного сопротивлений (рис. 13.12, а), рассмотренной ранее.
Покажем, что схемы рис. 13.12, а, б эквивалентны в том смысле, что при одинаковом напряжении сохраняются неизменными ток в неразветвленной части цепи, активная и реактивная мощности.

Вектор тока I можно разложить на две взаимно перпендикулярные составляющие и в соответствии со схемой и векторной диаграммой на рис. 13.12, б выразить векторным равенством

                                             I = I_G + I_L                                           (13.24)

Для схемы параллельного соединения активного и индуктивного элементов общим является приложенное напряжение, а токи разные: I_G —ток в ветви с активной проводимостью, по фазе совпадает с напряжением; I_L — ток в ветви с индуктивной проводимостью, по фазе отстает от напряжения на угол 90°.

Вектор тока I и его составляющие I_G и I_L образуют прямоугольный треугольник, поэтому

Составляющая тока в активном элементе

I_G = Icosφ

Проекция вектора тока I на направление напряжения называется активной составляющей вектора тока и обозначается I_а. Для катушки по схеме на рис. 13.12, б I_a = I_G.

Составляющая тока в реактивном элементе

I_L = Isinφ

Проекция вектора тока I на направление, перпендикулярное вектору напряжения, называется реактивной составляющей вектора тока и обозначается Iр. Для катушки I_р = I_L .

Стороны треугольника токов, выраженные в единицах тока, можно разделить на напряжение U и получить подобный треугольник проводимостей, катетами которого являются активная G = I_G/U и индуктивная В_L = I_L/U проводимости, а гипотенузой — величина Y = I/U, называемая полной проводимостью цепи.

Из треугольника проводимостей и с учетом ранее полученных выражений из треугольника сопротивлений получим