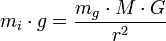Гравитационная и инертная масса тел.
Массу тела можно
определить, используя второй закон
Ньютона
Определяемая
таким путем масса mин
получила название инертной массы.
Инертная масса является мерой инертности
тела.
Массу того же
самого тела можно определить, используя
закон всемирного тяготения, путем
измерения силы тяготения к другому
телу, например к Земле:
Определяемая
этим способом масса mграв
носит название
гравитационной массы. Гравитационная
масса является, таким образом,
количественной мерой присущему всем
телам свойству гравитации.
Выясним теперь, в
каком отношении друг к другу находятся
обе массы тела. Опыты показали, что
инертные массы всех тел в пределах
достигнутой точности измерений
пропорциональны их гравитационным
массам.
Простейший
из этих опытов заключается в проверке,
действительно ли все тела (из любых
веществ) падают на Земле с одинаковым
ускорением. Пусть мы имеем два разнородных
тела, например из железа и гранита.
Обозначим их инертные и гравитационные
массы через m1ин,
m1грав
и m2ин,
m2грав.
Для первого тела
(3)
а для второго
(4)
После деления
уравнения (3) на (4) получим:
или
(5)
Полученное
соотношение показывает, что отношение
инертной массы тела к его гравитационной
массе будет для всех тел (из любых
веществ) одинаковым
(6)
если
будет доказано, что все тела независимо
от их размера и рода вещества падают в
вакууме с одинаковым ускорением (g1
=g2
=…=g)
Опыты по непосредственному
измерению ускорения свободного падения
показывают, что это ускорение в пределах
точности измерения одинаково для всех
тел.
Классические опыты
такого типа принадлежат Ньютону, который
использовал для этой цели метод маятника.
Среди
других, получивших известность опытов
отметим опыт Этвеша,
проведенный им в 1890
г. Идея опыта состоит в следующем.
Если к длинной нити, верхний конец
которой закреплен, подвесить груз,
то вследствие вращения Земли эта нить
отклонится от направления к центру
планеты на некоторый угол
.
Величина этого угла определяется
отношением
инертной
массы груза к его гравитационной массе.
Понятно, что если при повторении опыта
с различными грузами (отличающимися
размерами и материалом) будет получаться
каждыйpaз
один и тот же угол
отклонения нити, то из этого можно
заключить о постоянстве отношения
для
всех тел
=
const
(7)
или о наличии
прямой пропорциональности между инертной
и гравитационной массами.
Этвеш
провел измерения угла отклонения для
восьми различных тел. При этом точность
измерений была такова, что относительная
ошибка не превосходила 10-8.
Эти опыты, как и эксперименты, проведенные
уже в наше время с точностью до 10-10,
подтвердили равенство (7). Значит, для
всех тел, частиц и вообще для всех
материальных объектов имеется строгая
пропорциональность между инертной
и гравитационными массами:
.
При
строгой пропорциональности значение
коэффициента роли не играет и его можно
принять равным единице (k
= 1). При этом гравитационная
масса будет равна инертной массе тела
(именно равна, а не тождественна ей). По
этой причине обычно говорят о массе
тела, не уточняя, идет ли речь об инертной
или гравитационной массе.
Принимая,
что гравитационная масса равна инертной
массе, мы этим предопределяем единицу
измерения массы в законе всемирного
тяготения. Таким образом, единицы
измерения всех входящих в формулу (1)
величин установлены. При этих условиях
коэффициент пропорциональности
(постоянная
тяготения) должен иметь вполне
определенное значение и определенную
размерность. Значение постоянной
рассчитать
нельзя; оно устанавливается из опыта.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
У этого термина существуют и другие значения, см. Масса (значения).
Не следует путать с весом.
| Масса | |
|---|---|
 |
|
| Размерность | M |
| Единицы измерения | |
| СИ | кг |
| СГС | г |
Ма́сса — скалярная физическая величина, определяющая инерционные и гравитационные свойства тел в ситуациях, когда их скорость намного меньше скорости света[1]. В обыденной жизни и в физике XIX века масса синонимична весу[2].
Будучи тесно связанной с такими понятиями механики, как «энергия» и «импульс», масса проявляется в природе двумя качественно разными способами, что даёт основания для подразделения её на две разновидности:
- инертная масса характеризует инертность тел и фигурирует в выражении второго закона Ньютона: если заданная сила в инерциальной системе отсчёта одинаково ускоряет различные тела, им приписывают одинаковую инертную массу;
- гравитационная масса (пассивная и активная) показывает, с какой силой тело взаимодействует с внешними полями тяготения[3] и какое гравитационное поле создаёт само это тело[4], она входит в закон всемирного тяготения и положена в основу измерения массы взвешиванием.
Однако экспериментально с высокой точностью установлена пропорциональность гравитационной и инертной масс[5][6], и подбором единиц они сделаны в теории равными друг другу. Поэтому, когда речь не идёт об особой «новой физике», принято оперировать термином «масса» и использовать обозначение m без пояснений.
Массой обладают все макроскопические объекты, бытовые предметы, а также большинство элементарных частиц (электроны, нейтроны и др.), хотя среди последних имеются и безмассовые (например, фотоны). Наличие массы у частиц объясняется их взаимодействием с полем Хиггса.
Масса в классической механике[править | править код]
Простое определение инертной массы[править | править код]
Величина массы входит в нерелятивистское выражение второго закона Ньютона F = ma, дающее связь между силой и вызываемым ею ускорением свободного тела. Указанный закон, одновременно с утверждением линейности соотношения «сила—ускорение», по сути, выступает определением инертной массы. Сила при этом определяется логически независимо и от закона Ньютона, и от понятия «ускорение»[7]: она равна деформации специальной тестовой пружины (с точностью до калибровочного множителя).
Масса может измеряться в килограммах. Официальным эталоном массы «1 кг» по 2018 год служил конкретный объект (см. фото выше); по соглашению, если приложенная к эталону сила обеспечивает ускорение 1 м/с2, то такая сила имеет величину 1 Н. Данным соглашением задаётся единичная сила — приложив её к упомянутой пружине, можно прокалибровать последнюю и использовать для измерений. Инертная масса любого исследуемого тела находится затем как F / a: достаточно знать ускорение при каком-то одном значении силы.
В 2018 году учёные заменили эталон килограмма, хранящийся в Международном бюро мер и весов во Франции с 1889 года. Теперь единица массы определяется с помощью постоянной Планка. Для создания нового эталона массы применяются весы Киббла — устройство, которое определяет, какой ток нужен для того, чтобы создать электромагнитное поле, способное уравновесить чашу с тестируемым эталоном[8]. Старый эталон отныне играет роль очень точной гири.
Гравитационная масса. Принцип эквивалентности[править | править код]
По своему смыслу гравитационная масса — характеристика тел в классической механике, являющаяся мерой их гравитационного взаимодействия
где G — гравитационная постоянная (константа Ньютона), r — расстояние между материальными точками, обладающими гравитационными массами 
и 
. Она отличается по определению от инертной массы, определяющей динамические свойства тел, и априори ниоткуда не следует, что массы этих двух разновидностей должны быть пропорциональными друг другу. Данное обстоятельство является нетривиальным экспериментальным фактом.
Первая проверка пропорциональности двух видов массы была выполнена Галилеем, изучавшим свободное падение. Согласно опытам Галилея, все тела, независимо от их массы и материала, падают с одинаковым ускорением. Сейчас эти опыты можно трактовать так, что увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Позднее на пропорциональность инертной и гравитационной масс обратил внимание Ньютон, он же впервые доказал, что эта пропорциональность выдерживается с точностью не хуже 0,1 %[9].
С учётом сказанного раздельных единиц для гравитационной и инертной массы не вводят, а коэффициент их пропорциональности принят равным 1 с надлежащим подбором константы G. На сегодня пропорциональность (условно говоря, «равенство масс») экспериментально проверена с очень высокой точностью: чувствительность к относительной разности в лучшем эксперименте на 2009 год[5][6] имеет порядок 10−13.
Подобные эксперименты привели к формулированию принципа эквивалентности:
Все явления в гравитационном поле происходят точно так же, как в соответствующем поле сил инерции, если совпадают напряжённости этих полей и одинаковы начальные условия для тел системы.
имеющего два уровня глобальности охвата «всех явлений». Так называемый «сильный» принцип гласит: в каждой точке пространства-времени в произвольном гравитационном поле можно выбрать локально-инерциальную систему координат, такую, что в достаточно малой окрестности рассматриваемой точки законы природы будут иметь такую же форму, как и в неускоренных декартовых системах координат, где под «законами природы» подразумевают все законы природы. «Слабый» принцип отличается заменой слов «законы природы» словами «законы движения свободно падающих частиц». Слабый принцип — это не что иное, как другая формулировка наблюдаемого равенства гравитационной и инертной масс, в то время как сильный принцип представляет собой обобщение наблюдений за влиянием гравитации на любые физические объекты.
Единицы измерения массы[править | править код]
Килограмм является одной из семи основных единиц СИ. По современному определению, его величина выражается через величины трёх выбранных физических постоянных: постоянная Планка, скорость света и частота определённого электронного перехода.
В Международной системе единиц (СИ) масса измеряется в килограммах. Единицей измерения массы в системе СГС является грамм (1⁄1000 килограмма). Вообще говоря, в любой системе измерения выбор основных (первичных) физических величин, их единиц измерения и их числа произволен — зависит от принимаемого соглашения и масса не всегда входит в их состав — так в системе МКГСС единица массы была производной единицей и измерялась в кГс·с²/м (называлась «техническая единица массы» или «инерта»). В атомной физике и химии принято сравнивать [соотносить] массу с относительной атомной массой (а.е.м.), в физике твёрдого тела — с массой электрона (Атомная система единиц), в физике элементарных частиц массу измеряют в электронвольтах. Кроме этих единиц, используемых в науке, существует большое разнообразие исторических единиц измерения массы, которые сохранили свою отдельную сферу использования: фунт, унция, карат, тонна и др. В астрофизике единицей для сравнения масс небесных тел служит масса Солнца.
В некоторых естественных системах единиц в качестве единицы массы используются массы элементарных частиц: электрона или протона[10]. В планковской системе единиц, также относящейся к естественным системам, единицей массы является планковская масса.
Массы очень мелких частиц могут быть определены с помощью величины, обратной к комптоновской длине волны: 1 см-1 ≈ 3,52⋅10-41 кг. Масса очень большой звезды или чёрной дыры может быть отождествлена с её гравитационным радиусом: 1 см ≈ 6,73⋅1024 кг.
Основные свойства массы как величины[править | править код]
Масса — одна из важнейших величин в физике. Это скалярная неотрицательная релятивистски инвариантная величина. По современным представлениям, масса эквивалентна энергии покоя (mc2, где c — скорость света в вакууме). Масса входит в выражения кинетической энергии (mv2/2, где v — скорость) и импульса (mv) материальной точки.
Масса тела, выраженная в килограммах, численно примерно равна весу этого тела, выраженному в кгс (1 кгс ≈ 10 Н), когда оно покоится вблизи поверхности Земли. Поэтому в повседневных ситуациях слово «вес» нередко синонимизируется со словом «масса». Однако это разные понятия, и в общем случае численные значения массы и веса не совпадают, не говоря уже о различии размерностей. Например, при помещении предмета на обычные магазинные весы показания колеблются в течение нескольких секунд: в это время вес претерпевает изменения, а масса постоянна. Также возможны ситуации с нулевым весом и ненулевой массой одного и того же тела: в условиях невесомости вес всех тел равен нулю, а масса у каждого тела своя.
В классической механике масса инвариантна относительно смены системы отсчёта и аддитивна, то есть масса системы тел равна сумме масс составляющих её тел.
Масса в релятивистской механике[править | править код]
Строгое определение массы[править | править код]
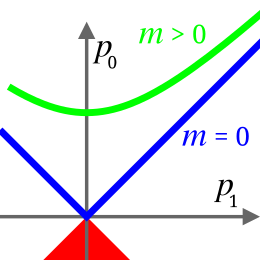
Возможные 4-импульсы тел с нулевой и положительной массой покоя. Векторы 4-импульса, построенные от точки пересечения осей до любой точки на зелёной гиперболе, имеют одну и ту же (положительную) длину, то есть массу частицы, несущей этот четырёхимпульс, и различаются энергией и 4-скоростью частицы. Ускорение частицы сводится к движению конца 4-импульса по гиперболе. Векторы четырёхимпульса, построенные от точки пересечения осей до любой точки на синих полупрямых, имеют нулевую длину и могут относиться только к частицам нулевой массы (например, фотонам); энергия этих частиц (с точностью до коэффициента
c) равна модулю их 3-импульса
Наиболее строгое определение массы даётся в специальной теории относительности (СТО): масса — это абсолютная величина 4-вектора энергии-импульса[11]:
где E — полная энергия свободного тела, p — его 3-импульс, c — скорость света. В СТО масса является неаддитивной, но, как и в классической физике, инвариантной величиной.
В случае произвольной метрики пространства-времени (как в общей теории относительности) это определение требует некоторого обобщения:
Здесь 
— метрический тензор, 
— 4-импульс.
Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то 
— масса определяется энергией покоя (Эквивалентность массы и энергии).
Особенно просто выглядят эти определения в системе единиц, в которой за единицу измерения скорости принята скорость света (например, в планковской или же в принятой в физике элементарных частиц для описания процессов при высоких энергиях релятивистской системе единиц, в которой масса, импульс и энергия имеют размерность энергии[12] и измеряются в электронвольтах):
- В СТО:
- В ОТО:
Частицы с нулевой массой (фотон и гипотетический гравитон) двигаются в вакууме со скоростью света (c ≈ 300 000 км/с), и поэтому не существует системы отсчёта, в которой бы они покоились. Напротив, частицы с ненулевой массой всегда движутся медленнее скорости света.
О «массе покоя» и «релятивистской массе»[править | править код]
В современной терминологии термин масса применяется вместо терминов инвариантная масса или масса покоя, являясь полностью эквивалентным им по смыслу. В некоторых ситуациях (особенно в популярной литературе) это, однако, уточняется явно, чтобы избежать путаницы из-за понимания термина масса в другом — устаревшем — смысле, описанном в этом подразделе.
В большом количестве источников[13][14], относящихся к началу и середине XX века, а также в научно-популярных[15], введённое выше понятие массы называли «массой покоя», при этом саму массу вводили на основе классического определения импульса
В таком случае 
, и поэтому говорили, что масса тела растёт с увеличением скорости. При таком определении понятие массы было эквивалентно понятию энергии, а также требовалось отдельно вводить «массу покоя», измеряемую в собственной СО, и «релятивистскую массу» движущегося тела. Такой подход был распространён в течение длительного времени[15] и позволял провести многочисленные аналогии с классической физикой, однако в современной научной литературе используется редко[16], так как вносит дополнительную путаницу в терминологию, не давая никаких новых результатов. Так называемая релятивистская масса оказывается аддитивной (в отличие от массы покоя системы, зависящей от состояния составляющих её частиц). Однако безмассовые частицы (например, фотоны) в такой терминологии оказываются имеющими переменную массу; кроме того, релятивистская масса ничуть не упрощает формулировку законов динамики частиц.
Полным аналогом классического определения импульса через массу и скорость в СТО следует считать ковариантное равенство
где m — инвариантная масса, а uμ — 4-скорость (производная от 4-координаты по собственному времени частицы 
; единичный вектор, направленный вдоль мировой линии частицы).
Также можно записать ковариантный эквивалент второго закона Ньютона:
где 
— 4-ускорение (кривизна мировой линии частицы).
Масса составных и нестабильных систем[править | править код]
В релятивистской механике, в отличие от классической, масса не является аддитивной физической величиной, то есть масса системы в общем случае не равна сумме масс её компонентов. Масса системы зависит от характера движения частиц друг относительно друга и в случае взаимодействующих частиц также включает в себя энергию связи[Комм 1].
Масса устойчивой системы взаимодействующих частиц, совершающих финитное движение (например, нуклонов в атомном ядре), может зависеть от внутреннего состояния этой системы. Она меньше суммы масс частиц на величину 
называемую дефектом массы, где 
— энергия связи системы, 
— скорость света[17].
Масса системы невзаимодействующих релятивистских частиц не меньше суммы их масс и равна данной сумме, только когда все частицы покоятся друг относительно друга[18]. Это утверждение следует из того, что в релятивистской механике массой системы частиц называется модуль её четырёхимпульса[19]: 
В системе отсчёта, для которой полный пространственный импульс системы частиц равен нулю 
для системы невзаимодействующих частиц, в силу аддитивности энергии, получаем 
(индекс 
нумерует частицы). Иными словами, 
причём равенство левой и правой частей обеспечивается, только когда все 
равны нулю.
Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: 
При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью, равной означенному Δm.
Классификация частиц по значению массы[править | править код]
- Масса частиц микромира
Масса всех известных на сей день частиц является неотрицательной величиной. В физике элементарных частиц понятие массы чрезвычайно важно, так как позволяет отделять безмассовые частицы (всегда двигающиеся со скоростью света, как фотоны) от массивных (скорость которых всегда ниже скорости света).
Кроме того, масса практически однозначно позволяет идентифицировать частицу (с точностью до зарядового сопряжения, меняющего частицы и античастицы). Наличие массы у кварков и лептонов объясняется их взаимодействием с полем Хиггса, и чем сильнее это взаимодействие, тем больше масса[20][21]. Масса элементарной частицы постоянна, она одинакова у всех частиц данного типа и их античастиц. В то же время в физике элементарных частиц рассматриваются объекты без определённой массы (которые также можно называть элементарными частицами); эти частицы являются линейными квантовомеханическими комбинациями частиц, имеющих определённую массу (массовых состояний). Так, нейтрино с определёнными флейворами (то есть электронное, мюонное и тау-нейтрино и соответствующие им антинейтрино) не имеют определённых масс, и наоборот, массовые состояния нейтрино не обладают определёнными флейворами, а являются смесью флейворных состояний; этот факт является причиной нейтринных осцилляций. То же относится и к ряду нейтральных мезонов (K0, B0– и D0-мезоны). В частности, K0
и K0
-мезоны, являющиеся собственными состояниями гамильтониана сильного взаимодействия, не обладают, строго говоря, определённой массой (и временем жизни), будучи суперпозицией двух массовых состояний K0
S и K0
L (см. Смешивание нейтральных каонов); однако разность масс m(K0
S) − m(K0
L) = 3,5·10−6 эВ настолько мала по сравнению с их массой mK ≈ m(K0
S) ≈ m(K0
L) ≈ 497,611 МэВ и даже с экспериментальной погрешностью её измерения (13 кэВ), что можно считать массу каона K0
и антикаона K0
определённой и равной mK[22].
- Положительная масса
К частицам с положительной массой (тардионам) относятся почти все частицы Стандартной модели: лептоны (включая нейтрино, которые в первоначальной версии Стандартной модели считались безмассовыми), кварки, W- и Z-бозоны, бозон Хиггса. Эти частицы могут двигаться с любой скоростью, меньшей скорости света, в том числе покоиться. К тардионам относятся также все известные составные частицы: барионы (в том числе протон и нейтрон) и мезоны.
- Нулевая масса
К известным на сегодняшний день частицам нулевой массы (безмассовым, люксонам) относятся фотоны и глюоны, а также гипотетические гравитоны. Такие частицы в свободном состоянии могут двигаться только со скоростью света. Но поскольку из квантовой хромодинамики следует, что глюоны в свободном состоянии не существуют, то непосредственно наблюдать движущимися со скоростью света можно только фотоны (собственно, именно поэтому говорят о «скорости света»). Долгое время считалось, что нейтрино также имеют нулевую массу, однако обнаружение вакуумных нейтринных осцилляций свидетельствует о том, что масса нейтрино хоть и очень мала, но не равна нулю.
Комбинация нескольких частиц нулевой массы может (а в случае, например, сцепленных частиц — должна) иметь ненулевую массу.
- Отрицательная масса
Частицы с отрицательной массой двигались бы с любой скоростью, меньшей скорости света, аналогично тардионам, и имели бы отрицательную энергию и импульс, направленный в сторону, противоположную направлению движения. Допущение существования отрицательных масс ведёт к определённым сложностям в интерпретации принципа эквивалентности и закона сохранения импульса. В то же время в общей теории относительности допускается существование локальных пространственных областей с отрицательной плотностью энергии-импульса. В частности, подобную область можно создать с помощью эффекта Казимира[23].
- Мнимая масса
В рамках специальной теории относительности математически возможно существование частиц с мнимой массой, так называемых тахионов. Такие частицы будут иметь реальные значения энергии и импульса, а их скорость должна всегда быть выше скорости света. Однако допущение возможности наблюдения одиночных тахионов вызывает ряд методологических трудностей (например, нарушение принципа причинности), поэтому в большинстве современных теорий одиночные тахионы не вводятся. Впрочем, в квантовой теории поля мнимая масса может быть введена для рассмотрения тахионной конденсации, не нарушающей принцип причинности.
Измерение массы[править | править код]
Методы и устройства для измерения[править | править код]
Основная статья: Весы
Большинство приборов для измерения массы основано на использовании принципа эквивалентности инертной и гравитационной массы. С помощью таких приборов, называемых весами, массу тел определяют по их весу. В пружинных весах вес измеряется по степени деформации гибкой пружины. В рычажных — вес определяется путём сравнения веса интересующего тела с весом эталонов (гирь) известной массы.
Однако в ситуации невесомости (скажем, на космических станциях) весы неприменимы, и используются другие устройства — массметры, действие которых основано на измерении периода свободных колебаний груза на пружине; этот период, как известно, зависит от массы тела.
Массы заряженных элементарных частиц определяют по их следам в камере Вильсона[24]. Массы короткоживущих элементарных частиц, не оставляющих следов в камере Вильсона, определяют, оценивая суммарную энергию продуктов их распада[25][26].
Массу Земли определяют на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной и радиуса Земли[27]. Массу Солнца определяют также на основе закона всемирного тяготения Ньютона, исходя из известных значений гравитационной постоянной, расстояния между Землёй и Солнцем и периода обращения Земли вокруг Солнца[28]. Масса нашей Галактики определяется исходя из периода обращения окрестностей Солнца вокруг центра Галактики и расстояния до центра Галактики[29].
Массы ближайших двойных звезд определяются по расстоянию между ними и периоду их обращения. Если звезда не имеет спутника и принадлежит главной последовательности, то её массу можно определить исходя из её светимости или температуры поверхности[30].
Значения масс различных объектов[править | править код]
| Объект | Масса (кг) | В других единицах | |
|---|---|---|---|
| Нейтрино | < 1,5⋅10−37 | < 0,12 | эВ |
| Электрон | 9,1⋅10−31 | 5,1⋅105 | эВ |
| Протон | 1,7⋅10−27 | 9,4⋅108 | эВ |
| Бозон Хиггса | 2,4⋅10−25 | 1,3⋅1011 | эВ |
| Вирус гриппа | 6⋅10−19 | 4⋅108 | а.е.м. |
| Снежинка | 1⋅10−7 | 0,1 | мг |
| Человек | 80 | 176 |
фунт |
| Слон | 4,5⋅103 | 4,5 | тонн |
| Кит | 1,5⋅105 | 150 | тонн |
| Пирамида Хеопса | 6,0⋅109 | 6,0⋅106 | тонн |
| Земля | 6,0⋅1024 |  |
масс Земли |
| Юпитер | 1,9⋅1027 |  |
масс Земли |
| Солнце | 2,0⋅1030 | |
масс Солнца |
| Другие звёзды | 4,0⋅1028—1,8⋅1032 | 0,02—90 | масс Солнца |
| Наша Галактика | 2,6⋅1041 | 1,3⋅1011 | масс Солнца |
| Другие галактики | 2,0⋅1036—2,0⋅1043 | 106—1013 | масс Солнца |
Этимология и история понятия[править | править код]
Слово масса (лат. massa, от др.-греч. μαζα) первоначально в античные времена обозначало кусок теста. Позднее смысл слова расширился, и оно стало обозначать цельный, необработанный кусок произвольного вещества; в этом смысле слово используется, например, у Овидия и Плиния[31]. В ряде областей науки и техники это слово (часто во множественном числе) до сих пор продолжает использоваться в значении какой-либо относительно однородной субстанции (воздушные массы, пластмасса, бумажная масса, селевая масса, народные массы).
Масса как научный термин для меры количества вещества была введена Ньютоном, до этого естествоиспытатели оперировали понятием веса. В труде «Математические начала натуральной философии» (1687) Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон ввёл массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что вес пропорционален массе[32]. Ньютон явно указал на эту пропорциональность и даже проверил её на опыте со всей возможной в те годы точностью: «Определяется масса по весу тела, ибо она пропорциональна весу, что мной найдено опытами над маятниками, произведенными точнейшим образом»[33] (эти опыты Ньютон подробно описал в III томе своих «Начал»).
Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения[34]. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, оно сохранялось в XVII—XIX веке, но затем подверглось критике как нефизическое и бессодержательное[35]. В настоящее время понятие «количество вещества» применяется, но имеет совершенно другой смысл.
Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии и во многих ситуациях не соблюдается.
Обобщения понятия массы[править | править код]
Прямые обобщения понятия массы включают в себя такие тензорные характеристики, как момент инерции, и такие показатели свойств системы «тело плюс среда», как массовое водоизмещение, присоединённая масса и эффективная масса, используемые в гидростатике, гидродинамике и квантовой теории.
Например, введение так называемой эффективной массы позволяет учесть взаимодействие электрона (или дырки) с периодическим электромагнитным полем кристаллической решетки в полупроводнике, что необходимо для корректного квантовомеханического описания движения носителей заряда.
См. также[править | править код]
- Эквивалентность массы и энергии
- Принцип эквивалентности сил гравитации и инерции
- Скрытая масса
- Сравнение массы и веса
- Эффективная масса
Комментарии[править | править код]
- ↑ Так, например, суммарная масса двух свободных частиц зависит от угла между их импульсами. В частности, масса системы, состоящей из двух фотонов, обладающих энергией Е каждый, равна нулю, если импульсы фотонов сонаправлены, и равна 2E/c2, если их импульсы направлены в противоположные стороны[15].
Примечания[править | править код]
- ↑ Окунь Л. Б. Масса // Физическая энциклопедия / Гл. ред. А. М. Прохоров. — М.: Большая Российская энциклопедия, 1992. — Т. 3. — С. 50—52. — 672 с. — 48 000 экз. — ISBN 5-85270-019-3.
- ↑ Дмитрий Иванович Сахаров, Михаил Иванович Блюдов. Физика для техникумов «Наука», 1969. С. 28.
- ↑ Неравенство пассивной гравитационной и инертной масс протяженного тела. Дата обращения: 23 июля 2014. Архивировано 13 августа 2014 года.
- ↑ Вебер Дж. — Общая теория относительности и гравитационные волны. Дата обращения: 25 июля 2014. Архивировано 27 июля 2014 года.
- ↑ 1 2 Phys. Rev. Lett. 100, 041101 (2008): Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ 1 2 [1]Архивная копия от 21 октября 2016 на Wayback Machine [0712.0607] Test of the Equivalence Principle Using a Rotating Torsion Balance
- ↑ Матвеев А. Н. Механика и теория относительности. — М.: ОНИКС, 2003. — 432 с. — ISBN 5-329-00742-9 [гл. 5, §§ 19—20].
- ↑ Мировой эталон килограмма заменили. lenta.ru. Дата обращения: 13 декабря 2018. Архивировано 18 ноября 2018 года.
- ↑ Кудрявцев П. С. Курс истории физики. — 2 изд., испр. и доп. М.: Просвещение, 1982. — 448 с. — Ч. 1, гл. 5. Дата обращения: 18 февраля 2011. Архивировано 4 января 2010 года.
- ↑ Tomilin K. A. Natural Systems of Units: To the Centenary Anniversary of the Planck System (англ.). Proc. of the XXII Internat. Workshop on high energy physics and field theory (июнь 1999). Дата обращения: 22 декабря 2016. Архивировано 12 мая 2016 года.
- ↑ Ландау Л. Д., Лифшиц Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7., § 9. Энергия и импульс.
- ↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 6.
- ↑ Фок В. А. Теория пространства, времени и тяготения. — М.: Государственное издательство технико-теоретической литературы, 1955. — 504 с.
- ↑ Мёллер К. Теория относительности = The theory of relativity. Clarendon Press. Oxford. 1972.. — М.: Атомиздат, 1975. — 400 с.
- ↑ 1 2 3 Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?» // Успехи физических наук. — 2000. — Т. 170, № 12. — С. 1366—1371. — doi:10.3367/UFNr.0170.200012j.1366.
- ↑
Окунь Л. Б. Понятие массы (Масса, энергия, относительность) (Методические заметки) // УФН. — 1989. — Т. 158. — С. 511—530. - ↑ Широков Ю. М. Ядерная физика. — М., Наука,1980. — С. 37.
- ↑ Наумов А. И. Физика атомного ядра и элементарных частиц. — М., Просвещение, 1984. — С. 25.
- ↑ В этом абзаце для простоты используется рассмотренная выше система единиц с = 1.
- ↑ Рубаков В. А. Долгожданное открытие: бозон Хиггса Архивная копия от 29 октября 2013 на Wayback Machine // Наука и жизнь. — 2012. — № 10. — С. 20—40. — ISSN 0028-1263. —
- ↑ Садовский М. В. Лекции по квантовой теории поля. — Москва-Ижевск : Институт компьютерных исследований, 2003. — С. 370 — ISBN 5-93972-241-5. — URL: http://eqworld.ipmnet.ru/ru/library/books/Sadovskij2002ru.pdf Архивная копия от 9 сентября 2016 на Wayback Machine
- ↑ Герштейн С. С., Захаров В. И. K-мезоны // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 384—388. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
- ↑ M. Morris, K. Thorne, and U. Yurtsever, Wormholes, Time Machines, and the Weak Energy Condition Архивировано 17 июля 2012 года., Physical Review, 61, 13, September 1988, pp. 1446—1449
- ↑ Завельский, 1970, с. 119.
- ↑ Завельский, 1970, с. 123.
- ↑ Копылов Г. И. Всего лишь кинематика. — М.: Атомиздат, 1968. — 176 с.
- ↑ Завельский, 1970, с. 136.
- ↑ Завельский, 1970, с. 150.
- ↑ Завельский, 1970, с. 161.
- ↑ Киппенхан Р. 100 миллиардов солнц. Рождение, жизнь и смерть звезд. — М.: Мир, 1990. — С. 281—284 — ISBN 5-03-001195-1.
- ↑ Джеммер, М., 1967, Глава I.
- ↑ Спасский Б. И. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
- ↑ Ньютон И. Математические начала натуральной философии, том I, определение 1.
- ↑ Тюлина И. А. Об основах ньютоновой механики (к трёхсотлетию «Начал» Ньютона) // История и методология естественных наук. — М.: Изд-во Моск. ун-та, 1989. — Вып. 36. — С. 184—196..
- ↑ Мах Э. Механика. Историко-критический очерк её развития. — Ижевск: НИЦ РХД, 2000. — 456 с. — ISBN 5-89806-023-5.
Литература[править | править код]
- Джеммер, Макс. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
- Переиздание: Едиториал УРСС, 2003, ISBN 5-354-00363-6.
- Окунь Л. Б. Понятие массы (Масса, энергия, относительность) Успехи физических наук, № 158 (1989)
- Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
- L. B. Okun. On the concepts of vacuum and mass and the search for higgs (англ.) // Modern Physics Letters A. — 2012. — Vol. 27. — P. 1230041. — doi:10.1142/S0217732312300418. — arXiv:1212.1031.
- Спасский Б. И.. История физики. М., «Высшая школа», 1977. Том 1, часть 1-я.
- Gordon Kane. The Mysteries of Mass. // Scientific American. June 27, 2005.
- Завельский Ф. С. Взвешивание миров, атомов и элементарных частиц. — М.: Атомиздат, 1970. — 176 с.
Статьи[править | править код]
- Государственный первичный эталон единицы массы ГЭТ 3-2008
Измерение массы и объема. Плотность вещества
- Закон инерции
- Инертность тела
- Инертная и гравитационная масса
- Измерение массы с помощью весов
- Плотность вещества
- Задачи
- Лабораторная работа №5. Определение плотности жидкостей
- Лабораторная работа №6. Определение плотности твердых тел
п.1. Закон инерции
Как свидетельствуют многочисленные эксперименты и наш повседневный опыт, чтобы неподвижное тело сдвинулось с места, на него должно подействовать другое тело. С другой стороны, чтобы остановить тело, уже находящееся в движении, или изменить его траекторию, также необходимо внешнее воздействие (обычно, причиной остановки в механике является трение; причиной изменения траектории – столкновение с другим телом и т.п.).
Возникает вопрос: а что будет с телом, если на него не действуют никакие другие тела?
Очевидно, если тело покоилось, то оно продолжит покоиться.
А если оно двигалось, что тогда произойдет?
А теперь представим себе идеальный случай: трение полностью отсутствует.
В этом случае шарик будет двигаться с постоянной скоростью бесконечно долго.
Закон инерции
Если на тело не действуют другие тела, оно либо покоится, либо движется прямолинейно и равномерно.
Закон инерции впервые был сформулирован Галилео Галилеем в его работе «Диалог о двух главнейших системах мира» (опубликована в 1632 г.). Однако Галилей ошибочно считал, что свободное равномерное движение тела возможно не только по прямой, но и по окружности.
В 1644 г. Рене Декарт уточнил формулировку Галилея, указав, что для изменения направления скорости также необходимо внешнее воздействие. Т.к. при равномерном движении по окружности направление скорости всё время меняется, оно не является свободным. Следовательно, свободное движение может быть только прямолинейным.
п.2. Инертность тела
Инертность – это свойство тела сохранять состояние покоя или прямолинейное и равномерное движение.
Благодаря инертности, тело не может мгновенно перейти из состояния покоя в движение или из состояния движения в покой. Для изменения скорости тела необходимо определенное время.
При взаимодействии инертность проявляется в том, что разные тела под одинаковым внешним воздействием получают разные ускорения (об ускорении – см. §11 данного справочника).
п.3. Инертная и гравитационная масса
Инертная масса – это количественная мера инертности, показатель того, в какой степени данное тело будет препятствовать изменению своей скорости.
Гравитационная масса – это количественная характеристика способности тела к взаимодействию по закону всемирного тяготения.
На сегодняшний день с высоким уровнем точности (относительная ошибка (sim 10^{-13}) в эксперименте 2009 г.) установлено, что значения инертной и гравитационной массы одного и того же тела равны. Поэтому инертную и гравитационную массы на практике не различают (принцип эквивалентности) и рассматривают «просто» массу тела.
Единицей массы в системе СИ является килограмм (кг).
Масса является одной из семи основных единиц системы СИ (см. §2 данного справочника).
При изучении очень больших или очень малых физических тел удобней использовать внесистемные единицы массы.
Например, в астрофизике единицей для сравнения масс небесных тел служит масса Солнца, (M_{odot}approx 1,99cdot 10^{30} text{кг}). А в физической химии при определении масс атомов и молекул используется атомная единица массы, равная 1/12 массы свободного покоящегося атома углерода, (1 text{а.е.м.}approx 1,66cdot 10^{-27} text{кг}).
п.4. Измерение массы с помощью весов
Весы – это прибор для измерения массы по весу тела на основании принципа эквивалентности инертной и гравитационной масс.
 Весы равноплечие рычажные лабораторные и наборы гирек к ним |
Вес тела определяется сравнением с весом эталонной массы (гири). Весы находятся в равновесии, если помещенные на их чаши тела одинаково притягиваются к Земле. Чтобы найти массу тела, его кладут на одну чашу весов, а на другую – гири известной массы, пока весы не уравновесятся. |
Метод двойного взвешивания (метод Гаусса)
Шаг 1. Поместить тело для взвешивания на левую чашку весов, а на правую чашку весов поставить гири до полного уравновешивания. Записать полученный результат (m_1).
Шаг 2. Переложить тело на правую чашку весов, а гири – на левую. Повторить уравновешивание. Записать полученный результат (m_2).
Шаг 3. Найти массу тела как среднее арифметическое $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ т.к. (delta_m=0,01text{%}) – относительная погрешность для весов класса точности III.
п.5. Плотность вещества
Плотность вещества однородного тела – это физическая величина, равная отношению массы тела к его объему: $$ rho=frac mv $$
Единицей плотности в системе СИ является килограмм на метр кубический (кг/м3).
Плотности различных веществ тщательно измерены и занесены в справочные таблицы.
Плотности в справочнике даны для химически чистых веществ (содержание основного вещества 98% и выше), при нормальных условиях (давление 760 мм рт.ст. и температура 0°С), если не указаны другие значения давления и температуры.
Плотность зависит от следующих свойств вещества:
- масса молекул (атомов) вещества. Например, масса атомов алюминия 27 а.е.м., а атомов золота 197 а.е.м. При этом плотность алюминия 2700 кг/м3, а плотность золота 19300 кг/м3, что приблизительно соответствует соотношению масс атомов. Небольшое различие можно объяснить большим расстоянием между более крупными атомами золота в кристаллической решетке (гранецентрированный куб, как для алюминия, так и для золота).
- расположение частиц вещества. Например, расстояния между слоями атомов углерода в графите в 3 раза больше, чем межатомные расстояния в самих слоях; а вот в алмазе атомы углерода упакованы очень плотно. В результате плотность графита 2160 кг/м3, а плотность алмаза 3510 кг/м3, хотя оба вещества состоят из атомов углерода.
- агрегатное состояние, в котором находится вещество. Наименьшие плотности у газов, наибольшие – у твердых веществ. Например, плотность воздуха (газ) 1,29 кг/м3, плотность воды (жидкость) 1000 кг/м3, плотность железа (твердое тело) 7900 кг/м3.
п.6. Задачи
Задача 1. Найдите плотность мела, если масса кусочка равна 7,2 г, а объем – 3,6 см3.
Дано:
(m=7,2 text{г}=7,2cdot 10^{-3} text{кг})
(V=3,6 text{см}^3=3,6cdot 10^{-6} text{м}^3)
__________________
(rho-?)
Плотность (rho=frac mv) $$ rho=frac{7,2cdot 10^{-3}}{3,6cdot 10^{-6}}=2cdot 10^3=2000 (text{кг/м}^3) $$ Ответ: (2000 text{кг/м}^3)
Задача 2. Найдите объем тела человека массой 60 кг, ели средняя плотность человеческого тела равна плотности воды. Ответ дайте в литрах.
Дано:
(m=60 text{кг})
(rho=1000 text{кг/м}^3)
__________________
(V-?)
Плотность (rho=frac mv Rightarrow) Объем (V=frac mp) $$ V=frac{60}{1000}=0,06 (text{м}^3)=60 (text{л}) $$ Ответ: 60 л.
Задача 3. Алюминиевая кастрюля имеет массу 0,5 кг. Если кастрюлю таких же размеров изготовить из стали, какая у неё будет масса?
Дано:
(m_1=0,5 text{кг})
(rho_1=2700 text{кг/м}^3)
(rho_2=7800 text{кг/м}^3)
__________________
(m_2-?)
У кастрюль одинаковых размеров одинаковый объем. Получаем: begin{gather*} V=frac{m_1}{rho_1}=frac{m_2}{rho_2}Rightarrow m_2=frac{rho_2}{rho_1}m_1\ m_2=frac{7800}{2700}cdot 0,5approx 1,4 (text{кг}) end{gather*} Ответ: ≈1,4 кг.
Задача 4*. В банку, до краев наполненную водой, опустили кусок золота массой 1 кг. В другую такую же банку опустили кусок меди массой 1 кг. Где больше вылилось воды и насколько больше? (ответ дайте в миллилитрах).
Дано:
(m=1 text{кг})
(rho_1=19320 text{кг/м}^3)
(rho_2=8940 text{кг/м}^3)
__________________
(Delta V-?)
Объем вытесненной воды равен объему погруженного тела: $$ V_1=frac{m}{rho_1}, V_2=frac{m}{rho_2} $$ Т.к. (rho_1gt rho_2, V_1lt V_2), объем воды, вытесненной медью, больше. $$ Delta V=V_2-V_1=frac{m}{rho_2}-frac{m}{rho_1}=mleft(frac{1}{rho_2}-frac{1}{rho_2}right)=mfrac{rho_1-rho_2}{rho_1rho_2} $$ Подставляем: begin{gather*} Delta V=1cdotfrac{19320-8940}{19320cdot 8940}approx 6,01cdot 10^{-5} text{м}^3\ 1 text{л}=10^{-3} text{м}^3, 1 text{мл}=1 text{cм}^3=10^{-3} text{л}=10^{-6} text{м}^3\ Delta Vapprox 60,1 text{мл} end{gather*} Ответ: ≈60,1 мл; больше вылилось во втором случае, для меди.
п.7. Лабораторная работа №5. Определение плотности жидкостей
Цель работы
Научиться измерять массу и объем жидкостей. Научиться определять жидкости по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Пусть масса стакана с жидкостью равна (M), абсолютная погрешность этого взвешивания (Delta M); масса пустого стакана (m_{text{ст}}), абсолютная погрешность (Delta m_{text{ст}}). Тогда масса жидкости $$ m=M-m_{text{ст}} $$ Абсолютная и относительная погрешности определения массы жидкости $$ Delta m=Delta M+Delta m_{text{ст}}, delta_m=frac{Delta m}{m}cdot 100text{%} $$ Мерный цилиндр проградуирован в миллилитрах. Для расчёта плотности жидкости в системе СИ необходимо помнить, что $$ 1 text{мл}=1 text{cм}^3=10^{-6} text{м}^3 $$ Абсолютная погрешность измерения объема жидкости равна половине цены деления мерного цилиндра $$ Delta V=frac d2 $$ Относительная погрешность равна $$ delta_V=frac{Delta V}{V}cdot 100text{%}. $$ Плотность жидкости равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$
Приборы и материалы
Два стакана с неизвестными жидкостями; мерный цилиндр; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Поставьте на весы первый стакан с жидкостью. Методом двойного взвешивания определите массу стакана и жидкости (M_1). Оцените абсолютную погрешность взвешивания.
3. Вылейте жидкость из первого стакан в мерный цилиндр и определите её объем (V_1). Оцените абсолютную погрешность измерения объема.
4. Методом двойного взвешивания определите массу первого стакана (m_{text{ст1}}). Оцените абсолютную погрешность взвешивания.
5. По формулам, данным в теоретической части, определите плотность жидкости, относительную и абсолютную погрешности полученного результата.
6. По таблице в справочнике определите, какая жидкость находится в первом стакане.
7.-11. Повторите шаги 2.-6. для второго стакана с жидкостью.
12. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра (d=1 text{мл}=1 text{см}^3)
Первый стакан
| Стадии двойного взвешивания | (M, text{г}) | (m_{text{ст}}, text{г}) |
| (m_1) | 151,2 | 50,1 |
| (m_2) | 150,8 | 49,9 |
| (m=frac{m_1+m_2}{2}) | 151,0 | 50,0 |
| (|m_1-m_2|) | 0,4 | 0,2 |
| (0,01text{%}m) | 0,015 | 0,005 |
| (Delta m) | 0,4 | 0,2 |
Масса первой жидкости
begin{gather*} m=151,0-50,0=101,0,\ Delta m=0,4+0,2=0,6,\ delta_m=frac{0,6}{101,0}cdot 100text{%}=0,59text{%} end{gather*}
Объем первой жидкости
begin{gather*} V=109 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{109}cdot 100text{%}=0,46text{%} end{gather*}
Плотность первой жидкости
begin{gather*} rho=frac mV=frac{101,0}{109}approx 0,927frac{text{г}}{text{см}^3}=927frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,59text{%}+0,46text{%}approx 1,1text{%},\ delta rho=rhocdotdelta_{rho}=927cdot 0,011approx 10frac{text{кг}}{text{м}^3},\ rho=(927pm 10)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,1text{%} end{gather*}
В первом стакане – подсолнечное масло.
Второй стакан
| Стадии двойного взвешивания | (M, text{г}) | (m_{text{ст}}, text{г}) |
| (m_1) | 100,4 | 50,0 |
| (m_2) | 100,2 | 49,9 |
| (m=frac{m_1+m_2}{2}) | 100,3 | 49,95≈50,0 |
| (|m_1-m_2|) | 0,2 | 0,1 |
| (0,01text{%}m) | 0,01 | 0,005 |
| (Delta m) | 0,2 | 0,1 |
Масса второй жидкости
begin{gather*} m=100,3-50,0=50,3,\ Delta m=0,2+0,1=0,3,\ delta_m=frac{0,3}{50,3}cdot 100text{%}=0,6text{%} end{gather*}
Объем второй жидкости
begin{gather*} V=50 text{мл},\ Delta V=frac d2=0,5 text{мл},\ delta_V=frac{0,5}{50}cdot 100text{%}=1,0text{%} end{gather*}
Плотность второй жидкости
begin{gather*} rho=frac mV=frac{50,3}{50,0}= 1,006frac{text{г}}{text{см}^3}=1006frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,6text{%}+1,0text{%}= 1,6text{%},\ delta rho=rhocdotdelta_{rho}=1006cdot 0,016approx 16frac{text{кг}}{text{м}^3},\ rho=(1006pm 16)frac{text{кг}}{text{м}^3},\ delta_{rho}=1,6text{%} end{gather*}
Во втором стакане – вода.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности жидкости в работе методом двойного взвешивания измерялась масса (стакана с жидкостью и пустого стакана) и объем жидкости в мерном цилиндре.
Результаты для двух данных жидкостей
begin{gather*} rho_1=(927pm 10)frac{text{кг}}{text{м}^3}, delta_{rho 1}=1,1text{%}\ rho_2=(1006pm 16)frac{text{кг}}{text{м}^3}, delta_{rho 2}=1,6text{%} end{gather*}
По таблицам в справочнике было определено, что в первом стакане – растительное масло, а во втором – вода. Полученные результаты также подтверждаются цветом (желтоватый – для масла, прозрачный – для воды) и запахом (характерный запах у масла и отсутствие запаха у воды).
п.8. Лабораторная работа №6. Определение плотности твердых тел
Цель работы
Научиться измерять массу и объем твердых тел неправильной формы. Научиться определять вещества твердых тел по плотности, оценивать погрешность полученных результатов.
Теоретические сведения
Для определения массы тел в данной работе используется метод двойного взвешивания (см. выше в данном параграфе).
Масса тела определяется как среднее арифметическое двух взвешиваний на разных чашках весов: $$ m=frac{m_1+m_2}{2}. $$ Абсолютная погрешность двойного взвешивания – это большая из двух величин $$ Delta m=max(|m_1-m_2|; 0,01text{%}m) $$ Относительная погрешность $$ delta_m=frac{Delta m}{m}cdot 100text{%} $$ Объем твердого тела неправильной формы определяется с помощью погружения в жидкость.
Пусть объем жидкости в мерном цилиндре до погружения тела (V_0), после погружения – (V’).
Тогда объем самого тела (V=V’-V_0).
Абсолютная погрешность измерения объема равна половине цены деления мерного цилиндра (Delta V_0=frac d2) для прямого измерения. Для разности двух прямых измерений общая абсолютная погрешность $$ Delta V=2Delta V_0=d $$ Относительная погрешность $$ delta_V=frac dVcdot 100text{%}. $$ Плотность твердого тела равна $$ rho=frac mv. $$ Относительная погрешность результата $$ delta_{rho}=delta_m+delta_V. $$ Абсолютная погрешность результата $$ Deltarho=rhocdot delta_{rho} $$ Перевод полученных результатов в систему СИ $$ 1frac{text{г}}{text{см}^3}= frac{10^{-3} text{кг}}{10^{-6} text{м}^3}=10^3frac{text{кг}}{text{м}^3}=1000frac{text{кг}}{text{м}^3} $$
Приборы и материалы
Мерный цилиндр, наполненный водой наполовину; два тела неправильной формы из металлов; весы с разновесом.
Ход работы
1. Приготовьте весы к взвешиванию.
2. Методом двойного взвешивания определите массу первого тела. Найдите абсолютную и относительную погрешность взвешивания.
3. С помощью погружения первого тела в жидкость найдите его объем. Абсолютная погрешность равна цене деления мерного цилиндра. Рассчитайте относительную погрешность.
4. По формулам, данным в теоретической части, определите плотность твердого тела, относительную и абсолютную погрешности полученного результата.
5. По таблице в справочнике определите, из какого вещества изготовлено первое тело.
6-9. Повторите шаги 2.-5. для второго твердого тела неправильной формы.
10. Сделайте выводы о проделанной работе.
Результаты измерений и вычислений
Цена деления мерного цилиндра (d=0,5 text{мл}=0,5 text{см}^3)
Первое тело
| Стадии двойного взвешивания | (m, text{г}) |
| (m_1) | 22,34 |
| (m_2) | 22,38 |
| (m=frac{m_1+m_2}{2}) | 22,36 |
| (|m_1-m_2|) | 0,04 |
| (0,01text{%}m) | 0,002 |
| (Delta m) | 0,04 |
| (delta m) | 0,18% |
| Стадии определения объема | (V, text{см}^3) |
| (V_0) | 50,0 |
| (V’) | 58,5 |
| (V=V’-V_0) | 8,5 |
| (Delta V=d) | 0,5 |
| (delta_V) | 5,9% |
Плотность первого тела
begin{gather*} rho=frac mV=frac{22,36}{8,5}approx 2,631frac{text{г}}{text{см}^3}=2631frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,18text{%}+5,9text{%}approx 6,1text{%},\ delta rho=rhocdotdelta_{rho}=2631cdot 0,061approx 160frac{text{кг}}{text{м}^3},\ rho=(2630pm 160)frac{text{кг}}{text{м}^3},\ delta_{rho}=6,1text{%} end{gather*}
Первое тело изготовлено из алюминия.
Второе тело
| Стадии двойного взвешивания | (m, text{г}) |
| (m_1) | 101,21 |
| (m_2) | 101,27 |
| (m=frac{m_1+m_2}{2}) | 101,25 |
| (|m_1-m_2|) | 0,06 |
| (0,01text{%}m) | 0,005 |
| (Delta m) | 0,06 |
| (delta m) | 0,06% |
| Стадии определения объема | (V, text{см}^3) |
| (V_0) | 50,0 |
| (V’) | 63,0 |
| (V=V’-V_0) | 13,0 |
| (Delta V=d) | 0,5 |
| (delta_V) | 3,8% |
Плотность второго тела
begin{gather*} rho=frac mV=frac{101,25}{13,0}approx 7,788frac{text{г}}{text{см}^3}=7788frac{text{кг}}{text{м}^3},\ delta_{rho}=delta_m+delta_V=0,06text{%}+3,8text{%}approx 3,9text{%},\ delta rho=rhocdotdelta_{rho}=7788cdot 0,039approx 300frac{text{кг}}{text{м}^3},\ rho=(7790pm 300)frac{text{кг}}{text{м}^3},\ delta_{rho}=3,9text{%} end{gather*}
Второе тело изготовлено из железа.
Выводы
На основании проделанной работы можно сделать следующие выводы.
Для определения плотности твердых металлических тел неправильной формы в работе методом двойного взвешивания измерялась масса тел. Объем определялся методом погружения в мерном цилиндре.
Результаты для двух данных тел
begin{gather*} rho_1=(2630pm 160)frac{text{кг}}{text{м}^3}, delta_{rho 1}=6,1text{%}\ rho_2=(7790pm 300)frac{text{кг}}{text{м}^3}, delta_{rho 2}=3,9text{%} end{gather*}
По таблицам в справочнике было определено, что первое тело изготовлено из алюминия, второе – из железа.
- Эта статья о физической величине. Статью об автогонщике см. Масса, Фелипе
Ма́сса — одна из важнейших физических величин. Первоначально (XVII–XIX века) она характеризовала «количество вещества» в физическом объекте, от которого, по представлениям того времени, зависели как способность объекта сопротивляться приложенной силе (инертность), так и гравитационные свойства — вес. В современной физике понятие «количество вещества» имеет другой смысл, а под массой понимают два различных свойства физического объекта:
- Гравитационная масса показывает, с какой силой тело взаимодействует с внешними гравитационными полями (пассивная гравитационная масса) и какое гравитационное поле создаёт само это тело (активная гравитационная масса) — эта масса фигурирует в законе всемирного тяготения.
- Инертная масса, которая характеризует меру инертности тел и фигурирует во втором законе Ньютона. Если произвольная сила в инерциальной системе отсчёта одинаково ускоряет разные тела, этим телам приписывают одинаковую инертную массу.
Теоретически, гравитационная и инертная масса равны, поэтому в большинстве случаев просто говорят о массе, не уточняя какую из них имеют в виду.
Масса тела не зависит от того, какие внешние силы и в какой момент на это тело действуют.
Содержание
- 1 Исследование единства понятия массы
- 2 Определение массы
- 2.1 Масса составных и нестабильных систем
- 3 Единицы массы
- 4 Измерение массы
- 5 Исторический очерк
- 6 Примечания
- 7 Литература
- 8 См. также
- 9 Ссылки
Исследование единства понятия массы
Гравитационная масса — характеристика материальной точки при анализе в классической механике, которая полагается причиной гравитационного взаимодействия тел, в отличие от инертной массы, которая определяет динамические свойства тел.
Как установлено экспериментально, эти две массы пропорциональны друг другу. Не было обнаружено никаких отклонений от этого закона, поэтому новых единиц измерения для инерционной массы не вводят (используют единицы измерения гравитационной массы) и коэффициент пропорциональности считают равным единице, что позволяет говорить и о равенстве инертной и гравитационной масс.
Можно сказать, что первая проверка пропорциональности двух видов массы была выполнена Галилео Галилеем, который открыл универсальность свободного падения. Согласно опытам Галилея по наблюдению свободного падения тел, все тела, независимо от их массы и материала, падают с одинаковым ускорением свободного падения. Сейчас эти опыты можно трактовать так: увеличение силы, действующей на более массивное тело со стороны гравитационного поля Земли, полностью компенсируется увеличением его инертных свойств. Следовательно, гравитационная масса пропорциональна инертной массе[1]
На равенство инертной и гравитационной масс обратил внимание ещё Ньютон, он же впервые доказал, что они отличаются не более чем на 0,1 % (иначе говоря, равны с точностью до 10−3).. На сегодняшний день это равенство экспериментально проверено с очень высокой степенью точности (3×10−13).
Фактически, равенство гравитационной и инертной масс было сформулировано А. Эйнштейном в виде слабого принципа эквивалентности — составной части принципов эквивалентности, положенных в основу общей теории относительности. Существует также сильный принцип эквивалентности — по которому в свободно падающей системе локально выполняется специальная теория относительности. Он на сегодняшний день проверен со значительно меньшей точностью.
В классической механике — масса есть величина аддитивная (масса системы равна сумме масс составляющих её тел) и инвариантная относительно смены системы отсчёта. В релятивистской механике масса неаддитивная величина, но тоже инвариантная, и хотя здесь под массой понимается абсолютная величина 4-вектора энергии-импульса, лоренц-инвариантная.
Введение так называемой релятивистской массы, зависящей от величины скорости тела в рассматриваемой системе отсчёта, использовалось в ранних работах по теории относительности. В настоящее время термины «релятивистская масса» и «масса покоя» считаются устаревшими[2].
Определение массы
В СТО масса тела m определяется из уравнения релятивистской динамики [3]:
- ,
,где E — полная энергия свободного тела, p — его импульс, c — скорость света.
Определённая выше масса является релятивистским инвариантом, то есть она одна и та же во всех системах отсчёта. Если перейти в систему отсчёта, где тело покоится, то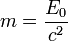 
— масса определяется энергией покоя.
Следует однако отметить, что частицы с нулевой инвариантной массой (фотон, гравитон…) двигаются в вакууме со скоростью света (c ≈ 300000 км/сек) и поэтому не обладают системой отсчёта, в которой бы покоились.
Масса составных и нестабильных систем
Инвариантная масса элементарной частицы постоянна, и одинакова у всех частиц данного типа и их античастиц. Однако, масса массивных тел, составленных из нескольких элементарных частиц (например, ядра или атома) может зависеть от их внутреннего состояния.
Для системы, подверженной распаду (например, радиоактивному), величина энергии покоя определена лишь с точностью до постоянной Планка, делённой на время жизни: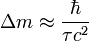 
. При описании такой системы при помощи квантовой механики удобно считать массу комплексной, с мнимой частью равной означенному Δm.
Единицы массы
В системе СИ масса измеряется в килограммах. В системе СГС используются граммы. Иногда используются также другие единицы измерения массы.
Измерение массы
-
Основная статья: Весы
Исторический очерк
Понятие массы было введено в физику Ньютоном, до этого естествоиспытатели оперировали с понятием веса. В труде «Математические начала натуральной философии» Ньютон сначала определил «количество материи» в физическом теле как произведение его плотности на объём. Далее он указал, что в том же смысле будет использовать термин масса. Наконец, Ньютон вводит массу в законы физики: сначала во второй закон Ньютона (через количество движения), а затем — в закон тяготения, откуда сразу следует, что масса пропорциональна весу [4].
Фактически Ньютон использует только два понимания массы: как меры инерции и источника тяготения. Толкование её как меры «количества материи» — не более чем наглядная иллюстрация, и оно подверглось критике ещё в XIX веке как нефизическое и бессодержательное.
Долгое время одним из главных законов природы считался закон сохранения массы. Однако в XX веке выяснилось, что этот закон является ограниченным вариантом закона сохранения энергии, и во многих ситуациях не соблюдается.
Примечания
- ↑ Например, это видно из закона всемирного тяготения Ньютона (связывающего силу и гравитационную массу), второго закона Ньютона (связывающего силу с массой инерционной), и замеченной Галилеем независимости ускорения свободного падения от материала:
- ↑ См., например, дискуссию в «Успехах физических наук», вып.12, 2000: письмо Окуня).
- ↑ Ландау, Л. Д., Лифшиц, Е. М. Теория поля. — Издание 7-е, исправленное. — М.: Наука, 1988. — 512 с. — («Теоретическая физика», том II). — ISBN 5-02-014420-7, § 9. Энергия и импульс.
- ↑ Спасский Б. И.. История физики. М., «Высшая школа», 1977, том I, с. 135—137.
Литература
- Окунь Л. Б. О письме Р. И. Храпко «Что есть масса?». Успехи физических наук, № 170, с.1366 (2000)
- Спасский Б. И.. История физики. М., «Высшая школа», 1977.
-
- Том 1, часть 1-я
- Макс Джеммер. Понятие массы в классической и современной физике. — М.: Прогресс, 1967.
См. также
- Эталон
Ссылки
Wikimedia Foundation.
2010.
Наверное, вы слышали о равенстве инертной* и гравитационной масс. Я тоже об этом слышал, и даже читал ещё в школе, но никак не мог понять, что же в этом такого?
И почему это равенство так тщательно проверяли, а ещё, к тому же, я не особо понимал в чем же кроется это равенство, как его понять?
Оказывается, все очень просто: у нас есть масса, та масса, которой мы обладаем – не вес(!), а именно масса, потому что вес может меняться, например, при свободном падении мы ничего не весим, или когда едем в лифте, то наш вес сначала становится больше, когда лифт трогается и едет вверх, а когда вниз – меньше.
Масса же всегда остаётся постоянной, если не учитывать ядерные взаимодействия. Теперь, возьмём два металлических шара (их любят физики, а ещё про шары есть анекдот). Бросим шары, большой и маленький шары (если не учитывать сопротивление воздуха) они упадут на землю одновременно. Почему так? По закону всемирного тяготения сила взаимодействия между Землёй и шаром равна F = GmM/r², где m – масса шара, а M – масса Земли. (Формулы… Терпите). А ускорение шара это F/m. Отсюда получаем: a = GM/r². Т.к. F и m у нас превратились в а – ускорение свободного падения шара на Землю за счёт притяжения.
Отсюда получаем интересное свойство: масса сократилась. Ускорение, которое придается Землёй телам, падающим на нее, зависит только от массы Земли и расстояния до тел. Но отсюда так же следует, что более тяжёлый шар испытывает более сильное тяготение (оно зависит от массы шара и земли, по закону всемирного тяготения и от расстояния между шарами).
Но, если у шара большая масса, значит нужно приложить большую силу, чтобы ускорить его! Он плохо ускоряется, ибо: F=ma. И, отсюда следует что, более массивный шар хуже ускоряется, и это компенсирует увеличенную силу, поэтому ускорение у обоих шаров будет одинаковым. У второго меньше масса и меньше тяготение.
И это просто потрясающее совпадение! Масса, которая идёт в формуле закона всемирного тяготения (гравитационная) и масса, которая идёт в формуле второго закона Ньютона (инертная, то есть какая сила нужна, чтобы сдвинуть тело, и какое ускорение ему будет передано этой силой) идентичны до какого-то большого знака после запятой. Попросту равны.
Вот это и есть то самое равенство гравитационной и инертной массы.
Примечание:
*) Инерция – это, простыми словами, способность тела сопротивляться изменению своей скорости под действием силы.
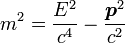