Как найти информационный объем одного сигнала

Обновлено: 24.05.2023

Давайте разберемся с этим, ведь нам придется измерять объем памяти и быстродействие компьютера.

Единицей измерения количества информации является бит – это наименьшая (элементарная) единица.

Байт – основная единица измерения количества информации.

Байт – довольно мелкая единица измерения информации. Например, 1 символ – это 1 байт.

Производные единицы измерения количества информации

1 килобайт (Кб)=1024 байта =2 10 байтов

1 мегабайт (Мб)=1024 килобайта =2 10 килобайтов=2 20 байтов

1 гигабайт (Гб)=1024 мегабайта =2 10 мегабайтов=2 30 байтов

1 терабайт (Гб)=1024 гигабайта =2 10 гигабайтов=2 40 байтов

Запомните, приставка КИЛО в информатике – это не 1000, а 1024, то есть 2 10 .

Методы измерения количества информации

Итак, количество информации в 1 бит вдвое уменьшает неопределенность знаний. Связь же между количеством возможных событий N и количеством информации I определяется формулой Хартли:

Алфавитный подход к измерению количества информации

Вероятностный подход к измерению количества информации

Этот подход применяют, когда возможные события имеют различные вероятности реализации. В этом случае количество информации определяют по формуле Шеннона:

I – количество информации,

N – количество возможных событий,

P_i – вероятность i-го события.

Задача 1.

Имеется 4 равновероятных события (N=4).

Задача 2.

Чему равен информационный объем одного символа русского языка?

В русском языке 32 буквы (буква ё обычно не используется), то есть количество событий будет равно 32. Найдем информационный объем одного символа. I=log₂ N=log₂ 32=5 битов (2 5 =32).

Примечание. Если невозможно найти целую степень числа, то округление производится в большую сторону.

Задача 3.

Чему равен информационный объем одного символа английского языка?

Задача 4.

Световое табло состоит из лампочек, каждая из которых может находиться в одном из двух состояний (“включено” или “выключено”). Какое наименьшее количество лампочек должно находиться на табло, чтобы с его помощью можно было передать 50 различных сигналов?

С помощью N лампочек, каждая из которых может находиться в одном из двух состояний, можно закодировать 2 N сигналов.

2 5 6 , поэтому пяти лампочек недостаточно, а шести хватит. Значит, нужно 6 лампочек.

Задача 5.

Метеостанция ведет наблюдения за влажностью воздуха. Результатом одного измерения является целое число от 0 до 100, которое записывается при помощи минимально возможного количества битов. Станция сделала 80 измерений. Определите информационный объем результатов наблюдений.

В данном случае алфавитом является множество чисел от 0 до 100, всего 101 значение. Поэтому информационный объем результатов одного измерения I=log₂101. Но это значение не будет целочисленным, поэтому заменим число 101 ближайшей к нему степенью двойки, большей, чем 101. это число 128=2 7 . Принимаем для одного измерения I=log₂128=7 битов. Для 80 измерений общий информационный объем равен 80*7 = 560 битов = 70 байтов.

Задача 6.

Определите количество информации, которое будет получено после подбрасывания несимметричной 4-гранной пирамидки, если делают один бросок.

Пусть при бросании 4-гранной несимметричной пирамидки вероятности отдельных событий будут равны: p₁=1/2, p₂=1/4, p₃=1/8, p₄=1/8.

Тогда количество информации, которое будет получено после реализации одного из них, можно вычислить по формуле Шеннона:

I = -[1/2 * log₂(1/2) + 1/4 * log₂(1/4) + 1/8 * log(1/8) + 1/8 * log(1/8)] = 14/8 битов = 1,75 бита.

Задача 7.

В книге 100 страниц; на каждой странице – 20 строк, в каждой строке – 50 символов. Определите объем информации, содержащийся в книге.

Задача 8.

Оцените информационный объем следующего предложения:

Тяжело в ученье – легко в бою!

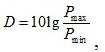
(2.10)

где P – максимальное и минимальное значения мгновенной мощности. Пик-фактором сигнала называют отношение максимальной мощности к средней

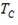
Р

ширина спектра сигнала –

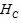
отношение сигнал/шум или превышение сигнала над помехой –

Таким образом, можно принять некоторое геометрическое представление сигнала как некоторого объема в трехмерном пространстве (рис.2.6).

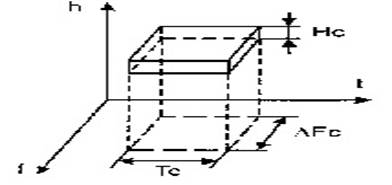
Рис. 2.6 Геометрическое представление сигнала Объемом сигнала принято называть произведение трех параметров

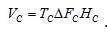
Введя понятие объема сигнала можно сравнительно просто представить соотношения между свойствами сигнала и свойствами системы связи.

Система связи может быть охарактеризована:

ü временем в течении которого канал связи предоставлен для передачи;

ü полосой частот, которую канал способен пропустить;

ü полосой уровней к зависящей от допустимой нагрузки на аппаратуру канала.

Очевидно, что передача сигнала с характеристиками с” с’ с по системе связи с каналом, имеющим параметры к’ к’ к возможна, лишь при условиях

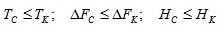
Динамический диапазон и пик-фактор сигналов

Чтобы охарактеризовать изменения мгновенной мощности сигналов вводятся понятия динамического диапазона и пик-фактора. Динамический диапазон сигнала. дБ. определяется выражением

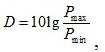
(2.10)

где P – максимальное и минимальное значения мгновенной мощности. Пик-фактором сигнала называют отношение максимальной мощности к средней

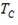
Р

ширина спектра сигнала –

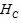
отношение сигнал/шум или превышение сигнала над помехой –

Таким образом, можно принять некоторое геометрическое представление сигнала как некоторого объема в трехмерном пространстве (рис.2.6).

Рис. 2.6 Геометрическое представление сигнала Объемом сигнала принято называть произведение трех параметров

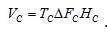
Введя понятие объема сигнала можно сравнительно просто представить соотношения между свойствами сигнала и свойствами системы связи.

Система связи может быть охарактеризована:

ü временем в течении которого канал связи предоставлен для передачи;

ü полосой частот, которую канал способен пропустить;

ü полосой уровней к зависящей от допустимой нагрузки на аппаратуру канала.

Очевидно, что передача сигнала с характеристиками с” с’ с по системе связи с каналом, имеющим параметры к’ к’ к возможна, лишь при условиях

Информационная емкость сигналов

Информационная емкость сигналов существенно зависит от типа сигналов и определяет требования к каналам передачи данных (каналам связи), равно как и технические характеристики каналов связи определяют требования к информационной емкости сигналов, передаваемых по этим каналам.

Для каналов передачи дискретных сигналов (дискретные канала связи) используют понятия технической и информационной скорости передачи данных.

Под технической скоростью передачи подразумевают число элементарных сигналов (символов), передаваемых по каналу в единицу времени. Простейший элементарный символ – однополярный электрический импульс длительностью t на тактовом интервале T. В дискретных каналах используют, как правило, двуполярные импульсы, положительные на первой половине интервала Т и отрицательные на второй половине. Это позволяет поддерживать нулевой потенциал кабеля и выполнять тактовую синхронизацию приемо-передачи сигналов. Единицей измерения технической скорости V t = 1/T служит БОД – один символ в секунду. Полоса пропускания канала связи обычно ограничивается определенной предельной частотой F пред по уровню затухания сигнала до уровня статистических помех, при этом значение технической скорости передачи данных, естественно, не может быть выше F пред без каких-либо специальных устройств выделения информационных сигналов.

При известной технической скорости V T скорость передачи информации измеряется в битах в секунду, и при уровне помех меньше амплитудных значений символьных импульсов задается соотношением:

где H(s) – энтропия символа. Для двоичных дискретных символов с возможными состояниями [0, 1] (однополярные – есть/нет импульс на такте, для двуполярных – порядок полярности импульсов на такте, например, 0: плюс/минус, 1: минус/плюс) при постоянной амплитуде импульсов значение H(s) равно 1. При числе L возможных равновероятных уровней амплитуды импульсов (уровень помех меньше разности уровней амплитуд импульсов) значение H(s) равно log L.

I t (S) = N log L = (t/T) log L. (1.4.7)

Увеличение числа уровней L увеличивает пропускную способность каналов связи, но усложняет аппаратуру кодирования данных и снижает помехоустойчивость связи.

Для непрерывных сигналов передача по каналам связи возможна только при условии, что максимальная информационная частота в сигнале F max не превышает предельной частоты F пред передачи сигналов каналом связи. Для оценки информационной емкости непрерывного сигнала выполним его дискретизацию с интервалом D t = 1/2F max . Как установлено Котельниковым в 1933 году, по мгновенным отсчетам непрерывного сигнала с таким интервалом дискретизации аналоговый сигнал может быть восстановлен без потери информации. При полной длительности сигнала T s число отсчетов:

N = T s / D t = 2F max T s .

Определим максимально возможное число выборок в каждом отсчете при наличии шума в канале со средней мощностью Р ш = d 2 . При средней мощности сигнала P s = s 2 :

Информационная емкость сигнала:

I(S) = 2F max T s log L. (1.4.8)

Информационные возможности сигнала возрастают с расширением его спектра и превышением его уровня над уровнем помех.

Знаете ли Вы, почему “черные дыры” – фикция?
Согласно релятивистской мифологии, “чёрная дыра – это область в пространстве-времени, гравитационное притяжение которой настолько велико, что покинуть её не могут даже объекты, движущиеся со скоростью света (в том числе и кванты самого света). Граница этой области называется горизонтом событий, а её характерный размер – гравитационным радиусом. В простейшем случае сферически симметричной чёрной дыры он равен радиусу Шварцшильда”.
На самом деле миф о черных дырах есть порождение мифа о фотоне – пушечном ядре. Этот миф родился еще в античные времена. Математическое развитие он получил в трудах Исаака Ньютона в виде корпускулярной теории света. Корпускуле света приписывалась масса. Из этого следовало, что при высоких ускорениях свободного падения возможен поворот траектории луча света вспять, по параболе, как это происходит с пушечным ядром в гравитационном поле Земли.
Отсюда родились сказки о “радиусе Шварцшильда”, “черных дырах Хокинга” и прочих безудержных фантазиях пропагандистов релятивизма.
Впрочем, эти сказки несколько древнее. В 1795 году математик Пьер Симон Лаплас писал:
“Если бы диаметр светящейся звезды с той же плотностью, что и Земля, в 250 раз превосходил бы диаметр Солнца, то вследствие притяжения звезды ни один из испущенных ею лучей не смог бы дойти до нас; следовательно, не исключено, что самые большие из светящихся тел по этой причине являются невидимыми.” [цитата по Брагинский В.Б., Полнарёв А. Г. Удивительная гравитация. – М., Наука, 1985]
Однако, как выяснилось в 20-м веке, фотон не обладает массой и не может взаимодействовать с гравитационным полем как весомое вещество. Фотон – это квантованная электромагнитная волна, то есть даже не объект, а процесс. А процессы не могут иметь веса, так как они не являются вещественными объектами. Это всего-лишь движение некоторой среды. (сравните с аналогами: движение воды, движение воздуха, колебания почвы). Подробнее читайте в FAQ по эфирной физике.

Единицу количественной меры информации – БИТ (сокращение binary digit – двоичная цифра), впервые предложил Р. Хартли в 1928 году. 1 бит – это информация о двух возможных равновероятных состояниях объекта, неопределенность выбора из двух равновероятных событий. Математически это отображается состоянием 1 или 0 одного разряда двоичной системы счисления. Количество информации Н (в битах), необходимое и достаточное для полного снятия неопределенности состояния объекта, который имеет N равновозможных состояний, измеряется как логарифм по основанию 2 из числа возможных состояний:

H = log ₂ N. (10)

Соответственно, двоичный числовой информационный код одного из N возможных состояний объекта занимает Н двоичных разрядов.

Требование аддитивности: неопределенность объединенного источника равна сумме неопределенностей исходных источников, что соответствует интуитивному требованию к информации: она должна быть однозначной, а ее количество должно быть одним и тем же независимо от способа задания.

Основание логарифма не имеет принципиального значения и определяет только масштаб или единицу неопределенности. Так, если за единицу неопределенности принять три равновероятных состояния, то для определения, например, одной фальшивой золотой монеты (более легкой) из 27 внешне неотличимых монет потребуется только H = log ₃27 = 3, т.е. три взвешивания на равноплечных весах.

Двоичная мера информации получила общее признание в связи с простотой реализации информационной техники на элементах с двумя устойчивыми состояниями.В десятичном исчислении единицей информации является один десятичный разряд – ДИТ.

Энтропия источника информации. Степень неопределенности состояния объекта (или так называемого источника информации) зависит не только от числа его возможных состояний, но и от вероятности этих состояний. При неравновероятных состояниях свобода выбора для источника ограничивается. Так, если из двух возможных состояний вероятность одного из них равна 0.999, то вероятность другого состояния соответственно равна 1-0.999 = 0.001, и при взаимодействии с таким источником результат практически предрешен.

В общем случае, в соответствии с теорией вероятностей, источник информации однозначно и полно характеризуется ансамблем состояний U = 1, u₂. u_N> с вероятностями состояний соответственно <р(u₁), р(u₂). р(u_N)> при условии, что сумма вероятностей всех состояний равна 1. Мера количества информации, как неопределенности выбора дискретным источником состояния из ансамбля U, предложена К. Шенноном в 1946 году и получила названиеэнтропии дискретного источника информацииили энтропии конечного ансамбля:

H(U) = -p_nlog₂p_n. (11)

Выражение Шеннона совпадает с выражением Больцмана для энтропии физических систем при оценке степени разнообразия их состояний. Мера энтропии Шеннона является обобщением меры Хартли на случай ансамблей с неравновероятными состояниями, в чем нетрудно убедиться, если в выражении (11) значение p_nзаменить значением p=1/N для ансамбля равновероятных состояний.Энтропия конечного ансамбля H(U) характеризует неопределенность, приходящуюся в среднем на одно состояние ансамбля.

Учитывая, что в дальнейшем во всех математических выражениях, касающихся энтропии, мы будем использовать только двоичное основание логарифма, индекс 2 основания логарифма в формулах будем подразумевать по умолчанию.

Основные свойства энтропии:

1. Энтропия является величиной вещественной и неотрицательной, т.к. значения вероятностей p_nнаходятся в интервале 0-1, значения log p_nвсегда отрицательны, а значения -p_nlog p_nв (1.4.2) соответственно положительны.

2. Энтропия – величина ограниченная, т.к. при p_n0 значение -p_nlog p_nтакже стремится к нулю, а при 0

Рисунок 20 – график изменения энтропии источника с двумя состояниями

5. Энтропия источника с двумя состояниями u₁и u₂при изменении соотношения их вероятностей p(u₁)=p и p(u₂)=1-p определяется выражением:

H(U) = -[p log p + (1-p) log (1-p)],

и изменяется от 0 до 1, достигая максимума при равенстве вероятностей. График изменения энтропии приведен на рис. 20.

6. Энтропия объединенных статистически независимых источников информации равна сумме их энтропий.

Рассмотрим это свойство на двух источниках информации u и v. При объединении источников получаем обобщенный источник информации (u,v), который описывается вероятностями p(u_nv_m) всех возможных комбинаций состояний u_nисточника u и v_mисточника v. Энтропия объединенного источника при N возможных состояниях источника u и М возможных состояниях источника v:

H(UV) = -p(u_nv_m) log p(u_nv_m),

Источники статистически независимы друг от друга, если выполняется условие:

С использованием этого условия соответственно имеем:

H(UV) = -p(u_n)p(v_m) log [p(u_n)p(v_m)] =

= -p(u_n) log p(u_n)p(v_m) -p(v_m) log p(v_m)p(u_m).

С учетом того, чтоp(u_n) = 1 иp(v_m) = 1, получаем:

7. Энтропия характеризует среднюю неопределенность выбора одного состояния из ансамбля, игнорируя содержательную сторону ансамбля. Это расширяет возможности использования энтропии при анализе самых различных явлений, но требует определенной дополнительной оценки возникающих ситуаций, т.к. из рисунка 20 следует, что энтропия состояний может быть неоднозначной.

Энтропия непрерывного источника информации должна быть бесконечна, т. к. неопределенность выбора из бесконечно большого числа возможных состояний бесконечно велика.

Разобьем диапазон изменения непрерывной случайной величины U на конечное число n малых интервалов u. При реализации значений u в интервале (u_n, u_n+u) будем считать, что реализовалось значение u_n дискретной случайной величины U’, вероятность реализации которой:

p(u_n 2 . При средней мощности сигнала P_s = s 2 :

L = =.

Информационная емкость сигнала:

I(S) = 2F_max T_s log L. (17)

Информационные возможности сигнала возрастают с расширением его спектра и превышением его уровня над уровнем помех.

Пространство сигналов

Множества сигналов.Сигналы обычно рассматриваются в составе определенных множеств L, объединенных каким-либо свойством Р, характерным для всех и каждого из сигналов данного множества. Условное отображение множества: L = – множество всех s, для которых справедливо свойство Р. Определив свойство Р, мы тем самым можем ограничивать сигналы, действующие в каких-либо системах, определенными типами, условиями, границами по параметрам и т.п.

Множества сигналов могут образовываться из других, ранее определенных множеств, логическими операциями объединения (индекс – ) и пересечения (индекс -):

Возможно разбиение множества сигналов на непересекающиеся подмножества, более удобные для обработки, при этом для множества S, разбитого на совокупность подмножеств 1, S₂, S₃, …, S_N>, должны выполняться условия:

Запись S₁Sозначает, что множествоS₁входит в состав множества S, т.е. является подмножеством в составе S.

Преобразование элементов v_i множества V в элементы g_i множества G называется отображением (трансформацией, преобразованием) V в G. Символьные записи преобразования: g = T[v] или v → g, при этом элементы v называют прообразом множества g, а элементы g – образом множества v.

Если преобразование выполняется над числами одного множества R (например, x = T[y]), то такое преобразование порождает функциональную зависимость x = f(y).

Если преобразование выполняется над функциями одного и того же множества L (например, f(t) = T[g(t)], f(t)  L и g(t)  L), то алгоритм преобразования T[..] называют оператором преобразования f(t) в g(t).

Преобразование g = T[f(t)] функций f(t) множества F называют функционалом, если результатом преобразования являются числовые значения g множества G. Примерами функционалов являются интегралы функций в определенных пределах.

Преобразование может выполняться функциональными операторами с переводом функций одной переменной, например t, в функции по другой переменной, например ω, Типичным примером функционального оператора является преобразование Фурье. В комплексной форме:

S(ω) = s(t) exp(-jωt) dt.

Пространство сигналов.Для анализа и обработки информации, которая может быть заключена в сигналах, требуется выделять из множества сигналов сигналы с определенными параметрами, сравнивать сигналы друг с другом, оценивать изменение сигналов при их прохождении через системы обработки данных, и т.п. Это может выполняться только при “помещении” множества сигналов в определенные метрические пространства с заранее оговоренными свойствами и единицами измерений.Положение на поверхности Земли любого объекта однозначно определяется по “координатному сигналу” в заранее сформированных метрических координатных пространствах с нулевыми точками и принятыми единицами измерений. Для практического использования сформированы также различные пространства картографических проекций с определенными структурными ограничениями, жестко установленная метрология которых позволяет трансформировать информацию из одного пространства в другое, более удобное для отображения или обработки определенными программами.

Главным условием превращения множество сигналов L₁(t), s₂(t), …>, которые имеют какие-то общие свойства, в функциональное пространство сигналов является выполнение условия однозначной реализации. Если пространство значений независимой переменной t задано выражением R:=(-,+), то пространство сигналов L P [R] определяет множество сигналов в этом пространстве, для которых условие однозначной реализации записывается в следующей форме:

|s(t)| p dt 2 dt 2 [0, 2π] одного периода:

|s(t)| 2 dt 3 можно только абстрактно, но с математических позиций такое пространство вполне реально и N-мерный сигнал s отображается вполне определенной точкой в этом пространстве с координатами s_nпо осям пространства. При уменьшении интервала дискретизации сигнала до бесконечно малой величины значение N стремится к бесконечности, и пространство сигналов превращается в бесконечномерное пространство аналоговых сигналов. Следовательно, и аналоговые сигналы могут рассматриваться как предельный случай бесконечномерных векторов.

Рисунок 21 – Пространства сигналов и функций.

С учетом вышеизложенного, для математического анализа систем и сигналов в линейном пространстве может использоваться математика векторов.

В линейном пространстве L_n; n=0,1,2,…,N> всегда можно выделить множество векторов _n; n=0,1,2,…,N>, для которых выполняется равенство нулю их линейной комбинации

_n x_n = 0 (18)

только при условии равенства нулю всех значений _k. Такое множество векторов называется линейно независимым. Ни один вектор линейно независимого множества не может быть выражен в виде какой-либо линейной комбинации других векторов этого пространства. Такое множество векторов называется базисом N-мерного пространства L_n; N>. Линейная комбинация таких линейно независимых векторов образует векторное пространство где каждый вектор U может быть выражен единственной линейной комбинацией векторовx_n:

U =_n x_n

Совокупность чисел _n> называется спектром вектора U в этом базисе. Спектр вектора в общем случае может быть комплексным.

Линейные пространства сигналов имеют, как правило, не единственный базис. Выбор базиса определяется простотой и удобством его использования при обработке сигналов.

Основными метрическими параметрами линейного пространства являются норма, метрика и скалярное произведение сигналов.

Норма сигналов в линейном пространстве является аналогом длины векторов, и обозначается индексом ||s(t)|| – норма. В математике существуют различные формы норм. При анализе сигналов обычно используются квадратичные нормы

||s(t)|| =. (19)

Для дискретных сигналов:

||s(n)|| =. (19′)

Для комплексных сигналов

||s(t)|| =, (19”)

где s*(t) – величины, комплексно сопряженные с s(t).

Линейное пространство сигналов L является нормированным, если каждому сигналу пространства s(t) однозначно сопоставлена его числовая норма ||s(t)||, и выполняются следующие аксиомы:

Норма неотрицательна (||s(t)|| ≥ 0) и равна нулю тогда и только тогда, когда сигнал равен нулю (||s(t)|| = , при s(t) =).

Для любого числа b должно быть справедливо равенство||bs(t)|| = |b|||s(t)||.

Если v(t) и u(t) – сигналы из пространства L, то должно выполняться неравенство треугольника||v(t)+u(t)||||v(t)|| + ||u(t)||.

Пример нормы для двумерных цифровых сигналов приведен на рисунке 22.

Рисунок 22 – Норма и метрика сигналов.

Метрика сигналов.Линейное пространство сигналов L является метрическим, если каждой паре сигналов s(t)  L и v(t)  L однозначно сопоставляется неотрицательное число (s,v) – метрика или расстояние между векторами. Пример метрики для двух векторов в двумерном пространстве приведен на рисунке 22.

Для метрик сигналов в метрическом пространстве любой размерности должны выполняться аксиомы:

(s,v) = (v,s) – рефлексивность метрики.

(s,s) = 0 для любых s(t)  L.

(s,v)  (s,a) + (a,v) для любых a  L.

Метрика определяется нормой разности двух сигналов (рисунок 22)

В свою очередь норму можно отождествлять с расстоянием от выбранного элемента пространства до нулевого||s(t)|| =(s(t),).

По метрике сигналов можно судить, например, о том, насколько точно один сигнал может быть аппроксимирован другим сигналом, или насколько изменяется выходной сигнал относительно входного при прохождении через какое-либо устройство. Пространство сигналов может иметь несколько метрик.

Тут вы можете оставить комментарий к выбранному абзацу или сообщить об ошибке.

ИНФОРМАЦИОННАЯ ЕМКОСТЬ средства отображения информации— максимальное количество информации, которое может быть отображено на СОИ. Значение И. е. зависит от структуры информационного поля, количества позиций в нем и числа символов в алфавите, закрепленном за позицией. И. е. определяет максимальные информационные возможности СОИ. Реальное же количество отображаемой информации обычно меньше И. е. Равенство возможно лишь в том случае ( если для каждой позиции информационного поля равновероятно появление любого из символов алфавита, относящегося к ней. Воспринимая И. м.г оператор производит анализ и оценку сложившейся ситуации, планирует управляющие воздействия, наблюдает и оценивает результаты их реализации. Технической основой для формирования И. м. являются системы и средства отображения информации. И. м. должна удовлетворять трем важнейшим требованиям: 1) по содержанию она должна адекватно отражать объект управления, рабочие процессы, окружающую среду и состояние самой системы управления; 2) по количеству информации И. м. должна обеспечивать оптимальный информационный баланс и не приводить к таким нежелательным явлениям, как дефицит или избыток информации; она должна отображать лишь те свойства, отношения и связи управляемых объектов, которые имеют существенное значение; 3) по форме и композиции И. м. должна соответствовать задачам трудового процесса и возможностям человека по приему и переработке поступающей информации и осуществлению управляющих воздействий. И. м., как правило, воспроизводит действительность в упрощенной форме и всегда является некоторой идеализацией действительности. Степень и характер упрощения и идеализации могут быть определены на основе анализа задач СЧМ в целом и анализа задач оператора. Однако при этом желательно, чтобы И. м. была наглядной, т. е. оператор должен иметь возможность быстрого понимания ситуации. Важным свойством И. м. является ее читаемость, что обеспечивается структурой И. м.: в нее не просто должны входить упорядоченные сведения, а должна быть представлена их взаимосвязь. И. м. различаются по модальности выдаваемых сигналов (визуальные, акустические, полимодальные), по характеру используемых элементов индикации, по степени детализации информации (детальные, интегральные, смешанные). Основными классами И. м. являются: наглядные (картинные) модели-изображения (фото-, кино-, телеизображение), абстрактные знаковые модели (печатный текст, табло, формуляр и т .п.), графические модели (график, диаграмма, чертеж, блок-схема) и комбинированные (мнемосхема, карта и др.).

Энциклопедический словарь по психологии и педагогике . 2013 .

Полезное

Смотреть что такое “ИНФОРМАЦИОННАЯ ЕМКОСТЬ” в других словарях:

Информационная емкость — Количество охраняемых объектов (для систем передачи извещений), контролируемых шлейфов сигнализации (для приемно контрольных приборов), охраняемых зон, о состоянии которых может оповестить оповещатель (для оповещателей), или защищаемых зон (для… … Словарь-справочник терминов нормативно-технической документации

информационная емкость — Общее число битов в информации в канале пользователя, поддерживаеиле одной ячейкой (или точечным лучом), которая является частью бесконечного набора идентичных ячеек (или большого числа точечных спутниковых лучей) в единообразном двумерном (или… … Справочник технического переводчика

информационная емкость кадра средства отображения информации — информационная емкость кадра Максимальное количество различимых элементов отображения информации в кадре средства отображения информации. [ГОСТ 27833 88] Тематики средства отображения информации Синонимы информационная емкость кадра … Справочник технического переводчика

информационная емкость устройства записи [воспроизведения, записи-воспроизведения] — Характеристика устройства записи [воспроизведения, записи воспроизведения], определяющая количество информации, которое может быть записано [воспроизведено] с помощью этого устройства без смены носителя записи [сигналограммы] или комплекта… … Справочник технического переводчика

информационная емкость устройства телемеханики — информационная емкость Число объектов измерения, сигнализации, управления и регулирования, от (для) которых может передавать информацию устройство телемеханики. [ГОСТ 26.005 82] Тематики телемеханика, телеметрия Синонимы информационная емкость EN … Справочник технического переводчика

информационная емкость носителя записи [сигналограммы] — Характеристика единицы носителя записи (сигналограммы), определяющая количество записываемой или записанной информации. Примечание Количественно информационная емкость может выражаться в битах или иных единицах, прямо или косвенно характеризующих … Справочник технического переводчика

информационная емкость запоминающего устройства — емкость Наибольшее количество единиц данных, которое одновременно может храниться в запоминающем устройстве. [ГОСТ 25492 82] Тематики устройства цифр. выч. машин запоминающие Синонимы емкость EN capacity … Справочник технического переводчика

информационная емкость (абонентского оборудования) — — [Е.С.Алексеев, А.А.Мячев. Англо русский толковый словарь по системотехнике ЭВМ. Москва 1993] Тематики информационные технологии в целом EN user data capacity … Справочник технического переводчика

информационная емкость дискретного сигнала — Максимум энтропии дискретного сигнала, равный логарифму числа возможных дискретных сигналов за единицу времени. [Сборник рекомендуемых терминов. Выпуск 94. Теория передачи информации. Академия наук СССР. Комитет технической терминологии. 1979 г.] … Справочник технического переводчика

Читайте также:

  

• Выбор жизненного пути обществознание 6 класс кратко

  

• Политические партии и движения их классификация кратко

  

• Меры центральной тенденции кратко

  

• Мусульманские кратко метражный видеоролики

  

• Применение каменного угля кратко

!!! Информационная емкость сигналов

Количественная
мера информации. При
неопределенности самого понятия
информации можно достаточно обоснованно
считать, чтоинформация проявляется,
хранится и передается от одного объекта
к другому в материально-энергетической
форме в виде сигналов.Сигналом как
материальным носителем информации
может быть любой физический процесс
(электрический, магнитный, оптический,
акустический и пр.), определенные
параметры которого (амплитуда, частота,
энергия, интенсивность и др.)однозначно
отображают информационные данные
(сообщения).

Единицу
количественной меры информации – БИТ
(сокращение binary
digit – двоичная
цифра), впервые предложил Р. Хартли в
1928 году. 1 бит – это информация о двух
возможных равновероятных состояниях
объекта, неопределенность выбора из
двух равновероятных событий. Математически
это отображается состоянием 1 или 0
одного разряда двоичной системы
счисления. Количество информации Н (в
битах), необходимое и достаточное для
полного снятия неопределенности
состояния объекта, который имеет N
равновозможных состояний, измеряется
как логарифм по основанию 2 из числа
возможных состояний:

H = log ₂
N. (10)

Соответственно,
двоичный числовой информационный код
одного из N возможных состояний объекта
занимает Н двоичных разрядов.

Требование
аддитивности: неопределенность
объединенного источника равна сумме
неопределенностей исходных источников,
что соответствует интуитивному требованию
к информации: она должна быть однозначной,
а ее количество должно быть одним и тем
же независимо от способа задания.

Основание логарифма
не имеет принципиального значения и
определяет только масштаб или единицу
неопределенности. Так, если за единицу
неопределенности принять три равновероятных
состояния, то для определения, например,
одной фальшивой золотой монеты (более
легкой) из 27 внешне неотличимых монет
потребуется только H = log ₃27 = 3, т.е.
три взвешивания на равноплечных весах.

Двоичная мера
информации получила общее признание в
связи с простотой реализации информационной
техники на элементах с двумя устойчивыми
состояниями.В десятичном исчислении
единицей информации является один
десятичный разряд – ДИТ.

Энтропия
источника информации. Степень
неопределенности состояния объекта
(или так называемого источника информации)
зависит не только от числа его возможных
состояний, но и от вероятности этих
состояний. При неравновероятных
состояниях свобода выбора для источника
ограничивается. Так, если из двух
возможных состояний вероятность одного
из них равна 0.999, то вероятность другого
состояния соответственно равна 1-0.999 =
0.001, и при взаимодействии с таким
источником результат практически
предрешен.

В общем случае, в
соответствии с теорией вероятностей,
источник информации однозначно и полно
характеризуется ансамблем состояний
U = {u₁, u₂,…, u_N} с
вероятностями состояний соответственно
{р(u₁), р(u₂),…, р(u_N)} при
условии, что сумма вероятностей всех
состояний равна 1. Мера количества
информации, как неопределенности выбора
дискретным источником состояния из
ансамбля U, предложена К. Шенноном в 1946
году и получила названиеэнтропии
дискретного источника информацииили энтропии конечного ансамбля:

H(U) = –p_nlog₂p_n.
(11)

Выражение Шеннона
совпадает с выражением Больцмана для
энтропии физических систем при оценке
степени разнообразия их состояний. Мера
энтропии Шеннона является обобщением
меры Хартли на случай ансамблей с
неравновероятными состояниями, в чем
нетрудно убедиться, если в выражении
(11) значение p_nзаменить значением p=1/N для ансамбля
равновероятных состояний.Энтропия
конечного ансамбля H(U) характеризует
неопределенность, приходящуюся в среднем
на одно состояние ансамбля.

Учитывая, что в
дальнейшем во всех математических
выражениях, касающихся энтропии, мы
будем использовать только двоичное
основание логарифма, индекс 2 основания
логарифма в формулах будем подразумевать
по умолчанию.

Основные
свойства энтропии:

1. Энтропия является
величиной вещественной и неотрицательной,
т.к. значения вероятностей p_nнаходятся в интервале 0-1, значения log p_nвсегда отрицательны, а значения -p_nlog p_nв
(1.4.2) соответственно положительны.

2. Энтропия – величина
ограниченная, т.к. при p_n0 значение -p_nlog p_nтакже стремится к нулю, а при 0 < p_n1 ограниченность
суммы всех слагаемых очевидна.

3. Энтропия равна
0, если вероятность одного из состояний
источника информации равна 1, и тем самым
состояние источника полностью определено
(вероятности остальных состояний
источника равны нулю, т.к. сумма
вероятностей должна быть равна 1).

4. Энтропия
максимальна при равной вероятности
всех состояний источника информации:

H_max(U)
= –(1/N)
log (1/N) = log N.

Рисунок 20 – график
изменения энтропии источника с двумя
состояниями

5. Энтропия источника с двумя
состояниями u₁и u₂при
изменении соотношения их вероятностей
p(u₁)=p и p(u₂)=1-p определяется
выражением:

H(U) = -[p
log p + (1-p) log (1-p)],

и изменяется от 0
до 1, достигая максимума при равенстве
вероятностей. График изменения энтропии
приведен на рис. 20.

6. Энтропия
объединенных статистически независимых
источников информации равна сумме их
энтропий.

Рассмотрим это
свойство на двух источниках информации
u и v. При объединении источников получаем
обобщенный источник информации (u,v),
который описывается вероятностями
p(u_nv_m)
всех возможных комбинаций состояний
u_nисточника u и v_mисточника v. Энтропия объединенного
источника при N возможных состояниях
источника u и М возможных состояниях
источника v:

H(UV) =
–p(u_nv_m)
log p(u_nv_m),

Источники
статистически независимы друг от друга,
если выполняется условие:

p(u_nv_m)
= p(u_n)p(v_m).

С
использованием этого условия соответственно
имеем:

H(UV) =
–p(u_n)p(v_m)
log [p(u_n)p(v_m)]
=

= –p(u_n)
log p(u_n)p(v_m)
–p(v_m)
log p(v_m)p(u_m).

С
учетом того, чтоp(u_n)
= 1 иp(v_m)
= 1, получаем:

H(UV) = H(U) + H(V).
(12)

7. Энтропия
характеризует среднюю неопределенность
выбора одного состояния из ансамбля,
игнорируя содержательную сторону
ансамбля. Это расширяет возможности
использования энтропии при анализе
самых различных явлений, но требует
определенной дополнительной оценки
возникающих ситуаций, т.к. из рисунка
20 следует, что энтропия состояний может
быть неоднозначной.

Энтропия
непрерывного источника информации
должна быть бесконечна, т. к. неопределенность
выбора из бесконечно большого числа
возможных состояний бесконечно велика.

Разобьем
диапазон изменения непрерывной случайной
величины U
на конечное число n
малых интервалов u.
При реализации значений u
в интервале (u_n,
u_n+u)
будем считать, что реализовалось значение
u_n
дискретной случайной величины U’,
вероятность реализации которой:

p(u_n<u<u_n+u)
=p(u)
du
p(u_n)
u.

Энтропия
дискретной
величины
U’:

H(U’)
= –p(u_n)
u
log (p(u_n)
u).

Заменяем
log
(p(u_n)
u)
= log
p(u_n)+log
u,
принимаем во внимание, что сумма p(u_n)
u
по всем возможным значениям u_n
равна 1, и получаем:

H(U’)
= –p(u_n)
u
log p(u_n)
– log u.
(13)

В пределе, при u

0, получаем выражение энтропии для
непрерывного источника:

H(U)
= –p(u)
log p(u) du –.(14)

Значение энтропии
в (1.4.5), как и ожидалось, стремится к
бесконечности за счет второго члена
выражения. Для получения конечной
характеристики информационных свойств
непрерывных сигналов используют только
первый член выражения (14), получивший
название дифференциальной энтропии.
Ее можно трактовать, как среднюю
неопределенность выбора произвольной
случайной величины по сравнению со
средней неопределенностью выбора
случайной величины U’,
имеющей равномерное распределение в
диапазоне (0-1). Действительно, для такого
распределения p(u_n)
= 1/N,
u
= 1/N,
и при N


из (13) следует:

H(U’)
= – (log N)/N – log u

–.

Соответственно,
разность энтропий дает дифференциальную
энтропию:

h(U) = H(U)
– H(U’) = –p(u)
log p(u) du.(15)

Дифференциальная
энтропия не зависит от конкретных
значений величины U:

h(U+a) =
h(U), a = const,

но зависит от
масштаба ее представления:

h(kU)
= h(U)
+ log
k.

Практика анализа
и обработки сигналов обычно имеет дело
с сигналами в определенном интервале
[a,
b]
их значений, при этом максимальной
дифференциальной энтропией обладает
равномерное распределение значений
сигналов:

h(U) =
–p(u)
log p(u) du = log (b-a).

По
мере сужения плотности распределения
значение h(U)
уменьшается, и в пределе при p(u)


(u-c),
a<c<b
стремится к нулю.

!!! Информационная
емкость сигналов
существенно
зависит от типа сигналов и определяет
требования к каналам передачи данных.

Для
каналов передачи дискретных сигналов
(дискретные каналы связи) используют
понятия технической и информационной
скорости передачи данных.

Под
технической скоростью передачи
подразумевают число элементарных
сигналов (символов), передаваемых по
каналу в единицу времени. Простейший
элементарный символ – однополярный
импульс длительностью 
на тактовом интервале T.
В дискретных каналах используют, как
правило, двуполярные импульсы,
положительные на первой половине
интервала Т и отрицательные на второй
половине. Это позволяет поддерживать
нулевой потенциал в кабеле и выполнять
тактовую синхронизацию приемо-передачи
сигналов. Единицей измерения технической
скорости V_t
= 1/T
служит БОД – один символ в секунду.
Полоса пропускания канала связи
ограничивается предельной частотой
F_пред
по уровню затухания сигнала до уровня
помех, при этом значение технической
скорости передачи данных не может быть
выше F_пред.

При известной
технической скорости V_t
скорость передачи информации измеряется
в битах в секунду и задается соотношением:

V_h
= V_t
H(s),

где H(s)
– энтропия символа. Для двоичных
дискретных символов [0, 1] при постоянной
амплитуде импульсов значение H(s)
равно 1. При числе L
возможных равновероятных уровней
амплитуды импульсов (уровень помех
меньше разности уровней амплитуд
импульсов) значение H(s)
равно log
L.

Информационная
емкость сигнала или полное количество
информации в сигнале S
(сообщении, кодовой последовательности/слове)
определяется полным количеством N
= t/T
энтропии символов в битах на интервале
задания сигнала t:

I_t(S)
= N log L = (t/T) log L.
(16)

Увеличение числа
уровней L
увеличивает пропускную способность
каналов связи, но усложняет аппаратуру
кодирования данных и снижает
помехоустойчивость связи.

Для
непрерывных сигналов передача по каналам
связи возможна только при условии, что
максимальная информационная частота
в сигнале F_max
не превышает предельной частоты F_пред
передачи сигналов каналом связи. Для
оценки информационной емкости непрерывного
сигнала выполним его дискретизацию с
интервалом t
= 1/2F_max.
Как установлено Котельниковым и Шенноном,
по мгновенным отсчетам непрерывного
сигнала с таким интервалом дискретизации
аналоговый сигнал может быть восстановлен
без потери информации. При полной
длительности сигнала T_s
число отсчетов:

N
= T_s/t
= 2F_max
T_s.

Определим
максимально возможное число выборок в
каждом отсчете при наличии шума в канале
со средней мощностью Р_ш
= ².
При средней мощности сигнала P_s
= s²:

L
= =.

Информационная
емкость сигнала:

I(S) =
2F_max
T_s
log L. (17)

Информационные
возможности сигнала возрастают с
расширением его спектра и превышением
его уровня над уровнем помех.

Пространство
сигналов

Важнейшее свойство
аналоговых и дискретных сигналов
заключается в том, что их линейные
комбинации также являются аналоговыми
или дискретными сигналами.Линейные
комбинации цифровых сигналов, в силу
их ограничения по разрядности, в принципе
относятся к разряду нелинейных операций,
однако последним фактором можно
пренебречь, если ошибки, которые вносятся
в результаты наблюдений при квантовании
отсчетов, достаточно малы по сравнению
с шумами зарегистрированной информации.
При дискретизации и квантовании данных
непосредственно на входах в ЭВМ это
условие выполняется практически всегда,
поскольку ошибки определяются разрядностью
ЭВМ и программными системами обработки
данных, которые обычно не ниже 6-12
десятичных разрядов.

Множества
сигналов.Сигналы обычно
рассматриваются в составе определенных
множеств L, объединенных каким-либо
свойством Р, характерным для всех и
каждого из сигналов данного множества.
Условное отображение множества: L = {s;
P} – множество всех s, для которых
справедливо свойство Р. Определив
свойство Р, мы тем самым можем ограничивать
сигналы, действующие в каких-либо
системах, определенными типами, условиями,
границами по параметрам и т.п.

Множества сигналов
могут образовываться из других, ранее
определенных множеств, логическими
операциями объединения (индекс – )
и пересечения (индекс -):

L = S₁
 S₂
= {s; s 
S₁ или
s 
S₂},

L = S₁S₂= {s; sS₁и sS₂}.

Возможно разбиение
множества сигналов на непересекающиеся
подмножества, более удобные для обработки,
при этом для множества S, разбитого на
совокупность подмножеств {S₁, S₂,
S₃, …, S_N}, должны выполняться
условия:

S=S₁S₂ S₃…S_N,

S_nS_m=дляn≠m.

Запись S₁Sозначает, что множествоS₁входит в состав
множества S, т.е. является подмножеством
в составе S.

Преобразование
элементов v_i
множества V в элементы g_i
множества G называется отображением
(трансформацией, преобразованием) V в
G. Символьные записи преобразования: g
= T[v] или v → g,
при этом элементы v
называют прообразом множества g,
а элементы g – образом множества v.

Если преобразование
выполняется над числами одного множества
R (например, x = T[y]), то такое преобразование
порождает функциональную зависимость
x = f(y).

Если преобразование
выполняется над функциями одного и того
же множества L (например, f(t) = T[g(t)], f(t) 
L и g(t)
 L),
то алгоритм преобразования T[..] называют
оператором преобразования f(t) в g(t).

Преобразование
g = T[f(t)] функций f(t) множества F называют
функционалом, если результатом
преобразования являются числовые
значения g множества G. Примерами
функционалов являются интегралы функций
в определенных пределах.

Преобразование
может выполняться функциональными
операторами с переводом функций одной
переменной, например t, в функции по
другой переменной, например ω, Типичным
примером функционального оператора
является преобразование Фурье. В
комплексной форме:

S(ω)
= s(t)
exp(-jωt) dt.

Пространство
сигналов.Для анализа и обработки
информации, которая может быть заключена
в сигналах, требуется выделять из
множества сигналов сигналы с определенными
параметрами, сравнивать сигналы друг
с другом, оценивать изменение сигналов
при их прохождении через системы
обработки данных, и т.п. Это может
выполняться только при “помещении”
множества сигналов в определенные
метрические пространства с заранее
оговоренными свойствами и единицами
измерений.Положение на поверхности
Земли любого объекта однозначно
определяется по “координатному
сигналу” в заранее сформированных
метрических координатных пространствах
с нулевыми точками и принятыми единицами
измерений. Для практического использования
сформированы также различные пространства
картографических проекций с определенными
структурными ограничениями, жестко
установленная метрология которых
позволяет трансформировать информацию
из одного пространства в другое, более
удобное для отображения или обработки
определенными программами.

Главным условием
превращения множество сигналов L{s₁(t),
s₂(t), …}, которые имеют
какие-то общие свойства, в функциональное
пространство сигналов является выполнение
условия однозначной реализации. Если
пространство значений независимой
переменной t задано выражением
R:=(-,+),
то пространство сигналов L^P[R]
определяет множество сигналов в этом
пространстве, для которых условие
однозначной реализации записывается
в следующей форме:

|s(t)|^p
dt < .

Для анализа
сигналов наиболее часто используется
гильбертово пространство, сигналы в
котором должны удовлетворять условию
интегрирования с квадратом:

|s(t)|²
dt < .

Периодические
сигналы обычно рассматриваются в
пространстве L² [0,
2π] одного периода:

|s(t)|²
dt < .

Метрические
пространства должны иметь определенную
систему координат, что позволяет
рассматривать любые произвольные
сигналы х и у, принадлежащие пространству,
в виде векторов, соединяющих начало
координат с определенными точками этого
пространства и определять расстояние
(x,y) между
этими точками (метрика). Так как расстояние
между точками должно быть числовым, а
сигналы х и у представляют собой функции,
то (x,y)
представляет собой функционал, для
которого в метрическом пространстве
должны быть справедливы следующие
аксиомы:

• (x,y)
  ≥ 0;  (x,y)
  = 0 при х = у,

•  (x,y)
  = 
  (y,x),

•  (x,z)
  ≤  (x,y)
  +  (y,z)
  – неравенство треугольника.

Каждый элемент
векторного пространства может отображаться
проекциями на координатные оси, а для
обработки и преобразований сигналов
могут использоваться операции векторной
алгебры. Достаточно простые алгебраические
взаимосвязи между сигналами характерны
для линейных пространств.

Линейное
пространство сигналов.Метрическое
пространство является линейным,
если в нём определены операции сложения
векторов и умножения вектора на скаляр,
в результате которых образуется новый
вектор в том же пространстве.Множество
сигналов L образует линейное пространство
сигналов, если для него справедливы
следующие аксиомы

1. Множество
   содержит такой нулевой элемент ,
   что для всех сигналов u(t) 
   L выполняется равенство u(t) + 
   = u(t).

2. Для любых
   сигналов u(t) 
   L и v(t)  L
   существует их сумма s(t) = u(t)+v(t), которая
   также содержится в L. При этом операция
   суммирования должна быть

– коммутативна:
u(t)+v(t) = v(t)+u(t),

– ассоциативна:
u(t)+(v(t)+x(t)) = (u(t)+v(t))+x(t),

– однородна: u(t)
+ (-u(t)) = .

1. Существует
   множество скалярных элементов ,
   на которые может выполняться умножение
   любого сигнала s(t) 
   L, при этом результат умножения является
   новым сигналом y(t) = s(t)
   в том же пространстве, у(t) 
   L. Операция умножения должна быть

–
ассоциативна:
(·s(t))
= ·s(t),

–
дистрибутивна:
(u(t)+s(t))
= u(t)+s(t),
(+)s(t)
= s(t)+s(t),

–
пропорциональна:
1·s(t) = s(t), 0·s(t) = 0.

Сигналы могут
описываться как вещественными, так и
комплексными функциями, и линейные
пространства также могут быть вещественными
или комплексными. Скалярные множества
обычно отождествляются с множествами
действительных или комплексных чисел,
но на них также могут накладываться
определенные ограничения. Так, например,
в теории связи широко применяется
бинарное скалярное множество{0, 1}.

Множество L, для
которого выполняются приведенные выше
аксиомы, при анализе сигналов и систем
может рассматриваться как специальным
образом сконструированное многомерное
(в пределе – бесконечномерное)
геометрическое пространство. Рассмотрим
это на конкретном примере.

Имеем произвольный
сигнал s(t), заданный на интервале [a, b].
Дискретизируем сигнал с равномерным
шагом дискретизации и переведем в
цифровую форму (представим сигнал N
последовательными выборками):

s = (s₁, s₂,
… , s_N).

В таком отображении
величина s может рассматриваться в виде
N-мерного вектора в N-мерном пространстве,
в котором значения s_nпредставляют
собой проекции s-вектора на координатные
оси данного пространства. Двумерный
вектор в двумерном пространстве – это
точка с координатами s₁и s₂на рис. 21. Соответственно, в трехмерном
пространстве сигнал s представлен точкой
в трехмерном пространстве. Представить
себе N-мерное пространство при N>3 можно
только абстрактно, но с математических
позиций такое пространство вполне
реально и N-мерный сигнал s отображается
вполне определенной точкой в этом
пространстве с координатами s_nпо
осям пространства. При уменьшении
интервала дискретизации сигнала до
бесконечно малой величины значение N
стремится к бесконечности, и пространство
сигналов превращается в бесконечномерное
пространство аналоговых сигналов.
Следовательно, и аналоговые сигналы
могут рассматриваться как предельный
случай бесконечномерных векторов.

Рисунок 21 –
Пространства сигналов и функций.

С учетом
вышеизложенного, для математического
анализа систем и сигналов в линейном
пространстве может использоваться
математика векторов.

В линейном
пространстве L{u_n;
n=0,1,2,…,N}
всегда можно выделить множество векторов
{x_n; n=0,1,2,…,N},
для которых выполняется равенство нулю
их линейной комбинации

_n
x_n = 0
(18)

только при условии
равенства нулю всех значений _k.
Такое множество векторов называется
линейно независимым. Ни один
вектор линейно независимого множества
не может быть выражен в виде какой-либо
линейной комбинации других векторов
этого пространства. Такое множество
векторов называется базисом
N-мерного пространства
L{u_n; N}.
Линейная комбинация таких линейно независимых векторов образует
векторное пространство где каждый
вектор U может быть выражен единственной
линейной комбинацией векторовx_n:

U =_n
x_n

Совокупность
чисел {_n}
называется спектром вектора
U в этом базисе.
Спектр вектора в общем случае может
быть комплексным.

Линейные
пространства сигналов имеют, как правило,
не единственный базис. Выбор базиса
определяется простотой и удобством его
использования при обработке сигналов.

Основными
метрическими параметрами линейного
пространства являются норма, метрика
и скалярное произведение сигналов.

Норма сигналов
в линейном
пространстве является аналогом длины
векторов, и обозначается индексом
||s(t)|| – норма.
В математике существуют различные формы
норм. При анализе сигналов обычно
используются квадратичные нормы

||s(t)|| =.
(19)

Для дискретных
сигналов:

||s(n)|| =.
(19′)

Для комплексных
сигналов

||s(t)|| =,
(19”)

где s*(t) – величины,
комплексно сопряженные с s(t).

Линейное пространство
сигналов L является нормированным, если
каждому сигналу пространства s(t)
однозначно сопоставлена его числовая
норма ||s(t)||, и выполняются следующие
аксиомы:

1. Норма неотрицательна
   (||s(t)|| ≥ 0) и равна нулю тогда и только
   тогда, когда сигнал равен нулю (||s(t)|| =
   , при s(t) =).

2. Для любого числа
   b должно быть справедливо равенство||bs(t)|| = |b|||s(t)||.

3. Если v(t) и u(t) –
   сигналы из пространства L, то должно
   выполняться неравенство треугольника||v(t)+u(t)||||v(t)|| +
   ||u(t)||.

Пример нормы для
двумерных цифровых сигналов приведен
на рисунке 22.

Рисунок 22 – Норма
и метрика сигналов.

Метрика
сигналов.Линейное пространство
сигналов L является метрическим, если
каждой паре сигналов s(t) 
L и v(t)  L
однозначно сопоставляется неотрицательное
число (s,v) –
метрика или расстояние
между векторами. Пример метрики для
двух векторов в двумерном пространстве
приведен на рисунке 22.

Для метрик сигналов
в метрическом пространстве любой
размерности должны выполняться аксиомы:

1. (s,v) = (v,s)
   – рефлексивность метрики.

2. (s,s) =
   0 для любых
   s(t) 
   L.

3. (s,v) 
   (s,a)
   + (a,v)
   для любых
   a 
   L.

Метрика определяется
нормой разности двух сигналов (рисунок
22)

(s,v) = || s(t) – v(t)
||. (20)

В свою очередь
норму можно отождествлять с расстоянием
от выбранного элемента пространства
до нулевого||s(t)||
=(s(t),).

По метрике
сигналов можно судить, например, о том,
насколько точно один сигнал может быть
аппроксимирован другим сигналом, или
насколько изменяется выходной сигнал
относительно входного при прохождении
через какое-либо устройство. Пространство
сигналов может иметь несколько метрик.

Соседние файлы в папке Лекции

• #
• #
• #
• #
• #
• #
• #
• #
• #

Автор материалов – Лада Борисовна Есакова.

При оцифровке звука в памяти запоминаются только отдельные значения сигнала. Чем чаще записывается сигнал, тем лучше качество записи.

Частота дискретизации f – это количество раз в секунду, которое происходит преобразование аналогового звукового сигнала в цифровой. Измеряется в Герцах (Гц).

Глубина кодирования (а также, разрешение) – это количество бит, выделяемое на одно преобразование сигнала. Измеряется в битах (Бит).

Возможна запись нескольких каналов: одного (моно), двух (стерео), четырех (квадро).

Обозначим частоту дискретизации – f (Гц), глубину кодирования – B(бит), количество каналов – k, время записи – t(Сек).

Количество уровней дискретизации d можно рассчитать по формуле: d = 2^B.

Тогда объем записанного файла V(бит)  = f * B * k * t.

Или, если нам дано количество уровней дискретизации,

V(бит)  = f * log₂d * k * t.

Единицы измерения объемов информации:

1 б (байт) = 8 бит

1 Кб (килобайт) = 2¹⁰ б

1 Мб (мегабайт) = 2²⁰ б

1 Гб (гигабайт) = 2³⁰ б

1 Тб (терабайт) = 2⁴⁰ б

1 Пб (петабайт) = 2⁵⁰ б

При оцифровке графического изображения качество картинки зависит от количества точек и количества цветов, в которые можно раскрасить точку.

Если X – количество точек по горизонтали,

Y – количество точек по вертикали,

I – глубина цвета (количество бит, отводимых для кодирования одной точки), то количество различных цветов в палитре N = 2^I. Соответственно, I = log₂N.

Тогда объем файла, содержащего изображение, V(бит) = X * Y * I

Или, если нам дано количество цветов в палитре, V(бит) = X * Y * log₂N.

Скорость передачи информации по каналу связи (пропускная способность канала) вычисляется как количество информации в битах, переданное за 1 секунду (бит/с).

Объем переданной информации вычисляется по формуле V = q * t, где q – пропускная способность канала, а t – время передачи.

Кодирование звука

Пример 1.

Производится двухканальная (стерео) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 32 бит. Запись длится 12 минут, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 30               2) 45           3)  75         4)  90

Решение:

V(бит)  = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования, k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³

Переведем все величины в требуемые единицы измерения:

V(Мб) = (16*1000 * 32 * 2 * 12 * 60 ) / 2²³

Представим все возможные числа, как степени двойки:

V(Мб) = (2⁴ * 2³ * 125 * 2⁵ * 2 * 2² * 3 * 15 * 2²) / 2²³ = (5625 * 2¹⁷) / 2²³ = 5625 / 2⁶ =

5625 / 64 ≈ 90.

Ответ: 4

!!! Без представления чисел через степени двойки вычисления становятся намного сложнее.

!!! Частота – это физическая величина, а потому 16 кГц = 16 * 1000 Гц, а не 16 * 2¹⁰. Иногда этой разницей можно пренебречь, но на последних диагностических работах она влияла на правильность ответа.

Пример 2.

В те­че­ние трех минут про­из­во­ди­лась четырёхка­наль­ная (квад­ро) зву­ко­за­пись с ча­сто­той дис­кре­ти­за­ции 16 КГц и 24-бит­ным раз­ре­ше­ни­ем. Сжа­тие дан­ных не про­из­во­ди­лось. Какая из при­ве­ден­ных ниже ве­ли­чин наи­бо­лее близ­ка к раз­ме­ру по­лу­чен­но­го файла?

1) 25 Мбайт

2) 35 Мбайт

3) 45 Мбайт

4) 55 Мбайт

Решение:

V(бит)  = f(Гц)* B(бит) * k * t(Сек),

где V – размер файла, f – частота дискретизации, B – глубина кодирования (или разрешение), k – количество каналов, t – время.

Значит, V(Мб) = (f * B * k * t ) / 2²³ = (16 * 1000 * 24 * 4 * 3 * 60) / 2²³ = (2⁴ * 2³ * 125 * 3 * 2³ * 2² * 3 * 15 * 2²) / 2²³ = (125 * 9 * 15 * 2¹⁴) / 2²³ = 16875 / 2⁹ = 32, 96 ≈ 35

Ответ: 2

Пример 3.

Ана­ло­го­вый зву­ко­вой сиг­нал был записан сна­ча­ла с ис­поль­зо­ва­ни­ем 64 уров­ней дис­кре­ти­за­ции сиг­на­ла, а затем с ис­поль­зо­ва­ни­ем 4096 уров­ней дис­кре­ти­за­ции сиг­на­ла. Во сколь­ко раз уве­ли­чил­ся ин­фор­ма­ци­он­ный объем оциф­ро­ван­но­го звука?

            1) 64

2) 8

3) 2

4) 12

Решение:

V(бит)  = f * log₂d * k * t, где V – размер файла, f – частота дискретизации, d – количество уровней дискретизации, k – количество каналов, t – время.

V₁ = f * log₂64 * k * t = f * 6 * k * t

V₂ = f * log₂4096 * k * t = f * 12 * k * t

V₂ / V₁ = 2

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

Кодирование изображения

Пример 4.

Какой минимальный объём памяти (в Кбайт) нужно зарезервировать, чтобы можно было сохранить любое растровое изображение размером 64×64 пикселей при условии, что в изображении могут использоваться 256 различных цветов? В ответе запишите только целое число, единицу измерения писать не нужно.

Решение:

V(бит) = X * Y * log₂N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

V (Кб) = (64 * 64 * log₂256) / 2¹³ = 2¹² * 8 / 2¹³ = 4

Ответ: 4

Пример 5.

Для хранения растрового изображения размером 64×32 пикселя отвели
1 килобайт памяти. Каково максимально возможное число цветов в палитре изображения?

Решение:

V(бит) = X * Y * log₂N, где V – объем памяти, X,Y – количество пикселей по горизонтали и вертикали, N – количество цветов.

log₂N = V /( X*Y) = 2¹³ / (2⁶ * 2⁵) = 4

N = 16

Ответ:16

Сравнение двух способов передачи данных

Пример 6.

До­ку­мент объ­е­мом 5 Мбайт можно пе­ре­дать с од­но­го ком­пью­те­ра на дру­гой двумя спо­со­ба­ми:

А) Сжать ар­хи­ва­то­ром, пе­ре­дать архив по ка­на­лу связи, рас­па­ко­вать.

Б) Пе­ре­дать по ка­на­лу связи без ис­поль­зо­ва­ния ар­хи­ва­то­ра.

Какой спо­соб быст­рее и на­сколь­ко, если

– сред­няя ско­рость пе­ре­да­чи дан­ных по ка­на­лу связи со­став­ля­ет 2¹⁸ бит в се­кун­ду,

– объем сжа­то­го ар­хи­ва­то­ром до­ку­мен­та равен 80% от ис­ход­но­го,

– время, тре­бу­е­мое на сжа­тие до­ку­мен­та – 35 се­кунд, на рас­па­ков­ку – 3 се­кун­ды?

В от­ве­те на­пи­ши­те букву А, если спо­соб А быст­рее или Б, если быст­рее спо­соб Б. Сразу после буквы на­пи­ши­те ко­ли­че­ство се­кунд, на­сколь­ко один спо­соб быст­рее дру­го­го. Так, на­при­мер, если спо­соб Б быст­рее спо­со­ба А на 23 се­кун­ды, в от­ве­те нужно на­пи­сать Б23. Слов «се­кунд», «сек.», «с.» к от­ве­ту до­бав­лять не нужно.

Решение:

Спо­соб А. Общее время скла­ды­ва­ет­ся из вре­ме­ни сжа­тия, рас­па­ков­ки и пе­ре­да­чи. Время пе­ре­да­чи t рас­счи­ты­ва­ет­ся по фор­му­ле t = V / q, где V — объём ин­фор­ма­ции, q — скорость пе­ре­да­чи дан­ных.

Объем сжатого документа: 5 * 0,8 = 4 Мб =4 * 2²³ бит.

Найдём общее время: t = 35 с + 3 с + 4 * 2²³ бит / 2¹⁸ бит/с = 38 + 2⁷ с = 166 с.

Спо­соб Б. Общее время сов­па­да­ет с вре­ме­нем пе­ре­да­чи: t = 5 * 2²³ бит / 2¹⁸ бит/с = 5 * 2⁵ с = 160 с.

Спо­соб Б быст­рее на 166 – 160 = 6 с.

Ответ: Б6

Определение времени передачи данных

Пример 7.

Ско­рость пе­ре­да­чи дан­ных через ADSL─со­еди­не­ние равна 128000 бит/c. Через дан­ное со­еди­не­ние пе­ре­да­ют файл раз­ме­ром 625 Кбайт. Опре­де­ли­те время пе­ре­да­чи файла в се­кун­дах.

Решение:

Время t = V / q, где V — объем файла, q — скорость пе­ре­да­чи дан­ных.

t = 625 * 2¹⁰ байт / (2 ⁷ * 1000) бит/c = 625 * 2¹³ бит / (125 * 2¹⁰) бит/c = 5 * 2³ с = 40 с.

Ответ: 40

Пример 8.

У Васи есть до­ступ к Ин­тер­нет по вы­со­ко­ско­рост­но­му од­но­сто­рон­не­му ра­дио­ка­на­лу, обес­пе­чи­ва­ю­ще­му ско­рость по­лу­че­ния им ин­фор­ма­ции 2¹⁷ бит в се­кун­ду. У Пети нет ско­рост­но­го до­сту­па в Ин­тер­нет, но есть воз­мож­ность по­лу­чать ин­фор­ма­цию от Васи по низ­ко­ско­рост­но­му те­ле­фон­но­му ка­на­лу со сред­ней ско­ро­стью 2¹⁵ бит в се­кун­ду. Петя до­го­во­рил­ся с Васей, что тот будет ска­чи­вать для него дан­ные объ­е­мом 4 Мбай­та по вы­со­ко­ско­рост­но­му ка­на­лу и ре­транс­ли­ро­вать их Пете по низ­ко­ско­рост­но­му ка­на­лу. Ком­пью­тер Васи может на­чать ре­транс­ля­цию дан­ных не рань­ше, чем им будут по­лу­че­ны пер­вые 512 Кбайт этих дан­ных. Каков ми­ни­маль­но воз­мож­ный про­ме­жу­ток вре­ме­ни (в се­кун­дах), с мо­мен­та на­ча­ла ска­чи­ва­ния Васей дан­ных, до пол­но­го их по­лу­че­ния Петей? В от­ве­те ука­жи­те толь­ко число, слово «се­кунд» или букву «с» до­бав­лять не нужно.

Решение:

Нужно опре­де­лить, сколь­ко вре­ме­ни будет пе­ре­да­вать­ся файл объ­е­мом 4 Мбай­та по ка­на­лу со ско­ро­стью пе­ре­да­чи дан­ных 2¹⁵ бит/с; к этому вре­ме­ни нужно до­ба­вить за­держ­ку файла у Васи (пока он не по­лу­чит 512 Кбайт дан­ных по ка­на­лу со ско­ро­стью 2¹⁷ бит/с).

Время скачивания дан­ных Петей: t₁= 4*2²³ бит / 2¹⁵ бит/с = 2¹⁰ c.

Время за­держ­ки: t₂ = 512 кб / 2¹⁷ бит/с = 2^{(9 + 10 + 3) – 17} c = 2⁵ c.

Пол­ное время: t₁ + t₂ = 2¹⁰ c + 2⁵ c = (1024 + 32) c = 1056 c.

Ответ: 1056

Пример 9.

Данные объемом 60 Мбайт передаются из пункта А в пункт Б по каналу связи, обеспечивающему скорость передачи данных 2¹⁹ бит в секунду, а затем из пункта Б в пункт В по каналу связи, обеспечивающему скорость передачи данных 2²⁰ бит в секунду. Задержка в пункте Б (время между окончанием приема данных из пункта А и началом передачи в пункт В) составляет 25 секунд. Сколько времени (в секундах) прошло с момента начала передачи данных из пункта А до их полного получения в пункте В? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Решение:

Полное время складывается из времени передачи из пункта А в пункт Б (t₁), задержки в пункте Б (t2) и времени передачи из пункта Б в пункт В (t₃).

t₁ = (60 * 2²³) / 2¹⁹ =60 * 16 = 960 c

t₂ = 25 c

t₃ = (60 * 2²³) / 2²⁰ =60 * 8 = 480 c

Полное время t₁ + t₂ +t₃ = 960 + 25 + 480 = 1465 c

Ответ: 1465

1. Найди информационный объём следующего сообщения, если известно, что один символ кодируется одним байтом.

Кто владеет информацией, тот владеет миром.

Решение: посчитаем количество символов в сообщении, будем учитывать буквы, знаки препинания и пробелы.

Всего (43) символа. Каждый символ кодируется (1) байтом.

(I = К · i), (43 · 1) байт (= 43) байта.

Ответ: (43) байта.

2. Найди информационный объём слова из (12) символов в кодировке Unicode (каждый символ кодируется двумя байтами). Ответ дайте в битах.

Решение.

Мы знаем из условия задачи, что каждый символ кодируется двумя байтами. Найдём сколько это бит.

(2) байта (·  8 = 16) бит; 

Слово состоит из (12) символов, поэтому

(16) бит (· 12) символов (= 192) бита.

Ответ: (192) бита.

3. Найди информационный вес книги, которая состоит из (700) страниц, на каждой странице (70) строк и в каждой строке (95) символов . Мощность алфавита — (256) символов. Ответ дать в Мб.

Найдём количество символов в книге: (700·70·95 = 4655000) символов.

Информационный вес сообщения: (4655000·8=37240000) бит.

Ответ нужно дать в Мб, поэтому переведём биты в Мб

(37240000:8:1024:1024 = 4,44) Мб

Ответ: (4,44) Мб.

Определение информационного объема сообщения. Информатика в 7 классе.

Тема: «Измерение информации»

Формулы

Для определения информационного объема сообщения потребуются две формулы:

1. ( N= 2^i )

N — мощность алфавита

i — информационный объём одного символа в алфавите

2. ( I = k * i )​

I — информационный объём сообщения

k — количество символов в сообщении

i — информационный объём одного символа в алфавите

Формула нахождения k:

( k = frac{mathrm I}{mathrm i} )​

Формула нахождения i:

( i = frac{mathrm I}{mathrm k} )​

Задачи

Задача №1. Сообщение, записанное буквами из 128-символьного алфавита, содержит 30 символов. Найти информационный объем всего сообщения?

Решение. Запишем, что дано по условию задачи и что необходимо найти:

N = 128

k = 30

( I = ? )​

( i = ? )​

Сначала найдем вес одного символа по формуле:

( N= 2^i ) = ( 128= 2^7 ) 

( i = 7  )​ бит. Какая степень двойки, такой вес одного символа в алфавите. Далее определяем информационный объем сообщения по формуле:

( I = k * i )​ = 30 * 7 = 210 бит

Ответ: 210 бит

Задача №2. Информационное сообщение объемом 4 Кбайта содержит 4096 символов. Сколько символов содержит алфавит, при помощи которого было записано это сообщение?

Решение. Запишем, что дано по условию задачи и что необходимо найти:

( I = 4 )​ Кб

k = 4096

( N = ? )​

( i = ? )​

Очень важно перевести все числа в степени двойки:

1 Кб = (  2^{13} ) бит

( I = 4 )​ Кб = (  2^2 ) * (  2^{13} ) = (  2^{15} ) бит

k = 4096 = (  2^{12} )

Сначала найдем вес одного символа по формуле:

( i = frac{mathrm I}{mathrm k} )​ = (  2^{15} ) : (  2^{12} ) = (  2^3 ) = 8 бит

Далее находим мощность алфавита по формуле:

( N= 2^i )  ( 2^8 =256)

Ответ: 256 символов в алфавите.

Задача №3. Сколько символов содержит сообщение, записанное с помощью 16-символьного алфавита, если его объем составляет 1/16 Мб?

Решение. Запишем, что дано по условию задачи и что необходимо найти:

N = 16

( I = frac{mathrm 1}{mathrm 16} )​ Мб

( k = ? )​

( i = ? )​

Представим ( I = frac{mathrm 1}{mathrm 16} )​ Мб в степень двойки:

1 Мб = (  2^{23} ) бит

( I = frac{mathrm 1}{mathrm 16} )​ Мб = ( 2^{23} ) : ​(  2^4  )   = (  2^{19} ) бит.

Сначала найдем вес одного символа по формуле:

( N= 2^i ) = (  2^4 = 16 ) 

( i = 4  )​ бит = (  2^2  )  

Теперь найдём количество символов в сообщении k:

( k = frac{mathrm I}{mathrm i} )​ = (  2^{19} )​ : (  2^2 ) = (  2^{17} ) = 131072

Ответ: 131072 символов в сообщении.