Как найти информационный объем памяти

Информатика

7 класс

Урок № 6

Единицы измерения информации

Перечень вопросов, рассматриваемых в теме:

• Алфавитный подход к измерению информации.
• Наименьшая единица измерения информации.
• Информационный вес одного символа алфавита и информационный объём всего сообщения.
• Единицы измерения информации.
• Задачи по теме урока.

Тезаурус:

Каждый символ информационного сообщения несёт фиксированное количество информации.

Единицей измерения количества информации является бит – это наименьшаяединица.

1 байт = 8 бит

1 Кб (килобайт) = 1024 байта= 2¹⁰байтов

1 Мб (мегабайт) = 1024 Кб = 2¹⁰Кб

1 Гб (гигабайт) = 1024 Мб = 2¹⁰ Мб

1 Тб (терабайт) =1024 Гб = 2¹⁰ Гб

Формулы, которые используются при решении типовых задач:

Информационный вес символа алфавита и мощность алфавита связаны между собой соотношением: N = 2ⁱ.

Информационный объём сообщения определяется по формуле:

I = К · i,

I – объём информации в сообщении;

К – количество символов в сообщении;

i – информационный вес одного символа.

Основная литература:

1. Босова Л. Л. Информатика: 7 класс. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2017. – 226 с.

Дополнительная литература:

1. Босова Л. Л. Информатика: 7–9 классы. Методическое пособие. // Босова Л. Л., Босова А. Ю., Анатольев А. В., Аквилянов Н.А. – М.: БИНОМ, 2019. – 512 с.
2. Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 1. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
3. Босова Л. Л. Информатика. Рабочая тетрадь для 7 класса. Ч 2. // Босова Л. Л., Босова А. Ю. – М.: БИНОМ, 2019. – 160 с.
4. Гейн А. Г. Информатика: 7 класс. // Гейн А. Г., Юнерман Н. А., Гейн А.А. – М.: Просвещение, 2012. – 198 с.

Теоретический материал для самостоятельного изучения.

Любое сообщение несёт некоторое количество информации. Как же его измерить?

Одним из способов измерения информации является алфавитный подход, который говорит о том, что каждый символ любого сообщения имеет определённый информационный вес, то есть несёт фиксированное количество информации.

Сегодня на уроке мы узнаем, чему равен информационный вес одного символа и научимся определять информационный объём сообщения.

Что же такое символ в компьютере? Символом в компьютере является любая буква, цифра, знак препинания, специальный символ и прочее, что можно ввести с помощью клавиатуры. Но компьютер не понимает человеческий язык, он каждый символ кодирует. Вся информация в компьютере представляется в виде нулей и единичек. И вот эти нули и единички называются битом.

Информационный вес символа двоичного алфавита принят за минимальную единицу измерения информации и называется один бит.

Алфавит любого понятного нам языка можно заменить двоичным алфавитом. При этом мощность исходного алфавита связана с разрядностью двоичного кода соотношением: N = 2ⁱ.

Эту формулу можно применять для вычисления информационного веса одного символа любого произвольного алфавита.

Рассмотрим пример:

Алфавит древнего племени содержит 16 символов. Определите информационный вес одного символа этого алфавита.

Составим краткую запись условия задачи и решим её:

Дано:

N=16, i = ?

Решение:

N = 2ⁱ

16 = 2ⁱ, 2⁴ = 2ⁱ, т. е. i = 4

Ответ: i = 4 бита.

Информационный вес одного символа этого алфавита составляет 4 бита.

Сообщение состоит из множества символов, каждый из которых имеет свой информационный вес. Поэтому, чтобы вычислить объём информации всего сообщения, нужно количество символов, имеющихся в сообщении, умножить на информационный вес одного символа.

Математически это произведение записывается так: I = К · i.

Например: сообщение, записанное буквами 32-символьного алфавита, содержит 180 символов. Какое количество информации оно несёт?

Дано:

N = 32,

K = 180,

I= ?

Решение:

I = К · i,

N = 2ⁱ

32 = 2ⁱ, 2⁵ = 2 ⁱ, т.о. i = 5,

I = 180 · 5 = 900 бит.

Ответ: I = 900 бит.

Итак, информационный вес всего сообщения равен 900 бит.

В алфавитном подходе не учитывается содержание самого сообщения. Чтобы вычислить объём содержания в сообщении, нужно знать количество символов в сообщении, информационный вес одного символа и мощность алфавита. То есть, чтобы определить информационный вес сообщения: «сегодня хорошая погода», нужно сосчитать количество символов в этом сообщении и умножить это число на восемь.

I = 23 · 8 = 184 бита.

Значит, сообщение весит 184 бита.

Как и в математике, в информатике тоже есть кратные единицы измерения информации. Так, величина равная восьми битам, называется байтом.

Бит и байт – это мелкие единицы измерения. На практике для измерения информационных объёмов используют более крупные единицы: килобайт, мегабайт, гигабайт и другие.

1 байт = 8 бит

1 Кб (килобайт) = 1024 байта= 2¹⁰байтов

1 Мб (мегабайт) = 1024 Кб = 2¹⁰Кб

1 Гб (гигабайт) = 1024 Мб = 2¹⁰ Мб

1 Тб (терабайт) =1024 Гб = 2¹⁰ Гб

Итак, сегодня мы узнали, что собой представляет алфавитный подход к измерению информации, выяснили, в каких единицах измеряется информация и научились определять информационный вес одного символа и информационный объём сообщения.

Материал для углубленного изучения темы.

Как текстовая информация выглядит в памяти компьютера.

Набирая текст на клавиатуре, мы видим привычные для нас знаки (цифры, буквы и т.д.). В оперативную память компьютера они попадают только в виде двоичного кода. Двоичный код каждого символа, выглядит восьмизначным числом, например 00111111. Теперь возникает вопрос, какой именно восьмизначный двоичный код поставить в соответствие каждому символу?

Все символы компьютерного алфавита пронумерованы от 0 до 255. Каждому номеру соответствует восьмиразрядный двоичный код от 00000000 до 11111111. Этот код ‑ просто порядковый номер символа в двоичной системе счисления.

Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки.Таблица для кодировки – это «шпаргалка», в которой указаны символы алфавита в соответствии порядковому номеру. Для разных типов компьютеров используются различные таблицы кодировки.

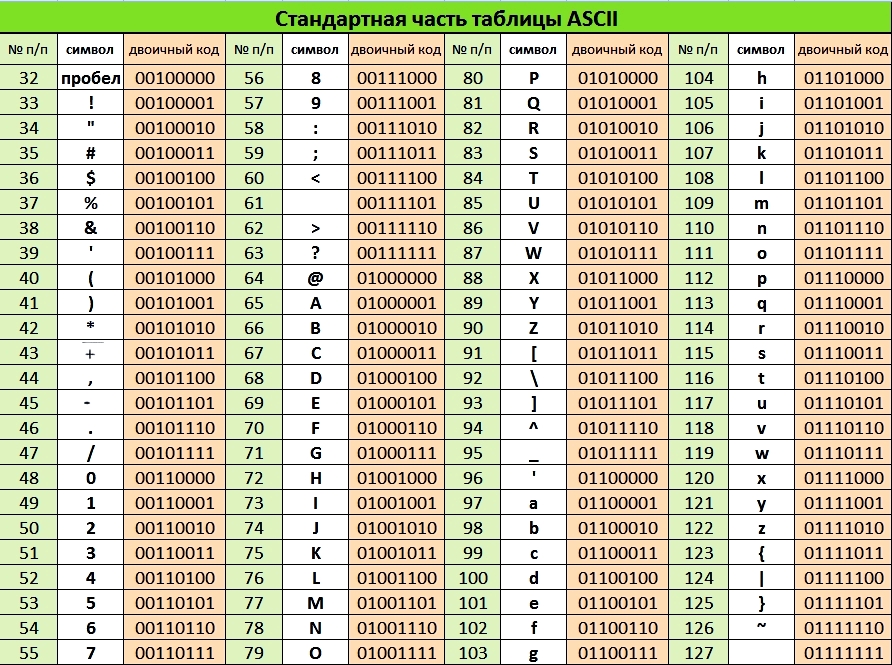
Таблица ASCII (или Аски), стала международным стандартом для персональных компьютеров. Она имеет две части.

В этой таблице латинские буквы (прописные и строчные) располагаются в алфавитном порядке. Расположение цифр также упорядочено по возрастанию значений. Это правило соблюдается и в других таблицах кодировки и называется принципом последовательного кодирования алфавитов. Благодаря этому понятие «алфавитный порядок» сохраняется и в машинном представлении символьной информации. Для русского алфавита принцип последовательного кодирования соблюдается не всегда.

Запишем, например, внутреннее представление слова «file». В памяти компьютера оно займет 4 байта со следующим содержанием:

01100110 01101001 01101100 01100101.

А теперь попробуем решить обратную задачу. Какое слово записано следующим двоичным кодом:

01100100 01101001 01110011 01101011?

В таблице 2 приведен один из вариантов второй половины кодовой таблицы АSСII, который называется альтернативной кодировкой. Видно, что в ней для букв русского алфавита соблюдается принцип последовательного кодирования.

Вывод: все тексты вводятся в память компьютера с помощью клавиатуры. На клавишах написаны привычные для нас буквы, цифры, знаки препинания и другие символы. В оперативную память они попадают в форме двоичного кода.

Из памяти же компьютера текст может быть выведен на экран или на печать в символьной форме.

Сейчас используют целых пять систем кодировок русского алфавита (КОИ8-Р, Windows, MS-DOS, Macintosh и ISO). Из-за количества систем кодировок и отсутствия одного стандарта, очень часто возникают недоразумения с переносом русского текста в компьютерный его вид. Поэтому, всегда нужно уточнять, какая система кодирования установлена на компьютере.

Разбор решения заданий тренировочного модуля

№1. Определите информационный вес символа в сообщении, если мощность алфавита равна 32?

Варианты ответов:

3

5

7

9

Решение:

Информационный вес символа алфавита и мощность алфавита связаны между собой соотношением: N = 2ⁱ.

32 = 2ⁱ, 32 – это 2⁵, следовательно, i =5 битов.

Ответ: 5 битов.

№2. Выразите в килобайтах 2¹⁶ байтов.

Решение:

2¹⁶ можно представить как 2⁶ · 2¹⁰.

2⁶ = 64, а 2¹⁰ байт – это 1 Кб. Значит, 64 · 1 = 64 Кб.

Ответ: 64 Кб.

№3. Тип задания: выделение цветом

8^х = 32 Кб, найдите х.

Варианты ответов:

3

4

5

6

Решение:

8 можно представить как 2³. А 32 Кб переведём в биты.

Получаем 2^3х=32 · 1024 ·8.

Или 2^3х = 2⁵ · 2¹⁰ · 2³.

2^3х = 2¹⁸.

3х = 18, значит, х=6.

Ответ: 6.

Как найти информационный объем

В курсе информатики визуальный, текстовый, графический и другие виды информации представлены в двоичном коде. Это «машинный язык» — последовательность нулей и единиц. Информационный объем позволяет сравнивать количество двоичной информации, входящей в состав разных носителей. Для примера можно рассмотреть, как вычисляются объемы текста и графики.

Инструкция

Для вычисления информационного объема текста, из которого состоит книга, определите начальные данные. Вы должны знать количество страниц в книге, среднее количество строк текста на каждой странице и число символов с пробелами в каждой строке текста. Пусть книга содержит 150 страниц, по 40 строк на странице, по 60 символов в строке.

Найдите количество символов в книге: перемножьте данные первого шага. 150 страниц * 40 строк * 60 символов = 360 тыс. символов в книге.

Определите информационный объем книги, исходя из того, что один символ весит один байт. 360 тысяч символов * 1 байт = 360 тысяч байт.

Перейдите к более крупным единицам измерения: 1 Кб (килобайт) = 1024 байт, 1 Мб (мегабайт) = 1024 Кб. Тогда 360 тысяч байт / 1024 = 351,56 Кб или 351,56 Кб / 1024 = 0,34 Мб.

Чтобы найти информационный объем графического файла, также определите начальные данные. Пусть изображение 10×10 см получено с помощью сканера. Надо знать разрешающую способность устройства — для примера, 600 dpi — и глубину цвета. Последнее значение, так же для примера, можно взять 32 бита.

Выразите разрешающую способность сканера в точках на см. 600 dpi = 600 точек на дюйм. 1 дюйм = 2,54 см. Тогда 600 / 2,54 = 236 точек на см.

Найдите размер изображения в точках. 10 см = 10 * 236 точек на см = 2360 точек. Тогда размер картинки = 10×10 см = 2360×2360 точек.

Вычислите общее количество точек, из которых состоит изображение. 2360 * 2360 = 5569600 штук.

Рассчитайте информационный объем полученного графического файла. Для этого умножьте глубину цвета на результат восьмого шага. 32 бита * 5569600 штук = 178227200 бит.

Перейдите к более крупным единицам измерения: 1 байт = 8 бит, 1 Кб (килобайт) = 1024 байта и т.д. 178227200 бит / 8 = 22278400 байт, или 22278400 байт / 1024 = 21756 Кб, или 21756 Кб / 1024 = 21 Мб. Из-за округления результаты получаются примерными.

Источники:

• Нахождение информационного объема графического файла
• определите информационный объём

Войти на сайт

или

Забыли пароль?
Еще не зарегистрированы?

1.     Информационный объём текстового
сообщения

Расчёт
информационного объёма текстового сообщения (количества информации,
содержащейся в информационном сообщении) основан на подсчёте количества
символов в этом сообщении, включая пробелы, и на определении
информационного веса одного символа, который зависит от кодировки, используемой
при передаче и хранении данного сообщения.

Для расчёта
информационного объёма текстового сообщения используется формула 

I=K*i, где

I  – это информационный объём текстового сообщения,
измеряющийся в байтах, килобайтах, мегабайтах; 

K  –  количество символов в
сообщении, 

i  –  информационный вес одного символа, который
измеряется в битах на один символ.

Информационный
объём одного символа связан с количеством символов в алфавите формулой

N=2ⁱ, где

N – это количество символов в алфавите (мощность
алфавита),

i – информационный
вес одного символа в битах на один символ.

2.     Информационный объём растрового
графического изображения

Расчёт
информационного объёма растрового графического изображения (количества
информации, содержащейся в графическом изображении) основан на подсчёте количества
пикселей в этом изображении и на определении глубины
цвета (информационного веса одного пикселя).

Для расчёта
информационного объёма растрового графического изображения используется
формула 

I=K*i, где

I  – это информационный объём растрового графического
изображения, измеряющийся в байтах, килобайтах, мегабайтах; 

K – количество пикселей (точек) в
изображении, определяющееся разрешающей способностью носителя информации
(экрана монитора, сканера, принтера); 

i – глубина цвета, которая
измеряется в битах на один пиксель.

         Глубина цвета связана с
количеством отображаемых цветов формулой 

N=2ⁱ, где

N – это количество цветов в палитре, 

i – глубина цвета в битах на
один пиксель.

Объем памяти для хранения объектов

Код ОГЭ по информатике: 2.1.3.  Оценка количественных параметров информационных объектов. Объем памяти, необходимый для хранения объектов

---

---

Оценка количества информации

Количество информации можно рассматривать как меру уменьшения неопределенности знания при получении информационных сообщений. Такой подход позволяет количественно измерять информацию.

Впервые объективный подход к измерению количества информации был предложен американским инженером Р. Хартли в 1928 г. Позже, в 1948 г., этот подход обобщил создатель общей теории информации К. Шеннон.

Формула Хартли устанавливает связь между количеством возможных равновероятных информационных сообщений N и количеством информации I, которое содержится в этих сообщениях: N = 2^I

При алфавитном подходе к определению количества информации рассматривают информационное сообщение как последовательность знаков определенной знаковой системы. При этом содержание информации значения не имеет.

По приведенной выше формуле можно рассчитать, какое количество информации I несет каждый из знаков этой системы. Если в алфавите знаковой системы N знаков, то каждый знак несет количество информации: I = log₂ N

Чем больше знаков содержит алфавит, тем больше информации несет один его знак. Если количество символов алфавита равно N, а количество символов в записи сообщения — М, то информационный объем этого сообщения вычисляется по формуле:  I = M • log₂ N

Таким образом, мерой объема любого сообщения в компьютере или на каком–либо носителе принято считать общую длину двоичного кода этого сообщения. Такая мера весьма удобна, поскольку она не связана ни с видом сообщения, ни с его смыслом. Текстовое, звуковое или иное сообщение одинаково характеризуется тем количеством двоичных знаков, которым оно представлено в выбранной системе кодировки.

Количество информации в текстовом сообщении

Текстовая информация состоит из букв, цифр, знаков препинания, различных специальных символов. Для кодирования текстовой информации используют различные коды. Таблица, в которой всем символам компьютерного алфавита поставлены в соответствие порядковые номера, называется таблицей кодировки. Существуют различные таблицы кодировок текстовой информации.

Распространенная таблица кодировки ASCII (читается «аски», American Standard Code for Information Interchange — стандартный американский код для обмена информацией) использует 1 байт для кодов информации. Если код каждого символа занимает 1 байт (8 бит), то с помощью такой кодировки можно закодировать 2⁸ = 256 символов.

Таблица ASCII состоит из двух частей. Первая, базовая часть, является международным стандартом и содержит значения кодов от 0 до 127 (для цифр, операций, латинского алфавита, знаков препинания). Вторая, национальная часть, содержит коды от 128 до 255 для символов национального алфавита, т. е. в национальных кодировках одному и тому же коду соответствуют различные символы.

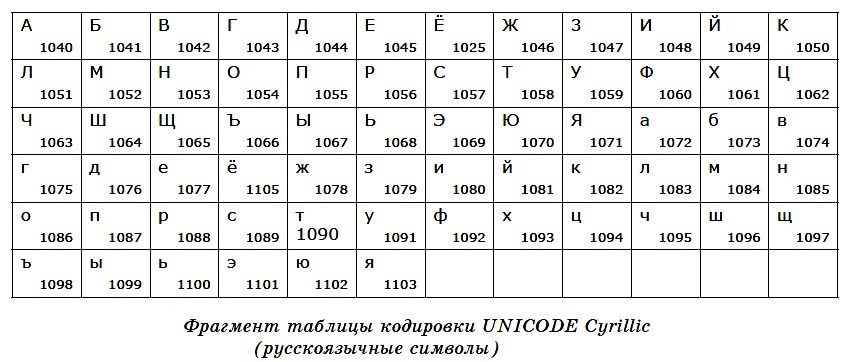
В настоящее время существует несколько различных кодировок второй части таблицы для кириллицы — КОИ8–Р, KOI8–U, Windows, MS–DOS, Macintosh, ISO. Наиболее распространенной является таблица кодировки Windows–1251. Из–за разнообразия таблиц кодировки могут возникать проблемы при переносе русского текста между компьютерами или различными программами.

Поскольку объем в 1 байт явно мал для кодирования разнообразных и многочисленных символов мировых алфавитов, была разработана система кодирования Unicode. В ней для кодирования символа отводится 2 байта (16 бит). Это означает, что система позволяет закодировать 2¹⁶ = 65 536 символов. Полная спецификация стандарта Unicode включает в себя все существующие, вымершие и искусственно созданные алфавиты мира, а также множество математических, музыкальных, химических и прочих символов.

---

Количество графической информации

Растровое графическое изображение состоит из отдельных точек — пикселей, образующих строки и столбцы.

Основные свойства пикселя — его расположение и цвет. Значения этих свойств кодируются и сохраняются в видеопамяти компьютера.

Качество изображения зависит от пространственного разрешения и глубины цвета.

Разрешение — величина, определяющая количество точек (пикселей) на единицу площади.

Глубина цвета — объем памяти (в битах), используемой для хранения и представления цвета при кодировании одного пикселя растровой графики или видеоизображения.

Для графических изображений могут использоваться различные палитры — наборы цветов. Количество цветов N в палитре и количество информации I, необходимое для кодирования цвета каждой точки, связаны соотношением: N = 2^I

Например, для черно–белого изображения палитра состоит из двух цветов. Можно вычислить, какое количество информации необходимо, чтобы закодировать цвет каждой точки (пикселя): 2 = 2^I —> I_{пикселя} = 1 бит

Чтобы определить информационный объем видеоизображения, необходимо умножить количество информации одного пикселя на количество пикселей в изображении: I = I_{пикселя} • X • Y,  где Х — количество точек изображения по горизонтали, Y — количество точек изображения по вертикали.

Существует несколько цветовых моделей для количественного описания цвета. В основе модели RGB (сокращение от англ. Red, Green, Blue) лежат три основных цвета: красный, зеленый и синий. Все другие цвета создаются с помощью смешения их оттенков. Например, при смешивании красного и зеленого цветов получим желтый, красного и синего — пурпурный, зеленого и синего — бирюзовый. Если смешать все три основные цвета максимальной яркости, получим белый цвет.

Если один цвет имеет 4 оттенка, то общее количество цветов в модели RGB будет составлять 4 • 4 • 4 = 64. При 256 оттенках для каждого цвета общее количество возможных цветов будет равно 256 • 256 • 256 = 16 777 216 ≈ 16,7 млн.

В современных компьютерах для представления цвета обычно используются от 2–х до 4–х байт. Два байта (16 бит) позволяют различать 2¹⁶, то есть 65 536 цветов и оттенков. Такой режим представления изображений называется High Color. Четыре байта (32 бита) обеспечивают цветную гамму в 2³², то есть 4 294 967 296 цветов и оттенков (приблизительно 4,3 миллиарда). Такой режим называется True Color.

В графических редакторах применяются и другие цветовые модели. Например, модель CMYK — она основана на цветах, получающихся при отражении белого света от предмета: бирюзовом (англ. Cyan), пурпурном (англ. Magenta), желтом (англ. Yellow). Эта модель применяется в полиграфии, где чаще всего употребляется черный цвет (ключевой, англ. Key).

---

Измерение объемов звуковой информации

Звук является непрерывным сигналом. Для использования звука в компьютере его преобразуют в цифровой сигнал. Это преобразование называется дискретизацией: для кодирования звука производят его измерение с определенной частотой (несколько раз в секунду). частота дискретизации и точность представления измеренных значений определяют качество представления звука в компьютере. Чем выше частота дискретизации и чем больше количество разных значений, которыми можно характеризовать сигнал, тем выше качество отображения звука.

В современных компьютерах обычно применяется частота дискретизации в 22 кГц или 44,1 кГц (1 кГц — это тысяча измерений за 1 секунду), а для представления значения сигнала выделяются 2 байта (16 бит), что позволяет различать 2¹⁶, то есть 65 536 значений.

---

Конспект урока по информатике «Объем памяти для хранения объектов».

Вернуться к Списку конспектов по информатике.

Здравствуйте! С вами Елена TeachYOU, и сегодня мы разберем задачи 11 из ЕГЭ по информатике. Задачи несложные, но почему-то у многих учеников с ними возникают проблемы.

Что такое равномерное кодирование

Для того, чтобы работать с какими-то объектами с помощью компьютера, необходимо их закодировать. Так как подавляющее большинство современных ЭВМ использует двоичную логику, разумно кодировать объекты с использованием двоичного кодирования.

Двоичное кодирование можно разделить на равномерное (когда кодовые слова, или коды, имеют одинаковую длину), и неравномерное (когда длина кодовых слов разная). Тема неравномерного кодирования поднимается в 4 задании ЕГЭ, можете посмотреть материал по нему в этой статье. Там разобраны примеры с разными вариантами кодирования. Если вам все еще непонятно, чем равномерное кодирование отличается от неравномерного, то перед тем, как читать материал по 11 заданию дальше, советую сначала просмотреть материал по ссылке выше.

Перевод битов в байты и далее

Прежде чем двигаться дальше, напомню правила перевода между единицами измерения информации. Основное:

• 1 байт = 8 бит
• 1 Кбайт = 1024 байт = 2^10 байт = 2^13 бит
• 1 Мбайт = 1024 Кбайт = 2^10 Кбайт = 2^23 бит

Что нужно знать про равномерное двоичное кодирование

Кодирование равномерное => все кодовые слова имеют одинаковую, минимально возможную, длину. Кодирование двоичное => кодовые слова состоят только из 0 и 1.

Сколько объектов можно закодировать, используя кодовые слова имеют длины i ?

Например, буква А может кодироваться кодовым словом 01101. В нем пять знаков (0 или 1). Говорят, что кодовое слово 01101 состоит из пяти бит. Бит – это ячейка, принимающая значение 0 или 1 (тире или точка, вкл или выкл и пр.).

Тогда кодовое слово 0110 состоит из 4 бит, слово 110011 – из 6 бит и т.д.

Посмотрим, сколько разных кодовых слов можно составить, если брать кодовые слова определенной длины (здесь нам поможет теория по теме “Комбинаторика” для 8 номера).

• Кодовые слова длины 1 – это 0 и 1. Их два (каждое занимает 1 бит).
• Кодовые слова длины 2 – это 00, 01, 10 и 11. Их четыре (каждое занимает 2 бит).
• Кодовые слова длины 3 я перечислять не буду. Их количество равно 2*2*2 = 2^3 = 8 (если непонятно, загляните в материал по комбинаторике). Каждое кодовое слово занимает 3 бита.
• ….
• Кодовые слова длины i – их 2^i. Каждое занимает i бит.

Получается, что, если для кодирования мы выберем кодовые слова длины i (i-битные), то сможем закодировать 2^i объектов.

Если в сообщении используется N символов, сколько бит нужно для кодирования каждого символа?

Количество i-битных кодовых слов равно 2^i.

Похоже, что, нужно подобрать такое i, чтобы N = 2^i.

Но на практике не всегда число N является степенью двойки. Поэтому для кодирования N объектов нужно взять такое минимальное i, чтобы выполнялось условие N <= 2^i.

Например:

• N = 14: 14 <= 16 = 2^4. Получается, что при кодировании 14 объектов с использованием равномерного двоичного кодирования на каждый объект будет приходиться 4 бита.
• N = 250: 250 <= 256 = 2^8 => 8 бит на объект.
• N = 2050: 2050 <= 4096 = 2^12 => 12 бит на объект.

Рассмотрим задачи 11 из ЕГЭ

Задача 1 (номер 1964 с компегэ)

При регистрации в компьютерной системе каждому объекту сопоставляется идентификатор, состоящий из 15 символов и содержащий только символы из 8-символьного набора: А, В, C, D, Е, F, G, H. В базе данных для хранения сведений о каждом объекте отведено одинаковое и минимально возможное целое число байт. При этом используют посимвольное кодирование идентификаторов, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственно идентификатора, для каждого объекта в системе хранятся дополнительные сведения, для чего отведено 24 байта на один объект.

Определите объём памяти (в байтах), необходимый для хранения сведений о 20 объектах. В ответе запишите только целое число – количество байт.

Из задачи следует, что нужно сохранить данные о 20 объектах. Для каждого из них хранится идентификатор (его информационный вес нужно вычислить) и дополнительные сведения (известны, 24 байта на один объект).

Начнем с вычисления количества байт, которое занимает один идентификатор.

Длина идентификатора 15 символов, а мощность алфавита равна восьми. Вспоминаем основную формулу информатики: N = 2^i, где N – количество кодируемых равномерным кодированием объектов, i – количество бит, которое приходится на один объект. N = 8 (нужно закодировать все символы из набора, поэтому N = мощности алфавита). Из 8 = 2^i находим i=3 бита. Каждый символ кодируется 3 битами, а идентификатор состоит из 15 символов. Получается, на один идентификатор приходится 15 * 3 = 45 бит = 5,625 байт.

Обращаем внимание, что в задаче говорится, что для хранения сведений о каждом объекте отведено одинаковое и минимально возможное целое число байт. Необходимо округлить 5,625 байт до целого значения. Но в большую или меньшую сторону?

Если округлим в меньшую, то получим 5 байт = 40 бит. Но для хранения идентификатора нужно 45 бит! 45 бит не помещаются в “коробочку” из 5 байт. Значит, нужно округлять в большую. Итого, на идентификатор приходится 6 байт.

Для вычисления информационного объема, необходимого для хранения сведений об одном объекте, найдем сумму байт, приходящихся на идентификатор и на дополнительные сведения:

6 + 24 = 30 (байт) – на 1 объект.

Вычислим объем информации для хранения сведений о 20 объектах:

30 (байт) * 20 (объектов) = 600 (байт).

Задача 2 (номер 212 с компегэ)

Для регистрации на сайте необходимо продумать пароль, состоящий из 9 символов. Он может содержать десятичные цифры, строчные или заглавные буквы латинского алфавита (алфавит содержит 26 букв) и символы из перечисленных: «.», «$», «#», «@», «%», «&». В базе данных для хранения сведения о каждом пользователе отведено одинаковое и минимальное возможное целое число байт. При этом используют посимвольное кодирование паролей, все символы кодируют одинаковым и минимально возможным количеством бит. Кроме собственного пароля, для каждого пользователя в системе хранятся дополнительные сведения, для чего выделено целое число байт одинаковое для каждого пользователя. Для хранения сведений о двадцати пользователях потребовалось 500 байт. Сколько байт выделено для хранения дополнительных сведений об одном пользователе. В ответе запишите только целое число – количество байт.

Сайт хранит данные о 20 пользователях. Они занимают 500 байт. Для каждого пользователя хранятся пароль (его информационный объем нужно вычислить) и дополнительные сведения (эту величину нужно найти и взять в качестве ответа).

Начнем с поиска количества байт, приходящихся на одного пользователя:

500 (байт) / 20 (польз.) = 25 (байт на 1 польз.)

Разберемся с паролем. Мощность алфавита символов, которые используются для его записи:

N = 10 (цифр) + 26 (строчных букв) + 26 (заглавных букв) + 6 (символов «.», «$», «#», «@», «%», «&») = 68 (символов).

Сколькими битами можно закодировать каждый из 78 символов при использовании равномерного кодирования?

68 <= 2^i, i = 7 (бит).

Тогда пароль занимает

7 (бит) * 9 (символов) = 63 (бит) = 8 (байт).

Для одного пользователя хранится пароль (8 байт) и доп. сведения. Всего на пользователя приходится 25 байт. Тогда доп. сведения занимают

25 – 8 = 17 (байт).

Задача 3 (номер 463 с компегэ)

Очень люблю эту задачу авторства Евгения Джобса за нацеленность на понимание темы

Автомобильный номер состоит из одиннадцати букв русского алфавита A, B,C, E, H, K, M, O, P, T, X и десятичных цифр от 0 до 9.  Каждый номер состоит из двух букв, затем идет 3 цифры и еще одна буква. Например, АВ901С.

В системе каждый такой номер кодируется посимвольно, при этом каждая буква и каждая цифра кодируются одинаковым минимально возможным количеством бит.

Укажите, сколько бит на один номер можно сэкономить, если кодировать с помощью одинакового минимально возможного количества бит каждую из трех групп – первые две буквы, три цифры и последняя буква.

В этой задаче есть “до” и “после”.

“До”: каждая буква и каждая цифра кодируются отдельно.

“После”: кодируются отдельно первые две буквы, три цифры и последняя буква.

Разберемся, сколько бит занимал автомобильный номер при выборе способа кодирования “до”.

• Буквы: N = 11 <= 16 = 2^4 => i = 4.
• Цифры: N = 10 <= 16 = 2^4 => i = 4.
• Весь номер состоит их трех цифр и трех букв, это 3 (буквы) * 4 (бита) + 3 (цифры) * 4 (бита) = 24 (бит на один номер)

Как кодируем номер “после”?

• Первые две буквы. Букв 11. Количество пар букв (АА, АВ, … , ХХ) равно 11*11 = 121. Нашли объекты – это пары букв. Их количество N = 121 <= 128 = 2^7 => i=7 бит. Раньше каждую букву мы кодировали 4 битами и две буквы занимали 8 бит. А теперь 7. Э – экономия!
• Три цифры. Цифр 10. Количество троек цифр (000, 001, … , 999) равно 10*10*10 = 1000. В этом случае кодируемые объекты – это тройки цифр. N = 1000 <= 1024 = 2^10 => i = 10 бит. “До” каждую цифру кодировали 4 битами, три цифры занимали 12 бит. А сейчас 10. И здесь сэкономили.
• Последняя буква. N = 11 <= 16 = 2^4 => i=4. Тут ничего не изменилось: “до” кодировали объекты-буквы и здесь поступили так же.
• Количество бит на номер “после”: 7 + 10 + 4 = 21 (бит).

Итого сэкономили 24 – 21 = 3 (бита).

Какие еще задачи посмотреть, чтобы закрепить материал?

Сайт kompege.ru покорил мое сердце, и теперь я считаю себя его амбассадором)

Если вы только знакомитесь с 11 номерами, решайте любые задачи (на сайте компегэ их можно отсортировать по сложности, начните с простых).

Для более продвинутых настоятельно советую прорешать задачи из списка ниже, так как в каждой есть свои тонкости.

Номера 11: 4468, 4323, 2119, 5433.

И традиционно – успехов!