Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 декабря 2019 года; проверки требуют 9 правок.
Информа́ция Фи́шера — математическое ожидание квадрата относительной скорости изменения условной плотности вероятности 
честь описавшего её Рональда Фишера.
Определение[править | править код]
Пусть 
,
где 




Если 

Для регулярных моделей: 
В этом случае, поскольку математическое ожидание функции вклада выборки равно нулю, выписанная величина равна её дисперсии.
Фишеровским количеством информации, содержащемся в одном наблюдении называют:
.
Для регулярных моделей все 
Если выборка состоит из одного элемента, то информация Фишера записывается так:
.
Из условия регулярности, а также из того, что в случае независимости случайных величин дисперсия суммы равна сумме дисперсий, следует, что для 

Свойства[править | править код]
- Из указанного выше свойства дисперсий следует, что в случае независимости случайных величин
(рассматриваемых в одной статистической модели) информация Фишера их суммы равна сумме информации Фишера каждой из них.
Сохранение информации достаточной статистикой[править | править код]
В общем случае, если 
Причем равенство достигается тогда и только тогда, когда T является достаточной статистикой.
Достаточная статистика содержит столько же информации Фишера, сколько и вся выборка X.
Это может быть показано с помощью факторизационного критерия Неймана для достаточной статистики. Если статистика 

Равенство информации следует из:
что следует из определения информации Фишера и независимости 

См. также[править | править код]
- Неравенство Крамера — Рао
- Информационное неравенство (математическая статистика)
Другие меры, используемые в теории информации:
- Информационная энтропия
- Расстояние Кульбака — Лейблера
- Собственная информация
Примечания[править | править код]
- ↑ Леман, 1991, с. 112.
- ↑
Lehmann, E. L. (англ.) (рус.; Casella, G. Theory of Point Estimation (неопр.). — 2nd ed. — Springer, 1998. — ISBN 0-387-98502-6.
, eq. (2.5.16).
Литература[править | править код]
- Леман Э. Теория точечного оценивания. — М.: Наука, 1991. — 448 с. — ISBN 5-02-013941-6.
В математической статистике и теории информации информа́цией Фи́шера называется дисперсия функции вклада выборки. Эта функция названа в честь описавшего её Рональда Фишера.
Определение
Пусть 
,
где 


Если выборка состоит из одного элемента, то информация Фишера записывается так:
.
Из того, что в случае независимости случайных величин дисперсия суммы равна сумме дисперсий, следует, что в случае 

Свойства
См. также
- Неравенство Крамера — Рао
In mathematical statistics, the Fisher information (sometimes simply called information[1]) is a way of measuring the amount of information that an observable random variable X carries about an unknown parameter θ of a distribution that models X. Formally, it is the variance of the score, or the expected value of the observed information.
The role of the Fisher information in the asymptotic theory of maximum-likelihood estimation was emphasized by the statistician Ronald Fisher (following some initial results by Francis Ysidro Edgeworth). The Fisher information matrix is used to calculate the covariance matrices associated with maximum-likelihood estimates. It can also be used in the formulation of test statistics, such as the Wald test.
In Bayesian statistics, the Fisher information plays a role in the derivation of non-informative prior distributions according to Jeffreys’ rule.[2] It also appears as the large-sample covariance of the posterior distribution, provided that the prior is sufficiently smooth (a result known as Bernstein–von Mises theorem, which was anticipated by Laplace for exponential families).[3] The same result is used when approximating the posterior with Laplace’s approximation, where the Fisher information appears as the covariance of the fitted Gaussian.[4]
Statistical systems of a scientific nature (physical, biological, etc.) whose likelihood functions obey shift invariance have been shown to obey maximum Fisher information.[5] The level of the maximum depends upon the nature of the system constraints.
Definition[edit]
The Fisher information is a way of measuring the amount of information that an observable random variable 
















Formally, the partial derivative with respect to 




The Fisher information is defined to be the variance of the score:[7]
Note that 
If log f(x; θ) is twice differentiable with respect to θ, and under certain regularity conditions, then the Fisher information may also be written as[8]
since
and
Thus, the Fisher information may be seen as the curvature of the support curve (the graph of the log-likelihood). Near the maximum likelihood estimate, low Fisher information therefore indicates that the maximum appears “blunt”, that is, the maximum is shallow and there are many nearby values with a similar log-likelihood. Conversely, high Fisher information indicates that the maximum is sharp.
Regularity conditions[edit]
The regularity conditions are as follows:[9]
- The partial derivative of f(X; θ) with respect to θ exists almost everywhere. (It can fail to exist on a null set, as long as this set does not depend on θ.)
- The integral of f(X; θ) can be differentiated under the integral sign with respect to θ.
- The support of f(X; θ) does not depend on θ.
If θ is a vector then the regularity conditions must hold for every component of θ. It is easy to find an example of a density that does not satisfy the regularity conditions: The density of a Uniform(0, θ) variable fails to satisfy conditions 1 and 3. In this case, even though the Fisher information can be computed from the definition, it will not have the properties it is typically assumed to have.
In terms of likelihood[edit]
Because the likelihood of θ given X is always proportional to the probability f(X; θ), their logarithms necessarily differ by a constant that is independent of θ, and the derivatives of these logarithms with respect to θ are necessarily equal. Thus one can substitute in a log-likelihood l(θ; X) instead of log f(X; θ) in the definitions of Fisher Information.
Samples of any size[edit]
The value X can represent a single sample drawn from a single distribution or can represent a collection of samples drawn from a collection of distributions. If there are n samples and the corresponding n distributions are statistically independent then the Fisher information will necessarily be the sum of the single-sample Fisher information values, one for each single sample from its distribution. In particular, if the n distributions are independent and identically distributed then the Fisher information will necessarily be n times the Fisher information of a single sample from the common distribution.
Informal derivation of the Cramér–Rao bound[edit]
The Cramér–Rao bound[10][11] states that the inverse of the Fisher information is a lower bound on the variance of any unbiased estimator of θ. H.L. Van Trees (1968) and B. Roy Frieden (2004) provide the following method of deriving the Cramér–Rao bound, a result which describes use of the Fisher information.
Informally, we begin by considering an unbiased estimator 
This expression is zero independent of θ, so its partial derivative with respect to θ must also be zero. By the product rule, this partial derivative is also equal to
For each θ, the likelihood function is a probability density function, and therefore 


Using these two facts in the above, we get
Factoring the integrand gives
Squaring the expression in the integral, the Cauchy–Schwarz inequality yields
The second bracketed factor is defined to be the Fisher Information, while the first bracketed factor is the expected mean-squared error of the estimator 
In other words, the precision to which we can estimate θ is fundamentally limited by the Fisher information of the likelihood function.
Alternatively, the same conclusion can be obtained directly from the Cauchy-Schwarz inequality for random variables, 


Single-parameter Bernoulli experiment[edit]
A Bernoulli trial is a random variable with two possible outcomes, “success” and “failure”, with success having a probability of θ. The outcome can be thought of as determined by a coin toss, with the probability of heads being θ and the probability of tails being 1 − θ.
Let X be a Bernoulli trial. The Fisher information contained in X may be calculated to be
Because Fisher information is additive, the Fisher information contained in n independent Bernoulli trials is therefore
This is the reciprocal of the variance of the mean number of successes in n Bernoulli trials, so in this case, the Cramér–Rao bound is an equality.
Matrix form[edit]
When there are N parameters, so that θ is an N × 1 vector 
The FIM is a N × N positive semidefinite matrix. If it is positive definite, then it defines a Riemannian metric on the N-dimensional parameter space. The topic information geometry uses this to connect Fisher information to differential geometry, and in that context, this metric is known as the Fisher information metric.
Under certain regularity conditions, the Fisher information matrix may also be written as
The result is interesting in several ways:
- It can be derived as the Hessian of the relative entropy.
- It can be used as a Riemannian metric for defining Fisher-Rao geometry when it is positive-definite.[12]
- It can be understood as a metric induced from the Euclidean metric, after appropriate change of variable.
- In its complex-valued form, it is the Fubini–Study metric.
- It is the key part of the proof of Wilks’ theorem, which allows confidence region estimates for maximum likelihood estimation (for those conditions for which it applies) without needing the Likelihood Principle.
- In cases where the analytical calculations of the FIM above are difficult, it is possible to form an average of easy Monte Carlo estimates of the Hessian of the negative log-likelihood function as an estimate of the FIM.[13][14][15] The estimates may be based on values of the negative log-likelihood function or the gradient of the negative log-likelihood function; no analytical calculation of the Hessian of the negative log-likelihood function is needed.
Information orthogonal parameters[edit]
We say that two parameter component vectors θ1 and θ2 are information orthogonal if the Fisher information matrix is block diagonal, with these components in separate blocks.[16] Orthogonal parameters are easy to deal with in the sense that their maximum likelihood estimates are asymptotically uncorrelated. When considering how to analyse a statistical model, the modeller is advised to invest some time searching for an orthogonal parametrization of the model, in particular when the parameter of interest is one-dimensional, but the nuisance parameter can have any dimension.[17]
Singular statistical model[edit]
If the Fisher information matrix is positive definite for all θ, then the corresponding statistical model is said to be regular; otherwise, the statistical model is said to be singular.[18] Examples of singular statistical models include the following: normal mixtures, binomial mixtures, multinomial mixtures, Bayesian networks, neural networks, radial basis functions, hidden Markov models, stochastic context-free grammars, reduced rank regressions, Boltzmann machines.
In machine learning, if a statistical model is devised so that it extracts hidden structure from a random phenomenon, then it naturally becomes singular.[19]
Multivariate normal distribution[edit]
The FIM for a N-variate multivariate normal distribution, 





where 

Note that a special, but very common, case is the one where 
In this case the Fisher information matrix may be identified with the coefficient matrix of the normal equations of least squares estimation theory.
Another special case occurs when the mean and covariance depend on two different vector parameters, say, β and θ. This is especially popular in the analysis of spatial data, which often uses a linear model with correlated residuals. In this case,[21]
where
Properties[edit]
Chain rule[edit]
Similar to the entropy or mutual information, the Fisher information also possesses a chain rule decomposition. In particular, if X and Y are jointly distributed random variables, it follows that:[22]
where ![{displaystyle {mathcal {I}}_{Ymid X}(theta )=operatorname {E} _{X}left[{mathcal {I}}_{Ymid X=x}(theta )right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0597b3e4e15806338f76e41e02af60263455c8d3)


As a special case, if the two random variables are independent, the information yielded by the two random variables is the sum of the information from each random variable separately:
Consequently, the information in a random sample of n independent and identically distributed observations is n times the information in a sample of size 1.
F-divergence[edit]
Given a convex function ![{displaystyle f:[0,infty )to (-infty ,infty ]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/6fb2206a6fa5ea459545ee7ff25b0495c0d9481b)








where 


In this form, it is clear that the Fisher information matrix is a Riemannian metric, and varies correctly under a change of variables. (see section on Reparametrization)
Sufficient statistic[edit]
The information provided by a sufficient statistic is the same as that of the sample X. This may be seen by using Neyman’s factorization criterion for a sufficient statistic. If T(X) is sufficient for θ, then
for some functions g and h. The independence of h(X) from θ implies
and the equality of information then follows from the definition of Fisher information. More generally, if T = t(X) is a statistic, then
with equality if and only if T is a sufficient statistic.[24]
Reparametrization[edit]
The Fisher information depends on the parametrization of the problem. If θ and η are two scalar parametrizations of an estimation problem, and θ is a continuously differentiable function of η, then
where 

In the vector case, suppose 



where the (i, j)th element of the k × k Jacobian matrix 
and where 

In information geometry, this is seen as a change of coordinates on a Riemannian manifold, and the intrinsic properties of curvature are unchanged under different parametrizations. In general, the Fisher information matrix provides a Riemannian metric (more precisely, the Fisher–Rao metric) for the manifold of thermodynamic states, and can be used as an information-geometric complexity measure for a classification of phase transitions, e.g., the scalar curvature of the thermodynamic metric tensor diverges at (and only at) a phase transition point.[27]
In the thermodynamic context, the Fisher information matrix is directly related to the rate of change in the corresponding order parameters.[28] In particular, such relations identify second-order phase transitions via divergences of individual elements of the Fisher information matrix.
Isoperimetric inequality[edit]
The Fisher information matrix plays a role in an inequality like the isoperimetric inequality.[29] Of all probability distributions with a given entropy, the one whose Fisher information matrix has the smallest trace is the Gaussian distribution. This is like how, of all bounded sets with a given volume, the sphere has the smallest surface area.
The proof involves taking a multivariate random variable 



where 




Applications[edit]
Optimal design of experiments[edit]
Fisher information is widely used in optimal experimental design. Because of the reciprocity of estimator-variance and Fisher information, minimizing the variance corresponds to maximizing the information.
When the linear (or linearized) statistical model has several parameters, the mean of the parameter estimator is a vector and its variance is a matrix. The inverse of the variance matrix is called the “information matrix”. Because the variance of the estimator of a parameter vector is a matrix, the problem of “minimizing the variance” is complicated. Using statistical theory, statisticians compress the information-matrix using real-valued summary statistics; being real-valued functions, these “information criteria” can be maximized.
Traditionally, statisticians have evaluated estimators and designs by considering some summary statistic of the covariance matrix (of an unbiased estimator), usually with positive real values (like the determinant or matrix trace). Working with positive real numbers brings several advantages: If the estimator of a single parameter has a positive variance, then the variance and the Fisher information are both positive real numbers; hence they are members of the convex cone of nonnegative real numbers (whose nonzero members have reciprocals in this same cone).
For several parameters, the covariance matrices and information matrices are elements of the convex cone of nonnegative-definite symmetric matrices in a partially ordered vector space, under the Loewner (Löwner) order. This cone is closed under matrix addition and inversion, as well as under the multiplication of positive real numbers and matrices. An exposition of matrix theory and Loewner order appears in Pukelsheim.[31]
The traditional optimality criteria are the information matrix’s invariants, in the sense of invariant theory; algebraically, the traditional optimality criteria are functionals of the eigenvalues of the (Fisher) information matrix (see optimal design).
Jeffreys prior in Bayesian statistics[edit]
In Bayesian statistics, the Fisher information is used to calculate the Jeffreys prior, which is a standard, non-informative prior for continuous distribution parameters.[32]
Computational neuroscience[edit]
The Fisher information has been used to find bounds on the accuracy of neural codes. In that case, X is typically the joint responses of many neurons representing a low dimensional variable θ (such as a stimulus parameter). In particular the role of correlations in the noise of the neural responses has been studied.[33]
Derivation of physical laws[edit]
Fisher information plays a central role in a controversial principle put forward by Frieden as the basis of physical laws, a claim that has been disputed.[34]
Machine learning[edit]
The Fisher information is used in machine learning techniques such as elastic weight consolidation,[35] which reduces catastrophic forgetting in artificial neural networks.
Fisher information can be used as an alternative to the Hessian of the loss function in second-order gradient descent network training.[36]
Relation to relative entropy[edit]
Fisher information is related to relative entropy.[37] The relative entropy, or Kullback–Leibler divergence, between two distributions 

Now, consider a family of probability distributions 

If 



But the second order derivative can be written as
Thus the Fisher information represents the curvature of the relative entropy of a conditional distribution with respect to its parameters.
History[edit]
The Fisher information was discussed by several early statisticians, notably F. Y. Edgeworth.[38] For example, Savage[39] says: “In it [Fisher information], he [Fisher] was to some extent anticipated (Edgeworth 1908–9 esp. 502, 507–8, 662, 677–8, 82–5 and references he [Edgeworth] cites including Pearson and Filon 1898 [. . .]).” There are a number of early historical sources[40] and a number of reviews of this early work.[41][42][43]
See also[edit]
- Efficiency (statistics)
- Observed information
- Fisher information metric
- Formation matrix
- Information geometry
- Jeffreys prior
- Cramér–Rao bound
- Minimum Fisher information
- Quantum Fisher information
Other measures employed in information theory:
- Entropy (information theory)
- Kullback–Leibler divergence
- Self-information
Notes[edit]
- ^ Lehmann & Casella, p. 115
- ^ Robert, Christian (2007). “Noninformative prior distributions”. The Bayesian Choice (2nd ed.). Springer. pp. 127–141. ISBN 978-0-387-71598-8.
- ^ Le Cam, Lucien (1986). Asymptotic Methods in Statistical Decision Theory. New York: Springer. pp. 618–621. ISBN 0-387-96307-3.
- ^ Kass, Robert E.; Tierney, Luke; Kadane, Joseph B. (1990). “The Validity of Posterior Expansions Based on Laplace’s Method”. In Geisser, S.; Hodges, J. S.; Press, S. J.; Zellner, A. (eds.). Bayesian and Likelihood Methods in Statistics and Econometrics. Elsevier. pp. 473–488. ISBN 0-444-88376-2.
- ^ Frieden & Gatenby (2013)
- ^ Suba Rao. “Lectures on statistical inference” (PDF).
- ^ Fisher (1922)
- ^ Lehmann & Casella, eq. (2.5.16), Lemma 5.3, p.116.
- ^ Schervish, Mark J. (1995). Theory of Statistics. New York, NY: Springer New York. p. 111. ISBN 978-1-4612-4250-5. OCLC 852790658.
- ^ Cramer (1946)
- ^ Rao (1945)
- ^ Nielsen, Frank (2010). “Cramer-Rao lower bound and information geometry”. Connected at Infinity II: 18–37. arXiv:1301.3578.
- ^ Spall, J. C. (2005). “Monte Carlo Computation of the Fisher Information Matrix in Nonstandard Settings”. Journal of Computational and Graphical Statistics. 14 (4): 889–909. doi:10.1198/106186005X78800. S2CID 16090098.
- ^ Spall, J. C. (2008), “Improved Methods for Monte Carlo Estimation of the Fisher Information Matrix,” Proceedings of the American Control Conference, Seattle, WA, 11–13 June 2008, pp. 2395–2400. https://doi.org/10.1109/ACC.2008.4586850
- ^ Das, S.; Spall, J. C.; Ghanem, R. (2010). “Efficient Monte Carlo Computation of Fisher Information Matrix Using Prior Information”. Computational Statistics and Data Analysis. 54 (2): 272–289. doi:10.1016/j.csda.2009.09.018.
- ^ Barndorff-Nielsen, O. E.; Cox, D. R. (1994). Inference and Asymptotics. Chapman & Hall. ISBN 9780412494406.
- ^ Cox, D. R.; Reid, N. (1987). “Parameter orthogonality and approximate conditional inference (with discussion)”. J. Royal Statistical Soc. B. 49: 1–39.
- ^ Watanabe, S. (2008), Accardi, L.; Freudenberg, W.; Ohya, M. (eds.), “Algebraic geometrical method in singular statistical estimation”, Quantum Bio-Informatics, World Scientific: 325–336, Bibcode:2008qbi..conf..325W, doi:10.1142/9789812793171_0024, ISBN 978-981-279-316-4.
- ^ Watanabe, S (2013). “A Widely Applicable Bayesian Information Criterion”. Journal of Machine Learning Research. 14: 867–897.
- ^ Malagò, Luigi; Pistone, Giovanni (2015). Information geometry of the Gaussian distribution in view of stochastic optimization. Proceedings of the 2015 ACM Conference on Foundations of Genetic Algorithms XIII. pp. 150–162. doi:10.1145/2725494.2725510. ISBN 9781450334341. S2CID 693896.
- ^ Mardia, K. V.; Marshall, R. J. (1984). “Maximum likelihood estimation of models for residual covariance in spatial regression”. Biometrika. 71 (1): 135–46. doi:10.1093/biomet/71.1.135.
- ^ Zamir, R. (1998). “A proof of the Fisher information inequality via a data processing argument”. IEEE Transactions on Information Theory. 44 (3): 1246–1250. CiteSeerX 10.1.1.49.6628. doi:10.1109/18.669301.
- ^ Polyanskiy, Yury (2017). “Lecture notes on information theory, chapter 29, ECE563 (UIUC)” (PDF). Lecture notes on information theory. Archived (PDF) from the original on 2022-05-24. Retrieved 2022-05-24.
- ^ Schervish, Mark J. (1995). Theory Statistics. Springer-Verlag. p. 113.
- ^ Lehmann & Casella, eq. (2.5.11).
- ^ Lehmann & Casella, eq. (2.6.16)
- ^ Janke, W.; Johnston, D. A.; Kenna, R. (2004). “Information Geometry and Phase Transitions”. Physica A. 336 (1–2): 181. arXiv:cond-mat/0401092. Bibcode:2004PhyA..336..181J. doi:10.1016/j.physa.2004.01.023. S2CID 119085942.
- ^ Prokopenko, M.; Lizier, Joseph T.; Lizier, J. T.; Obst, O.; Wang, X. R. (2011). “Relating Fisher information to order parameters”. Physical Review E. 84 (4): 041116. Bibcode:2011PhRvE..84d1116P. doi:10.1103/PhysRevE.84.041116. PMID 22181096. S2CID 18366894.
- ^ Costa, M.; Cover, T. (Nov 1984). “On the similarity of the entropy power inequality and the Brunn-Minkowski inequality”. IEEE Transactions on Information Theory. 30 (6): 837–839. doi:10.1109/TIT.1984.1056983. ISSN 1557-9654.
- ^ Cover, Thomas M. (2006). Elements of information theory. Joy A. Thomas (2nd ed.). Hoboken, N.J.: Wiley-Interscience. p. 256. ISBN 0-471-24195-4. OCLC 59879802.
- ^ Pukelsheim, Friedrick (1993). Optimal Design of Experiments. New York: Wiley. ISBN 978-0-471-61971-0.
- ^ Bernardo, Jose M.; Smith, Adrian F. M. (1994). Bayesian Theory. New York: John Wiley & Sons. ISBN 978-0-471-92416-6.
- ^ Abbott, Larry F.; Dayan, Peter (1999). “The effect of correlated variability on the accuracy of a population code”. Neural Computation. 11 (1): 91–101. doi:10.1162/089976699300016827. PMID 9950724. S2CID 2958438.
- ^ Streater, R. F. (2007). Lost Causes in and beyond Physics. Springer. p. 69. ISBN 978-3-540-36581-5.
- ^ Kirkpatrick, James; Pascanu, Razvan; Rabinowitz, Neil; Veness, Joel; Desjardins, Guillaume; Rusu, Andrei A.; Milan, Kieran; Quan, John; Ramalho, Tiago (2017-03-28). “Overcoming catastrophic forgetting in neural networks”. Proceedings of the National Academy of Sciences. 114 (13): 3521–3526. doi:10.1073/pnas.1611835114. ISSN 0027-8424. PMC 5380101. PMID 28292907.
- ^ Martens, James (August 2020). “New Insights and Perspectives on the Natural Gradient Method”. Journal of Machine Learning Research (21). arXiv:1412.1193.
- ^ Gourieroux & Montfort (1995), page 87
- ^ Savage (1976)
- ^ Savage(1976), page 156
- ^ Edgeworth (September 1908, December 1908)
- ^ Pratt (1976)
- ^ Stigler (1978, 1986, 1999)
- ^ Hald (1998, 1999)
References[edit]
- Cramér, Harald (1946). Mathematical methods of statistics. Princeton mathematical series. Princeton: Princeton University Press. ISBN 0691080046.
- Edgeworth, F. Y. (Jun 1908). “On the Probable Errors of Frequency-Constants”. Journal of the Royal Statistical Society. 71 (2): 381–397. doi:10.2307/2339461. JSTOR 2339461.
- Edgeworth, F. Y. (Sep 1908). “On the Probable Errors of Frequency-Constants (Contd.)”. Journal of the Royal Statistical Society. 71 (3): 499–512. doi:10.2307/2339293. JSTOR 2339293.
- Edgeworth, F. Y. (Dec 1908). “On the Probable Errors of Frequency-Constants (Contd.)”. Journal of the Royal Statistical Society. 71 (4): 651–678. doi:10.2307/2339378. JSTOR 2339378.
- Fisher, R. A. (1922-01-01). “On the mathematical foundations of theoretical statistics”. Philosophical Transactions of the Royal Society of London, Series A. 222 (594–604): 309–368. Bibcode:1922RSPTA.222..309F. doi:10.1098/rsta.1922.0009.
- Frieden, B. R. (2004) Science from Fisher Information: A Unification. Cambridge Univ. Press. ISBN 0-521-00911-1.
- Frieden, B. Roy; Gatenby, Robert A. (2013). “Principle of maximum Fisher information from Hardy’s axioms applied to statistical systems”. Physical Review E. 88 (4): 042144. arXiv:1405.0007. Bibcode:2013PhRvE..88d2144F. doi:10.1103/PhysRevE.88.042144. PMC 4010149. PMID 24229152.
- Hald, A. (May 1999). “On the History of Maximum Likelihood in Relation to Inverse Probability and Least Squares”. Statistical Science. 14 (2): 214–222. doi:10.1214/ss/1009212248. JSTOR 2676741.
- Hald, A. (1998). A History of Mathematical Statistics from 1750 to 1930. New York: Wiley. ISBN 978-0-471-17912-2.
- Lehmann, E. L.; Casella, G. (1998). Theory of Point Estimation (2nd ed.). Springer. ISBN 978-0-387-98502-2.
- Le Cam, Lucien (1986). Asymptotic Methods in Statistical Decision Theory. Springer-Verlag. ISBN 978-0-387-96307-5.
- Pratt, John W. (May 1976). “F. Y. Edgeworth and R. A. Fisher on the Efficiency of Maximum Likelihood Estimation”. Annals of Statistics. 4 (3): 501–514. doi:10.1214/aos/1176343457. JSTOR 2958222.
- Rao, C. Radhakrishna (1945). “Information and accuracy attainable in the estimation of statistical parameters”. Bulletin of the Calcutta Mathematical Society. Springer Series in Statistics. 37: 81–91. doi:10.1007/978-1-4612-0919-5_16. ISBN 978-0-387-94037-3. S2CID 117034671.
- Savage, L. J. (May 1976). “On Rereading R. A. Fisher”. Annals of Statistics. 4 (3): 441–500. doi:10.1214/aos/1176343456. JSTOR 2958221.
- Schervish, Mark J. (1995). Theory of Statistics. New York: Springer. ISBN 978-0-387-94546-0.
- Stigler, S. M. (1986). The History of Statistics: The Measurement of Uncertainty before 1900. Harvard University Press. ISBN 978-0-674-40340-6.[page needed]
- Stigler, S. M. (1978). “Francis Ysidro Edgeworth, Statistician”. Journal of the Royal Statistical Society, Series A. 141 (3): 287–322. doi:10.2307/2344804. JSTOR 2344804.
- Stigler, S. M. (1999). Statistics on the Table: The History of Statistical Concepts and Methods. Harvard University Press. ISBN 978-0-674-83601-3.[page needed]
- Van Trees, H. L. (1968). Detection, Estimation, and Modulation Theory, Part I. New York: Wiley. ISBN 978-0-471-09517-0.
Определение.
Свойства. Пусть
сообщение X
есть непрерывная случайная величина,
а сигнал
характеризуется условной плотностью
вероятности
Рассмотрим две гипотезы:
H1
– передано сообщение x1,
то есть
,
H2
– передано
сообщение x2,
то есть
.
Среднюю информацию
в пользу H1,
вычисленную по формуле (5.1.2)
|
|
(5.2.1) |
можно формально
рассматривать как функцию аргумента
x2,
зависящую от параметра x1.
На рис.5.2 в качестве примера приведен
возможный вид этой функции при различных
значениях x1.
Е
сли
существует вторая производная этой
функции по x2 в
точке x2= x1=
x,
|
|
(5.2.2) |
то ее величина
называется информацией по Фишеру о
параметре x,
содержащейся в сигнале y.
То же значение информации можно получить
в результате вычисления по формуле
|
|
(5.2.3) |
Выбор одной из
двух формул определяется только удобством
вычислений. Информация Фишера показывает,
насколько быстро возрастает функция
I(x1:x2)
при увеличении
и, следовательно, является мерой
различимости близких значений x1
и x2.
Информация Фишера,
как и информация Кульбака, обладает
свойствами выпуклости и аддитивности.
Единицы измерения информации Фишера –
это единицы измерения величины х-2.
Неравенство
Рао-Крамера.
Это – главный результат теории информации
по Фишеру.
Рассмотрим задачу
оценки непрерывного сообщения x.
Правило оценивания сводится к тому, что
каждому значению выборки
ставится в соответствие некоторое
значение оцениваемого параметра x.
Таким образом, оценка
является функцией выборочных данных и
поэтому также является случайной
величиной. Обычно вычисляют следующие
числовые характеристики оценки:
1) Математическое
ожидание при условии, что истинное
значение сообщения равно x,
|
|
(5.2.4) |
2) Смещение
|
|
(5.2.5) |
т.е. систематическую
ошибку, сопутствующую выбранному правилу
оценивания.
3) Дисперсию,
вычисляемую также при условии, что
истинное значение сообщения равно x,
|
|
(5.2.6) |
Дисперсия оценки
является основной количественной мерой
точности оценивания.
Пусть функция
правдоподобия
дифференцируема по параметру x,
информация Фишера (5.2.2) существует и не
равна нулю для всех значений параметра
в окрестности точки x,
тогда дисперсия и смещение любой оценки
связаны с информацией Фишера неравенством
Рао-Крамера
|
|
(5.2.7) |
Для несмещенных
оценок (b(x)=0)
или для оценок с постоянным, не зависящим
от x
смещением (b(x)=c),
числитель в (5.2.7) равен единице и
тогда
|
|
(5.2.8) |
Таким образом,
информация
Фишера является количественной мерой
предельной, потенциальной точности
оценивания непрерывного сообщения x,
так как дисперсия несмещенной оценки
не может быть меньше величины, обратной
информации Фишера.
Неравенства (5.2.7)
и (5.2.8) обращаются в равенства тогда и
только тогда, когда одновременно
выполняются два условия:
1) Функция
правдоподобия выборки может быть
представлена в виде
|
|
(5.2.9) |
где
– некоторая функция выборки y,
не зависящая от x
и
,
– функция, зависящая
только от x
и
.
Оценка
,
удовлетворяющая условию (5.2.9), называется
достаточной, поскольку она сохраняет
всю информацию о x,
содержащуюся в самой выборке.
-
Функция правдоподобия
выборки такова, что для любого x
выполняется соотношение
|
|
(5.2.10) |
где
– некоторая функция x.
Оценка, удовлетворяющая
этому уравнению, называется эффективной,
а семейство распределений, задаваемых
уравнением (5.2.10) при различных значениях
x,
называется экспоненциальным семейством.
Легко убедиться, что эффективная оценка
всегда достаточна, но обратное утверждение
неверно.
Среди всех оценок
с заданным смещением именно эффективные
оценки обладают минимальной дисперсией.
К сожалению, эффективная оценка существует
далеко не во всех случаях, и тогда
потенциальная точность оценивания
сообщения недостижима.
Оценка максимального
правдоподобия. Метод максимального
правдоподобия широко используется на
практике. В качестве оценки
выбирается такое значение x,
при котором функция правдоподобия
достигает наибольшего значения. Это
значит, что в качестве оценки максимального
правдоподобия выбирается решение
уравнения правдоподобия
|
|
(5.2.11) |
Доказано, что если
эффективная оценка существует, то она
может быть реализована методом
максимального правдоподобия.
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
В математическая статистика, то Информация Fisher (иногда просто называют Информация[1]) – способ измерения количества Информация что наблюдаемый случайная переменная Икс несет в себе неизвестный параметр θ распределения, моделирующего Икс. Формально это отклонение из счет, или ожидаемое значение из наблюдаемая информация. В Байесовская статистика, то асимптотическое распределение из задний Режим зависит от информации Fisher, а не от прежний (согласно Теорема Бернштейна – фон Мизеса, чего ожидал Лаплас за экспоненциальные семейства ).[2] Роль информации Фишера в асимптотической теории оценка максимального правдоподобия было подчеркнуто статистиком Рональд Фишер (после некоторых первоначальных результатов Фрэнсис Исидро Эджворт ). Информация Фишера также используется при вычислении Джеффрис приор, который используется в байесовской статистике.
Информационная матрица Фишера используется для расчета ковариационные матрицы связана с максимальная вероятность оценки. Его также можно использовать при составлении статистики тестов, например Тест Вальда.
Было показано, что статистические системы научного характера (физические, биологические и т. Д.), Функции правдоподобия которых подчиняются инвариантности сдвига, подчиняются максимальной информации Фишера.[3] Уровень максимума зависит от характера ограничений системы.
Определение
Информация Фишера – это способ измерения количества информации, которую можно наблюдать. случайная переменная Икс несет о неизвестном параметр θ на котором вероятность Икс зависит от. Позволять ж(Икс; θ) быть функция плотности вероятности (или же функция массы вероятности ) за Икс зависит от стоимости θ. Он описывает вероятность того, что мы наблюдаем данный результат Икс, данный известная стоимость θ. Если ж резко пик по отношению к изменению θ, легко указать “правильное” значение θ из данных или, что то же самое, что данные Икс предоставляет много информации о параметре θ. Если вероятность ж плоский и разложенный, то потребуется много образцов Икс для оценки действительной «истинной» стоимости θ который бы быть полученным с использованием всей выборки. Это предполагает изучение некой дисперсии по отношению к θ.
Формально частная производная относительно θ из натуральный логарифм функции правдоподобия называется счет. При определенных условиях регулярности, если θ является истинным параметром (т.е. Икс фактически распространяется как ж(Икс; θ)), можно показать, что ожидаемое значение (первый момент ) оценки, оцененной при истинном значении параметра 
В отклонение оценки определяется как Информация Fisher:[5]
Обратите внимание, что 
Если бревнож(Икс; θ) дважды дифференцируема по θ, а при определенных условиях регулярности[4] тогда информация Фишера также может быть записана как[6]
поскольку
и
Таким образом, информацию Фишера можно рассматривать как кривизну кривая поддержки (график логарифма правдоподобия). Недалеко от максимальная вероятность оценка, поэтому низкая информация Фишера указывает на то, что максимум кажется «тупым», то есть максимум неглубоким и есть много близких значений с аналогичной логарифмической вероятностью. И наоборот, высокая информация Фишера указывает на резкость максимума.
Расхождение в определении
Существует две версии определения информации Фишера. Некоторые книги и заметки определяют
куда 
куда
– функция логарифма правдоподобия для всех наблюдений.
В некоторых учебниках может даже использоваться один и тот же символ 



Неформальный вывод границы Крамера – Рао
В Граница Крамера – Рао[7][8] утверждает, что инверсия информации Фишера является нижней границей дисперсии любого объективный оценщик из θ. H.L. Van Trees (1968) и Б. Рой Фриден (2004) предлагают следующий метод получения Граница Крамера – Рао, результат, который описывает использование информации Фишера.
Неформально мы начнем с рассмотрения объективный оценщик 
Это выражение равно нулю независимо от θ, поэтому его частная производная по θ также должен быть равен нулю. Посредством правило продукта, эта частная производная также равна
Для каждого θ, функция правдоподобия является функцией плотности вероятности, и поэтому 
Используя эти два факта выше, мы получаем
Факторизация подынтегральной функции дает
Возводя выражение в интеграл в квадрат, Неравенство Коши – Шварца дает
Второй фактор в квадратных скобках определяется как информация Фишера, а первый фактор в квадратных скобках – это ожидаемая среднеквадратичная ошибка оценки. 
Другими словами, точность, с которой мы можем оценить θ фундаментально ограничен информацией Фишера о функции правдоподобия.
Однопараметрический эксперимент Бернулли
А Бернулли суд случайная величина с двумя возможными исходами: «успех» и «неудача», при этом вероятность успеха составляет θ. Результат можно представить как результат подбрасывания монеты с вероятностью выпадения орла. θ и вероятность выпадения хвостов 1 − θ.
Позволять Икс быть судом Бернулли. Информация Fisher, содержащаяся в Икс можно рассчитать как
Поскольку информация Fisher является аддитивной, информация Fisher, содержащаяся в п независимый Бернулли испытания следовательно является
Это обратное отклонение среднего числа успехов в п Бернулли испытания, поэтому в данном случае оценка Крамера – Рао является равенством.
Матричная форма
Когда есть N параметры, так что θ является N × 1 вектор 
FIM – это N × N положительно полуопределенная матрица. Если он положительно определен, то он определяет Риманова метрика на N-размерный пространство параметров. Тема информационная геометрия использует это для подключения информации Fisher к дифференциальная геометрия, и в этом контексте этот показатель известен как Информационная метрика Fisher.
При определенных условиях регулярности информационная матрица Фишера также может быть записана как
Результат интересен в нескольких отношениях:
- Его можно получить как Гессен из относительная энтропия.
- Его можно понимать как метрику, индуцированную Евклидова метрика, после соответствующей замены переменной.
- В комплекснозначной форме это Метрика Фубини – Этюд.
- Это ключевая часть доказательства Теорема Уилкса, что позволяет оценить доверительную область для оценка максимального правдоподобия (для тех условий, для которых он применяется) без необходимости Принцип правдоподобия.
- В случаях, когда аналитические расчеты FIM выше затруднены, можно сформировать среднее из простых оценок Монте-Карло для Гессен функции отрицательного логарифма правдоподобия как оценки FIM.[9][10][11] Оценки могут быть основаны на значениях функции отрицательного логарифмического правдоподобия или градиента функции отрицательного логарифма правдоподобия; не требуется аналитического вычисления гессиана функции отрицательного логарифмического правдоподобия.
Ортогональные параметры
Мы говорим, что два параметра θя и θj ортогональны, если элемент яй ряд и j-й столбец информационной матрицы Фишера равен нулю. С ортогональными параметрами легко иметь дело в том смысле, что их оценки максимального правдоподобия независимы и могут быть рассчитаны отдельно. При решении исследовательских задач исследователь часто тратит некоторое время на поиски ортогональной параметризации плотностей, задействованных в проблеме.[нужна цитата ]
Сингулярная статистическая модель
Если информационная матрица Фишера положительно определена для всех θ, то соответствующий статистическая модель как говорят обычный; в противном случае говорят, что статистическая модель единственное число.[12] Примеры сингулярных статистических моделей включают следующее: нормальные смеси, биномиальные смеси, полиномиальные смеси, байесовские сети, нейронные сети, радиальные базисные функции, скрытые марковские модели, стохастические контекстно-свободные грамматики, регрессии с пониженным рангом, машины Больцмана.
В машинное обучение, если статистическая модель разработана так, что она извлекает скрытую структуру из случайного явления, то она естественно становится сингулярной.[13]
Многомерное нормальное распределение
FIM для N-variate многомерное нормальное распределение, 





куда 

Обратите внимание, что особый, но очень распространенный случай – это случай, когда
В этом случае информационная матрица Фишера может быть отождествлена с матрицей коэффициентов нормальные уравнения из наименьших квадратов теория оценки.
Другой частный случай возникает, когда среднее значение и ковариация зависят от двух разных векторных параметров, скажем, β и θ. Это особенно популярно при анализе пространственных данных, который часто использует линейную модель с коррелированными остатками. В этом случае,[15]
куда
Характеристики
Правило цепи
Подобно энтропия или же взаимная информация, информация Фишера также обладает Правило цепи разложение. В частности, если Икс и Y являются совместно распределенными случайными величинами, отсюда следует, что:[16]
куда 

Как особый случай, если две случайные величины равны независимый, информация, полученная от двух случайных величин, представляет собой сумму информации от каждой случайной величины отдельно:
Следовательно, информация в случайной выборке п независимые и одинаково распределенные наблюдения п раз больше информации в выборке размером 1.
Достаточная статистика
Информация предоставлена достаточная статистика такой же, как у образца Икс. Это можно увидеть, используя Критерий факторизации Неймана для достаточной статистики. Если Т(Икс) достаточно для θ, тогда
для некоторых функций грамм и час. Независимость час(Икс) из θ подразумевает
тогда равенство информации следует из определения информации Фишера. В более общем смысле, если Т = т(Икс) это статистика, тогда
с равенством если и только если Т это достаточная статистика.[17]
Репараметризация
Информация Фишера зависит от параметризации проблемы. Если θ и η – две скалярные параметризации задачи оценивания, и θ это непрерывно дифференцируемый функция η, тогда
куда 

В векторном случае предположим 



где (я, j) th элемент k × k Матрица якобиана 
и где 
В информационная геометрия, это видится как изменение координат на Риманово многообразие, а внутренние свойства кривизны не изменяются при различной параметризации. В общем случае информационная матрица Фишера обеспечивает риманову метрику (точнее, метрику Фишера – Рао) для многообразия термодинамических состояний и может использоваться в качестве меры информационно-геометрической сложности для классификации фазовые переходы Например, скалярная кривизна термодинамического метрического тензора расходится в (и только в) точке фазового перехода.[20]
В термодинамическом контексте информационная матрица Фишера напрямую связана со скоростью изменения соответствующего параметры заказа.[21] В частности, такие соотношения идентифицируют фазовые переходы второго рода через расхождения отдельных элементов информационной матрицы Фишера.
Приложения
Оптимальный план экспериментов
Информация Fisher широко используется в оптимальный экспериментальный план. Из-за взаимности оценки дисперсии и информации Фишера, сведение к минимуму то отклонение соответствует максимизация то Информация.
Когда линейный (или же линеаризованный ) статистическая модель имеет несколько параметры, то иметь в виду оценщика параметров является вектор и это отклонение это матрица. Обратная матрица дисперсии называется «информационной матрицей». Поскольку дисперсия средства оценки вектора параметров является матрицей, проблема «минимизации дисперсии» усложняется. С помощью статистическая теория, статистики сжимают информационную матрицу, используя действительные значения сводные статистические данные; будучи функциями с действительным знаком, эти «информационные критерии» могут быть максимизированы.
Традиционно статистики оценивают оценки и планы, рассматривая некоторые сводная статистика ковариационной матрицы (несмещенной оценки), обычно с положительными действительными значениями (например, детерминант или же матричный след ). Работа с положительными действительными числами дает несколько преимуществ: если оценка одного параметра имеет положительную дисперсию, тогда и дисперсия, и информация Фишера являются положительными действительными числами; следовательно, они являются членами выпуклого конуса неотрицательных действительных чисел (ненулевые члены которого имеют обратные значения в этом же конусе).
Ковариационные и информационные матрицы для нескольких параметров являются элементами выпуклого конуса неотрицательно-определенных симметричных матриц в частично упорядоченное векторное пространство, под Loewner (Лёвнер) заказ. Этот конус замкнут при сложении и обращении матриц, а также при умножении положительных действительных чисел и матриц. Изложение теории матриц и порядка Лёвнера появляется в Пукельсхайме.[22]
Традиционными критериями оптимальности являются Информация матричные инварианты в смысле теория инвариантов; алгебраически традиционные критерии оптимальности функционалы из собственные значения информационной матрицы (Фишера) (см. оптимальный дизайн ).
Джеффрис приор в байесовской статистике
В Байесовская статистика, информация Фишера используется для расчета Джеффрис приор, который является стандартным неинформативным априорным методом для параметров непрерывного распределения.[23]
Вычислительная нейробиология
Информация Фишера использовалась для определения границ точности нейронных кодов. В таком случае, Икс обычно являются совместными ответами многих нейронов, представляющими низкоразмерную переменную θ (например, параметр стимула). В частности, изучалась роль корреляций в шуме нервных реакций.[24]
Вывод физических законов
Информация Фишера играет центральную роль в противоречивом принципе, выдвинутом Frieden как основание физических законов, требование, которое было оспорено.[25]
Машинное обучение
Информация Фишера используется в таких методах машинного обучения, как упругое уплотнение веса,[26] что уменьшает катастрофическое забывание в искусственные нейронные сети.
Отношение к относительной энтропии
Информация Fisher связана с относительная энтропия.[27] Относительная энтропия, или Дивергенция Кульбака – Лейблера, между двумя распределениями 

Теперь рассмотрим семейство вероятностных распределений 

Если 



Но производную второго порядка можно записать как
Таким образом, информация Фишера представляет собой кривизна относительной энтропии.
Schervish (1995: §2.3) говорит следующее.
Одним из преимуществ информации Кульбака-Лейблера перед информацией Фишера является то, что на нее не влияют изменения параметризации. Другое преимущество состоит в том, что информацию Кульбака-Лейблера можно использовать, даже если рассматриваемые распределения не все являются членами параметрического семейства.
…
Еще одно преимущество информации Кульбака-Лейблера заключается в том, что условия гладкости для плотностей … не требуются.
История
Информация Фишера обсуждалась несколькими ранними статистиками, в частности Ф. Я. Эджворт.[28] Например, Savage[29] говорит: «В нем [информация Фишера] он [Фишер] был в некоторой степени предвиден (Эджворт 1908–199, особенно 502, 507–8, 662, 677–8, 82–5 и ссылки, которые он [Эджворт] цитирует, включая Пирсона). и Филон 1898 […]) “. Есть ряд ранних исторических источников[30] и ряд обзоров этой ранней работы.[31][32][33]
Смотрите также
- Эффективность (статистика)
- Наблюдаемая информация
- Информационная метрика Fisher
- Матрица формирования
- Информационная геометрия
- Джеффрис приор
- Граница Крамера – Рао
- Минимальная информация Fisher
Другие меры, применяемые в теория информации:
- Энтропия (теория информации)
- Дивергенция Кульбака – Лейблера
- Самоинформация
Примечания
- ^ Леманн и Казелла, стр. 115
- ^ Люсьен Ле Кам (1986) Асимптотические методы в статистической теории принятия решений: Страницы 336 и 618–621 (фон Мизес и Бернштейн).
- ^ Фриден и Гатенби (2013)
- ^ а б Суба Рао. «Лекции по статистическому выводу» (PDF).
- ^ Фишер (1922)
- ^ Lehmann & Casella, ур. (2.5.16), лемма 5.3, с.116.
- ^ Крамер (1946)
- ^ Рао (1945)
- ^ Сполл, Дж. К. (2005). «Вычисление Монте-Карло информационной матрицы Фишера в нестандартных условиях». Журнал вычислительной и графической статистики. 14 (4): 889–909. Дои:10.1198 / 106186005X78800.
- ^ Сполл, Дж. К. (2008), “Улучшенные методы оценки информационной матрицы Фишера методом Монте-Карло”, Труды Американской конференции по контролю, Сиэтл, Вашингтон, 11–13 июня 2008 г., стр. 2395–2400. https://doi.org/10.1109/ACC.2008.4586850
- ^ Das, S .; Spall, J.C .; Ганем, Р. (2010). «Эффективное вычисление методом Монте-Карло информационной матрицы Фишера с использованием априорной информации». Вычислительная статистика и анализ данных. 54 (2): 272–289. Дои:10.1016 / j.csda.2009.09.018.
- ^ Watanabe, S. (2008), Accardi, L .; Freudenberg, W .; Охя, М. (ред.), “Алгебраико-геометрический метод в сингулярной статистической оценке”, Квантовая биоинформатика, Всемирный научный: 325–336, Bibcode:2008qbi..conf..325 Вт, Дои:10.1142/9789812793171_0024, ISBN 978-981-279-316-4.
- ^ Ватанабэ, S (2013). «Широко применимый байесовский информационный критерий». Журнал исследований в области машинного обучения. 14: 867–897.
- ^ Малаго, Луиджи; Пистоне, Джованни (2015). Информационная геометрия распределения Гаусса с учетом стохастической оптимизации. Материалы конференции ACM 2015 г. по основам генетических алгоритмов XIII. С. 150–162. Дои:10.1145/2725494.2725510. ISBN 9781450334341.
- ^ Mardia, K. V .; Маршалл, Р. Дж. (1984). «Оценка максимального правдоподобия моделей остаточной ковариации в пространственной регрессии». Биометрика. 71 (1): 135–46. Дои:10.1093 / biomet / 71.1.135.
- ^ Замир, Р. (1998). «Доказательство информационного неравенства Фишера с помощью аргумента обработки данных». IEEE Transactions по теории информации. 44 (3): 1246–1250. CiteSeerX 10.1.1.49.6628. Дои:10.1109/18.669301.
- ^ Шервиш, Марк Дж. (1995). Теоретическая статистика. Springer-Verlag. п. 113.
- ^ Lehmann & Casella, ур. (2.5.11).
- ^ Lehmann & Casella, ур. (2.6.16)
- ^ Janke, W .; Johnston, D.A .; Кенна, Р. (2004). «Информационная геометрия и фазовые переходы». Physica A. 336 (1–2): 181. arXiv:cond-mat / 0401092. Bibcode:2004PhyA..336..181J. Дои:10.1016 / j.physa.2004.01.023.
- ^ Прокопенко, М .; Лизье, Джозеф Т .; Lizier, J. T .; Обст, О .; Ван, X. Р. (2011). «Связь информации Fisher с параметрами заказа». Физический обзор E. 84 (4): 041116. Bibcode:2011PhRvE..84d1116P. Дои:10.1103 / PhysRevE.84.041116. PMID 22181096. S2CID 18366894.
- ^ Пукельсхайм, Фридрик (1993). Оптимальный план экспериментов. Нью-Йорк: Вили. ISBN 978-0-471-61971-0.
- ^ Бернардо, Хосе М .; Смит, Адриан Ф. М. (1994). Байесовская теория. Нью-Йорк: Джон Вили и сыновья. ISBN 978-0-471-92416-6.
- ^ Эбботт, Ларри Ф .; Даян, Питер (1999). «Влияние коррелированной изменчивости на точность кода населения». Нейронные вычисления. 11 (1): 91–101. Дои:10.1162/089976699300016827. PMID 9950724.
- ^ Стритер, Р. Ф. (2007). Утраченные причины в физике и за ее пределами. Springer. п. 69. ISBN 978-3-540-36581-5.
- ^ Киркпатрик, Джеймс; Паскану, Разван; Рабиновиц, Нил; Венесс, Джоэл; Дежарден, Гийом; Русу, Андрей А .; Милан, Киран; Куан, Джон; Рамальо, Тьяго (28 марта 2017 г.). «Преодоление катастрофического забывания в нейронных сетях». Труды Национальной академии наук. 114 (13): 3521–3526. Дои:10.1073 / pnas.1611835114. ISSN 0027-8424. ЧВК 5380101. PMID 28292907.
- ^ Гурье и Монфор (1995), стр. 87
- ^ Дикарь (1976)
- ^ Дикарь (1976), стр.156
- ^ Эджворт (сентябрь 1908 г., декабрь 1908 г.)
- ^ Пратт (1976)
- ^ Стиглер (1978, 1986, 1999)
- ^ Халд (1998, 1999)
Рекомендации
- Крамер, Харальд (1946). Математические методы статистики. Принстонский математический ряд. Принстон: Издательство Принстонского университета. ISBN 0691080046.
- Эджворт, Ф. (Июнь 1908 г.). «О вероятных ошибках частотных постоянных». Журнал Королевского статистического общества. 71 (2): 381–397. Дои:10.2307/2339461. JSTOR 2339461.
- Эджворт, Ф. (Сентябрь 1908 г.). “О вероятных ошибках частотных постоянных (продолжение)”. Журнал Королевского статистического общества. 71 (3): 499–512. Дои:10.2307/2339293. JSTOR 2339293.
- Эджворт, Ф. (Декабрь 1908 г.). “О вероятных ошибках частотных постоянных (продолжение)”. Журнал Королевского статистического общества. 71 (4): 651–678. Дои:10.2307/2339378. JSTOR 2339378.
- Фишер, Р.А. (1922-01-01). «О математических основах теоретической статистики». Философские труды Лондонского королевского общества. А. 222 (594–604): 309–368. Дои:10.1098 / рста.1922.0009. Получено 2020-08-12.
- Frieden, B.R. (2004) Наука от информации Фишера: объединение. Cambridge Univ. Нажмите. ISBN 0-521-00911-1.
- Frieden, B. Roy; Гейтенби, Роберт А. (2013). «Принцип максимума информации Фишера из аксиом Харди применительно к статистическим системам». Физический обзор E. 88 (4): 042144. arXiv:1405.0007. Bibcode:2013PhRvE..88d2144F. Дои:10.1103 / PhysRevE.88.042144. ЧВК 4010149. PMID 24229152.
- Халд, А. (май 1999 г.). «К истории максимума правдоподобия по отношению к обратной вероятности и наименьшим квадратам». Статистическая наука. 14 (2): 214–222. Дои:10.1214 / сс / 1009212248. JSTOR 2676741.
- Халд, А. (1998). История математической статистики с 1750 по 1930 гг.. Нью-Йорк: Вили. ISBN 978-0-471-17912-2.
- Леманн, Э.; Казелла, Г. (1998). Теория точечного оценивания (2-е изд.). Springer. ISBN 978-0-387-98502-2.
- Ле Кам, Люсьен (1986). Асимптотические методы в статистической теории принятия решений. Springer-Verlag. ISBN 978-0-387-96307-5.
- Пратт, Джон В. (май 1976 г.). “Ф. И. Эджворт и Р. А. Фишер об эффективности оценки максимального правдоподобия”. Анналы статистики. 4 (3): 501–514. Дои:10.1214 / aos / 1176343457. JSTOR 2958222.
- Рао, Ч. Радхакришна (1945). «Информация и достижимая точность при оценке статистических параметров». Бюллетень Калькуттского математического общества. 37: 81–91. Дои:10.1007/978-1-4612-0919-5_16.
- Сэвидж, Л. Дж. (Май 1976 г.). «О перечитывании Р. А. Фишера». Анналы статистики. 4 (3): 441–500. Дои:10.1214 / aos / 1176343456. JSTOR 2958221.
- Шервиш, Марк Дж. (1995). Теория статистики. Нью-Йорк: Спрингер. ISBN 978-0-387-94546-0.
- Стиглер, С.М. (1986). История статистики: измерение неопределенности до 1900 г.. Издательство Гарвардского университета. ISBN 978-0-674-40340-6.[страница нужна ]
- Стиглер, С.М. (1978). “Фрэнсис Исидро Эджворт, статистик”. Журнал Королевского статистического общества, серия A. 141 (3): 287–322. Дои:10.2307/2344804. JSTOR 2344804.
- Стиглер, С.М. (1999). Статистика на столе: история статистических концепций и методов. Издательство Гарвардского университета. ISBN 978-0-674-83601-3.[страница нужна ]
- Ван Трис, Х. Л. (1968). Обнаружение, оценка и теория модуляции, часть I. Нью-Йорк: Вили. ISBN 978-0-471-09517-0.







![frac{partial}{partialtheta} ln left[f(X ;theta)right]
= frac{partial}{partialtheta} ln left[g(T(X);theta)right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/592daabb0c231dae868657fc18d5b5d522bcd2f0)


![{displaystyle {begin{aligned}operatorname {E} left[left.{frac {partial }{partial theta }}log f(X;theta )right|theta right]={}&int _{mathbb {R} }{frac {{frac {partial }{partial theta }}f(x;theta )}{f(x;theta )}}f(x;theta ),dx\[3pt]={}&{frac {partial }{partial theta }}int _{mathbb {R} }f(x;theta ),dx\[3pt]={}&{frac {partial }{partial theta }}1\={}&0.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/dfcbb2c8b6da15b6589b7273830c90414cf88d38)
![{displaystyle {mathcal {I}}(theta )=operatorname {E} left[left.left({frac {partial }{partial theta }}log f(X;theta )right)^{2}right|theta right]=int _{mathbb {R} }left({frac {partial }{partial theta }}log f(x;theta )right)^{2}f(x;theta ),dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/4b7316935b31a3e0fbcf5bc89c0abc8c87532f29)
![{displaystyle {mathcal {I}}(theta )=-operatorname {E} left[left.{frac {partial ^{2}}{partial theta ^{2}}}log f(X;theta )right|theta right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/2d21830494acf6fa8b7a42febe29b2a7ead86af8)

![{displaystyle operatorname {E} left[left.{frac {{frac {partial ^{2}}{partial theta ^{2}}}f(X;theta )}{f(X;theta )}}right|theta right]={frac {partial ^{2}}{partial theta ^{2}}}int _{mathbb {R} }f(x;theta ),dx=0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/3097dc661879cfe3a25ac2a3c761d5786522155b)
![{displaystyle operatorname {E} left[left.{hat {theta }}(X)-theta right|theta right]=int left({hat {theta }}(x)-theta right),f(x;theta ),dx=0{text{ regardless of the value of }}theta .}](https://wikimedia.org/api/rest_v1/media/math/render/svg/8595cafc412fabfdfec68c61abc2bac6fc38a136)




![{displaystyle 1={biggl (}int left[left({hat {theta }}-theta right){sqrt {f}}right]cdot left[{sqrt {f}},{frac {partial log f}{partial theta }}right],dx{biggr )}^{2}leq left[int left({hat {theta }}-theta right)^{2}f,dxright]cdot left[int left({frac {partial log f}{partial theta }}right)^{2}f,dxright].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b8ee8002e46c71c03fbe279ea1045596543b4509)

![{displaystyle operatorname {Cov} [{hat {theta }}(X)partial _{theta }log f(X;theta )]=int dx({hat {theta }}(x)-mathrm {E} [{hat {theta }}])partial _{theta }f(x;theta )=partial _{theta }mathrm {E} [{hat {theta }}]=1.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ae414ba2bb24b25a45823215e0ebe8a4d8c9635a)
![{displaystyle {begin{aligned}{mathcal {I}}(theta )&=-operatorname {E} left[left.{frac {partial ^{2}}{partial theta ^{2}}}log left(theta ^{X}(1-theta )^{1-X}right)right|theta right]\[5pt]&=-operatorname {E} left[left.{frac {partial ^{2}}{partial theta ^{2}}}left(Xlog theta +(1-X)log(1-theta )right)right|theta right]\[5pt]&=operatorname {E} left[left.{frac {X}{theta ^{2}}}+{frac {1-X}{(1-theta )^{2}}}right|theta right]\[5pt]&={frac {theta }{theta ^{2}}}+{frac {1-theta }{(1-theta )^{2}}}\[5pt]&={frac {1}{theta (1-theta )}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/e3d60a256f3e0e36ab48f35ed6ed7956afe38fd6)

![{displaystyle {bigl [}{mathcal {I}}(theta ){bigr ]}_{i,j}=operatorname {E} left[left.left({frac {partial }{partial theta _{i}}}log f(X;theta )right)left({frac {partial }{partial theta _{j}}}log f(X;theta )right)right|theta right].}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a314d5608ec35463ba25013999bb11789816b96c)
![{displaystyle {bigl [}{mathcal {I}}(theta ){bigr ]}_{i,j}=-operatorname {E} left[left.{frac {partial ^{2}}{partial theta _{i},partial theta _{j}}}log f(X;theta )right|theta right],.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b50e0c89c59d58f892dd66d9fa0bd250e4242a4d)

![{displaystyle {begin{aligned}{frac {partial mu }{partial theta _{m}}}&={begin{bmatrix}{dfrac {partial mu _{1}}{partial theta _{m}}}&{dfrac {partial mu _{2}}{partial theta _{m}}}&cdots &{dfrac {partial mu _{N}}{partial theta _{m}}}end{bmatrix}}^{textsf {T}};\[8pt]{dfrac {partial Sigma }{partial theta _{m}}}&={begin{bmatrix}{dfrac {partial Sigma _{1,1}}{partial theta _{m}}}&{dfrac {partial Sigma _{1,2}}{partial theta _{m}}}&cdots &{dfrac {partial Sigma _{1,N}}{partial theta _{m}}}\[5pt]{dfrac {partial Sigma _{2,1}}{partial theta _{m}}}&{dfrac {partial Sigma _{2,2}}{partial theta _{m}}}&cdots &{dfrac {partial Sigma _{2,N}}{partial theta _{m}}}\vdots &vdots &ddots &vdots \{dfrac {partial Sigma _{N,1}}{partial theta _{m}}}&{dfrac {partial Sigma _{N,2}}{partial theta _{m}}}&cdots &{dfrac {partial Sigma _{N,N}}{partial theta _{m}}}end{bmatrix}}.end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b9563f25377f20a259795079006042014f62e2ee)


![{displaystyle {begin{aligned}{mathcal {I}}{(beta )_{m,n}}&={frac {partial mu ^{textsf {T}}}{partial beta _{m}}}Sigma ^{-1}{frac {partial mu }{partial beta _{n}}},\[5pt]{mathcal {I}}{(theta )_{m,n}}&={frac {1}{2}}operatorname {tr} left(Sigma ^{-1}{frac {partial Sigma }{partial theta _{m}}}{Sigma ^{-1}}{frac {partial Sigma }{partial theta _{n}}}right)end{aligned}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/ecebc33561ebf425962059511de15739d58b227f)



![{displaystyle {frac {partial }{partial theta }}log left[f(X;theta )right]={frac {partial }{partial theta }}log left[g(T(X);theta )right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/49cf755a988eba8851adf6724177890708a898fb)








![{displaystyle left({frac {partial ^{2}}{partial theta '_{i},partial theta '_{j}}}D(theta ,theta ')right)_{theta '=theta }=-int f(x;theta )left({frac {partial ^{2}}{partial theta '_{i},partial theta '_{j}}}log(f(x;theta '))right)_{theta '=theta },dx=[{mathcal {I}}(theta )]_{i,j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/02bab191b23a6d1a0812342f41d4e4eeec455bcb)
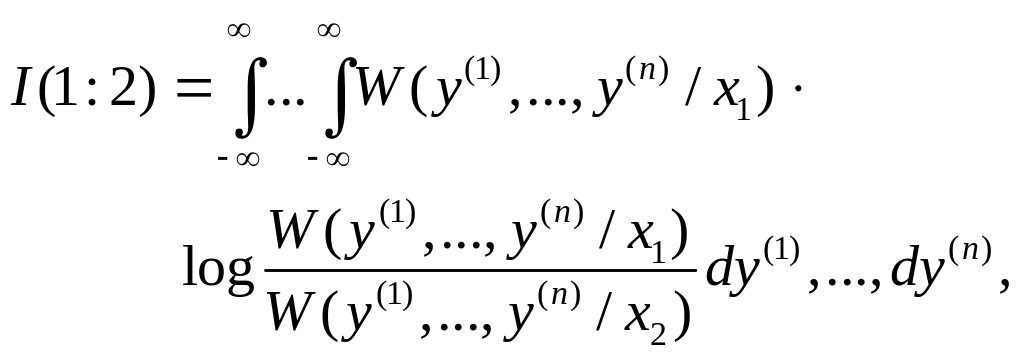
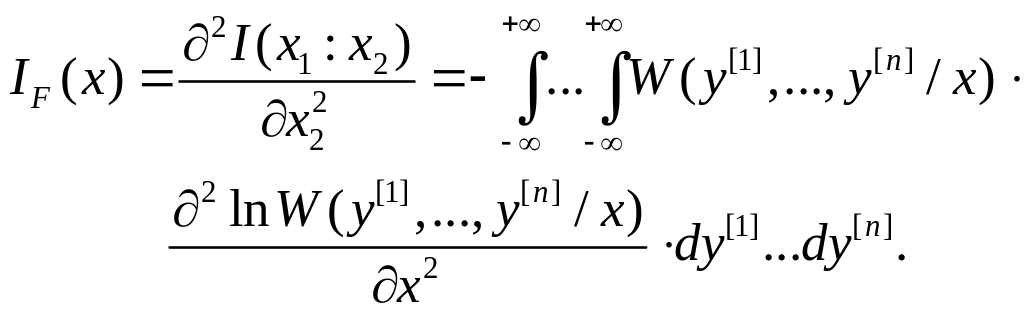
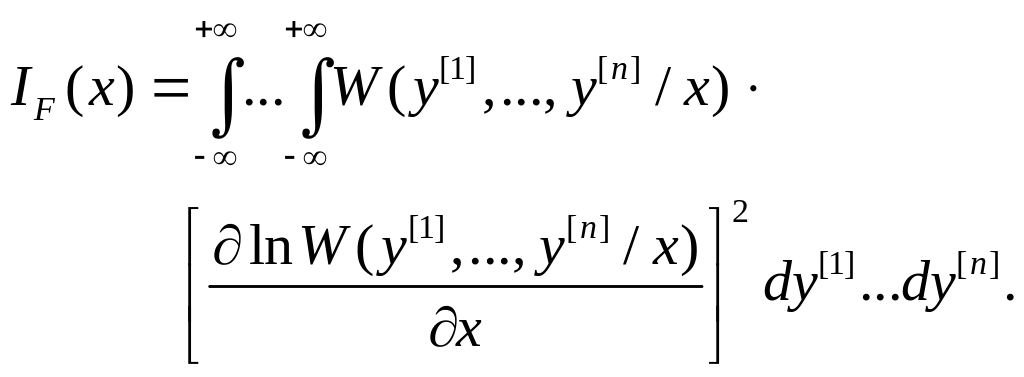
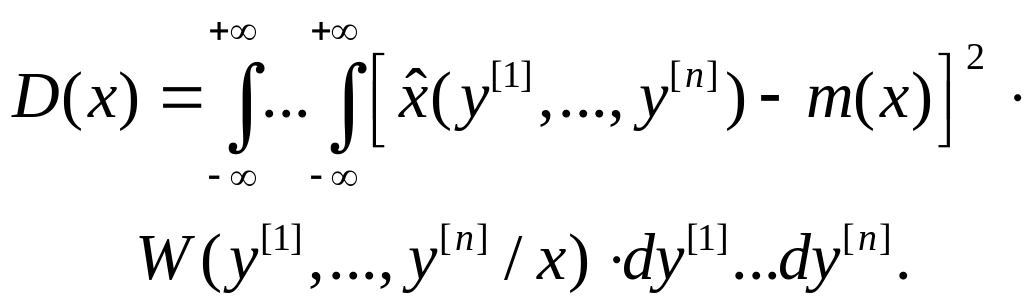
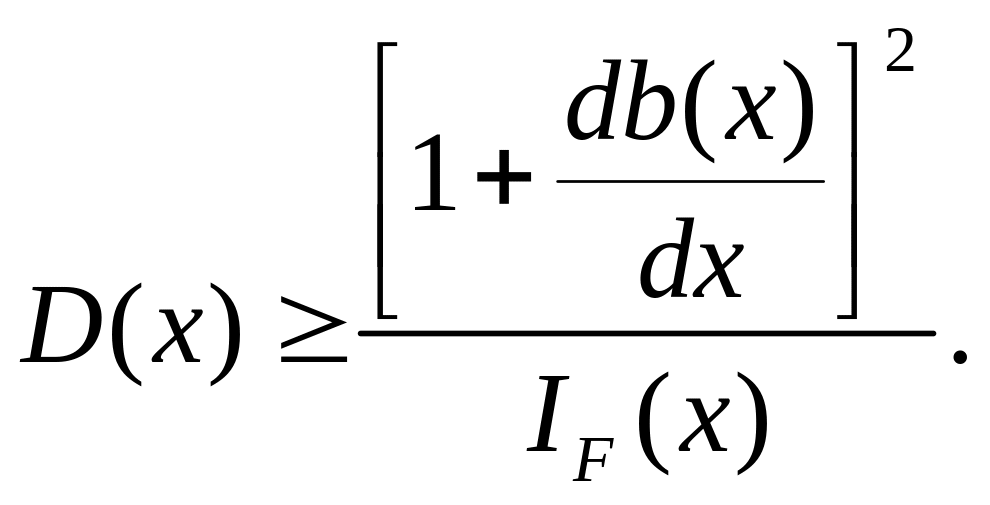
![{ displaystyle { begin {align} & operatorname {E} left [ left. { frac { partial} { partial theta}} log f (X; theta) right | theta справа] [3pt] = {} & int { frac {{ frac { partial} { partial theta}} f (x; theta)} {f (x; theta)}} f (x; theta) , dx [3pt] = {} & { frac { partial} { partial theta}} int f (x; theta) , dx [3pt] = {} & { frac { partial} { partial theta}} 1 = 0. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/a695c2fd53160ac791aa5df5fc27b5d8e7c3aa35)
![{ displaystyle { mathcal {I}} ( theta) = operatorname {E} left [ left. left ({ frac { partial} { partial theta}} log f (X; theta) right) ^ {2} right | theta right] = int left ({ frac { partial} { partial theta}} log f (x; theta) right) ^ {2} f (x; theta) , dx,}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d1cba9aa53478972d4382ff3ef80426ea0673118)
![{ displaystyle operatorname {E} left [ left. { frac {{ frac { partial ^ {2}} { partial theta ^ {2}}} f (X; theta)} {f (X; theta)}} right | theta right] = { frac { partial ^ {2}} { partial theta ^ {2}}} int f (x; theta) , dx = 0.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/34b6bb2ba863b0a3130736fb32d7320c433d4645)
![{ displaystyle { cal {I}} ( theta): = operatorname {E} left [- { frac { partial ^ {2}} { partial theta ^ {2}}} log f (X mid theta) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/56e2a7f7763f600c906553fbd2c75f5f3816683d)
![{ displaystyle { cal {I}} ( theta): = operatorname {E} left [- { frac { partial ^ {2}} { partial theta ^ {2}}} ell ( X mid theta) right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/1944674c2e88cd0e8d106b91bf2786f008537cb3)

![{ displaystyle { begin {align} { frac { partial mu} { partial theta _ {m}}} & = { begin {bmatrix} { frac { partial mu _ {1}} { partial theta _ {m}}} & { frac { partial mu _ {2}} { partial theta _ {m}}} & cdots & { frac { partial mu _ { N}} { partial theta _ {m}}} end {bmatrix}} ^ { extf {T}}; { frac { partial Sigma} { partial theta _ {m}} } & = { begin {bmatrix} { frac { partial Sigma _ {1,1}} { partial theta _ {m}}} & { frac { partial Sigma _ {1,2} } { partial theta _ {m}}} & cdots & { frac { partial Sigma _ {1, N}} { partial theta _ {m}}} [5pt] { frac { partial Sigma _ {2,1}} { partial theta _ {m}}} и { frac { partial Sigma _ {2,2}} { partial theta _ {m}}} & cdots & { frac { partial Sigma _ {2, N}} { partial theta _ {m}}} vdots & vdots & ddots & vdots { frac { partial Sigma _ {N, 1}} { partial theta _ {m}}} & { frac { partial Sigma _ {N, 2}} { partial theta _ {m}}} & cdots & { frac { partial Sigma _ {N, N}} { partial theta _ {m}}} end {bmatrix}}. end {align}}}](https://wikimedia.org/api/rest_v1/media/math/render/svg/f74d96bb3033167504b7ff02cb3089f1b6f57f43)


![{ displaystyle left ({ гидроразрыва { partial ^ {2}} { partial theta '_ {i} , partial theta' _ {j}}} D ( theta, theta ') справа) _ { theta '= theta} = - int f (x; theta) left ({ frac { partial ^ {2}} { partial theta' _ {i} , partial theta '_ {j}}} log (f (x; theta')) right) _ { theta '= theta} dx = [{ mathcal {I}} ( theta)] _ { i, j}.}](https://wikimedia.org/api/rest_v1/media/math/render/svg/0b3d58cdf933a6c40dd93514da68c186f719e21f)
