И снова здравствуйте, друзья!
Как я и обещал, с этого урока мы начнём бороздить бескрайние просторы поэтического мира интегралов и приступим к решению самых разнообразных (порой, очень красивых) примеров. 🙂
Чтобы грамотно ориентироваться во всём интегральном многообразии и не заблудиться, нам потребуется всего четыре вещи:
1) Таблица интегралов. Все подробности о ней — в предыдущем материале. Как именно с ней работать — в этом.
2) Свойства линейности неопределённого интеграла (интеграл суммы/разности и произведения на константу).
3) Таблица производных и правила дифференцирования.
Да-да, не удивляйтесь! Без умения считать производные, в интегрировании ловить совершенно нечего. Согласитесь, бессмысленно, например, учиться делению, не умея умножать. 🙂 И очень скоро вы увидите, что без отточенных навыков дифференцирования не посчитать ни один сколь-нибудь серьёзный интеграл, выходящий за рамки элементарных табличных.
4) Методы интегрирования.
Их очень и очень много. Для конкретного класса функций — свой. Но среди всего их богатого разнообразия выделяется три базовых:
– метод подведения функции под знак дифференциала,
– метод замены переменной,
– метод интегрирования по частям.
О каждом из них — в отдельных уроках.
А теперь, наконец, приступим к решению долгожданных примеров. Чтобы не скакать из раздела в раздел, я продублирую ещё разок весь джентльменский набор, который пригодится для нашей дальнейшей работы. Пусть весь инструментарий будет под рукой.)
Прежде всего, это таблица интегралов:

Кроме того, нам понадобятся базовые свойства неопределённого интеграла (свойства линейности):
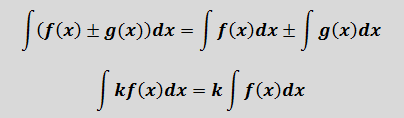
Что ж, необходимая снаряга подготовлена. Пора в путь! 🙂
Прямое применение таблицы
В данном параграфе будут рассматриваться самые простые и безобидные примеры. Алгоритм здесь прост до ужаса:
1) Смотрим в таблицу и ищем нужную формулу (формулы);
2) Применяем свойства линейности (где требуется);
3) Осуществляем превращение по табличным формулам и прибавляем в конце константу С (не забываем!);
4) Записываем ответ.
Итак, поехали.)
Пример 1
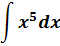
Такой функции в нашей таблице нет. Зато есть интеграл от степенной функции в общем виде (вторая группа). В нашем случае n = 5. Вот и подставляем пятёрку вместо n и аккуратно считаем результат:
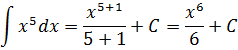
Готово. 🙂
Разумеется, этот пример совсем примитивный. Чисто для знакомства.) Зато умение интегрировать степени позволяет легко считать интегралы от любых многочленов и прочих степенных конструкций.
Пример 2
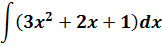
Под интегралом сумма. Ну и ладно. У нас на этот случай есть свойства линейности. 🙂 Разбиваем наш интеграл на три отдельных, выносим все константы за знаки интегралов и считаем каждый по таблице (группа 1-2):
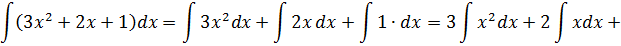
Прошу обратить внимание: константа С появляется именно в тот момент, когда исчезают ВСЕ знаки интеграла! Конечно, после этого приходится её постоянно таскать за собой. А что делать…
Разумеется, так подробно расписывать обычно не требуется. Это чисто для понимания сделано. Чтобы суть уловить.)
Например, очень скоро, особо не раздумывая, вы в уме будете давать ответ к монстрам типа:
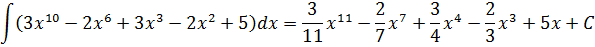
Многочлены — самые халявные функции в интегралах.) А уж в диффурах, в физике, в сопромате и прочих серьёзных дисциплинах интегрировать многочлены придётся постоянно. Привыкайте.)
Следующий примерчик будет чуть покруче.
Пример 3
Надеюсь, всем понятно, что наше подынтегральное выражение можно расписать вот так:
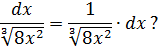
Подынтегральная функция отдельно, а множитель dx (значок дифференциала) — отдельно.
Замечание: в этом уроке множитель dx в процессе интегрирования пока никак не участвует, и мы на него пока что мысленно “забиваем”. 🙂 Работаем только с подынтегральной функцией. Но забывать про него не будем. Совсем скоро, буквально на следующем уроке, посвящённом подведению функции под знак дифференциала, мы про него вспомним. И ощутим всю важность и мощь этого значка в полную силу!)
А пока наш взор обращён на подынтегральную функцию
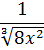
Не очень похоже на степенную функцию, но это она. 🙂 Если вспомнить школьные свойства корней и степеней, то вполне можно преобразовать нашу функцию:
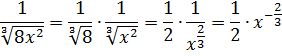
А икс в степени минус две трети — это уже табличная функция! Вторая группа, n=-2/3. А константа 1/2 нам не помеха. Выносим её наружу, за знак интеграла, и прямо по формуле считаем:
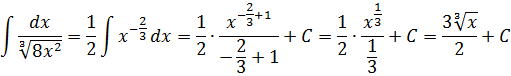
В этом примере нам помогли элементарные свойства степеней. И так надо делать в большинстве случаев, когда под интегралом стоят одинокие корни или дроби. Посему пара практических советов при интегрировании степенных конструкций:
Заменяем дроби степенями с отрицательными показателями;
Заменяем корни степенями с дробными показателями.
А вот в окончательном ответе переход от степеней обратно к дробям и корням — дело вкуса. Лично я перехожу обратно — так эстетичнее, что ли.
И, пожалуйста, аккуратно считаем все дроби! Внимательно следим за знаками и за тем, что куда идёт — что в числитель, а что знаменатель.
Что? Надоели уже скучные степенные функции? Ну ладно! Берём быка за рога!
Пример 4
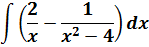
Если сейчас привести всё под интегралом к общему знаменателю, то можно застрять на этом примере всерьёз и надолго.) Но, присмотревшись повнимательнее к подынтегральной функции, можно заметить, что наша разность состоит из двух табличных функций. Так что не будем извращаться, а вместо этого разложим наш интеграл на два:
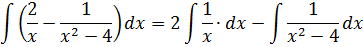
Первый интеграл — обычная степенная функция, (2-я группа, n = -1): 1/x = x-1.
Традиционная наша формула для первообразной степенной функции
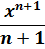
здесь не работает, но зато у нас для n = -1 есть достойная альтернатива — формула с натуральным логарифмом. Вот эта:
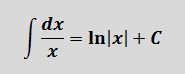
Тогда, согласно этой формуле, первая дробь проинтегрируется так:
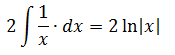
А вторая дробь — тоже табличная функция! Узнали? Да! Это седьмая формула с “высоким” логарифмом:
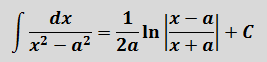
Константа “а” в этой формуле равна двойке: a=2.
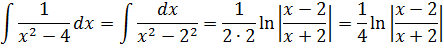
Важное замечание: Обратите внимание, константу С при промежуточном интегрировании я нигде не приписываю! Почему? Потому что она пойдёт в окончательный ответ всего примера. Этого вполне достаточно.) Строго говоря, константу надо писать после каждого отдельного интегрирования — хоть промежуточного, хоть окончательного: так уж неопределённый интеграл требует…)
Например, после первого интегрирования я должен был бы написать:
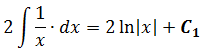
После второго интегрирования:
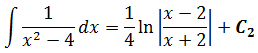
Но вся фишка в том, что сумма/разность произвольных констант — это тоже некоторая константа! В нашем случае для окончательного ответа нам надо из первого интеграла вычесть второй. Тогда у нас получится разность двух промежуточных констант:
С1-С2
И мы имеем полное право эту самую разность констант заменить одной константой! И просто переобозначить её привычной нам буквой “С”. Вот так:
С1-С2 = С
Вот и приписываем эту самую константу С к окончательному результату и получаем ответ:
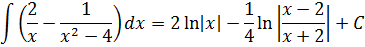
Да-да, дроби они такие! Многоэтажные логарифмы при их интегрировании — самое обычное дело. Тоже привыкаем.)
Запоминаем:
При промежуточном интегрировании нескольких слагаемых константу С после каждого из них можно не писать. Достаточно включить её в окончательный ответ всего примера. В самом конце.
Следующий пример тоже с дробью. Для разминки.)
Пример 5
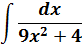
В таблице, понятное дело, такой функции нет. Но зато есть похожая функция:
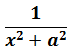
Это самая последняя, восьмая формула. С арктангенсом. 🙂
Вот эта:
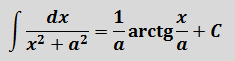
И нам сам бог велел подстроить наш интеграл под эту формулу! Но есть одна проблемка: в табличной формуле перед х2 никакого коэффициента нету, а у нас – девятка. Не можем пока что напрямую воспользоваться формулой. Но в нашем случае проблема вполне решаема. Вынесем эту девятку сначала за скобки, а потом вообще уведём за пределы нашей дроби.)
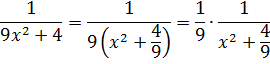
А новая дробь – уже нужная нам табличная функция под номером 8! Здесь а2=4/9. Или а=2/3.
Всё. Выносим 1/9 за знак интеграла и пользуемся восьмой формулой:
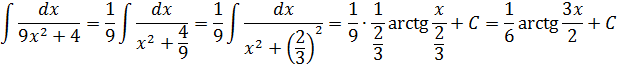
Вот такой ответ. Этот пример, с коэффициентом перед х2, я специально так подобрал. Чтобы ясно было, что делать в таких случаях. 🙂 Если перед х2 никакого коэффициента нет, то такие дроби тоже будут в уме интегрироваться.
Например:
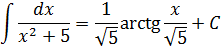
Здесь а2 = 5, поэтому само “а” будет “корень из пяти”. В общем, вы поняли.)
А теперь немного видоизменим нашу функцию: напишем знаменатель под корнем.) Вот такой интеграл теперь будем брать:
Пример 6
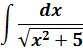
В знаменателе появился корень. Естественно, изменилась и соответствующая формула для интегрирования, да.) Опять лезем в таблицу и ищем подходящую. Корни у нас есть в формулах 5-й и 6-й групп. Но в шестой группе под корнями только разность. А у нас — сумма. Значит, работаем по пятой формуле, с “длинным” логарифмом:
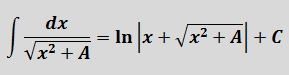
Число А у нас — пятёрка. Подставляем в формулу и получаем:
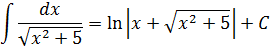
И все дела. Это ответ. Да-да, так просто!)
Если закрадываются сомнения, то всегда можно (и нужно) проверить результат обратным дифференцированием. Проверим? А то вдруг, лажа какая-нибудь?
Дифференцируем (на модуль внимания не обращаем и воспринимаем его как обычные скобки):
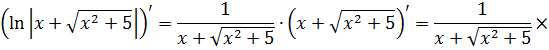
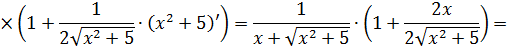
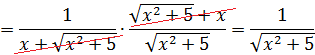
Всё честно. 🙂
Кстати, если в подынтегральной функции под корнем поменять знак с плюса на минус, то формула для интегрирования останется той же самой. Не случайно в таблице под корнем стоит плюс/минус. 🙂
Например:
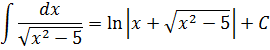
Важно! В случае минуса, на первом месте под корнем должно стоять именно х2, а на втором — число. Если же под корнем всё наоборот, то и соответствующая табличная формула будет уже другая!
Пример 7
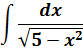
Под корнем снова минус, но х2 с пятёркой поменялись местами. Похоже, но не одно и то же… На этот случай в нашей таблице тоже есть формулка.) Формула номер шесть, с ней мы ещё не работали:
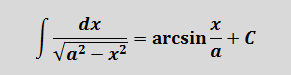
А вот теперь — аккуратно. В предыдущем примере у нас пятёрка выступала в роли числа A. Здесь же пятёрка будет выступать уже в роли числа а2!
Поэтому для правильного применения формулы не забываем извлечь корень из пятёрки:
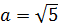
И теперь пример решается в одно действие. 🙂
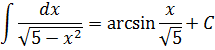
Вот так вот! Всего лишь поменялись местами слагаемые под корнем, а результат интегрирования изменился существенно! Логарифм и арксинус… Так что, пожалуйста, не путайте эти две формулы! Хотя подынтегральные функции и очень похожи…
Бонус:
В табличных формулах 7-8 перед логарифмом и арктангенсом присутствуют коэффициенты 1/(2а) и 1/а соответственно. И в тревожной боевой обстановке при записи этих формул даже закалённые учёбой ботаны частенько путаются, где просто 1/а, а где 1/(2а). Вот вам простой приёмчик для запоминания.
В формуле №7
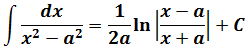
в знаменателе подынтегральной функции стоит разность квадратов х2 — а2. Которая, согласно боянной школьной формуле, раскладывается как (х-а)(х+а). На два множителя. Ключевое слово — два. И эти две скобки при интегрировании идут в логарифм: с минусом вверх, с плюсом — вниз.) И коэффициент перед логарифмом тоже 1/(2а).
А вот в формуле №8
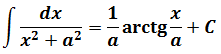
в знаменателе дроби стоит сумма квадратов. Но сумма квадратов x2+a2 неразложима на более простые множители. Поэтому, как ни крути, в знаменателе так и останется один множитель. И коэффициент перед арктангенсом тоже будет 1/а.
А теперь для разнообразия проинтегрируем что-нибудь из тригонометрии.)
Пример 8
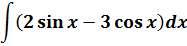
Пример простой. Настолько простой, что народ, даже не глядя в таблицу, тут же радостно ответ пишет и… приехали. 🙂
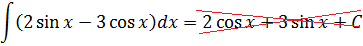
Следим за знаками! Это самая распространённая ошибка при интегрировании синусов/косинусов. Не путаем с производными!
Да, (sin x)’ = cos x и (cos x)’ = –sin x.
Но!
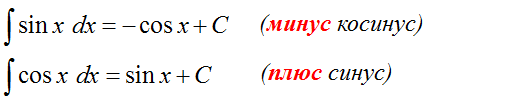
Поскольку производные народ обычно худо-бедно помнит, то, чтобы не путаться в знаках, приём для запоминания интегралов тут очень простой:
Интеграл от синуса/косинуса = минус производная от тех же синуса/косинуса.
Например, мы ещё со школы знаем, что производная синуса равна косинусу:
(sin x)’ = cos x.
Тогда для интеграла от того же синуса будет справедливо:
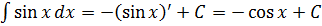
И всё.) С косинусом то же самое.
Исправляем теперь наш пример:
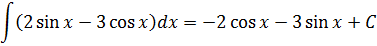
Предварительные элементарные преобразования подынтегральной функции
До этого момента были самые простенькие примеры. Чтобы прочувствовать, как работает таблица и не ошибаться в выборе формулы.)
Конечно, мы делали кое-какие простенькие преобразования — множители выносили, на слагаемые разбивали. Но ответ всё равно так или иначе лежал на поверхности.) Однако… Если бы вычисление интегралов ограничивалось только прямым применением таблицы, то вокруг была бы сплошная халява и жить стало бы скучно.)
А теперь разберём примеры посолиднее. Такие, где впрямую, вроде бы, ничего и не решается. Но стоит вспомнить буквально пару-тройку элементарных школьных формул или преобразований, как дорога к ответу становится простой и понятной. 🙂
Применение формул тригонометрии
Продолжим развлекаться с тригонометрией.
Пример 9
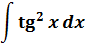
Такой функции в таблице и близко нет. Зато в школьной тригонометрии есть такое малоизвестное тождество:
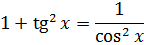
Выражаем теперь из него нужный нам квадрат тангенса и вставляем под интеграл:
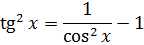
Зачем это сделано? А затем, что после такого преобразования наш интеграл сведётся к двум табличным и будет браться в уме!
Смотрите:
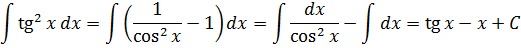
А теперь проанализируем наши действия. На первый взгляд, вроде бы, всё проще простого. Но давайте задумаемся вот над чем. Если бы перед нами стояла задача продифференцировать ту же самую функцию, то мы бы точно знали, что именно надо делать — применять формулу производной сложной функции:
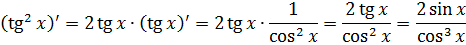
И всё. Простая и безотказная технология. Работает всегда и гарантированно приводит к успеху.
А что же с интегралом? А вот тут нам пришлось порыться в тригонометрии, откопать какую-то малопонятную формулу в надежде, что она нам как-то поможет выкрутиться и свести интеграл к табличному. И не факт, что помогла бы она нам, совсем не факт… Именно поэтому интегрирование — более творческий процесс, нежели дифференцирование. Искусство, я бы даже сказал. 🙂 И это ещё не самый сложный пример. То ли ещё будет!
Пример 10
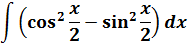
Что, внушает? Таблица интегралов пока бессильна, да. Но, если снова заглянуть в нашу сокровищницу тригонометрических формул, то можно откопать весьма и весьма полезную формулу косинуса двойного угла:
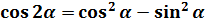
Вот и применяем эту формулу к нашей подынтегральной функции. В роли “альфа” у нас х/2.
Получаем:
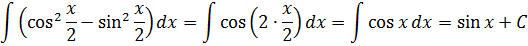
Эффект потрясающий, правда?
Эти два примера наглядно показывают, что предварительное преобразование функции перед интегрированием вполне допускается и порой колоссально облегчает жизнь! И в интегрировании эта процедура (преобразование подынтегральной функции) на порядок более оправдана, чем при дифференцировании. В дальнейшем всё увидите.)
Разберём ещё парочку типовых преобразований.
Формулы сокращённого умножения, раскрытие скобок, приведение подобных и метод почленного деления.
Обычные банальные школьные преобразования. Но порой только они и спасают, да.)
Пример 11
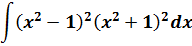
Если бы мы считали производную, то никаких проблем: формула производной произведения и — вперёд. Но стандартной формулы для интеграла от произведения не существует. И единственный выход здесь — раскрыть все скобки, чтобы под интегралом получился многочлен. А уж многочлен мы как-нибудь проинтегрируем.) Но скобки раскрывать тоже будем с умом: формулы сокращённого умножения — штука мощная!
(x2 — 1)2(x2 + 1)2 = ((x2 — 1)(x2 + 1))2 = ((x2)2 — 12)2 = (x4 — 1)2 = x8 — 2x4 + 1
А теперь считаем:
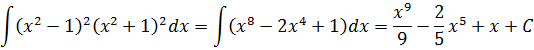
И все дела.)
Пример 12
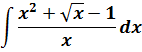
Опять же, стандартной формулы для интеграла от дроби не существует. Однако в знаменателе подынтегральной дроби стоит одинокий икс. Это в корне меняет ситуацию.) Поделим почленно числитель на знаменатель, сведя нашу жуткую дробь к безобидной сумме табличных степенных функций:
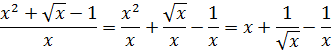
Особо комментировать процедуру интегрирования степеней не буду: не маленькие уже.)
Интегрируем сумму степенных функций. По табличке.)
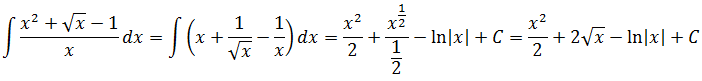
Вот и все дела.) Кстати, если бы в знаменателе сидел не икс, а, скажем, х+1, вот так:
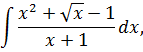
то этот фокус с почленным делением уже так просто не прошёл бы. Именно из-за наличия корня в числителе и единицы в знаменателе. Пришлось бы замену вводить и избавляться от корня. Но такие интегралы гораздо сложнее. О них — в других уроках.
Видите! Стоит только чуть-чуть видоизменить функцию — тут же меняется и подход к её интегрированию. Порой кардинально!) Нету чёткой стандартной схемы. К каждой функции — свой подход. Иногда даже уникальный.)
В некоторых случаях преобразования в дробях ещё более хитрые.
Пример 13
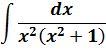
А здесь как можно свести интеграл к набору табличных? Здесь можно ловко извернуться добавлением и вычитанием выражения x2 в числителе дроби с последующим почленным делением. Очень искусный приём в интегралах! Смотрите мастер-класс! 🙂
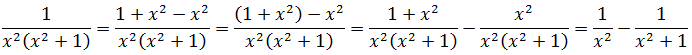
И теперь, если заменить исходную дробь на разность двух дробей, то наш интеграл распадается на два табличных — уже знакомую нам степенную функцию и арктангенс (формула 8):
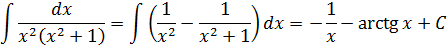
Ну, что тут можно сказать? Вау!
Этот трюк с добавлением/вычитанием слагаемых в числителе — очень популярен в интегрировании рациональных дробей. Очень! Рекомендую взять на заметку.
Пример 14
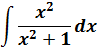
Здесь тоже рулит эта же технология. Только добавлять/вычитать надо единичку, чтобы из числителя выделить выражение, стоящее в знаменателе:
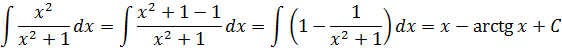
Вообще говоря, рациональные дроби (с многочленами в числителе и знаменателе) — отдельная очень обширная тема. Дело всё в том, что рациональные дроби – один из очень немногих классов функций, для которых универсальный способ интегрирования существует. Метод разложения на простейшие дроби вкупе с методом неопределённых коэффициентов. Но способ этот очень трудоёмкий и обычно применяется как тяжёлая артиллерия. Ему будет посвящён не один урок. А пока что тренируемся и набиваем руку на простых функциях.
Подытожим сегодняшний урок.
Сегодня мы подробно рассмотрели, как именно пользоваться таблицей, со всеми нюансами, разобрали множество примеров (и не самых тривиальных) и познакомились с простейшими приёмами сведения интегралов к табличным. И так мы теперь будем поступать всегда. Какая бы страшная функция ни стояла под интегралом, с помощью самых разнообразных преобразований мы будем добиваться того, чтобы, рано или поздно, наш интеграл, так или иначе, свёлся к набору табличных.
Несколько практических советов.
1) Если под интегралом дробь, в числителе которой сумма степеней (корней), а в знаменателе – одинокая степень икса, то используем почленное деление числителя на знаменатель. Заменяем корни степенями с дробными показателями и работаем по формулам 1-2.
2) В тригонометрических конструкциях в первую очередь пробуем базовые формулы тригонометрии — двойного/тройного угла, основные тригонометрические тождества:
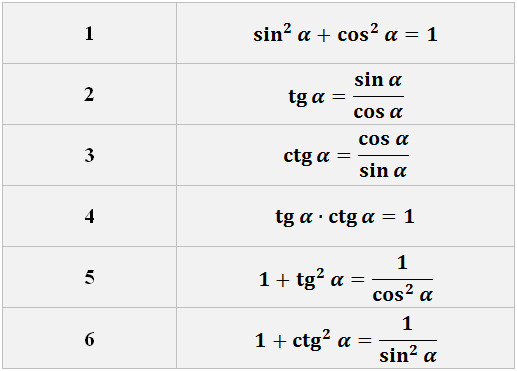
Может очень крупно повезти. А может и нет…
3) Где нужно (особенно в многочленах и дробях), применяем формулы сокращённого умножения:
(a+b)2 = a2+2ab+b2
(a-b)2 = a2-2ab+b2
(a-b)(a+b) = a2-b2
и так далее…
4) При интегрировании дробей с многочленами пробуем искусственно выделить в числителе выражение(я), стоящее(щие) в знаменателе. Очень часто дробь упрощается и интеграл сводится к комбинации табличных.
Ну что, друзья? Я вижу, интегралы вам начинают нравиться. 🙂 Тогда набиваем руку и решаем примеры самостоятельно.) Сегодняшнего материала вполне достаточно, чтобы успешно с ними справиться.
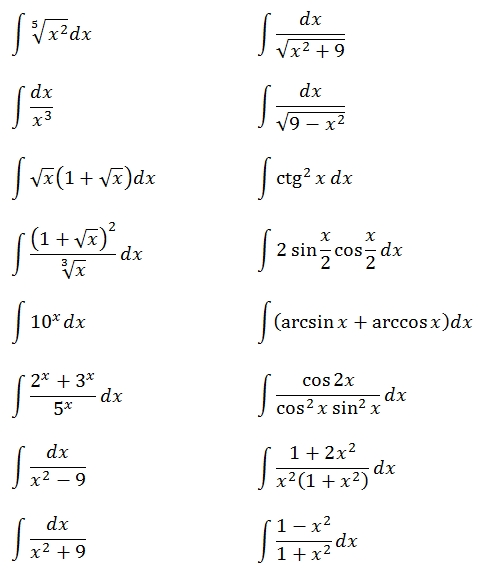
Что? Не знаете, как интегрировать арксинус/арккосинус? Да! Мы этого ещё не проходили.) Но здесь их напрямую интегрировать и не нужно. И да поможет вам школьный курс!)
Ответы (в беспорядке):
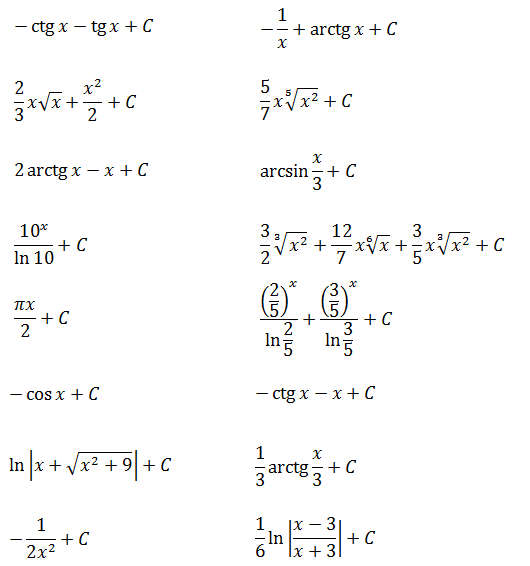
Для лучших результатов настоятельно рекомендую приобрести сборник задач по матану Г.Н. Бермана. Классная штука!
А у меня на сегодня всё. Успехов!
$begingroup$
Can someone please walk me through the steps to find the following integral? I’m not sure what to do when $dx$ is at the top.
$$ int frac{ x^{2}dx }{ (x^{3} + 5)^{2}} $$
![]()
Justin
2,5054 gold badges20 silver badges38 bronze badges
asked Feb 8, 2014 at 22:41
Darren FindlayDarren Findlay
5972 gold badges5 silver badges11 bronze badges
$endgroup$
2
$begingroup$
The $dx$ inside an integral expression can appear in various places, even if when integrals are introduced, it is (usually) always written at the end. An informal but intuitive (but probably dangerous!) way is to think of the expression as a multiplication of the integrand by the differential $dx$.
So
$$ int frac{ x^{2}dx }{ (x^{3} + 5)^{2}} = int frac{ x^{2} }{ (x^{3} + 5)^{2}} dx.$$
In fact, many people, at least many physicists, often write e.g.
$$ int_a^b dxleft{ frac{ x^{2} }{ (x^{3} + 5)^{2}} right},$$
so the reader (one who is familiar with this notation) will immediately see what is the variable of integration.
answered Feb 8, 2014 at 22:44
$endgroup$
6
$begingroup$
Having $dx$ in the numerator is the same as having it appear as if it is multiplying the integrand:
$$ int frac{ x^{2}dx }{ (x^{3} + 5)^{2}} = int frac{ x^{2} }{ (x^{3} + 5)^{2}}dx$$
So just start with something like $u = x^3 + 5$ and $du = 3x^2 dx$, and go to town.
answered Feb 8, 2014 at 22:45
JohnJohn
25.9k3 gold badges38 silver badges62 bronze badges
$endgroup$
$begingroup$
Put $u = x^3 + 5$ and then we will have $du = 3x^2dx$. Thus we have $x^2dx = du/3$. Thus, we will get the integral $$frac{1}{3}int frac{du}{u^2} $$ which you can then evaluate.
answered Feb 8, 2014 at 22:43
AyeshaAyesha
2,62021 silver badges40 bronze badges
$endgroup$
$begingroup$
What do you mean? It is its “usual place”, $int_D f(x)dx$…
answered Feb 8, 2014 at 22:43
![]()
Clement C.Clement C.
65.5k7 gold badges67 silver badges152 bronze badges
$endgroup$
You must log in to answer this question.
Not the answer you’re looking for? Browse other questions tagged
.
Not the answer you’re looking for? Browse other questions tagged
.
Рустам Искендеров
Искусственный Интеллект
(133392)
10 лет назад
Это – самый удобный вариант решения, хотя преподавателя он наверняка не устроит: они все почему-то хотят, чтобы ученики или студенты побольше мучились.
NataliaМастер (2080)
10 лет назад
Вы неправы… самый удобный – вынести за знак интеграла все, что “мешает” интегрировать, и проинтегрировать остальное, более покладистое. ))
Рустам Искендеров
Искусственный Интеллект
(133392)
Вот видите: варианты есть. Лишь бы проявить смекалку.
Cheery
Высший разум
(200421)
10 лет назад
dx и может стоять только в числителе, если речь об интеграле )
все выражение интегрируется, но на записи нужно смотреть как указан знак интеграла – если он только наверху, в числителе, тогда вот интегрируется только он.
ps: просто, как пример ) 
Men qazaqpynМыслитель (5249)
10 лет назад
есть примеры где дикс стоял за всей дробью!!!!или вы скажите что нет разницы?!
Cheery
Высший разум
(200421)
нет разницы
Интегрирование рациональных дробей
Формула
Дробь называется правильной, если старшая степень числителя меньше старшей степени знаменателя. Интеграл правильной рациональной дроби имеет вид:
$$ int frac{mx+n}{ax^2+bx+c}dx $$
Формула на интегрирование рациональных дробей зависит от корней многочлена в знаменателе. Если многочлен $ ax^2+bx+c $ имеет:
- Только комплексные корни, то из него необходимо выделить полный квадрат: $$ int frac{mx+n}{ax^2+bx+c} dx = int frac{mx+n}{x^2 pm a^2} $$
- Различные действительные корни $ x_1 $ и $ x_2 $, то нужно выполнить разложение интеграла и найти неопределенные коэффициенты $ A $ и $ B $: $$ int frac{mx+n}{ax^2+bx+c} dx = int frac{A}{x-x_1} dx + int frac{B}{x-x_2} dx $$
- Один кратный корень $ x_1 $, то выполняем разложение интеграла и находим неопределенные коэффициенты $ A $ и $ B $ для такой формулы: $$ int frac{mx+n}{ax^2+bx+c} dx = int frac{A}{(x-x_1)^2}dx + int frac{B}{x-x_1} dx $$
Если дробь является неправильной, то есть старшая степень в числителе больше либо равна старшей степени знаменателя, то сначала её нужно привести к правильному виду путём деления многочлена из числителя на многочлен из знаменателя. В данном случае формула интегрирования рациональной дроби имеет вид:
$$ int frac{P(x)}{ax^2+bx+c}dx = int Q(x) dx + int frac{mx+n}{ax^2+bx+c}dx $$
Примеры решений
| Пример 1 |
| Найти интеграл рациональной дроби: $$ int frac{dx}{x^2-10x+16} $$ |
| Решение |
|
Дробь является правильной и многочлен имеет только комплексные корни. Поэтому выделим полный квадрат: $$ int frac{dx}{x^2-10x+16} = int frac{dx}{x^2-2cdot 5 x+ 5^2 – 9} = $$ Сворачиваем полный квадрат и подводим под знак дифференциала $ x-5 $: $$ = int frac{dx}{(x-5)^2 – 9} = int frac{d(x-5)}{(x-5)^2-9} = $$ Пользуясь таблицей интегралов получаем: $$ = frac{1}{2 cdot 3} ln bigg | frac{x-5 – 3}{x-5 + 3} bigg | + C = frac{1}{6} ln bigg |frac{x-8}{x-2} bigg | + C $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
| $$ int frac{dx}{x^2-10x+16} = frac{1}{6} ln bigg |frac{x-8}{x-2} bigg | + C $$ |
| Пример 2 |
| Выполнить интегрирование рациональных дробей: $$ int frac{x+2}{x^2+5x-6} dx $$ |
| Решение |
|
Решим квадратное уравнение: $$ x^2+5x-6 = 0 $$ $$ x_{12} = frac{-5pm sqrt{25-4cdot 1 cdot (-6)}}{2} = frac{-5 pm 7}{2} $$ Записываем корни: $$ x_1 = frac{-5-7}{2} = -6; x_2 = frac{-5+7}{2} = 1 $$ С учётом полученных корней, преобразуем интеграл: $$ int frac{x+2}{x^2+5x-6} dx = int frac{x+2}{(x-1)(x+6)} dx = $$ Выполняем разложение рациональной дроби: $$ frac{x+2}{(x-1)(x+6)} = frac{A}{x-1} + frac{B}{x+6} = frac{A(x-6)+B(x-1)}{(x-1)(x+6)} $$ Приравниваем числители и находим коэффициенты $ A $ и $ B $: $$ A(x+6)+B(x-1)=x+2 $$ $$ Ax + 6A + Bx – B = x + 2 $$ $$ begin{cases} A + B = 1 \ 6A – B = 2 end{cases} $$ $$ begin{cases} A = frac{3}{7} \ B = frac{4}{7} end{cases} $$ Подставляем в интеграл найденные коэффициенты и решаем его: $$ int frac{x+2}{(x-1)(x+6)}dx = int frac{frac{3}{7}}{x-1} dx + int frac{frac{4}{7}}{x+6} dx = $$ $$ = frac{3}{7} int frac{dx}{x-1} + frac{4}{7} int frac{dx}{x+6} = frac{3}{7} ln |x-1| + frac{4}{7} ln |x+6| + C $$ |
| Ответ |
| $$ int frac{x+2}{x^2+5x-6} dx = frac{3}{7} ln |x-1| + frac{4}{7} ln |x+6| + C $$ |
Прежде, чем приступить к интегрированию простейших дробей для нахождения неопределенного интеграла дробно рациональной функции, рекомендуется освежить в памяти раздел «Разложение дроби на простейшие».
Найдем неопределенный интеграл ∫2×3+3×3+xdx .
Решение
Выделим целую часть, проведя деление столбиком многочлена на многочлен, учитывая тот факт, что степень числителя подынтегральной функции равна степени знаменателя:
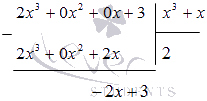
Поэтому 2×3+3×3+x=2+-2x+3×3+x . Мы получили правильную рациональную дробь -2x+3×3+x , которую теперь разложим на простейшие дроби -2x+3×3+x=3x-3x+2×2+1 . Следовательно,
∫2×3+3×3+xdx=∫2+3x-3x+2×2+1dx=∫2dx+∫3xdx-∫3x+2×2+1dx=2x+3lnx-∫3x+2×2+1dx
Мы получили интеграл простейшей дроби третьего типа. Взять его можно методом подведения под знак дифференциала.
Так как dx2+1=2xdx , то 3xdx=32dx2+1 . Поэтому
∫3x+2×2+1dx=∫3xx2+1dx+∫2×2+1=32∫dx2+1×2+1+2∫dxx2+1=32lnx2+1+2arctg x+C1
Следовательно,
∫2×3+3×3+xdx=2x+3lnx-∫3x+2×2+1dx=2x+3lnx-32lnx2+1-2arctan x+C, где С=-С1
Опишем методы интегрирования простейших дробей каждого из четырех типов.
Интегрирование простейших дробей первого типа Ax-a
Используем для решения этой задачи метод непосредственного инетгрирования:
∫Ax-adx=A∫dxx-a=A·lnx-a+C
Найдите множество первообразных функции y=32x-1.
Решение
Испльзуя правило интегрирования, свойства первообразной и таблицу первообразных, найдем неопределенный интеграл ∫3dx2x-1: ∫fk·x+bdx=1k·Fk·x+b+C
∫3dx2x-1=3∫dx2x-12=32∫dxx-12=32lnx-12+C
Ответ: ∫3dx2x-1=32lnx-12+C
Интегрирование простейших дробей второго типа Ax-an
Здесь также применим метод непосредственного интегрирования:∫Ax-andx=A∫x-a-ndx=A-n+1x-a-n+1+C=A1-nx-an-1+C
Необходимо найти неопределенный интеграл ∫dx2x-37 .
Решение
∫dx2x-37=∫dx2x-327=127∫x-32-7dx==127·1-7+1·x-32-7+1+C=127·-6·x-326+C==12·-6·26·x-326+C=-112·12x-36+C
Ответ: ∫dx2x-37=-112·12x-36+C
Интегрирование простейших дробей третьего типа Mx+Nx2+px+q, D=p2-4q<0
Первым шагом представим неопределенный интеграл ∫Mx+Nx2+px+q в виде суммы:
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q
Для того, чтобы взять первый интеграл, используем метод подведения под знак дифференциала:
∫Mxx2+px+qdx=dx2+px+q=2x+pdx=2xdx+pdx⇒2xdx=dx2+px+q-pdx⇒Mxdx=M2dx2+px+q-pM2dx==∫M2dx2+px+q-pM2dxx2+px+q==M2∫dx2+px+qx2+px+q-pM2∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q
Поэтому,
∫Mx+Nx2+px+qdx=∫Mxx2+px+qdx+N∫dxx2+px+q==M2lnx2+px+q-pM2∫dxx2+px+q+N∫dxx2+px+q==M2lnx2+px+q+2N-pM2·∫dxx2+px+q
Мы получили интеграл ∫dxx2+px+q. Проведем преобразование его знаменателя:
∫dxx2+px+q=∫dxx2+px+p22-p22+q==∫dxx+p22-p24+q=∫dxx+p22-p24+q==∫dxx+p22+4q-p24=24q-p2·arctg2x+p24q-p2+C1
Следовательно,
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM2·∫dxx2+px+q==M2lnx2+px+q+2N-pM2·24q-p2·arctg2x+p24q-p2+C1
Формула интегрирования простейших дробей третьего типа принимает вид:
∫Mx+Nx2+px+qdx=M2lnx2+px+q+2N-pM4q-p2·arctg2x+p24q-p2+C
Необходимо найти неопределенный интеграл ∫2x+13×2+6x+30dx.
Решение
Применим формулу:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=M=2,N=1,p=2,q=10==1322lnx2+2x+10+2·1-2·24·10-22arctg2x+224·10-22+C==13lnx2+2x+10-19arctgx+13+C
Второй вариант решения выглядит следующим образом:
∫2x+13×2+6x+30dx=13∫2x+1×2+2x+10dx=d(x2+2x+10=(2x+2)dx==13∫2x+2-1×2+2x+10dx=13∫d(x2+2x+10)x2+2x+10=13∫dxx2+2x+10==преобразуем знаменатель=13lnx2+2x+10-13∫d(x)x+12+9==13lnx2+2x+10-19arctgx+13+C
Ответ: ∫2x+13×2+6x+30dx=13lnx2+2x+10-19arctgx+13+C
Интегрирование простейших дробей четвертого типа Mx+N(x2+px+q)n, D=p2-4q<0
Первым делом выполняем подведение под знак дифференциала:
∫Mx+Nx2+px+qdx=d(x2+px+q)=(2x+p)dx==M2∫d(x2+px+q)(x2+px+q)n+N-pM2∫dx(x2+px+q)n==M2(-n+1)·1(x2+px+q)n-1+N-pM2∫dx(x2+px+q)n
Затем находим интеграл вида Jn=∫dx(x2+px+q)n с использованием рекуррентных формул. Информацию о рекуррентных формулах можно посмотреть в теме «Интегрирование с использованием рекуррентных формул».
Для решения нашей задачи подходит рекуррентная формула вида Jn=2x+p(n-1)(4q-p2)(x2+px+q)n-1+2n-3n-1·24q-p2·Jn-1.
Необходимо найти неопределенный интеграл ∫dxx5x2-1 .
Решение
∫dxx5x2-1=∫x-5(x2-1)-12dx
Мы будем использовать для этого вида подынтегральной функции метод подстановки. Введем новую переменную x2-1=z2x=(z2+1)12dx=z(z2+1)-12dx
Получаем:
∫dxx5x2-1=∫x-5(x2-1)-12dx==∫(z2+1)-52·z-1·z·(z2+1)-12dz=∫dz(z2+1)3
Пришли к нахождению интеграла дроби четвертого типа. В нашем случае имеем коэффициенты М = 0, р = 0, q = 1, N = 1 и n = 3. Применяем рекуррентную формулу:
J3=∫dz(z2+1)3=2z+0(3-1)·(4·1-0)·z2+13-1+2·3-33-1·24·1-0·∫dz(z2+1)2==z4(z2+1)2+342z(2-1)·(4·1-0)·(z2+1)2-1+2·2-32-11·24·1-0·∫dzz2+1==z4(z2+1)2+38zz2+1+38arctg(z)+C
После обратной замены z=x2-1 получаем результат:
∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
Ответ: ∫dxx5x2-1=x2-14×4+38×2-1×2+38arctgx2-1+C
![]()
Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта
