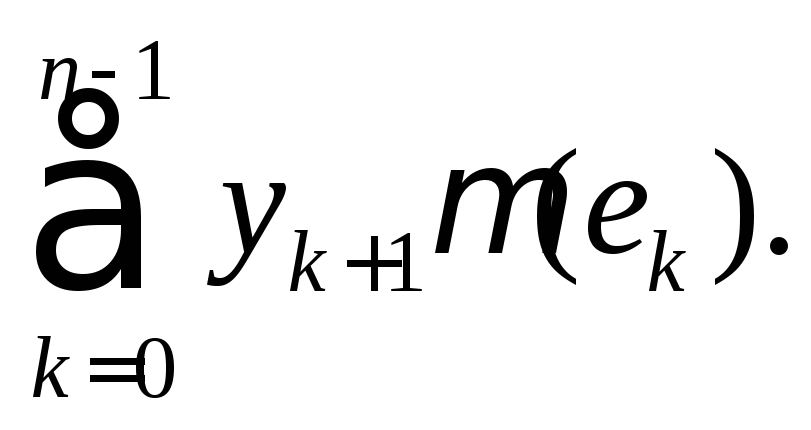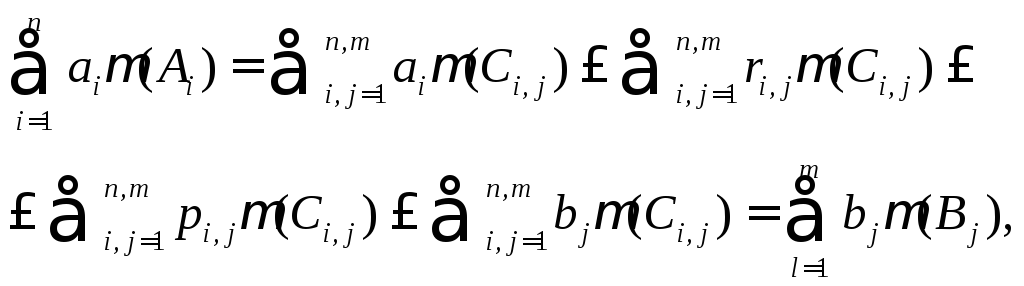Как найти интеграл лебега

Интеграл Лебе́га — это обобщение интеграла Римана на более широкий класс функций.

Все функции, определённые на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако существует большой класс функций, определённых на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах (интеграл Фреше).

Идея построения интеграла Лебега^[1] состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

Определение[править | править код]

Интеграл Лебега определяют пошагово, переходя от более простых функций к сложным. Будем считать, что дано пространство с мерой , и на нём определена измеримая функция , где — борелевская -алгебра на вещественной оси.

Определение 1. Пусть  — индикатор некоторого измеримого множества, то есть , где .
Тогда интеграл Лебега функции по определению:

Определение 2. Пусть  — простая функция, то есть , где , а  — конечное разбиение на измеримые множества.
Тогда

.

Определение 3. Пусть теперь  — неотрицательная функция, то есть .
Рассмотрим все простые функции , такие что .
Обозначим это семейство . Для каждой функции из этого семейства уже определён интеграл Лебега.
Тогда интеграл от задаётся формулой:

Наконец, если функция произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:

где

.

Определение 4. Пусть  — произвольная измеримая функция.
Тогда её интеграл задаётся формулой:

.

Определение 5. Пусть наконец произвольное измеримое множество. Тогда по определению

,

где  — индикатор-функция множества .

Пример[править | править код]

Рассмотрим функцию Дирихле , заданную на , где  — борелевская σ-алгебра на , а  — мера Лебега. Эта функция принимает значение в рациональных точках и в иррациональных. Легко увидеть, что не интегрируема в смысле Римана. Однако, она является простой функцией на пространстве с конечной мерой, ибо принимает только два значения, а потому её интеграл Лебега определён и равняется:

Действительно, мера отрезка равна 1,
и так как множество рациональных чисел счётно, то его мера равна 0,
а значит мера иррациональных чисел равна .

Замечания[править | править код]

Свойства[править | править код]

• Интеграл Лебега линеен, то есть

  ,

где  — произвольные константы;

Интегральные суммы Лебега[править | править код]

Интегральными суммами Лебега для функции и меры называются суммы вида

,

где  — разбиение области значений функции .

Каждая такая сумма является интегралом Лебега от простой функции, аппроксимирующей функцию – в каждой точке она принимает одно из значений (а именно, на подмножестве ). Поэтому, если функция интегрируема по Лебегу, эти суммы сходятся к её интегралу, когда , , и диаметр разбиения стремится к нулю.

Особенность интегральных сумм Лебега состоит в том, что для их вычисления не требуется вычислять значения интегрируемой функции — нужна на самом деле лишь функция распределения её значений:

Тогда интегральные суммы Лебега для функции и меры становятся интегральными суммами Римана-Стилтьеса для функции и функции распределения :

.

Если функция распределения имеет плотность: , то интегральные суммы Лебега преобразуются в интегральные суммы Римана:

.

Поскольку функции распределения естественным образом возникают в теории вероятностей, статистической и квантовой физике, то и интегральные суммы Лебега фактически используются для вычисления интеграла Лебега, в основном, в приложениях этих теорий. Чаще же всего интеграл Лебега вычисляется как равный ему интеграл Римана (в тех случаях, когда последний имеет смысл).

Сходимость интегралов Лебега от последовательностей функций[править | править код]

• Теорема Леви о монотонной сходимости
• Теорема Лебега о мажорируемой сходимости
• Лемма Фату

Примечания[править | править код]

Литература[править | править код]

• Колмогоров А.Н., Фомин С.В. Элементы теории функций и функционального анализа. — изд. четвёртое, переработанное. — М.: Наука, 1976. — 544 с.
• Треногин В. А. Функциональный анализ. — М.: Наука, 1980. — 495 с.
• Шилов Г.Е. Математический анализ. Специальный курс. — 2-е. — М.: Физматлит, 1961. — 436 с.

• Фролов Н. А. Теория функций действительного переменного. — 2-е. — М.: ГУПИМПР, 1961. — 173 с.

Интеграл Лебега

Рассмотрим одно из центральных понятий математического анализа — интеграл Лебега.

Понятие интеграла Лебега

Чтобы понять принцип устройства этого интеграла, рассмотрим следующий пример. Пусть имеется большое количество монет различного достоинства и требуется сосчитать общую сумму денег, заключенную в этих монетах. Это можно сделать двумя способами. Можно откладывать монеты подряд и прибавлять стоимость каждой новой монеты к общей стоимости всех ранее отложенных. Однако можно поступить и иначе: сложить монеты стопочками так, чтобы в каждой стопочке были монеты одного достоинства, затем сосчитать число монет в каждой стопочке, умножить это число на стоимость соответствующей монеты, а затем сложить полученные числа. Первый способ счета денег соответствует процессу интегрирования Римана, а второй — процессу интегрирования Лебега.

Переходя от монет к функциям, мы можем сказать, что для вычисления интеграла Римана производится деление на мелкие части области задания функции (оси абсцисс, рис. 2а), а для вычисления интеграла Лебега производится деление области значений функции (оси ординат, рис. 2б). Последний принцип применялся практически задолго до Лебега при вычислении интегралов от функций, имеющих колебательный характер, однако Лебег впервые развил его во всей общности и дал его строгое обоснование при помощи теории меры.

Рассмотрим, как связаны между собою мера множеств и интеграл Лебега. Пусть — какое-либо измеримое множество, расположенное та некотором отрезке . Построим функцию равную 1 для , принадлежащих , и равную 0 для , не принадлежащих . Иными словами, зададим функцию

Функцию принято называть характеристической функцией множества . Рассмотрим интеграл

Мы уже привыкли считать, что интеграл равен площади фигуры , ограниченной осью абсцисс, прямыми и кривой . Так как в данном случае “высота” фигуры отлична от нуля и равна 1 для точек и только для этих точек, то (согласно формуле, площадь равна длине, умноженной на ширину) её площадь должна быть численно равна длине (мере) множества . Итак, должно быть равно мере множества

Именно так и определяет Лебег интеграл от функции .

Мы должны твердо уяснить себе, что равенство (1) является определением интеграла как интеграла Лебега. Может случиться, что интеграл не будет существовать в том смысле, как это понималось для интеграла Римана, т. е. как предел интегральных сумм. Даже если это последнее имеет место, интеграл как интеграл Лебега существует и равен .

В качестве примера подсчитаем интеграл от функции Дирихле , равной 0 в рациональных точках отрезка [0, 1] и равной 1 в иррациональных точках этого отрезка. Так как, согласно (5), мера множества иррациональных точек отрезка [0, 1] равна 1, то интеграл Лебега равен 1. Нетрудно проверить, что интеграл Римана от этой функции не существует.

Пусть теперь — произвольная ограниченная измеримая функция, заданная на отрезке . Покажем, что всякую такую функцию можно сколь угодно точно представить в виде линейной комбинации характеристических функций множеств. Чтобы убедиться в этом, разобьем отрезок оси ординат между нижней и верхней гранями значений функции и точками , на отрезки длины меньшей , где — произвольное фиксированное положительное число. Далее, если в точке

то положим в этой точке

а если в точке б то положим . Построение функции показано на рис. 3.

Согласно построению функции , в любой точке отрезка

Кроме того, так как функция принимает лишь конечное число значений , то её можно записать в виде

где — характеристическая функция того множества, где , т. е. (в каждой точке лишь одно слагаемое в правой части формулы (2) отлично от нуля!).

---

Определение интеграла Лебега

Переходим к определению интеграла Лебега от произвольной ограниченной измеримой функции. Так как функция мало отличается от функции , то в качестве приближенного значения интеграла от функции можно принять интеграл от функции . Но, замечая, что функции являются характеристическими функциями множеств, и пользуясь формально обычными правилами вычисления интеграла, получаем

где есть мера множества тех , для которых выполняется неравенство .

Итак, приближенным значением интеграла Лебега от функции является интегральная сумма Лебега

В соответствии с этим интеграл Лебега определяется как предел интегральных сумм Лебега , когда

что соответствует равномерной сходимости функций к функции .

Можно показать, что интегральные суммы Лебега имеют предел для любой ограниченной измеримой функции, т. е. любая ограниченная измеримая функция интегрируема по Лебегу. Интеграл Лебега можно также распространить на некоторые классы неограниченных измеримых функций, но мы не будем этим заниматься.

---

Свойства интеграла Лебега

Интеграл Лебега обладает всеми хорошими свойствами обычного интеграла, именно, интеграл от суммы равен сумме интегралов, постоянный множитель можно выносить за знак интеграла и т. д. Однако интеграл Лебега обладает еще одним замечательным свойством, которым обычный интеграл не обладает : если измеримые функции ограничены в совокупности:

для любого и любого из отрезка и последовательность сходится почти всюду к функции , то

Иными словами, интеграл Лебега допускает безотказный переход к пределу. Именно это свойство интеграла Лебега делает его весьма удобным, а часто и неизбежным инструментом во многих исследованиях. В частности, интеграл Лебега совершенно необходим в теории тригонометрических рядов, в теории функциональных пространств и других разделах математики.

Приведем пример. Пусть — периодическая функция с периодом и

— ее ряд Фурье.

Если, например, функция непрерывна, то, как нетрудно показать,

Это тождество носит название равенства Парсеваля.

Рассмотрим такой вопрос: для какого класса периодических функций справедливо равенство Парсеваля (3)? Ответ на этот вопрос гласит: равенство Парсеваля (3) выполняется в том и только в том случае, если функция измерима на отрезке и функция интегрируема по Лебегу на этом отрезке.

Математический форум (помощь с решением задач, обсуждение вопросов по математике).

Если заметили ошибку, опечатку или есть предложения, напишите в комментариях.

Интеграл Лебега — это обобщение интеграла Римана на более широкий класс функций. Все функции, определенные на конечном отрезке числовой прямой и интегрируемые по Риману, являются также интегрируемыми по Лебегу, причём в этом случае оба интеграла равны. Однако, существует большой класс функций, определенных на отрезке и интегрируемых по Лебегу, но неинтегрируемых по Риману. Также интеграл Лебега может иметь смысл для функций, заданных на произвольных множествах.

Идея построения интеграла Лебега состоит в том, что вместо разбиения области определения подынтегральной функции на части и составления потом интегральной суммы из значений функции на этих частях, на интервалы разбивают её область значений, а затем суммируют с соответствующими весами меры прообразов этих интервалов.

Определение

Интеграл Лебега определяют индуктивно, переходя от более простых функций к сложным. Будем считать, что дано пространство с мерой , и на нем определена измеримая функция .

Определение 1. Пусть — индикатор некоторого измеримого множества, т.е. , где .
Тогда интеграл Лебега функции по определению:

Определение 2. Пусть — простая функция, т.е. , где , а — конечное разбиение на измеримые множества.
Тогда

.

Определение 3. Пусть теперь — неотрицательная функция, т.е. .
Рассмотрим все простые функции , такие что .
Обозначим это семейство . Для каждой функции из этого семейства уже определен интеграл Лебега.
Тогда интеграл от задаётся формулой:

Наконец, если функция произвольного знака, то её можно представить в виде разности двух неотрицательных функций. Действительно, легко видеть, что:

где

.

Определение 4. Пусть — произвольная измеримая функция.
Тогда ее интеграл задаётся формулой:

.

Определение 5. Пусть наконец произвольное измеримое множество. Тогда по определению

,

где — индикатор-функция множества .

Пример

Рассмотрим функцию Дирихле , заданную на , где – борелевская σ-алгебра на , а – мера Лебега. Эта функция принимает значение в рациональных точках и в иррациональных. Легко увидеть, что не интегрируема в смысле Римана. Однако, она является простой функцией на пространстве с конечной мерой, ибо принимает только два значения, а потому её интеграл Лебега определён и равняется:

Замечания

Простейшие свойства интеграла Лебега

• Интеграл Лебега линеен, т.е.

,

где – произвольные константы;

;

• Интеграл Лебега не зависит от поведения функции на множестве меры нуль, т.е. если п.в., то

.

Сходимость интегралов Лебега от последовательностей функций

• Теорема Леви о монотонной сходимости;
• Теорема Лебега о мажорируемой сходимости;
• Лемма Фату.

Эта статья содержит материал из статьи Интеграл Лебега русской Википедии.

1. Интеграл Лебега для простых и ограниченных функций на пространстве с конечной мерой

Понятие интеграла
Римана, известное из элементарного
курса анализа, применимо лишь к таким
функциям, которые или непрерывны или
имеют «не слишком много» точек разрыва.
Для измеримых функций, которые могут
быть разрывными всюду, где они определены
(или же вообще могут быть заданы на
аб­страктном множестве, так что для
них понятие непрерывности просто не
имеет смысла), римановская конструкция
интеграла становится непригодной.
Вместе с тем для таких функций имеется
весьма совершенное и гибкое понятие
интеграла, вве­денное Лебегом.

Основная идея
построения интеграла Лебега состоит в
том, что здесь, в отличие от интеграла
Римана, точки х
группируют­ся не по признаку их
близости на оси х,
а по признаку близости значений функции
в этих точках. Это сразу же позволяет
рас­пространить понятие интеграла
на весьма широкий класс функций.

Всюду, где не
оговорено противное, будет рассматриваться
некоторая полная -аддитивная
мера ,
определенная на -алгебре

множеств с единицей X.
Все рассматриваемые множества А

Х
будут предполагаться измеримыми, а
функции f(x)
–
определенными
для x
Х и
измеримыми. Далее предполагается, что
(Х)
< .

Классическое
определение интеграла, данное О. Коши
и разви­тое Б. Риманом, состоит, как
известно, в следующем: рассматри­вается
конечная функция f(x),
заданная на отрезке [a,
b];
этот отрезок разбивается на части
точками x₀
= a

x₁

x₂



x_n
= b,
в
каждой части [x_k,
x_k+1]
выбирается
точка _k
и составляется риманова сумма

 =
.

Если сумма 
при стремлении к нулю числа 
=
(x_k+1
– x_k)
стремится
к конечному пределу I,
не зависящему ни от способа дробления
[a,
b],
ни от выбора точек _k,
то этот предел I
назы­вается интегралом Римана функции
f(x)
и обозначается символом

.

Иногда, желая
подчеркнуть, что речь идет именно о
римановом интеграле, пишут

(R).

Функции, для которых
интеграл Римана существует, называются
интегрируемыми
в смысле Римана
или, короче, интегрируемыми
(R).
Для
интегрируемости (R)
функции f(x)
необходимо, чтобы она была ограниченной.

Еще Коши установил,
что всякая непрерывная функция
интегри­руема (R).
Существуют также и разрывные функции,
интегрируе­мые (R).
В частности, такова любая разрывная
монотонная функция.

Легко построить,
однако, ограниченную функцию, которая
не будет интегрируемой (R).
Рассмотрим, например, функцию
Ди­рихле
,
которая определяется на отрезке [0,
1] следующим
образом

Легко видеть, что
эта функция не интегрируема (R),
ибо сумма 
обращается в 0, если все точки 
иррациональны и 
= 1, если все
рациональны.

Таким образом,
риманово определение интеграла страдает
суще­ственными недостатками – даже
очень простые функции оказываются
неинтегрируемыми. Нетрудно разобраться
в причинах этого обстоятельства. Дело
заключается в следующем: при составлении
сумм Римана ,
мы дробим сегмент [a,
b]
на мелкие части [x₀,
x₁],
[x₁,
x₂],

, [x_n-1,
x_n]
(назовем их
через e₀,
e₁,

, e_n–1),
в каждой части e_k
берем точку
_k
и, составив
сумму 
=
,требуем,
чтобы она имела предел, не зависящий от
выбора точек _k
в множествах е_k.
Иначе говоря, каждая точка х
из множества е_k
может быть
взята за _k,
а варьирование этой точки не должно
заметно влиять на значение суммы .
А это возможно лишь в том случае, когда
варьирование точки _k
мало изменяет величину f(_k).
Но что же объединяет между собой различные
точки х
множества e_k?
Их объединяет то, что они близки друг
другу, ибо е_k
есть малый отрезок [x_k,
x_k+1].

Если функция f(x)
непрерывна, то достаточная близость
абсцисс х
влечет за
собой и близость соответствующих
значений функции, и мы вправе ждать, что
изменение точки _k
в пределах множества e_k
мало влияет на величину суммы ,
но для функция разрывной это вовсе не
так.

Иначе можно сказать,
что множества e_k
составлены так, что только для непрерывных
функций значение f(_k)
можно считать естественным представителем
других значений функции на e_k.

Таким образом,
самое определение риманова интеграла
можно считать вполне оправданным лишь
для функций непрерывных, для прочих же
функций оно выглядит довольно случайным.
Ниже мы убедимся, что для интегрируемости
(R)
необходимо, чтобы рас­сматриваемая
функция не была «слишком разрывной».

Желая
обобщить понятие интеграла на более
широкие классы функций, Лебег предложил
другой процесс интегрирования, в котором
точки x
объединяются
в множества e_k
не
по случайному признаку своей близости
на оси Ох,
а
по признаку достаточной близости
соответствующих значений функции. С
этой целью Лебег разбивает на части не
отрезок [a,
b],
расположенный
на оси абсцисс, а отрезок [А,
В],
лежащий
на оси ординат и включающий все значения
функции f(x):

A
= y₀

y₁



y_n
= B

Если
составить множества e_k
так:
e_k
= E(y_k

f

y_k+1),
то
ясно, что различным точкам х

е_k
и
в самом деле отвечают близкие значения
функции, хотя, в отличие от римановского
процесса, сами точки x
могут
быть весьма далеки друг от друга.

В
частности, хорошим представителем
значений функции на мно­жестве e_k
может
служить, например, y_k,
так
что естественно поло­жить в основу
понятия интеграла сумму

.

Перейдем
теперь к точному изложению вопроса.
Пусть на измеримом множестве E
задана измеримая ограниченная функция
f(x),
причем
A

f(x)

B.
Разобьем
отрезок [А,
В]
на
части точками y_o
= A

y₁

y₂



y_n
= B
и
соотнесем каждому полусегменту [у_k
,
у_k+1)
множество
e_k
= E(y_k

f

y_k+1).
Легко
проверить четыре свойства множеств e_k:

1)
Множества e_k
попарно
не пересекаются: e_ke_i
= 
(k

i).

2) Эти множества
измеримы.

3) E
=

4) (Е)
=

Введем
теперь нижнюю
и верхнюю суммы Лебега
s
и
S:

s
=
S =

Если
мы положим 
=
(y_k+1
– y_k),
то
будем иметь

0 
S
– s


(E).

Основное свойство
сумм Лебега выражает

Лемма
1.
Пусть
некоторому способу дробления сегмента
[А,
В]
отвечают суммы Лебега s₀
и S₀.
Если
ми добавим новую точку дробления
и
снова найдем суммы Лебега
s
и S,
то
окажется s₀

s,
S

S₀.

Иначе говоря, от
добавления новых точек деления нижняя
сумма не уменьшается, а верхняя не
увеличивается.

Доказательство.
Допустим, что

y_i


y_i+1.
(1)

Тогда
при k

i
полусегменты
[y_k,
у_k+1),
а
с ними и множества e_k,
фигурируют
и в новом способе дробления. Полусегмент
же [y_i,
y_i+1)
при
переходе к новому способу заменяется
двумя полусегментами [y_i,),
[,y_i+1),
в
связи с чем и множество e_i
разбивается на два множества
=
E(y_i

f


),

=
E(
f

y_i+1).
Очевидно,
что e_i
=+,=,
так
что

 (e_i)
= 
()
+
().
(2)

Из
сказанного ясно, что сумма s
получается из суммы s₀
заменой
слагаемого y_i
(e_i)
двумя слагаемыми
y_i
()
+

(),
откуда,
в связи с (1) и (2), следует, что s

s₀.

Для верхних сумм
рассуждение аналогично.

Следствие.
Ни
одна нижняя сумма
s
не
больше ни одной верхней суммы
S.

Доказательство.
Рассмотрим два каких-нибудь способа
дробления I
и II,
отрезка [А,
В].
Пусть
этим способам отвечают соответственно
нижние суммы s₁
и s₂
и верхние суммы S₁
и S₂.

Составим
третий способ дробления [А,
В]
– способ
III,
в котором точками деления служат точки
деления обоих способов I
и II. Если способу III отвечают суммы s₃
и
S₃,
то, в силу леммы, s₁

s₃,
S₃

S₂,
откуда, в связи с тем, что s₃

S₃,
ясно, что s₁

S₂,
а это и тре­бовалось доказать.

Выберем
какую-нибудь определенную верхнюю сумму
S₀.
Так как для всякой нижней суммы s
будет
s

S₀,
то множество {s}
всех нижних сумм Лебега оказывается
ограниченный сверху. Пусть U
есть
его точная верхняя граница U
= sup{s}.
Тогда, ясно, что U

S₀.

Ввиду
произвольности суммы S₀,
последнее неравенство доказы­вает,
что множество {S}
всех верхних сумм Лебега ограничено
снизу. Обозначим через V
его
точную нижнюю границу V
= inf{S}.

Очевидно,
при любом способе дробления будет
s

U

V

S.
Но,
как мы отмечали, S
– s


(E),
откуда 0

V
– U


(E)
и,
так как 
произвольно
мало, то U
= V.

Определение
1.
Чисело U
=
V
называется
инте­гралом
Лебега
функции
f(x)
по множеству Е
и
обозначается символом

(L)

В тех случаях,
когда смешение с другими видами интеграла
исключено, пишут просто

В
частности, если Е
есть
сегмент [а,
b],
употребляют
символы

(L)

Из
сказанного выше следует, что каждая
измеримая ограни­ченная функция
интегрируема в смысле Лебега.
Уже из этого замечания видно, что процесс
интегри­рования (L)
приложим к гораздо более широкому классу
функций, чем процесс интегрирования
(R).

К тому
же интегралу Лебега можно подойти с
другой стороны, используя суммы Дарбу,
но в отличие от интеграла Римана,
разбиения берутся по произвольным
измеримым множествам, а не только по
отрезкам. Дадим более точное определение.

Пусть

=
и
=
два разбиенияЕ
измеримыми множествами:
иf(x)
– ограниченная измеримая функция на
Е.
Для каждого разбиения и функции определим
нижнюю d(,
f
)
и верхнюю D(,
f
)
суммы Дарбу:

d(,
f
)
=
,D(,
f
)
=
,

где
,.
Точные грани существуют в силу
ограниченности функцииf.

Разбиение

множества Е,
полученное в результате пересечения
элементов разбиений 
и 

 =

=
,
C_i,
j
= A_iB_j,

называется
произведением
разбиений.

Лемма
2.
Пусть разбиение 
= 
является произведением разбиений 
и .
Тогда справедливы неравенства

d(,
f
)

d(,
f
)

D(,
f
)

D(,
f
).

Доказательство.
Обозначим через r_i,
j
и р_i,
j
– нижнюю и верхнюю грани функции f
на множестве C_i,
j.
Так как a_i

r_i,
j
и p_i,
j

b_j
при всех i
и j,
то используя аддитивность меры, мы имеем

откуда следует
утверждение леммы.

Из
доказанной леммы вытекает, что нижние
суммы Дарбу ограничены сверху, а верхние
– снизу. Вместе с тем, так как разбиения
Лебега и суммы Лебега являются частными
случаями разбиений и сумм Дарбу, легко
получаем

.

Так
как U
= V,
то мы получаем еще одно определение
интеграла Лебега.

Теорема
1.
В приведенных выше условиях справедливы
равенства

.

Следствие
1.
Для
произвольного 
> 0 всегда
существует разбиение ,для
которого D(,
f
)
– d(,
f
)
< .

Доказательство.
Из
теоремы вытекает, что для любого 
> 0 существуют разбиения 
и ,
для которых D(,
f
)
– d(,
f
)
< .
Если 
= 
есть произведение этих разбиений, то
по лемме 3 получим D(,
f
)
– d(,
f
)

D(,
f
)
– d(,
f
)
< .

Из
этой теоремы также следует, что значение
инте­грала Лебега, которое в силу
изначального определения связано с
числами А
и
В, на
самом
деле от них не зависит.

Теорема
2.
Если


0,
то
суммы Лебега
s
и
S
стремятся
к интегралу

Теорема непосредственно
вытекает из неравенств

s




S,
S
– s



(E).