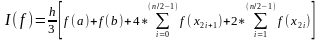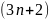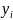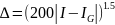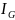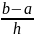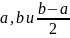При вычислении определенного интеграла не всегда получаем точное решение. Не всегда удается представление в виде элементарной функции. Формула Ньютона-Лейбница не подходит для вычисления, поэтому необходимо использовать методы численного интегрирования. Такой метод позволяет получать данные с высокой точностью. Метод Симпсона является таковым.
Для этого необходимо дать графическое представление выведению формулы. Далее идет запись оценки абсолютной погрешности при помощи метода Симпсона. В заключении произведем сравнение трех методов: Симпсона, прямоугольников, трапеций.
Метод парабол – суть, формула, оценка, погрешности, иллюстрации
Задана функция вида y=f(x), имеющая непрерывность на интервале [a; b], необходимо произвести вычисление определенного интеграла ∫abf(x)dx
Необходимо разбить отрезок [a; b] на n отрезков вида x2i-2;x2i, i=1, 2,…, n с длиной 2h=b-an и точками a=x0<x2<x4<…<x2π-2<x2π=b. Тогда точки x2i-1, i=1, 2,…, n считаются серединами отрезков x2i-2; x2i, i=1, 2,…, n. Данный случай показывает, что определение узлов производится через xi=a+i·h, i=0, 1,…, 2n.
Суть метода парабол
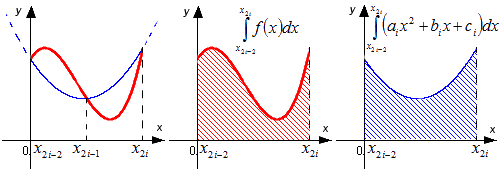
Каждый интервал x2i-2; x2i, i=1, 2,…, n подынтегральной функции приближен при помощи параболы, заданной y=aix2+bix+ci, проходящей через точки с координатами x2i-2; f(x2i-2), x2i-1; x2i-1, x2i; f(x2i). Поэтому метод и имеет такое название.
Данные действия выполняются для того, чтобы интеграл ∫x2i-2x2iaix2+bix+cidx взять в качестве приближенного значения ∫x2i-2x2if(x)dx. Можем вычислить при помощи формулы Ньютона-Лейбница. Это и есть суть метода парабол. Рассмотрим рисунок, приведенный ниже.
Графическая иллюстрация метода парабол (Симпсона)
При помощи красной линии изображается график функции y=f(x), синей – приближение графика y=f(x) при помощи квадратичных парабол.
Вывод формулы метода Симпсона (парабол)
Исходя из пятого свойства определенного интеграла получаем ∫abf(x)dx=∑i=1n∫x2i-2x2if(x)dx≈∑i=1n∫x2i-2x2i(aix2+bix+ci)dx
Для того чтобы получить формулу методом парабол, необходимо произвести вычисление:
∫x2i-2x2i(aix2+bix+ci)dx
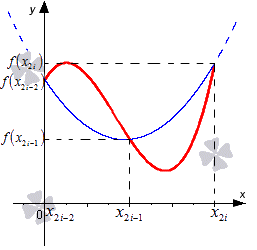
Пусть x2i-2=0. Рассмотрим рисунок, приведенный ниже.
Изобразим, что через точки с координатами x2i-2; f(x2i-2), x2i-1; x2i-1, x2i; f(x2i) может проходить одна квадратичная парабола вида y=aix2+bix+ci. Иначе говоря, необходимо доказать, что коэффициенты могут определяться только единственным способом.
Имеем, что x2i-2; f(x2i-2), x2i-1; x2i-1, x2i; f(x2i) являются точками параболы, тогда каждое из представленных уравнений является справедливым. Получаем, что
ai(x2i-2)2+bi·x2i-2+ci=f(x2i-2)ai(x2i-1)2+bi·x2i-1+ci=f(x2i-1)ai(x2i)2+bi·x2i+ci=f(x2i)
Полученная система разрешается относительно ai, bi, ci, где необходимо искать определитель матрицы по Вандермонду. Получаем, что
(x2i-2)2x2i-21x2i-1)2x2i-11(x2i)2x2i1, причем он считается отличным от нуля и не совпадает с точками x2i-2, x2i-1, x2i. Это признак того, что уравнение имеет только одно решение, тогда и выбранные коэффициенты ai; bi; ci могут определяться только единственным образом, тогда через точки x2i-2; f(x2i-2), x2i-1; x2i-1, x2i; f(x2i) может проходить только одна парабола.
Можно переходить к нахождению интеграла ∫x2i-2x2i(aix2+bix+ci)dx.
Видно, что
f(x2i-2)=f(0)=ai·02+bi·0+ci=cif(x2i-1)=f(h)=ai·h2+bi·h+cif(x2i)=f(0)=4ai·h2+2bi·h+ci
Для осуществления последнего перехода необходимо использовать неравенство вида
∫x2i-2x2i(aix2+bix+ci)dx=∫02h(aix2+bix+ci)dx==aix33+bix22+cix02h=8aih33+2bih2+2cih==h38aih2+6bih+6ci=h3fx2i-2+4f22i-1+fx2i
Значит, получаем формулу, используя метод парабол:
∫abf(x)dx≈∑i=1n∫x2i-2x2iaix2+bix+cidx==∑i=1nh3(f(x2i-2)+4f(x2i-1)+f(x2i))==h3f(x0)+4f(x1)+f(x2)+f(x2)+4f(x3)+f(x4)+…++f(x2n-2)+4f(x2n-1)+f(x2n)==h3f(x0)+4∑i=1nf(x2i-1)+2∑i=1n-1f(x2i)+f(x2n)
Формула метода Симпсона имеет вид ∫abf(x)dx≈h3f(x0)+4∑i=1nf(x2i-1)+2∑i=1n-1f(x2i)+f(x2n).
Формула оценки абсолютной погрешности имеет вид δn≤max[a;b]f(4)(x)·(b-a)52880n4.
Примеры приближенного вычисления определенных интегралов методом парабол
Метод Симпсона предполагает приближенное вычисление определенных интегралов. Чаще всего имеются два типа задач, для которых применим данный метод:
- при приближенном вычислении определенного интеграла;
- при нахождении приближенного значения с точностью δn.
На точность вычисления влияет значение n, чем выше n, тем точнее промежуточные значения.
Вычислить определенный интеграл ∫05xdxx4+4 при помощи метода Симпсона, разбивая отрезок интегрирования на 5 частей.
Решение
По условию известно, что a = 0; b = 5; n = 5, f(x)=xx4+4.
Тогда запишем формулу Симпсона в виде
∫abf(x)dx≈h3f(x0)+4∑i=1nf(x2i-1)+2∑i=1n-1f(x2i)+f(x2n)
Чтобы применить ее в полной мере, необходимо рассчитать шаг по формуле h=b-a2n, определить точки xi=a+i·h, i=0, 1,…, 2n и найти значения подынтегральной функции f(xi), i=0, 1,…, 2n.
Промежуточные вычисления необходимо округлять до 5 знаков. Подставим значения и получим
h=b-a2n=5-02·5=0.5
Найдем значение функции в точках
i=0: xi=x0=a+i·h=0+0·0.5=0⇒f(x0)=f(0)=004+4=0i=1: xi=x1=a+i·h=0+1·0.5=0.5⇒f(x1)=f(0.5)=0.50.54+4≈0.12308…i=10: xi=x10=a+i·h=0+10·0.5=5⇒f(x10)=f(5)=554+4≈0.00795
Наглядность и удобство оформляется в таблице, приведенной ниже
| i | 0 | 1 | 2 | 3 | 4 | 5 |
| xi | 0 | 0.5 | 1 | 1.5 | 2 | 2.5 |
| fxi | 0 | 0.12308 | 0.2 | 0.16552 | 0.1 | 0.05806 |
| i | 6 | 7 | 8 | 9 | 10 |
| xi | 3 | 3.5 | 4 | 4.5 | 5 |
| fxi | 0.03529 | 0.02272 | 0.01538 | 0.01087 | 0.00795 |
Необходимо подставить результаты в формулу метода парабол:
∫05xdxx4+4≈h3f(x0)+4∑i=1nf(x2i-1)+2∑i=1n-1f(x2i)+f(x2n)==0.530+4·0.12308+0.16552+0.05806++0.02272+0.01087+2·0.2+0.1++0.03529+0.01538+0.00795≈≈0.37171
Для вычисления мы выбрали определенный интеграл, который можно вычислить по Ньютону-Лейбницу. Получим:
∫05xdxx4+4=12∫05d(x2)x22+4=14arctgx2205=14arctg252≈0.37274
Ответ: Результаты совпадают до сотых.
Вычислить неопределенный интеграл∫0πsin3x2+12dx при помощи метода Симпсона с точностью до 0,001.
Решение
По условию имеем, что а=0, b=π, f(x)=sin3x2+12, δn≤0.001. Необходимо определить значение n. Для этого используется формула оценки абсолютной погрешности метода Симпсона вида δn≤max[a;b]f(4)(x)·(b-a)52880n4≤0.001
Когда найдем значение n, то неравенство max[a;b]f(4)(x)·(b-a)52880n4≤0.001 будет выполняться. Тогда, применив метод парабол, погрешность при вычислении не превысит 0.001. Последнее неравенство примет вид
n4≥max[a;b]f(4)(x)·(b-a)52.88
Теперь необходимо выяснить, какое наибольшее значение может принимать модуль четвертой производной.
f'(x)=sin3x2+12’=32cos3x2⇒f”(x)=32cos3x2’=-94sin3x2⇒f”'(x)=-94sin3x2’=-278cos3x2⇒f(4)(x)=-278cos3x2’=8116sin3x2
Область определения f(4)(x)=8116sin3x2 принадлежит интервалу -8116;8116, а сам отрезок интегрирования [0;π) имеет точку экстремума, из этого следует, что max[0;π]f(4)(x)=8116.
Производим подстановку:
n4≥max[a;b]f(4)(x)·(b-a)52.88⇔n4≥8116·π-052.88⇔⇔n4>537.9252⇔n>4.8159
Получили, что n – натуральное число, тогда его значение может быть равным n=5, 6, 7… для начала необходимо взять значение n=5.
Действия производить аналогично предыдущему примеру. Необходимо вычислить шаг. Для этого
h=b-a2n=π-02·5=π10
Найдем узлы xi=a+i·h, i=0, 1,…, 2n, тогда значение подынтегральной функции будет иметь вид
i=0: xi=x0=a+i·h=0+0·π10=0⇒f(x0)=f(0)=sin3·02+12=0.5i=1: xi=x1=a+i·h=0+1·π10=π10⇒f(x1)=f(π10)=sin3·π102+12≈0.953990…i=10: xi=x10=a+i·h=0+10·π10=π⇒f(x10)=f(π)=sin3·π2+12≈-0.5
Для объединения результатов запишем данные в таблицу.
| i | 0 | 1 | 2 | 3 | 4 |
| xi | 0 | π10 | π5 | 3π10 | 2π5 |
| f(xi) | 0.5 | 0.953990 | 1.309017 | 1.487688 | 1.451056 |
| i | 5 | 6 | 7 | 8 | 9 | 10 |
| xi | π2 | 3π5 | 7π10 | 4π5 | 9π10 | π |
| f(xi) | 1.207107 | 0.809017 | 0.343566 | -0.087785 | -0.391007 | -0.5 |
Осталось подставить значения в формулу решения методом парабол и получим
∫0πsin3x2+12≈h3f(x0)+4∑i=1nf(x2i-1)+2∑i=1n-1f(x2i)+f(x2n)==π30·0,5+4·0.953990+1.487688+1.207107++0.343566-0.391007+2·1.309017+1.451056++0.809017-0.87785-0.5==2.237650
Метод Симпсона позволяет нам получать приближенное значение определенного интеграла ∫0πsin3x2+12dx≈2.237 с точностью до 0,001.
При вычислении формулой Ньютона-Лейбница получим в результате
∫0πsin3x2+12dx=-23cos3x2+12×0π==-32cos3π2+π2–23cos0+12·0=π2+23≈2.237463
Ответ: ∫0πsin3x2+12dx≈2.237
Замечание
В большинстве случаях нахождение max[a;b]f(4)(x) проблематично. Поэтому применяется альтернатива – метод парабол. Его принцип подробно разъясняется в разделе метода трапеций. Метод парабол считается предпочтительным способом для разрешения интеграла. Вычислительная погрешность влияет на результат n. Чем меньше его значение, тем точнее приближенное искомое число.
Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 28 декабря 2019 года; проверки требуют 20 правок.
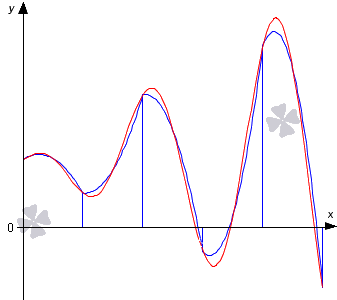
Суть метода — аппроксимация функции f (x) (синий график) квадратичным полиномом P (x) (красный)
Формула Симпсона (также Ньютона-Симпсона[1]) относится к приёмам численного интегрирования. Получила название в честь британского математика Томаса Симпсона (1710—1761).
Суть метода заключается в приближении подынтегральной функции на отрезке ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

Формула[править | править код]
Формулой Симпсона называется интеграл от интерполяционного многочлена второй степени на отрезке ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)
где 


Погрешность[править | править код]
При условии, что у функции 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

В связи с тем, что значение 
Представление в виде метода Рунге-Кутты[править | править код]
Формулу Симпсона можно представить в виде таблицы метода Рунге-Кутты следующим образом:
Составная формула (формула Котеса)[править | править код]
Для более точного вычисления интеграла интервал ![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)

- где
— величина шага, а
— чередующиеся границы и середины составных отрезков, на которых применяется формула Симпсона. Один подобный составной отрезок
состоит из двух элементарных отрезков
. Таким образом, если проводить параллели с простой формулой Симпсона, то в данном случае серединой отрезка, на котором применяется формула Симпсона, становится
.
- Обычно для равномерной сетки данную формулу записывают в других обозначениях (отрезок
разбит на
отрезков) в виде
Также формулу можно записать используя только известные значения функции, то есть значения в узлах:
- где
означает что индекс меняется от единицы с шагом, равным двум.
Общая погрешность 
![[a,b]](https://wikimedia.org/api/rest_v1/media/math/render/svg/9c4b788fc5c637e26ee98b45f89a5c08c85f7935)



.
При невозможности оценить погрешность с помощью максимума четвёртой производной (например, на заданном отрезке она не существует, либо стремится к бесконечности), можно использовать более грубую оценку:
.
Проверка составной формулы Симпсона в случае интегрирования узких пиков[править | править код]
Составная формула Симпсона не проходит проверку на величину погрешности в случае узких (малое число точек на пик) пикоподобных функций, оказываясь значительно менее эффективной[3], чем правило трапеций. Именно, для достижения той же погрешности, что и в случае правила трапеций, составному правилу Симпсона требуется в 1.8 раз больше точек. Интеграл по составному правилу Симпсона может быть разложен на суперпозицию двух интегралов: 2/3 интеграла по правилу трапеций с шагом h, и 1/3 интеграла по правилу центральных прямоугольников с шагом 2h, и погрешность составного правила Симпсона соответствует второму слагаемому. Можно построить удовлетворительную модификацию правила Симпсона путём усреднения схем этого правила, полученных со сдвигом рамки суммирования на одну точку, при этом получаются следующие правила[3]:
в котором используются значения, выходящие за границу интервала интегрирования, или
в котором значения, находящиеся за границей интервала интегрирования, не используются. Приложение второго из правил к участку из трёх точек порождает правило Симпсона 1/3, к участку из 4 точек – 3/8.
В этих правилах веса точек внутри интервала интегрирования равны единице, отличия наблюдаются только на концах участка. Эти правила могут быть ассоциированы с формулой Эйлера-Маклорена, при условии учета первой производной и названы правилами Эйлера-Маклорена первого порядка[3]. Разница между правилами состоит в способе вычисления первой производной на краях интервала интегрирования. Разница первых производных на краях участка интегрирования учитывает вклад второй производной в интеграл функции. Формула Эйлера-Маклорена аналогично приведённым выше правилам первого порядка может быть использована для конструирования правил интегрирования третьего, пятого и более высоких порядков.
См. также[править | править код]
- Метод прямоугольников
- Метод трапеций
- Список квадратурных формул
Примечания[править | править код]
- ↑ Формула Ньютона-Симпсона. Дата обращения: 14 августа 2009. Архивировано из оригинала 22 мая 2010 года.
- ↑ Численные методы / Н. С. Бахвалов, Н. П. Жидков, Г. М. Кобельков. — 4-е изд. — М.: БИНОМ, Лаборатория знаний, 2006. — С. 122. — 636 с. — ISBN 5-94774-396-5.
- ↑ 1 2 3 Comparison of integration rules in the case of very narrow chromatographic peaks (англ.) // Chemometrics and Intelligent Laboratory Systems. — 2018-08-15. — Vol. 179. — P. 22–30. — ISSN 0169-7439. — doi:10.1016/j.chemolab.2018.06.001.
Литература[править | править код]
- Костомаров Д. П., Фаворский А. П. Вводные лекции по численным методам. М.: Логос, 2004. 184 с. ISBN 5-94010-286-7
- Петров И. Б., Лобанов А. И. Лекции по вычислительной математике. М.: Интуит, Бином, 2006. 523 с. ISBN 5-94774-542-9
Щебетун Виктор
Эксперт по предмету «Математика»
Задать вопрос автору статьи
В случае с методом Симпсона для вычисления интегралов в отличие от метода прямоугольников и метода трапеций, функция кривой $y=f(x)$ на элементарных отрезках $left[x_{i-1};x_iright]$ заменяется не отрезками прямых, а дугами парабол, в результате получается более точная формула для приближённого вычисления интеграла $int_a^b f(x)dx$.
Вывод формулы Симпсона
Для начала рассмотрим, как найти площадь криволинейной трапеции, ограниченной сверху функцией $y=ax^2+bx+c$, по бокам прямыми, параллельными оси ординат $x=-h$, $x=h$, а снизу отрезком, параллельным оси абсцисс.
Рисунок 1. Вычисление площади криволинейной трапеции
Сдай на права пока
учишься в ВУЗе
Вся теория в удобном приложении. Выбери инструктора и начни заниматься!
Получить скидку 3 000 ₽
Парабола проходит через три точки $M_1, M_2$ и $M_3$ c координатами соответственно $(-h; y_0), (0; y_1)$ и $(h;y_2)$. При этом функция $y$ в точке $(-h; y_0)$ будет равна $y_0=ah^2-bh+c$, в точке $(0; y_1)$ она равна $y_1=c$, так как $x=0$, а в точке $(h;y_2)$ она имеет значение $y_2= ah^2+bh+c$.
Соответственно, площадь $S$ равна:
$int_{-h}^h (ax^2 + bx + c)dx=(afrac{x^3}{3} + bfrac{x^2}{2}+cx)|^h_{-h}=frac{2}{3}ah^3+2chleft(1right).$
Из формул, описывающих значения функций в рассматриваемых точках, получаем, что $c=y_1, a =frac{1}{2h^2}(y_0-2y_1+y_2)$. Подставим эти значения в выражение $(1)$, получим:
$S=frac{2}{3}h^3 cdot frac{1}{2h^2}(y_0-2y_1+y_2)+2hy_1= frac{h}{3}(y_0-2y_1+y_2) + 2hy_1 = frac{h}{3} cdot (y_0 + 4y_1+y_2)left(2right)$
Полученная формула является формулой для вычисления площади криволинейной трапеции. Перейдём от неё к формуле парабол для приближённого вычисления определённого интеграла.
Сначала разобьём отрезок $left[a;bright]$ на $2n$ равных отрезков длиной $h=frac{b-a}{2n}$, для этого отложим точки $x_i=x_0+ih, (i=0…2n)$, причём $x_0=a$, a $x_{2n}=b$. Получим $2n$ элементарных трапеций (рис. 2). В каждой из этих точек с абсциссой $x_i$ вычисляем значение функции $y$.
«Метод Симпсона» 👇
Рисунок 2. Вычисление площади фигуры, ограниченной линиями, по методу Симпсона
Теперь перейдём от элементарных трапеций к формуле Cимпсона для вычисления интеграла. Для этого каждую пару элементарных криволинейных трапеций, основания у которых равны $h$, заменяем на одну трапецию с основанием $2h$. Рассматриваем кривую $y=f(x)$ на отрезке $left[x_0;x_2right]$, она проходит через 3 точки с координатами $(x_0;y_0), (x_1;y_1), (x_2;y_2)$. Подставим их в формулу $(2)$:
$S_1=int^{x_2}_{x_0} f(x)dx=frac{h}{3}(y_0 + 4y_1+y_2)$.
Аналогично находим все остальные площади:
$S_n=int^{x_{2n}}_{x_{2n-2}} f(x)dx=frac{h}{3}(y_{2n-2}+ 4y_{2n-1}+y_{2n})$.
Теперь складываем полученные равенства и получаем:
Замечание 1
$int^b_a f(x)dx≈frac{b-a}{6n}((y_0+y_{2n}+4(y_1+y_3+…+y_{2n-1})+2(y_2+y_4+…+y_{2n-2}))left(3right)$
Полученная формула носит название метода парабол или иначе формула Симпсона.
Оценка погрешности при использовании метода парабол
Погрешность для метода парабол вычисляется по формуле:
Определение 1
$|R_n|≤frac{b-a)^5}{180 cdot (2n)^4} cdot M_4$, где $M_4=max_{a≤x≤ b}|f^{IV}(x)|$
Формула Симпсона даёт точное значение для всех функций, в которых максимальная степень при $x$ меньше или равна $3$, так как четвёртая производная в этом случае равна нулю.
Нахождение определённого интеграла не всегда удобно из-за трудности вычисления $M_4$, поэтому при возникновении сложностей пользуются методом трапеций.
Пример 1
Вычислите интеграл $int^2_0 x^3dx$ при этом разбив отрезок интегрирования на 4 элементарных.
Решение:
Для начала проведём подготовительные вычисления для функции $f(x)=x^3$:
$a=0=x_0, b=2=x_4$, следовательно, длина элементарного отрезка составит:
$h=frac{b-a}{4}=frac{1}{2}$.
Определяем координаты границ элементарных отрезков:
$x_0=0; y_0= 0$
$x_1=frac{1}{2}; y_1=frac{1}{8}$
$x_2=1; y_2=1$
$x_3=frac{3}{2}; y_3=frac{27}{8}$
$x_4=2; y_4=8$.
Теперь воспользуемся формулой парабол и вычислим интеграл:
$int^2_0 x^3dx≈frac{2}{12}(0+8+4(frac{1}{8}+ frac{27}{8}) + 2) = 4$
Так как четвёртая производная функции $y(x)=x^3$ равна нулю, погрешность метода в данном случае также будет нулевой.
Находи статьи и создавай свой список литературы по ГОСТу
Поиск по теме
Метод Симпсона
Более
высокая точность определения численного
значения определенного интеграла
получается при аппроксимации функции
f(x)
квадратичным интерполяционным полиномом,
который совпадает с f(x)
в крайних точках a
и b,
а также в средней точке
.
Интеграл от этого квадратичного
полинома выражается формулой:
,
(5)
которая
называется формулой Симпсона.
Р
ис.
4. Метод Симпсона.
В
методе Симпсона площадь криволинейной
трапеции рассчитывается как сумма
площадей ряда криволинейных трапеций,
у которых криволинейная сторона
представляет собой участок параболы.
Это можно видеть на рис.4.
Каждая
парабола может быть проведена только
через три граничные точки, принадлежащие
двум соседним отрезкам. Поэтому число
участков разбиения отрезка [a,b] в
отличие от предыдущих методов обязательно
должно быть четным. Таким образом, вместо
каждых двух элементарных прямолинейных
трапеций будем рассматривать одну
элементарную трапецию, ограниченную
параболической дугой. Исходя из этого,
определенный интеграл на случай разбиения
интервала
на n участков с шагом h. приближенно
вычисляется по формуле:
(6)
–
полная формула Симпсона.
Таким образом,
для реализации метода прямоугольников,
трапеции и Симпсона для вычисления
определенного интеграла необходимо:
Задать в явном
виде определенный интеграл, площадь
которого необходимо определить. После
этого задаются пределы интегрирования,
и шаг интегрирования. Затем проводится
расчет по формулам (2), (4) и (6).
Для метода
Симпсона число разбиений n должно быть
четным, что подлежит проверке при
составлении программы.
Метод Гаусса.
Приближение
функции одним полиномом на всем отрезке
интегрирования, как правило, приводит
к большой ошибке в оценке значения
интеграла.
Для
уменьшения погрешности отрезок
интегрирования разбивают на части и
применяют численный метод для оценки
интеграла на каждой из них.
При
стремлении количества разбиений к
бесконечности, оценка интеграла стремится
к его истинному значению для любого
численного метода.
Приведённые выше методы допускают
простую процедуру уменьшения шага в
два раза, при этом на каждом шаге требуется
вычислять значения функции только во
вновь добавленных узлах. Для оценки
погрешности вычислений используется
правило Рунге.
Описанные выше методы используют
фиксированные точки отрезка (концы и
середину) и имеют низкий порядок точности
(0 – методы правых и левых прямоугольников,
1 – методы средних прямоугольников и
трапеций, 3 – метод парабол (Симпсона)).
Если мы можем выбирать точки, в которых
мы вычисляем значения функции
,
то можно при том же количестве вычислений
подынтегральной функции получить методы
более высокого порядка точности. Так
для двух (как в методе трапеций) вычислений
значений подынтегральной функции, можно
получить метод уже не 1-го, а 3-го порядка
точности:

В
общем случае, используя
точек, можно получить метод с порядком
точности
.
Значения узлов метода Гаусса по
точкам являются корнями полинома
Лежандра степени
.
Значения
узлов метода Гаусса и их весов приводятся
в справочниках специальных функций.
Наиболее известен метод Гаусса по пяти
точкам.
Недостаток
метода Гаусса состоит в том, что он не
имеет лёгкого (с вычислительной точки
зрения) пути оценки погрешности
полученного значения интеграла.
Использование правила Рунге требует
вычисления подынтегральной функции
примерно в таком же числе точек, не давая
при этом практически никакого выигрыша
точности, в отличие от простых методов,
где точность увеличивается в разы при
каждом новом разбиении. Кронродом был
предложен следующий метод оценки
значения интеграла
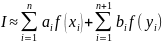
где
– узлы метода Гаусса по
точкам, а
параметров
,
,
подобраны таким образом, чтобы порядок
точности метода был равен
.
Тогда
для оценки погрешности можно использовать
эмпирическую формулу:
,
где
– приближённое значение интеграла,
полученное методом Гаусса по
точкам.
Сравнение
методов по эффективности:
Возьмем
пять произвольных промежутков и вычислим
погрешность для каждого из методов по
формуле:

Были
выбраны следующие промежутки:





Так
как средние значения погрешностей и
итераций имеют большой интервал, строить
график не имеет смысла, поэтому составим
таблицу:
|
Метод |
Метод |
Метод |
|||
|
Δ |
Количество итераций |
Δ |
Количество итераций |
Δ |
Количество итераций |
|
4,794001 |
4,6 |
4,916453 |
5,8 |
0,1203142 |
61,4 |
|
0,216836 |
63,4 |
0,000009 |
46 |
0,0088742 |
198,2 |
|
0,004717 |
630,2 |
0,000004 |
452,4 |
0,0056248 |
637,4 |
|
0,003569 |
6300,8 |
0,000016 |
4500,6 |
0,0000448 |
1991 |
|
0,0000042 |
6692,6 |
||||
|
0,0000002 |
97819,4 |
||||
|
0,0000000 |
125448,5 |
Как
видно из таблицы, самым лучшим соотношением
точность/количество итераций обладает
метод Симпсона, но при дальнейшем
повышении количества итераций в
переменные записываются выходящие за
пределы значения, что вносит погрешность
в вычисления. Именно поэтому в методе
трапеций и Симпсона нижние ячейки
оставлены пустыми. Метод Гаусса работает
дольше, но при этом может вычислить
значение интеграла со сколь угодно
большой точностью.
Описание
алгоритма решения задачи
Для удобства
построения алгоритма была введена
функция подсчета значения функции,
указанной в задании.
-
Как и в предыдущем задании,
был реализован выбор метода решения
задачи. -
До перехода к конкретному
методу у пользователя запрашиваются
пределы интегрирования. Так как функция
определена на промежутке
ограничений ввода нет.
-
Метод трапеции начинается
с ввода шага с терминала. Далее в
результирующую переменную подсчитывается
первое слагаемое метода
.
-
Стартует цикл, где счетчик
выступает в роли аргумента, соответственно
он пробегает значения от нижнего предела
к верхнему, увеличиваясь каждый раз на
шаг. К результирующей переменной каждый
раз прибавляется значение
.
Примечание:
для сокращения кода можно было использовать
неупрощенную формулу, тем самым
избавиться от строчки, указанной в
пункте 3. В самом цикле слагаемое приняло
бы вид
.
-
Результаты записываются
в файл. -
В методе трапеций запросы
вводы и вывод те же самые. -
Для удобства вычисляется
количество разбиений по формуле
. -
По требованию, в методе
Симпсона количество разбиений должно
быть четным, поэтому в противном случае
количество разбиений увеличивается
на 1(чтобы не понижать точность) и
вычисляется новый шаг.
Примечание:
опять же, программу можно упростить,
избавившись от этого условия. Для этого
достаточно вычислять каждый отрезок
не по первой, второй и третьей точке, а
по первой третьей и второй, то есть
.
-
В цикле выполняются
операции, указанные в вышеприведенной
формуле для метода Симпсона. -
Для метода Гаусса введены
две функции:
-
Первая из них просчитывает
значение интеграла на задаваемом в
качестве параметра промежутке a,
b по формуле

где m=
, n=
,
и
–
нули полинома Лежандра со степенью 6,
значения которых взяты из таблицы:






-
Рекурсивная функция,
вычисляющая интеграл методом Гаусса
с заданной точностью. В качестве
параметров используются пределы, ранее
вычисленный интеграл и точность.
Сначала область интегрирования делится
на два, вычисляется по ранее описанной
функции, результаты складываются. Если
разность суммы и ранее вычисленного
интеграла оказывается меньше точности,
два раза рекурсивно вызывается функция,
первая считает первую половину с
точностью, деленной на два и вычисленным
интегралом от первой половины, вторая,
соответственно от второй. В конце
функция возвращает сумму значений
вычисленных половинок от интегралов
-
Пользователю предлагается
выбрать точность, далее вызывается
рекурсивная функция, с параметрами
введенных пределов интегрирования,
заданной точностью и функцией,
вычисляющей значение интеграла на
всем заданном промежутке. -
Результаты записываются
в файл -
С помощью цикла можно еще
раз повторить операцию.
Руководство
программиста
Программный код приложения разрабатывался
на языке СИ.
В программе использованы следующие
пользовательские функции:
-
float f(float x) вычисляет значение
функции от х -
float
calcGauss(float
a, float b)
Вычисляет интеграл методом Гаусса по
шести точкам -
float gauss(float
a,float b,
точность, ранее вычисленный
интеграл)
Рекурсивная
функция, разбивающая область от a
до b на две половинки и
считающая интеграл на каждой из них,
пока не достигнет нужной точности.
Так же в глобальный массив с двумя
строками записаны вышеприведенные
точки следующим методом:
double
pnt[2][G]={{
,
,
},
{
,
,
}};
где G
– количество точек деленное на два.
То есть внешними скобками объединены
строки, а внутренними элементы
соответствующей строки. Если потребуется
изменить порядок метода Гаусса, нужно
во-первых изменить значение константы
G и вписать в массив новые
значения точек для соответствующего
порядка, которые являются табличными
значениями.
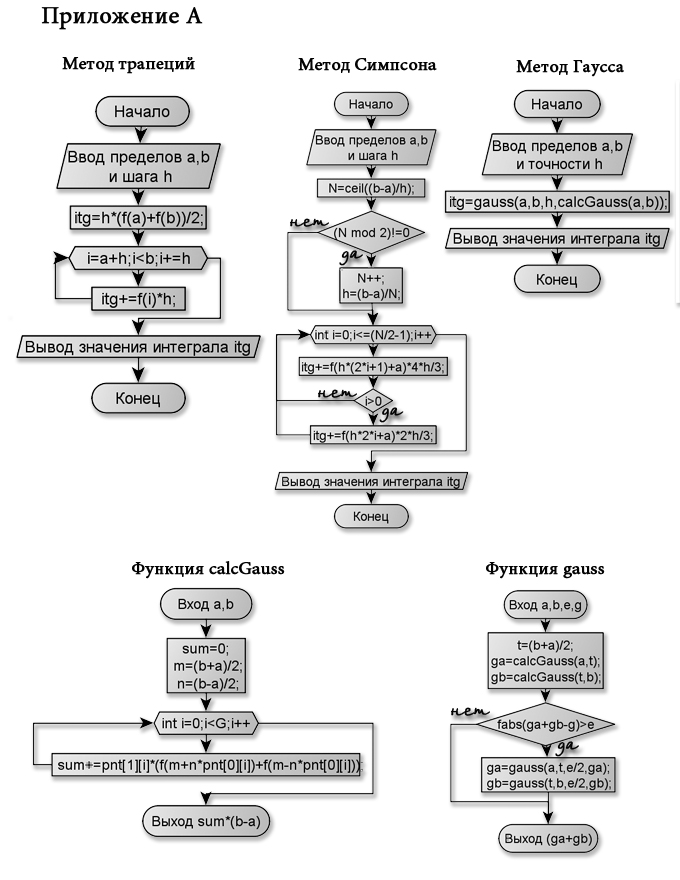
Блок-схема алгоритма программы приведена
в приложении А.
Листинг программы приведен в приложении
В.
Пример входного и выходного файла в
приложении С.
Руководство пользователя
После запуска программа потребует
выбрать метод нахождения интеграла от
указанной функции. Далее необходимо
задать область интегрирования, после
чего для методов Симпсона и трапеции
указывается шаг, а для метода Гаусса с
шестью узлами – точность. Процедуру
можно повторять сколь угодно раз, после
чего посмотреть результаты в файле
integral.txt
Вывод: В ходе
лабораторной работы были изучены
некоторые численные методы вычисления
определенных интегралов, а так же они
были реализованы программно на языке
СИ и при помощи специализированных
программных пакетов (Matcad).
Приложение
В
#include
<stdio.h>
#include
<stdio.h>
#include
<math.h>
#define
G 3
double
pnt[2][G]={{0.932469514203152/2,0.661209386966265/2,0.238619186083197/2},
{0.171324492379170/2,0.360761573048139/2,0.467913934572691/2}};
float
f(float x)
{
float
y=(pow(x,2)+sin(2*x))/(cos(x)+3);
return
y;
}
float
calcGauss(float a,float b)
{
float
m,n,sum=0;
m=(b+a)/2;
n=(b-a)/2;
for(int
i=0;i<G;i++)
sum+=pnt[1][i]*(f(m+n*pnt[0][i])+f(m-n*pnt[0][i]));
return
sum*(b-a);
}
float
gauss(float a,float b,float e,float g)
{
float
ga,gb,t=(b+a)/2;
ga=calcGauss(a,t);
gb=calcGauss(t,b);
if
(fabs(ga+gb-g)>e)
{
ga=gauss(a,t,e/2,ga);
gb=gauss(t,b,e/2,gb);
}
return
(ga+gb);
}
void
main()
{
float
a,b,h,itg;
int
N;
char
P;
FILE
*out;
out=fopen(“Integral.txt”,”w”);
printf(”
x^2+sin(2*x)n”);
printf(“Definite
integral of the function Y(x)= ————n”);
printf(”
cos(x)+3nn”);
printf(“can
be calculated with “);
do
{
do
{
printf(“Simpson
method(S), trapetion method(T), Gauss method with 6 nodes(G)n”);
scanf(”
%c”,&P);
}
while(P!=’t’
&& P!=’T’ && P!=’g’ && P!=’G’ &&
P!=’s’ && P!=’S’);
printf(“Input
limits(a,b)n”);
scanf(“%f
%f”,&a,&b);
if(P==’t’
|| P==’T’)
{
printf(“Input
step(h)n”);
scanf(“%f”,&h);
itg=h*(f(a)+f(b))/2;
for(float
i=a+h;i<b;i+=h)
itg+=f(i)*h;
fprintf(out,”
x^2+sin(2*x)n”);
fprintf(out,”Y(x)=
—————– = %fn”,itg);
fprintf(out,”
cos(x)+3nn”);
fprintf(out,”Integral
was calculated from %.3f to %.3f with trapetion method;nStep was
equal %fnn”,a,b,h);
}
if(P==’S’
|| P==’s’)
{
printf(“Input
step(h)n”);
scanf(“%f”,&h);
N=ceil((b-a)/h);
if
((N%2)!=0)
{
N++;
h=(b-a)/N;
}
itg=(f(a)+f(b))*h/3;
for(int
i=0;i<=(N/2-1);i++)
{
itg+=f(h*(2*i+1)+a)*4*h/3;
if(i>0)itg+=f(h*2*i+a)*2*h/3;
}
fprintf(out,”
x^2+sin(2*x)n”);
fprintf(out,”Y(x)=
—————– = %fn”,itg);
fprintf(out,”
cos(x)+3nn”);
fprintf(out,”Integral
was calculated from %.3f to %.3f with Simpson’s method;nStep was
equal %fnn”,a,b,h);
}
if(P==’G’
|| P==’g’)
{
printf(“Input
accuracy(h)n”);
scanf(“%f”,&h);
itg=gauss(a,b,h,calcGauss(a,b));
fprintf(out,”
x^2+sin(2*x)n”);
fprintf(out,”Y(x)=
—————– = %fn”,itg);
fprintf(out,”
cos(x)+3nn”);
fprintf(out,”Integral
was calculated from %.3f to %.3f with Gauss method;nAccuracy was
equal %fnn”,a,b,h);
}
printf(“You
may check results in ‘Integral.txt file’nDo you want to try
again?(Y/N)n”);
scanf(”
%c”,&P);
}
while(P==’Y’
|| P==’y’);
fclose(out);
}
Приложение
C
Выходной
файл Integral.txt:
x^2+sin(2*x)
Y(x)=
—————– = 17.123938
cos(x)+3
Integral
was calculated from 0.000 to 5.000 with trapetion method;
Step
was equal 0.001000
x^2+sin(2*x)
Y(x)=
—————– = 17.116716
cos(x)+3
Integral
was calculated from 0.000 to 5.000 with Simpson’s method;
Step
was equal 0.001000
x^2+sin(2*x)
Y(x)=
—————– = 17.116722
cos(x)+3
Integral
was calculated from 0.000 to 5.000 with Gauss method;
Accuracy
was equal 0.001000
x^2+sin(2*x)
Y(x)=
—————– = 0.276663
cos(x)+3
Integral
was calculated from 0.000 to 1.000 with trapetion method;
Step
was equal 0.000100
15
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Вычисление определённых интегралов: базовые алгоритмы
Время на прочтение
13 мин
Количество просмотров 82K
В этой публикации описаны простейшие методы вычисления интегралов функций от одной переменной на отрезке, также называемые квадратурными формулами. Обычно эти методы реализованы в стандартных математических библиотеках, таких как GNU Scientific Library для C, SciPy для Python и других. Публикация имеет целью продемонстрировать, как эти методы работают “под капотом”, и обратить внимание на некоторые вопросы точности и производительности алгоритмов. Также хотелось бы отметить связь квадратурных формул и методов численного интегрирования обыкновенных дифференциальных уравнений, о которых хочу написать ещё одну публикацию.
Определение интеграла
Интегралом (по Риману) от функции на отрезке
называется следующий предел:
где — мелкость разбиения,
,
,
— произвольное число на отрезке
.
Если интеграл от функции существует, то значение предела одно и то же вне зависимости от разбиения, лишь бы оно было достаточно мелким.
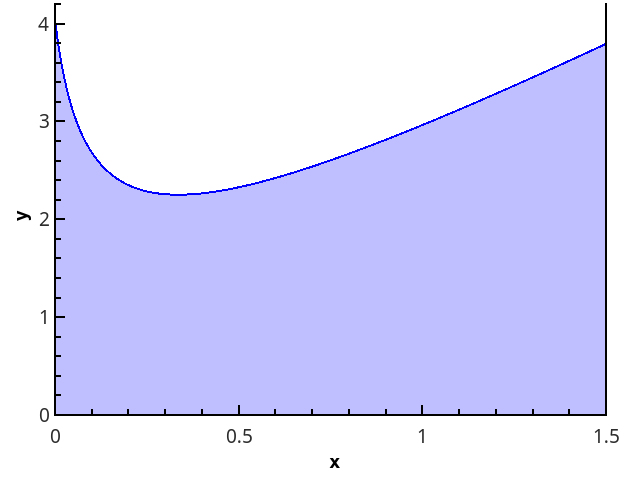
Более наглядно геометрическое определение — интеграл равен площади криволинейной трапеции, ограниченной осью 0x, графиком функции и прямыми x = a и x = b (закрашенная область на рисунке).
Квадратурные формулы
Определение интеграла (1) можно переписать в виде
где — весовые коэффициенты, сумма которых должна быть равна 1, а сами коэффициенты — стремиться к нулю при увеличении числа
точек, в которых вычисляется функция.
Выражение (2) — основа всех квадратурных формул (т.е. формул для приближенного вычисления интеграла). Задача состоит в том, чтобы выбрать точки и веса
таким образом, чтобы сумма в правой части приближала требуемый интеграл как можно точнее.
Вычислительная задача
Задана функция , для которой есть алгоритм вычисления значений в любой точке отрезка
(имеются в виду точки, представимые числом с плавающей точкой — никаких там функций Дирихле!).
Требуется найти приближённое значение интеграла .
Решения будут реализованы на языке Python 3.6.
Для проверки методов используется интеграл .
Кусочно-постоянная аппроксимация
Идейно простейшие квадратурные формулы возникают из применения выражения (1) “в лоб”:
Т.к. от метода разбиения отрезка точками и выбора точек
значение предела не зависит, то выберем их так, чтобы они удобно вычислялись — например, разбиение возьмём равномерным, а для точек вычисления функции рассмотрим варианты: 1)
; 2)
; 3)
.
Получаем методы левых прямоугольников, правых прямоугольников и прямоугольников со средней точкой, соответственно.
Реализация
def _rectangle_rule(func, a, b, nseg, frac):
"""Обобщённое правило прямоугольников."""
dx = 1.0 * (b - a) / nseg
sum = 0.0
xstart = a + frac * dx # 0 <= frac <= 1 задаёт долю смещения точки,
# в которой вычисляется функция,
# от левого края отрезка dx
for i in range(npoints):
sum += func(xstart + i * dx)
return sum * dx
def left_rectangle_rule(func, a, b, nseg):
"""Правило левых прямоугольников"""
return _rectangle_rule(func, a, b, nseg, 0.0)
def right_rectangle_rule(func, a, b, nseg):
"""Правило правых прямоугольников"""
return _rectangle_rule(func, a, b, npoints, 1.0)
def midpoint_rectangle_rule(func, a, b, nseg):
"""Правило прямоугольников со средней точкой"""
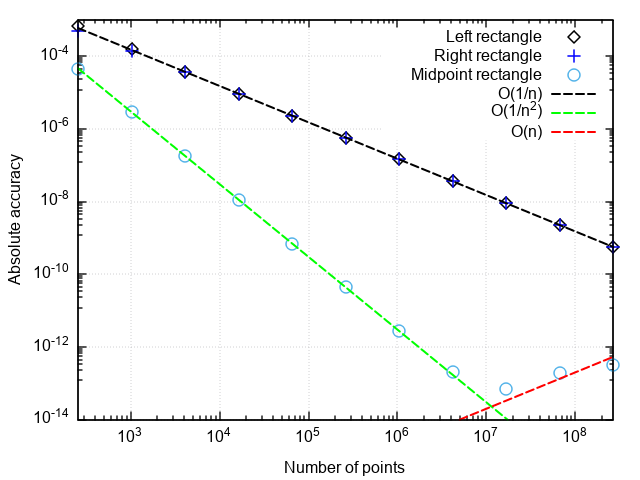
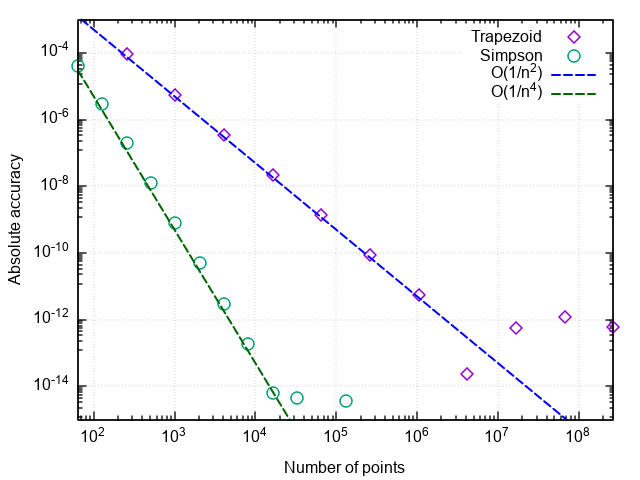
return _rectangle_rule(func, a, b, nseg, 0.5)Для анализа производительности квадратурных формул построим график погрешности в координатах “число точек — отличие численного результата от точного”.
Что можно заметить:
- Формула со средней точкой гораздо точнее, чем с правой или левой точками
- Погрешность формулы со средней точкой падает быстрее, чем у двух остальных
- При очень мелком разбиении погрешность формулы со средней точкой начинает возрастать
Первые два пункта связаны с тем, что формула прямоугольников со средней точкой имеет второй порядок аппроксимации, т.е., а формулы правых и левых прямоугольников — первый порядок, т.е.
.
Возрастание погрешности при измельчении шага интегрирования связано с нарастанием погрешности округления при суммировании большого числа слагаемых. Эта ошибка растёт как, что не даёт при интегрировании достигнуть машинной точности.
Вывод: методы прямоугольников с правой и левой точками имеют низкую точность, которая к тому же медленно растёт с измельчением разбиения. Поэтому они имеют смысл разве что в демонстрационных целях. Метод прямоугольников со средней точкой имеет более высокий порядок аппроксимации, что даёт ему шансы на использование в реальных приложениях (об этом чуть ниже).
Кусочно-линейная аппроксимация
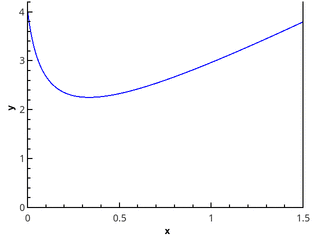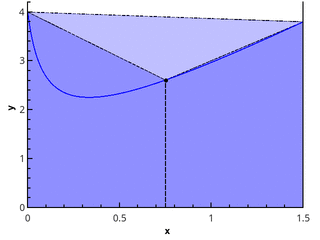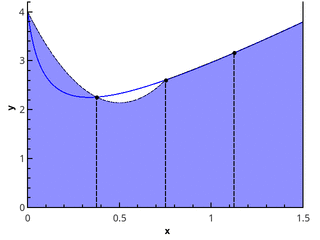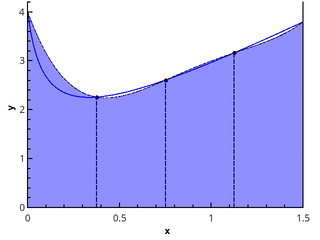
Следующий логический шаг — аппроксимировать интегрируемую функцию на каждом из подотрезков линейной функцией, что даёт квадратурную формулу трапеций:
Иллюстрация метода трапеций для n=1 и n=2.
В случае равномерной сетки длины всех отрезков разбиения равны, и формула имеет вид
Реализация
def trapezoid_rule(func, a, b, nseg):
"""Правило трапеций
nseg - число отрезков, на которые разбивается [a;b]"""
dx = 1.0 * (b - a) / nseg
sum = 0.5 * (func(a) + func(b))
for i in range(1, nseg):
sum += func(a + i * dx)
return sum * dxПостроив график ошибки от числа точек разбиения, убеждаемся, что метод трапеций тоже имеет второй порядок аппроксимации и вообще даёт результаты, слабо отличающиеся от метода прямоугольников со средней точкой (в дальнейшем — просто метод прямоугольников).
Контроль точности вычисления
Задание в качестве входного параметра числа точек разбиения не слишком практично, поскольку обычно требуется вычислить интеграл не с заданной плотностью разбиения, а с заданной погрешностью. Если подынтегральная функция известна наперёд, то можно оценить погрешность заранее и выбрать такой шаг интегрирования, чтобы заданная точность заведомо достигалась. Но так редко бывает на практике (и вообще, не проще ли при известной наперёд функции и сам интеграл протабулировать наперёд?), поэтому необходима процедура автоматической подстройки шага под заданную погрешность.
Как это реализовать? Один из простых методов оценки погрешности — правило Рунге — разность значений интегралов, рассчитанных по n и 2n точкам, даёт оценку погрешности: . Метод трапеций удобнее для удвоения мелкости разбиения, чем метод прямоугольников с центральной точкой. При расчёте методом трапеций для удвоения числа точек нужны новые значения функции только в серединах отрезков предыдущего разбиения, т.е. предыдущее приближение интеграла можно использовать для вычисления следующего.
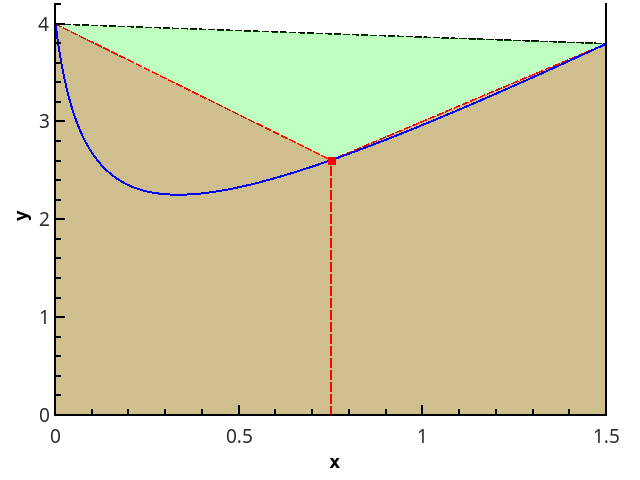
Чем ещё хорош метод прямоугольников
Метод прямоугольников не требует вычислять значения функции на концах отрезка. Это означает, что его можно использовать для функций, имеющих на краях отрезка интегрируемые особенности (например, sinx/x или x-1/2 от 0 до 1). Поэтому показанный далее метод экстраполяции будет работать точно так же и для метода прямоугольников. Отличие от метода трапеций лишь в том, что при уменьшении шага вдвое отбрасывается результат предыдущих вычислений, однако можно утроить число точек, и тогда предыдущее значение интеграла также можно использовать для вычисления нового. Формулы для экстраполяции в этом случае необходимо скорректировать на другое соотношение шагов интегрирования.
Отсюда получаем следующий код для метода трапеций с контролем точности:
def trapezoid_rule(func, a, b, rtol = 1e-8, nseg0 = 1):
"""Правило трапеций
rtol - желаемая относительная точность вычислений
nseg0 - начальное число отрезков разбиения"""
nseg = nseg0
old_ans = 0.0
dx = 1.0 * (b - a) / nseg
ans = 0.5 * (func(a) + func(b))
for i in range(1, nseg):
ans += func(a + i * dx)
ans *= dx
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
ans = 0.5 * (ans + midpoint_rectangle_rule(func, a, b, nseg)) # новые точки для уточнения интеграла
# добавляются ровно в середины предыдущих отрезков
nseg *= 2
err_est = abs(ans - old_ans)
return ansС таким подходом подынтегральная функция не будет вычисляться по нескольку раз в одной точке, и все вычисленные значения используются для окончательного результата.
Но нельзя ли при том же количестве вычислений функции добиться более высокой точности? Оказывается, что можно, есть формулы, работающие точнее метода трапеций на той же самой сетке.
Кусочно-параболическая аппроксимация
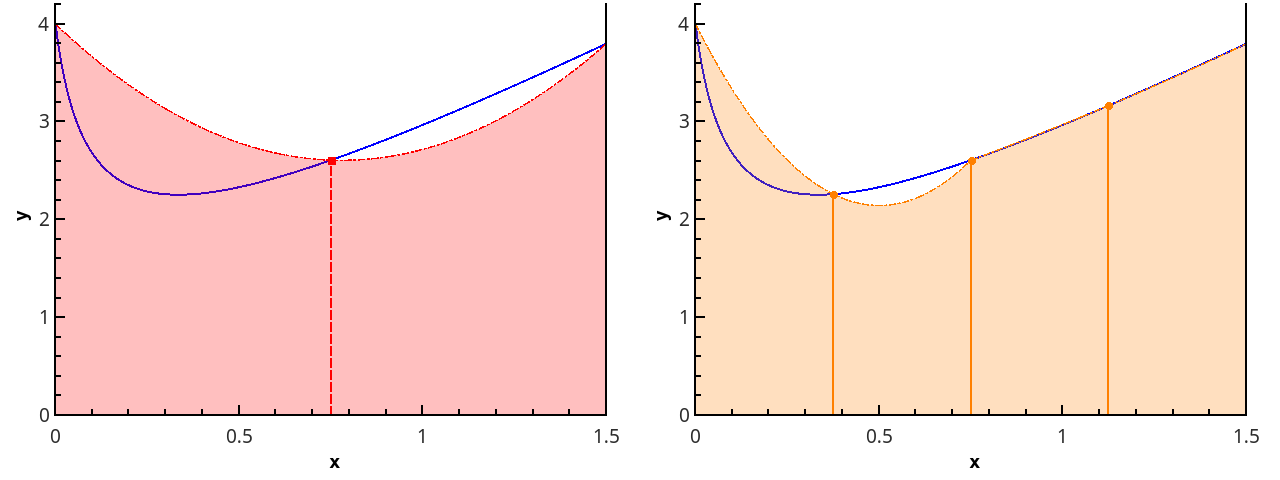
Следующим шагом аппроксимируем функцию элементами парабол. Для этого требуется, чтобы число отрезков разбиения было чётным, тогда параболы могут быть проведены через тройки точек с абсциссами {(x0=a, x1, x2), (x2, x3, x4), …, (xn-2, xn-1, xn=b)}.
Иллюстрация кусочно-параболического приближения на 3 и 5 точках (n=2 и n=3).
Приближая интеграл от функции на каждом из отрезков [xk;xk+2] интегралом от параболической аппроксимации на этом отрезке и считая точки равномерно распределенными (xk+1=xk+h), получаем формулу Симпсона:
Из формулы (4) напрямую получается “наивная” реализация метода Симпсона:
Заголовок спойлера
def simpson_rule(func, a, b, nseg):
"""Правило трапеций
nseg - число отрезков, на которые разбивается [a;b]"""
if nseg%2 = 1:
nseg += 1
dx = 1.0 * (b - a) / nseg
sum = (func(a) + 4 * func(a + dx) + func(b))
for i in range(1, nseg / 2):
sum += 2 * func(a + (2 * i) * dx) + 4 * func(a + (2 * i + 1) * dx)
return sum * dx / 3Для оценки погрешности можно использовать точно так же вычисление интеграла с шагами h и h/2 — но вот незадача, при вычислении интеграла с более мелким шагом результат предыдущего вычисления придётся отбросить, хотя половина новых вычислений функции будет в тех же точках, что и раньше.
Бесполезной траты машинного времени, к счастью, можно избежать, если реализовать метод Симпсона более хитроумным образом. Присмотревшись повнимательнее, заметим, что интеграл по формуле Симпсона может быть представлен через два интеграла по формуле трапеций с разными шагами. Яснее всего это видно на базовом случае аппроксимации интеграла по трём точкам :
Таким образом, если реализовать процедуру уменьшения шага вдвое и хранить два последних вычисления методом трапеций, метод Симпсона с контролем точности реализуется более эффективно.
Как-то так…
class Quadrature:
"""Базовые определения для квадратурных формул"""
__sum = 0.0
__nseg = 1 # число отрезков разбиения
__ncalls = 0 # считает число вызовов интегрируемой функции
def __restart(func, x0, x1, nseg0, reset_calls = True):
"""Обнуление всех счётчиков и аккумуляторов.
Возвращает интеграл методом трапеций на начальном разбиении"""
if reset_calls:
Quadrature.__ncalls = 0
Quadrature.__nseg = nseg0
# вычисление суммы для метода трапеций с начальным числом отрезков разбиения nseg0
Quadrature.__sum = 0.5 * (func(x0) + func(x1))
dx = 1.0 * (x1 - x0) / nseg0
for i in range(1, nseg0):
Quadrature.__sum += func(x0 + i * dx)
Quadrature.__ncalls += 1 + nseg0
return Quadrature.__sum * dx
def __double_nseg(func, x0, x1):
"""Вдвое измельчает разбиение.
Возвращает интеграл методом трапеций на новом разбиении"""
nseg = Quadrature.__nseg
dx = (x1 - x0) / nseg
x = x0 + 0.5 * dx
i = 0
AddedSum = 0.0
for i in range(nseg):
AddedSum += func(x + i * dx)
Quadrature.__sum += AddedSum
Quadrature.__nseg *= 2
Quadrature.__ncalls += nseg
return Quadrature.__sum * 0.5 * dx
def trapezoid(func, x0, x1, rtol = 1e-10, nseg0 = 1):
"""Интегрирование методом трапеций с заданной точностью.
rtol - относительная точность,
nseg0 - число отрезков начального разбиения"""
ans = Quadrature.__restart(func, x0, x1, nseg0)
old_ans = 0.0
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
ans = Quadrature.__double_nseg(func, x0, x1)
err_est = abs(old_ans - ans)
print("Total function calls: " + str(Quadrature.__ncalls))
return ans
def simpson(func, x0, x1, rtol = 1.0e-10, nseg0 = 1):
"""Интегрирование методом парабол с заданной точностью.
rtol - относительная точность,
nseg0 - число отрезков начального разбиения"""
old_trapez_sum = Quadrature.__restart(func, x0, x1, nseg0)
new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
ans = (4 * new_trapez_sum - old_trapez_sum) / 3
old_ans = 0.0
err_est = max(1, abs(ans))
while (err_est > abs(rtol * ans)):
old_ans = ans
old_trapez_sum = new_trapez_sum
new_trapez_sum = Quadrature.__double_nseg(func, x0, x1)
ans = (4 * new_trapez_sum - old_trapez_sum) / 3
err_est = abs(old_ans - ans)
print("Total function calls: " + str(Quadrature.__ncalls))
return ansСравним эффективность метода трапеций и парабол:
>>> import math
>>> Quadrature.trapezoid(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 65537
4.250000001385811
>>> Quadrature.simpson(lambda x: 2 * x + 1 / math.sqrt(x + 1 / 16), 0, 1.5, rtol=1e-9)
Total function calls: 2049
4.2500000000490985Как видим, обоими методами ответ можно получть с достаточно высокой точностью, но количество вызовов подынтегральной функции разительно отличается — метод более высокого порядка эффективнее в 32 раза!
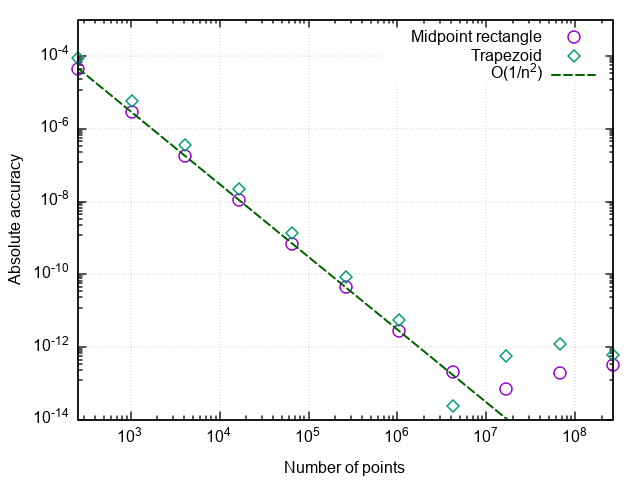
Построив график погрешности интегрирования от числа шагов, можно убедиться, что порядок аппроксимации формулы Симпсона равен четырём, т.е. ошибка численного интегрирования (а интегралы от кубических многочленов с помощью этой формулы вычисляются с точностью до ошибок округления при любом чётном n>0!).
Отсюда и возникает такой рост эффективности по сравнению с простой формулой трапеций.
Что дальше?
Дальнейшая логика повышения точности квадратурных формул, в целом, понятна — если функцию продолжать приближать многочленами всё более высокой степени, то и интеграл от этих многочленов будет всё точнее приближать интеграл от исходной функции. Этот подход называется построением квадратурных формул Ньютона-Котеса. Известны формулы вплоть до 8 порядка аппроксимации, но выше среди весовых коэффициентов wi в (2) появляются знакопеременные члены, и формулы при вычислениях теряют устойчивость.
Попробуем пойти другим путём. Ошибка квадратурной формулы представляется в виде ряда по степеням шага интегрирования h. Замечательное свойство метода трапеций (и прямоугольников со средней точкой!) в том, что для неё этот ряд состоит только из чётных степеней:
На нахождении последовательных приближений к этому разложению основана экстраполяция Ричардсона: вместо того, чтобы приближать подынтегральную функцию многочленом, по рассчитанным приближениям интеграла строится полиномиальная аппроксимация, которая при h=0 должна давать наилучшее приближение к истинному значению интеграла.
Разложение ошибки интегрирования по чётным степеням шага разбиения резко ускоряет сходимость экстраполяции, т.к. для аппроксимации порядка 2n нужно всего n значений интеграла методом трапеций.
Если считать, что каждое последующее слагаемое меньше предыдущего, то можно последовательно исключать степени h, имея приближения интеграла, рассчитанные с разными шагами. Поскольку приведённая реализация легко позволяет дробить разбиение вдвое, удобно рассматривать формулы для шагов h и h/2.
Легко показать, что исключение старшего члена погрешности формулы трапеций в точности даст формулу Симпсона:
Повторяя аналогичную процедуру для формулы Симпсона, получаем:
Если продолжить, вырисовывается такая таблица:
| 2 порядок | 4 порядок | 6 порядок | … |
|---|---|---|---|
| I0,0 | |||
| I1,0 | I1,1 | ||
| I2,0 | I2,1 | I2,2 | |
| … | … | … |
В первом столбце стоят интегралы, вычисленные методом трапеций. При переходе от верхней строки вниз разбиение отрезка становится вдвое мельче, а при переходе от левого столбца вправо повышается порядок аппроксимации интеграла (т.е. во втором столбце находятся интегралы по методу Симпсона и т.д.).
Элементы таблицы, как можно вывести из разложения (5), связаны рекуррентным соотношением:
Погрешность приближения интеграла можно оценить по разности формул разных порядков в одной строке, т.е.
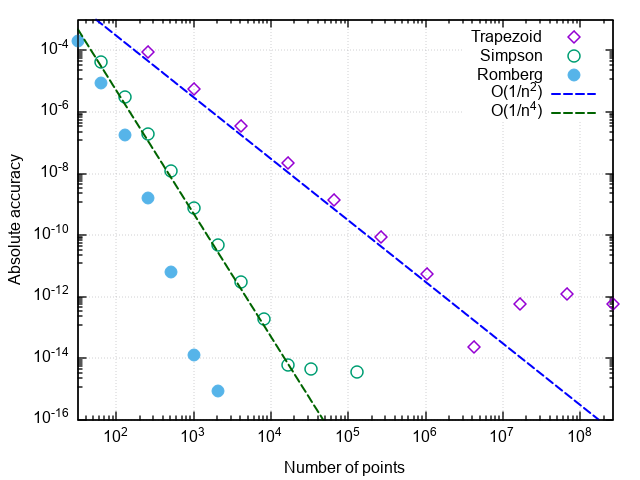
Применение экстраполяции Ричардсона вместе с интегрированием методом трапеций называется методом Ромберга. Если метод Симпсона учитывает два предыдущих значения по методу трапеций, то метод Ромберга использует все ранее вычисленные методом трапеций значения для получения более точной оценки интеграла.
Реализация
Дополнительный метод добавляется в класс Quadrature
class Quadrature:
"""Базовые определения для квадратурных формул"""
__sum = 0.0
__nseg = 1 # число отрезков разбиения
__ncalls = 0 # считает число вызовов интегрируемой функции
def __restart(func, x0, x1, nseg0, reset_calls = True):
"""Обнуление всех счётчиков и аккумуляторов.
Возвращает интеграл методом трапеций на начальном разбиении"""
if reset_calls:
Quadrature.__ncalls = 0
Quadrature.__nseg = nseg0
# вычисление суммы для метода трапеций с начальным разбиением на nseg0 отрезков
Quadrature.__sum = 0.5 * (func(x0) + func(x1))
dx = 1.0 * (x1 - x0) / nseg0
for i in range(1, nseg0):
Quadrature.__sum += func(x0 + i * dx)
Quadrature.__ncalls += 1 + nseg0
return Quadrature.__sum * dx
def __double_nseg(func, x0, x1):
"""Вдвое измельчает разбиение.
Возвращает интеграл методом трапеций на новом разбиении"""
nseg = Quadrature.__nseg
dx = (x1 - x0) / nseg
x = x0 + 0.5 * dx
i = 0
AddedSum = 0.0
for i in range(nseg):
AddedSum += func(x + i * dx)
Quadrature.__sum += AddedSum
Quadrature.__nseg *= 2
Quadrature.__ncalls += nseg
return Quadrature.__sum * 0.5 * dx
def romberg(func, x0, x1, rtol = 1e-10, nseg0 = 1, maxcol = 5, reset_calls = True):
"""Интегрирование методом Ромберга
nseg0 - начальное число отрезков разбиения
maxcol - максимальный столбец таблицы"""
# инициализация таблицы
Itable = [[Quadrature.__restart(func, x0, x1, nseg0, reset_calls)]]
i = 0
maxcol = max(0, maxcol)
ans = Itable[i][i]
error_est = max(1, abs(ans))
while (error_est > abs(rtol * ans)):
old_ans = ans
i += 1
d = 4.0
ans_col = min(i, maxcol)
Itable.append([Quadrature.__double_nseg(func, x0, x1)] * (ans_col + 1))
for j in range(0, ans_col):
diff = Itable[i][j] - Itable[i - 1][j]
Itable[i][j + 1] = Itable[i][j] + diff / (d - 1.0)
d *= 4.0
ans = Itable[i][ans_col]
if (maxcol <= 1): # методы трапеций и парабол обрабатываются отдельно
error_est = abs(ans - Itable[i - 1][-1])
elif (i > maxcol):
error_est = abs(ans - Itable[i][min(i - maxcol - 1, maxcol - 1)])
else:
error_est = abs(ans - Itable[i - 1][i - 1])
print("Total function calls: " + str(Quadrature.__ncalls))
return ansПроверим, как работает аппроксимация высокого порядка:
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 0) # трапеции
Total function calls: 65537
4.250000001385811
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 1) # параболы
Total function calls: 2049
4.2500000000490985
>>> Quadrature.romberg(lambda x: 2 * x + 1 / math.sqrt(x + 1/16), 0, 1.5, rtol=1e-9, maxcol = 4)
Total function calls: 257
4.250000001644076Убеждаемся, что, по сравнению с методом парабол, число вызовов подынтегральной функции снизилось ещё в 8 раз. При дальнейшем увеличении требуемой точности преимущества метода Ромберга проявляются ещё заметнее:
Некоторые замечания
Замечание 1. Количество вызовов функции в этих задачах характеризует число суммирований при вычислении интеграла. Уменьшение числа вычислений подынтегрального выражения не только экономит вычислительные ресурсы (хотя при более оптимизированной реализации и это тоже), но и уменьшает влияние погрешностей округления на результат. Так, при попытке вычислить интеграл тестовой функции метод трапеций зависает при попытке достигнуть относительной точности 5×10-15, метод парабол — при желаемой точности 2×10-16(что является пределом для чисел в двойной точности), а метод Ромберга справляется с вычислением тестового интеграла вплоть до машинной точности (с ошибкой в младшем бите). То есть, повышается не только точность интегрирования при заданном числе вызовов функции, но и предельно достижимая точность вычисления интеграла.
Замечание 2. Если метод сходится при задании некоторой точности, это не означает, что вычисленное значение интеграла имеет ту же самую точность. В первую очередь, это относится к случаям, когда задаваемая погрешность близка к машинной точности.
Замечание 3. Хотя метод Ромберга для ряда функций работает почти магическим образом, он предполагает наличие у подынтегральной функции ограниченных производных высоких порядков. Это значит, что для функций с изломами или разрывами он может оказаться хуже простых методов. Например, проинтегрируем f(x)=|x|:
>>> Quadrature.trapezoid(abs, -1, 3, rtol=1e-5)
Total function calls: 9
5.0
>>> Quadrature.simpson(abs, -1, 3, rtol=1e-5)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 2)
Total function calls: 17
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 3)
Total function calls: 33
5.0
>>> Quadrature.romberg(abs, -1, 3, rtol=1e-5, maxcol = 4)
Total function calls: 33
5.000001383269357Замечание 4. Может показаться, что чем выше порядок аппроксимации, тем лучше. На самом деле, лучше ограничить число столбцов таблицы Ромберга на уровне 4-6. Чтобы понять это, посмотрим на формулу (6). Второе слагаемое представляет собой разность двух последовательных элементов j-1-го столбца, поделенную на примерно 4j. Т.к. в j-1-м столбце находятся аппроксимации интеграла порядка 2j, то сама разность имеет порядок (1/ni)2j ~ 4–ij. C учётом деления получается ~4-(i+1)j ~ 4–j2. Т.е. при j~7 второе слагаемое в (6) теряет точность после приведения порядков при сложении чисел с плавающей точкой, и повышение порядка аппроксимации может вести к накоплению ошибки округления.
Замечание 5. Желающие могут ради интереса применить описанные методы для нахождения интеграла и эквивалентного ему
. Как говорится, почувствуйте разницу.
Заключение
Представлено описание и реализация базовых методов численного интегрирования функций на равномерной сетке. Продемонстрировано, как с помощью несложной модификации получить на базе метода трапеций класс квадратурных формул по методу Ромберга, что значительно ускоряет сходимость численного интегрирования. Метод хорошо работает для интегрирования “обычных” функций, т.е. слабо меняющихся на отрезке интегрирования, не имеющих особенностей на краях отрезка (см. Замечание 5), быстрых осцилляций и т.д.
Продвинутые методы численного интегрирования для более сложных случаев можно найти в книгах из списка литературы (в [3] — с примерами реализации на C++).
Литература
- А.А. Самарский, А.В. Гулин. Численные методы. М.: Наука. 1989.
- J. Stoer, R. Bulirsch. Introduction to Numerical Analysis: Second Edition. Springer-Verlag New York. 1993.
- W.H. Press, S.A. Teukolsky, W.T. Vetterling, B.P. Flannery. Numerical Recipes: Third Edition. Cambridge University Press. 2007.


![E(f)=-{frac {(b-a)^{5}}{2880}}{{f^{{(4)}}(zeta )}}, zeta in [a,b].](https://wikimedia.org/api/rest_v1/media/math/render/svg/f433d5ee51bf8430229b9d4b9461ee9f457929dc)
![left|E(f)right|leqslant {frac {(b-a)^{5}}{2880}}max limits _{{xin [a,b]}}{left|f^{{(4)}}(x)right|}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/0286f6a0dbc988cdd1a83b0303ac005d3e490372)

![{displaystyle int _{a}^{b}f(x),dxapprox {frac {h}{3}}left[f(x_{0})+2sum _{j=1}^{N/2-1}f(x_{2j})+4sum _{j=1}^{N/2}f(x_{2j-1})+f(x_{N})right],}](https://wikimedia.org/api/rest_v1/media/math/render/svg/9d56e22c1c27c88d58eec2e54929f524d69aa1f5)


![{displaystyle [x_{j-1},x_{j+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/662ade106e57ea7bf0999c9600edb80f2d5e9fa9)
![{displaystyle [x_{j-1},x_{j}],[x_{j},x_{j+1}]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/b1999f53bbec26a0bdd09d31943eb43fb13bd5d3)


![int _{a}^{b}f(x),dxapprox {frac {h}{3}}{bigg [}f(x_{0})+4f(x_{1})+2f(x_{2})+4f(x_{3})+2f(x_{4})+cdots +4f(x_{{N-1}})+f(x_{N}){bigg ]}.](https://wikimedia.org/api/rest_v1/media/math/render/svg/66c8c4e7dbfcaf9b3045745b4fd7b9240f1cae71)
![{int limits _{a}^{b}f(x)dx}approx {frac {h}{3}}cdot sum _{{k=1,2}}^{{N-1}}left[f(x_{{k-1}})+4f(x_{k})+f(x_{{k+1}})right]](https://wikimedia.org/api/rest_v1/media/math/render/svg/e7f315f4a998aa231b1a8873ac449772d1907ca1)

![left|E(f)right|leqslant {frac {(b-a)}{2880}}h^{4}max limits _{{xin [a,b]}}|f^{{(4)}}(x)|](https://wikimedia.org/api/rest_v1/media/math/render/svg/ec21769097e7f35df4c82f8eecbb44142061301e)
![left|E(f)right|leqslant {frac {(b-a)}{288}}h^{3}max limits _{{xin [a,b]}}|f^{{(3)}}(x)|](https://wikimedia.org/api/rest_v1/media/math/render/svg/7d8a735a238d91d8943f1686a97dd9ce08a72663)
![{displaystyle int _{a}^{b}f(x),dxapprox {tfrac {h}{24}}left[-f(x_{-1})+12f(x_{0})+25f(x_{1})+24sum _{i=2}^{n-2}f(x_{i})+25f(x_{n-1})+12f(x_{n})-f(x_{n+1})right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/5fc5347b4c60f196ec77e48ad2daaab1bc90c8fc)
![{displaystyle int _{a}^{b}f(x),dxapprox {tfrac {h}{24}}left[9f(x_{0})+28f(x_{1})+23f(x_{2})+24sum _{i=3}^{n-3}f(x_{i})+23f(x_{n-2})+28f(x_{n-1})+9f(x_{n})right]}](https://wikimedia.org/api/rest_v1/media/math/render/svg/d134f5a6cae73f7e38d5ffe1900ebb728c0d4ed8)