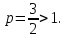-
Свойства определённого интеграла
Монотонность
интеграла.Если


то
Действительно,
в этом случае


в анализ»), получаем искомое соотношение
между интегралами.
Как следующее
свойство отметим одно простое равенство,
вытекающее из определения определенного
интеграла:
Оценка
интеграла.Если


то
Действительно,

монотонность интеграла, его линейность
и равенство (1). Аналогично доказывается
первое из неравенств в (2).
Например,
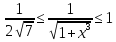

что следует из монотонности функции

Теорема о среднем. Если функция
то найдётся точка
что
Величина



Доказательство.
По теореме Вейерштрасса, функция

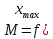
и наименьшего значения
Здесь

Применяя оценку интеграла (2), выводим
Интегральное
среднее оказывается промежуточным
значением между наименьшим и наибольшим
значениями. Применим теорему Больцано-Коши
о промежуточном значении к непрерывной
функции


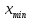


такую, что
Пример.
Пусть
Тогда
интегральное среднее функции (4) на
отрезке

Однако
точки

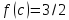

-
Формула Ньютона-Лейбница
Интеграл
вида
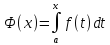
верхним пределом.
Теорема.
Пусть

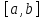
Тогда
есть первообразная функции

для любого

Доказательство.
Пусть
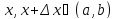
Тогда по теореме о среднем
для некоторой
точки
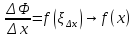

ибо в этом случае
а функция
Формула
Ньютона-Лейбница. Пусть


Тогда
Доказательство.
Для функции



1 )найдется константа
Подставим
в соотношение (3) вместо

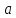

а затем подставим
что и
требовалось доказать.
Пример.

-
Замена переменной и интегрирование по частям в определённом интеграле
Замена
переменной. Пусть

а
отрезке
Тогда
Доказательство.
Пусть


Тогда по формуле замена переменной в
неопределенном интеграле функция

Применим формулу Ньютона-Лейбница
дважды:
— что и
требовалось доказать. □
Пример
1.Вычислим площадь верхнего полукруга
радиусаR.
Интегрирование по частям. Пусть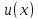


Тогда
Доказательство.
Соотношение
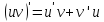



Пример
2.Вычислим
Заметим,
что

-
Несобственные интегралы
Пусть
функция


где
а величина

Предположим, что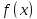


Полагаем по определению
и называем
это число несобственным интегралом.
В случае, когда предел (1) существует, то
говорим, что соответствующий интеграл
сходится; в противном случае будем
говорить, что онрасходится.
Несобственный
интеграл (1) применяется в двух типичных
ситуациях.
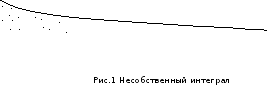
1) Пусть

2) Пусть d∈ℝи функция

Если

то несобственный интеграл равен площади
неограниченной фигуры — криволинейной
трапеции, ограниченной сверху графиком
функции
снизу – осью Ох и слева – вертикальной
прямой
(см. рис. 1)
Отметим,
что если функция


— несобственный интеграл в смысле (1)
будет равен определенному интегралу
функции

Аналогично
определяется несобственный интеграл
для функций, определенных на полуинтервале
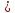
где

В примере
§8 мы фактически
вычислили несобственный интеграл
Формула
Ньютона-Лейбница для несобственных
интегралов. Пусть

существуют пределы
Тогда
несобственный интеграл

Равенство
(5) вытекает из формулы Ньютона-Лейбница
для обычных интегралов и соотношений
(4).
Пример.
Вычислим
Предложение
об “эталонных” интегралах . Пусть
a>0.
-
Интеграл
сходится тогда и только тогда, когда
p>1. -
Интеграл
сходится тогда и только тогда, когдаp<1.
Доказательство.
1. Если
то первообразная


По формуле Ньютона-Лейбница для
несобственных интегралов, получаем,
что интеграл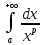
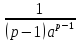
Если

то первообразной подинтегральной
функции служит

Для

Аналогично,
прямыми вычислениями доказывает второе
утверждение.
Примеры
1. Интеграл
так как здесь
2. Докажем,
что интегралы


Интеграл

дифференциала

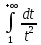
который сходится согласно предложению
об эталонных интегралах и равен 1.
Интегралы


приводит их к несобственным эталонным
интегралам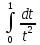

с
Соседние файлы в папке ЛЕКЦИИ2
- #
- #
- #
- #
- #
- #
- #
|
|
Макеты страниц
а. Одна общая оценка интеграла.
Начнем с одной общей оценки интеграла, которая, как потом выяснится, справедлива не только для интегралов от действительнозначных функций.
Теорема 3. Если а 


Если при этом 


При 



Переходя к пределу при 

b. Монотонность интеграла и первая теорема о среднем.
Все дальнейшее специфично для интегралов от действительнозначных функций.
Теорема 4. Если а 


При 


справедливое, поскольку 

Теорему 4 можно трактовать как утверждение о монотонности зависимости интеграла от подынтегральной функции.
Из теоремы 4 получается ряд полезных следствий.
Следствие 1. Если а 


и, в частности, если 

Соотношение (12) получается, если проинтегрировать каждый член неравенств 
Следствие 


Если 






Следствие 3. Если 


По теореме о промежуточном значении для непрерывной функции, на отрезке 



Таким образом, (14) следует из (13).
Равенство (14) часто называют первой теоремой о среднем для интеграла. Мы же зарезервируем это название для следующего, несколько более общего утверждения.
Теорема 5 (первая теорема о среднем для интеграла). Пусть 



где 
Если, кроме того, известно, что 


Поскольку перестановка пределов интегрирования приводит к изменению знака одновременно в обеих частях равенства (15), то достаточно проверить это равенство в случае 



Поскольку 


Поскольку 

Бели 
Если же 

из (17) находим, что

но это равносильно соотношению (15).
Равенство (16) теперь следует из (15) и теоремы о промежуточном значении для функции 


Заметим, что равенство (13) получается из (15), если 

с. Вторая теорема о среднем для интеграла. Значительно более специальной и деликатной в рамках теории интеграла Римана является так называемая вторая теорема о среднем.
Чтобы не осложнять доказательство этой теоремы, сделаем несколько полезных заготовок, представляющих и самостоятельный интерес.
Преобразование Абеля. Так называется следующее преобразование суммы 




Итак,

или, поскольку 

На основе преобразования Абеля легко проверяется следующая
Лемма 2. Если числа 





Используя то, что 


Аналогично проверяется и левое неравенство в соотношении (20).
Лемма 3. Если 


Существование интеграла (21) при любом 






Мы воспользовались неравенством (10) с учетом того, что при 

Итак, мы показали, что если 

откуда, очевидно, следует непрерывность функции 

Теперь докажем лемму, которая уже является вариантом второй теоремы о среднем.
Лемма 4. Если 



Прежде чем переходить к доказательству, отметим, что, в отличие от соотношения (16) первой теоремы о среднем, в (23) под знаком интеграла осталась функция 

Для доказательства формулы (23), как и в уже рассмотренных выше случаях, постараемся оценить соответствующую интегральную сумму.
Пусть Р — разбиение отрезка 

и покажем, что при 
Поскольку 



при 


Оценим теперь сумму, стоящую в правой части равенства (24). Положив

по лемме 3 получаем функцию, непрерывную на отрезке 
Пусть

Поскольку 

Учитывая неотрицательность и невозрастание функции 


по лемме 2 находим, что

поскольку

Мы показали, что суммы (25) удовлетворяют неравенствам (26). Вспоминая соотношение (24), теперь имеем

Если 
Если же 

Из (27) следует, что 




Теорема 6 (вторая теорема о среднем для интеграла). Если 



Равенство (28) (как, впрочем, и равенство 
Пусть 




Но

Учитывая эти соотношения и свойство аддитивности интеграла, из (29) получаем доказываемое равенство (28).
Бели 



Задачи и упражнения
(см. скан)
(см. скан)
Оглавление
- ПРЕДИСЛОВИЕ КО ВТОРОМУ ИЗДАНИЮ
- ИЗ ПРЕДИСЛОВИЯ К ПЕРВОМУ ИЗДАНИЮ
- ГЛАВА I. НЕКОТОРЫЕ ОБЩЕМАТЕМАТИЧЕСКИЕ ПОНЯТИЯ И ОБОЗНАЧЕНИЯ
- § 1. Логическая символика
- § 2. Множество и элементарные операции над множествами
- 2. Отношение включения.
- 3. Простейшие операции над множествами.
- Упражнения
- § 3. Функция
- 2. Простейшая классификация отображений.
- 3. Композиция функций и взаимно обратные отображения.
- 4. Функция как отношение. График функции.
- § 4. Некоторые дополнения
- 2. Об аксиоматике теории множеств.
- 3. Замечания о структуре математических высказываний и записи их на языке теории множеств.
- Упражнения
- ГЛАВА II. ДЕЙСТВИТЕЛЬНЫЕ (ВЕЩЕСТВЕННЫЕ) ЧИСЛА
- § 1. Аксиоматика и некоторые общие свойства множества действительных чисел
- 2. Некоторые общие алгебраические свойства действительных чисел.
- 3. Аксиома полноты и существование верхней (нижней) грани числового множества
- § 2. Важнейшие классы действительных чисел и вычислительные аспекты операций с действительными числами
- 2. Рациональные и иррациональные числа
- 3. Принцип Архимеда.
- 4. Геометрическая интерпретация множества действительных чисел и вычислительные аспекты операций с действительными числами
- Задачи и упражнения
- § 3. Основные леммы, связанные с полнотой множества действительных чисел
- 2. Лемма о конечном покрытии (принцип Бореля — Лебега)
- 3. Лемма о предельной точке (принцип Больцано—Вейерштрасса).
- Задачи и упражнения
- § 4. Счетные и несчетные множества
- 2. Мощность континуума
- Задачи и упражнения
- ГЛАВА III. ПРЕДЕЛ
- 2. Свойства предела последовательности
- 3. Вопросы существования предела последовательности
- 4. Начальные сведения о рядах
- § 2. Предел функции
- 2. Свойства предела функции.
- 3. Общее определение предела функции (предел по базе).
- 4. Вопросы существования предела функции
- ГЛАВА IV. НЕПРЕРЫВНЫЕ ФУНКЦИИ
- 2. Точки разрыва.
- § 2. Свойства непрерывных функций
- 2. Глобальные свойства непрерывных функций.
- ГЛАВА V. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ
- 2. Функция, дифференцируемая в точке.
- 3. Касательная; геометрический смысл производной и дифференциала.
- 4. Роль системы координат.
- 5. Некоторые примеры
- Задачи и упражнения
- § 2. Основные правила дифференцирования
- 2. Дифференцирование композиции функций
- 3. Дифференцирование обратной функции
- 4. Таблица производных основных элементарных функций.
- 5. Дифференцирование простейшей неявно заданной функции.
- 6. Производные высших порядков.
- § 3. Основные теоремы дифференциального исчисления
- 2. Теоремы Лагранжа и Коши о конечном приращении.
- 3. Формула Тейлора.
- § 4. Исследование функций методами дифференциального исчисления
- 2. Условия внутреннего экстремума функции.
- 3. Условия выпуклости функции
- 4. Правило Лопиталя.
- 5. Построение графика функции.
- § 5. Комплексные числа и взаимосвязь элементарных функций
- 2. Сходимость в С и ряды с комплексными членами.
- 3. Формула Эйлера и взаимосвязь элементарных функций.
- 4. Представление функции степенным рядом, аналитичность.
- 5. Алгебраическая замкнутость поля С комплексных чисел.
- § 6. Некоторые примеры использования дифференциального исчисления в задачах естествознания
- 2. Барометрическая формула.
- 3. Радиоактивный распад, цепная реакция и атомный котел.
- 4. Падение тел в атмосфере.
- 5. Еще раз о числе e и функции exp(x).
- 6. Колебания.
- § 7. Первообразная
- 2. Основные общие приемы отыскания первообразной.
- 3. Первообразные рациональных функций.
- 4. Первообразные вида …
- 5. Первообразные вида …
- ГЛАВА VI. ИНТЕГРАЛ
- § 1. Определение интеграла и описание множества интегрируемых функций
- 2. Определение интеграла Римана
- 3. Множество интегрируемых функций.
- § 2. Линейность, аддитивность и монотонность интеграла
- 2. Интеграл как аддитивная функция отрезка интегрирования.
- 3. Оценка интеграла, монотонность интеграла, теоремы о среднем
- § 3. Интеграл и производная
- 2. Формула Ньютона—Лейбница
- 3. Интегрирование по частям в определенном интеграле и формула Тейлора
- 4. Замена переменной в интеграле.
- 5. Некоторые примеры.
- § 4. Некоторые приложения интеграла
- 2. Длина пути.
- 3. Площадь криволинейной трапеции.
- 4. Объем тела вращения.
- 5. Работа и энергия.
- § 5. Несобственный интеграл
- 2. Исследование сходимости несобственного интеграла
- 3. Несобственные интегралы с несколькими особенностями.
- ГЛАВА VII. ФУНКЦИИ МНОГИХ ПЕРЕМЕННЫХ, ИХ ПРЕДЕЛ И НЕПРЕРЫВНОСТЬ
- 2. Открытые и замкнутые множества в R^m
- 3. Компакты в R^m
- § 2. Предел и непрерывность функции многих переменных
- 2. Непрерывность функции многих переменных и свойства непрерывных функций.
- ГЛАВА VIII. ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИЙ МНОГИХ ПЕРЕМЕННЫХ
- 2. Линейные отображения L : R^m -> R^n.
- 3. Норма в R^m.
- 4. Евклидова структура в R^m.
- § 2. Дифференциал функции многих переменных
- 2. Дифференциал и частные производные вещественнозначной функции.
- 3. Координатное представление дифференциала отображения. Матрица Якоби.
- 4. Непрерывность, частные производные и дифференцируемость функции в точке.
- § 3. Основные законы дифференцирования
- 2. Дифференцирование композиции отображений
- 3. Дифференцирование обратного отображения
- § 4. Основные факты дифференциального исчисления вещественнозначных функций многих переменных
- 2. Достаточное условие дифференцируемости функции многих переменных
- 4. Формула Тейлора
- 5. Экстремумы функций многих переменных.
- 6. Некоторые геометрические образы, связанные с функциями многих переменных
- § 5. Теорема о неявной функции
- 2. Простейший вариант теоремы о неявной функции.
- 3. Переход к случаю зависимости
- 4. Теорема о неявной функции.
- § 6. Некоторые следствия теоремы о неявной функции
- 2. Локальное приведение гладкого отображения к каноническому виду.
- 3. Зависимость функций
- 4. Локальное разложение диффеоморфизма в композицию простейших.
- 5. Лемма Морса.
- § 7. Поверхность в R^n и теория условного экстремума
- 2. Касательное пространство.
- 3. Условный экстремум
- НЕКОТОРЫЕ ЗАДАЧИ КОЛЛОКВИУМОВ
- ВОПРОСЫ К ЭКЗАМЕНУ
- ЛИТЕРАТУРА
Требуемые условия завершения
Предыдущая
Следующая
15. Монотонность определенного интеграла
Предыдущая
Следующая
◄ Итоговые схемы
Перейти на…
Вычисление определенных интегралов ►










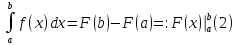




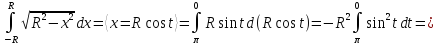


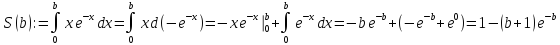

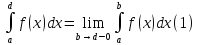




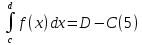

 сходится тогда и только тогда, когда
сходится тогда и только тогда, когда сходится тогда и только тогда, когдаp<1.
сходится тогда и только тогда, когдаp<1.