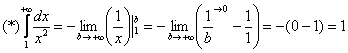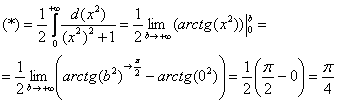Как найти интеграл от 0 до бесконечности - Сайт, где вы сможете решить свои вопросы

К
изучению несобственных интегралов
лучше приступать в последнюю очередь
в ходе изучения интегрального исчисления
функции одной переменной. Читатель
данного урока должен быть хорошо подкован
в неопределенных
интегралах, определенных
интегралах,
уметь находить площадь
плоской фигуры с помощью определенного
интеграла.
Кроме того, потребуются знания
простейших пределов и графиков
элементарных функций.
По логике изложения материала эта статья
является продолжением урока
Определенный
интеграл. Как вычислить площадь фигуры.
Тема несобственных интегралов – очень
хорошая иллюстрация тому, как важно не
запускать высшую математику и другие
точные науки.

Образно говоря,
несобственный интеграл – это «продвинутый»
определенный интеграл, к тому же у
несобственного интеграла есть очень
хороший геометрический смысл.

Что
значит вычислить несобственный интеграл?

Вычислить
несобственный интеграл – это значит,
найти ЧИСЛО (точно
так же, как в определенном интеграле),
или доказать, что
он расходится (то
есть, получить в итоге бесконечность
вместо числа).

Несобственные
интегралы бывают двух видов: первого и
второго рода.

5.3.1. Несобственный интеграл с бесконечным пределом (ами) интегрирования

Иногда
такой несобственный интеграл еще
называют несобственным
интегралом первого рода.
В общем виде несобственный интеграл с
бесконечным пределом чаще всего выглядит
так:

В чем его отличие
от определенного интеграла? В верхнем
пределе.

Он
бесконечный:

Встречаются
интегралы и с бесконечным нижним пределом

или с двумя
бесконечными пределами:

Мы
рассмотрим самый популярный случай

.
Техника работы с другими разновидностями
– аналогична.

Всегда
ли существует несобственный интеграл

Нет,
не всегда.

Подынтегральная
функция

должна быть непрерывной на интервале

.
Строго
говоря, последнее утверждение неверно:
если есть разрывы функции, то в ряде
случаев можно разбить интервал на
несколько частей и вычислить несколько
несобственных интегралов.

Изобразим
на чертеже график подынтегральной
функции

.
Типовой график и криволинейная трапеция
для данного случая выглядит так:

Здесь
всё хорошо, подынтегральная функция

непрерывна на интервале

,
а, значит, несобственный интеграл
существует. Обратите внимание, что
криволинейная трапеция у нас –
бесконечная (не
ограниченная справа) фигура.

Несобственный
интеграл

численно равен
площади заштрихованной фигуры, при этом
возможны два случая:

1)
Первая мысль, которая приходит в голову:
«Раз фигура бесконечная, то и

»,
иными словами, площадь тоже бесконечна.
Так быть может.
В этом случае говорят,
что, что несобственный интеграл
расходится.

2) Но!
Как это ни парадоксально прозвучит,
площадь бесконечной фигуры может
равняться… конечному числу! Например:

Может
ли так быть? Да. В этом случае несобственный
интеграл сходится.

В каких
случаях несобственный интеграл
расходится, а в каком сходится? Это
зависит от подынтегральной функции

А что будет, если
бесконечная криволинейная трапеция
расположена ниже оси? В этом случае,
несобственный интеграл

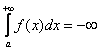
«расходится»,
либо равен отрицательному числу.

Несобственный
интеграл может быть отрицательным.

Важно!
Когда Вам для решения
предложен ПРОИЗВОЛЬНЫЙ несобственный
интеграл, то, вообще говоря,
ни о какой площади
речи не идет и чертежа строить не нужно.
Ваша задача найти ЧИСЛО, либо доказать,
что несобственный интеграл расходится.
Геометрический смысл несобственного
интеграла рассказан только для того,
чтобы легче было понять материал.

Поскольку
несобственный интеграл очень похож на
определенный интеграл, то вспомним
формулу Ньютона- Лейбница:

На
самом деле формула применима и к
несобственным интегралам, только ее
нужно немного модифицировать. В чем
отличие? В бесконечном верхнем пределе
интегрирования:
.
Наверное, многие догадались, что здесь
необходимо применение теории пределов,
и формула запишется так:

В чем
отличие от определенного интеграла? Да
ни в чем особенном! Как и в определенном
интеграле, нужно уметь находить
первообразную функцию

(неопределенный интеграл) и уметь
применять формулу Ньютона-Лейбница.
Единственное, что добавилось – это
вычисление предела. У кого с ними плохо,
изучите урок Пределы
функций. Примеры решений,
ибо лучше поздно, чем в армии. Рассмотрим
два классических примера:

Пример 1

Вычислить
несобственный интеграл или установить
его расходимость.

Для
наглядности построим чертеж, хотя, еще
раз подчеркиваю, на
практике строить
чертежи в данном задании не нужно.

Подынтегральная
функция

непрерывна на интервале

,
значит, всё нормально и несобственный
интеграл можно вычислить «штатным»
методом.

Применение нашей
формулы

и решение задачи
выглядит так:

То есть, несобственный
интеграл расходится, и площадь
заштрихованной криволинейной трапеции
равна бесконечности.

В
рассмотренном примере у нас простейший
табличный интеграл и такая же техника
применения формулы Ньютона-Лейбница,
как в определенном интеграле. Но
применятся эта формула под знаком
предела. Вместо привычной
буквы
«динамической»
переменной выступает буква «бэ». Это
не должно смущать или ставить в тупик,
потому-что любая буква ничем не хуже
стандартного «икса».

Если
Вам непонятно почему

при

,
то это очень плохо, либо Вы не понимаете
простейшие пределы (и вообще не понимаете,
что такое предел), либо не знаете, как
выглядит график логарифмической функции.
Во втором случае посетите урок Графики
и свойства элементарных функций.

При
решении несобственных интегралов очень
важно знать, как выглядят графики
основных элементарных функций!

Чистовое оформление
задания должно выглядеть примерно так:

Подынтегральная
функция непрерывна на «полубесконечном»
интервале

Несобственный
интеграл расходится.

При
оформлении примера всегда прерываем
решение, и указываем, что происходит с
подынтегральной функцией на границах
интервала.

Этим мы идентифицируем
тип несобственного интеграла.

Если Вам встретится
интеграл вроде

то с
вероятностью, близкой к 100%, можно сказать,
что это опечатка. Здесь подынтегральная
функция не является непрерывной на
интервале интегрирования

,
она терпит разрыв в точке

.
Теоретически и практически допустимо
вычислить два несобственных интеграла
на интервалах

и

,
а потом их сложить, но со здравой точки
зрения такая вещь выглядит довольно
абсурдно. Опечатка.

Иногда
вследствие опечатки несобственного
интеграла может вообще не существовать.
Например, если в знаменатель вышеуказанного
интеграла поставить квадратный корень
из «икс», то часть интервала интегрирования
вообще не войдёт в область определения
подынтегральной функции.

Всегда
смотрим и записываем, является ли
подынтегральная функция непрерывной
на интервале интегрирования.

Пример 2

Вычислить
несобственный интеграл или установить
его расходимость:

Выполним
чертеж:

Во-первых, замечаем
следующее: подынтегральная функция

непрерывна
на интервале

.
Хорошо. Решаем с помощью формулы

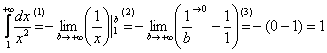
(1) Берем простейший
интеграл от степенной функции (этот
частный случай есть во многих таблицах).
Минус лучше сразу вынести за знак
предела, чтобы он не путался под ногами
в дальнейших вычислениях.

(2) Подставляем
верхний и нижний пределы по формуле
Ньютона-Лейбница.

(3)
Указываем, что

,
если

(это нужно понимать) и упрощаем ответ.

Вот здесь площадь
бесконечной криволинейной трапеции
равна конечному числу! Невероятно, но
факт.

Чистовое оформление
примера должно выглядеть примерно так:

“

Подынтегральная
функция непрерывна на полубесконечном
интервале

“

Пример 3

Вычислить
несобственный интеграл или установить
его расходимость.

Подынтегральная
функция непрерывна на

.

Интеграл
не так прост, особенно для чайника. Что
делать, если интеграл кажется не самым
простым или не сразу понятно как его
решать? В этом случае целесообразно
применить алгоритм, о котором я уже
рассказал в статье Определенный
интеграл. Примеры решений.

Сначала
попытаемся найти первообразную функцию
F(X)
(неопределенный интеграл). Если нам не
удастся этого сделать, то несобственный
интеграл мы, естественно, тоже не решим.

На какой из табличных
интегралов похожа подынтегральная
функция? Напоминает она арктангенс:

Из этих соображений
напрашивается мысль, что неплохо бы в
знаменателе получить квадрат. Делается
это путем замены.

Проведем
замену
,
тогда:

Неопределенный
интеграл найден, константу C
в данном случае
добавлять не имеет смысла.

На
черновике всегда полезно выполнить
проверку, то есть продифференцировать
полученный результат:

Получена исходная
подынтегральная функция, значит,
неопределенный интеграл найден правильно.

Теперь находим
несобственный интеграл:

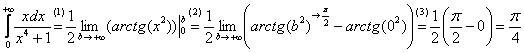
(1) Записываем
решение в соответствии с формулой

Константу лучше
сразу вынести за знак предела, чтобы
она не мешалась в дальнейших вычислениях.

(2) Подставляем
верхний и нижний пределы в соответствии
с формулой Ньютона-Лейбница.

Почему

при

?
Смотрите график арктангенса.

(3)
Получаем окончательный ответ. Тот факт,
что arctg(0)
= 0, полезно
знать наизусть.

Продвинутые
студенты могут не находить отдельно
неопределенный интеграл, и не использовать
метод замены, а использовать метод
подведения функции под знак дифференциала
и решать несобственный интеграл «сразу».
В этом случае решение должно выглядеть
примерно так:

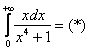
Подынтегральная
функция непрерывна на интервале

А сейчас два примера
для самостоятельного решения.

Пример 4

Вычислить
несобственный интеграл или установить
его расходимость.

ВНИМАНИЕ!
Это типовой пример,
и похожие интегралы встречаются очень
часто. Хорошо его проработайте!
Первообразная функция здесь находится
методом выделения полного квадрата,
более подробно с методом можно ознакомиться
на уроке Интегрирование
некоторых дробей.

Пример 5

Вычислить
несобственный интеграл или установить
его расходимость.

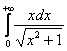
Этот
интеграл можно решить подробно, то есть
сначала найти неопределенный интеграл,
проведя замену переменной. А можно
решить «сразу» – подведением функции
под знак дифференциала. У кого какая
математическая подготовка. Полные
решения и ответы в конце урока.

Примеры
решений несобственных интегралов с
бесконечным нижним пределом интегрирования
можно посмотреть на странице Эффективные
методы решения определённых и несобственных
интегралов.
Там же разобран случай, когда оба предела
интегрирования бесконечны.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
08.02.20157.31 Mб91.rtf
#
#
#
#
#
#
#
#
#
#

Источник

Содержание:

Несобственный интеграл – Основные понятия и теоремы
Свойства несобственного интеграла
Несобственные интегралы
Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)
Интегралы от неограниченных функций (несобственные интегралы II типа)

Несобственный интеграл – Основные понятия и теоремы

Пусть функция определена на промежутке и интегрируема на отрезке при любом . Если существует предел

(1.1)

то его называют несобственным интегралом от функции по промежутку и обозначают символом

(1.2)

Символ (1.2) также называется несобственным интегралом. Если предел (1.1) существует, то несобственный интеграл называется сходящимся, в противном случае — расходящимся.

Аналогично определяется несобственный интеграл с бесконечным нижним пределом:

(1.3)

Интегралы (1.2) и (1.3) называются несобственными интегралами по неограниченному множеству.

Пусть функция определена на промежутке , интегрируема на отрезке при любом и не ограничена в левой полуокрестности точки . Тогда интеграл (1.4)

называют несобственным интегралом от неограниченной функции и по определению полагают

(1.5)

По этой ссылке вы найдёте полный курс лекций по высшей математике:

Если предел (1.5) существует, то несобственный интеграл (1.4) называется сходящимся, в противном случае — расходящимся.

Аналогично определяется несобственный интеграл по промежутку .

Обозначим через один из символов и сформулируем определение несобственного интеграла в общем случае.

Пусть функция определена на промежутке и интегрируема на каждом отрезке. Если существует предел

(1.6)

то его называют несобственным интегралом от функции по промежутку и обозначают символом

(1.7)

Несобственный интеграл по промежутку , где — один из символов определяется аналогично. Далее все утверждения будем формулировать для промежутка . Они очевидным образом переносятся на интегралы по промежутку .

Несобственные интегралы возникают в задачах на геометрические приложения интегрального исчисления: при вычислении площадей неограниченных фигур; объемов тел и площадей поверхностей вращения, если вращающаяся фигура неограничена.

Пусть функция непрерывна и неотрицательна в промежутке . Рассмотрим фигуру

(1.8)

которую назовем неограниченной криволинейной трапецией.

Если несобственный интеграл сходится, то площадью фигуры называется число

(1.9)

Возможно вам будут полезны данные страницы:

Объем тела, образованного вращением фигуры вокруг оси равен несобственному интегралу

(1.10)

Площадь поверхности, полученной вращением непрерывной кривой

вокруг оси , вычисляется по формуле

(1.11)

Формулы (1.10), (1.11), как и формула (1.9), применимы при условии сходимости соответствующих несобственных интегралов.

При решении геометрических задач используются и несобственные интегралы от неограниченных функций.

Свойства несобственного интеграла

3. При любом

Свойства 1 и 2 называют линейными, а свойство 3 — аддитивностью.

Теорема 1.1 (о замене переменной в несобственном интеграле). Пусть выполнены следующие условия:

1) непрерывно дифференцируемая и строго монотонная функция отображает промежуток в промежуток , где и при

2) функция непрерывна в промежутке . Тогда интегралы

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

(1.12)

Теорема 1.2 (об интегрировании по частям в несобственном интеграле). Пусть функции и непрерывно дифференцируемы на промежутке и существует .

Тогда интегралы

либо оба сходятся, либо оба расходятся. В случае сходимости справедливо равенство

(1.13)

где

Определенный интеграл считается неуместным, если выполнено хотя бы одно из следующих условий: Поля интеграции бесконечны. Например, бесконечный разрыв. Функция не ограничена вблизи некоторых точек области интегрирования.

Примеры с решением

Вычислить несобственный интеграл или установить его расходимость.

Пример 1.

Решение:

Вычислим несобственный интеграл по определению:

Следовательно, данный интеграл интеграл сходится.

Пример 2.

Решение: По определению несобственного интеграла с бесконечным верхним пределом имеем

Следовательно, данный интеграл интеграл расходится.

Пример 3.

Решение:

По определению несобственного интеграла с бесконечным нижним пределом имеем

Итак, интеграл сходится и равен 1.

Пример 4.

Решение:

Интеграл является несобственным, поскольку верхний предел бесконечен. Рассмотрим два случая.

1). Пусть Тогда по определению имеем

2). Пусть . Тогда Итак, интеграл сходится при и расходится при

Пример 5.

Решение:

Данный интеграл является несобственным, поскольку подынтегральная функция не определена в точке и . По определению несобственного интеграла от неограниченной функции имеем

Итак, данный интеграл сходится и равен

Пример 6.

Решение:

Подынтегральная функция не ограничена в правой полуокрестности нижнего предела. Поэтому данный интеграл – несобственный. Рассмотрим два случая.

1). Пусть . По определению несобственного интеграла от неограниченной функции имеем

2). Пусть . Тогда

Итак, интеграл сходится при и расходится при

Пример 7.

Решение:

Применим к данному интегралу формулу интегрирования по частям: Пример 1.8.

Данный интеграл является несобственным, поскольку

подынтегральная функция не определена в точке

и . Воспользуемся формулой замены переменной в несобственном интеграле. Положим . Имеем

Заметим, что в результате замены переменной несобственный интеграл преобразовался в определенный интеграл от непрерывной функции по отрезку.

Пример 8.

Найти площадь фигуры, ограниченной графиком функции и прямой .

Решение:

Функция непрерывна и неотрицательна в промежутке . Поэтому заданная фигура является неограниченной криволинейной трапецией вида (1.8). Площадь фигуры находится по формуле (1.9):

Для вычисления интеграла применим формулу (1.13) интегрирования по частям. Положим Тогда . Функции и непрерывно дифференцируемы в промежутке и существует

По формуле (1.13) имеем

Пример 9.

Найти объем тела, образованного вращением вокруг оси фигуры, ограниченной графиком функции

и прямыми

Решение: Функция непрерывна, неотрицательна в промежутке (1,2] и не ограничена на нем, так как . Поэтому объем тела вращения выражается через несобственный интеграл:

Итак,

Несобственные интегралы

Понятие «несобственные интегралы» связано с нарушением условий теоремы 23.1 о существовании определенного интеграла. В зависимости от того, какая именно условие существования нарушена, рассматривают несобственные интегралы I и II типов.

Различают следующие случаи:

1) вместо конечного отрезка рассматриваются бесконечные пол интервалы или интервал
2) вместо подынтегральной функции, которая является непрерывной или ограниченной на отрезке интегрирования и имеет конечное число точек разрыва первого рода, рассматривают функцию, имеет на этом отрезке бесконечный разрыв, то есть разрыв второго рода.

Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)

Пусть функция определена и непрерывна на промежутке Тогда согласно теореме 23.1 она интегрируема на любом отрезке где – произвольное действительное число, большее Итак, существует определенный интеграл от этой функции на отрезке

где

то есть является первоначальной для подынтегральной функции

Несобственным интегралом I типа функции на промежутке называется предел определенного интеграла при условии, что верхняя граница интегрирования стремится к плюс бесконечности, то есть

Если граница конечна, то несобственный интеграл I типа называется сходящимся, или говорят, что он совпадает. Если граница в соотношении (25.1) является бесконечной или вовсе не существует, то несобственный интеграл I типа называется расходящимся, то есть разбегается.

С учетом формулы Ньютона-Лейбница соотношение (25.1) можно записать так:

где применяется обозначения:

Аналогично определяется несобственный интеграл I типа для случая, когда вместо отрезка интегрирования рассматривается интервал с бесконечной нижней границей.

Пусть функция определена и непрерывна на промежутке тогда для любого действительного существует определенный интеграл:

Несобственным интегралом I типа функции на промежутке называется предел определенного интеграла при условии, что нижняя граница интегрирования стремится к минус бесконечности, то есть

где применяется обозначение

Пусть функция определена и непрерывна на промежутке Тогда представим интеграл на этом промежутке как сумму двух несобственных интегралов на промежутках и

Если в соотношении (25.4) обе границы существуют, то несобственный интеграл I типа с бесконечными пределами совпадает.

С учетом формулы Ньютона-Лейбница несобственный интеграл на промежутке определяется соотношением:

Общий порядок нахождения несобственного интеграла I типа состоит из двух шагов:

1) вычисляем определенный интеграл от на где – переменная нижняя граница интегрирования ( – переменная верхний предел интегрирования)
2) находим границу определенного интеграла при

Под исследованием несобственных интегралов на сходимость понимают установления факта его сходимости или разногласия. Для этого во многих случаях бывает достаточна не вычислять самый интеграл (а он может быть таким, что и «не берется»), а сравнить его с несобственным интегралом, сходимость (или расхождение) которого известна.

Приведем признаки сравнения несобственных интегралов (которые примем без доказательства).

Теорема 25.1. Если функции и для всех связанные соотношением и несобственный интеграл совпадает, то совпадает и несобственный интеграл при этом

Теорема 25.2. Если функции и для всех связанные соотношением и несобственный интеграл расходится, то расходится и несобственный интеграл

Несобственный интеграл от функции сходимость или расхождение которого известна заранее, называется эталонным интегралом, а – эталонной функцией.

В предыдущих теоремах рассматривались несобственные интегралы от неотъемлемых функций. Для знакопеременной функции на бесконечном промежутке справедлива следующая теорема.

Теорема 25.3. Если несобственный интеграл от модуля заданной функции совпадает, то совпадает и интеграл от самой функции

В этом случае несобственный интеграл от на называется абсолютно сходящимся.

Рассмотрим некоторые примеры несобственных интегралов I типа. Одним из таких интегралов является интеграл Эйлера-Пуассона:

Этот интеграл нельзя представить в виде конечного числа элементарных функций, поэтому по общему алгоритму проблему вычисления интеграла Эйлера – Пуассона решить невозможно. Докажем, что этот интеграл совпадает, применив теорему 25.1.

Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции Как эталонную функцию выберем функцию φ () x e x = -. Учтем также парность подынтегральной функции (рис. 25.1):

Рис. 25.1

Сравним функции и Обе функции положительные на числовой оси, и для выполняется неравенство тогда относительно функций и имеет место соотношение:

Следовательно, применить теорему 25.1 можно только на промежутке
Исследуем на сходимость интеграл от эталонной функции на

Эталонный интеграл совпадает на промежутке тогда по признаку сравнения сходится есть интеграл Поскольку несобственный интеграл отличается от несобственного интеграла постоянной, равной площади криволинейной трапеции для то интеграл Эйлера-Пуассона тоже является сходящимся.

В главе 26 будет доказано, что:

При исследовании вопроса о сходимости несобственных интегралов I типа часто в роли эталонного интеграла принимают интеграл вида:

Свойства этого интеграла зависят от значений параметра

Интеграл (25.8) при разбегается:

Следовательно, несобственный интеграл от степенной функции совпадает, если и расходится, если

Исследовать на сходимость несобственный интеграл I типа:

По определению:

Мы доказали, что несобственный интеграл совпадает, поскольку соответствующая граница равна конечном числу.

Исследовать на сходимость несобственный интеграл I типа:

По определению имеем:

Эта граница не существует, поскольку не существует следовательно, заданный несобственный интеграл расходится.

Исследовать на сходимость несобственный интеграл I типа:

По определению:

то есть данный интеграл расходится.

Интегралы от неограниченных функций (несобственные интегралы II типа)

Пусть на имеет конечное число точек разрыва второго рода. Это означает, что хотя бы одна из односторонних пределов функции в этих точках равна бесконечности, то есть при приближении к точкам разрыва функция неограниченно приходит или растет. Такие точки называются особыми точками функции. На рис. 25.2 приведены примеры расположения особых точек c на отрезке Так, особой точкой может быть как левый, так и правый конец отрезка, а также любая внутренняя точка. В геометрическом смысле прямая является вертикальной асимптотой графика функции

Рис. 25.2

Выберем некоторое положительное число и рассмотрим, соответственно, отрезки (рис. 25.2 а, б и в), на которых подынтегральная функция ограничена и непрерывная, следовательно, существует определенный интеграл от этой функции.

Несобственным интегралом II типа от функции на промежутке где при функция имеет разрыв второго рода, называется предел определенного интеграла на промежутке при условии, что стремится к нулю:

Аналогично определяют несобственные интегралы II типа для случая, когда особой точкой является верхняя граница отрезка интегрирования:

а также для случая, когда особая точка является внутренней точкой отрезка интегрирования:

Несобственный интеграл II типа называется сходящимся, если существуют конечные границы в правых частях формул (25.10) – (25.12). В противном случае их называют расходящимися.

Порядок исчисления несобственных интегралов II типа принципиально ничем не отличается от порядка определения несобственных интегралов I типа: вычисляют определенный интеграл на конечном отрезке и находят его границу при условии, что или Если для подынтегральной функции не существует первоначальная в виде конечной суммы элементарных функций, то для исследования несобственных интегралов II типа на сходимость применяются признаки сравнения их с эталонными интегралами, то есть такими, о которых заранее известно, совпадают они или разбегаются. Часто в качестве эталонных берут несобственные интегралы от степенных функций:

и его обобщения:

где

Для первого и второго эталонных интегралов особой точкой является нижняя граница отрезка интегрирования, а для третьего – верхний предел.

Проведем исследование на сходимость первого интеграла с (25.13):

Если то

Следовательно, несобственный интеграл II типа совпадает при и расходится при

Определим, совпадает ли несобственный интеграл

Его подынтегральная функция имеет разрыв второго рода в точке то есть ее особой точкой является верхняя граница отрезка интегрирования. По определению имеем:

Заданный интеграл совпадает, потому соответствующая граница равна конечном числу.

Исследуем на сходимость несобственный интеграл

Подынтегральная функция непрерывна на промежутке по исключением точки в которой знаменатель равен нулю, следовательно, в окрестности этой точки функция не ограничена, поэтому интеграл записываем в таком виде:

Если каждый интеграл в правой части совпадает, то выходной интеграл тоже будет совпадать.

Рассмотрим первый интеграл:

Поскольку первый интеграл расходится, то нет необходимости вычислять второй. Окончательно делаем вывод, что заданный несобственный интеграл расходится.

Лекции:

Определенный интеграл и объем фигур вращения
Уравнение гиперболы
Уравнение эллипса
Степенные ряды
Случайные события и вероятность
Свойства пределов функции
Решение пределов со степенями
Теория сплайнов примеры решения
Жорданова форма матрицы
Скрещивающиеся прямые

Источник

Это «родственник» определённого интеграла. …Нормальное такое определение :). И сразу возникает вопрос: чем отличается несобственный интеграл от «собрата»? Он может отличаться пределами интегрирования:
– то есть, один или даже оба предела бесконечны, при этом подынтегральная функция непрерывна на промежутке интегрирования.

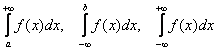
Такие интегралы получили название несобственные интегралы первого рода.

Кроме того, несобственный интеграл может быть «внешне похож» на определённый интеграл и иметь вид 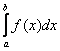. Но есть один нюанс. Подынтегральная функция не определена в точке или . Или на обоих концах. Или даже во внутренних точках отрезка .

Это так называемые несобственные интегралы второго рода.

Что значит решить несобственный интеграл? В отличие от определённого интеграла, тут есть три варианта. Решить несобственный интеграл – это значит найти конечное число, либо получить бесконечность, либо выяснить, что несобственного интеграла не существует.

1) Если несобственный интеграл равен конечному числу, то говорят, что он сходится. Число может быть как положительным, так и отрицательным. Или нулём.

2) Если несобственный интеграл равен бесконечности (со знаком «плюс» или «минус»), то говорят, он расходится.

3) И в ряде случаев несобственного интеграла может вовсе не существовать. Даже если подынтегральная функция непрерывна на промежутке интегрирования! (вспоминаем, что определённый интеграл при этом условии существует всегда).

Как решить несобственный интеграл? С помощью той же формулы Ньютона-Лейбница. С некоторыми особенностями.

И здесь вы должны понимать и уметь решать несложные пределы функций.

В чём смысл несобственного интеграла? Геометрически – это тоже площадь (если интеграл существует). Но площадь своеобразная. И с этим своеобразием мы познакомимся прямо на следующей странице:

2.2. Несобственный интеграл первого рода

1.11. А если подынтегральная функция нечётная?

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Определённый интеграл называется несобственным, если выполняется хотя бы одно из двух условий:

Один (или оба) из пределов интегрирования равен

или
. В этом случае, интеграл называется
несобственным интегралом первого рода, например:
.

В любой точке на отрезке интегрирования, подинтегральная функция терпит бесконечный разрыв. В этом случае, интеграл называется
несобственным интегралом второго рода, например:

в точке
.

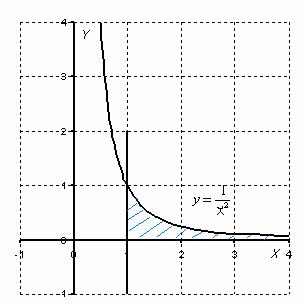
Рассмотрим в качестве примера
несобственный интеграл
первого рода
. График подинтегральной функции

на отрезке интегрирования

имеет вид:

Геометрически, данный несобственный интеграл равен площади под графиком функции

на отрезке
. Рассматриваемый интеграл является сходящимся, потому что указанная площадь равна

– конечному числу. Однако, несобственные интегралы бывают и расходящимися, например:

Алгоритм вычисления несобственного интеграла первого рода выглядит следующим образом:

Сначала мы заменяем бесконечный предел на некоторый параметр, например

и получаем определенный интеграл. Этот интеграл мы вычисляем обычным образом: берем
неопределенный интеграл
и далее используем формулу Ньютона-Лейбница. На завершающем этапе, мы вычисляем
предел
при
и, если, данный предел существует и конечен, тогда исходный несобственный интеграл является сходящимся, а в противном случае – расходящимся.

Алгоритм вычисления несобственного интеграла второго рода заключается в разбивке интервала интегрирования на отрезки в каждом из которых подинтегральная функция является непрерывной (разрывы допускаются только на концах отрезка). Далее, вычисляются полученные
определенные интегралы, а при подстановке значений в формулу Ньютона-Лейбница вычисляются соответствующие пределы. И если все эти пределы существуют и конечны, тогда, как и раньше, интеграл является сходящимся, а в противном случае – расходящимся. Приведем пример:

Наш онлайн калькулятор, построенный на основе системы Wolfram Alpha способен вычислить очень многие типы несобственных интегралов. При этом, если интеграл расходится, калькулятор выдает сообщение:
integral does not converge.

Источник

Определённый интеграл называется несобственным, если выполняется по крайней мере одно из следующих условий.

Область интегрирования является бесконечной. Например, является бесконечным промежутком .
Функция является неограниченной в окрестности некоторых точек области интегрирования.

Если интервал [a,b] конечный и функция интегрируема по Риману, то значение несобственного интеграла совпадает со значением определённого интеграла.

Несобственные интегралы I рода[править | править код]

Несобственный интеграл первого рода

Пусть f(x) определена и непрерывна на интервале и ${displaystyle forall A>a exists int limits _{a}^{A}f(x)dx}$ . Тогда:

Если $exists lim_{A to +infty}intlimits_{a}^{A} f(x)dx = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{+infty} f(x)dx$ и интеграл называется несобственным интегралом Римана первого рода. В этом случае $I=intlimits_{a}^{+infty} f(x)dx$ называется сходящимся.
Если не существует конечного $lim_{A to +infty}intlimits_{a}^{A} f(x)dx$ ( или ), то интеграл $intlimits_{a}^{+infty} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Пусть f(x) определена и непрерывна на множестве от и $forall B < b Rightarrow exists intlimits_{B}^{b} f(x)dx$ . Тогда:

Если $exists lim_{B to -infty}intlimits_{B}^{b} f(x)dx = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{-infty}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана первого рода. В этом случае $I=intlimits_{-infty}^{b} f(x)dx$ называется сходящимся.
Если не существует конечного $lim_{B to -infty}intlimits_{B}^{b} f(x)dx$ ( или ), то интеграл $intlimits_{-infty}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Если функция f(x) определена и непрерывна на всей числовой прямой, то может существовать несобственный интеграл данной функции с двумя бесконечными пределами интегрирования, определяющийся формулой:

$intlimits_{-infty}^{+infty} f(x)dx = intlimits_{-infty}^{c} f(x)dx + intlimits_{c}^{+infty} f(x)dx$ , где с — произвольное число.

Геометрический смысл несобственного интеграла I рода[править | править код]

Несобственный интеграл первого рода выражает площадь бесконечно длинной криволинейной трапеции.

Примеры[править | править код]

${displaystyle int limits _{-infty }^{-1}{1 over x^{2}}dx=lim _{ato -infty }int limits _{a}^{-1}{1 over x^{2}}dx=lim _{ato -infty }{Bigl .}-{frac {1}{x}}{Bigr |}_{a}^{-1}=1+lim _{ato -infty }{frac {1}{a}}=1+0=1}$

Несобственные интегралы II рода[править | править код]

Несобственный интеграл Римана второго рода

Пусть f(x) определена на (a,b] , терпит бесконечный разрыв в точке x = a и $forall delta > 0 Rightarrow exists intlimits_{a + delta}^{b} f(x)dx = mathcal{I}(delta)$ . Тогда:

Если $exists lim_{delta to 0+0} mathcal{I}(delta) = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если $lim_{delta to 0+0} mathcal{I}(delta) = infty ; (pminfty$ или , то обозначение сохраняется, а $mathcal{I}=intlimits_{a}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Пусть f(x) определена на [a,b) , терпит бесконечный разрыв при x = b и $forall delta > 0 Rightarrow exists intlimits_{a}^{b-delta} f(x)dx = mathcal{I}(delta)$ . Тогда:

Если $exists lim_{delta to 0+0} mathcal{I}(delta) = Iinmathbb{R}$ , то используется обозначение $I=intlimits_{a}^{b} f(x)dx$ и интеграл называется несобственным интегралом Римана второго рода. В этом случае интеграл называется сходящимся.
Если $lim_{delta to 0+0} mathcal{I}(delta) = infty ; (pminfty$ или , то обозначение сохраняется, а $mathcal{I}=intlimits_{a}^{b} f(x)dx$ называется расходящимся к «», «», или просто расходящимся.

Если функция f(x) терпит разрыв во внутренней точке отрезка [a;b] , то несобственный интеграл второго рода определяется формулой:

${displaystyle int limits _{a}^{b}f(x)dx=int limits _{a}^{c}f(x)dx+int limits _{c}^{b}f(x)dx.}$

Геометрический смысл несобственных интегралов II рода[править | править код]

Несобственный интеграл второго рода выражает площадь бесконечно высокой криволинейной трапеции.

Пример[править | править код]

$intlimits_{0}^{1} {dx over x} = lim_{delta to 0+0} Bigl. ln |x| Bigr|_{0+delta }^1 = 0 - lim_{delta to 0+0} ln delta = + infty$

Отдельный случай[править | править код]

Пусть функция f(x) определена на всей числовой оси и имеет разрыв в точках .

Тогда можно найти несобственный интеграл $intlimits_{-infty }^{+infty} f(x)dx = intlimits_{-infty }^{x_1} f(x)dx + sum_{j=1}^{k-1} {intlimits_{x_j}^{x_{j+1}} f(x)dx}+ intlimits_{x_k}^{+infty} f(x)dx$

Критерий Коши[править | править код]

1. Пусть f(x) определена на множестве от и ${displaystyle forall A>a exists int limits _{a}^{A}f(x)dx}$ .

Тогда $mathcal{I}=intlimits_{a}^{+infty} f(x)dx$

сходится ${displaystyle Leftrightarrow forall varepsilon >0 exists A(varepsilon )>a:forall (A_{2}>A_{1}>A)Rightarrow left|,int limits _{A_{1}}^{A_{2}}f(x)dxright|<varepsilon }$

2. Пусть f(x) определена на (a,b] и ${displaystyle forall delta >0 exists int limits _{a+delta }^{b}f(x)dx}$ .

Тогда $mathcal{I}=intlimits_{a}^{b} f(x)dx$

сходится ${displaystyle Leftrightarrow forall varepsilon >0Rightarrow exists delta (varepsilon )>0:forall (0<delta _{1}<delta _{2}<delta )Rightarrow left|,int limits _{a+delta _{1}}^{a+delta _{2}}f(x)dxright|<varepsilon }$

Абсолютная сходимость[править | править код]

Интеграл $intlimits_{a}^{+infty} f(x)dx left(intlimits_{a}^{b} f(x)dxright)$ называется абсолютно сходящимся, если $intlimits_{a}^{+infty} |f(x)|dx left(intlimits_{a}^{b} |f(x)|dxright)$ сходится.
Если интеграл сходится абсолютно, то он сходится.

Условная сходимость[править | править код]

Интеграл $intlimits_{a}^{+infty} f(x)dx$ называется условно сходящимся, если $intlimits_{a}^{+infty} f(x)dx$ сходится, а $intlimits_{a}^{+infty} |f(x)|dx$ расходится.

См. также[править | править код]

Интеграл Римана
Интеграл Лебега
Метод Самокиша — численный метод для вычисления интегралов с особенностями.

Литература[править | править код]

Дмитрий Письменный. Конспект лекций по высшей математике, часть 1. — Айрис Пресс, 2007. — С. 233-237.

Источник

5.3.1. Несобственный интеграл с бесконечным пределом (ами) интегрирования

Несобственный интеграл – Основные понятия и теоремы

Свойства несобственного интеграла

Примеры с решением

Пример 1.

Пример 2.

Пример 3.

Пример 4.

Пример 5.

Пример 6.

Пример 7.

Пример 8.

Пример 9.

Несобственные интегралы

Интегралы с бесконечными пределами интегрирования (несобственные интегралы І типа)

Интегралы от неограниченных функций (несобственные интегралы II типа)

Несобственные интегралы I рода[править | править код]

Геометрический смысл несобственного интеграла I рода[править | править код]

Примеры[править | править код]

Несобственные интегралы II рода[править | править код]

Геометрический смысл несобственных интегралов II рода[править | править код]

Пример[править | править код]

Отдельный случай[править | править код]

Критерий Коши[править | править код]

Абсолютная сходимость[править | править код]

Условная сходимость[править | править код]

См. также[править | править код]

Литература[править | править код]

Вам также может понравиться

Как исправить ямки на ягодицах

Как составить рабочую программу по информатике

Как найти шепот вальгалла

Добавить комментарий Отменить ответ