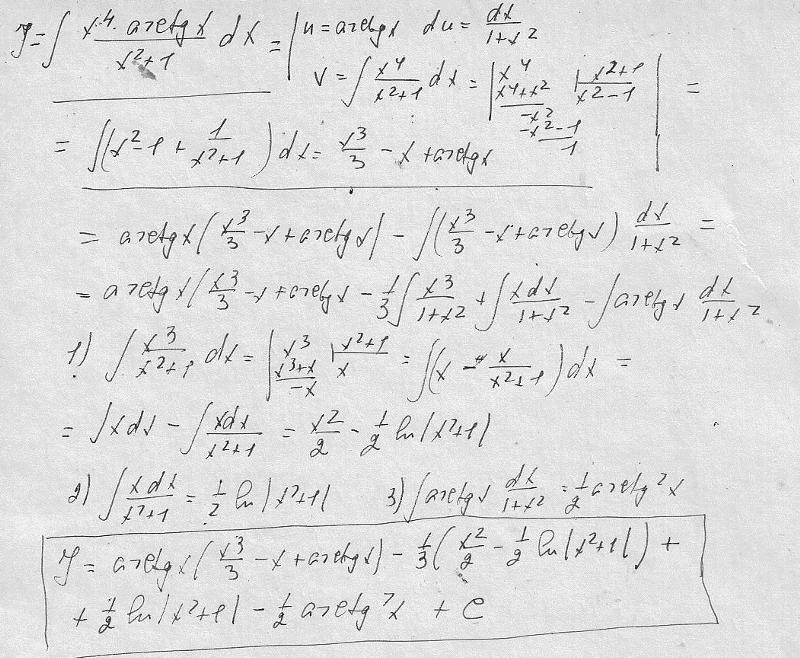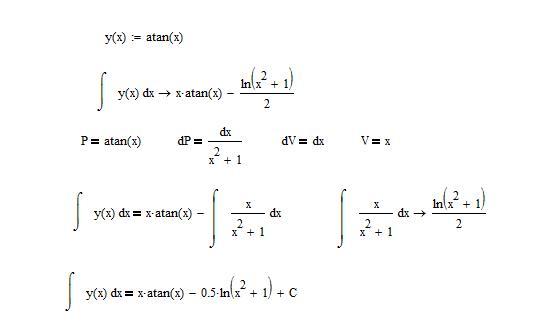Интеграл арктангенса
Интеграл от арктангенса равен переменной интегрирования, умноженной на этот арктангенс, за вычетом естественного логарифма корня суммы единицы и переменной интегрирования в квадрате плюс константа интегрирования
(
int operatorname{arctg} x d x=x cdot operatorname{arctg} x-ln sqrt{1+x^{2}}+C
)
Примеры решения проблем
ПРИМЕР 1
Чтобы доказать это (
int operatorname{arctg} x d x=x cdot operatorname{arctg} x-ln sqrt{1+x^{2}}+C
)
(
int operatorname{arctg} x d xleft|u=frac{d x}{1+x^{2}}, quad v=xright|=x cdot operatorname{arctg} x-int frac{x d x}{1+x^{2}}left|begin{array}{l}{1+x^{2}=t |} \ {2 x d x=d t} \ {x d x=frac{d t}{2}}end{array}right|=
)
(
=x cdot operatorname{arctg} x-frac{1}{2} int frac{d t}{t}=x cdot operatorname{arctg} x-frac{1}{2} ln |t|+C=x cdot operatorname{arctg} x-ln sqrt{left|1+x^{2}right|}+C=
)
(
=x cdot operatorname{arctg} x-ln sqrt{1+x^{2}}+C
)
ПРИМЕР 2
Найти интеграл (
int x operatorname{arctg} x^{2} d x
)
Чтобы свести интеграл к известной формуле, применим метод замены переменных:
(
int x operatorname{arctg} x^{2} d xleft|begin{array}{c}{x^{2}=t} \ {2 x d x=d t} \ {x d x=frac{d t}{2}}end{array}right|=int operatorname{arctg} t cdot frac{d t}{2}=frac{1}{2} int operatorname{arctg} t d t=
)
(
=frac{1}{2}left(t cdot operatorname{arctg} t-ln sqrt{1+t^{2}}right)+C=frac{1}{2}left(x^{2} cdot operatorname{arctg} x^{2}-ln sqrt{1+left(x^{2}right)^{2}}right)+C=
)
(
=frac{x^{2} operatorname{arctg} x^{2}}{2}-frac{1}{2} ln sqrt{1+x^{4}}+C
)
(
int x operatorname{arctg} x^{2} d x=frac{x^{2} operatorname{arctg} x^{2}}{2}-frac{1}{2} ln sqrt{1+x^{4}}+C
)
Ниже приведён список интегралов (первообразных функций) от обратных тригонометрических функций.
Содержание
- 1 Арксинус
- 2 Арккосинус
- 3 Арктангенс
- 4 Арккотангенс
- 5 Арксеканс
- 6 Арккосеканс
- 7 Библиография
Арксинус[править | править код]
Арккосинус[править | править код]
Арктангенс[править | править код]
Арккотангенс[править | править код]
Арксеканс[править | править код]
Арккосеканс[править | править код]
Библиография[править код]
- Книги
- Градштейн И. С., Рыжик И. М. Таблицы интегралов, сумм, рядов и произведений. — 4-е изд. — М.: Наука, 1963.
- Двайт Г. Б. Таблицы интегралов. — СПб.: Издательство и типография АО ВНИИГ им. Б. В. Веденеева, 1995. — 176 с. — ISBN 5-85529-029-8.
- Zwillinger D. CRC Standard Mathematical Tables and Formulae (англ.). — 31st ed. — 2002. — ISBN 1-58488-291-3.
- Справочник по специальным функциям с формулами, графиками и таблицами / Под ред. М. Абрамовица и И. Стиган; пер. с англ. под ред. В. А. Диткина и Л. Н. Карамзиной. — М.: Наука, 1979. — 832 с. — 50 000 экз.
- Корн Г. А., Корн Т. М. Справочник по математике для научных работников и инженеров. — М.: «Наука», 1974. — 832 с.
- Таблицы интегралов
- Интегралы на EqWorld
- S.O.S. Mathematics: Tables and Formulas
- Вычисление интегралов
- The Integrator (на Wolfram Research)
- Империя Чисел
- Методы вычисления неопределённых интегралов
Списки интегралов по типам функций |
|---|
|
Тригонометрия |
|
|---|---|
| Общее |
|
| Справочник |
|
| Законы и теоремы |
|
| Математический анализ |
|
Помогите с интегралом
-
MidaS
- Сообщения: 3
- Зарегистрирован: 15 апр 2016, 00:39
Помогите с интегралом
Здравствуйте! Подскажите, как можно найти интеграл arctg от корня (7х-1)? Какую замену сделать?
-
Алексей
- Администратор
- Сообщения: 1680
- Зарегистрирован: 18 янв 2014, 03:13
Re: Помогите с интегралом
Сообщение
Алексей » 15 апр 2016, 01:20
Добрый вечер! Насколько я понимаю, речь идет об интеграле (intmathrm{arctg}sqrt{7x-1}dx). В таком случае замены можно не делать, а интегрировать по частям. Возьмите (u=mathrm{arctg}sqrt{7x-1}) и (dv=dx).
“Именно то, что наиболее естественно, менее всего подобает человеку.” Братья Стругацкие, “Хромая судьба”
-
Алексей
- Администратор
- Сообщения: 1680
- Зарегистрирован: 18 янв 2014, 03:13
Re: Помогите с интегралом
Сообщение
Алексей » 15 апр 2016, 11:27
Полагаю, что именно та Это формула интегрирования по частям. На сайте эта тема здесь.
“Именно то, что наиболее естественно, менее всего подобает человеку.” Братья Стругацкие, “Хромая судьба”
-
MidaS
- Сообщения: 3
- Зарегистрирован: 15 апр 2016, 00:39
Лучший ответ по мнению автора |
|
|||||||||||||
|
|
Посмотреть всех экспертов из раздела Учеба и наука > Математика
Будим ли мы в месте придёте ли он назад
Решено
Электрон находится в однородном электрическом поле с напряженностью 0,5 В/м.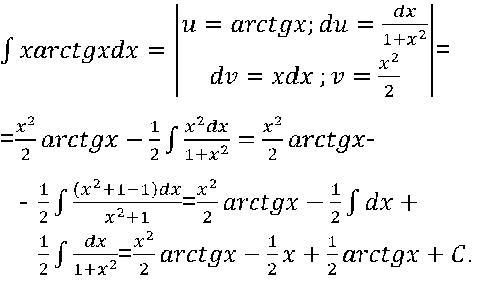
Решено
Здравствуйте.Скажите, пожалуйста, если сейчас прекратить общение с этим мужчиной, будет ли у меня другой мужчина для поддержки, или просто общаться с ним дальше? Юлия 17.01.1998 Дмитрий 07.06.1974
Купил автомобиль, есть доровор купли продажи, на автомобиле стоит запрет на рег действия по задолжности штрафа, запрет наложен судебным приставом в карачаево черкесии , если я захочу его оформить на
Здравствуйте, мое позывное Андрей 06.13.1933. Я служил в военно-морском флоте целых 34 с половиной года. У меня уже давно есть проблема
Пользуйтесь нашим приложением
Основные методы интегрирования — презентация онлайн
Похожие презентации:
Методы интегрирования
Основные методы интегрирования
Основные методы интегрирования
Неопределенный интеграл.
Методы интегрирования
Неопределенный интеграл. Методы интегрирования. Лекция 2
Неопределённый интеграл, его свойства . Непосредственное интегрирование. Метод замены переменной в неопределенном интеграле
Основные методы интегрирования. Интегрирование по частям
Методы интегрирования. (Семинар 14)
Первообразная функция и неопределенный интеграл. Методы интегрирования
1. ОСНОВНЫЕ МЕТОДЫ ИНТЕГРИРОВАНИЯ
Замена переменной
( подведение под знак дифференциала )
ПОВТОРЕНИЕ
Правило дифференцирования сложной функции
Сложная функция (или функция от функции) y f g x дифференцируется
по правилу
y’ f ‘ g x g ‘ x
Восстановление сложной первообразной функции
Проблема состоит в том, что изначально все интегралы задаются в виде
f x dx
Вы сами должны представить подынтегральную функцию в виде
произведения двух сомножителей.
(отличная от f x ) сложная функция h от внутренней функции g x , а
второй сомножитель – это производная внутренней функции g’ x .
f x h g x g ‘ x
Если такое представление сделать удалось, то процесс интегрирования можно
оформить цепочкой равенств.
Предполагается, что новый интеграл
него преобразуется.
h t d t — либо табличный, либо легко в
Главный вопрос – какую часть подынтегральной функции обозначить за
новую переменную? Однозначного ответа нет. Но следует помнить, что внутренняя
функция g x может стоять где угодно – в знаменателе, под корнем, под знаком
логарифма, в степени показательной функции, в аргументе тригонометрической
функции, а её производная может быть только сомножителем.
Пример 1. Найти интеграл
Решение.
x dx
1 x2
x dx
1 x2
Самое главное и одновременно самое сложное в начале решения – увидеть
дифференциальную связь между двумя частями подынтегральной функции.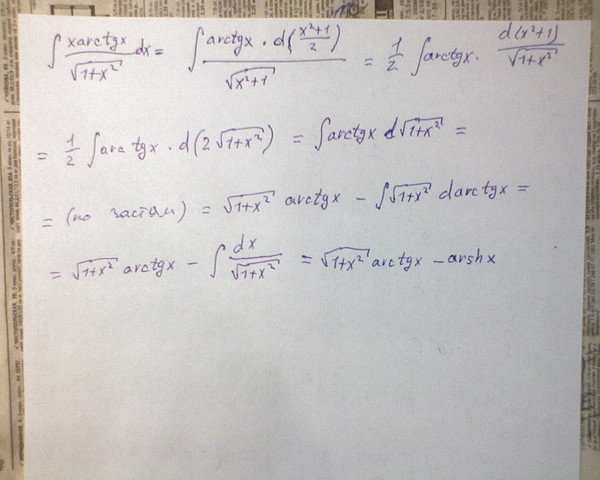
В данном примере такими частями являются числитель х и сумма в знаменателе
(1 + х2). Важно вспомнить, что производная этой суммы (1 + х2) = 2х, т.е. почти
равна числителю х. Можно сказать и иначе : выражение (1 + х2) – это почти
первообразная для числителя х. Забудьте на время, что в подынтегральной
функции есть ещё операция деления. На этапе замены переменной она роли не
играет. Не старайтесь сразу учесть все действия, которые есть в подынтегральной
функции
За новую переменную t нужно обозначить ту часть
подынтегральной функции, производная которой равна (или
очень близка ) к другой части подынтегральной функции.
Замена
x dx
t 1 x2
1 x2
dt 1 x 2 dx 2 x dx
Замечание. Если Вы ввели новую переменную t, то все подынтегральное
выражение должно содержать только переменную t , в том числе и
дифференциал должен быть dt. Но нельзя просто механически заменить dх
на dt. Выражение, которое Вы замените на dt, находится в заготовке
замены.
В примере 1 в подынтегральном выражении есть только хdx, а нужно 2хdx. Здесь
у Вас два способа.
Способ1: выразить произведение xdx из равенства dt = 2xdx как x dx dt .
2
Замена
t 1 x2
x dx x dx
2
dt
1
x
dx 2 x dx
2
2
1 x
1 x
x dx dt
2
dt
2 dt 1 dt 1 ln t C 1 ln 1 x 2 C
t
2t 2 t 2
2
Способ2: искусственно сделать в числителе подынтегральной дроби 2xdx,
умножив числитель на 2, а весь интеграл на 1 .
2
x dx 1 2 x dx
2 1 x2
1 x2
Замена
t 1 x2
1 dt 1 ln t C 1 ln 1 x 2 C
2 t 2
2
2
dt 1 x dx 2 x dx
ЗАМЕНА ПЕРЕМЕННОЙ
как подведение под знак дифференциала
Замену переменной интегрирования можно сделать и без переобозначения
внутренней функции g x новой буквой t. Последовательность действий в этом
случае задается цепочкой равенств.
f x dx h g x g’ x dx h g x dg x H g x C
Использовали понятие дифференциала функции
d g x g ‘ x dx
Этот метод ещё называется подведением под знак дифференциала (ППЗД).
Образно говоря, производная g ‘ x перемещается за букву d вправо,
превращаясь при этом в свою первообразную g x и становясь новой переменной
интегрирования вместо х.
x dx
1 x2
1
2
x 1 dx 1
2
1 x2
1
1
2
2 x
dx
1 x 1 dx
2
1 x2
1 x2
1 1 x 2 dx 1
2
2
1 x
1
2
1 d 1 x2
1 x2
d 1 x2 1
ln 1 x 2 C
2
1 x2
Можно было бы ……
x dx x 1 dx x arctg x dx x d arctg x
1 x2
1 x2
Верно. Но! Бесполезно, т.к. оставшаяся после подведения под знак дифференциала
функция сократилась до х и выражение её через arctg x возможно, но не рационально.
Пример 2. Найти интеграл
x
dx
2
x 3
Решение.
x
dx
2
x 3
dt
2
t
Замена
t x2 3
dt ( x 2 3) ‘ dx 2 xdx
xdx dt
2
dt
2 t
t C
x2 3 C
ЗАМЕНА ПЕРЕМЕННОЙ
методом определения независимой переменной х как новой функции
новой переменной t.
f x dx .
x t
Пусть требуется найти интеграл
новой переменной t, а именно,
. Предположим, что функция
дифференцируема, т.е. существует производная
dx d t t ‘ dt
Определим х как функцию
x ‘ ‘ t
x t
и её дифференциал
. Тогда переход к новой переменной интегрирования в
искомом интеграле задается цепочкой равенств.
f x dx f t d t f t t ‘ dt y t dt Y t C
Разумеется, последним шагом в решении будет возврат к старой переменной х
по формуле t -1 x . Например, x t 6 t 6 x .
x
Или x 2 sin t t arcsin
2
Внимание! -1
Символом x здесь обозначается функция, обратная функции t ,
как на калькуляторах.
Но!!
Именно с помощью такой замены находятся интегралы от функций, содержащих
корни разных степеней (или иначе от иррациональностей).
Интегрирование простейших иррациональностей
Пример . Найти интеграл
Решение.
dx
x 4 x
x t4
dx
3
dx
4
t
dt
4
x x
t 4 x
2
t
dt 4
4
t 1
Цель замены –
чтобы все корни извлеклись!
4 t 3dt
t4 4 t4
t 2 1 1 dt 4 t 2 1 dt 4
t 1
t 1
3
3
t
dt
t
dt
4 2
4
t t 1
t t
dt 4
t 1
4 x 2
t2
4 t 4 ln t 1 C 4
4 x 4 ln
2
2
4 x 4 x 4 ln
2
4
x 1 C
4
t 1 dt 4 ln t 1
x 1 C
Пример .
5 x 2 dx
Решение.
5 x
2
Замена
dx x 5 sin t
dx 5 costdt
5 1 sin t 2
5 5 sin t
2
5 cost dt
5 cost dt 5 cost cost dt 5 cos2 t dt
5 1 cos 2t dt 5 dt cos 2t dt 5 t 1 sin 2t C
2
2
2 2
5 arcsin x 1 sin 2 arcsin x C
2
5 2
5
x
5 sin t
t arcsin x
5
English
Русский
Правила
Интеграл арктангенса – Примеры, интегрирование обратного тангенса x
Интеграл арктангенса представляет собой интегрирование тангенса обратного х, которое также называется первообразной арктангенса и определяется как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C, где C — постоянная интегрирования. Интеграл от арктангенса можно вычислить методом интегрирования по частям. Интегрирование – это процесс обратного дифференцирования, т. е. определения первообразной.
Изучим интегрирование тангенса обратного x, докажем, что интеграл арктангенса равен ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C и определите определенный интеграл арктангенса вместе с некоторыми решенными примерами для лучшего понимания.
| 1. | Что такое интеграл арктангенса? |
| 2. | Интеграл доказательства арктангенса с использованием интегрирования по частям |
| 3. | Определенный интеграл обратного коэффициента загара x От 0 до 1 |
| 4. | Часто задаваемые вопросы по Integral of Arctan |
Что такое интеграл арктангенса?
Интеграл арктангенса, также называемый интегралом тангенса, обратному х, равен x tan -1 x — ½ ln |1+x 2 | + C. Математически это записывается как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C. Здесь C — константа интегрирования, dx обозначает, что интегрирование тангенса, обратное x, производится по отношению к x, а ∫ обозначает символ интегрирования. Интеграл от arctan можно вычислить методом ILATE, то есть интегрированием по частям.
Интеграл формулы арктангенса
Формула интеграла арктангенса дана,
Интеграл доказательства арктангенса с использованием интегрирования по частям
Теперь, когда мы знаем, что интеграл от arctan равен x tan -1 x — ½ ln |1+x 2 | + C, докажем это методом интегрирования по частям. Мы будем использовать следующие формулы и факты, чтобы доказать интеграл от arctan.
- Формула интегрирования по частям: ∫f(x)g(x)dx = f(x) ∫g(x)dx — ∫[d(f(x))/dx × ∫g(x) dx ] дх.
- Обратите внимание, что tan -1 x может быть записан как tan -1 x = tan -1 x.1
- Имеем f(x) = tan -1 x, g(x) = 1
- д (загар -1 х)/дх = 1/(1 + х 2 )
Используя эти формулы и факты, мы имеем
∫tan -1 x dx = ∫tan -1 x,1 dx
= tan -1 x ∫1dx — ∫0[d 1 x)/dx × ∫1 dx] dx
= x tan -1 x — ∫[1/(1 + x 2 ) × x] dx
= x tan -1 x — ∫x/(1 + x 2 ) dx
= x tan -1 x — (1/2) ∫2x/(1 + x 2 ) dx [Умножение и деление на 2]
= x tan -1 x — (1/2) ln |1 + x 2 | + C {Используя формулу ∫f'(x)/f(x) dx = ln |f(x)| + C}
Следовательно, мы доказали, что интеграл от tan, обратный x, равен x tan -1 x — (1/2) ln |1 + x 2 | + C, где C — постоянная интегрирования.
Определенный интеграл обратного коэффициента загара x От 0 до 1
Теперь определим определенный интеграл арктангенса в пределах от 0 до 1. Мы будем использовать интеграл тангенса, обратный формуле х, то есть ∫тангенс 92|+C)\&=dfrac{pi}{4}-ln2+C-0+0-C\&=dfrac{pi}{4}-ln2 end{align} )
Следовательно, определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2.
Важные замечания относительно интеграла арктангенса
- ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + С
- Определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2
- Интеграл арктангенса (x/a) определяется как ∫tan -1 (x/a) dx = x tan -1 (x/a) — (a 2 /2) ln |a 2 + x 2 | + С
Связанные темы по интегралу арктангенса
- Интегральное исчисление
- Формулы интегрирования
- Формула арктангенса
Часто задаваемые вопросы по Integral of Arctan
Что такое интеграл арктангенса в исчислении?
Интеграл от арктангенса представляет собой интегрирование тангенса, обратное х, которое определяется как ∫тангенс -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C, где C — постоянная интегрирования.
Какова формула интеграла арктангенса?
Формула интеграла арктангенса задается как ∫tan -1 x dx = x tan -1 x — ½ ln |1+x 2 | + C.
Как найти интеграл от арктангенса?
Интеграл арктангенса можно вычислить методом ILATE, то есть интегрированием по частям.
Что такое интеграл обратного тангенса х от 0 до 1?
Определенный интеграл арктангенса от 0 до 1 равен π/4 — ln 2.
Является ли интеграл арктангенса тем же самым, что и интеграл тангенса, обратный x?
Арктан также называют инверсным загаром. Следовательно, интеграл от арктангенса такой же, как и интеграл от обратного тангенса.
Является ли интеграл от Arctan равным интегралу от Arccot?
Теперь интеграл от arctan не равен интегралу от arccot, поскольку интеграл от arctan равен x tan -1 x — ½ ln |1+x 2 | + C, а интеграл от arccot равен x cot -1 x + ½ ln |1+x 2 | + К.
Ниже в табличном виде представлены формулы неопределенных интегралов тригонометрических функций: прямых, производных и обратных.
Прямые и производные функции: синус (sin), косинус (cos), тангенс (tg) и котангенс (ctg).
| Действие | Формула |
| Интеграл синуса | ∫ sin x dx = -cos x + C |
| Интеграл косинуса | ∫ cos x dx = sin x + C |
| Интеграл тангенса | ∫ tg x dx = -ln |cos x| + C |
| Интеграл котангенса | ∫ ctg x dx = ln |sin x| + C |
microexcel.ru























![{displaystyle int x^{n}operatorname {arcsec} x,dx={frac {1}{n+1}}left(x^{n+1}operatorname {arcsec} x-{frac {1}{n}}left[x^{n-1}{sqrt {x^{2}-1}}+[1-n]left(x^{n-1}operatorname {arcsec} x+(1-n)int x^{n-2}operatorname {arcsec} x,dxright)right]right)}](https://wikimedia.org/api/rest_v1/media/math/render/svg/df6b1b242f587f4c7d8f44f63fddc972c62ba510)