Заказать задачи по любым предметам можно здесь от 10 минут
Интегрирование по частям
Интегрирование по частям – метод для решения интегралов от произведения двух элементарных функций. Одна из них легко дифференцируема, а другая интегрируема. Работает техника для неопределенных и определенных интегралов.
Формула для неопределенного интеграла:
$$ int udv = uv – int vdu $$
Формула для определенного интеграла:
$$ int limits_{a}^{b} udv = uv bigg |_{a}^{b} – int limits_{a}^{b} vdu $$
Рассмотрим на практике примеры решения интегрирования по частям, которые часто предлагаются преподавателями на контрольных работах. Обратите внимание ещё раз на то, что под значком интеграла стоит произведение двух функций. Это как признак того, что для решения подойдет данный метод.
| Пример 1 |
| Найти интеграл $ int xe^xdx $ |
| Решение |
|
Видим, что подынтегральная функция состоит из двух функций, одна из которых при дифференцировании моментально превращается в единицу, а другая легко интегрируется. Для решения интеграла используем метод интегрирования по частям. Положим, $ u = x rightarrow du=dx $, а $ dv = e^x dx rightarrow v=e^x $ Подставляем найденные значения в первую формулу интегрирования и получаем $$ int xe^x dx = xe^x – int e^x dx = xe^x – e^x + C. $$ Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя! |
| Ответ |
|
$$ int xe^x dx = xe^x – e^x + C $$ |
| Пример 2 |
| Найти интеграл $ int xcos x dx $ |
| Решение |
|
В качестве неизвестных функций $ u $ и $ v $ возьмем следующие: $ u=x rightarrow du=dx $ и $ dv = cos x dx rightarrow v = sin x $. Подставим функции $ u $ и $ v $ в первую формулу $$ int x cos x dx = x sin x – int sin x dx = x sin x + cos x + C. $$ |
| Ответ |
|
$$ int x cos x dx = x sin x + cos x + C $$ |
| Пример 3 |
| Вычислить интеграл $ int limits_1 ^e xln x dx $ |
| Решение |
|
В данном задании имеем интеграл с пределами, а поэтому будем применять формулу для определенного интеграла. Введём обозначения $$ u = ln x rightarrow du = frac{dx}{x}, text{a за } dv = xdx rightarrow v = frac{x^2}{2}. $$ Осталось подставить это в формулу $$ int limits_1 ^e xln x dx = frac{x^2}{2} ln x bigg |_1 ^e – int limits_1 ^e frac{x^2}{2}frac{dx}{x} = frac{e^2}{2} – 0 – frac{1}{2} int limits_1 ^e xdx = $$ $$ =frac{e^2}{2} – frac{1}{2} frac{x^2}{2}bigg |_1 ^e = frac{e^2}{2} – frac{1}{2}(frac{e^2}{2} – frac{1}{2}) = frac{e^2}{2} – frac{e^2}{4} + frac{1}{4} = frac{e^2+1}{4} .$$ |
| Ответ |
|
$$ int limits_0 ^1 x ln x dx = frac{e^2+1}{4} $$ |
| Пример 4 |
| Вычислить интеграл $ int limits_0 ^1 (x+5) 3^x dx $ |
| Решение |
|
По аналогии с предыдущими решенными примерами разберемся какую функцию без проблем интегрировать, какую дифференцировать. Обращаем внимание, что если продифференцировать $ (x+5) $, то произойдет автоматическое преобразования этого выражения в единицу, что нам будет “на руку”. Поэтом поступаем так $$ u=x+5 rightarrow du=dx, dv=3^x dx rightarrow v=frac{3^x}{ln3} .$$ Теперь все неизвестные функции стали найдены и могут быть поставлены во вторую формулу $$ int limits_0 ^1 (x+5) 3^x dx = (x+5) frac{3^x}{ln 3} bigg |_0 ^1 – int limits_0 ^1 frac{3^x dx}{ln 3} = $$ $$ = frac{18}{ln 3} – frac{5}{ln 3} – frac{3^x}{ln^2 3}bigg| _0 ^1 = frac{13}{ln 3} – frac{3}{ln^2 3}+frac{1}{ln^2 3} = frac{13}{ln 3}-frac{4}{ln^2 3}. $$ |
| Ответ |
| $$ intlimits_0 ^1 (x+5)3^x dx = frac{13}{ln 3}-frac{4}{ln^2 3} $$ |
Метод интегрирования по частям.
Продолжаем осваивать базовые приёмы интегрирования. В предыдущих уроках мы рассмотрели три таких приёма – непосредственное интегрирование (то бишь, по таблице), метод подведения функции под знак дифференциала и метод замены переменной. Три ножки для стула. Сидеть уже можно, но… как-то неудобно.)
Сегодняшний наш урок будет началом изучения ещё одной обширной темы интегрального исчисления. Последней, четвёртой ножки для нашего стула.) А именно – метода интегрирования по частям. Великого и могучего. Фраза “интегрируем по частям” вселяет уверенность и так же обнадёживает студентов, как и фраза “решаем через дискриминант” у школьников. 🙂
В чём же заключается столь сильная мощь данного метода и почему именно он так популярен при вычислении львиной доли неопределённых интегралов? А дело вот в чём.
Ключевой момент №1
Как мы уже знаем, в отличие от производных, в матанализе не существует стандартных правил для интегралов от произведения, частного и сложной функции. Но в процессе интегрирования такие операции с функциями встречаются сплошь и рядом. И очень часто именно метод интегрирования по частям позволяет свести вычисление интеграла от навороченной функции к совсем простенькому выражению, проинтегрировать которое не составит труда. Если таблицу знать, конечно.
Ключевой момент №2
Нередко под интегралом могут стоять всякие нехорошие трансцендентные конструкции — логарифмы, арксинусы, арктангенсы и прочие ужасы. Таблица интегралов не катит: нету в ней ни логарифмов, ни арков. И замена не годится тоже.
И в таких случаях тоже надо уметь как-то выкручиваться, да…
Какие же именно интегралы берутся по частям?
Вот типовые схемы подынтегральных функций:
Например, что-то в таком духе:
Что общего во всех таких интегралах? А общее то, что подынтегральная функция представляет собой произведение (а в ряде случаев и частное) “разнородных” функций. Многочлена и логарифма, синуса и экспоненты и так далее… Или же под интегралом тусуются всякие там арксинусы, арктангенсы и прочая жесть.
Под последним шестым пунктом стоит слово “прочие”. Это такие функции, которые не относятся к предыдущим пяти типам, но которые также вполне можно проинтегрировать по частям (а иногда и только по частям). Как правило, сочетая в себе и другие способы интегрирования — замену переменной, подведение под дифференциал и т.п. Это всякие сложные экзотические функции, а также некоторые дроби и функции с корнями.
Например:
И тому подобные примеры. Их разберём в соответствующем уроке.
Ну вот. Про таинственный метод упомянули, какие именно интегралы с его помощью вычисляются — тоже. Пора бы уже начать более близкое знакомство. Знакомимся? Поехали!
Формула интегрирования по частям — вывод и смысл.
Итак, прошу любить и жаловать:
Это и есть формула интегрирования по частям собственной персоной.)
Откуда же она берётся и почему так называется? Она берётся из обычного правила дифференцирования произведения.
Все вы (надеюсь) его хорошо помните ещё со школы:
Или почти то же самое, только по-взрослому, через дифференциалы:
Все формулы в матанализе, если слева и справа стоят функции или их производные (или дифференциалы), можно почленно интегрировать. Вот и проинтегрируем левую и правую части нашего правила. Имеем полное право!
Подвешиваем на крючки левую и правую части и получаем:
Осталось сообразить, что значок интеграла всегда “съедает” значок дифференциала (согласно соответствующему свойству). Стало быть, слева останется просто произведение u∙v. А справа приведём первый интеграл к приличному виду и отправим его влево к u·v (со сменой знака, разумеется). Получим:
И, наконец, финальный бросок. Меняем местами левую и правую части и получаем:
Всё! Больше никаких научных хитростей.)
Собственно, формула производной произведения и формула интегрирования по частям — это две взаимно обратных формулы. 🙂 Так же, как и операции дифференцирования сложной функции и подведения функции под знак дифференциала. Вот и вся суть.
Запоминается формула на удивление легко и просто. Чаще всего, в виде секретного заклинания:
Интеграл у-дэ-вэ равен у на вэ минус интеграл вэ-дэ-у. 🙂
Итак, будем считать, что с происхождением формулы разобрались. Теперь разбираемся с названием – что ещё там за части какие-то. 🙂
Смотрим на формулу ещё разок:
В чём основная суть? Исходное подынтегральное выражение (то, что слева) разбивается на два кусочка. Или две части.) Причём только с помощью умножения! Именно поэтому в общей формуле я отдельно и выделяю знаки умножения.
Первая часть (первый множитель) — это некоторая функция u. Функция как функция. Выражаемая какой-то формулой.
Вторая часть (второй множитель) — это не функция, а дифференциал некоторой другой функции v. То есть, dv.
Что это за таинственные u и v? Об этом дальше подробненько будет. Никаких тайн.)
Что же происходит при применении формулы? С точки зрения математики ничего особенного не происходит:
1. Первый множитель — u — дифференцируется. Было u, а становится du.
2. Второй множитель – dv – наоборот, интегрируется. Было dv, а после интегрирования стало просто v.
Зато с точки зрения наших хотелок происходит оч-чень много полезного! Исходный интеграл:
который, по каким-то причинам, нам не очень нравится, заменяется на другой интеграл
вычисление которого должно оказаться проще исходного.
Вот и всё. Вот и вся ключевая идея применения формулы!
Что брать за u, а что за dv?
Вопрос хороший! Этот момент – стратегически самый важный при применении формулы. Давайте разбираться. В самых общих чертах.) Выпишем ещё раз формулу:
Как видно из формулы, нам надо интегрировать новое выражение v∙du. И оно должно оказаться проще старого подынтегрального выражения u∙dv. Вот такая ключевая идея — упростить исходное подынтегральное выражение!
Поскольку в новом подынтегральном выражении стоит дифференциал du, то за функцию u всегда принимается функция, упрощающаяся при дифференцировании.
И какие же функции упрощаются при дифференцировании? Как правило, это всякие ужасы типа логарифмов или “арков”. Почему же они упрощаются при дифференцировании? А потому, что их производные — гораздо более простые функции! Рациональные дроби или, в худшем случае, выражения с корнями (для арксинуса/арккосинуса). Вспоминаем нашу старую добрую таблицу производных:
И так далее. С дробью 1/х всяко проще работать в процессе интегрирования, чем с логарифмом, правда? И с арками та же история.
Точно так же упрощаются при дифференцировании и многочлены, степень которых после каждого дифференцирования понижается на единичку:
В общем, принцип выбора функции u предельно ясен — упрощение после дифференцирования. А что же со вторым множителем dv?
Поскольку множитель dv нам придётся интегрировать, то за dv всегда берётся конструкция, не усложняющаяся при интегрировании!
Например, это вполне может быть экспонента. Или же тригонометрическая функция — синус там или косинус… Или степенная функция или многочлен. Эти функции никак не усложняются при интегрировании! Почему? Вспоминаем теперь уже таблицу интегралов (первообразных): экспонента при интегрировании превращается сама в себя, синус/косинус — друг в друга (с точностью до знака), а любой многочлен степени n — также в многочлен, но степени n+1.
Запоминаем:
За функцию u всегда принимаем выражение, упрощающееся при дифференцировании.
За dv принимаем выражение, не усложняющееся при интегрировании.
Разумеется, сразу увидеть и сообразить в уме, что упростится/усложнится после дифференцирования/интегрирования, не всегда возможно. Всё от конкретного примера и от опыта зависит. Не всегда с первого раза получается. Бывает.)
Но для некоторых типовых схем я всё же приведу небольшую сводную табличку. Пользуйтесь на здоровье! 🙂
Что ж, думаю, хватит грузной теории, давайте перейдём к конкретным примерам — всё станет куда понятнее.) В этом уроке рассмотрим интегралы из группы №1.
Произведение многочлена и показательной/тригонометрической функции.
Это интегралы из первой группы нашей сводной таблички.
Общий рецепт здесь следующий:
Если под интегралом стоит произведение многочлена и показательной/тригонометрической функции, то за функцию u всегда берётся МНОГОЧЛЕН.
А что берётся за dv? А за dv всегда берётся оставшаяся часть подынтегрального выражения вместе с dx! Что уж там осталось, то и берётся, так уж формула интегрирования по частям устроена: всё подынтегральное выражение надо по кусочкам распределить между u и dv.
Вот так:
Ну что, посмотрим на формулу интегрирования по частям в действии?)
Например, пусть надо найти вот такой интересный интеграл:
Пример 1
Казалось бы, всё просто. Под знаком интеграла стоит произведение знакомых табличных функций — икса и ex. Вроде, всё хорошо. Но есть одна проблемка: общей стандартной формулы для интеграла от произведения не существует! По отдельности каждая функция интегрируется без проблем, а вот произведение — уже проблема, да…) Как быть?
Как-как… Надо разделить разные типы функций!
Вот и разбиваем наше подынтегральное выражение на кусочки! Наша задача представить конструкцию
xexdx
в виде произведения функции u и дифференциала другой функции dv.
Определяемся, что выбираем за u и за dv!
Работаем прямо по правилу для группы №1. В роли показательной функции у нас, очевидно, ex. А множитель х служит как раз тем самым многочленом, который целесообразно брать в качестве функции u. Не так очевидно, что это многочлен, но это именно он.) Состоящий всего из одного члена — икса. Бывает.)
А вот к dv мы должны отнести то, что осталось — выражение exdx.
Так и пишем:
Да-да, именно так и выделяем, прямо в тетрадке!
Итак, выбор u и dv сделан. Вот он:
Теперь следующим шагом мы начинаем операцию, которую я условно называю “миграция дифференциала”: функцию u мы будем дифференцировать и превращать в du, а dv — наоборот интегрировать и превращать в v. Таким образом, под дифференциалом вместо функции v окажется функция u. Вспоминаем нашу картинку с пляшущими человечками.)
Поехали!
Дифференцируем функцию u, считаем du:
Интегрируем множитель dv и ищем функцию v:
Внимание! Не прибавляем константу С после отыскания функции v! Ведь в качестве функции v нам нужна только какая-то одна конкретная первообразная! А не всё бесконечное множество, да…) Самая простая такая первообразная — очевидно, с константой С, равной нулю (С=0). Именно поэтому я и пишу
v = ex,
а не
v = ex + C.
А теперь берём формулу интегрирования по частям
и аккуратно подставляем все исходные данные на свои места:
И считаем:
Вот и все дела.)
Ответ:
Как всегда, для пущей уверенности, дифференцируем результат:
Ура! Совпало! 🙂
Что у нас произошло после применения формулы интегрирования по частям? А произошло то, что мешающий нам множитель х исчез из примера, и исходный интеграл от нехорошего произведения
свёлся к табличному (!) интегралу от безобидной экспоненты
Берущемуся в уме. Если таблицу знать.) Здорово, правда?
Именно так и работает формула интегрирования по частям. Разделяет разнотипные функции и превращает ужасный на вид интеграл в белый и пушистый. Вот и вся суть метода интегрирования по частям.)
А что будет, если поступить наоборот – за u принять ex, а за dv — xdx?
Не вопрос, давайте посмотрим:
Тогда, подставляя всё в формулу, получим:
Хм… И что нам с таким интегралом делать?! Даже ещё хуже стало, чем было…
Да! При таком выборе u и dv новый интеграл не упрощается, а, наоборот, усложняется! Экспоненте-то всё равно, что с ней делают — дифференцируют/интегрируют. У неё ко всем воздействиям врождённый иммунитет.) В отличие от многочлена, который при таком раскладе не понижает свою степень, а повышает. Что никак не делает пример проще, да…)
Собственно в этом-то и кроется причина выбора именно многочлена в качестве функции u для интегралов первой группы — понизить его степень.
А для общего развития запоминаем:
Если после применения формулы новый интеграл получился сложнее исходного, то, скорее всего, неудачно сделан выбор u и dv. Не падаем духом и пробуем другую комбинацию.
Эта рекомендация относится не только к этому уроку, на примеры из первой группы, а ко всему интегрированию по частям вообще.
Но самое надёжное — не бездумно расчленять подынтегральное выражение и комбинировать кусочки, задумчиво глядя на пример, а понимать общий смысл формулы и принцип выбора u и dv для конкретного типа интеграла. Уметь заранее просчитывать ситуацию и оценивать последствия того или иного выбора. Такой опыт только с практикой приходит. Прорешаете хотя бы 20-30 примеров — и проблема выбора u и dv отпадёт сама собой.)
Ну вот. Первый пример разобран по косточкам. Разумеется, так подробно расписывать следующие примеры я уже не буду. Это чисто для знакомства сделано. Чтобы общую идею уловить.)
А теперь можно записать и общий алгоритм вычисления неопределённых интегралов по частям.
Алгоритм вычисления неопределённых интегралов по частям.
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
Ну что, потренируемся в применении алгоритма?)
Пример 2
И опять под интегралом стоит произведение функций разной природы — икса и косинуса. Значит, разделяем разнородные функции и интегрируем по частям: у нас просто нет других вариантов!
Работаем строго по пунктам.
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
Очевидно, это интеграл из первой группы — типа “многочлен на синус/косинус”. Переходим к пункту 2.
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
Наше правило для первой группы гласит, что за функцию u следует принимать многочлен — то есть, просто множитель x.
Ну, а за dv, ясен перец, принимаем то что осталось, т.е. cos x dx.
Вот так:
Итак, выбор сделан. Переходим к пунктам 3 и 4. Тут всё просто, без фокусов:
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
Итак, все исходные данные для применения формулы подготовлены. Подставляем:
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
Вперёд!
Ответ:
Готово дело.)
Проверяем ответ дифференцированием:
Всё путём.)
Мы видим, что новый интеграл опять оказался табличным и берущимся в уме! От синуса. Халява! 🙂 Но далеко не всегда выпадает такое счастье. Иногда при поиске функции v надо дополнительно потрудиться. Поэтому теперь решим что-нибудь посложнее. Чтобы в ступор не впасть, в случае чего…
Пример 3
Чем-то похоже на предыдущий пример, правда? Только синус ещё затесался, в качестве третьего множителя. Поскольку перед нами снова произведение разнородных функций — икса и тригонометрии, то такой интеграл можно попробовать взять только по частям. Но под интегралом произведение трёх функций, а не двух, как обычно! Что делать?
Что-что… Не бояться, вот что! Ибо из трёх множителей всегда можно сделать два. Нас спасут… скобочки! Вот так:
А дальше опять по алгоритму. Поехали!
1. Внимательно осматриваем подынтегральную функцию и определяем, к какой группе относится данный интеграл.
Всё ясно. Это первая группа, т.к. под интегралом произведение многочлена (икса) и тригонометрии (sinx∙cosx).
2. Разбиваем подынтегральное выражение на две части (u и dv), согласно правилу именно для данной группы.
И здесь вопросов нет. Икс — это u. То, что осталось (т.е. sinx∙cosxdx) — это dv.
Итого имеем следующее:
3. Дифференцируем функцию u и считаем дифференциал du.
4. Интегрируем дифференциал dv и ищем саму функцию v.
А вот здесь начинается самое интересное.) Для поиска v нам надо проинтегрировать выражение sinx∙cosxdx.
Вот так:
Вот тут уже с ходу, в уме, этот интеграл не возьмёшь. В одно действие. Подумать надо.)
Варианта два. Можно внести косинус (или синус) под знак дифференциала и старым добрым способом, но в данном случае гораздо выгоднее искусственно выделить под интегралом синус двойного угла:
А проинтегрировать синус двойного угла уже никакого труда не составляет. В уме интегрируется. Как это делается, смотрим этот урок. Самое главное — не забываем про дополнительные коэффициенты и про знаки.
Всё. Функцию v мы нашли. Идём дальше по алгоритму.
5. Подставляем исходные данные (u, du, v, dv) в формулу интегрирования по частям.
6. Срабатываем по формуле, берём новый, более простой, интеграл ∫vdu, подставляем результат, упрощаем (если надо) и записываем окончательный ответ примера.
И снова мы видим, что новый интеграл, от косинуса двойного угла, много проще старого интеграла от сборной солянки x∙sinx∙cosx. Интегрируем косинус двойного угла, “причёсываем” ответ и добиваем наш злой пример.
Пишу подробно, со всеми знаками и коэффициентами, поскольку именно в них народ и косячит на 99%:
Ответ:
Вот и все дела.) Кому не нравятся двойные углы, те могут перейти обратно к одинарным по соответствующим формулам, но в таком виде ответ выглядит гораздо компактнее.
Что, сомнения нахлынули? Не ленимся, дифференцируем:
Нет, всё честно.)
Всё бы ничего, но… могут случаться и такие сюрпризы, когда по частям приходится интегрировать несколько раз. Разберём ещё один пример.
Пример 4
Надеюсь, общий алгоритм интегрирования по частям уже запомнился? Можно не расписывать подробно в четвёртый раз?)
В этот раз на экспоненту умножается не одинокий икс, а вполне себе полноценный многочлен. Но схема выбора u и dv та же самая.
Действуем в соответствии с алгоритмом:
Отлично. Функции u и v, а также их дифференциалы du и dv найдены. Пора приступать к интегрированию по частям. Снова прямо по формуле вставляем все исходные данные, упрощаем что упрощается и получаем:
А вот и обещанный сюрприз! Что делать с новым интегралом
В таблице такого и близко нет, обычными преобразованиями с подынтегральной функцией тоже ничего не сделаешь… Но! Можно заметить, что под новым интегралом у нас опять произведение многочлена и экспоненты! Поэтому… снова интегрируем по частям (да-да!). Утешает то, что новый многочлен (2х+1) стал уже линейным (а не квадратичным, как был изначально)! Казалось бы, мелочь, но очень существенная: новый интеграл в целом проще старого! Как и должно быть.)
Если мы сейчас отдельно возьмём этот интеграл по частям и упростим до упора, то получим такой результат:
Что, у вас не так получилось? А за знаками следили? А за коэффициентами? Не забываем, что е-2х — сложная функция! Со всеми вытекающими.)
Вот практически и всё. Возвращаемся к исходному примеру, вставляем результат промежуточного интегрирования по частям на своё место и константу не забываем.)
Получим:
В принципе, интеграл мы уже нашли. Если требуются дальнейшие упрощения и наведение марафета, то, раскрыв скобки и приведя подобные, окончательно получим:
Ответ:
Вот такой ответ. Проверочное обратное дифференцирование предлагаю провести самостоятельно.)
Чем поучителен этот пример? Как видите, здесь нам пришлось интегрировать по частям два раза! Почему? Всему виной является вторая степень нашего многочлена x2+x+1. Проблема в том, что после каждого применения формулы (т.е. взятии дифференциала du) степень многочлена понижается лишь на единичку. Как и при любом дифференцировании, да.
Например, если бы под интегралом стоял многочлен 10-й степени (да даже хотя бы простое произведение x10ex), то последовательно интегрировать по частям пришлось бы (о, ужас!) десять раз! Это огорчает. Но зато при каждом новом интегрировании степень многочлена будет становиться всё ниже. Пускай на единичку, но — ниже. Это радует.)
Запоминаем:
Интегрировать по частям требуется столько раз, какова степень многочлена.
Между прочим, в качестве показательной функции совершенно не обязательно должна стоять именно экспонента (ex, е2х и тому подобные конструкции). Запросто может оказаться вообще не “е”, а что-то типа 23х и т. п. Не надо пугаться. Принцип интегрирования тот же самый. Отличие состоит лишь в том, что при вычислении функции v будут всплывать дополнительные коэффициенты с логарифмами, которые ни в коем случае нельзя терять.
Например:
И так далее…
Итак, с первой группой интегралов, берущихся по частям, поработали. Переходим ко второй группе — логарифмам, аркам и прочим питомцам нашего зоопарка элементарных функций. В следующей теме.)
Интеграл произведения функций
ОПРЕДЕЛЕНИЕ
Интеграл произведения функций (
int f(x) g(x) d x
) в общем случае не равен произведению интегралов от каждого из факторов:
(
int f(x) g(x) d x neq int f(x) d x cdot int g(x) d x
)
В зависимости от того, какие функции находятся под знаком интеграла, интеграл от произведения в некоторых случаях может быть выражен через элементарные функции, а в некоторых случаях можно оценить определенный интеграл произведения функций. Для этого используются теоремы о среднем значении.
Средние теоремы
Теорема 1. Пусть функции (
f(x)
)и (
g(x)
) интегрируемы на отрезке (
[a ; b]
), с (
m leq f(x) leq M, x in[a ; b]
) и (
g(x) geq 0
) на (
[mathrm{a} ; mathrm{b}]
), затем
(
m(b-a) leq int_{a}^{b} f(x) g(x) d x leq M(b-a)
)
Следствие 1. Пусть функция (
f(x)
) интегрируема на отрезке (
[a ; b]
) и ограничены на этом отрезке: (
m leq f(x) leq M
) . затем
(
m(b-a) leq int_{a}^{b} f(x) g(x) d x leq M(b-a)
)
Теорема 2. Пусть функция (
f(x)
) непрерывна на отрезке (
[mathrm{a} ;mathrm{b}]
), функция (
g(x) geq 0
) интегрируема на этом сегменте. Тогда существует точка (
c in[a ; b]
) такая, что имеет место равенство:
(
int_{a}^{b} f(x) g(x) d x=f(c) cdot int_{a}^{b} g(x) d x
)
Следствие 2. Пусть функция (
f(x)
) непрерывна на отрезке (
[mathrm{a} ; mathrm{b}]
). Тогда существует (
c in[a ; b]
) такое, что
(
int_{a}^{b} f(x) g(x) d x=f(c)(b-a)
)
Примеры решения проблем на тему «Интегральные работы»
ПРИМЕР 1
Задача
Оцените Интеграл
(
int_{0}^{2} frac{5-x}{9-x^{2}} d x
)
Подынтегральная функция (
f(x)=frac{5-x}{9-x^{2}}
) определена на отрезке (
[0 ; 2]
). Используя дифференциальное исчисление, можно показать, что на этом отрезке функция принимает наименьшее значение, равное (
frac{1}{2}
) ; и самый маленький (
-frac{3}{5}
) . Тогда, согласно следствию 1, мы можем написать:
(
frac{1}{2} cdot(2-0) leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{3}{5} cdot(2-0)
)
или же
(
1 leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{6}{5}
)
1 leq int_{0}^{2} frac{5-x}{9-x^{2}} d x leq frac{6}{5}
)
ПРИМЕР 2
Оценить Интеграл
(
int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x
)
Интегральная функция (
f(x)=frac{sin x}{x}
) убывает на сегменте интегрирования (
left[frac{pi}{4} ; frac{pi}{2}right]
), поэтому справедлива оценка:
(
fleft(frac{pi}{2}right) leq f(x)=frac{sin x}{x} leq fleft(frac{pi}{4}right) Rightarrow frac{2}{pi} leq f(x)=frac{sin x}{x} leq frac{2 sqrt{2}}{pi}
)
Тогда, согласно следствию 1, имеем:
(
frac{2}{pi} cdotleft(frac{pi}{2}-frac{pi}{4}right) leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{2 sqrt{2}}{pi} cdotleft(frac{pi}{2}-frac{pi}{4}right)
)
или же
(
frac{2}{pi} cdot frac{pi}{4} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{2 sqrt{2}}{pi} cdot frac{pi}{4} Rightarrow frac{1}{2} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{sqrt{2}}{2}
)
(
frac{1}{2} leq int_{frac{pi}{4}}^{frac{pi}{2}} frac{sin x}{x} d x leq frac{sqrt{2}}{2}
)

Онлайн калькуляторы
На нашем сайте собрано более 100 бесплатных онлайн калькуляторов по математике, геометрии и физике.

Справочник
Основные формулы, таблицы и теоремы для учащихся. Все что нужно, чтобы сделать домашнее задание!

Заказать решение
Не можете решить контрольную?!
Мы поможем! Более 20 000 авторов выполнят вашу работу от 100 руб!
Интеграл произведения функций
В зависимости от того, какие функции стоят под знаком интеграла, интеграл от произведения в некоторых случаях можно выразить через элементарные функции, а в некоторых определенный интеграл произведения функций можно оценить. Для этого используются теоремы про среднее.
Теоремы про среднее
Следствие 1. Пусть функция интегрируема на отрезке
и является ограниченной на этом отрезке:
Тогда
Следствие 2. Пусть функция непрерывна на отрезке
Тогда существует
такое, что
Примеры решения задач по теме «Интеграл произведения»
| Понравился сайт? Расскажи друзьям! | |
Содержание:
- Интегральное исчисление функций одной и нескольких переменных
- Понятие первоначальной функции и неопределенного интеграла
- Неопределенный интеграл. Определение и свойства, таблица основных интегралов
- Непосредственное интегрирование
- Метод интегрирования заменой переменной
- Метод интегрирования по частям
- Интегрирование элементарных рациональных алгебраических дробей
- Интегрирование рациональных алгебраических дробей
- Интегрирование некоторых видов иррациональных функций
- Интегрирование простейших иррациональностей
- Интегрирования функций, рационально зависящих от тригонометрических функций
- Интегральное исчисление функции одной переменной
- Первоначальная функция и неопределенный интеграл
- Основные свойства неопределенного интеграла
- Таблица неопределенных интегралов
- Методы вычисления интегралов
- Непосредственное интегрирование
- Метод разложения
- Метод подстановки (метод замены переменной)
- Метод интегрирования по частям
- Интегрирование рациональных дробей
- Метод неопределенных коэффициентов
- Интегралы от простейших рациональных дробей
- Интегрирование неправильных рациональных дробей
- Метод Остроградского интегрирования рациональных функций
- Интегрирование тригонометрических функций
- Интегрирование некоторых иррациональных функций
- Понятие о неопределенном интеграле, не имеющем первообраных в элементарных функциях
- Определенный интеграл
- Задачи, приводящие к понятию определенного интеграла
- Задача об объеме производства с переменной производительностью труда
- Определенный интеграл, как предел интегральных сумм
- Основные свойства определенного интеграла
- Теорема о среднем значении определенного интеграла
- Геометрический смысл определенного интеграла
- Связь неопределенного и определенного интегралов. Формула Ньютона-Лейбница
- Методы вычисления определенного интеграла
- Замена переменной в определенном интеграле
- Метод интегрирования по частям
- Приближенное вычисление определенных интегралов
- Разложение подынтегрального выражения
- Интегрирование с помощью таблиц
- Численное интегрирование
- Несобственные интегралы и их нахождение
- Интеграл с бесконечными пределами интегрирования
- Интеграл от разрывной функции
- Применение определенных интегралов
- Вычисление площадей
- Задача о распределении доходов населения государства
- Вычисление объемов
- Понятие о двойном интеграле. Сведение двойного интеграла к повторному
- Повторный интеграл. Переход от двойного интеграла к повторному
- Интеграл Эйлера-Пуассона
Интегральное исчисление функций одной и нескольких переменных
Одной из основных задач дифференциального исчисления является нахождение производной заданной функции. Исследования во многих областях науки, в том числе и экономической, приводят к обратной задачи, а именно: возникает необходимость по данной функцией найти такую функцию, производная от которой равнялась бы исходной функции. В экономике это означает, что по предельным характеристикам (скоростями) процессов необходимо воссоздать их общие свойства (общие расходы, общая прибыль и т.д.).
После изучения данной темы вы сможете:
- ● интерпретировать содержание интегралов в математических моделях экономических процессов;
- ● владеть методами интегрирования различных функций;
- ● распознавать типы задач в экономике, для решения которых целесообразно применять интегралы;
- ● применять инструменты интегрального исчисления для нахождения исходных величин по известным функциями факторов, влияющих на них;
- ● исследовать экономическую динамику процессов с применением интегралов.
Понятие первоначальной функции и неопределенного интеграла
Функция 





Первоначальной для 

Проверить это утверждение можно, если продифференцировать функцию 

Нахождение для 

Теорема 21.1 (о множестве первичных). Если для функции 

1) их бесконечно много;
2) все они отличаются друг от друга только постоянной величиной.
Доказательство.
1. Пусть функция 







2. Пусть 






Поскольку для любого 





Например, для функции 



Следовательно, для нахождения первичных заданной функции достаточно знать только одну, а каждая другая представляет собой сумму найденной первоначальной и произвольной действительной постоянной.
Неопределенный интеграл. Определение и свойства, таблица основных интегралов
Множество всех первобытных для 


где 



Относительно выражения 
Современное обозначение неопределенного интеграла знаком 

С геометрической точки зрения любая первоначальная – это линия 


Рис. 21.1
По геометрическим содержанием производной имеем, что 






Теорема 21.2 (теорема существования неопределенного интеграла). Если функция 


Основные свойства неопределенного интеграла вытекают из определения первичной, соотношение (21.3) с привлечением свойств производной.
1 (о производной интеграла). Производная от неопределенного интеграла по переменной интегрирования равна под интегральной функции:
Действительно, согласно (21.3) и (21.2) имеем:
2 (о дифференциал интеграла). Дифференциал от неопределенного интеграла по переменной интегрирования равна подынтегральному выражению:
потому что дифференциал функции – это произведение производной функции и дифференциала аргумента.
3 (о неопределенном интеграле от дифференциала). Неопределенный интеграл от дифференциала любой функции, имеет производную, которая является однопараметрической семьей этой функции:
Обоснование такое же, как и для свойства 2.
4 (о интеграле от производной). Неопределенный интеграл от производной любой дифференцируемой функции является однопараметрической семьей этой функции:
Ниже приведены свойства, которые называют также правилами интегрирования, доводятся посредством сравнения множеств, соответствующих левой и правой частям равенств, или дифференцированием левой и правой частей равенств, которые надо доказать.
5 (об устойчивом множителе). Постоянный множитель можно выносить за знак неопределенного интеграла:
Найдем производные от обеих частей равенства. Для левой части по свойству 1 имеем: 


6 (о интеграле от алгебраической суммы функций). Неопределенный интеграл от алгебраической суммы двух функций равен сумме неопределенных интегралов от слагаемых этой суммы:
Снова найдем производные от обеих частей этого равенства. Так, для левой части имеем:
Для правой части имеем:
Как видим, производные от обеих частей равенств совпали, значит, правильная и самая равенство.
Свойство 6 обобщается на любое конечное число слагаемых.
7 (о интеграле от функции составного линейного аргумента). Если неопределенный интеграл от функции 




Для доказательства свойства 7 найдем производные от обеих частей равенства (21.11):
где 
Например, непосредственное применение формулы (21.11) дает:
8 (об инвариантности формулы неопределенного интеграла). Вид формулы интегрирования не зависит от того, является ли переменная интегрирования независимой переменной или функцией от нее:
В таблицу основных интегралов относят, как правило, те интегралы, которые можно получить непосредственно по таблице производных, если прочитать ее справа налево. В таблице 21.1 к таким интегралов еще добавлены формулы (7), (8), (15) и (16). Полный перечень интегралов от элементарных функций можно найти в справочнике по высшей математике.
Таблица основных интегралов Таблица 21.1
Справедливость каждой формулы таблицы, как и вообще результата интегрирования, проверяется дифференцированием по свойством 1 (о производной неопределенного интеграла).
Например, проверим справедливость формулы (16). Для этого найдем производную от правой части этого равенства:
Действительно, мы получили подынтегральную функцию, что и требовалось доказать.
Интегрирования функций как операция, является обратной к дифференцировке, является более сложной задачей, чем нахождение производной. Для определения производных от произведения или частного функций существуют определенные соотношения, а для интегрирования таких соотношений нет. Каким бы ни было сложным выражение, для которого нужно найти производную, это всегда можно сделать, чего нельзя утверждать относительно интегрирования. Овладение техникой интегрирования требует, прежде всего, знания неопределенных интегралов основных элементарных функций, приведены в
таблицы 21.1 и свойств неопределенных интегралов 1-8.
Непосредственное интегрирование
Непосредственным интегрированием называется нахождение неопределенных интегралов с помощью таблицы основных интегралов и основных свойств неопределенного интеграла с привлечением тождественных преобразований подынтегральной функции. Этот подход, как правило, не вызывает затруднений, но охватывает лишь узкий класс функций.
Общий порядок непосредственного интегрирования таков:
1) анализируем подынтегральное выражение с целью установления того, какие свойства неопределенных интегралов надо учесть и которые алгебраические преобразования следует предпринять, чтобы воспользоваться табличным интегралом;
2) выполняем соответствующие действия;
3) применяем соответствующие табличные формулы.
Процесс нахождения неопределенного интеграла записывается цепочкой, возможно, с указанием справочных сведений.
Приведем несколько примеров непосредственного интегрирования.
Например, найдем интеграл:
Разность двух параметров 



Проверяем правильность интегрирования с помощью дифференцирования полученной первоначальной:
Поскольку получено подынтегральная функция, то интегрирование выполнено верно.
В данном примере при интегрировании использованы свойства 3, 5 и 6, а затем были применены соответствующие формулы таблицы интегралов. Предлагаем самостоятельно проверить, является ли полученный результат правильным.
При преобразовании подынтегральной функции было использовано соотношение 

Метод интегрирования заменой переменной
Если неопределенный интеграл не является табличным, то во многих случаях цели приведет метод интегрирования заменой переменной. Нахождение неопределенного интеграла с помощью перехода от переменной интегрирования 

Основой этого метода является свойство 8 (об инвариантности формулы неопределенного интеграла).
Связь между переменными интегрирования – выходной 




1. Подстановка 


После нахождения интеграла по переменной 

На базе соотношений (21.13) и (21.14) получаем:
Найдем неопределенный интеграл:
Подынтегральная функция содержит составленную функцию 



Заметим, что без предварительных тождественных преобразований подынтегральной функции не всегда сразу удается осуществить выбор соответствующей подстановки:
2. Подстановка 

Найдем неопределенный интеграл:
Чтобы избавиться иррациональности, выполняем подстановку 

Подстановка, которая помогает упростить подынтегральная функцию и свести интеграл к табличному, может быть и не единственной.
Как обобщение того, что рассматривалось выше, приведем общий порядок интегрирования методом подстановки:
1) выбираем тип замены переменной 

2) переходим в подынтегральное выражение в новой переменной 
3) находим неопределенный интеграл по новой переменной интегрирования;
4) возвращаемся к исходной переменной
Приведем иллюстративный пример.
Соотношение (21.18) часто используется как готовая формула. Итак, если под интегральной функцией является дробь, числитель которой является производной знаменателя, то одна из первоначальных – это натуральный логарифм модуля знаменателю.
Метод интегрирования по частям
Теорема 21.3 (формула интегрирования по частям). Если в неопределенном интеграле 




Доказательство. Если 


В формуле (21.19) произвольную постоянную 
Нахождение неопределенного интеграла 
Вполне понятно, что представление подынтегрального выражения 

Общий порядок интегрирования по частям:
1) разбиваем подынтегральное выражение на части 



2) находим дифференциал функции 


3) применяем формулу интегрирования по частям (21.19)
4) берем неопределенный интеграл 
Рассмотрим примеры интегрирования по частям и образец оформления символических записей:
Формула интегрирования по частям имеет более ограниченную область применения, чем метод подстановки. Однако существуют такие типы подынтегральных функций, интегралы от которых можно найти только интегрированием по частям. В таблице 21.2 приведены три типа стандартных интегралов, к которым применяется метод интегрирования по частям с особенностями разбиения подынтегрального выражения на 
Типы интегралов, для нахождения которых применяется метод интегрирования по частям Таблица 21.2
К первому типу относят неопределенные интегралы, подынтегральные функции которых являются произведением многочлена 









Второй тип охватывает неопределенные интегралы, подынтегральные функции которых представляют собой произведение многочлена 




К третьему типу относятся неопределенные интегралы, при двукратном интегрировании которых по формуле (21.19) получаем линейное уравнение относительно исходного интеграла. Решение этого уравнения и дает искомый интеграл. Для произведений показательной функции 








Приведем примеры нахождения неопределенных интегралов каждого типа.
где
Для 
В заключении:
Следовательно, неопределенный интеграл первого типа требует применения формулы интегрирования по частям 

Итак, окончательный ответ:
До последнего интеграла тоже применяем формулу интегрирования по частям:
Таким образом, получаем уравнение относительно исходного интеграла:
Решаем его и записываем окончательный результат:
Интегрирование элементарных рациональных алгебраических дробей
Простейшими рациональными алгебраическими дробями называются дроби четырех типов, а именно:
где 

При нахождении неопределенных интегралов от дробей первого и второго типов не возникает трудностей, они легко берутся методом непосредственного интегрирования:
На практике такие неопределенные интегралы, как правило, берутся устно: условие – ответ.
Например:
Аналогично действуют, когда знаменатели дробей являются линейными функциями от 



При интегрировании простого дроби третьего типа сначала в знаменателе выделяем полный квадрат, а затем вводим новую переменную.

Выделяем в знаменателе полный квадрат двучлена
Выполняем замену переменной 

Поскольку 

Возвращаясь к исходной переменной, получаем:

Приведем пример взятия неопределенного интеграла от дроби 
Рассмотрен подход к интегрированию простейших дробей третьего типа без принципиальных изменений переносят на некоторые не элементарные дроби, знаменатель которых содержит квадратный трехчлен, а именно:













Рекуррентная формула для случая 
По известному 

Интегрирование рациональных алгебраических дробей
Рациональной алгебраической дробью 
где 



Если все коэффициенты при степенях 
Правильной рациональной дробью называется дробь, степень числителя 



Если дробь неправильный, то его всегда можно представить в виде суммы многочлена 
где 
Представление дроби в виде (22.8) называется выделением целой части.
Для этого надо выполнить деление «ступеньками» числителя дроби на его знаменатель. Рассмотрим это на примере.
Найдем целую часть неправильной дроби
Деление «ступеньками» дает:
Следовательно,
Поскольку интегрирование многочлена как суммы степенных функций не вызывает затруднений, то для интегрирования любых – правильных и неправильных – рациональных дробей надо уметь интегрировать правильные дроби.
Примем без доказательства теорему высшей алгебры, которая позволяет свести интегрирования любого дроби к интегрированию рассмотренных выше простых дробей.
Теорема 22.1. Любой правильный рациональный алгебраический дробь можно представить как сумму элементарных дробей – разложить на сумму элементарных дробей.
Разложение 

1) раскладываем знаменатель дроби – многочлен 
где однотипные множители могут повторяться (например, множитель 



2) ставим в соответствие каждому множителю самый рациональный алгебраический дробь или их сумму (табл. 22.1)
3) записываем 
Соответствие между множителями знаменателя и простейшими дробями Таблица 22.1
Следовательно, получаем:
где 
Надо заметить, что в этом раскладе будет столько дробей, сколько корней имеет многочлен 

4) определяем числовые параметры расписания, то есть его коэффициенты.
Реализацию этого шага осуществляют с помощью так называемого метода неопределенных коэффициентов, согласно которому нахождение коэффициентов разложения сводится к решению системы линейных уравнений. В основе метода лежат следующие свойства:
а) равенство не нарушится, если обе его части умножить на одно и то же выражение, определенное на множестве действительных чисел;
б) в равных многочленов коэффициенты при одинаковых степенях переменной равны между собой.
Рассмотрим примеры интегрирования рациональных алгебраических дробей.
Подынтегральная функция является правильным рациональным дробью. Разложим эту дробь на простейшие дроби:
Умножим обе части равенства на знаменатель 
Находим коэффициенты 
Осталось найти 

Следовательно,
Под знаком интеграла знаменатель правильной дроби имеет только один действительный корень 

Опять умножим обе части равенства на знаменатель
Определяем коэффициенты
Следовательно, исходный интеграл запишется в виде суммы двух интегралов от простых дробей, которые легко берутся:
Интегрирование некоторых видов иррациональных функций
Иррациональным называется алгебраическое выражение, содержащее операцию извлечения корня.
Интегрирование простейших иррациональностей
Так называют нахождения неопределенного интеграла от функций, зависящих от дробных степеней переменной 

1. Неопределенный интеграл функции, рационально зависит от дробных степеней переменной 
Такой интеграл сводится к интеграла от рациональной функции относительно новой переменной 





Выполним в интеграле (22.10) подстановку:
где 

Рассмотрим интеграл:
Анализ степеней переменной 


Обратите внимание, что выделение целой части неправильной дроби в данном примере осуществлялось не делением «ступеньками», а путем тождественных преобразований.
2. Неопределенный интеграл от функции, рационально зависит от дробных степеней линейной функции переменной 
Такой неопределенный интеграл рационализируется с помощью подстановки 

Нахождение неопределенного интеграла (22.11) ничем принципиально не отличается от интегрирования по формуле (22.10), но соответствующие изложения – символические записи – более громоздкие, особенно при возвращении к исходной переменной.
Пусть в предыдущем примере вместо 


и первоначальная под знаком радикала содержать не просто 
3. Неопределенный интеграл от функции, рационально зависит от дробных степеней дробно-линейной функции переменной 

рационализируется подстановкой: 

Замена переменной осуществляется с учетом преобразований:
где 

Найдем неопределенный интеграл:
Осуществляем подстановку:
Получили подынтегральную функцию, которая является правильным рациональным алгебраическим дробью.
Вместо трех отдельных неопределенных интегралов от простейших иррациональностей можно было бы рассматривать только (22.12), поскольку все другие являются его частными случаями.
Неопределенные интегралы, первобытные которых не выражаются через конечное число элементарных функций, называют интегралами, которые не берутся в конечном виде. К таким интегралов, например, относятся:
Интегрирования функций, рационально зависящих от тригонометрических функций
І. Интегрирование произвольных рациональных функций от
Рассмотрим способы, с помощью которых берутся интегралы вида
где 

Общий подход к интегрированию таких функций заключается в применении подстановки 
Действительно:
как видим, 

Привлечем тригонометрические формулы представления функций 
Заданный интеграл принимает вид:
так результатом арифметических операций над дробями есть дроби.
Применим эту подстановку к интегралам вида:

Найдем
Сделаем подстановку
Тогда получим:
Найдем
Используя универсальную тригонометрическую подстановку 

Найдем
Надо отметить, что интегралы, содержащие в знаменателе степени 

и получим:
Найдем
С помощью подстановки 
Подынтегральная функция является правильным рациональным дробью.
Раскладываем его на сумму простейших:
После умножения обеих частей равенства на 
Если



Для нахождения 


Подставляем в систему 
Следовательно,
Универсальная тригонометрическая подстановка часто приводит к сложным, громоздких выражений, поэтому целесообразно рассмотреть отдельные случаи интегралов типа 
ІІ. Интегрирования функций, нечетных (четных) относительно синуса или (и) косинуса. Функция 

есть знак функции меняется на противоположное, если в ней заменить или 


Функция 


есть функция не меняется, если в ней одновременно заменить 



Правило введения новой переменной. Если функция
1) нечетная относительно функции 

2) парная относительно функций 



Найдем неопределенный интеграл
Поскольку подынтегральная функция нечетная относительно функции 
Предлагаем интегрирование суммы дробей осуществить самостоятельно.
Если в подынтегральной функции 


ІІІ. Интегрирование произведения целых степеней синуса и косинуса:

Такие неопределенные интегралы являются частным случаем рассмотренных выше (см. II), поэтому если:



В третьем случае часто вместо предложенных подстановок используют формулы снижения степени (тригонометрических функций):
Они позволяют в ряде случаев избежать введения новой переменной.
Найдем интеграл
Поскольку подынтегральная функция содержит 


Неопределенные интегралы, для нахождения которых используются формулы преобразования произведения тригонометрических функций на сумму, выделяют в отдельный вид.
IV. Интегрирование произведения первых степеней синусов и косинусов, имеющих различные аргументы.
Так называют взятие неопределенных интегралов вида:
где 

Нахождение неопределенных интегралов (22.21) сводится к непосредственному интегрированию благодаря применению таких тригонометрических формул:
Найдем, например, интеграл от произведения синусов:
V. Интегрирование натуральных степеней тангенса и котангенса:
Нахождение таких интегралов можно осуществлять введением новой переменной 

Подынтегральная функция 
Аналогично поступают при взятии интегралов от натуральных степеней функции
Найдем интеграл
Вводим новую переменную 
К нахождению рассмотренных интегралов сводятся неопределенные интегралы вида:
Действительно, если использовать соотношение (22.16) и (22.17), получим:
Раскрыв скобки, получим интеграл от суммы степеней 
VІ. Интегрирование квадратичных иррациональностей (тригонометрические подстановки).
Общий подход к рационализации соответствующих интегралов
где рассматриваются все пары знаков, кроме 

Анализируя подынтегральное выражение, убеждаемся, что благодаря тригонометрическим подстановки переменная 

Например:
Для того чтобы избавиться от радикала в интегралах 1, 2, 3 (табл. 22.2), используют соответственно такие тригонометрические формулы:
Таблица 22.2 Тригонометрические подстановки для рационализации неопределенных интегралов

Найдем неопределенный интеграл
Под знаком радикала имеем двучлен 

Ответ значительно упрощается, если задействовать формулу тангенса половинного угла и некоторые другие соотношения:


Интегральное исчисление функции одной переменной
Одной из основных задач раздела IV “Дифференциальное исчисление функций одной переменной” является задача нахождения производной от заданной функции. Раздел математики, который решает обратную задачу — нахождение функции по ее производной (интегрирование), а также другие задачи, непосредственно связанные с интегрированием, называется интегральным исчислением. Предметом изучения данного раздела являются интегралы: определенный, неопределенный, поверхностный, криволинейный, двойной, тройной, и их свойства, методы нахождения,
их применение к решению различных задач.
Интегральное исчисление практически возникло из задач вычисления площадей и объемов различных фигур и тел. Впервые такие задачи пытались решить ученые Древней Греции (Евдокс Книдский, Архимед и др.). В XVI – XVII вв. интенсивное промышленное развитие в Европе привел к развитию интегрального исчисления и его применения. Труды ученых И. Кеплера, Б. Кавальери, П. Ферма, Э. Торричелли, Дж. Валлиса, Б. Паскаля, Х. Гюйгенса углубили теоретические основы интегрального исчисления. Ученые И. Ньютон и Лейбниц создали ряд общих методов нахождения интегральных сумм. Их работы много
задач интегрального исчисления свели к чисто технического уровня. Г. Лейбниц ввел удобную символику, которая применяется и сейчас. А формула Ньютона-Лейбница, которая связала неопределенный и определенный интегралы, является центральной формулой интегрального исчисления. Дальнейшее историческое развитие интегрального исчисления связано с именами И. Бернулли, Л. Эйлера, П. Чебышева, О. Коши, В. Буняковского. Существенными для развития интегрального исчисления являются работы
выдающегося украинского математика М. В. Остроградского (12.09.1801–20.12.1861, родился в с. Пашеновка, Козельского р-на Полтавской обл.), учился в Харьковском университете, где его учителями были Т. Ф. Осиповский и А.Ф. Павловский. Во время пребывания в Париже слушал лекции А. М. Ампера, О. Л. Коши, П. С. Лапласа, С. Д. Пуассона, Ж. Б. Ж. Фурье. Друг В. Я. Буняковского. Находясь в Петербурге, подружился с Т. Г. Шевченко. Основные труды М. В. Остроградского касаются математической физики, математического анализа (формула связи интеграла по объему с интегралом по поверхности, принцип разложения функций в ряд по собственными функциями, принцип локализации для тригонометрических рядов, правило преобразования переменных в двойных интегралах, метод интегрирования рациональных функций и др.), теоретической механики. Решил некоторые задачи по теории чисел, алгебры, дифференциальных уравнений, теории рядов.
Первоначальная функция и неопределенный интеграл
Задача нахождения для функции f (x) такой функции F (x), что F’ (x) = f (x) является основной задачей интегрального исчисления. Операция интегрирования (нахождение интеграла) является обратной операцией к дифференцированию (нахождение производной). Термин
“интеграл” происходит от латинского integer — целый. Иногда использует термин “антипроизводная”.
Определение 1. Функция F (x) называется первообразной для функции f (x), если для любого х из области определения f (x),
F’ (x) = f (x) или dF (x) = f (x) dx. (6.1)
Например,
а) для f (x) = 2cos x, первообразной есть F (x) = 2 sin x, потому что
F’ (x) = (2 sin x) ‘= 2cos x = f (x).
б) для f (x) = 4x3 — F (x) = x4, потому что F’ (x) = (x4) ‘= 4x3 = f (x).
Отыскание первообразной является операцией неоднозначной. Так F (x) = x4 + 5, F (x) = x4 – 24,3 и F (x) = x4 + 179 и т. д. и вообще, F (x) = x4 + C, где С — произвольное постоянное число является первообразной для f (x) = 4 x3.
ТЕОРЕМА 1. Если F1 (x) и F2 (x) — две первообразные для функции f (x) на отрезке [a; b], то разница между ними равна постоянному числу.
Доказательство. Пусть 




Определение 2. Совокупность всех первообразных для функции f (x) называется неопределенным интегралом от этой функции и обозначается

При этом F’ (x) = f (x), f (x) называется подынтегральной функцией, f (x) dx —подынтегральным выражением, ∫ — знак неопределенного интеграла.
Операция отыскания первообразной для данной функции называется интегрированием. Таким образом, неопределенный интеграл — это множество всех функций, производная которых равна подынтегральной функции, а дифференциал равен подынтегральному выражению.
Основой для интегрального исчисления является такая теорема.
ТЕОРЕМА 2. Если функция непрерывна, то для нее существует первообразная, а следовательно, и неопределенный интеграл.
(Доказывается в фундаментальных курсах высшей математики). С геометрической точки зрения неопределенный интеграл — это семейство кривых, каждая из которых образуется смещением одной из них параллельно себе вверх или вниз (рис. 1).
Рис. 1.
Основные свойства неопределенного интеграла
ТЕОРЕМА 3. (Свойство 1) Производная от неопределенного интеграла равна подынтегральной функции:

Доказательство. Согласно определению (6.2), 
Итак производная от первообразной равна подынтегральной функции.
ТЕОРЕМА 4. (Свойство 2) Дифференциал от неопределенного интеграла равен подынтегральному выражению:

Доказательство. По определению дифференциала d (f (x)) = f ‘(x) dx.
Поэтому
ТЕОРЕМА 5. (Свойство 3) Неопределенный интеграл от дифференциала некоторой функции F (x) равен этой функции с точностью до произвольной постоянной:

Доказательство. Продифференцируем левую и правую части равенства.
Получим: 

Правые части равенств одинаковы. Значит равны и левые. Теорему доказано.
Аналогично, дифференцированием левой и правой частей равенства доказываются теоремы 6 и 7.
ТЕОРЕМА 6. (Свойство 4) Постоянный множитель можно выносить за знак неопределенного интеграла:

ТЕОРЕМА 7. (Свойство 5) Интеграл от алгебраической суммы конечного числа функций равен алгебраической сумме интегралов от этих функций:

Таблица неопределенных интегралов
Интегрирования является операцией, обратной к дифференцированию. Поэтому формулы интегрирования получают из формул для нахождения производных. А универсальность применения формул интегрирования следует из теоремы о независимости вида неопределенного интеграла от выбора аргумента (инвариантность неопределенного интеграла относительно переменной интегрирования).
ТЕОРЕМА 8. Пусть f (x) — некоторая непрерывная функция на данном промежутке, х — независимая переменная, F (x) — ее первообразная, ∫ f (x) dx = F (x) + C , и пусть u = φ (x) непрерывно дифференцируемая функция. Тогда ∫ f (u) du = F (u) + C. (6.9)
Доказательство. Рассмотрим интеграл ∫ f (u) du = ∫ f (u) u’dx. В этом случае сложная функция F (u) = F (φ (x)) является первообразной для f (u).
Действительно, вследствие независимости дифференциала первого порядка от выбора независимой переменной, получаем
dF (u) = F’ (u) du = f (u) du. При этом

Поэтому, из справедливости формулы (6.3), следует справедливость формулы

Итак формулами интегрирования можно пользоваться при любой переменной интегрирования. Используя таблицу дифференциалов основных элементарных функций, выведем некоторые формулы интегрирования. Другие выводятся аналогично.
1) Интегрируя формулу 

2) В случае показательной функции, используем формулу 




3) Выведем формулу интегрирования из формулы:

Получим 
Итак, 
4) Интегрируя формулу дифференцирования 


Используя эту формулу, будем иметь:

5)
Для вывода этой формулы используют формулу для нахождения дифференциала 

Интегрируя эту формулу (левую и правую часть) и, сделав преобразование, получим

6) Формулы 
и 
доказываются дифференцированием левой и правой частей равенства.
Такой метод доказательства формул можно использовать для любой формулы интегрирования.
7) Докажем справедливость формулы 
Пусть х > 0. Тогда 

Для компактности все формулы сводят в таблицу.
Методы вычисления интегралов
Непосредственное интегрирование
Непосредственное интегрирование — это метод, который заключается в прямом применении табличной формулы и свойств неопределенного интеграла.
Пример 1.
Использовали формулу 
Пример 2. 
Для нахождения этого интеграла использована формула

Пример 3. 
В данном случае, после элементарных преобразований, интегрируем по формуле 
Метод разложения
Метод разложения заключается в том, что интеграл раскладывают на сумму (разность) табличных интегралов.
Пример 4.


При интегрировании этого выражения учтено то, что постоянный множитель выносится за знак интеграла, а также то, что сумма произвольных постоянных интегрирования тоже постоянна, и ее записывают как одну.
Метод подстановки (метод замены переменной)
Метод заключается в том, что вводится новая переменная x = φ (t), или t = ψ (x). Удачной заменой часто удается существенно упростить интеграл и даже свести его к табличному.
Пусть x = φ (t) — дифференцируемая функция от t, производная φ’ (t) которой сохраняет знак на промежутке интегрирования.
Формулу замены переменной 

Пример 5. Найти ∫ tg (x – 3) dx.
Решение. При интегрировании данного выражения вводим замену t = cos (x-3). Тогда dt = dcos (x – 3) = –sin (x – 3) dx. Получаем:
Пример 6. Найти 
Решение. Вводим замену x2 + 3 = t. Определяем dt = 2xdx. Учитывая, что 

Рассмотрим еще две важные формулы, которые существенно ускоряют интегрирование: 
и 
Выведем их. Если ∫ f (u) du = F (u) + C и u = ax + b — линейная функция от х, то du = d (ax + b) = adx. Подставив в выражение для интеграла, получим ∫ f (ax + b) d (ax + b) = a∫ f (ax + b) dx = F (ax + b) + C.
Из последнего равенства следует, что
Вторая формула выводится на основании формулы 

Пример 7. 
Пример 8. Найти 
Решение.
Метод интегрирования по частям
Пусть заданы две непрерывно дифференцированные функции u (x) и v (x). Рассмотрим дифференциал произведения: d (u ⋅ v) = udv + vdu. Проинтегрируем это выражение: ∫d (u⋅ v) = ∫ udv + ∫vdu. Преобразовав, получаем формулу интегрирования по частям:
∫ udv = uv – ∫ vdu. (6.19)
Применяя эту формулу, подынтегральное выражение f (x) dx подают в виде произведения множителей u и dv. Для данного метода имеет большое значение правильный выбор функций u и v. Необходимо, чтобы множитель dv был выражением, которое интегрируется. Есть несколько видов интегралов, для которых правила выбора функций u и v известны.
а)
Подынтегральное выражение содержит произведение многочлена на тригонометрическую, или многочлена на показательную функцию. Выбираем за u многочлен, а за dv — оставшееся выражение.
Пример 9. Вычислить ∫ x sin 3 xdx.
Решение. Применяем метод интегрирования по частям (6.19): ∫udv = uv-∫vdu. Выбираем: u = x, dv = sin 3x dx. Тогда du = dx, 

б) 
Подынтегральное выражение — произведение многочлена на логарифмическую или многочлена на аркфункцию. За dv берем произведение многочлена на dx, а за u — логарифмическую или аркфункцию.
Пример 10. Вычислить ∫ arctg xdx.
Решение. За u берем arctg x, за dv — dx. Тогда 
в)
В этом случае выбор u и v несущественны.
Пример 11. Найти
Решение. Выберем u = e3x, а dv = sin xdx. Тогда du = 3e3xdx, v = –cos x. Итак,

Тогда dv = cos xdx, v = sin x. Получаем
Искомый интеграл есть в правой и в левой частях равенства. Определим его:
Итак
Такие интегралы иногда называют циклическими или круговыми. При их интегрировании обязательно по u дважды выбирать ту же самую функцию.
Примечание: В случае, если подынтегральное выражение является произведением многочлена на одну из рассмотренных функций, можно интеграл разложить на сумму нескольких интегралов. Например,
Интегрирование рациональных дробей
Функциями, которые всегда интегрируются, есть рациональные дроби. Пусть 


Если степень числителя меньше степени знаменателя, то дробь называется правильной. Если же степень числителя больше или равна степени знаменателя, то дробь называется неправильной. Так, например, 

Теорема Вейерштрасса о приближении. Любую функцию f (x), непрерывную на (а, b), можно с заранее заданной произвольной погрешностью заменить многочленом
То есть, практически, много интегралов можно свести к интегрированию рациональных функций. Из алгебры известно, что всякий многочлен можно разложить на произведение множителей вида (x – b) и (x2 + px + q), так называемых неприводимых многочленов, где (x2 + px + q) — квадратный трехчлен, который имеет действительные корни. И всякую правильную дробь можно разложить на сумму простых:

Это делают методом неопределенных коэффициентов.
Метод неопределенных коэффициентов
Метод неопределенных коэффициентов дает алгоритм для нахождения коэффициентов разложения правильной рациональной дроби на сумму простых.
Пусть

Сводим правую часть равенства к общему знаменателю. Приравниваем соответствующие коэффициенты числителя левой части к коэффициентам числителя правой. Получаем систему линейных алгебраических уравнений. Ее решения являются коэффициентами разложения.
Пример 12.
Это пример разложения правильной рациональной дроби на сумму простых, где А1, А2, В, Мi, Ni — неопределенные коэффициенты.
Пример 13. Найти интеграл 
Решение.

х3 + х – 10 = (х – 2) (х2 + 2 х + 5). Для уравнения х2 + 2х + 5 = 0, D = 4 – 20 < 0. Поэтому уравнение не имеет действительных корней.
Итак, 
Сведя к общему знаменателю и приравняв числительные
получим: 
Приравнивая соответствующие коэффициенты получаем:
N = 9 + 4M; – 13M – 18 = 8; – 13M = 26; M = -2; N = 1; A = 2.
Мы получили интегралы от дробей (6.20). Итак:

Найдем, соответствующие простым дробям (6.20) интегралы, а затем завершим пример, использовав полученные результаты.
Интегралы от простейших рациональных дробей
а)
При решении использована формула (6.7) и табличный интеграл 
б) 
в) 

Пример 14. Найти
Используя формулу (6.23), запишем

Однако, на практике это громоздкую формулу применяют редко, а интеграл ищут, выделив в знаменателе полный квадрат.
x2 – 4x + 8 = x2 – 4x + 4 + 4 = (x – 2) 2 + 22. Сделаем замену (х – 2) = u.
Тогда

г) 


Интеграл 
Интеграл 


понижается порядок знаменателя. Использовав ее (к – 1) раз, приходим к интегралу 
Мы рассмотрели четыре случая, к которым сводится интегрирование правильных рациональных дробей. Завершим решение примера 13, используя выведенные формулы:

Интегрирование неправильных рациональных дробей
Интегрирования неправильных рациональных дробей сводится (после выделения целой части дроби) к интегрированию многочлена и интегрированию правильной рациональной дроби.
Пример 15. Вычислить интеграл
Решение. Рациональная дробь неправильная. Выделяем целую часть и записываем ее в виде суммы целой и дробной частей.

Тогда
Используя метод неопределенных коэффициентов, раскладываем дробь на сумму простых:

Итак 
Метод Остроградского интегрирования рациональных функций
Это метод выделения алгебраической части в неопределенных интегралах от рациональных функций. Пусть Р (х) и Q (x) — многочлены с действительными коэффициентами. Степень Р (х) меньше степень Q (x). То есть 
Пусть, также 

многочлены Р1 (х), Р2 (х), степени которых меньше степени Q1 (x), Q2 (x) соответственно, такие что 
Коэффициенты многочленов Р1 (х) и Р2 (х) можно найти методом неопределенных
коэффициентов, продифференцировав (6.25). Q1 (x) является наибольшим общим делителем Q (x) и его производной Q’ (x) и можно определить с помощью метода Евклида.
Q2 (x) = Q (x) / Q1 (x). Формула сводит интегрирование правильной рациональной дроби к интегрированию правильной рациональной дроби, знаменатель которой имеет простые
корни.
Пример 16. Найти интеграл 
Решение. Разложим многочлен (x3 + 1) на простые множители: x3 + 1 = (x + 1) (x2 – x + 1). Тогда, по методу Остроградского, запишем:
Дифференцируем это выражение и сводим к общему знаменателю.
Приравниваем числители:
1 = -Ax4 – 2Bx3 – 3Cx2 + 2Ax + B + D (x5 – x4 + x3 + x2 – x + 1) + (Mx + N) (x4 + x2 + x + 1). Приравнивая соответствующие коэффициенты, получаем
0 = D + N; 0 = –A – D + M + N; 0 = –2B + D + N; 0 = –3C + D + M; 0 = 2A – D + M + N; 1 = B + D + N.
Решением этой системы уравнений является: A = C = 0; B = 1/3; D = 2/9; M = -2/9; N = 4/9.
Итак
Интегрирование тригонометрических функций
При интегрировании тригонометрических функций важно уметь использовать тригонометрические формулы, удачно подобранной заменой или подстановкой свести
интеграл к более простому (дробно-рациональному выражению), а в результате — и к табличному. Есть некоторые виды интегралов (однако не все), для которых существуют правила их нахождения.
а) Интегралы вида
Если хотя бы одно из чисел m или n — положительное целое нечетное число, например
m, то вводим замену cosx = t. Тогда
Если же n — положительное нечетное, то sin x = t,
Пример 17. Найти 
Решение.
Если m и n — четные неотрицательные числа, то понижают степени по формулам:
Пример 18. Найти ∫ cos2 xdx
Решение.
б) интегралы вида 
Эти интегралы упрощаются применением формул преобразования произведения тригонометрических функций в сумму:
Такие интегралы имеют широкое применение в теории рядов Фурье.
Пример 19. Найти ∫ sin5 x cos 3x dx.
в) интегралы вида ∫ R (sin x, cos x) dx, универсальная тригонометрическая подстановка.
Для интегралов вида 


Тогда:
Пример 20. Найти 
и дальше интегрируем как рациональную дробь (пункт 6.1.5.). Интегрирование тригонометрических функций и интегрирование иррациональных функций удачно подобранной заменой часто сводится к интегралу от рациональной дроби, который и всегда интегрируется.
Интегрирование некоторых иррациональных функций
Интегралы вида 
Пример 21. Найти
Решение. Использована замена: x – 3 = t6, dx = 6t5dt, 
А дальше ищем интеграл от рациональной функции (пункт 6.1.5.).
Интегралы 



Для интегралов вида 

В заключение следует заметить, что различные способы интегрирования
могут привести к различным аналитическим выражениям первообразной. Однако мы
получаем выражения, которые отличаются разве что на постоянную.
Понятие о неопределенном интеграле, не имеющем первообраных в элементарных функциях
До этого момента мы удачно решали задачу нахождения неопределенного интеграла для функции. Однако, мы увидели, что эта задача не является простой. Более того, доказано, что есть ряд функций, первообразная для которых не может быть представлена, как выражение, образованное “элементарными” функциями. Приведем в качестве примера некоторые такие интегралы: 
Определенный интеграл
При решении некоторых важных задач необходимо находить бесконечную сумму бесконечно малых слагаемых. Это приводит к одному из центральных понятий математики — определенному интегралу.
Задачи, приводящие к понятию определенного интеграла
Задача о площади криволинейной трапеции
Рис. 2.
Найдем площадь фигуры, ограниченной графиком непрерывной функции y = f (x) на
отрезке [a, b], осью абсцисс, и прямыми x = a и x = b. Назовем ее криволинейной трапецией (рис. 2). Для простоты, рассмотрим случай, когда f (x) ≥ 0 на данном отрезке [a, b]. Разобьем промежуток [a, b] на n отрезков [xi-1 , xi] (i = 1, 2, 3 … n), x0 = a , xn = b. На каждом из отрезков [xi-1 , xi] — выберем по произвольной точке 






Доказано, что выбор точек разбиения на площадь S не влияет.
Задача об объеме производства с переменной производительностью труда
Анализируя любое производство видно, что производительность есть величина переменная и в разные моменты разная. Пусть производительность за период от 0 до t (определенный период времени) описывается функцией f (t). Разобьем промежуток [0; t] на n промежутков продолжительностью Δti и считая производительность за время Δti постоянной и равной f (ti) определим, приблизительно, объем продукции произведенной за промежуток времени (tk; tl) как 


Определенный интеграл, как предел интегральных сумм
Проведем рассуждения аналогично соображениям предыдущего пункта. Для непрерывной функции f (x) , определенной на [a, b], и для разбиения 

Сумму (6.27) называют интегральной суммой. Введем еще одну величину maxΔxi — это длина наибольшего из отрезков Δxi = xi – xi-1
Определение 3. Функция f (x) называется интегрируемой на [a, b], если существует конечный предел

Определение 4. Число I называется пределом интегральной суммы 


Определение 5. Определенным интегралом от функции f (x) на промежутке [a, b] называется предел 
Обозначается 
Числа a i b называются, соответственно, нижним и верхним пределами интегрирования, а [a, b] — промежуток интегрирования.
На основе этих определений можно записать, что


Для пределов интегральных сумм сохраняются многие свойства пределов последовательностей или функций. Однако, из определения определенного интеграла не следует, что любая функция интегрируема на любом интервале. Есть такие функции, для которых не существует определенный интеграл. Ответ на вопрос о существовании определенного интеграла дает такая теорема.
ТЕОРЕМА 9. Если функция f (x) непрерывна на замкнутом промежутке [a, b], то она интегрируема на этом промежутке, то есть для нее существует определенный интеграл
Теорема доказывается в широких курсах высшей математики.
ТЕОРЕМА 10. Если по [a, b] функция ограничена и имеет лишь конечное число точек разрывов, то она интегрируема на [a, b].
Эта теорема дает возможность интегрировать разрывные функции.
Интеграл 
Дополним определение. Если a > b, то 
а если a = b, то 
Основные свойства определенного интеграла
Из определения 
Свойство 1. 
Свойство 2. 
Докажем еще несколько других свойств.
ТЕОРЕМА 11. (Свойство 3) Пусть c — промежуточная точка промежутка [a, b] (a < c < b). Тогда выполняется равенство



Доказательство. По условию a < c < b , и все три интеграла, о которых идет речь, существуют. Разобьем промежуток [a, b] на n частичных промежутков: 



Перейдя к пределу при 

ТЕОРЕМА 12. (Свойство 4) Постоянный множитель можно выносить за знак определенного интеграла.

Доказательство. По определению
На основании свойства пределов, о том, что константу можно выносить за знак предела, и определения интеграла, получаем:
ТЕОРЕМА 13. (Свойство 5) Определенный интеграл от алгебраической суммы нескольких непрерывных функций равен алгебраической сумме определенных интегралов от этих функций.
Доказательство. В общем случае все можно свести к рассмотрению такого выражения [f 
По определению интеграла, и учитывая свойство пределов (пункт 3.4.1.), получаем:
Теорема о среднем значении определенного интеграла
ТЕОРЕМА 14. (О среднем значении определенного интеграла). Если функция f (x) непрерывна на промежутке [a, b], то внутри него найдется такая точка с, что

Доказательство. Если функция f (x) непрерывна на промежутке [a, b], то она достигает своих наибольшего и наименьшего значений М и m на промежутке [a, b] (пункт 3.6.2.). Разобьем промежуток [a, b] на n частичных промежутков длиной 




Получим 
Аналогично, 

Объединив эти два неравенства (6.36) и (6.37), получим
Если 
или
Учтем теорему о том, что функция f (x), непрерывная на промежутке [a, b] и приобретает на нем все промежуточные значения между своим наибольшим и наименьшим значениями, соответственно M и m. Пусть в точке с: m ≤ f (c) ≤ M, где (а ≤ с ≤ b).
Тогда 

А это и требовалось доказать.
Геометрический смысл определенного интеграла
Ранее мы выяснили, что площадь криволинейной трапеции, которая ограничена сверху кривой y = f (x), снизу — промежутком [a, b] оси Ох (a ≤ x ≤ b) и с боковых сторон — прямыми х = а и х = в, равна: 
Если же функция на (а; b) меняет знак — на (а; с) и (d; b) — положительная, а на (c; d) — отрицательная, то и соответствующие значения интегралов будут положительными и отрицательным (рис. 3).
Рис. 3.
Поэтому площадь криволинейной трапеции, изображенной на рисунке, вычисляют по формуле:
Это нужно учитывать при нахождении площадей с помощью определенного интеграла и при вычислении определенного интеграла. В случае, если y = f (x) — нечетная функция, то 

Связь неопределенного и определенного интегралов. Формула Ньютона-Лейбница
Одним из важных моментов этого раздела является нахождение связи между определенным и неопределенным интегралами. Неопределенный интеграл ∫ f (x) dx — это функция, а определенный интеграл 

ТЕОРЕМА 15. Если функция f (x) непрерывна на [a, b], то производная определенного интеграла 

Доказательство. Рассмотрим функцию 


Рис. 4.
Но 
Поэтому 
На основании теоремы (11) получим
Значит 
где x < c <x + Δx. Отсюда следует, что
Направим 


Переходя к пределу в равенстве (6.40), получим

Но 
Однако, базовой при вычислении определенного интеграла, является следующая теорема.
ТЕОРЕМА 16. (Ньютона-Лейбница). Определенный интеграл от непрерывной функции f (x) равна разности значений ее первообразной F (x) при x = b и x = a, где a и b — нижний и верхний пределы интегрирования, то есть имеет место формула:

Доказательство. Рассмотрим функцию 


Поскольку 
А значит 
При x = b получим 
Эта формула называется формулой Ньютона-Лейбница и дает самый простой метод для нахождения определенного интеграла. Ее принято записывать так:
Методы вычисления определенного интеграла
В большинстве случаев вычисления определенного интеграла сводится к нахождению первообразной для соответствующего неопределенного интеграла, а затем используется формула Ньютона-Лейбница. Поэтому все методы, которые используются для нахождения неопределенного интеграла, используются для нахождения определенного интеграла.
Замена переменной в определенном интеграле
Пусть дано 

Пример 22. Вычислить 
Решение. Вводим новую переменную по формуле x = 2 sin t. Определим новые пределы интегрирования. Если х = 0, то 2 sin t = 0 и t = 0 — нижняя граница интегрирования. Если х = 2, то 2 sin t = 2 и 

Метод интегрирования по частям
Заключается в применении формулы: 
Пример 23. Вычислить
Решение. Используем формулу интегрирования по частям. Пусть u = x, dv = e-xdx. Получим du = dx, v = -e-x.
Приближенное вычисление определенных интегралов
Нахождению интеграла посвящены все предыдущие выкладки этого раздела. Однако, как мы уже знаем, есть ряд функций, для которых первообразную невозможно выразить в элементарных функциях. С другой стороны, в применении определенного интеграла не обязательно иметь ему соответствующий неопределенный интеграл. Достаточно иметь его значение или найти его определенное численное приближение. Рассмотрим некоторые методы приближенного вычисления определенных интегралов.
Разложение подынтегрального выражения
При нахождении определенного интеграла раскладывают подынтегральную функцию по формулам Тейлора или Маклорена и интегрированием разложения находят соответствующий интеграла.
Пример 24. Вычислить 
Интегрирование с помощью таблиц
Ряд интегралов хорошо изучены и для них составлены таблицы. Это так называемые табулированные не элементарные “специальные” функции. Например интегралы Френеля: 

Интегралы, для которых найдено точное значение определенного интеграла, без нахождения неопределенного интеграла
Например, 

Численное интегрирование
Методы численного интегрирования дают приближенное численное значение определенного интеграла, если возможно вычислить значение подынтегральной функции в некоторых точках промежутка интегрирования.
Пусть надо найти 







Рис. 5.
Рис. 6. Рис. 7. Рис. 8. Рис. 9.

Если же дугу 



Несобственные интегралы и их нахождение
При определении 
1. промежуток интегрирования [a, b] конечный.
2. подынтегральная функция f (x) определена и непрерывна на [a, b].
В случае если хотя бы одно из условий не выполняется, интеграл называется несобственным. Рассмотрим два самых простых случаях.
Интеграл с бесконечными пределами интегрирования
Определение 6. Пусть f (x) определена на [a, 

несобственный интеграл с бесконечными границами интегрирования.
По формуле Ньютона-Лейбница
Если, при Z → 

Аналогично рассматривается и интеграл вида 


Интеграл от разрывной функции
Пусть f (x) определена на [a, b) и имеет точку разрыва при x = b. Итак 


Если для интегралов пунктов (6.3.1) и (6.3.2) соответствующие им пределы существуют, то интегралы называются сходящимися. Если границы не существуют или бесконечные, то интегралы называются расходящимися.
Пример 26.

Значит, данный интеграл расходится при p ≤ 1 и сходится при p > 1. Его часто используют при исследовании рядов на сходимость.
Применение определенных интегралов
Вычисление площадей
Площадь фигуры, ограниченной графиком функции y = f (x), прямыми x = a и x = b, а также осью Ox, определяется по формуле


Пример 28. Найти площадь фигуры, ограниченной линиями у = 2 – х2, у = х (рис. 10).
Решение. а) Строим эскиз графиков функций: у = 2 – х2 (парабола, которая пересекает ось Ох в точках 

Рис. 10.
б) Найдем точки пересечения графиков данных функций (границы интегрирования). Решим уравнение: 2 – х2 = х; –х2 – х + 2 = 0.
Получаем решения: х1 = 1, х2 = –2.
в) далее, по формуле (6.46) вычисляем площадь фигуры:

Пример 29. Вычислить площадь фигуры, ограниченной линиями y = sin x, y = 0, 
Решение. Строим графики функций (рис. 11). Записываем формулу для нахождения площади 


Рис. 11.
Поэтому
= – (-1 + 0) + (0 + 1) = 2 (кв. ед.).
Интеграл же 
Задача о распределении доходов населения государства
Уровень развития государства характеризуется тем, как оно обеспечивает уровень жизни своих граждан. Одним из таких показателей является материальное благосостояние. Легко и достаточно точно проводить такой сравнительный анализ, имея определенные количественные характеристики. Хорошей характеристикой для этого есть коэффициент Джини, показывающий неравенство в распределении доходов населения. Он непосредственно связан с кривой Лоренца, отражающей зависимость процента доходов от процента тех, которые эти доходы имеют. Рассмотрим это на примере.
Пример 30. Пусть 
Рис. 14.
Решение. Из рисунка видно, что 
Для нахождения 


Поэтому 
Вычисление объемов
Определение и вычисление объема тел по площадям параллельных сечений
Пусть в пространстве дано тело, находящееся между двумя плоскостями x = a и x = b, и
известно, что всякая плоскость, параллельная плоскости Oyz и которая находится от нее на расстоянии x, пересекает тело по плоской фигуре, площадь которой является функцией S (x) (рис. 12).
Рис. 12.
Спроецируем тело на плоскость Oxy. Получим плоскую фигуру, которую снова спроецируем на ось Ох (а < b).
Разобьем промежуток [a, b] точками x1, x2, … xn-1. Через точки деления проведем перпендикулярные плоскости σ1, σ2, σ3, …, σn-1 — к плоскости Oxy и обозначим S (x1), S (x2), … S (xn-1) — площади соответствующих параллельных друг другу сечений. Построим на каждом сечении, как на основании, цилиндр высотой, соответственно, Δx1, Δx2, …, Δxi = x– xi-1 Таким образом, получим n цилиндров. Запишем сумму, которая является интегральной:
Перейдем к пределу при 
Если такой предел существует, то говорят, что данное тело имеет объем.
Вычисление объема тела вращения
Пусть криволинейная трапеция образована линией y = f (x), прямыми х = а и х = b и осью Ох, вращается в пространстве вокруг оси Ох. Найти объем фигуры вращения, которая образовалась.
Учитывая, что для объема тела вращения площадь поперечного сечения S (x) = πf 2 (x) получим:

Если же криволинейная трапеция образована линией x = φ (y), прямыми y = с и у = d и осью Оу, вращается в пространстве вокруг оси Оу то
Рис. 13.
Пример 31. Найти объем тела, образованного вращением вокруг оси абсцисс фигуры, ограниченной линиями

Решение. Объем тела вращения вычисляем по формуле 

Вычисления длины дуги плоской кривой
Запишем, без вывода, формулу для нахождения дуги плоской кривой, заданной уравнением y = f (x), при условии непрерывности на [a, b] функций f (x) и f’ (x).

Пример 32. Найти длину дуги плоской кривой линии 
Решение. В задачи а = 0, b = 4, 




Задача о максимизации прибыли по времени
Целью всякого производства является достижение максимальной прибыли. То есть, достижение максимальной разницы между доходами и расходами. Обозначим P (t), D (t), V(t) — соответственно функции прибыли, дохода и расходов от времени. Тогда P (t) = D (t) -V (t). Функция достигает своего экстремума, если ее производная равна 0. То есть P ‘(t) = D'(t) -V'(t) = 0. То есть D’ (t) = V’ (t). Определим момент tk , в который скорость изменения дохода и расходов уравниваются. Общую прибыль за время tk можно найти по формуле:

Пример 33. Скорости изменения затрат и дохода предприятия после начала его деятельности определялись формулам: 
Решение. Оптимальное время t1 для прибыли предприятия получим из условия D’ (t) = V’ (t). Из уравнения 

Таким образом, предприятие было прибыльным 1 год. За это время получено прибыли:

Задача о расходах, доход и прибыль
Пусть теперь V (х) — функция общих расходов на производство х единиц продукции, V’ (х) — функция маржинальных расходов. P’ (x), D’ (х) — функции, соответственно, маржинальных прибыли и дохода. Тогда при росте количества единиц продукции от a до b,
изменение общих расходов исчисляется по формуле

При возрастании реализации продукции изменения прибыли и дохода определим по формулам: 
Понятие о двойном интеграле. Сведение двойного интеграла к повторному
Понятие о двойном интеграле:
При введении понятия определенного интеграла мы решали задачу о нахождении площади криволинейной трапеции. Однако, часто необходимо найти объем некоторой пространственной фигуры. Решим задачу: найти объем тела, ограниченного сверху непрерывной поверхностью z = f (x, y) (f (x, y) ≥ 0), снизу — конечной замкнутой областью S плоскости Oxy, по бокам — прямой цилиндрической поверхностью, построенной на границе области S, перпендикулярно к плоскости Oxy. Найдем объем V тела изображенного на рисунке 14.
Рис. 14.
Разобьем область S несколькими линиями на n частей с площадями соответственно S1, S2, …, Sn. В каждой из частей выберем по одной точке P1 (x1, y1), P2 (x2, y2), …, Pn (xn, yn) и построим цилиндры с основами Si и высотами Pi Qi = f (xi, yi). Тогда объем V:

Эта сумма называется двухмерной интегральной суммой для функции z = f (x, y) по области S. Для этой суммы выполняется теорема существования двойного интеграла:
Если функция z = f (x, y) непрерывна в ограниченной замкнутой области S, и если число частиц n, на которые разбита область S, неограниченно возрастает, а наибольшее
расстояние между двумя точками каждой частицы, которые лежат на границе (diamSi), стремится к 0, то существует предел двухмерной интегральной суммы (6.50), величина которого не зависит ни от способа разбиения S, ни от выбора точки Pi внутри частицы с площадью Si.
Этот предел называется двойным интегралом от функции z = f (x, y), распространенным на область S и обозначается 

Надо отметить, что если 


Повторный интеграл. Переход от двойного интеграла к повторному
Подойдем к задаче о нахождении объема V поверхности z = f (x, y) по иному. Учтем, что область S в плоскости Oxy ограничена сверху и снизу определенными линиями y = φ1 (x) и y = φ2 (x) . Вместе с тем, функции φ1 (x) и φ2 (x) непрерывные на [а; b]. Проведем сечение нашего тела плоскостью х = хi, параллельно координатной плоскости Oyz так, что a<x<b (рис. 15). Площадь пересекается и обозначается как некоторая функция от х, то есть S = F(x).
Рис. 14
В таком случае объем тела

Определим теперь функцию F (x). Так 

Объединив формулы (6.53) и (6.54) получаем

Интеграл (6.55) называется повторным интегралом, распространенным на произвольную
область S. Заметим, что если бы область была ограничена кривыми x = ψ1 (y) и x = ψ2 (y) (непрерывными на (c; d)) то получили бы, что 
Итак, вычисления двойного интеграла можно свести к вычислению повторного.
Интеграл Эйлера-Пуассона
В теории вероятности и математической статистике большую роль играет интеграл
Эйлера-Пуассона:

Он относится к интегралам, которые не выражаются в элементарных функциях. Вычислим его с помощью двойного интеграла. Применим формулы связи
между декартовыми и полярными координатами:
Учтем, что определенный интеграл не зависит от обозначения переменной (инвариантность определенного интеграла относительно переменной).
Поэтому можем записать 
Перемножив формулы (6.56) и (6.57), получим
Геометрически, интеграл Пуассона выражает собой площадь фигуры (рис. 16.), ограниченной графиком функции 
Рис. 16.
Лекции:
- Предел сложной функции
- Нахождение предела функции по таблице значений функции и по графику
- Производная частного
- Экстремум функции нескольких переменных
- Интегрирование некоторых классов функций
- Векторное произведение примеры решения
- Найти производную функцию
- Поток вектора через незамкнутую поверхность. Теорема Гаусса—Остроградского
- Элементарные преобразования графиков функций
- Нормальный закон распределения случайной величины

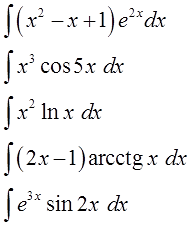
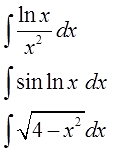
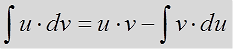
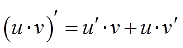
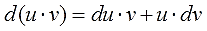
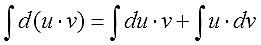
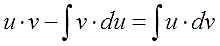
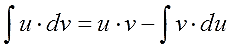
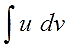
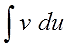
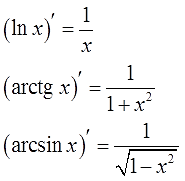
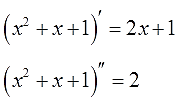
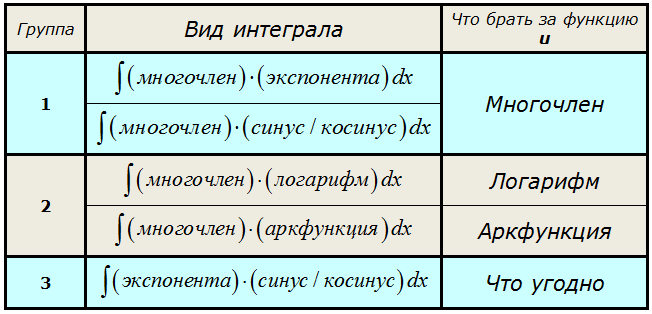
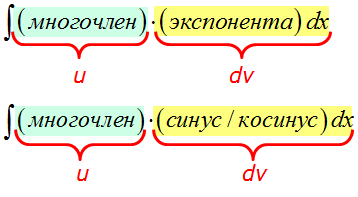
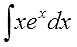
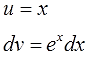
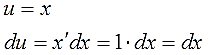
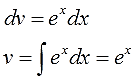
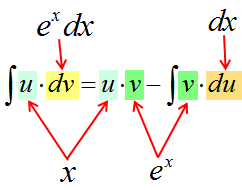
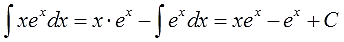
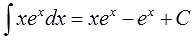
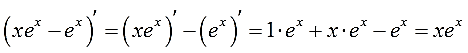
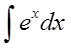
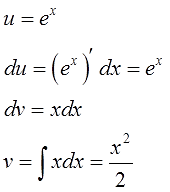
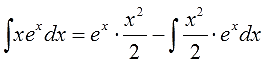
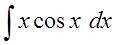
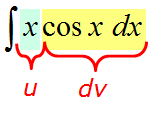
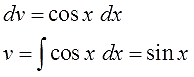
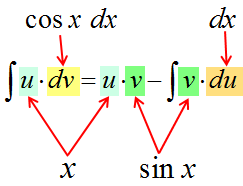
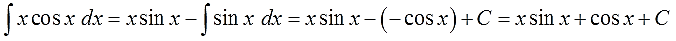
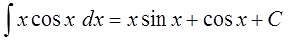
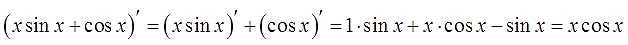
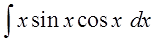
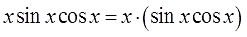
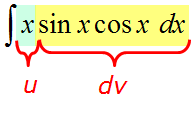
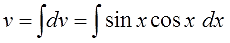
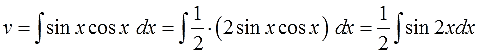
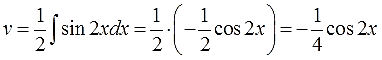
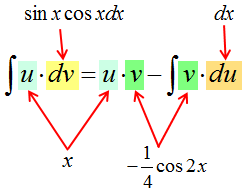
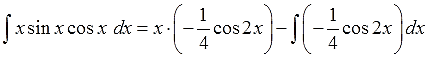
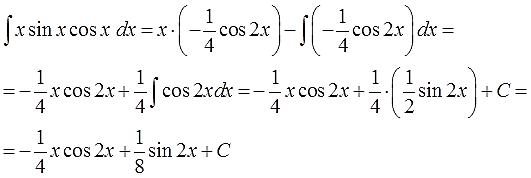
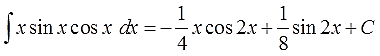
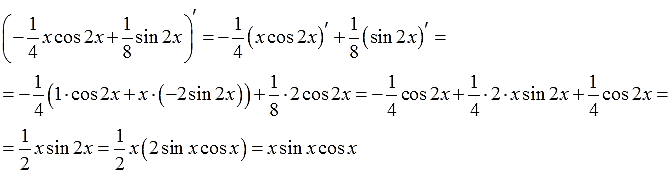
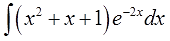
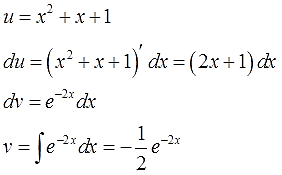
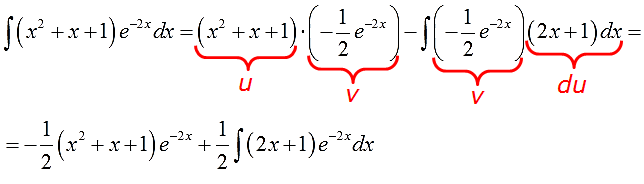
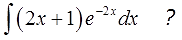
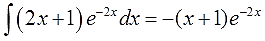
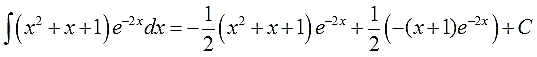
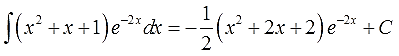
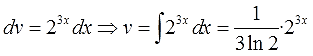
![Rendered by QuickLaTeX.com [mleft( b-a right)le intlimits_{a}^{b}{fleft( x right)gleft( x right)dx}le Mleft( b-a right)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-d316d887131c4eb15f6604daa05834ca_l3.png)
![Rendered by QuickLaTeX.com [intlimits_{a}^{b}{fleft( x right)gleft( x right)dx}=fleft( c right)left( b-a right)]](http://ru.solverbook.com/wp-content/ql-cache/quicklatex.com-8a78f8261c037b4a7adcc53dcafaba0b_l3.png)












































































































































































































































































































