Содержание:
- Формула
- Примеры вычисления интеграла тангенса
Формула
$$int operatorname{tg} x d x=-ln |cos x|+C$$
Интеграл от тангенса равен минус
логарифму натуральному от косинуса плюс константа интегрирования.
Примеры вычисления интеграла тангенса
Пример
Задание. Найти неопределенный интеграл $int 2 operatorname{tg} x d x$
Решение. Согласно
свойствам интеграла, константу можно выносить за знак интеграла, тогда
$$int 2 operatorname{tg} x d x=2 int operatorname{tg} x d x=2(-ln |cos x|)+C=-2 ln |cos x|+C$$
Ответ. $int 2 operatorname{tg} x d x=-2 ln |cos x|+C$
236
проверенных автора готовы помочь в написании работы любой сложности
Мы помогли уже 4 396 ученикам и студентам сдать работы от решения задач до дипломных на отлично! Узнай стоимость своей работы за 15 минут!
Пример
Задание. Найти интеграл $int(x-operatorname{tg} x) d x$
Решение. Интеграл от разности равен
разности интегралов, тогда
$$int(x-operatorname{tg} x) d x=int x d x-int operatorname{tg} x d x$$
Первый интеграл берем как интеграл от степенной функции, а второй как от тангенса. В итоге будем иметь:
$$int(x-operatorname{tg} x) d x=frac{x^{1+1}}{1+1}-(-ln |cos x|)+C=$$
$$=frac{x^{2}}{2}+ln |cos x|+C$$
Ответ. $int(x-operatorname{tg} x) d x=frac{x^{2}}{2}+ln |cos x|+C$
Читать дальше: интеграл котангенса.
Интеграл тангенса
Интеграл тангенса равен минус натуральному логарифму косинуса того же аргумента плюс константа интегрирования
(
int operatorname{tg} x d x=-ln |cos x|+C
)
Примеры решения задач
ПРИМЕР 1
Доказать формулу (
int operatorname{tg} x d x=-ln |cos x|+C
)
Указанный интеграл находится методом замены переменной:
(
int operatorname{tg} x d x=int frac{sin x d x}{cos x}|-sin x d x=-d t|=int frac{-d t}{t}=-ln |t|+C=-ln |cos x|+C
)
ПРИМЕР 2
Найти интеграл (
int operatorname{tg} 2 x d x
)
Данный интеграл сведем к указанной выше формуле заменой переменной:
(
int operatorname{tg} 2 x d x |left|begin{array}{c}{2 x=t} \ {2 d x=d t} \ {d x=frac{d t}{2}}end{array}right|=int operatorname{tg} t cdot frac{d t}{2}=frac{1}{2} int operatorname{tg} t d t=frac{1}{2}(-ln |cos t|)+C=-frac{ln |cos 2 x|}{2}+C
)
(
int operatorname{tg} 2 x d x=-frac{ln |cos 2 x|}{2}+C
)
Интегрирование сложных тригонометрических функций
Прилагательное
«сложный» для большинства примеров
вновь носит во многом условный характер.
Начнем с тангенсов и котангенсов в
высоких степенях. С точки зрения
используемых методов решения тангенс
и котангенс – почти одно и тоже, поэтому
я больше буду говорить о тангенсе,
подразумевая, что продемонстрированный
прием решения интеграла справедлив и
для котангенса тоже.
На
уроке Интегралы
от тригонометрических функций мы
разобрали интеграл от тангенса в
квадрате. На уроке Как
вычислить площадь фигуры? в
примере 10 фигурировал тангенс в кубе.
В том примере для нахождения интеграла
от тангенса в кубе мы применяли
тригонометрическую формулу 
.
Интеграл от тангенса в четвертой, пятой
степени (редко в более высоких степенях)
решается с помощью этой же формулы!
Пример
15
Найти
неопределенный интеграл
Идея
решения подобных интегралов состоит в
том, чтобы с помощью формулы
«развалить»
исходный интеграл на несколько более
простых интегралов:
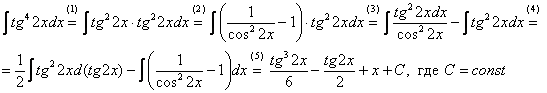
(1)
Готовим подынтегральную функцию к
применению формулы.
(2) Для одного из
множителей используем формулу
(3)
Раскрываем скобки и сразу же используем
свойство линейности неопределенного
интеграла.
(4) В первом интеграле
используем метод
подведения функции под знак дифференциала.
Во втором интеграле еще раз используем
формулу 
,
в данном случае 
.
(5)
Берём все три интеграла и получаем
ответ.
Пример
16
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Для котангенса существует аналогичная
формула: 
.
Полное решение и ответ в конце урока.
Если
возникли затруднения или недопонимание,
следует вернуться к уроку Интегралы
от тригонометрических функций.
На
вышеупомянутом уроке мы
рассматривали универсальную
тригонометрическую подстановку для
решения определенного вида интегралов
от тригонометрических функций. Недостаток
универсальной тригонометрической
подстановки заключается в том, что при
её применении часто возникают громоздкие
интегралы с трудными вычислениями. И в
ряде случаев универсальной тригонометрической
подстановки можно избежать!
Рассмотрим
еще один канонический пример, интеграл
от единицы, деленной на синус:
Пример
17
Найти
неопределенный интеграл
Здесь
можно использовать универсальную
тригонометрическую подстановку и
получить ответ, но существует более
рациональный путь. Я приведу полное
решение с комментами к каждому шагу:
(1)
Используем тригонометрическую формулу
синуса двойного угла 
.
(2)
Проводим искусственное преобразование:
В знаменателе делим и умножаем на 
.
(3)
По известной формуле в знаменателе
превращаем дробь в тангенс.
(4) Подводим
функцию под знак дифференциала.
(5)
Берём интеграл.
Пара
простых примеров для самостоятельного
решения:
Пример
18
Найти
неопределенный интеграл
Указание:
Самым первым действием следует
использовать формулу приведения 
и
аккуратно провести аналогичные
предыдущему примеру действия.
Пример
19
Найти
неопределенный интеграл
Ну,
это совсем простой пример.
Полные
решения и ответы в конце урока.
Думаю,
теперь ни у кого не возникнет проблем
с интегралами:
и
т.п.
В
чём состоит идея метода? Идея состоит
в том, чтобы с помощью преобразований,
тригонометрических формул организовать
в подынтегральной функции только
тангенсы и производную тангенса 
.
То есть, речь идет о замене: 
.
В Примерах 17-19 мы фактически и применяли
данную замену, но интегралы были настолько
просты, что дело обошлось эквивалентным
действием – подведением функции под
знак дифференциала.
Примечание:
аналогичные рассуждения, как я уже
оговаривался, можно провести и для
котангенса.
Существует
и формальная предпосылка для применения
вышеуказанной замены:
Сумма
степеней косинуса и синуса – целое
отрицательное число.
Для
интеграла 
–
целое отрицательное число.
Для
интеграла 
–
целое отрицательное число.
Для
интеграла 
–
целое отрицательное число.
Рассмотрим
пару более содержательных примеров на
это правило:
Пример
20
Найти
неопределенный интеграл
Сумма
степеней синуса и косинуса 
:
2 – 6 = –4 – целое отрицательное число,
значит, интеграл можно свести к тангенсам
и его производной:
(1)
Преобразуем знаменатель.
(2) По
известной формуле получаем 
.
(3)
Преобразуем знаменатель.
(4) Используем
формулу 
.
(5)
Подводим функцию под знак дифференциала.
(6)
Проводим замену 
.
Более опытные студенты замену могут и
не проводить, но все-таки лучше заменить
тангенс одной буквой – меньше риск
запутаться.
Далее
берётся простой интеграл и проводится
обратная замена.
Пример
21
Найти
неопределенный интеграл
Это
пример для самостоятельного решения.
Держитесь,
начинаются чемпионские раунды =)
Зачастую
в подынтегральной функции находится
«солянка»:
Пример
22
Найти
неопределенный интеграл
В
этом интеграле изначально присутствует
тангенс, что сразу наталкивает на уже
знакомую мысль:
Искусственное
преобразование в самом начале и остальные
шаги оставлю без комментариев, поскольку
обо всем уже говорилось выше.
Пара
творческих примеров для самостоятельного
решения:
Пример
23
Найти
неопределенный интеграл
Пример
24
Найти
неопределенный интеграл
Да,
в них, конечно, можно понизить степени
синуса, косинуса, использовать
универсальную тригонометрическую
подстановку, но решение будет гораздо
эффективнее и короче, если его провести
через тангенсы. Полное решение и ответы
в конце урока
У
многих читателей могло сложиться
впечатления, что я немного подустал.
Отнюдь. За окном февральский ветер –
самая атмосфера для лекций. Естественно,
данная страничка создана не за один
день, я успел несколько раз побриться,
регулярно кушаю и так далее. К тому же,
загружать студентов – удовольствие
бесконечное =). …Шутка! На самом деле
моя миссия – разгружать посетителей
сайта. Вагонами.
Переходим
к заключительному пункту познавательного
путешествия в мир сложных интегралов:
Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
- #
Среди простых формул интегрирования отсутствуют готовые зависимости, позволяющих найти интеграл от тангенса (tg (x)) и котангенса (ctg (x)). Но такие примеры в задачах встречаются и нужно знать: “Как вычислить интеграл от тангенса и котангенса?“.
Начнем с тангенса, распишем его в виде частки синуса на косинус
tg(x)=sin(x)/cos(x)
и подставим в интеграл.
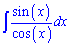Сейчас Вам понятно. Далее нужно внести синус под дифференциал, чтобы свести интеграции в логарифма
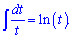В результате получим
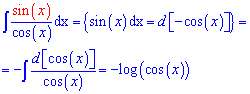Таким образом вывели простую и нужную на практике формулу – интеграл от тангенса равен логарифму косинуса со знаком минус.
Int(tan(x),x)=-log(cos(x)).
По приведенной схеме выведем формулу для интеграла от котангенса. Записываем частку косинуса на синус в интеграл и после внесения косинуса под дифференциал сводим интеграл к логарифму
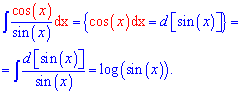Интеграл от котангенса равный логарифму от синуса.
Int(cot(x),x)=log(sin(x)).
Простые на вид формулы интегралов от тангенса и котангенса позволяют решить немало сложных примеров, например интегрирования тангенса двойного угла или котангенса половины угла.
Примеры интегрирования тангенса и котангенса
Пример 1. Найти интеграл от тангенса tan(4*x).
Вычисления: Применяем приведенную выше методику для интегрирования тангенса
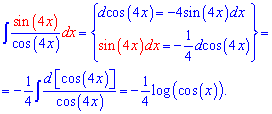
Здесь в скобках мы сначала вычисляем дифференциал от косинуса, а дальше выделяем значение, которое нам нужно достать. Далее интегрирования сводим к логарифму.
Таким образом можем записать обобщенную формулу для интегралаtan(k*x)
Int(tan(k*x),x)=-1/k*(log(cos(x)).
По этой формуле интеграл от тангенса двойного угла равен логарифму косинуса двойного угла умноженному на -0,5.
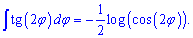Для тангенса половины угла tan (phi / 2) интеграл равен -2 умножить на логарифм косинуса половины угла
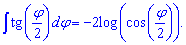По индукции получим формулу интеграла для тангенса одной третьей угла tan(phi/3)
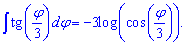
Пример 2. Проинтегрировать котангенс двойного угла
Вычисления: По аналогии с формулами для тангенса мы могли бы выписать готовую формулу, но лучше выполнить промежуточные переходы чтобы Вы лучше поняли и заучили методику внесения под дифференциал
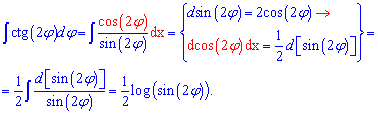
Таким образом, если имеем котангенс тройного угла то перед интегралом получим множителем 1/3
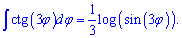Интегралы от котангенса половины и трети угла будут иметь множителями перед логарифмом соответственно двойку и тройку
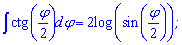
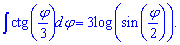При нахождении первоначальной от тангенса и котангенса следует справа добавить постоянную
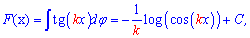
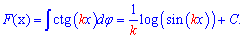Зная данную методику, Вы знаете как найти интеграл от тангенса, аргумент которого содержит множителем произвольное число.
Вычисления определенных интегралов от тангенса и котангенса в данной статье рассматривать не будем. Если Вы вычисляли такие интегралы от простых функций то, зная синусы и косинусы углов найти определенный интеграл от тангенса или котангенса сможете без проблем.
С методикой интегрирования обратных тригонометрических функций, иррациональных и показательных Вы можете ознакомиться на страницах категории “Интегрирование функции” в левом меню сайта.
Профи
(674),
закрыт
11 лет назад
Юрик
Высший разум
(117860)
11 лет назад
Сделайте с заменой, и всё станет ясно.
∫(sinx/cosx)dx=
t=cosx => dt=-sinxdx
=-∫dt/t=-ln|t|+C=-ln|cosx|+C.
Gagarin614Профи (674)
11 лет назад
если выразить t=cosx тогда я все понял и все получится, а если выражать числитель то получается бред и не решается так и должно или я не так делаю?
Serg
Высший разум
(170536)
11 лет назад
Производная cosx=-sinx, т. е. dcosx=-sindx и в обратном порядке
-sinxdx=dcosx, значит sinxdx=-dcosx.
SergВысший разум (170536)
11 лет назад
Ваууу! Скажите пожалуйста, а где у меня ошибка? Я объяснил почему так. Это называется внести синус в знак дифференциала, то что сделано в решении, или замена cosx=t, в 1 ответе.
