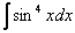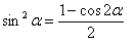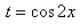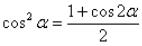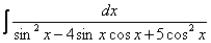Как найти интеграл от тригонометрической функции - Сайт, где вы сможете решить свои вопросы

Подставим все в формулу интегрирования по частям и приведем интеграл к табличному, тогда будем иметь:

Методы не применяются для интегрирования функций вида

; ; ; ;

; , т.е. от тригонометрических функций,

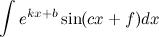
умноженных на многочлен. Такие интегралы интегрируются по частям.

При нахождении интегралов от тригонометрических функций используется ряд методов:

Использование тригонометрических формул Понижение степени подынтегральной функции Метод замены переменной Универсальная тригонометрическая подстановка

При работе с тригонометрическими функциями следует помнить, что:

Косинус – это четная функция, то есть , минус исчезает без всяких последствий.

Синус – функция нечетная: – здесь минус, наоборот – не пропадает, а выносится.

Использование тригонометрических формул

Пример34

Найти интеграл.

Используем формулу: и метод подведения под знак дифференциала

Пример 35

Найти интеграл

Для упрощения подынтегральной функции воспользуемся тригонометрическими функциями. Затем с помощью свойств интеграла приведем данный интеграл к табличному виду.

Пример 36

Найти интеграл.

Используем формулу: 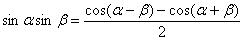и метод подведения под знак дифференциала.

Пример 37

Найти интеграл.

Используем формулу:

Пример 38

Найти неопределенный интеграл

Используем формулы преобразования произведения функций сначала для произведения 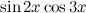, а затем для произведения синусов в каждом из интегралов :

В результате искомый интеграл будет равен

Понижение степени подынтегральной функции

Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в чётных степенях. Для понижения степени используют

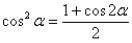
тригонометрические формулы , и , причем последняя формула чаще используется в обратном

направлении:

Интеграл вида ʃ sinn (x) cosm (x), где n и m – чётные числа, решается методом

понижения степени подынтегральной функции.

Пример 39

Найти интеграл

∫cos2xdx = ∫1+cos2x2	dx =	21	∫(1 + cos2x)dx = 21 x + 21 sin2x + C
Используем формулу:
Пример 40
Найти интеграл		dx =	21 ∫(1 −cos3x)dx = 21 x −31 sin3x + C
∫sin2 23 xdx = ∫1−cos3x2
Используем формулу:

Пример 41

Найти интеграл

Выражаем sin4 x как (sin2 x)2 и применяем формулу

Используем формулу

В третьем слагаемом снова понижаем степень с помощью формулы .

Пример 42

Найти интеграл

Метод замены переменной

Данный приём используют, когда в подынтегральных функциях присутствуют синусы и косинусы в нечётных степенях.

Общие рекомендации :

1.за t нужно обозначить функцию, которая находится в знаменателе.

2.за t нужно обозначить ту функцию, которая, является более сложной.

3.Если в подынтегральной функции одна из тригонометрических функций (синус или косинус) находится в нечетной степени, то нужно от нечетной степени «откусить» одну функцию, а за t – обозначить другую функцию

Интеграл вида ʃ sinn (x) cosm (x), где n или m – нечётные числа, решается методом замены переменной

Пример 43

Найти интеграл

Проведем замену:

Примечание: здесь можно было сделать замену , но гораздо выгоднее обозначить за весь знаменатель.

Пример 44

Найти интеграл 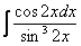Проводим замену

Пример 45

Найти интеграл Проведем замену:

Пример 46

Найти интеграл

Представляем cos3 x dx как cos2 x cos x dx, а cos2x выражаем через синус с помощью основного тригонометрического тождества:

Делаем замену:

Пример 47

Найти интеграл Преобразуем подынтегральное выражение:

Проведем замену:

Пример 48

Найти интеграл Проведем замену:

Пример 49

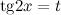
Найти неопределенный интеграл Для вычисления исходного интеграла введем замену , тогда

Подставляя это в искомый интеграл, получим

Сделаем обратную замену

Пример 50

Найти неопределенный интеграл Преобразуем подынтегральную функцию, используя основное тригонометрическое тождество

Введем замену , тогда исходный интеграл примет вид

Сделаем обратную замену и окончательно получим

Пример 51

Найти неопределенный интеграл Преобразуем подынтегральную функцию, используя вначале формулу для синуса двойного угла:

а затем, формулу для понижения степени

Универсальная тригонометрическая подстановка

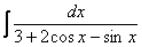
Универсальная тригонометрическая подстановка – это частый случай метода замены переменной. Её можно попробовать применить, когда «не знаешь, что делать». Интегралами, где нужно применить универсальную тригонометрическую подстановку, являются интегралы вида:

, , , и т.д.

Указанная замена позволяет свести интеграл от тригонометрической функции к интегралу от рациональной функции.

При этом следует учесть, что из равенства получаем:

;

Обратите внимание, что аргумент под тангенсом должен быть в два раза меньше, чем под синусом и косинусом, т.е., в общем виде, если присутствуют функции вида:

sin(kx), cos(kx), делается подстановка tg(kx/2) = t. Еще раз, при sin2x ‒ tg(2x/2), при sin3x ‒ tg(3x/2) и т.д.

Пример 52

Найти неопределенный интеграл Воспользуемся универсальной тригонометрической подстановкой:

Пример 53

Найти неопределенный интеграл 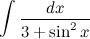Для решения данного интеграла сделаем упрощенную тригонометрическую замену, положив что

выразим из равенства

то есть Подставим все в искомый интеграл

Сделаем обратную замену

Пример 54

Найти неопределенный интеграл Преобразуем подынтегральную функцию следующим образом:

Для нахождения первого интеграла будем использовать универсальную тригонометрическую замену

Тогда первый интеграл преобразуется следующим образом

Разложим подынтегральную функцию полученного интеграла на элементарные дроби:

Приведем к общему знаменателю дроби в правой части равенства и приравниваем числители:

Приравнивая коэффициенты при соответствующих степенях, получим такую систему для нахождения и

Тогда подынтегральная функция имеет следующее разложение на простые дроби

а соответствующий интеграл равен

Делаем обратную замену

Окончательно искомый интеграл равен:

Пример 55

Найти неопределенный интеграл. Перед применением универсальной тригонометрической подстановки необходимо понизить степени в знаменателе при помощи формул

Универсальная тригонометрическая подстановка:

Применение универсальной тригонометрической подстановки часто приводит к длинным и трудоемким вычислениям. Поэтому на практике универсальной тригонометрической подстановки стараются избегать (если возможно).

В ряде случаев целесообразно свести подынтегральное выражение, содержащее sinn(α) и cosm(α), к tg(α) и ее производной 1/cos2(α) т.е. произвести замену:

. Для этого можно воспользоваться формулами

; .

Метод работает, если сумма показателей степеней n+m ‒ целое четное отрицательное число .

Пример56

Найти неопределенный интеграл

Пример57

Найти неопределенный интеграл

Замена tgх =t (чтобы не запутаться)

Пример58

Найти неопределенный интеграл

Пример59

Найти неопределенный интеграл

Пример60

Найти неопределенный интеграл

Пример61

Интеграл из примера55

4 2 − 5 2

(4 2 − 5 2 ) 2

(4 2 − 5) 2

( )

2 − √5

4 2 − 5

= 4 2 − 5 =

(2 )2 − (√5)2

= 2

2√5

2 + √5 + =

= 4√1

5 22 +−√√55 +

Решение значительно быстрее и проще.

6.Интегралы от дробей

Суть методов решения интегралов от дроби сводится к преобразованию дроби в сумму элементарных дробей табличного вида:

Для преобразования дроби используется комплекс приемов, основными из которых будут выделение полного квадрата, подстановка, разложение на множители, с дальнейшим преобразованием в сумму элементарных дробей.

Для решения интегралов от дроби можно придерживаться следующего алгоритма:

Определяем тип подынтегрального выражения.
1.	Для простейших дробей вида		применяется способ подведения функции
под знак дифференциала с дальнейшим интегрированием с помощью таблицы.
				( + )
		( + )		( + )−+	,
∫( + ) = ∫( + )	=	−+	+

Примеры:

2. Для дробей вида

(коэффициенты

a и c не равны нулю) также применяется способ подведения функции под знак дифференциала с дальнейшим интегрированием с помощью таблицы. (Формулы 2 – 6, см. выше).

Примеры:

3. Для дробей вида	сначала представляем
интеграл в виде суммы:

Первый интеграл берем методом подведения под знак дифференциала:

В интегралах вида	выделяем в знаменателе полный квадрат и приводим
выражение к табличному виду.
В ряде случаев, неразложимый многочлен			целесообразно представить в
	необходимо вынести коэффициент за знак интеграла,
виде полного квадрата (перед этим		(		+ + )
поделив все выражение на ) по формуле:

и свести интеграл к виду:

или

Пример62

Найти неопределенный интеграл Квадратный трехчлен, который стоит в знаменателе подынтегральной функции, не

раскладывается на множители . Поэтому для нахождения данного интеграла выделим в знаменателе полный квадрат.

Пример63

Найти неопределенный интеграл . Для начала вынесем двойкуиз под знака радикала:

т.е. вида

В подкоренном выражении выделяем полный квадрат:

Поэтому

Пример64

4. Для дробей вида

используют метод интегрирования по частям n раз, каждый раз понижая степень знаменателя и применяя предыдущие способы. Вычисления получаются очень длинные и долгие. Или пользуемся рекуррентными формулами.

5. Дроби( ) , у которых многочлены и в числителе и в знаменателе,

( ) , где Pn(x) и Pm(x) многочлены степени n и m соответственно, перед

собственно взятием интеграла необходимо разложить на множители, а затем, преобразовать в сумму элементарных дробей.

Определяем что дробь правильная. Правильной называется дробь, у которой степень числителя меньше степени знаменателя. Если дробь неправильная, то выделяем целую часть, с оставшейся частью работаем как с правильной дробью.

Раскладываем знаменатель правильной дроби на множители и преобразуем дробь в сумму элементарных дробей.

Для преобразования дроби в сумму элементарных дробей в большинстве случаев используют метод неопределенных коэффициентов.

Метод неопределенных коэффициентов.

т.е.
Любую дробь вида	( + )( + )( + )	можно представить в виде
		2+ +
	2 + +
( + )( + )( + ) =	+ + + + + ,

+ ++ + +

где A, B, C неизвестные коэффициенты.

Приводим правую часть уравнения к общему знаменателю:

( + )( + ) + ( + )( + ) ( + )( + )

+Тогда

( + )( + )( + )

+ +

( + )( + ) + ( + )( + ) + ( + )( + )

( + )( + )( + )

+ + = ( + )( + ) + ( + )( + ) ( + )( + )

Если дроби равны= и равны их знаменатели, то должны быть равны и их числители,

+ + =

= 2

Раскрываем скобки

( + ) + + 2 +

( + ) + =

( + ) + + 2 +

= ( + + )

( + + + + + ) + ( + + )

= + +

Приравниваем коэффициенты в выражениях:

= ( + )

+ ( + ) + ( + )

= + +

Решая систему уравнений, находим неизвестные коэффициенты A, B, C и раскладываем

+ +

дробь на сумму элементарных дробей:

( + )( + )( + )

он приравнивается к

(

+ + )

квадратный.

многочлен вида:

Если в знаменателе встречается=

+неразложимый+

( + )(

1 + )

, где

– неразложимый квадратный многочлен (D<0), то

( + )(

сумме дробей по формуле:

+ + )

(

+ + )

Если в знаменателе2

встречаются=

+кратные2

множители.

вида:

( 1+ )

то они раскладываются по формуле:

( + ) =

2 + +

+ ( + ) +

( + )2

+ +

( + )

Пример65

Найти неопределенный интеграл 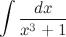Преобразуем подынтегральную функцию, расписав знаменатель согласно формуле сокращенного умножения для суммы кубов:

Тогда интеграл примет вид:

Далее разложим подынтегральную функцию на простые дроби с неопределенными коэффициентами. В нашем случае имеет место следующее разложение:

Найдем неопределенные коэффициенты, для этого приведем к общему знаменателю дроби в правой части равенства, а затем приравняем соответствующие числители

Далее приравняем коэффициенты при соответствующих степенях

Подставим, выраженные через , коэффициенты и во второе уравнение системы:

, тогда , а Таким образом, искомый интеграл будет равен:

1	1		(2 − 1) − 3
= 3	\| + 1\| − 6		2 − + 1	=
1	1			2 − 1		−3	=
= 3	\| + 1\| − 6	2	− + 1 −	6	2 − + 1
1	1	\|	2		1
= 3	\| + 1\| − 6		− + 1\| + 2	2 − + 1

Квадратный трехчлен, стоящий в знаменателе последнего интеграла, не раскладывается на

множители	1				1	2						. Поэтому для его нахождения выделим в
											1
знаменателе полный квадрат:
	3 + 1	= = 3	\| + 1\| − 6	\|		− + 1\| +	2 2 − + 1 =
1	\| + 1\| −	1	\|	2			1					+ 3 =
= 3	6	2	− + 1\| + 2	( − 1)2
1	\| + 1\| −	1	\|			1	1	2			4
= 3	6		− + 1\| + 2	3	3	+ =
1	\| + 1\| −	1	\|	2				1	4	2	4
= 3	6		− + 1\| + √3	√3 +

Пример66

Найти неопределенный интеграл Дробь является правильной

Раскладываем знаменатель на множители, используя формулу сокращенного умножения

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

Приводим дробь к общему знаменателю:

Составим и решим систему:

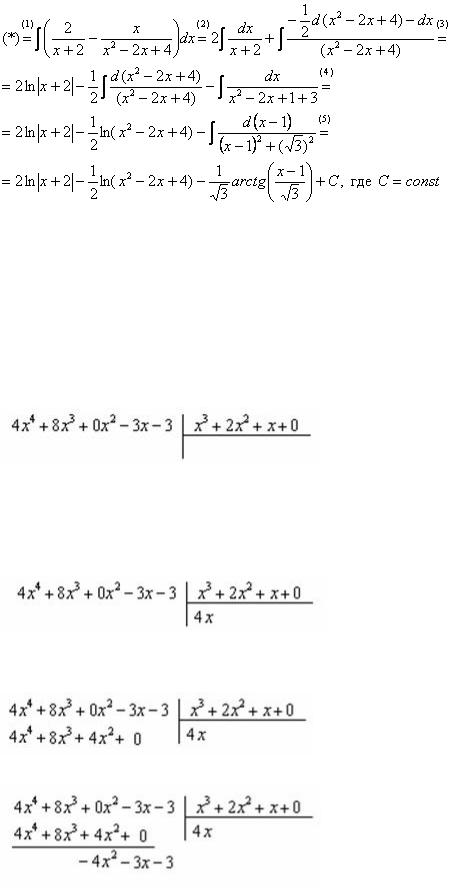
Пример67

Найти неопределенный интеграл Данная дробь является неправильной.

Основной метод решения интеграла с неправильной дробно-рациональной функцией – это

деление числителя на знаменатель.

Сначала рисуем «заготовку» для деления:

ВСЕ недостающие степени (и (или) свободные члены) без пропусков записываем в ОБОИХ многочленах с нулевыми коэффициентами

Теперь маленькая задачка, на какой множитель нужно умножить , чтобы получить ? Очевидно, что на :

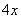
Далее умножаем сначала на , потом – на , потом – на , потом – на 0 и записываем результаты слева:

Проводим черточку и производим вычитание (из верха вычитаем низ):

Старшая степень остатка равна двум, старшая степень делителя

– больше, она равна трём, значит, больше разделить не удастся. Если бы

изначально унас был в числителе многочлен пятой степени, то алгоритм деления увеличился бы на один шаг.

Итак, у нас получилась целая часть плюс остаток:

Методом неопределенных коэффициентов разложим подынтегральную функцию в сумму элементарных дробей:

6. Неопределенные интегралы иррациональных функций вида находятся методом подстановки.

В зависимости от рациональных чисел m, n и p вводят следующие новые переменные:

Если p – целое число, то принимают

, где N – общий знаменатель чисел m и n.

– целое число, то

, где N – знаменатель числа p.

Если +

знаменатель

+ p

– целое число, то вводят новую переменную

, где N –

Если

числа .

привести к виду:

−

которые можно

Очень часто в вычислениях встречаются дроби вида

+ −

+ =

= +

− + = − +

+ −

−

− =

−

= −

+ − = − −

+ − = −1 + − = − −

+ −

−

− =

−

= −

+ − = + −

Пример68

Найти неопределенный интеграл

То есть, m = -1, n = 1, p = 1/2. Так как 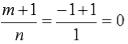– целое число, то вводим новую

переменную (N = 2 – знаменатель числа p). Выражаем х через z:

Выполняем подстановку в исходный интеграл:

Пример 69

Найти неопределенный интеграл Проведем замену: . Навешиваем дифференциалы на обе части:

Вот почему дифференциалы нужно именно НАВЕШИВАТЬ на обе части и добросовестно

раскрывать эти дифференциалы. Немало чайников здесь формально напишет и допустит ошибку.

Пример70

Найти неопределенный интеграл

Проведем замену: 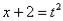Навешиваем дифференциалы на обе части:

С числителем разобрались. Что делать с в знаменателе? Берем нашу замену и выражаем из неё: Если , то

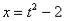
Пример71

Найти неопределенный интеграл Задача состоит в следующем: провести удачную замену, чтобы сразу избавиться от ВСЕХ корней.

Когда даны разные корни удобно придерживаться следующей схемы решения. Сначала выписываем на черновике подынтегральную функцию, при этом все корни представляем в

виде : . Нас будут интересовать знаменатели степеней. Записываем эти знаменатели: 2, 3, 3.

Теперь нужно найти наименьшее общее кратное чисел 2, 3, 3 – такое число, чтобы оно делилось и на 2 и на 3 (в данном случае), кроме того, это число должно быть как можно меньше.

Очевидно, что наименьшим общим кратным является число 6. Оно делится и на 2 и на 3, кроме того, меньше шестерки ничего не придумать.

Замена в рассматриваемом интеграле будет следующей: 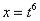Оформляем решение:

Проведем замену:

Источник

Интегрирование тригонометрических функции

Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x)=t и тогда sin(x)dx = -dt.
При R(sin(x),-cosx) = – R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t), , или замену ctg(x)=t, если это удобнее.

Интегрирование функций рационально зависящих от тригонометрических функций

1. Интегралы вида ∫sinⁿxdx, ∫cosⁿxdx, n>0

a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.

б) Если n чётное, то пользуемся формулами понижения степени

2sin²x=1-cos2x, 2cos²x=1+cos2x.

2. Интегралы вида ∫tgⁿxdx, ∫ctgⁿxdx, где n – целое.

Необходимо использовать формулы

3. Интегралы вида ∫sinⁿx·cos^mx dx

а) Пусть m и n разной чётности. Применяем подстановку t=sin x, если n – нечётное либо t=cos x, если m – нечётное.

б) Если m и n чётные, то пользуемся формулами понижения степени

2sin²x=1-cos2x, 2cos²x=1+cos2x.

4. Интегралы вида

Если числа m и n одинаковой чётности, то используем подстановку t=tg x. Часто бывает удобным применить приём тригонометрической единицы.

5. ∫sin(nx)·cos(mx)dx, ∫cos(mx)·cos(nx)dx, ∫sin(mx)·sin(nx)dx

Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:

sin α·cos β = ½(sin(α+β)+sin(α-β))
cos α·cos β = ½(cos(α+β)+cos(α-β))
sin α·sin β = ½(cos(α-β)-cos(α+β))

Решение онлайн
Видеоинструкция

С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

Также рекомендуется ознакомиться с возможностью нахождения интегралов онлайн.

Примеры

1. Вычислить интеграл ∫cos⁴x·sin³xdx.

Делаем замену cos(x)=t. Тогда ∫cos⁴x·sin³xdx =

2. Вычислить интеграл .

Делая замену sin x=t, получаем

3. Найти интеграл .

Делаем замену tg(x)=t. Подставляя, получаем

Заметим, что замена ctg(x)=t здесь удобнее, так как тогда , и поэтому

Интегрирование выражений вида R(sinx, cosx)

Пример №1. Вычислить интегралы:

Решение.

а) Интегрирование выражений вида R(sinx, cosx), где R — рациональная функция от sin x и cos x, преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t.

Тогда имеем

Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx, то применяется подстановка cos x = t.
Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx, то подстановка sin x = t.
Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx, то подстановка tgx = t или ctg x = t.

В данном случае для нахождения интеграла

применим универсальную тригонометрическую подстановку tg(x/2) = t.

Тогда

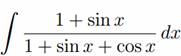
или

Так как дробь правильная, то, представляем в виде суммы интегралов:

Возвращась к исходной переменной будем иметь

b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫R(sinx, cosx) dx имеет вид ∫sin^mx·cosⁿxdx. В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:

В данном случае

Источник

На практике часто приходится вычислять интегралы трансцендентных функций, которые содержат тригонометрические функции. В рамках этого материала мы опишем основные виды подынтегральных функций и покажем, какие методы можно использовать для их интегрирования.

Интегрирование синуса, косинуса, тангенса и котангенса

Начнем с методов интегрирования основных тригонометрических функций – sin, cos, tg, ctg. Используя таблицу первообразных, сразу запишем, что ∫sin xdx=-cos x+C, а ∫cos xdx=sin x+C.

Для вычисления неопределенных интегралов функций tg и ctg можно воспользоваться подведением под знак дифференциала:

∫tg xdx=∫sin xcos xdx=d(cos x)=-sin xdx==-∫d(cos x)cos x=-lncos x+C∫ctg xdx=∫cos xsin xdx=d(sin x)=cos xdx==∫d(sin x)sin x=lnsin x+C

Как же у нас получились формулы ∫dxsin x=ln1-cos xsin x+C и ∫dxcos x=ln1+sin xcos x+C, взятые из таблицы первообразных? Поясним только один случай, поскольку второй будет понятен по аналогии.

Используя метод подстановки, запишем:

∫dxsin x=sinx=t⇒x=arcsin y⇒dx=dt1-t2=dtt1-t2

Здесь нам нужно интегрировать иррациональную функцию. Берем тот же метод подстановки:

∫dtt1-t2=1-t2=z2⇒t=1-z2⇒dt=-zdz1-z2==∫-zdzz1-z2·1-z2=∫dzz2-1=∫dz(z-1)(z+)==12∫dzz-1-12∫dzz+1=12lnz-1-12z+1+C==12lnz-1z+1+C=lnz-1z+1+C

Теперь производим обратную замену z=1-t2 и t = sin x:

∫dxsin x=∫dtt1-t2=lnz-1z+1+C==ln1-t2-11-t2+1+C=ln1-sin2 x-11-sin2 x+1+C==lncos x-1cos x+1+C=ln(cos x-1)2sin2x+C==lncos x-1sin x+C

Отдельно разберем случаи с интегралами, которые содержат степени тригонометрических функций, таких, как ∫sinn xdx, ∫cosn xdx, ∫dxsinn x, ∫dxcosn x.

О том, как их правильно вычислять, можно прочесть в статье об интегрировании с использованием рекуррентных формул. Если вы знаете, каким образом выведены эти формулы, то легко сможете брать интегралы вроде ∫sinn x·cosm xdx с натуральными m и n.

Если у нас имеется комбинация тригонометрических функций с многочленами или показательными функциями, то их придется интегрировать по частям. Советуем прочесть статью, посвященную методам нахождения интегралов ∫Pn(x)·sin (ax)dx, ∫Pn(x)·cos (ax)dx, ∫ea·x·sin (ax)dx, ∫ea·x·cos (ax)dx.

Наиболее сложными являются задачи, в которых подынтегральная функция включает в себя тригонометрические функции с разными аргументами. Для этого нужно пользоваться основными формулами тригонометрии, так что желательно помнить их наизусть или держать запись под рукой.

Пример 1

Найдите множество первообразных функции y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x).

Решение

Воспользуемся формулами понижения степени и запишем, что cos2x2=1+cos x2, а cos22x=1+cos 4×2. Значит,

y=sin (4x)+2cos2 (2x)sin x·cos (3x)+2cos2x2-1·sin (3x)=sin (4x)+2·1+cos 4x2sin x·cos (3x)+2·1+cos x2-1·sin (3x)==sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)

В знаменателе у нас стоит формула синуса суммы. Тогда можно записать так:

y=sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)=sin (4x)+cos(4x)+1sin(4x)==1+cos (4x)sin (4x)

У нас получилась сумма 3-х интегралов.

∫sin (4x)+cos(4x)+1sin x·cos (3x)+cos x·sin (3x)dx==∫dx+cos(4x)dxsin (4x)+∫dxsin (4x)==x+14ln∫d(sin(4x))sin(4x)+14lncos (4x)-1sin (4x)==14lnsin (4x)+14lncos (4x)-1sin (4x)+C=x+14·lncos4x-1+C

В некоторых случаях тригонометрические функции, находящиеся под интегралом, можно свести к дробно рациональным выражениям с использованием метода стандартной подстановки. Для начала возьмем формулы, которые выражают sin, cos и tg через тангенс половинного аргумента:

sin x=2tgx21+tg2x2, sin x=1-tg2x21+tg2x2, tg x=2tgx21-tg2x2

Также нам нужно будет выразить дифференциал dx через тангенс половинного угла:

Поскольку dtgx2=tgx2’dx=dx2cos2x2, то

dx=2cos2x2dtgx2=2dtgx21cos2x2=2dtgx2cos2x2+sin2x2cos2x2=2dtgx21+tg2x2

Таким образом, sin x=2z1+z2, cos x1-z21+z2, tg x2z1-z2, dx=2dz1+z2 при z=tgx2.

Пример 2

Найдите неопределенный интеграл ∫dx2sin x+cos x+2.

Решение

Используем метод стандартной тригонометрической подстановки.

2sin x+cos x+2=22z1+z2+1-z21+z2=z2+4z+31+z2⇒dx2sin x+cos x+2=2dz1+z2z2+4z+31+z2=2dzz2+4z+3

Получим, что ∫dx2sin x+cos x+2=2dzz2+4z+3.

Теперь мы можем разложить подынтегральную функцию на простейшие дроби и получить сумму двух интегралов:

∫dx2sin x+cos x+2=2∫2dzz2+4z+3=2∫121z+1-1z+3dz==∫dzz+1-∫Cz+3=lnz+1-lnz+3+C=lnz+1z+3+C

Далее производим обратную замену z=tgx2:

∫dx2sin x+cos x+2=lnz+1z+3+C=lntgx2+1tgx2+3+C

Ответ: ∫dx2sin x+cos x+2=lntgx2+1tgx2+3+C

Важно отметить, что те формулы, которые выражают фукнции через тангенс половинного аргумента, не являются тождествами, следовательно, получившееся в итоге выражение lntgx2+1tgx2+3+C – это множество первообразных функции y=12sin x+cos x+2 только на области определения.

Для решения других типов задач можно использовать основные методы интегрирования.

Преподаватель математики и информатики. Кафедра бизнес-информатики Российского университета транспорта

Источник

Интегрирование тригонометрических функций

Формула

Формула интегрирования тригонометрических функций в общем виде:

$$ int sin^n x cos^n x dx $$

где $ m $ и $ n $ – неотрицательные целые числа.

Рассмотрим пару случаев:

Хотя бы один из показателей $ m $ или $ n $ нечётный
Оба показателя $ m $ и $ n $ чётные

В первом случае применяем непосредственное интегрирование, а во втором могут помочь тригонометрические формулы:

$$ sin^2 x = frac{1}{2}(1-cos 2x); cos^2x = frac{1}{2}(1+cos 2x); sin x cos x = frac{1}{2}sin 2x; $$

Так же существуют интегралы вида:

$$ int sin mx sin nx dx; int cos mx cos nx dx; int sin mx cos nx dx $$

Их можно находить с помощью использования тригонометрических формул:

$$ sin alpha sin beta = frac{1}{2}[cos(alpha-beta)-cos(alpha+beta)] $$

$$ cos alpha cos beta = frac{1}{2}[cos(alpha-beta)+cos(alpha+beta)] $$

$$ sin alpha cos beta = frac{1}{2}[sin(alpha-beta)+sin(alpha+beta)] $$

Примеры решений

Пример 1

Найти интеграл: $$ int sin^3 x cos^2 x dx $$

Решение

Замечаем, что одна из степеней является нечетной, поэтому интегрирование тригонометрических функций вместе с методом непосредственного интегрирования должно помочь получить ответ к данной задаче.

Прежде выполним подведение под знак дифференциала:

$$ int sin^3 x cos^2 x dx = int sin^2 x cos^2 x sin x dx = -int sin^2 x cos^2 x d(cos x) = $$

Избавляемся от синуса через тригонометрическое тождество и выполняем разложение на два интеграла:

$$ = -int (1-cos^2 x) cos^2 x d(cos x) = -int cos^2 x d(cos x) + int cos^4 x d(cos x) = $$

Так как полученные интегралы содержат табличные функции, то записываем ответ:

$$ = -frac{1}{3} cos^2 x + frac{1}{5} cos^5 x + C $$

Если не получается решить свою задачу, то присылайте её к нам. Мы предоставим подробное решение онлайн. Вы сможете ознакомиться с ходом вычисления и почерпнуть информацию. Это поможет своевременно получить зачёт у преподавателя!

Ответ

$$ int sin^3 x cos^2 x dx = -frac{1}{3} cos^2 x + frac{1}{5} cos^5 x + C $$

Пример 2

Найти интеграл произведения тригонометрических функций: $$ int sin^2 x cos^4 x dx $$

Решение

Учитывая, что $ cos^4 x = cos^2 x cdot cos^2 x $ преобразуем выражение под знаком интеграла:

$$ int sin^2 x cos^4 x dx = int sin^2 x cos^2 x cos^2 x dx = int (sin x cos x)^2 cos^2 x dx = $$

Выполняем преобразование под синус двойного угла $ (sin x cos x)^2 = frac{1}{4}sin^2 2x $:

$$ = frac{1}{4} int sin^2 2x cos^2 x dx = frac{1}{4} int sin^2 2x frac{1+cos 2x}{2} dx = $$

Раскладываем интеграл на два интеграла:

$$ = frac{1}{8} int sin^2 2x dx + frac{1}{8} int sin^2 2x cdot cos 2x dx = $$

С помощью формулы понижения степени синуса $ sin^2 2x = frac{1-cos 4x}{2} $ получаем:

$$ = frac{1}{8} int frac{1-cos 4x}{2} dx + frac{1}{16} int sin^2 2x d(sin 2x) dx = $$

Выполняем интегрирование:

$$ = frac{1}{16} int dx – frac{1}{16} int cos 4x dx +frac{1}{16} frac{sin^3 2x}{3} = $$

$$ = frac{1}{16} x – frac{1}{64} sin 4x +frac{1}{48} sin^3 2x + C $$

Ответ

$$ int sin^2 x cos^4 x dx = frac{1}{16} x – frac{1}{64} sin 4x +frac{1}{48} sin^3 2x + C $$

Пример 3

Найти интеграл тригонометрической функции: $$ int (cos 5x cos x) dx $$

Решение

С помощью формулы произведения косинусов преобразуем:

$$ cos 5x cos x = frac{1}{2}[cos(5x-x)+cos(5x+x)] = frac{1}{2}[cos4x+cos6x] $$

Добавляем знак интеграла и выполняем разложение:

$$ int frac{1}{2}[cos4x+cos6x] dx = frac{1}{2}int cos 4x dx + frac{1}{2}int cos 6x dx = $$

Зная таблицу интегрирования элементарных функций получаем ответ:

$$ = frac{1}{8} sin 4x + frac{1}{12} sin 6x + C $$

Ответ

$$ int (cos 5x cos x) dx = frac{1}{8} sin 4x + frac{1}{12} sin 6x + C $$

Источник

Простое объяснение принципов нахождения интегралов тригонометрических функций и 10 наглядных примеров. В каждом примере поэтапный ход решения и ответ.

Алгоритм решения интегрирования тригонометрических функций

Для нахождения интегралов тригонометрических функций используются свойства интегралов, а также таблица неопределённых интегралов и, в частности, табличные интегралы тригонометрических функций.

Интегралы, содержащие произведения тригонометрических функций, вычисляются путём преобразования к сумме нескольких функций с помощью следующих формул.

Таблица основных интегралов

Таблица основных интегралов, – постоянная величина

$[int x^{n}dx = frac{x^{n + 1}}{n + 1} + C, (n = const, n neq -1)]$

$[int frac{dx}{x^{n}} = -frac{1}{n - 1}cdotfrac{1}{x^{n-1}} + C, (n = const, n neq -1)]$

$[int frac{dx}{sqrt{x}} = 2sqrt{x} + C]$

$[int frac{dx}{x} = ln{|x|} + C]$

$[int a^{x}dx = frac{a^{x}}{ln a} + C, (a > 0, a neq 1)]$

$[int e^{x}dx = e^{x} + C]$

$[int frac{dx}{cos^{2}x} = tg{x} + C]$

$[int frac{dx}{sin^{2}x} = - ctg{x} + C]$

$[int frac{dx}{1 + x^{2}} = arctg{x} + C]$

$[int frac{dx}{sqrt{1 - x^{2}}} = arcsin{x} + C]$

$[int frac{dx}{1 - x^{2}} = frac{1}{2}cdotlnleft | frac{1 + x}{1 - x} right | + C]$

$[int frac{dx}{sqrt{x^{2} pm a^{2}}} = ln | x + sqrt{x^{2} pm a^{2}} | + C]$

$[int frac{dx}{ ch^{2}x} = th{x} + C]$

$[int frac{dx}{ sh^{2}x} = - cth{x} + C]$

Примеры решений интегрирования тригонометрических функций

Задача

Вычислить интеграл:

Решение

Преобразуем подынтегральную функцию:

$[int sin6xcos7xdx = frac{1}{2}intsin-x + sin13xdx =]$

$[= frac{1}{2}int(-sin x + sin13x)dx = frac{1}{2}(cos x - frac{1}{13}cos13x) + C]$

Ответ

$[int sin6xcos7xdx = frac{1}{2}(cos x - frac{1}{13}cos13x) + C]$

Задача

Вычислить интеграл:

Решение

Преобразуем подынтегральную функцию:

$[int cos3xcos9xdx = frac{1}{2}int(cos(-6x) + cos12x)dx =]$

$[= frac{1}{2}int(cos6x + cos12x)dx = frac{1}{2}(frac{1}{6}sin6x + frac{1}{12}sin12x) + C]$

Ответ

$[int cos3xcos9xdx = frac{1}{2}(frac{1}{6}sin6x + frac{1}{12}sin12x) + C]$

Задача

Вычислить интеграл:

Решение

Преобразуем подынтегральную функцию:

$[int sin2xsin5xdx = frac{1}{2}int(cos(-3x) - cos7x)dx =]$

$[= frac{1}{2}(frac{1}{3}sin3x + frac{1}{7}sin7x) + C]$

Ответ

$[int sin2xsin5xdx = frac{1}{2}(frac{1}{3}sin3x + frac{1}{7}sin7x) + C]$

Задача

Вычислить интеграл:

$[int sin^{3}xdx]$

Решение

Преобразуем подынтегральную функцию:

$sin^{3}x = sin^{3}xsin x = (1 - cos^{2}x)sin x$

$[int(1 - cos^{2}x)sin xdx]$

Сделаем подстановку

$[-int(1 - z^{2})dz = -z + frac{z^{3}}{3} + C]$

Производя обратную подстановку получаем:

$-cos x + frac{cos^{3}x}{3} + C$

Ответ

$[int sin^{3}xdx = -cos x + frac{cos^{3}x}{3} + C]$

Задача

Вычислить интеграл:

$[int cos^{5}xdx]$

Решение

Преобразуем подынтегральную функцию:

$cos^{5}x = cos^{4}xcos x = (cos^{2}x)^{2}cos x = (1 - sin^{2}x)^{2}cos x = (1 - 2sin^{2}x + sin^{4})cos x$

$[int(1 - 2sin^{2}x + sin^{4})cos xdx]$

Сделаем подстановку

$[-int(1 - 2z^{2} + z^{4})dz = z - frac{2z^{3}}{3} + frac{z^{5}}{5} + C]$

Производя обратную подстановку получаем:

$sin x - frac{2sin^{3}x}{3} + frac{sin^{5}}x{5} + C$

Ответ

$[int cos^{5}xdx = sin x - frac{2sin^{3}x}{3} + frac{sin^{5}}x{5} + C]$

Задача

Вычислить интеграл:

$[int sin^{7}xdx]$

Решение

Преобразуем подынтегральную функцию:

$sin^{7}x = sin^{6}xsin x = (sin^{2}x)^{3}sin x = (1 - cos^{2}x)^{3}sin x$

$[int(1 - cos^{2}x)^{3}sin xdx]$

Сделаем подстановку

$[-int(1 - z^{2})^{3}dz = -int(1 - 3z^{2} + 3z^{4} - z^{6})dz =]$

$[= -(z - z^{3} + frac{3}{5}z^{5} - frac{1}{7}z^{7}) + C]$

Производя обратную подстановку получаем:

$-(cos x - cos^{3}x + frac{3}{5}cos^{5}x - frac{1}{7}cos^{7}x) + C$

Ответ

$[int sin^{7}xdx = -(cos x - cos^{3}x + frac{3}{5}cos^{5}x - frac{1}{7}cos^{7}x) + C]$

Задача

Вычислить интеграл:

$[int cos^{9}xdx]$

Решение

Преобразуем подынтегральную функцию:

$cos^{7}x = cos^{8}xcos x = (cos^{2}x)^{4}cos x = (1 - sin^{2}x)^{4}cos x$

$[int(1 - sin^{2}x)^{4}cos xdx]$

Сделаем подстановку

$[-int(1 - z^{2})^{4}dz = -int(1 - 4z^{2} + 6z^{4} - 4z^{6} + z^{8})dz =]$

$[= z - frac{4}{3}z^{3} + frac{6}{5}z^{5} - frac{4}{7}z^{7} + frac{1}{9}z^{9} + C]$

Производя обратную подстановку получаем:

$sin x - frac{4}{3}sin^{3}x + frac{6}{5}cos^{5}x - frac{4}{7}cos^{7}x) + frac{1}{9}sin^{9}x + C$

Ответ

$[int cos^{9}xdx = sin x - frac{4}{3}sin^{3}x + frac{6}{5}cos^{5}x - frac{4}{7}cos^{7}x + frac{1}{9}sin^{9}x + C]$

Задача

Вычислить интеграл:

$[int sin^{4}xcos^{3}xdx]$

Решение

Преобразуем подынтегральную функцию:

$sin^{4}xcos^{3}x = sin^{4}xcos^{2}xcos x = sin^{4}x(1 - sin^{2})cos x = (sin^{4} - sin^{6})cos x$

$[int(sin^{4} - sin^{6})cos xdx]$

Сделаем подстановку

$[int(z^{4} - z^{6})dz = frac{z^{5}}{5} - frac{z^{7}}{7} + C]$

Производя обратную подстановку получаем:

$frac{sin^{5}x}{5} - frac{sin^{7}x}{7} + C$

Ответ

$[int sin^{4}xcos^{3}xdx = frac{sin^{5}x}{5} - frac{sin^{7}x}{7} + C]$

Задача

Вычислить интеграл:

$[int sin^{2}xsin^{5}xdx]$

Решение

Преобразуем подынтегральную функцию:

$sin^{2}xsin^{5}x = cos^{2}xsin^{4}xsin x = cos^{2}x(sin^{2})^{2}sin x = cos^{2}x(1 - cos^{2}x)^{2}sin x = cos^{2}x(1 - 2cos^{2}x + cos^{4}x)sin x = (cos^{2}x - 2cos^{4}x + cos^{6}x)sin x$

$[int(cos^{2}x - 2cos^{4}x + cos^{6}x)sin xdx]$

Сделаем подстановку

$[-int(z^{2} - 2z^{4} + z^{6})dz = -(frac{z^{3}}{3} - frac{2z^{5}}{5} + frac{z^{7}}{7}) + C]$

Производя обратную подстановку получаем:

$-(frac{cos^{3}x}{3} - frac{2cos^{5}x}{5} + frac{cos^{7}x}{7}) + C$

Ответ

$[int sin^{2}xsin^{5}xdx = -(frac{cos^{3}x}{3} - frac{2cos^{5}x}{5} + frac{cos^{7}x}{7}) + C]$

Задача

Вычислить интеграл:

$[int sin^{4}xcos^{7}xdx]$

Решение

Преобразуем подынтегральную функцию:

$sin^{4}xcos^{7}x = sin^{4}xcos^{6}xcos x = sin^{4}x(cos^{2}x)^{3}cos x = sin^{4}x(1 - sin^{2}x)^{3}cos x = sin^{4}x(1 - 3sin^{2}x + 3sin^{4}x - sin^{6}x)^{3}cos x = (sin^{4}x - 3sin^{6}x + 3sin^{8}x - sin^{10}x)^{3}cos x$