Как найти интеграл по замкнутому контуру – Сайт, где вы сможете решить свои вопросы

3.4. Криволинейный интеграл по замкнутому контуру

Продолжаем решать криволинейные интегралы 2-го рода. Новизна будет состоять

в особенности пути интегрирования, а именно в его замкнутости. Наверное, всем интуитивно понятно, что это значит –

встаньте с места и прогуляйтесь, как вам захочется. После чего вернитесь в исходную точку. Это и есть замкнутый контур. В

рамках данной книги я рассмотрю элементарные маршруты без самопересечений, такие как окружность, треугольник, квадрат

и т.п.

Криволинейный интеграл по замкнутому контуру так и обозначают – с символической окружностью посередине:

Нередко на окружности рисуют стрелочку, указывая направление движения:
– против часовой стрелки;
– либо по часовой стрелке.

На практике чаще всего встречается первый вариант, который принято называть положительным направлением обхода

контура. Впрочем, чтобы послать по контуру – стрелка не обязательна:)

Пример 62

Вычислить интеграл по контуру , ограниченному линиями . Интегрировать против часовой стрелки.

Выполнить чертёж.

Решение: Слушаемся и повинуемся:)

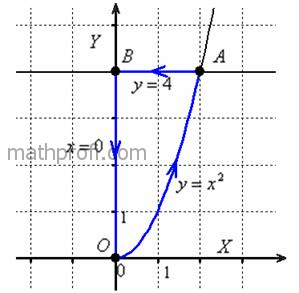
! Напоминаю, что для криволинейного интеграла 2-го рода принципиально важнО направление интегрирования, и поэтому на

чертеже крайне желательно проставлять стрелочки.

В силу свойства аддитивности, криволинейный интеграл по контуру можно представить в виде суммы трёх

интегралов:

И теперь, вы, наверное, поняли, что нас ждёт дальше:

1) Вычислим интеграл по дуге параболы. Если , то:

В соответствии с направлением, изменяется от 0 до 2:

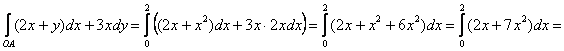
Желающие могут выполнить проверку: выразить нужный кусок параболы: , найти и проинтегрировать по «игрек» от 0 до 4.

2) Вычислим интеграл по отрезку прямой . С дифференциалом тут всё просто: , а вот с пределами интегрирования не очень – интегрировать нужно

строго по заданному направлению, то есть от 2 до 0 (см. чертёж выше):

3) И, наконец, интеграл по фрагменту оси ординат. Если , то, понятно, что , и «игрек» изменяется (внимание!) от 4 до 0:

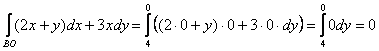
Осталось просуммировать три куска и получить результат по всему контуру:

Ответ:

Если контур обойти по часовой стрелке, то получится противоположное значение:
.

Другой очевидный факт состоит в том, что если мы начнём свой путь из любой другой точки контура и совершим «оборот» (в

том или ином направлении), то значение интеграла не изменится.

Что можно сказать по поводу выполненного задания?

Решение хорошее, решение логичное, однако у него есть существенный недостаток. Оно длинное.

…Но это не беда! Если нет беды с двойными интегралами :). Для простых контуров

существует:

3.5. Формула Грина – Остроградского

3.3.2. Если линия задана параметрически

| Оглавление |

Полную и свежую версию данного курса в pdf-формате,
а также курсы по другим темам можно найти здесь.

Также вы можете изучить эту тему подробнее – просто, доступно, весело и бесплатно!

С наилучшими пожеланиями, Александр Емелин

Источник

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 11 ноября 2019 года; проверки требуют 5 правок.

Теорема Грина устанавливает связь между криволинейным интегралом по замкнутому контуру $C$ и двойным интегралом по односвязной области $D$ , ограниченной этим контуром. Фактически, эта теорема является частным случаем более общей теоремы Стокса. Теорема названа в честь английского математика Джорджа Грина.

Формулировка[править | править код]

Пусть $C$ — положительно ориентированная кусочно-гладкая замкнутая кривая на плоскости, а $D$ — область, ограниченная кривой $C$ . Если функции $P = P(x,y)$ , $Q = Q(x,y)$ определены в области $D$ и имеют непрерывные частные производные $frac{partial P}{partial y}$ , $frac{partial Q}{partial x}$ , то

$ointlimits_{C} P ,dx + Q ,dy = iintlimits_{D} left( frac{partial Q}{partial x} - frac{partial P}{partial y} right) ,dx,dy$

На символе интеграла часто рисуют окружность, чтобы подчеркнуть, что кривая $C$ замкнута.

Доказательство для простой области[править | править код]

$D$ — область, правильная в направлении $OY$ , ограниченная замкнутой кривой $C$

Пусть область $D$ — криволинейная трапеция (область, правильная в направлении $OY$ ):

$D = { (x,y)|a le x le b, y_1(x) le y le y_2(x) }$

Для кривой $C$ , ограничивающей область $D$ зададим направление обхода по часовой стрелке.

Тогда:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = intlimits_{a}^{b}dx intlimits_{y_1(x)}^{y_2(x)} frac{partial P}{partial y} ,dy = intlimits_{a}^{b} (P(x,y_2(x)) - P(x,y_1(x))) ,dx =$

$= intlimits_{a}^{b} P(x,y_2(x)) ,dx - intlimits_{a}^{b} P(x,y_1(x)) ,dx quad (1)$

Заметим, что оба полученных интеграла можно заменить криволинейными интегралами:

$intlimits_{C_1} P(x,y) ,dx = -intlimits_{-C_1} P(x,y) ,dx = -intlimits_{a}^{b} P(x,y_1(x)) ,dx quad (2)$

$intlimits_{C_3} P(x,y) ,dx = intlimits_{a}^{b} P(x,y_2(x)) ,dx quad (3)$

Интеграл по $C_{1}$ берётся со знаком «минус», так как согласно ориентации контура $C$ направление обхода данной части — от $b$ до $a$ .

Криволинейные интегралы по $C_{2}$ и $C_{4}$ будут равны нулю, так как $x = operatorname{const}$ :

$intlimits_{C_2} P(x,y) ,dx = 0 quad (4)$

$intlimits_{C_4} P(x,y) ,dx = 0 quad (5)$

Заменим в (1) интегралы согласно (2) и (3), а также прибавим (4) и (5), равные нулю и поэтому не влияющие на значение выражения:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = intlimits_{C_1} P(x,y) ,dx + intlimits_{C_3} P(x,y) ,dx + intlimits_{C_2} P(x,y) ,dx + intlimits_{C_4} P(x,y) ,dx$

Так как обход по часовой стрелке при правой ориентации плоскости является отрицательным направлением, то сумма интегралов в правой части является криволинейным интегралом по замкнутой кривой $C$ в отрицательном направлении:

$iintlimits_{D} frac{partial P}{partial y} ,dx,dy = -intlimits_{C} P(x,y) ,dx quad (6)$

Аналогично доказывается формула:

$iintlimits_{D} frac{partial Q}{partial x} ,dx,dy = intlimits_{C} Q(x,y) ,dy quad (7)$

если в качестве области $D$ взять область, правильную в направлении $OX$ .

Складывая (6) и (7), получим:

$intlimits_{C} P ,dx + Q ,dy = iintlimits_{D} left( frac{partial Q}{partial x} - frac{partial P}{partial y} right) ,dx,dy$

Формулы Грина[править | править код]

Если бы в электростатических задачах мы всегда имели дело с дискретным или непрерывным распределением заряда без всяких граничных поверхностей, то общее решение для скалярного потенциала

$Phi (x)=int {frac {rho (x')}{|x-x'|}}d^{3}x$

было бы самой удобной и непосредственной формой решения таких задач и не нужны были бы ни уравнение Лапласа, ни уравнение Пуассона. Однако
в действительности в целом ряде, если не в большинстве, задач электростатики мы имеем дело с конечными областями пространства (содержащими или не содержащими заряд), на граничных поверхностях которых заданы определённые граничные («краевые») условия. Эти граничные условия могут быть заменены некоторым соответственно подобранным распределением зарядов вне рассматриваемой области (в частности, в бесконечности), однако приведённое выше соотношение в этом случае уже непригодно для расчёта потенциала, за исключением некоторых частных случаев (например, в методе изображений).

Для рассмотрения задач с граничными условиями необходимо расширить используемый нами математический аппарат, а именно вывести так называемые формулы, или теоремы Грина (1824 г.).
Они получаются непосредственно из теоремы о дивергенции

$intlimits_V operatorname{div}~A,d^3x=ointlimits_S A cdot n,da$ ,

которая справедлива для любого векторного поля А, определённого в объёме V, ограниченном замкнутой поверхностью S. Пусть $A=varphi operatorname{grad} ~psi$ , где $varphi$ и $psi$ — произвольные дважды непрерывно-дифференцируемые скалярные функции.
Тогда

$operatorname{div} , (varphi ; operatorname{grad} , psi)=varphi nabla^2 psi + operatorname{grad} ~varphi cdot operatorname{grad} ~psi qquad (1)$

$varphi ; operatorname{grad} , psi cdot n=varphi frac{partial psi}{partial n} qquad (2)$ ,

где $frac{partial}{partial n}$ — нормальная производная на поверхности S (по
направлению внешней нормали по отношению к объёму V). Подставляя (1) и (2) в теорему о дивергенции, мы придем к первой формуле Грина

$intlimits_V (varphi ; nabla^2 psi + operatorname{grad} , varphi cdot operatorname{grad} , psi),d^3x = ointlimits_S varphi frac{partial psi}{partial n} ,da qquad (3)$ .

Напишем такую же формулу, поменяв в ней местами $varphi$ и $psi$ ,
и вычтем её из (3). Тогда члены с произведением $operatorname{grad} ~varphi cdot operatorname{grad} ~psi$
сократятся и мы получим вторую формулу Грина, называемую иначе теоремой Грина:

$intlimits_V (varphi nabla^2 psi - psi nabla^2 varphi),d^3x = ointlimits_S left[varphi frac{partial psi}{partial n} - psi frac{partial varphi}{partial n}right] ,da$ .

В физике и математике теорема Грина дает соотношение между криволинейным интегралом простой ограниченной кривой С и двойным интегралом по плоской поверхности D ограниченной кривой С. И в общем виде записывается следующим образом

$intlimits_{C} L, dx + M, dy = iintlimits_{D} left(frac{partial M}{partial x} - frac{partial L}{partial y}right), dA.$

В физике Теорема Грина в основном используется для решения двумерных потоковых интегралов, исходя из того, что сумма исходящих потоков в любой точке области равна результирующему потоку, суммируемому по всей ограничивающей поверхности.

Третья формула Грина получается из второй путём замены $psi = frac{1}{|mathbf{x} - mathbf{y}|}$ и замечания о том, что $nabla^2 psi = - 4 pi delta left( mathbf{x} - mathbf{y} right)$ в ${{mathbb{R}}^{3}}$ . Если ${displaystyle phi ,}$ дважды дифференцируема на U.

$ointlimits_{partial U} left[ {1 over |mathbf{x} - mathbf{y}|} {partial phi over partial n} (mathbf{y}) - phi(mathbf{y}) {partial over partial n_mathbf{y}} {1 over |mathbf{x} - mathbf{y}|}right], dS_mathbf{y} - intlimits_U left[ {1 over |mathbf{x} - mathbf{y}|} nabla^2 phi(mathbf{y})right], dV_mathbf{y} = k$

${displaystyle k=4pi phi (x),}$ если $x in Int U$ (здесь Int обозначает внутренность множества),

${displaystyle 2pi phi (x),}$ если $x in partial U$
и в точке $x$ к граничной поверхности имеется касательная плоскость.

См. также[править | править код]

Дельта-функция
Теорема Стокса
Формула Остроградского
Дискретная теорема Грина

Литература[править | править код]

Д. Ж. Джексон Классическая электродинамика (1965 г.)
Тихонов А. Н., Самарский А. А. Уравнения математической физики. — М.: Наука, 1977. — 735 с.

Источник

Лекция 22

22. Криволинейные
интегралы

22.1. Определение
и существование криволинейного интеграла
2-го рода

Пусть в некоторой
области D задано плоское силовое поле.
Т. е. в области D вектор силы задается
формулой:

F=P(x,y)
i+Q(x,y)
j=(P(x,y);Q(x,y)).

Проведем в области
D некоторый контур AB. Разобьем контур
на достаточно большое число достаточно
малых частей системой точек
A=M₀,M₁,M₂,…,M_n=B.
На каждом элементарном перемещении
вычислим значения

P(x_i
,y_i)
x_i
+ Q(x_i
,y_i)y_i

и просуммируем
полученные значения.

(1)

Обозначим =
maxM_i_-1M_i.
Начнем строить различные интегральные
суммы так, чтобы 0
и, соответственно, n.

Определение. Предел
интегральных сумм вида (1) при 0,
если этот предел существует и не зависит
ни от способа разбиения контура L на
части, ни от выбора значений M_i(_i,_i)L_i
на этих частях, называется криволинейным
интегралом
2-го рода по контуру AB. Обозначается

(2)

Теорема. Если
функция z=f(x,y) непрерывна в области D и
область D ограничена, то интеграл (2)
существует. (Без доказательства).

22.2. Свойства
криволинейного интеграла 2-го рода

Свойства
криволинейного интеграла 2-го рода
аналогичны общим свойствам интегралов.
Поэтому отметим отличительные свойства.
Пусть указанные интегралы существуют.
Тогда выполняются следующие свойства.

Постоянный
сомножитель можно выносить за знак
криволинейного
интеграла
по контуру AB от каждого из слагаемых.

При изменении
направления движения по контуру знак
интеграла изменяется на противоположный.

Если контур AB
разбить на два контура AC и CB, не имеющие
общих внутренних точек, то

Это правило верно
и для случая любого числа частей.

Разобрать
доказательство по учебнику самостоятельно.

22.3. Вычисление
криволинейного интеграла 2-го рода

Пусть нам дан
интеграл (2). Рассмотрим случай, когда
контур задан параметрически

Тогда

(3)

(Без доказательства)

Если контур задан
в явном виде с помощью кривой, то можно
свести этот случай к параметрическому,
считая

Тогда

Пример. Вычислить

22.4. Определение
и существование криволинейного интеграла
1-го рода

Пусть в некоторой
области D задана z=f(x,y). Проведем в области
D некоторый контур AB. Разобьем контур
на достаточно большое число достаточно
малых частей системой точек
A=M₀,M₁,M₂,…,M_n=B.
На каждом элементарном перемещении
вычислим значения z=f(x_i,y_i).
Найдем элементарную длину контура

вычислим произведения
f (x_i,y_i)s_iи просуммируем
полученные значения.

(4)

Обозначим =
maxM_i_-1M_i.
Начнем строить различные интегральные
суммы так, чтобы 0
и, соответственно, n.

(5)

22.5. Свойства
криволинейного интеграла 1-го рода

Свойства
криволинейного интеграла 1-го рода
аналогичны общим свойствам интегралов.
Поэтому отметим отличительные свойства.
Пусть указанные интегралы существуют.
Тогда выполняются следующие свойства.

При изменении
направления движения по контуру величина
интеграла не изменяется.

Если контур AB
разбить на два контура AC и CB, не имеющие
общих внутренних точек, то

Это правило верно
и для случая любого числа частей.

Разобрать
доказательство по учебнику самостоятельно.

22.6. Вычисление
криволинейного интеграла 1-го рода

Пусть нам дан
интеграл (2). Рассмотрим случай, когда
контур задан параметрически

Тогда

(Без доказательства)

Если контур задан
в явном виде с помощью кривой , то можно
свести этот случай к параметрическому,
считая

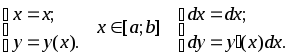
Тогда

22.7. Криволинейные
интегралы по замкнутому контуру

Если начало и конец
контура совпадают, то контур называется
замкнутым. Пусть нам дан криволинейный
интеграл по замкнутому контуру. Разобьем
контур на две части точками и . Тогда

Для криволинейного
интеграла 2-го рода по замкнутому контуру
нужно различать направление обхода.
Будем считать направление обхода
положительным, если при движении вдоль
контура область остается слева.
Противоположное направление обхода
является отрицательным.

22.8. Формула
Грина

Теорема. Если
область D ограничена замкнутым контуром
и функции z=P(x,y) и z=Q(x,y) непрерывна в
области D, включая границу, то

Доказательство.
Рассмотрим область D и обозначим уравнения
границ контура

Вторая часть
равенства доказывается аналогично.

Пример. Вычислить

где контур
треугольника с вершинами

Решение. Применим
формулу Грина

22.9. Криволинейные
интегралы по контурам в пространстве

Контур может быть
задан и в пространстве. Пусть в некоторой
области заданы функции и некоторый
контур. Тогда

Тогда криволинейный
интеграл 2-го рода равен

Криволинейный
интеграл 1-го рода равен

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

Источник

Интеграл по замкнутому контуру, формула Грина, примеры

Если дан криволинейный интеграл, а кривая, по которой происходит интегрирование – замкнутая (называется контуром), то такой интеграл называется интегралом по замкнутому контуру и обозначается следующим образом:

Область, ограниченную контуром L обозначим D. Если функции P(x, y) , Q(x, y) и их частные производные и – функции, непрерывные в области D, то для вычисления криволинейного интеграла можно воспользоваться формулой Грина:

Таким образом, вычисление криволинейного интеграла по замкнутому контуру сводится к вычислению двойного интеграла по области D.

Формула Грина остаётся справедливой для всякой замкнутой области, которую можно проведением дополнительных линий на конечное число простых замкнутых областей.

Пример 1. Вычислить криволинейный интеграл

если L – контур треугольника OAB , где О(0; 0) , A(1; 2) и B(1; 0) . Направление обхода контура – против часовой стрелки. Задачу решить двумя способами: а) вычислить криволинейные интегралы по каждой стороне треугольника и сложить результаты; б) по формуле Грина.

а) Вычислим криволинейные интегралы по каждой стороне треугольника. Сторона OB находится на оси Ox , поэтому её уравнением будет y = 0 . Поэтому dy = 0 и можем вычислить криволинейный интеграл по стороне OB :

Уравнением стороны BA будет x = 1 . Поэтому dx = 0 . Вычисляем криволинейный интеграл по стороне BA :

Уравнение стороны AO составим, пользуясь формулой уравнения прямой, проходящей через две точки:

Таким образом, dy = 2dx . Вычисляем криволинейный интеграл по стороне AO :

Данный криволинейный интеграл будет равен сумме интегралов по краям треугольника:

б) Применим формулу Грина. Так как , , то . У нас есть всё для того, чтобы вычислить данный интеграл по замкнутому контуру по формуле Грина:

Как видим, получили один и тот же результат, но по формуле Грина вычисление интеграла по замкнутому контуру происходит значительно быстрее.

Пример 2. Пользуясь формулой Грина, вычислить криволинейный интеграл

где L – контур OAB , OB – дуга параболы y = x² , от точки О(0; 0) до точки A(1; 1) , AB и BO – отрезки прямых, B(0; 1) .

Решение. Так как функции , , а их частные производные , , D – область, ограниченная контуром L , у нас есть всё, чтобы воспользоваться формулой Грина и вычислить данный интеграл по замкнутому контуру:

Пример 3. Пользуясь формулой Грина, вычислить криволинейный интеграл

, если L – контур, который образуют линия y = 2 − |x| и ось Oy .

Решение. Линия y = 2 − |x| состоит из двух лучей: y = 2 − x , если x ≥ 0 и y = 2 + x , если x .

Имеем функции , и их частные производные и . Подставляем всё в формулу Грина и получаем результат:

Пример 4. С помощью формулы Грина вычислить криволинейный интеграл

если L – окружность .

Решение. Функции , и их частные производные и непрерывны в замкнутом круге . Подставляем всё в формулу Грина и вычисляем данный интеграл:

Интеграл по контуру окружности

Учасники групи мають 10% знижку при замовленні робіт, і ще багато бонусів!

Контакты

Администратор, решение задач
Роман

Tel. +380685083397
[email protected]
skype, facebook:
roman.yukhym

Решение задач
Андрей

facebook:
dniprovets25

Криволинейные интегралы в математике с примерами решения и образцами выполнения

При изучении темы «Криволинейные интегралы» вы познакомитесь с понятиями криволинейных интегралов первого рода (по длине дуги) и второго рода (по координатам) от функций двух и трех переменных и научитесь вычислять их вдоль различных плоских и пространственных кривых, заданных параметрически, в декартовых и в полярных координатах, приводя криволинейные интегралы к определенным.

Криволинейные интегралы первого рода

Постановка задачи. Вычислить криволинейный интеграл

где L — часть гладкой кривой, заданной параметрически

и dl — дифференциал длины дуги.

План решения. Криволинейный интеграл первого рода по кривой L определяется формулой

Подчеркнем, что криволинейный интеграл первого рода не зависит
от направления обхода кривой и всегда

1.Вычисляем и

2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений

Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

то ее необходимо параметризовать.

Замечание:

Если плоская кривая задана уравнением у = у(х)
то дифференциал длины дуги равен и формула (1) имеет вид

Если плоская кривая задана в полярных координатах уравнением то дифференциал длины дуги равен

и формула (1) имеет вид

Пример:

Вычислить криволинейный интеграл

где L — первый виток винтовой линии

Решение:

1.Вычисляем: x'(t) = — sin t, y'(t) = cos t, z'(t) = 1, и

2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

Ответ.

Пример:

Вычислить криволинейный интеграл

где L — отрезок прямой от точки А(0, 0) до точки В(4, 3).

Решение:

1.В данном случае уравнение прямой есть и, следовательно, и

2.Подставляем эти результаты в формулу (1) и вычисляем определенный интеграл:

Ответ.

Пример:

Вычислить криволинейный интеграл

где L — часть спирали Архимеда

Решение:

1.Вычисляем: так как при

2.Подставляем эти результаты в формулу (1″) и вычисляем определенный интеграл:

Ответ.

Криволинейные интегралы второго рода

Постановка задачи. Вычислить криволинейный интеграл

где L — часть гладкой кривой, заданной параметрически

План решения. Криволинейный интеграл второго рода по кривой L определяется формулой

1.Вычисляем x'(t), y'(t) и z'(t).

2.Вычисляем криволинейный интеграл по формуле (1) и записываем ответ.

Замечание:

Если граничные точки кривой L и
заданы в декартовых координатах, то и определяем, решая системы уравнений

Замечание:

Если кривая задана как линия пересечения двух
поверхностей:

то ее необходимо параметризовать.

Пример:

Вычислить криволинейный интеграл

по части кривой L, заданной параметрически

Решение:

1.Вычисляем: x'(t) = — 2sin t, y'(t) = 2cos t и

2.Вычисляем криволинейный интеграл по формуле (1):

Ответ.

Пример:

Вычислить криволинейный интеграл

от точки М(2,0, 4) до точки N(—2,0,4) по кривой L, образованной пересечением параболоида и плоскости z = 4,

Решение:

В сечении получается окружность

Поэтому параметрические уравнения кривой L имеют вид

1.Вычисляем: х'(t) = -2sin t, у'(t) = 2cos t и z'(t) = 0.

Определяем из условий

Учитывая, что получаем и

2.Вычисляем криволинейный интеграл по формуле (1):

Ответ.

Дополнение к криволинейному интегралу

Решение криволинейных интегралов

Кривая АВ, заданная параметрическими уравнениями

называется гладкой, если функции φ(t) и ψ(t) имеют на отрезке [tо, t1] непрерывные производные φ'(t) и ψ'(t), причем

Если в конечном числе точек отрезка [tо, t1] эти производные не существуют или одновременно обращаются в нуль, то кривая называется кусочно-гладкой.

Пусть АВ — плоская кривая, гладкая или кусочно-гладкая. Пусть f(M) — функция, заданная на кривой АВ или в некоторой области D, содержащей эту кривую. Рассмотрим разбиение кривой АВ на части точками

Выберем на каждой из дуг AkAk+1 произвольную точку Мk и составим сумму

где ∆lk — длина дуги AkAk+1 и назовем ее интегральной суммой для функции f(M) по длине дуги кривой. Пусть ∆l — наибольшая из длин частичных дуг, т.е.

Определение:

Если при ∆l —► 0 интегральная сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ на части, ни от выбора точек на каждой из дуг разбиения, то этот предел называется криволинейным интегралом 1 -го рода от функции f(M) по кривой АВ (интеграл по длине дуги кривой) и обозначается символом

(точка М(х, у) лежит на кривой АВ).
В этом случае функция f(M) называется интегрируемой вдоль кривой АВ, кривая АВ называется контуром интегрирования, А — начальной, В — конечной точками интегрирования. Таким образом, по определению,
(2)

Пример:

Пусть вдоль некоторой гладкой кривой L распределена масса с переменной линейной плотностью f(M). Найти массу т кривой L.

Разобьем кривую L на п произвольных частей MkMk+1 (k = 0,1,… , n —1) и вычислим приближенно массу каждой части, предполагая, что на каждой из частей MkMk+1 плотность постоянна и равна плотности в какой-нибудь из ее точек, например, в крайней левой точке f(Mk). Тогда сумма

где ∆lk — длина k-ой части, будет приближенным значением массы т. Ясно, что погрешность будет тем меньше, чем мельче разбиение кривой L. В пределе при ∆l → 0 () получим точное значение массы всей кривой L, т.е.

Но предел справа есть криволинейный интеграл 1-го рода. Значит,

Существование криволинейного интеграла 1-го рода

Примем на кривой АВ за параметр длину дуги I, отсчитываемую от начальной точки А (рис. 2). Тогда кривую АВ можно описать уравнениями
(3)

где L — длина кривой АВ.

Уравнения (3) называются натуральными уравнениями кривой АВ. При переходе к натуральным уравнениям функция f(x, у), заданная на кривой АВ, сведется к функции переменной l: f(x(l), y(l). Обозначив через lk (k = 0, 1,…, п — 1) значение параметра l, отвечающее точке Мk, перепишем интегральную сумму (1) в виде

Это — интегральная сумма, отвечающая определенному интегралу

Поскольку интегральные суммы (1) и (4) равны между собой, то равны и отвечающие им интегралы. Таким образом,
(5)

Теорема:

Если функция f(M) непрерывна вдоль гладкой кривой АВ, то существует криволинейный интеграл

(поскольку при этих условиях существует определенный интеграл, стоящий в равенстве (5) справа ).

Свойства криволинейных интегралов 1-го рода

1, Из вида интегральной суммы (1) следует, что

т.е. величина криволинейного интеграла 1-го рода не зависит от направления интегрирования.

2. Линейность. Если для каждой из функций f(M) и д(М) существует криволинейный интеграл по кривой АВ, то для функции af(M) + βg<М), где а и β — любые постоянные, также существует криволинейный интеграл по кривой АВ, причем

3. Аддитивность. Если кривая АВ состоит из двух кусков АС и С В и для функции f(М) существует криволинейный интеграл по AВ, то существуют интегралы

4. Если f(M) ≥ 0 на кривой AB, то

5. Если функция f(M) интегрируема на кривой АВ, то функция |f(М)| также интегрируема на АВ, и при этом

6. Формула среднего значения. Если функция f(M) непрерывна вдоль кривой АВ, то на этой кривой найдется точка Мс такая, что

где L — длина кривой AB.

Вычисление криволинейного интеграла 1-го рода

Пусть кривая АВ задана параметрическими уравнениями

причем точке А соответствует значение t = t0, а точке В — значение t = t1. Будем предполагать, что функции φ(t) и ψ(t) непрерывны на [to, t1] вместе со своими производными φ'(t) и ψ'(t) и выполнено неравенство

Тогда дифференциал дуги кривой вычисляется по формуле

В частности, если кривая АВ задана явным уравнением

причем функция g(х) непрерывно дифференцируема на [а, b] и точке А соответствует значение х = а, а точке В — значение х = b, то, принимая х за параметр, получаем

Криволинейные интегралы 1-го рода для пространственных кривых

Определение криволинейного интеграла 1-го рода, сформулированное выше для плоской кривой, дословно переносится на случай, когда функция f(M) задана вдоль некоторой пространственной кривой АВ.

Пусть кривая АВ задана параметрическими уравнениями

Тогда криволинейный интеграл 1-го рода от функции f, взятый вдоль этой кривой, можно свести к определенному интегралу при помоши следующей формулы:

Пример:

Вычислить криволинейный интеграл

где L — контур треугольника с вершинами в точках O(0,0), A(1,0), B(0, I) (рис. 3).

По свойству аддитивности имеем

Вычислим каждый из интегралов в отдельности. Так как на отрезке OA имеем: 0 ≤ x ≤ 1, у = 0 и dl = dx, то

На отрезке АВ имеем х + у = 1, откуда у = 1 — х, т.е.

причем 0 ≤ х ≤ 1, тогда

Замечание:

При вычислении интегралов

мы воспользовались свойством 1, согласно которому

Криволинейные интегралы 2-го рода

Пусть АВ — гладкая или кусочно-гладкая ориентированная кривая на плоскости хОу и пусть

F(M) = Р(М) i + Q(M) j

— вектор-функция, определенная в некоторой области D, содержащей кривую АВ. Разобьем кривую АВ на части точками

координаты которых обозначим соответственно через

На каждой из элементарных дуг АkАk+1, возьмем произвольно точку Мk(ξk, ηk) и составим сумму

Пусть ∆l — длина наибольшей из дуг АkАk+1.

Определение:

Если при ∆l → 0 сумма (1) имеет конечный предел, не зависящий ни от способа разбиения кривой АВ. ни от выбора точек (ξk, ηk) на элементарных дугах, то этот предел называется криволинейным интегралом 2-го рода от вектор-функции F(M) по кривой АВ и обозначается символом

Так что по определению (2)

Теорема:

Если в некоторой области D, содержащей кривую АВ, функции Р(х,у) и Q(х, у) непрерывны, то криволинейный интеграл 2-го рода

r(М) = xi + yj

— радиус-вектор точки М(х, у). Тогда

dr = i dx + j dy,

и подынтегральное выражение

Р(х, у) dx + Q(x, у) dy

в формуле (2) можно представить в виде скалярного произведения векторов F(Af) и dr. Так что интеграл 2-го рода от вектор-функции

по кривой АВ можно записать коротко так:

Вычисление криволинейного интеграла 2-го рода

Пусть кривая АВ задана параметрическими уравнениями,

где функции φ(t) и ψ(t) непрерывны вместе с производными φ'(t), ψ'(t) на отрезке [to, t1] причем изменению параметра t от to до t1 соответствует движение точки М(х, у) по кривой АВ от точки А к точке В.

Если в некоторой области D, содержащей кривую АВ, функции Р(х, у) и Q(x, у) непрерывны, то криволинейный интеграл 2-го рода

сводится к следующему определенному интегралу:
(3)

Таким образом, вычисление криволинейного интеграла 2-го рода также может быть сведено к вычислению определенного интеграла.

Пример:

1) вдоль прямолинейного отрезка, соединяющего точки A(0,0) и В<1, 1);

2) вдоль параболы у = х , соединяющей те же точки (рис.5).

1) Уравнение линии АВ: у = х (х — параметр, 0 ≤ х ≤ 1), откуда dy = dx. Так что

2) Уравнение линии AB:

dy = 2х dx,

x dy = 2x 2 dx

Рассмотренный пример помазывает, что величина криволинейного интеграла 2-го рода, вообще говоря, зависит от формы пути интегрирования.

Свойства криволинейного интеграла 2-го рода

1. Линейность. Если существуют криволинейные интегралы

то при любых действительных а и β существует и интеграл

2. Аддитивность. Если кривая АВ разбита на части АС и С В и криволинейный интеграл

существует, то существуют интегралы

Криволинейный интеграл второго рода (в отличие от криволинейного интеграла 1-го рода) зависит от того, в каком направлении (от A к В или от В к А) проходится кривая АВ, и меняет знак при изменении направления движения по кривой, т. е.

Замечание:

Последнее свойство cotrmrrayer физической интерпретации криволинейного интеграла 2-го рода как работы силового паля F вдоль некоторого путь: при изменении направления движения по кривой работа силового поля вдоль этой кривой меняет знак на противоположный.

Связь между криволинейными интегралами 1-го и 2-го рода

Рассмотрим криволинейный интеграл 2-го рода

где ориентированная кривая АВ (А — начальная точка, В — конечная точка) задана векторным уравнением

r = r(l)

(здесь l — длина кривой, отсчитываемая в том направлении, в котором ориентирована кривая АВ) (рис. 6).

где т = т(l) — единичный вектор касательной к кривой АВ в точке М(l). Тогда

Заметим, что последний интеграл в этой формуле — криволинейный интеграл 1-го рода. При изменении ориентации кривой АВ единичный вектор касательной т заменяется на противоположный вектор (—т), что влечет изменение знака его подынтегрального выражения и, значит, знака самого интеграла.

Формула Грина

Выведем формулу Грина, связывающую криволинейный интеграл

по границе L некоторой плоской области D с двойным интегралом по этой области.

Теорема:

Если в замкнутой области D, ограниченной кусочно-гладким контуром L, функции Р(х, у) и Q и то справедливо равенство (формула Грина):

Здесь символ означает интегрирование по границе L области D, причем граница L проходится так, что область D остается слева (рис. 7).

Граница L плоской области D может состоять из одной или нескольких простых замкнутых кривых (компонент). В первом случае она называется односвязной, а во втором — многосвязной. Если граница L состоит из конечного числа кусочно-гладких замкнутых кривых Li, то кривые L, называются связными компонентами границы. На рис. 8 изображена трехсвязная область.

Односвязная область D (область «без дырок») обладает тем свойством, что любая лежащая в ней замкнутая кривая может быть стянута в точку Р ∈ D, оставаясь в процессе стягивания в области D.
Доказательство теоремы проведем для односвязной области.

В силу свойства линейности достаточно доказать, что

Докажем первую из этих формул.

Предположим сначала, что кривая L пересекается каждой прямой, параллельной оси Оу, не более чем в двух точках или по целому отрезку (рис. 9). Если каждая такая прямая пересекает кривую L не более чем в двух точках, то кривую L можно разбить на две части L1 и L2 (верхнюю и нижнюю), каждая из которых проектируется взаимно однозначно на некоторый отрезок [а, b] оси Ох. В силу аддитивности криволинейного интеграла имеем

На каждой из кривых L1 и L2 возьмем в качестве параметра абсциссу х и запишем уравнения этих кривых соответственно в виде

По предположению производная непрерывна в D, и значит, в силу известной формулы интегрального исчисления, приращение функции можно записать через интеграл от производной этой функции:

Из формул (4) и (5) получаем

Повторный интеграл в правой части последнего соотношения равен двойному интегралу от функции по области D, так что окончательно имеем

Формула (2) доказана.

Соотношение (3) доказывается аналогично. Складывая почленно соотношения (2) и (3), получаем формулу Грина (1).

Отметим, что формула Грина имеет место и для более сложных контуров L, и для неодносвязных областей D. Рассмотрим, например, случай двухсвязной области (рис. 10). Сделаем разрез АВ этой области, превращающий ее в односвязную. Тогда

Отсюда, учитывая, что

где интегрирование по кривой L1 ведется в направлении против движения часовой стрелки, а по кривой L2 — в направлении движения часовой стрелки. Отметим, что при этом кривые L1 и L2 проходятся так, что область D остается слева. Такое направление обхода контура принимается за положительное.

Площадь плоской области

Р(х, y) = -y и Q(x,y) = x.

и по формуле Грина (1) получаем

где S — площадь области D.

Отсюда получаем формулу для вычисления площади S плоской области D с помощью криволинейного интеграла по границе L этой области: (7)

Пример:

Вычислить площадь области, ограниченной эллипсом L:

Запишем уравнение эллипса в параметрической форме

Искомая площадь находится no формуле (7), где криволинейный интеграл берется по эллипсу при обходе контура в положительном направлении, что соответствует изменен ию параметра t от 0 до 2 π. Так как

то отсюда получаем, что

Замечание:

Пусть в пространстве задана ориентированная кусочно-гладкая кривая АВ и пусть, кроме того, в некоторой области Ω, содержащей кривую А В, задана вектор-функция

где Р, Q, R — непрерывные в Ω функции. Аналогично плоскому случаю криволинейный интеграл от вектор-функции F по ориентированной кривой АВ определим выражением

Это — криволинейный интеграл 2-го рода в пространстве.

Приложения криволинейных интегралов

Масса кривой

В примере 1 из § 1 было показано, что масса кривой L вычисляется с помощью интеграла 1-го рода

где f(M) — переменная линейная плотность на кривой L. (Мы предполагаем, что f(М) — непрерывная функция на АВ.)

Площадь цилиндрической поверхности

Пусть в плоскости хОу задана некоторая спрямляемая (т. е. имеющая длину) кривая АВ и на этой кривой определена непрерывная функция f(М) ≥ 0. Тогда совокупность точек (х, y, f(x, у)), или (М, f(M)), составит некоторую кривую, лежащую на цилиндрической поверхности, для которой кривая АВ является направляющей, а ее образующая параллельна оси Oz. Требуется определить площадь цилиндрической поверхности ABDC, ограниченной снизу кривой АВ, сверху — кривой z = f(M), где М ∈ АВ, и вертикальными прямыми АС и BD (рис. 11).

Для решения этой задачи поступим так:

1) разобьем кривую АВ на п частей точками

так, как показано на рис. 11;

2) из каждой точки Мk проведем перпендикуляр к плоскости хОу высотой f(Mk) (при этом цилиндрическая поверхность ABDC разобьется на n полосок);

3) каждую полоску заменим прямоугольником с основанием ∆lk, где ∆lk — длина дуги МkМk+1, и высотой, равной значению функции f

Тогда площадь k-ой полоски будет приближенно равна f(Mk) ∆lk, а площадь всей поверхности ABDC

Это приближенное равенство будет тем точнее, чем мельче будут частичные дуги МkМk+1, на которые разбита кривая АВ. Пусть ∆l — наибольшая из длин ∆lk частичных дуг MkMk+1. Тогда при ∆l —> 0 в пределе получим точное значение искомой площади

Предел справа по определению есть криволинейный интеграл первого рода от функции f(М) по кривой АВ. Итак, (2)

Пример:

Вычислить площадь части боковой поверхности цилиндра

срезанного сверху поверхностью

ху = 2Rz.

Сведем задачу к вычислению криволинейного интеграла 1-го рода от функции

вдоль дуги окружности, расположенной в первой четверти. Будем иметь

Параметрические уравнения линии АВ —

Площадь плоской фигуры

Ранее мы установили, что площадь S плоской фигуры D, ограниченной линией L, вычисляется по формуле

Правая часть есть криволинейный интеграл 2-го рода.

Работа силы:

Пусть в некоторой плоской области D, содержащей кривую АВ, задана сила

F(M) = P(M)i + Q(M)J, (4)

где функции Р(М) и Q(M), а следовательно, и F(M) предполагаются непрерывными функциями точки М. Требуется найти работу силы F, если под действием этой силы материальная точка М, имеющая единичную массу, переместилась из точки А в точку В по кривой АВ.

Для решения этой задачи разделим кривую АВ на п частей точками

(рис. 12), заменим каждую дугу хордой MkMk+1 и, предполагая для простоты, что на участке кривой (а значит, и на хорде MkMk+1) сила Fk имеет постоянное значение, например, равное ее значению в точке Мk,

получим приближенное выражение работы силы на участке пути :

где |Fk| — длина вектора Fk, |∆lk| — длина вектора ∆lk

Из формулы (4) с учетом (5) получим

Так как правая часть формулы (6) есть скалярное произведение векторов Fk и ∆lk, то, учитывая (7) и (8), будем иметь

Суммируя по всем значениям k(k = 0,1,2,…, п — 1), получим величину

приближенно выражающую работу силы F(M) на всем пути от А до В.

Предел этой суммы при ∆хk → 0 и ∆уk → 0 принимают за точное значение работы. Но с другой стороны, предел этой суммы есть криволинейный интеграл 2-го рода от вектор-функции F(M) по кривой АВ. Итак, работа силы вычисляется по формуле
(9)

Пример:

Найти работу силы

при перемещении единичной массы по параболе

от точки A(1,0) до точки В(0,1) (рис. 13). 4 Применим формулу (9), положив в ней

то искомую работу можно вычислить так:

Обобщение на случай пространственной кривой(рис. 14),

Если в некоторой пространственной области Ω, содержащей пространственную кривую АВ, задана сила

F(M) = Р(М)i + Q(M)j + R(M)k,

где Р(М), Q(M) и R(M) — непрерывные функции в области Ω, то работа, совершаемая силой F(М) по перемещению материальной точки М с единичной массой из точки А в точку В по пространственной кривой АВ, равна

Решение заданий и задач по предметам:

Дополнительные лекции по высшей математике:

Образовательный сайт для студентов и школьников

Копирование материалов сайта возможно только с указанием активной ссылки «www.lfirmal.com» в качестве источника.

[spoiler title=”источники:”]

http://yukhym.com/ru/integrirovanie-funktsii/formula-hryna-perekhod-ot-kryvolyneinoho-yntehrala-k-dvoinomu.html

http://lfirmal.com/krivolinejnye-integraly/

[/spoiler]

Источник

Краткая теория

Пусть
функция

непрерывна в каждой точке

гладкой кривой

. Разбив произвольным
образом кривую

на

частей

и выбрав в каждой из них произвольно точку

, построим интегральные
суммы:

где

– длины проекций частичных дуг

, на соответствующие
координатные оси. Тогда пределы:

называются
криволинейными интегралами II рода или криволинейными
интегралами по координатам.

Сумма
интегралов:

обозначается
как криволинейный интеграл

Если
кривая замкнутая, то обозначают:

Основные свойства криволинейных интегралов II рода

При
изменении направления интегрирования интеграл меняет свой знак:

Сказанное
верно и для замкнутой кривой, при этом выбор точки начала обхода безразличен.
Положительным направлением обхода считается то, при котором область,
ограниченная этой кривой, остается слева (для плоской кривой это движение против
часовой стрелки).

Остальные свойства такие же, как и у криволинейного интеграла I рода.

Вычисление криволинейного интеграла II рода

1. Если
пространственная кривая

задана параметрическими уравнениями

причем
перемещение от точки

к точке

происходит при изменении параметра

от

до

, то

2. В частном случае для плоской кривой

причем
перемещение от точки

к точке

происходит при изменении параметра

от

до

. Криволинейный интеграл
вычисляется по формуле:

3. Если
плоская кривая

определена уравнением

, причем перемещение от
точки

к точке

происходит при изменении

от

до

, то

Формула Грина

Интеграл по замкнутому контуру

можно
преобразовать в двойной интеграл по области

, ограниченной этим контуром, и наоборот, используя
формулу Грина:

где функции

и их частные производные первого порядка
должны быть непрерывными в области

и на контуре

При этом обход контура

выбирается таким образом, что область

остается слева.

Условие независимости криволинейного интеграла от пути интегрирования

Для того, чтобы
криволинейный интеграл

не зависел от пути
интегрирования, необходимо и достаточно, чтобы выполнялось равенство

Если же, кроме
того,

есть замкнутая кривая, то

Примеры решения задач

Задача 1

Вычислить
криволинейный интеграл

вдоль
дуги циклоиды

от точки

до точки

Решение

Искомый
криволинейный интеграл можно вычислить по формуле:

Получаем:

Ответ:

Задача 2

Вычислить
данный криволинейный интеграл вдоль линии

. Сделать чертеж.

где

– дуга кривой

от точки

до точки

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Криволинейный интеграл можно вычислить
по формуле:

Получаем:

Ответ:

Задача 3

Вычислить
криволинейный интеграл:

вдоль отрезка

прямой от точки

до точки

. Сделать чертеж.

Решение

Вычислим уравнение
прямой

Криволинейный
интеграл 2-го рода можно свести к определенному интегралу по следующей формуле:

Получаем:

Ответ:

Задача 4

Вычислить
непосредственно и с помощью формулы Грина:

где

-контур четырехугольника

Решение

Сделаем
чертеж области:

Вычислим
криволинейный интеграл непосредственно:

Криволинейный интеграл можно
вычислить по формулам:

или

Уравнение прямой

Искомый
интеграл:

По формуле
Грина:

Искомый
интеграл:

Ответ:

Задача 5

Применяя
формулу Грина, вычислить интеграл

для
заданной линии

(пробегаемой в положительном направлении) и
подынтегральных функций

Решение

По формуле
Грина:

Сделаем чертеж
области

Искомый
интеграл:

Ответ:

Источник

3.4. Криволинейный интеграл по замкнутому контуру

Формулировка[править | править код]

Доказательство для простой области[править | править код]

Формулы Грина[править | править код]

См. также[править | править код]

Литература[править | править код]

Лекция 22

22. Криволинейные интегралы

Интеграл по замкнутому контуру, формула Грина, примеры

Интеграл по контуру окружности

Контакты

Криволинейные интегралы в математике с примерами решения и образцами выполнения

Криволинейные интегралы первого рода

Криволинейные интегралы второго рода

Дополнение к криволинейному интегралу

Решение криволинейных интегралов

Существование криволинейного интеграла 1-го рода

Свойства криволинейных интегралов 1-го рода

Вычисление криволинейного интеграла 1-го рода

Криволинейные интегралы 1-го рода для пространственных кривых

Криволинейные интегралы 2-го рода

Вычисление криволинейного интеграла 2-го рода

Свойства криволинейного интеграла 2-го рода

Связь между криволинейными интегралами 1-го и 2-го рода

Формула Грина

Площадь плоской области

Приложения криволинейных интегралов

Масса кривой

Площадь цилиндрической поверхности

Площадь плоской фигуры

Основные свойства криволинейных интегралов II рода

Вычисление криволинейного интеграла II рода

Формула Грина

Условие независимости криволинейного интеграла от пути интегрирования

Примеры решения задач

Задача 1

Задача 2

Задача 3

Задача 4

Задача 5

Вам также может понравиться

Как найти свидетелей при дтп

Как найти whatsapp в моем телефоне whatsapp

Сталкер лост альфа как найти инструменты

Добавить комментарий Отменить ответ

22. Криволинейные
интегралы