Как найти интеграл sinx cosx

Как найти интеграл sinx cosx

Integration of sin x cos x is a process of determining the integral of sin x cos x with respect to x. Integration of sin x cos x can be done using different methods of integration. Before evaluating the integral of sin x cos x, let us recall the trigonometric formula which consists of sin x cos x, which is sin 2x = 2 sin x cos x. Integration is the reverse process of differentiation, and hence the integration of sin x cos x is also called the anti-derivative of sin x cos x.

In this article, we will study the integration of sin x cos x and derive its formula using the substitution method and sin 2x formula. We will also calculate the integration of sin x cos x from 0 to π.

1. What is Integration of Sin x Cos x?
2. Integration of Sin x Cos x Formula
3. Integration of Sin x Cos x Using Sin 2x Formula
4. Integration of Sin x Cos x Using Substitution Method
5. Integration of Sin x Cos x From 0 to π
6. FAQs on Integration of Sin x Cos x

What is Integration of Sin x Cos x?

The integration of sin x cos x gives the area under the curve of the function f(x) = sin x cos x and yields different equivalent answers when evaluated using different methods of integration. The integration of sin x cos x yields (-1/4) cos 2x + C as the integral of sin x cos x using the sin 2x formula of trigonometry. Mathematically, the integral fo sin x cos x is written as ∫sin x cos x dx = (-1/4) cos 2x + C, where C is the constant of integration, ∫ denotes the sign of integration and dx shows that the integration is with respect to x. Let us go through the formulas for the integration of sin x cos x.

Integration of Sin x Cos x Formula

Now, we will write the formulas for the integration of sin x cos x when evaluated using different formulas and methods of integration. Integral of sin x cos x can be determined using the sin 2x formula, and substitution method. Integration of sin x cos x given by:

  • ∫ sin x cos x dx = (-1/4) cos 2x + C [When evaluated using the sin 2x formula]
  • ∫ sin x cos x dx = (-1/2) cos2x + C [When evaluated by substituting cos x]
  • ∫ sin x cos x dx = (1/2) sin2x + C [When evaluated by substituting sin x]

integration of sin x cos x

Integration of Sin x Cos x Using Sin 2x Formula

We have studied the formulas for the integration of sin x cos x. Next, we will derive the formula for the integration of sin x cos x using the sin 2x formula. We will use the following trigonometric and integration formulas:

  • sin 2x = 2 sin x cos x
  • ∫sin (ax) dx = (-1/a) cos (ax) + C

Using the above formulas, we have

∫ sin x cos x dx = ∫(2/2) sin x cos x dx [Multiplying and dividing sin x cos x by 2]

⇒ ∫ sin x cos x dx = (1/2) ∫2 sin x cos x dx

⇒ ∫ sin x cos x dx = (1/2) ∫sin 2x dx [Using sin 2x = 2 sin x cos x]

⇒ ∫ sin x cos x dx = (1/2) (-1/2) cos 2x + C

⇒ ∫ sin x cos x dx = (-1/4) cos 2x + C

Hence we have derived the integral of sin x cos x using the sin 2x formula.

Integration of Sin x Cos x Using Substitution Method

Now, we will prove the integration of sin x cos x using the substitution method. We will substitute sin x and cos x separately to determine the integral of sin x cos x.

Integration of Sin x Cos x by Substituting Sin x

We will use the following formulas to determine the integral of sin x cos x:

  • d(sin x)/dx = cos x
  • ∫xn dx = xn+1/(n + 1) + C

Assume sin x = u, then we have cos x dx = du. Using the above formulas, we have

∫ sin x cos x dx = ∫udu

= u2/2 + C

⇒ ∫ sin x cos x dx = (1/2) sin2x + C

Hence we obtained the integration of sin x cos x by substituting sin x.

Integration of Sin x Cos x by Substituting Cos x

We will use the following formulas to determine the integral of sin x cos x:

  • d(cos x)/dx = -sin x
  • ∫xn dx = xn+1/(n + 1) + C

Assume cos x = v, then we have -sin x dx = dv ⇒ sin x dx = -dv. Using the above formulas, we have

∫ sin x cos x dx = ∫-vdv

= -v2/2 + C

⇒ ∫ sin x cos x dx = (-1/2) cos2x + C

Hence we obtained the integration of sin x cos x by substituting cos x.

Integration of Sin x Cos x From 0 to π

Now, that we have calculated the integration of sin x cos x using different methods, we will use the formula ∫ sin x cos x dx = (-1/4) cos 2x + C to determine the value of the definite integral of sin x cos x from 0 to π.

(begin{align}int_{0}^{pi}sin x cos x&=left [ dfrac{-1}{4}cos 2x + C right ]_0^pi \&= left ( dfrac{-1}{4}cos 2pi + C right )-left ( dfrac{-1}{4}cos 0 + C right )\&=left ( dfrac{-1}{4}+C right )-left ( dfrac{-1}{4}+C right )\&=0end{align})

Hence the integration of sin cos x from 0 to π is equal to 0.

Important Notes on Integration of Sin x Cos x

  • ∫ sin x cos x dx = (-1/4) cos 2x + C [When evaluated using the sin 2x formula]
  • ∫ sin x cos x dx = (-1/2) cos2x + C [When evaluated by substituting cos x]
  • ∫ sin x cos x dx = (1/2) sin2x + C [When evaluated by substituting sin x]
  • The integration of sin cos x from 0 to π is equal to 0.

Related Topics on Integration of Sin x Cos x

  • Integral of Tan 2x
  • Arctan Integral
  • Integral of Sin Inverse

FAQs on Integration of Sin x Cos x

What is Integration of Sin x Cos x in Trigonometry?

The integration of sin x cos x gives the area under the curve of the function f(x) = sin x cos x and yields different equivalent answers when evaluated using different methods of integration. The integral of sinx cosx is given by ∫ sin x cos x dx = (-1/4) cos 2x + C.

How to Find the Integral of Sin x Cos x?

We can derive the integral of sin x cos x formula using the substitution method and sin 2x formula.

What are the Formulas for Integration of Sin x Cos x?

Integration of sin x cos x given by:

  • ∫ sin x cos x dx = (-1/4) cos 2x + C [When evaluated using the sin 2x formula]
  • ∫ sin x cos x dx = (-1/2) cos2x + C [When evaluated by substituting cos x]
  • ∫ sin x cos x dx = (1/2) sin2x + C [When evaluated by substituting sin x]

What is the Integration of Sin x + Cos x?

The integration of sin x + cos x is cos x – sin x + C.

Is the Integration of Sin x Cos x the Same as the Anti Derivative of Sin x Cos x?

Integration is nothing but the reverse process of differentiation, so an integral of a function is the same as its anti-derivative. Hence, the integration of sin x cos x is the same as the anti-derivative of sin x cos x.

Источник

bold{mathrm{Basic}} bold{alphabetagamma} bold{mathrm{ABGamma}} bold{sincos} bold{gedivrightarrow} bold{overline{x}spacemathbb{C}forall} bold{sumspaceintspaceproduct} bold{begin{pmatrix}square&square\square&squareend{pmatrix}} bold{H_{2}O}
square^{2} x^{square} sqrt{square} nthroot[msquare]{square} frac{msquare}{msquare} log_{msquare} pi theta infty int frac{d}{dx}
ge le cdot div x^{circ} (square) |square| (f:circ:g) f(x) ln e^{square}
left(squareright)^{‘} frac{partial}{partial x} int_{msquare}^{msquare} lim sum sin cos tan cot csc sec
alpha beta gamma delta zeta eta theta iota kappa lambda mu
nu xi pi rho sigma tau upsilon phi chi psi omega
A B Gamma Delta E Z H Theta K Lambda M
N Xi Pi P Sigma T Upsilon Phi X Psi Omega
sin cos tan cot sec csc sinh cosh tanh coth sech
arcsin arccos arctan arccot arcsec arccsc arcsinh arccosh arctanh arccoth arcsech
begin{cases}square\squareend{cases} begin{cases}square\square\squareend{cases} = ne div cdot times < > le ge
(square) [square] ▭:longdivision{▭} times twostack{▭}{▭} + twostack{▭}{▭} – twostack{▭}{▭} square! x^{circ} rightarrow lfloorsquarerfloor lceilsquarerceil
overline{square} vec{square} in forall notin exist mathbb{R} mathbb{C} mathbb{N} mathbb{Z} emptyset
vee wedge neg oplus cap cup square^{c} subset subsete superset supersete
int intint intintint int_{square}^{square} int_{square}^{square}int_{square}^{square} int_{square}^{square}int_{square}^{square}int_{square}^{square} sum prod
lim lim _{xto infty } lim _{xto 0+} lim _{xto 0-} frac{d}{dx} frac{d^2}{dx^2} left(squareright)^{‘} left(squareright)^{”} frac{partial}{partial x}
(2times2) (2times3) (3times3) (3times2) (4times2) (4times3) (4times4) (3times4) (2times4) (5times5)
(1times2) (1times3) (1times4) (1times5) (1times6) (2times1) (3times1) (4times1) (5times1) (6times1) (7times1)
mathrm{Радианы} mathrm{Степени} square! ( ) % mathrm{очистить}
arcsin sin sqrt{square} 7 8 9 div
arccos cos ln 4 5 6 times
arctan tan log 1 2 3 –
pi e x^{square} 0 . bold{=} +

Подпишитесь, чтобы подтвердить свой ответ

Подписаться

Войдите, чтобы сохранять заметки

Войти

Номер Строки

Примеры

  • int xln(x)dx

  • int sin (2x)dx

  • int frac{x}{x^2+1}dx

  • int cos (sqrt{x})dx

  • int sin ^2(x)+cos ^2(x)dx

  • int :xe^xdx

  • Показать больше

Описание

Поэтапное решение первообразной функции

antiderivative-calculator

int sinx+cosxdx

ru

Блог-сообщения, имеющие отношение к Symbolab

  • High School Math Solutions – Polynomial Long Division Calculator

    Polynomial long division is very similar to numerical long division where you first divide the large part of the…

    Read More

    • Введите Задачу

    Сохранить в блокнот!

    Войти

    Источник

    Калькулятор интегралов

    Интеграл от sin(x)*cos(x) по x:
    -cos(x)^2/2  Нарисовать график     Редактировать LaTeX выражение     Прямая ссылка на страницу

    Калькулятор Интегралов вычисляет неопределенный интеграл (первообразную) от функции по заданной переменной с использованием аналитического интегрирования. Также он позволяет построить график функции и её интеграла.

    Показать правила синтаксиса

     

    Калькулятор интегралов, примеры

    Больше примеров неопределенных интегралов Математические настройки для вашего сайта Выберите язык:
    Deutsch
    English
    Español
    Français
    Italiano
    Nederlands
    Polski
    Português
    Русский
     中文
    日本語
    한국어 Империя чисел – мощные математические инструменты для каждого | Связь с веб-мастером
    Используя этот сайт, вы подтверждаете свое согласие с Условиями и соглашениями и Политикой приватности.

    © 2023
    numberempire.com
    Все права защищены
        
    Источник

    Tip: See my list of the Most Common Mistakes in English. It will teach you how to avoid mis­takes with com­mas, pre­pos­i­tions, ir­reg­u­lar verbs, and much more.

    The function $sin(x)cos(x)$ is one of the easiest functions to integrate. All you need to do is to use a simple substitution $u = sin(x)$, i.e. $frac{du}{dx} = cos(x)$, or $dx = du/cos(x)$, which leads to

    $$
    ∫ sin(x)cos(x),dx = l.∫ u,dur|_{u = sin(x)} = frac{u^2}2 + C = frac12 sin^2(x)+C,.
    $$

    Another way to integrate the function is to use the formula

    $$
    sin(2x) = 2sin(x)cos(x) quad ⇒ quad sin(x)cos(x) = frac12 sin(2x),
    $$

    so

    $$
    ∫ sin(x)cos(x),dx = frac12 ∫ sin(2x),dx = -frac14 cos(2x)+C
    $$

    It is worth mentioning that the $C$ in the equality above is not the same $C$ as in our original expression. In fact, it is possible to calculate that $frac12 sin^2(x) – (-frac14 cos(2x)) = 1/4$, so the two solutions lead to the same result, just shifted by a constant.

    By the way, I have written several educational ebooks. If you get a copy, you can learn new things and support this website at the same time—why don’t you check them out?

    Subscribe to my educational newsletter

    to receive a weekly summary of new articles

    Enter your email address below:

    Please, enter a valid email address:

    You tried to submit the form very quickly after opening this page. To confirm that you are a human, please, click on the button below again:

    Use the image

    You can use the image on another website, provided that you link to the source article. If you share it on Twitter or Facebook, I kindly ask you to tag my profile @JakubMarian.

    If you share it on reddit, please, share a link to the whole article and give credit to my subreddit r/JakubMarian in the comments.

    Источник

    Интегрирование тригонометрических функции

    Для интегрирования рациональных функций вида R(sin x, cos x) применяют подстановку , которая называется универсальной тригонометрической подстановкой. Тогда . Универсальная тригонометрическая подстановка часто приводит к большим вычислениям. Поэтому, по возможности, пользуются следующими подстановками.

    1. Если R(-sin(x),cosx) = -R(sin(x),cosx), то делают замену cos(x)=t и тогда sin(x)dx = -dt.
    2. При R(sin(x),-cosx) = – R(sin(x),cosx), полагают sin(x)=t при этом cos(x)dx=dt
    3. В случае R(-sin(x),-cosx) = R(sin(x),cosx) делают замену tg(x)=t, при которой x=arctg(t), 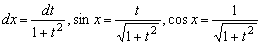, или замену ctg(x)=t, если это удобнее.

    Интегрирование функций рационально зависящих от тригонометрических функций

    1. Интегралы вида ∫sinnxdx, ∫cosnxdx, n>0

    a) Если n нечётное, то одну степень sinx (либо cosx) следует внести под знак дифференциала, а от оставшейся чётной степени следует перейти к противоположной функции.

    б) Если n чётное, то пользуемся формулами понижения степени

    2sin2x=1-cos2x, 2cos2x=1+cos2x.

    2. Интегралы вида ∫tgnxdx, ∫ctgnxdx, где n – целое.

    Необходимо использовать формулы



    3. Интегралы вида ∫sinnx·cosmx dx

    а) Пусть m и n разной чётности. Применяем подстановку t=sin x, если n – нечётное либо t=cos x, если m – нечётное.

    б) Если m и n чётные, то пользуемся формулами понижения степени

    2sin2x=1-cos2x, 2cos2x=1+cos2x.

    4. Интегралы вида

    Если числа m и n одинаковой чётности, то используем подстановку t=tg x. Часто бывает удобным применить приём тригонометрической единицы.

    5. ∫sin(nx)·cos(mx)dx, ∫cos(mx)·cos(nx)dx, ∫sin(mx)·sin(nx)dx

    Воспользуемся формулами преобразования произведения тригонометрических функций в их сумму:

    • sin α·cos β = ½(sin(α+β)+sin(α-β))
    • cos α·cos β = ½(cos(α+β)+cos(α-β))
    • sin α·sin β = ½(cos(α-β)-cos(α+β))
    • Решение онлайн
    • Видеоинструкция

    С помощью данного онлайн-калькулятора можно вычислять интегралы по частям. Решение сохраняется в формате Word.

    Также рекомендуется ознакомиться с возможностью нахождения интегралов онлайн.

    Примеры

    1. Вычислить интеграл ∫cos4x·sin3xdx.

    Делаем замену cos(x)=t. Тогда ∫cos4x·sin3xdx =

    2. Вычислить интеграл .

    Делая замену sin x=t, получаем

    3. Найти интеграл .

    Делаем замену tg(x)=t. Подставляя, получаем



    Заметим, что замена ctg(x)=t здесь удобнее, так как тогда , и поэтому

    Интегрирование выражений вида R(sinx, cosx)

    Пример №1. Вычислить интегралы:



    Решение.

    а) Интегрирование выражений вида R(sinx, cosx), где R — рациональная функция от sin x и cos x, преобразуются в интегралы от рациональных функций с помощью универсальной тригонометрической подстановки tg(x/2) = t.

    Тогда имеем

    Универсальная тригонометрическая подстановка дает возможность перейти от интеграла вида ∫R(sinx, cosx) dx к интегралу от дробно-рациональной функции, но часто такая замена ведет к громоздким выражениям. При определенных условиях эффективными оказываются более простые подстановки:

    • Если выполняется равенство R(-sin x, cos x) = -R(sin x, cos x)dx, то применяется подстановка cos x = t.
    • Если выполняется равенство R(sin x, -cos x) = -R(sin x, cos x)dx, то подстановка sin x = t.
    • Если выполняется равенство R(-sin x, -cos x) = R(sin x, cos x)dx, то подстановка tgx = t или ctg x = t.

    В данном случае для нахождения интеграла

    применим универсальную тригонометрическую подстановку tg(x/2) = t.

    Тогда

    =

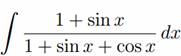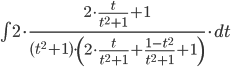
    или

    Так как дробь правильная, то, представляем в виде суммы интегралов:





    Возвращась к исходной переменной будем иметь

    b) Во втором примере рассмотрим важный частный случай, когда общее выражение ∫R(sinx, cosx) dx имеет вид ∫sinmx·cosnxdx. В этом частном случае, если m нечетно, следует применить подстановку cos x = t. Если нечетно n, следует применить подстановку sin x = t. Если оба показателя тип — четные неотрицательные числа (в частности, одно из них может быть равным нулю), то выполняют замену по известным тригонометрическим формулам:

    В данном случае

    Источник

    Добавить комментарий