Как найти интегральную функцию распределения от плотности

Кратко рассмотрим, как между собой
связаны функция плотности и функция
распределения двумерной непрерывной
случайной величины.

Зная дифференциальную
функцию

можно найти интегральную
функцию

по формуле (12)

,

что непосредственно следует
из определения плотности распределения
двумерной непрерывной с.в.
(свойство
3).

Пример 7. Найти
интегральную функцию распределения
двумерной случайной величины
по
данной плотности распределения
вероятности совместного распределения

.

Решение.
Воспользуемся формулой (9), с учётом


имеем

Далее, найти вероятность
попадания случайной точки в прямоугольник
с вершинами K
(1;1),
L,M(1;
0) и N
(;
0).

Решение.
Искомая вероятность

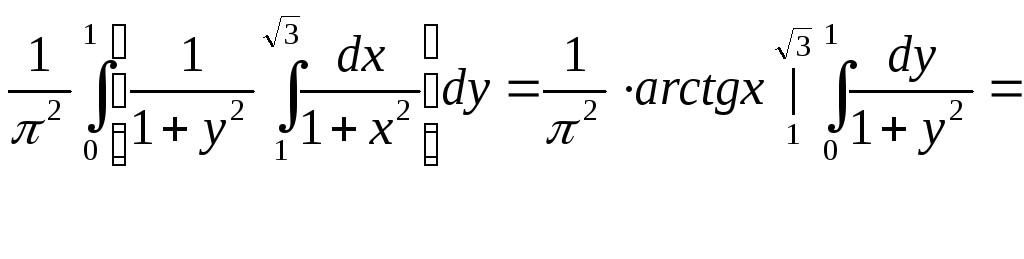
7. Зависимость и независимость двух случайных величин

Зная законы распределения
двух с.в.
и,
входящих в системуможно найти закон распределения системылишь в случае, когда
случайные величины
иявляются
независимы.

С понятием независимых
случайных величин мы уже встречались
неоднократно: две с.в. называются
независимыми,
если закон распределения каждой из них
не зависит от того, какие значения
принимает вторая с.в. В противном случае
случайные величины называются зависимыми.
Не приводя пока точных определений,
рассмотрим несколько примеров. Они
иллюстрируют разные степени зависимости
между случайными величинами – от сильной
почти функциональной зависимости до
практической независимости.

– пусть
рост
наугад выбранного взрослого человека
(в сантиметрах), аего вес (в килограммах). Зависимость
между ростом и весом является весьма
сильной, в начале её можно даже считать
функциональной. Формула, приближённо
выражающая эту зависимость, обычно
пишется:

– пусть
высота
выбранного наугад дерева в лесу, адиаметр
его основания. И здесь кажется зависимость
сильной, хотя в реальности и в не такой
степени, как в предыдущем примере.

– из груди камней нестандартной
формы выбирают один камень. Пусть
его
масса, амаксимальная
длина (скажем в диаметре). Зависимость
между ними носит сугубо вероятностный
характер.

–
рост
наугад выбранного взрослого человека
(в сантиметрах), аего возрасть. Проведенные опыты
показывают, что эти величины практически
независимы.

Таким образом, степень зависимости
между двумя с.в. могут быть как угодно
и каким угодно.

Сформулируем общее определение
независимости случайных величин с
помощью событий:
и.

Случайные величины
иназываютсянезависимыми,
если независимыми являются события:
идля любых действительных чиселиВ противном случае с.в.иназываютсязависимыми.

Справедливо следующее условие
независимости случайных величин.

Теорема 11.1. Для
того, чтобы случайные величины
ибыли независимы, необходимо и достаточно,
функция распределения системыбыла равна произведению функций
распределения её составляющих, т.е.
выполнялось равенство:

(19)
.

Доказательство. Пусть
случайные величины
инезависимы,
тогда событияинезависимы. Отсюда следует, что,
т.е.
.
Если же имеет место (16) , то

Значит
с.в.
инезависимы.

Сформулируем два утверждения
относительно независимости двух
случайных величин
и(д.с.в. и н.с. в. соответственно), образующих
систему.

Теорема 11.2. Необходимым
и достаточным условием
независимости двух дискретных случайных
величин
и,
образующих систему,
является равенство

(20)
,

для
любых

На практике, как правило, легко проверять
зависимость или независимость двух
д.с.в.

Здесь
ограничимся рассмотрением примера.

Пример 8. В
двух ящиках
находятся по шесть
шаров; в 1-м ящике: один
шар с номером 1, два шара с номером 2, три
шара с номером 3. Во втором ящике: два
шара с номером 1, три шара с номером 2,
один шар с номером 3. Пусть
номер
шара, случайно вынутого из первого
ящика,номер шара, случайно вынутого из второго
ящика. Из каждого ящика вынули по одному
шару. Составить таблицу закона
распределения системы случайных величин.

Решение. Случайная
точка (1;1)
имеет кратность 12
=2;

Случайная точка
(1;2) имеет кратность
13
=3;

Случайная точка
(1;3) имеет кратность
11
=1;

Случайная точка
(2;1) имеет кратность
22
=4;

Случайная точка
(2;2) имеет кратность
23
=6;

Случайная точка
(2;3) имеет кратность
21
=2;

Случайная точка
(3;1) имеет кратность
32
=6;

Случайная точка
(3;2) имеет кратность
33
=9;

Случайная точка
(3;3) имеет кратность
31
=3;

Всего случайных точек 66=36
. Так как кратности точек отношение
точки ко всему количеству точек равно
вероятности появления этой точки, то
таблица закона распределения системы
с.в. имеет вид

X Y	1	2	3
1
2
3

Сумма
всех вероятностей
,
указанных в таблице равна 1.(Проверьте!).

Случайные величины независимы.
Поскольку выполняется равенство (17).
Проще проверять
по следующей таблице:

(21)

Отсюда
легко видеть, что Таким образом,

Пример 9. В
урне 4
шара: 2 белых, 1 чёрный, 1 синий. Из них
наудачу извлекают два шара. Пусть
с.в.число
чёрных шаров в выборке, с.в.число
синих шаров в выборке.

Составить
закон распределения для системы
Найти:

1) таблицу распределения
системы
;

2) законы распределения
и;

3) выяснить зависимость
или независимость
и.

Решение. Случайная
величина
с.в..
Вычислим соответствующие вероятности:

;

Следовательно,
таблица распределения системы
имеет
вид

Y
0
1

Отсюда следует:

.

Законы распределения составляющих
и

X	0	1	и	Y	0	1
p	0,5	0,5	p	0,5	0,5

Теорема 11. 3. Необходимым
и достаточным условием независимости
двух непрерывных случайных величин
и,
образующих систему,
является равенство

(22)

Доказательство.
Если
инезависимые непрерывные случайные
величины, то имеет место равенство (19).

Дифференцируя это равенство
по
,
а затем по(с учётом равенства (9)), получим

,

Следовательно, необходимость равенство
(22) получено. Покажем, что оно и достаточно.

Действительно,
пусть выполняется равенство (22). Интегрируя
по
и по
получаем

,

или
.
Достаточность доказана.

Пример 10. Двумерная
случайная величина
задана с плотностью распределения
вероятностей
.
Найти:

1)
–
чтобы выполнялась условие нормированности;

2)

3)

4)

5) Убедитесь в выполнении условии
нормировки для найденных функций:

и

1) Легко может быть показано,
что величина
,
для этой цели следует проверить условие
нормировки (см. равенство (13)):

.

Следовательно,

2) Используя свойство 3, (см. равенство
(12)), находим

3)

4) По формуле (17) получаем

Аналогично,
по формуле (18) получаем

.

Следовательно,
.
Поэтому на основании равенство (20)
(теорема 11.2), заключаем, что случайные
величиныинезависимы.

Теперь вернёмся к нашим примерам,
рассмотренные в начале пункта (см.
пример1).

Пример 11. Пусть наосновании
некоторого опыта получены данные
относительно человеческого роста и
веса, которые представлены в виде
следующей таблицы, и они могут быть
описаны двумерной случайной величины,
где
обозначаетрост,вес.

X Y

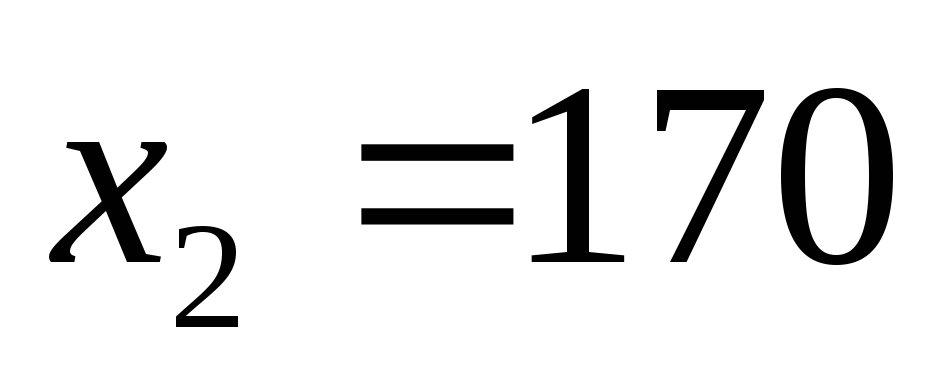
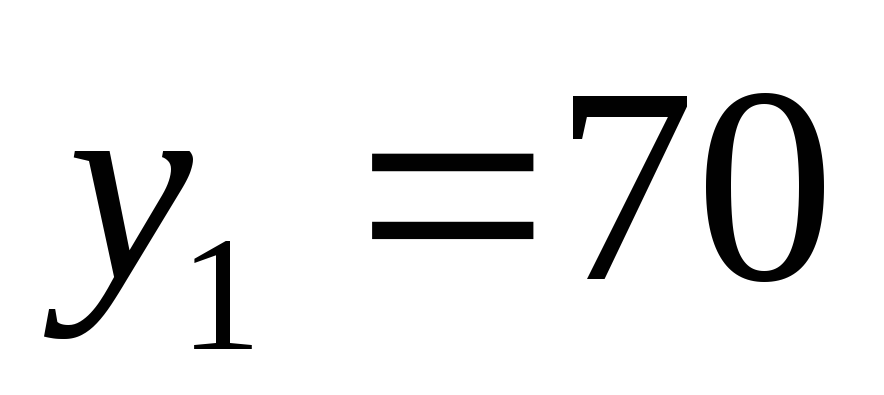
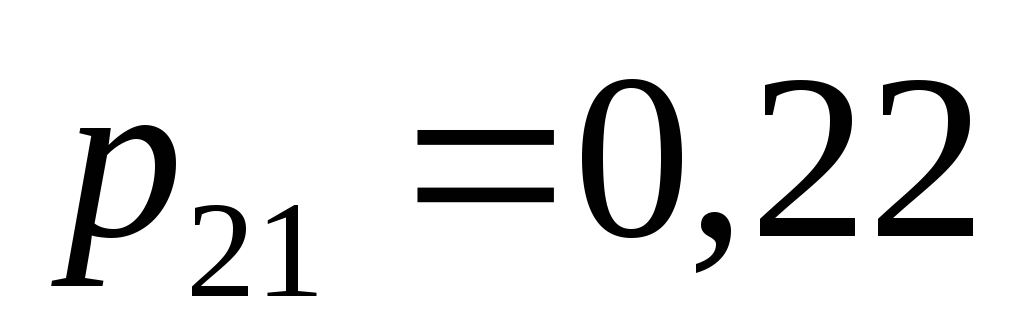
В этой таблице
обозначает
вероятность того, что человек, обладающим
ростом,
обладает весом

Требуется найти одномерные законы
распределения каждой из случайных
величин системы
.

Решение. Сложив вероятности по
столбцам, получим вероятности возможных
значений веса:

Закон распределения составляющей
запишется
так:распределение вероятности роста

Контроль: 0,26+ 0,38+0,36=1.

Закон распределения составляющей
запишется
так:распределение вероятности веса

Контроль: 0,56+ 0,44=1.

Пример 12. Система случайных величинхарактеризует рост и вес человека в
отклонениях от средних значений: роствеси имеет функцию распределения

Найти плотность распределения вероятностей
системы с.в.

Решение. На основании равенство (6)
сначала берём частную производную поа
затем пополучим:

Задания.

1. Найти функций плотностей одномерных
распределений с.в.и.

Воспользуйтесь
равенствами (14).

2. Система двух случайных величинподчинена равномерной плотности
распределения внутри круга радиусомНаписать выражение для плотности
распределения системы с.в.и отдельных случайных величини.

Указание.Воспользуйтесь равенством:

Плотность распределения вероятностей непрерывной случайной величины

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Краткая теория

---

Ранее
непрерывная случайная величина задавалась с помощью функции распределения. Этот
способ задания не является единственным. Непрерывную случайную величину можно
также задать, используя другую функцию, которую называют плотностью
распределения или плотностью вероятности (иногда ее называют дифференциальной
функцией).

Плотностью распределения вероятностей непрерывной случайной величины

 называют функцию

 – первую производную от функции распределения

:

Из этого определения следует, что
функция распределения является первообразной для плотности распределения.

Заметим, что для описания
распределения вероятностей дискретной случайной величины плотность
распределения неприменима.

Зная плотность распределения, можно
вычислить вероятность того, что непрерывная случайная величина примет значение,
принадлежащее заданному интервалу.

Вероятность того, что непрерывная
случайная величина

 примет
значение, принадлежащее интервалу

 равна
определенному интегралу от плотности распределения, взятому в пределах от

 до

:

Геометрически полученный результат
можно истолковать так: вероятность того, что непрерывная случайная величина
примет значение, принадлежащее интервалу

, равна площади криволинейной трапеции, ограниченной
осью

, кривой распределения

 и прямыми

 и

.

В частности, если

 – четная
функция и концы интервала симметричны относительно начала координат, то:

Зная плотность распределения

 можно найти
функцию распределения

 по формуле:

Свойства плотности распределения

Свойство 1.

Плотность
распределения – неотрицательная функция:

Свойство 2.

Несобственный
интеграл от плотности распределения в пределах от

 до

 равен единице:

Смежные темы решебника:

• Дискретная случайная величина
• Непрерывная случайная величина
• Интегральная функция распределения вероятностей

Примеры решения задач

---

Пример 1

Задана
плотность распределения вероятностей f(x) непрерывной случайной
величины X. Требуется:

1)
определить коэффициент A;

2) найти
функцию распределения F(x);

3)
схематично построить графики F(x) и f(x);

4) найти
математическое ожидание и дисперсию X;

5) найти
вероятность того, что X примет значение из
интервала (α,β):

α=1;  β=1.7

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

1)
Постоянный параметр

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Получаем:

2)
Функцию распределения

 найдем из
формулы:

Учитывая
свойства

,  сразу можем
отметить, что:

Остается
найти выражение для

, когда

 принадлежит
интервалу

.

Получаем:

3) Построим графики

 и

:

График плотности распределения

График функции распределения

4)
Математическое ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле:

5)
Вероятность того, что случайная величина примет значение из интервала

:

---

Пример 2

Плотность
распределения вероятности непрерывной случайной величины равна

, x∈(0,∞). Найти нормировочный множитель C,
математическое ожидание M(X) и дисперсию D(X).

Решение

Нормировочный множитель

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Дисперсию
можно найти по формуле: 

---

Пример 3

Непрерывная
случайная величина

 имеет плотность распределения:

Найти
величину a, вероятность P(X<0) и математическое
ожидание X.

Решение

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Постоянный
параметр

 найдем из
свойства плотности вероятности:

В
нашем случае эта формула имеет вид:

Плотность
вероятности имеет вид:

Вероятность:

Математическое
ожидание находим по формуле:

Для
нашего примера:

Задачи контрольных и самостоятельных работ

---

Задача 1

Плотность
распределения непрерывной случайной величины X имеет вид:

Найти:

а)
параметр a;

б)
функцию распределения F(x);

в)
вероятность попадания случайной величины X в интервал (6.5;  11);

г)
математическое ожидание M(X) и дисперсию D(X);

Построить
график функций f(x) и F(x).

---

Задача 2

Задана
функция распределения непрерывной случайной величины:

Найти и
построить график функции плотности распределения вероятностей.

---

Задача 3

Случайная
величина X задана функцией распределения F(x).
Найти плотность распределения вероятностей, математическое ожидание и дисперсию
случайной величины. Построить график функции
F(x).

---

Задача 4

Задана
плотность вероятности f(x) или функции распределения
непрерывной случайной величины X. Найти a, M[X], D[X], P(α<x<β).

α=1,β=2

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 5

Непрерывная
случайная величина

 задана плотностью распределения вероятностей.

Требуется
найти:

– функцию
распределения вероятностей;

–
математическое ожидание;

–
дисперсию;

– среднее
квадратическое отклонение;

– вероятность
того, что случайная величина отклонится от своего математического ожидания не
более, чем на одну четвертую длины всего интервала возможных значений этой
величины;

–
построить графики функции распределения и плотности распределения вероятностей.

---

Задача 6

Случайная
величина X равномерно распределена на интервале (2;7).
Составить f(x),F(x), построить графики. Найти
M(X),D(X).

---

Задача 7

Случайная
величина X~N(a,σ)

a=25;
σ=4; α=13; β=30; δ=0.1.

Требуется:

–
составить функцию плотности распределения и построить ее график;

– найти
вероятность того, что случайная величина в результате испытания примет
значение, принадлежащее интервалу (α; β);

– найти
вероятность того, что абсолютная величина отклонения значений случайной
величины от ее математического ожидания не превысит δ.

---

Задача 8

Плотность
вероятности непрерывной случайной величины ξ задана следующим выражением:

Найти
постоянную C, функцию распределения Fξ (x), математическое
ожидание и дисперсию Dξ случайной величины ξ.

---

На сайте можно заказать решение контрольной или самостоятельной работы, домашнего задания, отдельных задач. Для этого вам нужно только связаться со мной:

ВКонтакте
WhatsApp
Telegram

Мгновенная связь в любое время и на любом этапе заказа. Общение без посредников. Удобная и быстрая оплата переводом на карту СберБанка. Опыт работы более 25 лет.

Подробное решение в электронном виде (docx, pdf) получите точно в срок или раньше.

Задача 9

Случайная
величина X задана функцией распределения вероятностей F(x).

Требуется:

1. Найти
функцию плотности распределения f(x).

2. Найти M(X).

3. Найти
вероятность P(α<X<β)

4.
Построить графики f(x) и F(x).

α=2, β=4.5

---

Задача 10

Найти
функцию плотности нормально распределенной случайной величины X и
постройте ее график, зная M(X) и D(X).

M(X)=-1; D(X)=8

---

Задача 11

Случайная
величина X задана интегральной F(x) или дифференциальной f(x)
функцией. Требуется:

а) найти
параметр C;

б) при
заданной интегральной функции F(x) найти дифференциальную функцию f(x), а при
заданной дифференциальной функции f(x) найти интегральную функцию F(x);

в)
построить графики функций F(x) и f(x);

г) найти
математическое ожидание M(X), дисперсию D(X) и
среднее квадратическое отклонение σ(x);

д)
вычислить вероятность попадания в интервал P(a≤x≤b)

е)
определить, квантилем какого порядка является точка xp;

ж)
вычислить квантиль порядка p

a=π/4; b=π/3; xp=π/2; p=0.75

 

• Краткая теория
• Примеры решения задач
• Задачи контрольных и самостоятельных работ

Функция распределения вероятностей случайной величины. Плотность
распределения вероятности непрерывной случайной величины

8.1. Функция распределения вероятностей случайной величины

8.1.1. Определение функции распределения

Вспомним, что дискретная случайная величина может быть
задана перечнем всех ее возможных значений и их вероятностей. Такой способ
задания не является общим: он неприменим, например, для непрерывных случайных
величин.

Действительно, рассмотрим случайную величину ,
возможные значения которой сплошь заполняют интервал .
Можно ли составить перечень всех возможных значений ?
Очевидно, что этого сделать нельзя. Этот пример указывает на целесообразность
дать общий способ задания любых типов случайных величин. С этой целью и вводят
функции распределения вероятностей случайной величины.

Пусть  —
действительное число. Вероятность события, состоящего в том, что  примет
значение, меньшее ,
т.е. вероятность события ,
обозначим через .
Разумеется, если  изменяется,
то, вообще говоря, изменяется и ,
т.е.  —
функция от .

Функцией распределения называют функцию ,
определяющую вероятность того, что случайная величина  в
результате испытания примет значение, меньшее ,
т.е.

Геометрически это равенство можно истолковать так:  есть
вероятность того, что случайная величина примет значение, которое изображается
на числовой оси точкой, лежащей левее точки .

Иногда вместо термина «функция распределения» используют
термин «интегральная функция».

Теперь можно дать более точное определение непрерывной
случайной величины: случайную величину называют непрерывной, если ее
функция распределения есть непрерывная, кусочно-дифференцируемая функция с
непрерывной производной.

8.1.2. Свойства функции распределения

Свойство 1.
Значения функции распределения принадлежат отрезку :

Доказательство.
Свойство вытекает из определения функции распределения как вероятности:
вероятность всегда есть неотрицательное число, не превышающее единицы.

Свойство 2.  —неубывающая
функция, т.е.

,
если

Доказательство.
Пусть .
Событие, состоящее в том, что  примет
значение, меньшее ,
можно подразделить на следующие два несовместных события: 1)  примет
значение, меньшее ,
с вероятностью ;
2)  примет
значение, удовлетворяющее неравенству ,
с вероятностью .

По теореме сложения имеем

Отсюда

или

Так как любая вероятность есть число неотрицательное, то ,
или ,
что и требовалось доказать.

Следствие 1.
Вероятность того, что случайная величина примет значение, заключенное в
интервале ,
равна приращению функции распределения на этом интервале:

Это важное следствие вытекает из формулы (8.1), если
положить  и
.

Пример 8.1.
Случайная величина  задана
функцией распределения

Найти вероятность того, что в результате испытания  примет
значение, принадлежащее интервалу

Решение. Так как
на интервале ,
по условию,

то

Итак,

Следствие 2.
Вероятность того, что непрерывная случайная величина  примет
одно определенное значение, равна нулю.

Действительно, положив в формуле (8.2)  ,
имеем

Устремим  к
нулю. Так как  —
непрерывная случайная величина, то функция  непрерывна.
В силу непрерывности  в
точке  разность
 также
стремится к нулю; следовательно,  Используя
это положение, легко убедиться в справедливости равенств

Например, равенство  доказывается
так:

Таким образом, не представляет интереса говорить о
вероятности того, что непрерывная случайная величина примет одно определенное
значение, но имеет смысл рассматривать вероятность попадания ее в интервал,
пусть даже сколь угодно малый. Этот факт полностью соответствует требованиям
практических задач. Например, интересуются вероятностью того, что размеры
деталей не выходят за дозволенные границы, но не ставят вопроса о вероятности их
совпадения с проектным размером.

Заметим, что было бы неправильным думать, что равенство
нулю вероятности  означает,
что событие  невозможно
(если, конечно, не ограничиваться классическим определением вероятности).
Действительно, в результате испытания случайная величина обязательно примет одно
из возможных значений; в частности, это значение может оказаться равным .

Свойство 3.
Если возможные значения случайной величины принадлежат интервалу ,
то: 1)  при
;
2)  при
.

Доказательство.

1) Пусть .
Тогда событие  невозможно
(так как значений, меньших  величина
 по
условию не принимает) и, следовательно, вероятность его равна нулю.

2) Пусть .
Тогда событие  достоверно
(так как все возможные значения  меньше
)
и, следовательно, вероятность его равна единице.

Следствие.
Если возможные значения непрерывной случайной величины расположены на всей оси
,
то справедливы следующие предельные соотношения:

8.1.3. График функции распределения

Доказанные свойства позволяют представить, как выглядит
график функции распределения непрерывной случайной величины.

График расположен в полосе, ограниченной прямыми ,
 (первое
свойство).

При возрастании  в
интервале ,
в котором заключены все возможные значения случайной величины, график
«подымается вверх» (второе свойство).

При  ординаты
графика равны нулю; при  ординаты
графика равны единице (третье свойство).

График функции распределения непрерывной случайной величины
изображен на рис. 2.

Рис. 8.1

Замечание.
График функции распределения дискретной случайной величины имеет ступенчатый
вид. Убедимся в этом на примере.

Пример 8.1.
Дискретная случайная величина  задана
таблицей распределения

	1	4	8
	0,3	0,1	0,6

Найти функцию распределения и вычертить ее график.

Решение. Если ,
то  (третье
свойство).

Если ,
то .
Действительно,  может
принять значение 1 с вероятностью 0,3.

Если ,
то .
Действительно, если  удовлетворяет
неравенству ,
то  равно
вероятности события  которое
может быть осуществлено, когда  примет
значение 1 (вероятность этого события равна 0,3) или значение 4 (вероятность
этого события равна 0,1). Поскольку эти два события несовместны, то по теореме
сложения вероятность события  равна
сумме вероятностей .

Если ,
то .
Действительно, событие  достоверно,
следовательно, его вероятность равна единице.

Итак, функция распределения аналитически может быть
записана так:

График этой функции приведен на рис. 8.2.

Рис. 8.2.

8.2. Плотность распределения вероятностей
непрерывной случайной величины

8.2.1. Определение плотности распределения

Выше непрерывная случайная величина задавалась с помощью
функции распределения. Этот способ задания не является единственным. Непрерывную
случайную величину можно также задать, используя другую функцию, которую
называют плотностью распределения или плотностью вероятности (иногда ее называют
дифференциальной функцией).

Плотностью распределения вероятностей непрерывной
случайной величины  называют
функцию  —
первую производную от функции распределения :

Из этого определения следует, что функция распределения
является первообразной для плотности распределения.

Заметим, что для описания распределения вероятностей
дискретной случайной величины плотность распределения неприменима.

8.2.2. Вероятность попадания непрерывной случайной величины в заданный
интервал

Зная плотность распределения, можно вычислить вероятность
того, что непрерывная случайная величина примет значение, принадлежащее
заданному интервалу. Вычисление основано на следующей теореме.

Теорема 8.1.
Вероятность того, что непрерывная случайная величина  примет
значение, принадлежащее интервалу ,
равна определенному интегралу от плотности распределения, взятому в пределах от
 до
:

Доказательство.
Используем соотношение (8.2)

По формуле Ньютона–Лейбница,

Таким образом,

Так как ,
то окончательно получим

Геометрически полученный результат можно истолковать так:
вероятность того, что непрерывная случайная величина примет значение,
принадлежащее интервалу ,
равна площади криволинейной трапеции, ограниченной осью ,
кривой распределения  и
прямыми  и
.

Замечание. В
частности, если  —
четная функция и концы интервала симметричны относительно начала координат, то

Пример 8.2.
Задана плотность вероятности случайной величины  

Найти вероятность того, что в результате испытания  примет
значение, принадлежащее интервалу .

Решение. Искомая
вероятность

8.2.3. Нахождение функции распределения по известной плотности распределения

Зная плотность распределения ,
можно найти функцию распределения  по
формуле

Действительно, мы обозначили через  вероятность
того, что случайная величина примет значение, меньшее ,
т.е.

Очевидно, неравенство  можно
записать в виде двойного неравенства ,
следовательно,

Полагая в формуле (8.1) ,
,
имеем

Наконец, заменив  на
,
в силу (8.5), окончательно получим

Таким образом, зная плотность распределения, можно найти
функцию распределения. Разумеется, по известной функции распределения может быть
найдена плотность распределения, а именно:

Пример 8.3.
Найти функцию распределения по данной плотности распределения:

Построить график найденной функции.

Решение.
Воспользуемся формулой

Если ,
то ,
следовательно, .
Если ,
то ,
следовательно,

Если  то

Итак, искомая функция распределения

График этой функции изображен на рис. 8.3.

Рис. 8.3.

8.2.4. Свойства плотности распределения

Свойство 1.
Плотность распределения — неотрицательная функция:

Доказательство.
Функция распределения — неубывающая функция, следовательно, ее производная  —
функция неотрицательная.

Геометрически это свойство означает, что точки,
принадлежащие графику плотности распределения, расположены либо над осью ,
либо на этой оси.

График плотности распределения называют кривой
распределения.

Свойство 2.
Несобственный интеграл от плотности распределения в пределах от -∞ до  равен
единице:

Доказательство.
Несобственный интеграл

выражает вероятность события,
состоящего в том, что случайная величина примет значение, принадлежащее
интервалу .
Очевидно, такое событие достоверно, следовательно, вероятность его равна
единице.

Геометрически это означает, что вся площадь криволинейной
трапеции, ограниченной осью  и
кривой распределения, равна единице.

В частности, если все возможные значения случайной величины
принадлежат интервалу ,
то

Пример 8.4.
Плотность распределения случайной величины  задана:

Найти постоянный параметр .

Решение.
Плотность распределения должна удовлетворять условию

поэтому потребуем, чтобы
выполнялось равенство

Отсюда

Найдем неопределенный интеграл:

Вычислим несобственный интеграл:

Таким образом, искомый параметр

8.2.5. Вероятностный смысл плотности распределения

Пусть  —
функция распределения непрерывной случайной величины .
По определению плотности распределения, ,
или в иной форме

Как уже известно, разность  определяет
вероятность того, что  примет
значение, принадлежащее интервалу .
Таким образом, предел отношения вероятности того, что непрерывная случайная
величина примет значение, принадлежащее интервалу .,
к длине этого интервала (при )
равен значению плотности распределения в точке .

По аналогии с определением плотности массы в точке[1]
целесообразно рассматривать значение функции  в
точке  как
плотность вероятности в этой точке.

Итак, функция  определяет
плотность распределения вероятности для каждой точки .

Из дифференциального исчисления известно, что приращение
функции приближенно равно дифференциалу функции, т.е.

или

Так как  и
,
то

Вероятностный смысл этого равенства таков: вероятность
того, что случайная величина примет значение, принадлежащее интервалу ,
приближенно равна (с точностью до бесконечно малых высшего порядка относительно )
произведению плотности вероятности в точке  на
длину интервала .

Геометрически этот результат можно истолковать так:
вероятность того, что случайная величина примет значение, принадлежащее
интервалу ,
приближенно равна площади прямоугольника с основанием  и
высотой .

На рис. 8.4 видно, что площадь заштрихованного
прямоугольника, равная произведению ,
лишь приближенно равна площади криволинейной трапеции (истинной вероятности,
определяемой определенным интегралом ).
Допущенная при этом погрешность равна площади криволинейного треугольника .

Рис. 8.4.

8.2.6. Закон равномерного распределения вероятностей

При решении задач, которые выдвигает практика, приходится
сталкиваться с различными распределениями непрерывных случайных величин.
Плотности распределений непрерывных случайных величин называют также законами
распределений. Часто встречаются, например, законы равномерного, нормального
и показательного распределений. В настоящем параграфе рассматривается закон
равномерного распределения вероятностей.

Нормальному и показательному законам посвящены следующие
две главы.

Распределение вероятностей называют равномерным, если на
интервале, которому принадлежат все возможные значения случайной величины,
плотность распределения сохраняет постоянное значение.

Приведем пример равномерно распределенной непрерывной
случайной величины.

Пример 8.5.
Шкала измерительного прибора проградуирована в некоторых единицах. Ошибку при
округлении отсчета до ближайшего целого деления можно рассматривать как
случайную величину ,
которая может принимать с постоянной плотностью вероятности любое значение между
двумя соседними целыми делениями. Таким образом,  имеет
равномерное распределение.

Найдем плотность равномерного распределения ,
считая, что все возможные значения случайной величины заключены в интервале ,
на котором функция  сохраняет
постоянные значения:

По условию,  не
принимает значений вне интервала ,
поэтому  при
 и
.

Найдем постоянную .
Так как все возможные значения случайной величины принадлежат интервалу ,
то должно выполняться соотношение

или

Отсюда

Итак, искомая плотность вероятности равномерного
распределения

График плотности равномерного распределения изображен на
рис. 8.5, а график функции распределения — на рис. 8.3.

Рис. 8.5.

Замечание.
Обозначим через  непрерывную
случайную величину, распределенную равномерно в интервале ,
а через  —
ее возможные значения. Вероятность попадания величины  (в
результате испытания) в интервал ,
принадлежащий интервалу ,
равна его длине:

Действительно, плотность рассматриваемого равномерного
распределения

Следовательно, вероятность попадания случайной величины  в
интервал  

Далее
случайная величина  используется
неоднократно.

Содержание:

Непрерывные случайные величины: функция распределения случайной величины:

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Функция распределения непрерывной случайной величины

Зная функцию распределения непрерывной случайной величины, задача определения вероятности её попадания на интервал (а; b) может быть решена следующим образом.

По известной функции распределения вероятность попадания непрерывной случайной величины на интервал (а; b) равна приращению функции распределения на этом участке (рис. 1).

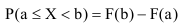
Во всех рассмотренных выше случаях случайная величина определялась путём задания значений самой величины и вероятностей этих значений.

Однако такой метод применим далеко не всегда. Например, в случае непрерывной случайной величины, её значения могут заполнять некоторый произвольный интервал. Очевидно, что в этом случае задать все значения случайной величины просто нереально.

Даже в случае, когда это сделать можно, зачастую задача решается чрезвычайно сложно. Рассмотренный только что пример даже при относительно простом условии (приборов только четыре) приводит к достаточно неудобным вычислениям, а если в задаче будет несколько сотен приборов?

Поэтому встает задача по возможности отказаться от индивидуального подхода к каждой задаче и найти по возможности наиболее общий способ задания любых типов случайных величин.

Пусть х – действительное число. Вероятность события, состоящего в том, что X примет значение, меньшее х, т.е. X

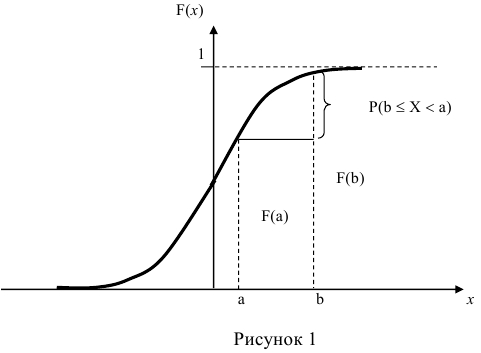
Определение. Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина X в результате испытания примет значение, меньшее х.

F(x) = Р(Х < х)

Функцию распределения также называют интегральной функцией. Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет

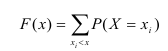
Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины X разрывна и возрастает скачками при переходе через каждое значение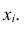

Так для примера, который мы будем рассматривать на следующем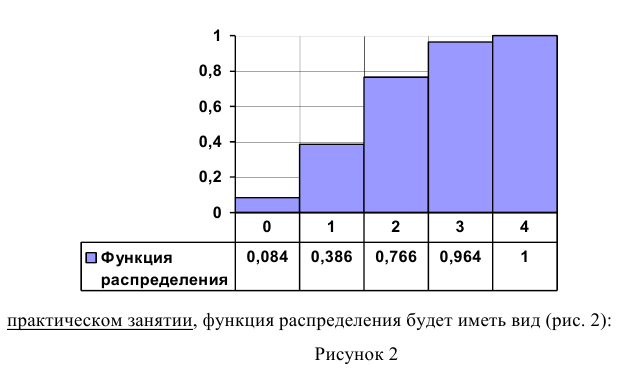

Свойства функции распределения

1)    значения функции распределения принадлежат отрезку [0, 1].

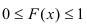
2)    F(x) – неубывающая функция.

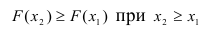
3)    Вероятность того, что случайная величина примет значение, заключенное в интервале (а, b) , равна приращению функции распределения на этом интервале.

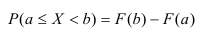
4)    На минус бесконечности функция распределения равна нулю, на плюс бесконечности функция распределения равна единице.

5)    Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равна нулю.

Таким образом, не имеет смысла говорить о каком – либо конкретном значении случайной величины. Интерес представляет только вероятность попадания случайной величины в какой – либо интервал, что соответствует большинству практических задач.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью функции распределения.

Плотность вероятности. Числовые характеристики. Моменты случайных величин

Если вычислить вероятность появления непрерывной случайной величины не составляет особого труда, то решение основной задачи теории вероятностей для непрерывной случайной величины несёт большие трудности. Поэтому в материалах сегодняшней лекции мы рассмотрим методы определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности
распределения.

Плотность распределения

Функция распределения полностью характеризует случайную величину, однако, имеет один недостаток. По функции распределения трудно судить о характере распределения случайной величины в небольшой окрестности той или иной точки числовой оси.

Определение. Плотностью распределения вероятностей непрерывной случайной величины X называется функция f(x) – первая производная от функции распределения F(x).

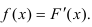
Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

Смысл плотности распределения состоит в том, что она показывает как часто появляется случайная величина X в некоторой окрестности точки х при повторении опытов.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Определение. Случайная величина X называется непрерывной, если её функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением (может быть, конечного числа точек).

Зная плотность распределения, можно вычислить вероятность того, что некоторая случайная величина X примет значение, принадлежащее заданному интервалу.

Теорема. Вероятность того, что непрерывная случайная величина X примет значение, принадлежащее интервалу (а, b), равна определенному интегралу от плотности распределения, взятому в пределах от а до b.

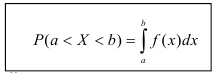
Доказательство этой теоремы основано на определении плотности распределения и третьем свойстве функции распределения (см. лекцию тема № 10).

Геометрически это означает, что вероятность того, что непрерывная случайная величина примет значение, принадлежащее интервалу (а, b), равна площади криволинейной трапеции, ограниченной осью ОХ, кривой распределения f(x) и прямыми х=а и х=b.

Геометрически вероятность Р(а < X < b) представляется в виде заштрихованной области, ограниченной кривой распределения и осью Ох на интервале(а; b) (рис 1).

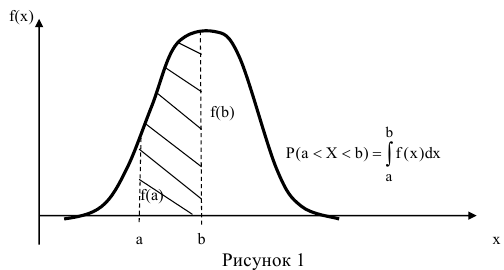
Функция распределения может быть легко найдена, если известна плотность распределения, по формуле:

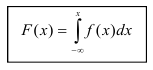
Свойства плотности распределения

1) Плотность распределения – неотрицательная функция.

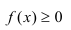
2) Несобственный интеграл от плотности распределения в пределах от –
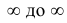равен единице.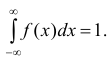

Плотность распределения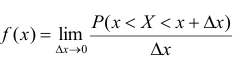
можно представить как:

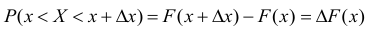
тогда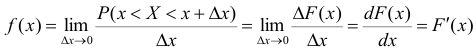
Поэтому иногда функцию плотности распределения f(x) называют также дифференциальной функцией распределения или дифференциальным законом распределения величины X, а функцию распределения F(x) -интегральной функцией распределения или интегральным законом распределения.

Следует заметить, что интеграл 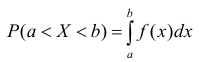возможно трактовать как сумму бесконечно большого числа несовместных элементарных событий, каждое из которых заключается в попадании случайной величины в бесконечно малый участок (х, х + dx) и имеет вероятность:

Р(х < X < х + dx) = dF(x) = f(x)dx

Величину f(x)dx называют элементом вероятности.

По своему содержанию элемент вероятности есть вероятность попадания случайной величины X на элементарный участок dx, прилежащий к точке X.

Функция распределения случайной величины X по известной плотности распределения может быть найдена, как интеграл от плотности распределения в интервале от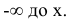

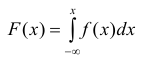
В схеме непрерывных случайных величин можно вывести аналогии формулы полной вероятности и формулы Бейеса, рассмотренные при изучении темы 4.

Обозначим Р(А /х) условную вероятность события А при условии Х= х. Заменяя в формуле полной вероятности вероятность гипотезы элементом вероятности f(x)dx, а сумму – интегралом, получим полную вероятность события А.

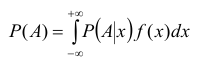
Данная формула называется интегральной формулой полной вероятности.

Соответствующий аналог в схеме непрерывных случайных величин имеет и формула Бейеса. Обозначив условную плотность распределения случайной величины X при условии, что в результате опыта появилось событие A через 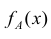, получим:

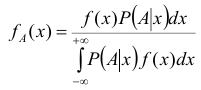
Данная формула называется интегральной формулой Бейеса.

Числовые характеристики непрерывных случайных величин

Пусть непрерывная случайная величина X задана функцией распределения f(x). Допустим, что все возможные значения случайной величины принадлежат отрезку [а,b].

Математическое ожидание

Определение. Математическим ожиданием непрерывной случайной величины X, возможные значения которой принадлежат отрезку [а,b], называется определенный интеграл

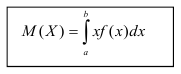
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

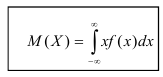
При этом, конечно, предполагается, что несобственный интеграл сходится.

Дисперсия

Определение. Дисперсией непрерывной случайной величины называется математическое ожидание квадрата её отклонения.

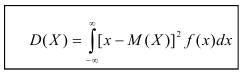
По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

 

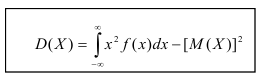
Среднеквадратичное отклонение

Определение. Средним квадратичным отклонением называется квадратный корень из дисперсии.

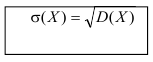
Мода

Определение. Модой 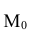дискретной случайной величины называется её наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

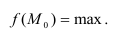
Если многоугольник распределения для дискретной случайной величины или кривая распределения для непрерывной случайной величины имеет два или несколько максимумов, то такое распределение называется двухмодальным или многомодальным.

Если распределение имеет минимум, но не имеет максимума, то оно
называется антимодальным.

Медиана

Определение. Медианой 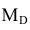случайной величины X называется такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины.

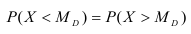
Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Отметим, что если распределение одномодальное, то мода и медиана совпадают с математическим ожиданием.

Начальный момент

Определение. Начальным моментом порядка k случайной величины X называется математическое ожидание величины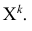

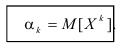
Для дискретной случайной величины: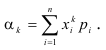
Для непрерывной случайной величины: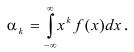

Начальный момент первого порядка равен математическому ожиданию.

Центральный момент

Определение. Центральным моментом порядка k случайной величины X называется математическое ожидание величины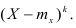

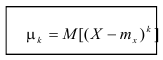
Для дискретной случайной величины: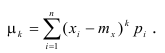

Для непрерывной случайной величины: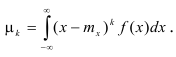
Центральный момент первого порядка всегда равен нулю, а центральный момент второго порядка равен дисперсии. Центральный момент третьего порядка характеризует асимметрию распределения.
 

Коэффициент асимметрии

Определение. Отношение центрального момента третьего порядка к среднеквадратическому отклонению в третьей степени называется коэффициентом асимметрии.

 

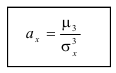
Эксцесс

Определение. Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

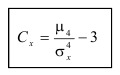
Кроме рассмотренных величин используются также так называемые абсолютные моменты:

Абсолютный начальный момент: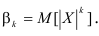 

Абсолютный центральный момент: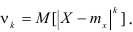

Абсолютный центральный момент первого порядка называется средним арифметическим отклонением.

Заключение по лекции:

В лекции мы рассмотрели методы решения основной задачи теории вероятностей – определения вероятности попадания непрерывной случайной величины на интервал с помощью плотности распределения.

Законы распределения непрерывных величин: нормальное, равномерное, показательное

В материалах сегодняшней лекции мы рассмотрим законы распределения непрерывных величин.

Равномерное распределение

Определение. Непрерывная случайная величина имеет равномерное распределение на отрезке [а,b], если на этом отрезке плотность

распределения случайной величины постоянна, а вне его равна нулю.

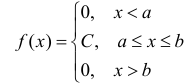
Постоянная величина С может быть определена из условия равенства единице площади, ограниченной кривой распределения, представленной на рис. 1
        

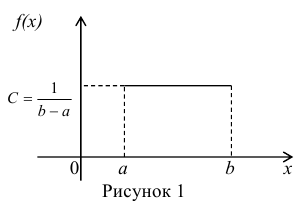
Получаем        .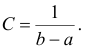

Найдём функцию распределения F(x) на отрезке [а,b] (рис. 2).

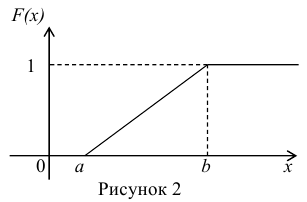
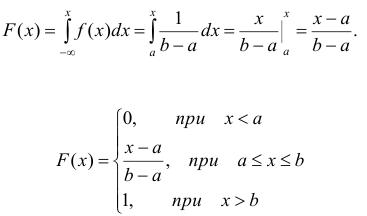
Для того, чтобы случайная величина подчинялась закону равномерного распределения необходимо, чтобы её значения лежали внутри некоторого определенного интервала, и внутри этого интервала значения этой случайной величины были бы равновероятны.

Определим математическое ожидание и дисперсию случайной величины, подчиненной равномерному закону распределения.

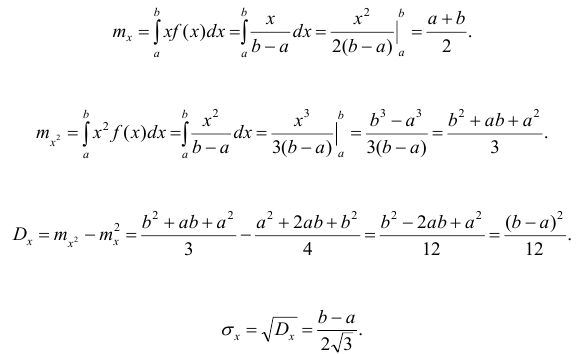
Вероятность попадания случайной величины в заданный интервал:

 

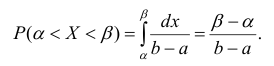
Показательное распределение

Определение. Показательным (экспоненциальным) называется распределение вероятностей непрерывной случайной величины X, которое описывается плотностью    

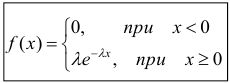
где 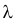– положительное число.

Найдём закон распределения.

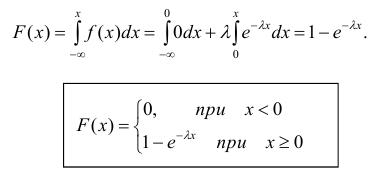
Графики функции распределения и плотности распределения представлены на рис. 3, 4.

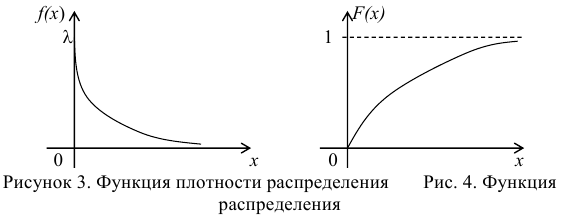
Найдём математическое ожидание случайной величины, подчинённой показательному распределению.

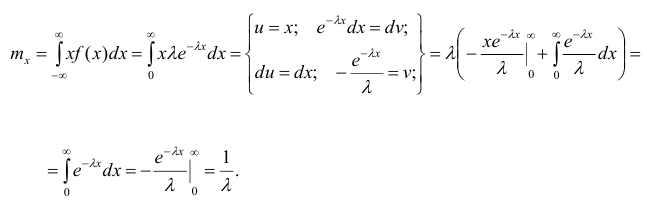
Результат получен с использованием того факта, что

Для нахождения дисперсии найдём величину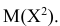

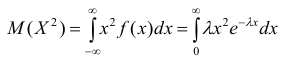
Дважды интегрируя по частям, аналогично рассмотренному случаю, получим:

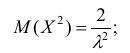
Тогда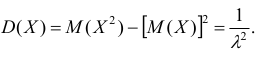
Итого: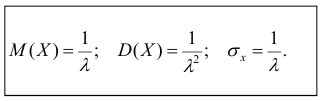

Видно, что в случае показательного распределения математическое ожидание и среднеквадратическое отклонение равны.

Также легко определить и вероятность попадания случайной величины, подчиненной показательному закону распределения, в заданный интервал.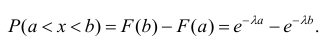

Показательное распределение широко используется в теории надёжности.

Допустим, некоторое устройство начинает работать в момент времени to=0, а через какое- то время t происходит отказ устройства.

Обозначим Т непрерывную случайную величину – длительность безотказной работы устройства.

Таким образом, функция распределения F(t) = P(T

Вероятность противоположного события (безотказная работа в течение времени t) равна R(t) = P(T>t) – l – F(t).

Функция надежности

Определение. Функцией надёжности R(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Часто на практике длительность безотказной работы подчиняется показательному закону распределению.

Вообще говоря, если рассматривать новое устройство, то вероятность отказа в начале его функционирования будет больше, затем количество отказов снизится и будет некоторое время иметь практически одно и то же значение. Затем (когда устройство выработает свой ресурс) количество отказов будет возрастать.

Другими словами, можно сказать, что функционирование устройства на протяжении всего существования (в смысле количества отказов) можно описать комбинацией двух показательных законов (в начале и конце функционирования) и равномерного закона распределения.

Функция надёжности для какого- либо устройства при показательном законе распределения равна:

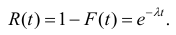
Данное соотношение называют показательным законом надежности.

Важным свойством, позволяющим значительно упростить решение задач теории надежности, является то, что вероятность безотказной работы устройства на интервале времени t не зависит от времени предшествующей работы до начала рассматриваемого интервала, а зависит только от длительности времени t.

Таким образом, безотказная работа устройства зависит только от интенсивности отказов 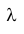и не зависит от безотказной работы устройства в
прошлом.

Так как подобным свойством обладает только показательный закон распределения, то этот факт позволяет определить, является ли закон распределения случайной величины показательным или нет.

Нормальный закон распределения

Определение. Нормальным называется распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности

Нормальный закон распределения также называется законом Гаусса.

Нормальный закон распределения занимает центральное место в теории вероятностей. Это обусловлено тем, что этот закон проявляется во всех случаях, когда случайная величина является результатом действия большого числа различных факторов. К нормальному закону приближаются все остальные законы распределения.

Можно легко показать, что параметры 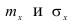входящие в плотность распределения являются соответственно математическим ожиданием и среднеквадратическим отклонением случайной величины X.

Найдём функцию распределения F(x).

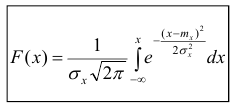
График плотности нормального распределения называется нормальной кривой или кривой Гаусса.

Нормальная кривая обладает следующими свойствами:

1)    Функция определена на всей числовой оси.

2)    При всех х функция распределения принимает только положительные значения.

3)    Ось ОХ является горизонтальной асимптотой графика плотности вероятности, т.к. при неограниченном возрастании по абсолютной величине аргумента л значение функции стремится к нулю.

4)    Найдём экстремум функции.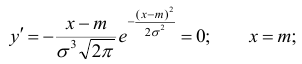

Т.к. при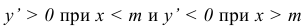 , то в точке х = m функция имеет максимум, равный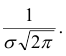

5)    Функция является симметричной относительно прямой x = а, т.к. разность

(х – а) входит в функцию плотности распределения в квадрате.

6)    Для нахождения точек перегиба графика найдем вторую производную функции плотности.

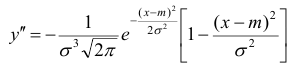
При 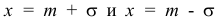вторая производная равна нулю, а при переходе через эти точки меняет знак, т.е. в этих точках функция имеет перегиб.

В этих точках значение функции равно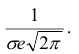     
Построим график функции плотности распределения (рис. 5).

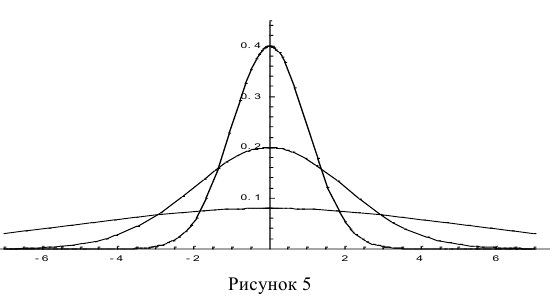
Построены графики при м =0 и трёх возможных значениях среднеквадратичного отклонения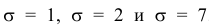. Как видно, при увеличении значения среднего квадратичного отклонения график становится более пологим, а максимальное значение уменьшается.

Если а > 0, то график сместится в положительном направлении, если а < 0 – в отрицательном.

При а = 0 и 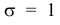кривая называется нормированной. Уравнение нормированной кривой:

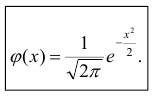
Функция Лапласа

Найдём вероятность попадания случайной величины, распределенной по нормальному закону, в заданный интервал.

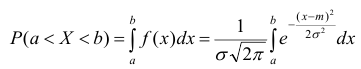
Обозначим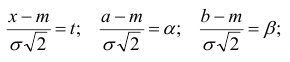

Тогда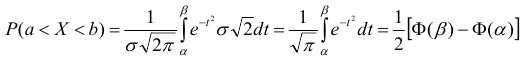
Т.к. интеграл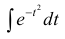 не выражается через элементарные функции, то вводится в рассмотрение функция

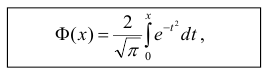
которая называется функцией Лапласа или интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

На рис. 6 показан график функции Лапласа.

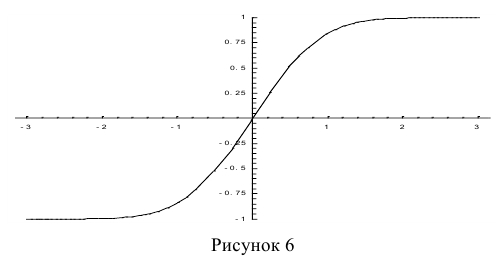
Функция Лапласа обладает следующими свойствами:

• 1)    Ф(0) = 0;
• 2)    Ф(-х) = – Ф(х);
• 3)  

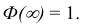
Функцию Лапласа также называют функцией ошибок и обозначают
erf х.

Ещё используется нормированная функция Лапласа, которая связана с функцией Лапласа соотношением:

На рис. 7 показан график нормированной функции Лапласа.

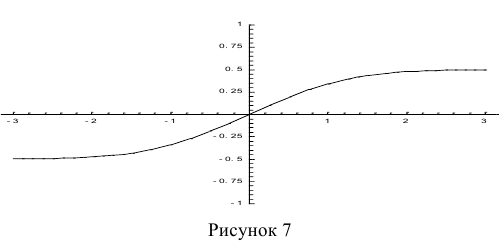
Правило трёх сигм

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

Запишем вероятность того, что отклонение нормально распределенной случайной величины от математического ожидания меньше заданной величины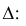

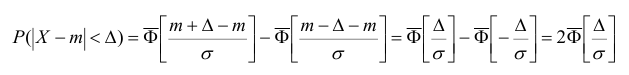
Если принять 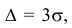, то получаем с использованием таблиц значений функции Лапласа:

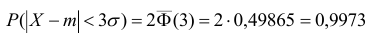
Т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую, чем утроенное среднее квадратичное отклонение, практически равна нулю.

Это правило называется правилом трех сигм.

Не практике считается, что если для какой-либо случайной величины выполняется правило трёх сигм, то эта случайная величина имеет нормальное распределение.

Пример:

Случайная величина Х задана плотностью распределения вероятностей:

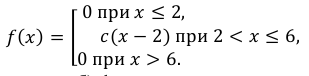
Найти: а) значение с; б) функцию распределения F(х) и построить ее график; в)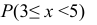
 

Решение:

а) Значение с найдем из условия нормировки: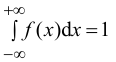
Следовательно,

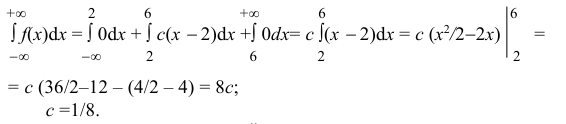
б) Известно, что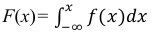 

Поэтому, если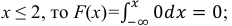 

если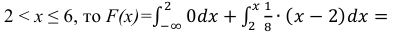 

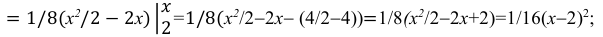
если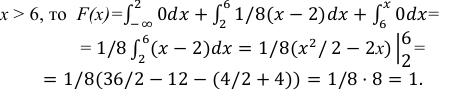 

Таким образом,

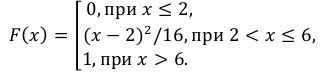
График функции F(х) изображен на рис. 5. 3.

в)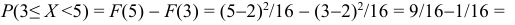 

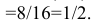
Пример:

Случайная величина Х задана функцией распределения:

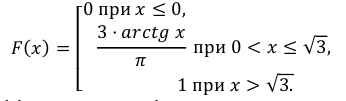
Найти дифференциальную функцию распределения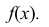  
 

Решение:  

Так как 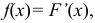 то

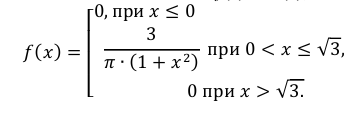
Пример:

Случайная величина Х задана дифференциальной функцией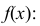

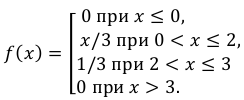
Найти 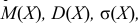 а также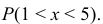 

Решение:

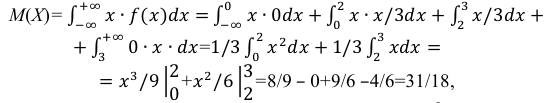
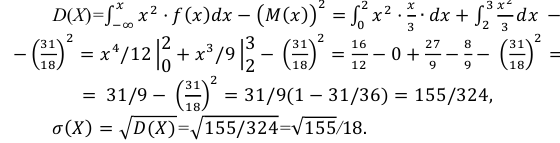
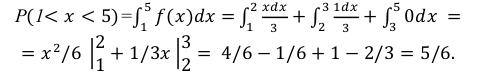
Некоторые законы распределения непрерывной случайной величины 

Пример:

Случайная величина Х равномерно распределена на отрезке [3;7]. Найти:

а) плотность распределения вероятностей 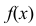 и построить ее график;

б) функцию распределения 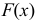 и построить ее график;

в)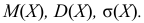
Решение: Воспользовавшись формулами, рассмотренными выше, при а = 3, b = 7, находим:

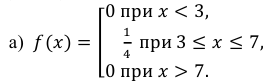
Построим ее график (рис. 6.3):

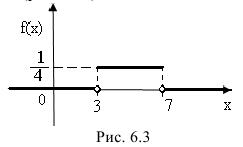
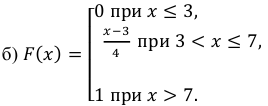
Построим ее график (рис. 6.4):

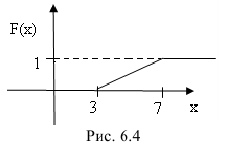
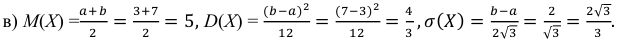
Пример:

Среднее время безотказной работы прибора равно 100 ч.
Полагая, что время безотказной работы прибора имеет показательный закон распределения, найти:

а) плотность распределения вероятностей;

б) функцию распределения;

в) вероятность того, что время безотказной работы прибора превысит 120 ч.
 

Решение.

По условию математическое ожидание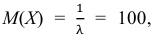
откуда 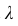 = 1/100 = 0,01.
Следовательно,

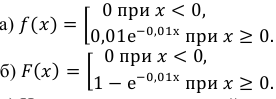
в) Искомую вероятность найдем, используя функцию распределения: 

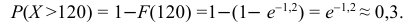
Пример:

Случайная величина Х распределена нормально с математическим ожиданием 32 и дисперсией 16. Найти: а) плотность распределения вероятностей 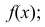 б) вероятность того, что в результате испытания Х примет значение из интервала (28;38).
 

Решение:

По условию m = 32, σ2 = 16, следовательно, σ = 4, тогда

а)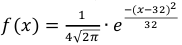 

б) Воспользуемся формулой:

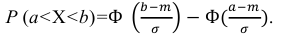
Подставив a = 28, b = 38, m = 32, σ = 4, получим

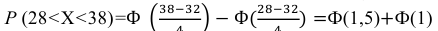
По   таблице   значений   функции   Ф(х)   находим   Ф(1,5) = 0,4332, Ф(1) = 0,3413.
Итак, искомая вероятность:

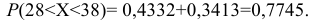
Заключение по лекции:

В лекции мы рассмотрели законы распределения непрерывных величин.

Формулы онлайн: Случайные величины

В данном разделе вы найдете формулы по теории вероятностей в онлайн-варианте (в формате для скачивания – см. на странице Таблицы и формулы по теории вероятностей).

Каталог формул по теории вероятности онлайн

Случайные величины. Способы задания

Ряд распределения дискретной случайной величины

Табличный вид:

$$
begin{array}{|c|c|}
hline
X_i & x_1 & x_2 & dots & x_n \
hline
p_i & p_1 & p_2 & dots & p_n \
hline
end{array}
$$

Сумма вероятностей всегда равна 1 (условие нормировки):

$$sum_{i=1}^{n} p_i=1$$

Примеры решенных задач с табличным законом распределения ДСВ

Функция распределения (интегральная функция распределения)

Функция распределения случайной величины $X$ определяется по формуле $F(x)=P(Xlt x)$. Это неубывающая функция, принимающая значения от 0 до 1. Если задана плотность распределения $f(x)$, то функция распределения выражается как интеграл от плотности:

$$
F(x)=int_{-infty}^x f(t), dt.
$$

Плотность распределения (дифференциальная функция распределения)

Плотность распределения случайной величины $X$ определяется по формуле $f(x)=F'(x)$. Существует только для непрерывной случайной величины. Для нее выполняется условие нормировки (площадь под кривой вероятности равна 1):

$$
int_{-infty}^{+infty} f(x), dx=1.
$$

Примеры решенных задач о НСВ

Вероятность попадания случайной величины в заданный интервал

Может быть вычислена двумя способами:

1) через функцию распределения

$$P(alpha lt X lt beta) = F(beta)-F(alpha).$$

2) через плотность распределения

$$P(alpha lt X lt beta) = int_{alpha}^{beta} f(x), dx.$$

Случайные величины. Числовые характеристики

Математическое ожидание случайной величины

1) Для дискретной случайной величины $X$, заданной рядом распределения:

$$M(X) = sum_{i=1}^{n} x_i cdot p_i.$$

2) Для непрерывной случайной величины $X$, заданной плотностью распределения:

$$M(X)=int_{-infty}^{+infty} f(x)cdot x, dx.$$

Статья и калькулятор о математическом ожидании

Дисперсия случайной величины

По определению дисперсия – это второй центральный момент:

$$ D(X) =Mleft[ left(X-M(X)right)^2 right] =M(X^2)-left(M(X)right)^2.$$

1) Для дискретной случайной величины $X$:

$$ D(X)= sum_{i=1}^{n} x_i^2 cdot p_i – left(M(X)right)^2.$$

2) Для непрерывной случайной величины $X$:

$$M(X)=int_{-infty}^{+infty} f(x)cdot x^2, dx – left(M(X)right)^2.$$

Статья и калькулятор о дисперсии

Среднее квадратическое отклонение случайной величины

$$sigma (X) = sqrt{D(X)}.$$

Статья и калькулятор о СКО

Коэффициент вариации случайной величины

$$V(X) = frac{sigma(X)}{M(X)}.$$

Начальный момент r–го порядка случайной величины

определяется по формуле:

$$nu_r = M(X^r)$$

В частности, первый начальный момент – это математическое ожидание: $nu_1=M(X^1)=M(X).$

Центральный момент r – го порядка случайной величины

определяется по формуле:

$$mu_r = Mleft[ left(X-M(X)right)^r right]$$

В частности, второй центральный момент – это дисперсия:

$$mu_2 = Mleft[ left(X-M(X)right)^2 right] = D(X).$$

Асимметрия

$$
A_s = frac{mu_3}{sigma^3}.
$$

Коэффициент асимметрии положителен, если правый хвост распределения длиннее левого (правая часть кривой более пологая), и отрицателен в противном случае. Если распределение симметрично относительно математического ожидания, то его коэффициент асимметрии равен нулю.

Эксцесс

$$
E = frac{mu_4}{sigma^4}-3.
$$

Коэффициент эксцесса нормального распределения равен нулю. Он положителен, если пик распределения около математического ожидания острый, и отрицателен, если пик гладкий.

Решенные задачи по теории вероятностей

Нужна готовая задача по терверу? Найдите на сайте-решебнике:

Полезные ссылки

Онлайн калькуляторы Формулы комбинаторики

Статьи по теории вероятностей Более 200 готовых примеров